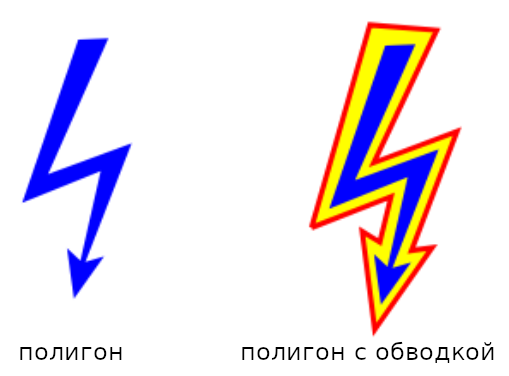
Привет, Хабр. Я хотел бы поделиться своим опытом, как сделать внешнюю обводку у полигона. Проблема заключается в том, что имеется полигон, который нужно обвести внешней обводкой и при этом обводка может не касаться граней полигона. В этой статье разбирается алгоритм по обводке, и предоставляется код на js для подтверждения работы алгоритма на практике. В результате работы алгоритма должна получится такая разноцветная обводка у полигона:
Теория
Полигон — замкнутая фигура, состоящая из вершин и ребер. Для прорисовки обводки полигона требуется найти точки, которые равноудалены от вершин полигона и соединить их линиями. В нахождении точек нам поможет линейная алгебра. Для демонстрации алгоритма по поиску точек обводки у полигона представим произвольный полигон:

В алгоритме для каждой вершины находим нормализованные вектора отстояния. Вектором отстояния, Я называю вектор, который при сложении с вершиной полигона даст точку обводки. Для нахождения вектора отстояния требуется взять два ребра вершины и представить их нормализованными векторами. Направление этих векторов должно быть исходящим из вершины. При сложении нормализованных векторов, получиться вектор отстояния. Этот вектор будет исходить из вершины под углом биссектрисы, так как при нормализации получаются два вектора с одинаковой длиной при сложении которых результирующий вектор будет выходить из вершины и делить угол пополам. Получившийся вектор отстояния потребуется нормализовать для равномерной обводки контура. Для демонстрации этапов по нахождению нормализованного вектора отстояния, этапы проиллюстрированы в пошаговом рисунке ниже:

Получившиеся нормализованные вектора отстояния могут иметь неправильные направления. Быть направленными внутрь контура или из вне:

При сложении векторов с вершинами полигона, получившиеся точки обводки могут быть внутри контура или снаружи. И в следствии получается неправильная обводка. Для того чтобы этого избежать для начала нужно определить, как точки полигона обходят контур по часовой стрелки или против часовой стрелки. Это даст возможность сделать обводку либо внутри полигона, либо снаружи. Чтобы определять направление обхода контура у полигона находим его крайнюю левую вершину по координате x. И представляем два ребра вершины векторами. Вектора направлены по следованию точек на контуре. Над векторами производим векторное умножение. Знак получившегося результата умножения покажет, как задается контур. Если число положительное, то против часовой стрелки, если отрицательное — по часовой стрелке:

Теперь осталось определить направление у нормализованных векторов отстояния. Для этого у каждой вершины надо взять два ребра направленные по направлению обхода контура и векторно их умножить. У получившегося результата узнаем арифметический знак. Арифметический знак покажет менять направление у вектора отстояния или оставить прежним. Пусть у нас точки полигона задают контур против часовой стрелки. Тогда если знак у результата векторного умножения положительный, то направление у вектора отстояния меняется, если отрицательный, то направление остается прежним. Для изменения направления вектора достаточно его координаты умножить на -1. Если точки полигона задают контур по часовой стрелки, то алгоритм определения направления вектора отстояния меняется. У положительного результата умножения, вектор не меняет направления, а у отрицательного меняет.

Получившиеся направленные вектора надо сложить с вершинами полигона, чтобы получить точки обводки:

Практика
Работоспособность алгоритма приведу кодом на js. Не буду голословным и приведу код с комментариями:
<!DOCTYPE html>
<html lang="">
<head>
<meta charset="utf-8">
<title></title>
</head>
<body>
<canvas id="polygon"></canvas>
</body>
<!-- входные данные -->
<script>
const points = [
{x: 0.36229, y: 0.64789},
{x: 0.51492, y: 0.58590},
{x: 0.47563, y: 0.76014},
{x: 0.44950, y: 0.73590},
{x: 0.46292, y: 0.83392},
{x: 0.52162, y:0.75190},
{x: 0.48531, y:0.76230},
{x: 0.57529, y: 0.53189},
{x: 0.41261, y: 0.59189},
{x: 0.53001, y: 0.32786},
{x: 0.47131, y: 0.32986},
{x: 0.36229, y: 0.64789}
];
const canvas = document.getElementById('polygon');
const ctx = canvas.getContext('2d')
const size = 300;
canvas.width = size;
canvas.height = size;
</script>
<!-- рисуем обводку -->
<script>
//функция нормализация вектора
const doNorm = (vec) => {
const len = Math.sqrt(vec.x * vec.x + vec.y * vec.y)
return {x: vec.x / len, y: vec.y / len}
}
//функция возращает соседние индексы вершин у выбранного индеска
const getNeighboringIndices = (selectIndex, maxIndex) => {
if (selectIndex === 0) {
selectIndex = maxIndex
}
const lastIndex = selectIndex + 1
return {
beginIndex: selectIndex - 1,
middleIndex: selectIndex,
lastIndex: lastIndex > maxIndex ? 1 : lastIndex
}
}
//узнаем направление обхода контура
const indexOnMinX = points.reduce((res, point, index, array) => { //Узнаем индекс c самым маленьким x
if(points[res].x > point.x) {
return index
}
return res
}, 0)
const inds = getNeighboringIndices(indexOnMinX, points.length - 1)
const v1 = {x: points[inds.middleIndex].x - points[inds.beginIndex].x, y: points[inds.middleIndex].y - points[inds.beginIndex].y}
const v2 = {x: points[inds.lastIndex].x - points[inds.middleIndex].x, y: points[inds.lastIndex].y - points[inds.middleIndex].y}
const multiVec = v1.x * v2.y - v2.x * v1.y //Векторное произведение
const isClockwise = multiVec < 0
//суммирование веторов, вычисление нормализованного вектора отстояния, получение точек отстояния от полигона
const borderPoints = []
for (let i = 0; i < points.length; ++i) {
//получение направлющий ветора с длинной
const inds = getNeighboringIndices(i, points.length - 1)
const v1_norm = doNorm( {x: points[inds.beginIndex].x - points[inds.middleIndex].x, y: points[inds.beginIndex].y - points[inds.middleIndex].y} )
const v2_norm = doNorm ( {x: points[inds.lastIndex].x - points[inds.middleIndex].x, y: points[inds.lastIndex].y - points[inds.middleIndex].y })
const resVec_norm = doNorm( {x: v1_norm.x + v2_norm.x, y: v1_norm.y + v2_norm.y} )
const k = 0.05 //коэффициент увеличивает длину нормализованного вектора отстояния
const resVec = { x: resVec_norm.x * k, y: resVec_norm.y * k }
//Расчет направления для направлюящего вектора
v1_norm.x = -v1_norm.x; v1_norm.y = -v1_norm.y //меняем знак у вектора v1, чтобы v1 и v2 были последовательно направлены по контуру
const multiVec = v1_norm.x * v2_norm.y - v2_norm.x * v1_norm.y //векторное произведение
if (isClockwise && multiVec < 0) {
resVec.x = -resVec.x; resVec.y = -resVec.y
}
if(!isClockwise && multiVec > 0) {
resVec.x = -resVec.x; resVec.y = -resVec.y
}
//добавляем в массив точки обводки
borderPoints.push( {x: points[i].x + resVec.x, y: points[i].y + resVec.y } )
}
ctx.beginPath();
ctx.moveTo( size * borderPoints[0].x, size * borderPoints[0].y)
for (let i = 1; i < borderPoints.length; ++i) {
ctx.lineTo(size * borderPoints[i].x, size * borderPoints[i].y)
}
ctx.fillStyle = 'yellow';
ctx.fill();
ctx.strokeStyle = "red";
ctx.lineWidth = 3;
ctx.stroke();
</script>
<!-- рисуем изначальную фигуру -->
<script>
ctx.beginPath();
ctx.moveTo( size * points[0].x, size * points[0].y)
for (let i = 1; i < points.length; ++i) {
ctx.lineTo(size * points[i].x, size * points[i].y)
}
ctx.fillStyle = "blue";
ctx.fill()
</script>
</html>Таким образом, алгоритм делиться на несколько этапов. В первом этапе, нужно найти вектора отстояния у каждой вершины полигона. Во втором определить как задают точки полигона обход контура — это либо по часовой стрелке или против часовой. И в последнем этапе изменить, если это требуется, направление найденных векторов отстояния и сложить их с каждой вершиной, к которой он принадлежит.
Комментарии (4)

AndrewSu
21.04.2023 10:44+2Интересная статья. Но ваш алгоритм на выходе может выдать результат с самопересечением для контуров с "петельками" радиусом менее отступа.
Вообще, эта тема хорошо представлена по ключевым словам "Offset curve".

fransua
21.04.2023 10:44Кажется вот эту либу https://www.npmjs.com/package/polygon-offset я использовал для этого успешно.


mobi
Мне кажется, там нужно не смещать узел вдоль вектора нормали на заданную величину, а находить точку пересечения прямых, параллельных ребрам, но отстоящих от них на заданную величину. Например, для вот такого треугольника с узкой выемкой
видно, что вдоль сторон треугольника ширина обводки меньше, чем у основания.
mobi
С другой стороны, ваш вариант дает немного нестандартный "ломаный" эффект, и именно этим привлекает к себе внимание.