Научный мир состоит из великого множества исследований и разработок, которые направлены на улучшение жизни человека, сохранение экологии планеты, поиски альтернативных источников энергии и т. д. Проще говоря, цели таких трудов весьма серьезны, чего нельзя сказать о некоторых других исследованиях, хоть их результаты от того не становятся менее интересными. Так ученые из Брауновского университета (США) провели исследование, в котором попытались объяснить, почему пузыри газа в шампанском ведут себя не так, как в других газированных напитках. Чем же уникально шампанское с точки зрения механики жидкостей, и как это было установлено? Ответы на эти вопросы мы найдем в докладе ученых.

Основа исследования

Вкусовые предпочтения касательно напитков могут разительным образом отличаться от человека к человеку. Тем не менее, несмотря на отличия во вкусах, каждый напиток символизирует определенный аспект жизни человека. Чай ассоциируют с теплом, уютом и заботой, кофе ассоциируют с бодростью и началом нового дня, а вот шампанское — неотъемлемый символ торжественных мероприятий, будь то свадьба, новогодняя ночь или празднование успешной сделки. Почему именно шампанское так тесно связывают с празднествами? Ответ сокрыт не в его вкусовых характеристиках, а в его эстетически приятных качествах. Одним из них является перляж — движение пузырьков углекислого газа в бокале.

Пузырьки в газированных напитках, а не только в шампанском, образуются при выделении избытка углекислого газа из перенасыщенной жидкости. Условия пересыщения легко достигаются, поскольку давление при розливе выше атмосферного, следовательно, в жидкости может быть растворено больше газа. Цепочки пузырьков образуются по мере того, как формируются отдельные пузырьки: как только пузырек достигает определенного критического размера, при котором плавучесть преодолевает силу поверхностного натяжения, удерживающую пузырек на месте, пузырек начинает свободно всплывать. Сразу же после того, как пузырек был вытеснен, сформируется новый, в результате чего и появляются эти цепочки. Этот процесс продолжается в течение нескольких минут, пока большая часть растворенного газа не выйдет из раствора. Скорость подъема пузырьков в жидкости зависит от их размера и свойств жидкости. Достигнув поверхности жидкости, пузырьки ненадолго остаются на ней, пока пленка жидкости стекает. Когда пленка жидкости становится достаточно тонкой, она самопроизвольно взрывается с характерным звуком и образует капли аэрозоля.

Все это эстетически приятное действо является сложным физико-химическим процессом, который зависит от множества факторов. И самое любопытное то, что цепочки пузырьков в шампанском поднимаются на поверхность ровными линиями, что не наблюдается в других газированных напитках. Учитывая это, ученые решили изучить стабильность цепочек пузырьков и попытаться ответить на вопрос — поскольку пузырьки формируются последовательно из одного и того же места зарождения, должны ли они оставаться на одной линии или нет? Помимо интереса к цепочкам пузырьков в напитках, эти результаты важны для выяснения ключевых механизмов, которые приводят к распределению пузырьков в пузырьковых потоках в целом. Природа гидродинамических взаимодействий между пузырьками определяет, будут ли образовываться кластеры, которые, в свою очередь, сильно влияют на уровни перемешивания и распределения пузырьковых потоков.

Для начала ученые предлагают рассмотреть случай двух сферических пузырей с чистыми границами раздела, поднимающихся на одной линии. Если число Рейнольдса выше 10, линейное движение неустойчиво, поскольку пузырьки выбрасываются после любого предыдущего пузыря. Процесс объясняется наличием следа* от лидирующего пузыря.

След (следовая волна)* — область рециркуляционного потока непосредственно за движущимся или неподвижным затупленным телом, обусловленная вязкостью, которая может сопровождаться отрывом потока и турбулентностью.

Его взаимодействие со следующим за ним пузырем приводит к возникновению подъемной силы (F_L):



где V_L — поле скорости следа ведущего пузырька, V_B — поле скорости следующего пузырька, а C_L — коэффициент подъемной силы (положительный) для сферических и чистых пузырьков.

Такое нестабильное взаимодействие пузырьков в потоке было подтверждено экспериментами и моделированием, которое показало, что взаимодействие между двумя пузырьками в инерционном режиме полно тонкостей.

В случае пузырьков в шампанском и других газированных напитках на водной основе число Рейнольдса пузыря монотонно увеличивается после его образования, поскольку пузырь продолжает расти. Однако, и это самое главное, оно достигает значения Re > 10 уже через несколько миллиметров после формирования. Следовательно, можно было бы ожидать, что в бокале для шампанского не будет наблюдаться устойчивых цепочек пузырьков. В этом исследовании ученые утверждают, что стабильная цепочка пузырьков возможна только в том случае, если подъемная сила, действующая на следующий пузырь, меняет знак. В таком случае пузырьки останутся на одной линии, несмотря на небольшие возмущения.

Ранее уже проводились исследования процесса реверсирования подъемной силы. Известно два механизма, вызывающих реверсирование, деформацию пузырьков и загрязнение поверхности. Либо одно, либо оба могут привести к изменению направления подъемной силы. Некоторые ученые предполагают, что поверхностно-активные вещества (ПАВ) фактически ответственны за стабилизацию цепочек пузырьков, наблюдаемую в обычных напитках, но не смогли дать физического механизма для объяснения стабилизации.

Как говорят ученые, основная задача их труда — прояснить происхождение цепочки пузырьков в линейном потоке.

Результаты исследования

Для характеризации системы использовались пузырьки азота миллиметрового размера, образующиеся в капиллярной трубке и поднимающиеся в различных вязких жидкостях.


Изображение №1

Выше показаны изображения цепочек пузырьков, полученные с использованием капиллярной трубки и чистой смеси воды и глицерина при различных расходах газа. Исходя из соображений подобия, размер пузырьков, свойства жидкости и скорость потока газа эквивалентны пузырькам, движущимся в шампанском и других газированных напитках. Другими словами, числа Архимеда и Бонда для этих экспериментов максимально приближены к числам для газированных напитков.

Боковое рассеивание пузырьков от места образования свидетельствует о неустойчивости этих цепочек. По мере увеличения расхода газа увеличивается частота пузырьков и, в свою очередь, уменьшается расстояние между пузырьками. Боковое движение пузырьков появляется тем раньше, чем меньше расстояние между пузырьками. Это ожидаемо, так как гидродинамическое взаимодействие сильнее на более коротких расстояниях.


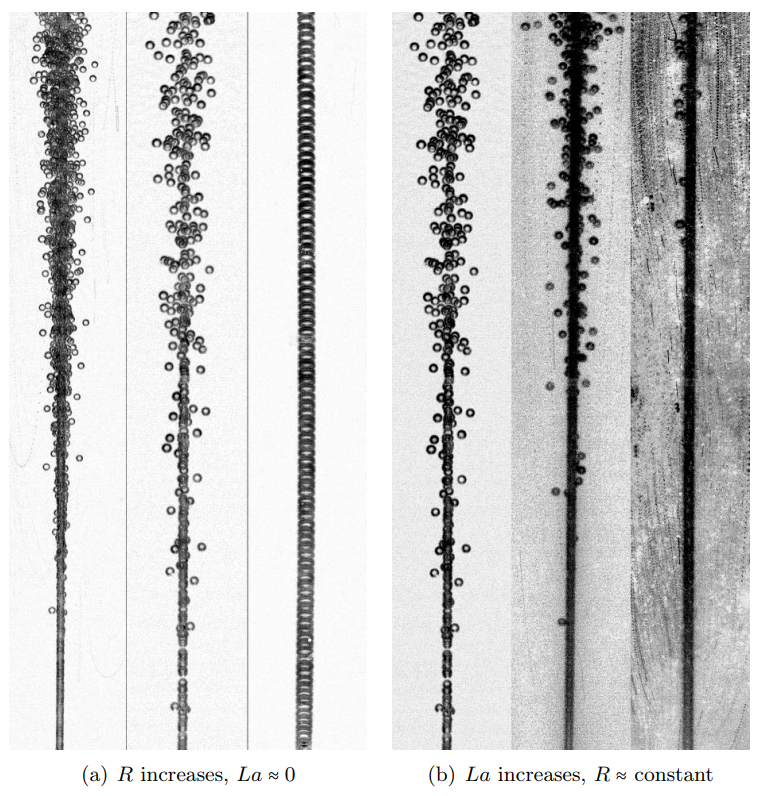
Изображение №2

Чтобы выяснить причину наблюдаемого нестабильного поведения цепочек пузырьков, ученые провели два типа экспериментов.

В первом эксперименте размер пузырьков был увеличен с учетом той же чистой жидкости за счет изменения размера капилляра, через который образуются пузырьки (2a). В этом случае цепочка пузырьков нестабильна для небольших размеров (слева и посередине на 2a), но переходит в устойчивое линейное поведение цепочки для больших пузырьков (справа на 2a). Стоит отметить, что числа Бонда* (Bo) и Архимеда* (Ar) для этих крупных пузырьков больше, чем ожидаемые для цепочек пузырьков на шампанском и других напитках.

Число Бонда* — критерий подобия в гидродинамике, определяющий соотношение между внешними силами (обычно силой тяжести) и силами поверхностного натяжения.

Число Архимеда* — критерий подобия, характеризующий соотношение между архимедовой силой, обусловленной различием плотностей в отдельных областях рассматриваемой системы, и вязкими силами в основном потоке.

Во втором эксперименте сохранялся относительно фиксированный размер пузырьков, используя ту же капиллярную трубку. Следовательно, Bo и Ar существенно не изменились. Но в этом опыте постепенно добавлялось поверхностно-активное вещество (додецилсульфат натрия), чтобы увеличить загрязнение поверхности. На 2b видно, что по мере увеличения количества ПАВ цепочки пузырьков из неустойчивых становятся устойчивыми.

Эти два эксперимента ясно показывают, что есть две возможности стабилизировать цепочку пузырьков. Однако физические механизмы, приводящие к стабилизации, остаются невыясненными. Чтобы помочь разобраться в этом вопросе, ученые провели численное моделирование.


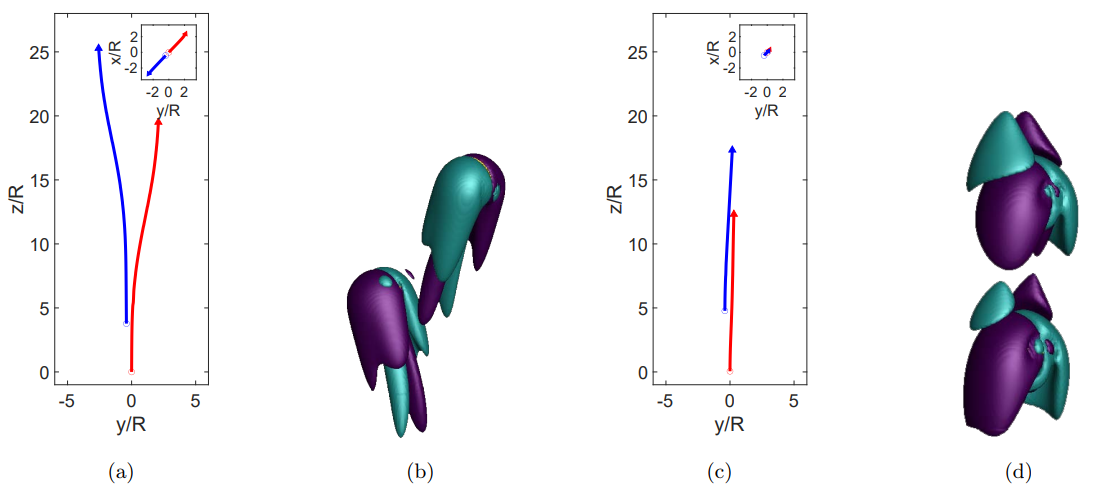
Изображение №3

При моделировании рассматривалась пара пузырьков газа, первоначально находящихся в покое, поднимающихся за счет плавучести. Для моделирования условий, обнаруженных в цепочке пузырьков, на верхнюю и нижнюю стенки области накладывались периодические граничные условия. Было проведено множество симуляций с учетом различных размеров пузырьков и уровней загрязнения. Пара пузырьков изначально расположена немного в стороне от линейной конфигурации (меньше 0.2 R).

На 3a и 3b показаны результаты почти сферической пары пузырьков (Ar = 400) без поверхностно-активных веществ (La = 0). Пузырьки начинаются близко к встроенной конфигурации в начале моделирования. Через некоторое время они перестают оставаться вертикально выровненными, удаляясь друг от друга (3a). Во время этого начального переходного периода за пузырьками развивается след (3b). Взаимодействие пузырька со следом перед ним приводит к возникновению подъемной силы. Для случая сферических пузырьков и отсутствия поверхностно-активных веществ след имеет две полосы встречно вращающейся завихренности*.

Завихренность* — свойство движения жидкости или газа, при котором в среде существуют «вихри», т.е. вращающиеся элементы объема.

Эта структура следа создает подъемную силу в противоположных направлениях для каждого последующего пузыря. Таким образом, пузырьки отталкиваются в стороны, что приводит к увеличению разделения и к отклонению от линейной конфигурации. Как вывод, эти цепочки являются неустойчивыми.

Напротив, при рассмотрении также сферических пузырьков (Ar = 400), но с учетом влияния поверхностно-активных веществ (La = 1), поведение значительно меняется. На 3c показана траектория двух пузырей. Тут видно, что начальная линейная конфигурация остается неизменной даже после начального переходного периода. Структура следа вокруг пузырьков в этом случае (3d) существенно отличается от случая без ПАВ. В частности, вихревая пара, развивающаяся за следующим и лидирующим пузырьком, имеет одинаковое направление вращения. Эта конфигурация вызывает подъемную силу одного направления для обоих пузырей. Следовательно, подъемная сила не дестабилизирует линейную конфигурацию.

Как и в случае экспериментов, моделирование проводилось для различных Ar, Bo и La, чтобы определить условия, которые приводят к стабильности или к ее отсутствию. В соответствии с экспериментами устойчивые цепочки наблюдались для более крупных пузырьков (более деформированных) или при наличии поверхностно-активных веществ. Что еще более важно, поскольку известно все поле течения вокруг пары пузырьков, можно легко получить поле завихренности. Изменение направления подъемной силы можно объяснить величиной завихренности, создаваемой на поверхности пузырька. Поэтому можно предложить критерий устойчивости, основанный на максимальной поверхностной завихренности для каждого случая.

Анализ результатов исследования

Для диапазона чисел Бонда и Архимеда, относящихся к газированным напиткам, конфигурация чистых пузырьков в линии нестабильна. Другими словами, устойчивые пузырьковые цепочки не могут наблюдаться, поскольку гидродинамические взаимодействия приводят к диспергированию. Дисперсия является результатом подъемной силы, вызванной следом пузырьков. Увеличение частоты инжекции пузырьков увеличивает боковую дисперсию. Увеличение частоты пузырьков приводит к меньшему разделяющему расстоянию между последовательными пузырьками, для которых подъемная сила, вызванная следом, больше. Ранее было доказано, что величина подъемной силы, вызванной следом, пропорциональна вращательной части поля скорости следа.

Эксперименты также показали, что при увеличении размера пузырьков без поверхностно-активных веществ может наблюдаться стабильная конфигурация цепочки пузырьков (2a). Цепочка становится устойчивой, поскольку подъемная сила меняет знак. Положительный эффект подъемной силы является результатом механизмов наклона и растяжения завихренности восходящего потока в следе за пузырьком. Завихренность, возникающая на поверхности пузырька, также наклоняется и растягивается в следе. Однако его вклад приводит к возникновению продольной завихренности противоположного знака и, таким образом, к вкладу индуцированной подъемной силы противоположного направления. Когда поверхностная завихренность превышает определенную величину, ее вклад становится доминирующим, и поэтому индуцированная подъемная сила меняет направление. По мере увеличения размера пузырька его форма становится более сплюснутой, что, в свою очередь, увеличивает завихренность поверхности. Следовательно, по мере увеличения деформации пузырьков происходит реверсирование подъемной силы. Такое изменение направления подъемной силы наблюдалось экспериментально для пузырьков воздуха в различных жидкостях, в том числе и в воде.

В случае пузырьков в шампанском и других газированных напитках размер пузырьков слишком мал, чтобы объяснить реверсирование подъемной силы, вызванное деформацией. Обычно для пузырька в воде изменение подъемной силы наблюдается при числе Рейнольдса пузырька (Re) равном 1000, соответствующем соотношению размеров пузырька χ ≈ 2. Эксперименты и моделирование показали, что стабильные цепочки могут наблюдаться для небольших сферических пузырьков, если поверхность загрязнена поверхностно-активными веществами. Следовательно, поверхностно-активные вещества также могут вызывать реверсирование подъемной силы. При наличии достаточного количества ПАВ поверхность пузырька становится неподвижной. Другими словами, поверхность пузыря больше не может поддерживать скольжение. Это приводит к увеличению образования завихренности на поверхности, которая переносится в след за пузырьком и достаточна для изменения структуры следа. В этом случае подъемная сила меняет знак, в результате чего следующий пузырек в следе выталкивается, чтобы оставаться на линии, образуя устойчивую цепь.

Ученые отмечают, что наличие данных моделирования позволяет рассчитать величину завихренности, создаваемой на поверхности пузырька. Ожидалось, что поверхностная завихренность превысит определенное значение для увеличения деформации пузырька, загрязнения или того и другого.


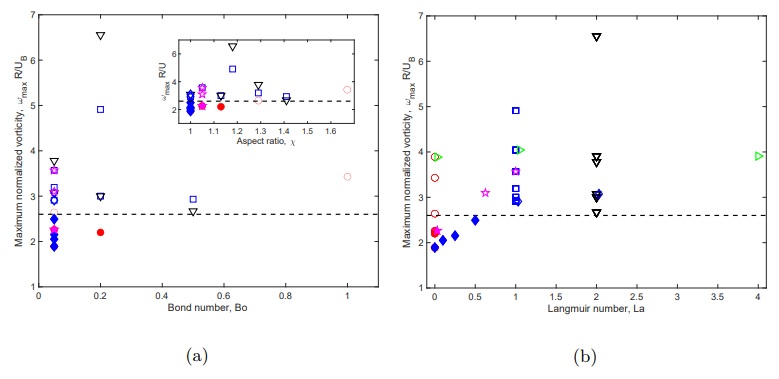
Изображение №4

Деформацию пузырька воздуха в воде можно описать с помощью числа Бонда (Bo) или отношения размеров пузырька (χ). На 4a максимальное значение поверхностной завихренности для каждого моделирования показано как функция числа Бонда и отношения размеров пузырька. Например, для определенного размера пузыря число Бонда является фиксированным. При постепенном добавлении поверхностно-активных веществ максимальное количество поверхностной завихренности увеличивается. Было установлено, что во всех случаях пара пузырьков становится стабильной, как только максимальная поверхностная завихренность превышает пороговое значение ω_maxR/U_B = 2.65.

Учитывая влияние поверхностно-активного вещества на границе раздела, на 4b максимальная завихренность показана как функция числа Ленгмюра* для различных значений числа Бонда.

Число Ленгмюра (La)* — величина, характеризующая количество газа, которое воздействует на поверхность образца. Определяется как произведение давления газа на время экспозиции.

Как и в предыдущем случае пузырьки остаются в линейной конфигурации, когда завихренность поверхности превышает пороговое значение. Как показано выше, пороговое значение для ω_max ~ 2.65 U_B/R наблюдается при переходе от неустойчивой к устойчивой линии пузырьков. Такая же величина завихренности требуется для изменения направления подъемной силы, когда деформация пузырька или загрязнение поверхности пузырька увеличиваются. Это подтверждает, что переход от неустойчивого состояния к устойчивому связан с изменением направления подъемной силы следа за пузырем.


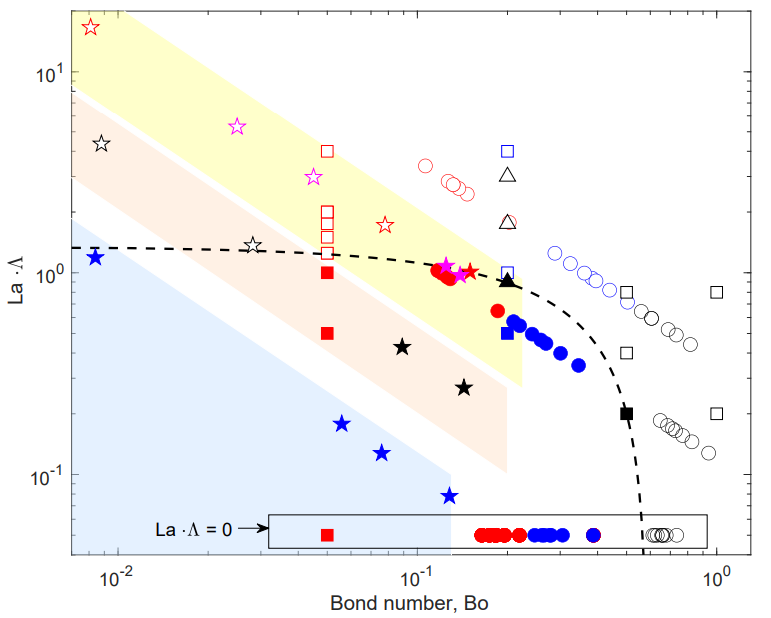
Изображение №5

На графике выше показаны результаты экспериментов и моделирования при разных значениях Bo и La. Закрашенные и пустые метки показывают нестабильные и стабильные цепи соответственно. Сочетание деформации пузырьков и жесткости поверхности четко определяет условия устойчивости цепочки пузырьков. Кроме того, переход является результатом величины завихрения, создаваемого на поверхности пузырька, как показано пороговым значением (пунктирная линия). Если известны уровень загрязнения и размер пузырьков, представленный график можно использовать для определения стабильности цепочки пузырьков. Опять же, маленькие пузырьки, которые обычно наблюдаются в газированных напитках, не должны быть стабильными в чистых жидкостях. Однако присутствие поверхностно-активных веществ приводит к иммобилизации поверхности, что приводит к образованию стабильных цепей.

Чтобы подтвердить вышеописанные выводы, ученые провели несколько опытов с различными газированными жидкостями для количественной оценки числа Бонда (Bo), параметров жесткости (Λ) и числа Ленгмюра (La) для каждой из жидкостей. Расчет Bo прост, поскольку известны значения плотности, размера и поверхностного натяжения. С другой стороны, для расчета Λ и La необходимо сделать некоторые предположения о поверхностной абсорбции и природе типичных поверхностно-активных веществ в исследуемых напитках.

Учитывая наличие пузырьков радиусом от 0.25 до 1 мм, ожидается, что газированная вода (синяя область на графике выше) не будет образовывать устойчивых цепей, поскольку присутствует небольшое количество поверхностно-активных веществ.

Для шампанского (желтая область на графике) тип поверхностно-активных веществ и их количество хорошо изучены и известны. Следовательно, можно определить диапазон ожидаемых значений Λ и Bo для одного и того же диапазона размеров. Как видно на графике, для шампанского ожидается стабильность цепочек для мелких пузырьков.

С пивом ситуация достаточно изменчивая, так как типичные поверхностно-активные вещества очень разные. Тем не менее ученые предположили, что для одного и того же диапазона размеров пузырьков (оранжевая область на графике) цепочки пузырьков могут быть либо стабильными, либо нет.

Эксперименты, проведенные с очень маленькими пузырьками в воде, пиве, игристом вине и шампанском, показаны на графике выше звездочками. Размер пузырьков в каждом из напитков отличался. Цепочки пузырьков были стабильны для игристых вин и шампанского, учитывая их небольшой размер. Для пива пузырьки наименьшего размера давали стабильные цепочки, в то время как два других размера давали нестабильные цепочки. В случае воды пузырьки такого же малого размера давали нестабильные цепочки.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.

Эпилог

Порой говорят, что истина лежит на дне бокала. В случае рассмотренного нами исследования это выражение вполне обосновано. В своем труде ученые продемонстрировали, что стабильные цепочки пузырьков, обычно наблюдаемые в шампанском, возникают из-за присутствия поверхностно-активных веществ. Пузырьки определенных размеров могут двигаться прямолинейно только в том случае, если на их поверхности создается достаточная завихренность. Если пузырьки маленькие, деформации недостаточно для создания достаточной завихренности. Следовательно, поверхностная иммобилизация (в результате присутствия поверхностно-активных веществ) обеспечивает второй источник завихренности, который приводит к стабильной цепи. Результаты исследования объясняют, почему в бокале шампанского наблюдаются стабильные цепочки пузырьков, что не наблюдается в других газированных напитках.

На первый взгляд это исследование кажется пустой тратой времени. Однако, как отмечают сами ученые, их труд не только является интересным примером источников завихренности в пузырьковых двухфазных потоках, но и может стать основой для нового метода оценки уровня загрязнения поверхностно-активными веществами в любой жидкости. Следовательно, даже самое странное и, казалось бы, лишнее исследование может иметь вполне себе практическое применение.

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?