????, Хабр!

После небольшого перерыва продолжим нашу экскурсию по различным вариациям классической конфигурации клеточных автоматов. Сегодня мы рассмотрим правила с «деструктивными клетками». Первоначальный вид подобной модификации, известной как BSFK, предложил энтузиаст под ником c0b0p0, всего 9 лет назад, спустя более чем 40 лет, после первого описания «Жизни» Джона Конвея.
Рассматриваемая модификация предполагает три состояния клеток – мёртвые, живые и деструктивные, и добавляет два числовых параметра в наше правило – F и K. Переходы говорят, что если у живой клетки есть как минимум K деструктивных соседей («киллеров»), она умирает. Если это условие не выполняется, то, как и в прошлых конфигурациях, происходит проверка на вхождение в множество S, но с тем отличием, что при отсутствии вхождения такая клетка не умирает, а сама превращается в киллера. Киллеры же умирают, если у них есть как минимум один живой сосед.

К условию зарождения жизни на пустых (мёртвых) клетках по числу живых соседей B добавляется «и количество соседей-киллеров не больше F».

Данная модификация также может быть без изменений в идее расширена радиусом, альтернативными окрестностями и нотацией Хенселя, но сообщество пока не начинало исследование этой области. Модификация в данном виде несовместима с поколениями, однако может быть адаптирована и под них. Но сегодня мы не будем затрагивать ничего из перечисленного.

❯ B2/S/F2/K1

Де-факто классический пример данной модификации, с которого и начал c0b0p0 – адаптированные «семена», на которые мы смотрели ещё в первой статье серии.

В этом примере, жизнь зарождается рядом с исключительно двумя живыми клетками (B2), если в числе прочих соседей меньше двух киллеров (F2). Живые клетки умирают, если среди соседей есть хоть один киллер (K1), в противном случае сами становятся ими (S-). Киллеры же сохраняют своё состояние, пока рядом нет живых клеток.
В данной конфигурации правило выглядит менее хаотично, и мы можем разглядеть все типы структур, в разных вариантах – корабли, паровозы, грабли, репликаторы, …. Можно даже принять за натюрморты группы затаившихся киллеров, но их структуры могут быть любого вида, так как они не влияют друг на друга.

❯ BSFKL

Первым пользователем, заинтересовавшимся BSFK модификацией, стал другой энтузиаст КА – Brian Prentice, который через месяц предложил расширение BSFKL. Предложенные дополнения: параметры F и K больше не числа-ограничители, а перечисления множества, по общему с B и S синтаксису. Новый параметр L, также содержащий множество, регулирует количество живых соседей, которые «нейтрализуют» клетку-киллера (в BSFK это значение было «любым ненулевым»).

Подытожим:
0→1 Рождение, если число живых соседей ∈ B и число соседей-киллеров ∈ F
1→0 Смерть, если число соседей-киллеров ∈ K
1→2 Криминализация, если клетка осталась жива и число живых соседей ∉ S
2→0 Смерть, если число живых соседей ∈ L
В любом другом варианте состояние клетки остаётся неизменным.

Таким образом, прошлый пример в BSFKL расширении выглядит как B2/S/F01/K12345678/L12345678. Данная запись выглядит более громоздко, но в то же время более явно, и с куда большей вариативностью.

Одним из первых рассмотренных Брайаном правил было B2358/S04567/F0456/K2567/L01235.

На конфигурации известно много различных правил с простыми и частыми генераторами и репликаторами, быстро заполняющими всю сетку. Правило выше, как раз, одно из них. Взглянем на вариант с заданным стартовым состоянием:


^{27с., 237×237, 2×50% | B2358/S04567/F0456/K2567/L01235}

❯ B2/F0

На основе параметров B2/F0 без S1, появляются простейшие направленные корабли из четырёх клеток – две живые и два «догоняющих» киллера. С дополнениями к этой основе корабли становятся всё причудливее и разнообразнее.

Прошлое правило, к примеру, превратило эти корабли в репликаторы: первое поколение живых клеток в блоке 2×1 превращается в киллеров через S-1 (отсутствие 1 в параметре S) и K-0, и этой же итерацией через B2/F0 порождает по такому же живому блоку с каждой стороны от себя. L-4 не даёт умереть блоку киллеров, который, форсируя смерть от одиночества (L0), с K2 убивает блоки соседей. Но от невинно убиенных успевают прорасти колосья ещё на один шаг дальше. На следующей итерации, как и первое поколение, живые блоки сами становятся киллерами, и дают потомство на следующие клетки (но не на прошлые, так как там ещё доживают последнюю итерацию криминальные соседи, а F-2). Получившийся квадрат из киллеров и живых клеток взаимно уничтожается с K2/L2, порождая стартовое состояние репликатора и всё начинается заново, но уже в раздвоенном виде.

Разумеется, это пример лишь для одного из бесчисленных расположений группы клеток, но на его основе, будь то намеренно или нет, было описано немало правил:


<sup>56с. x1.5, 237×237, 100×2% | B23458/S035678/F0456/K1235678/L01357


27с. x1.5, 237×237, 100×2% | B23478/S03567/F025678/K1345678/L028


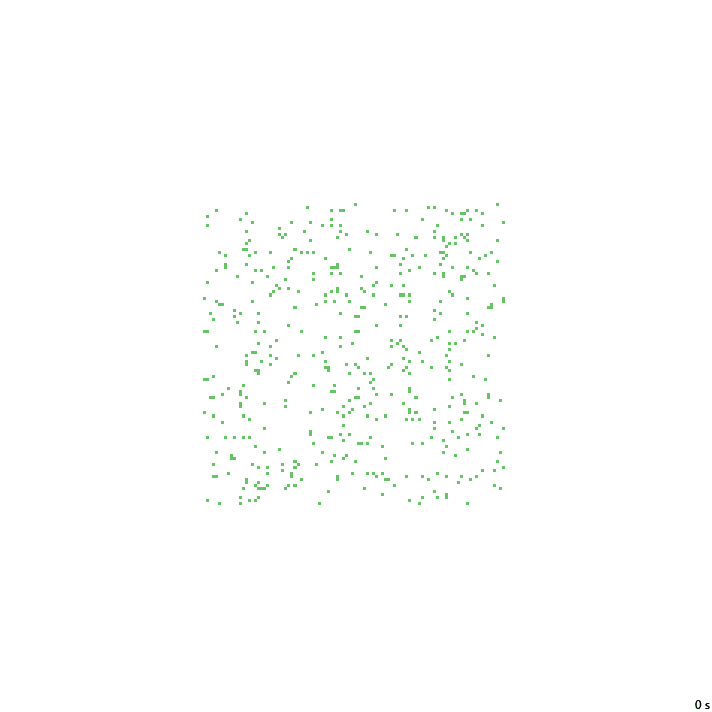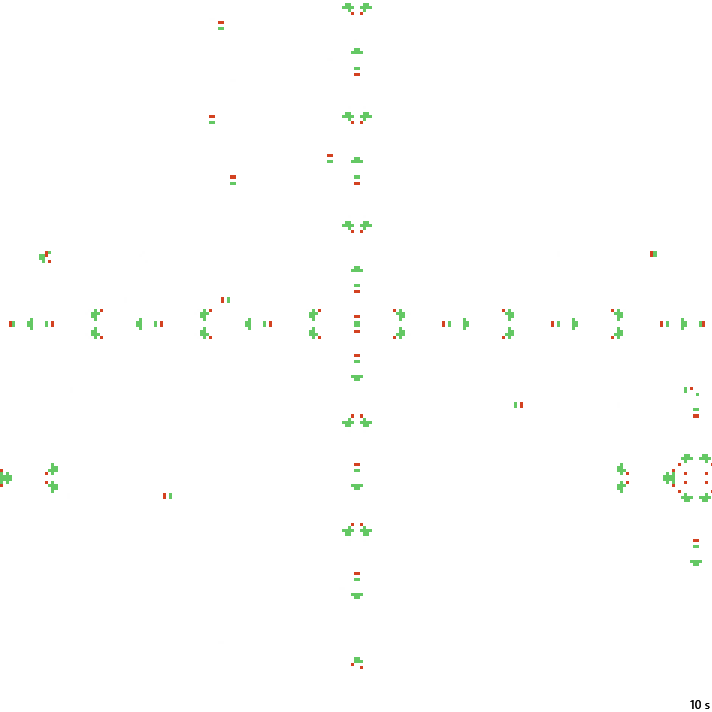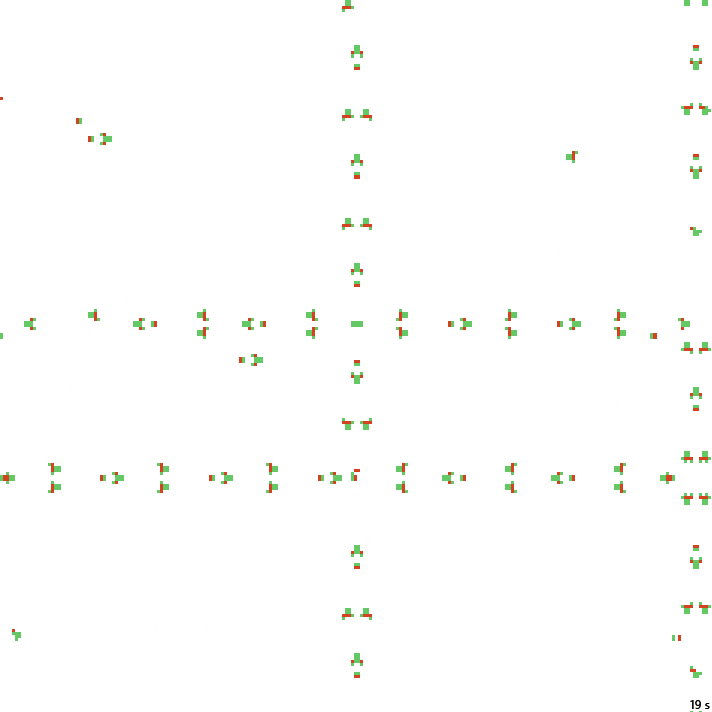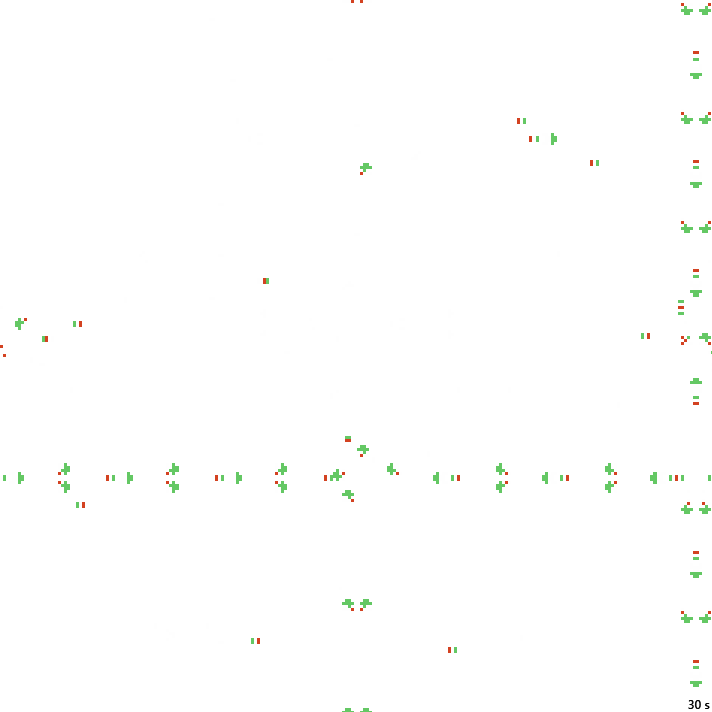
30с. x1.5, 237×237, 150×5% | B2/S34/F067/K12478/L01368


60с. x2, 237×237, 150×5% | B2/S34/F0124/K35/L0146</sup>

Конечно, есть и множество других правил, с другими типами кораблей:


<sup>19с. x3, 237×237, 100×10% | B1/S235/F23/K4/L0


64с. x2, 237×237, 150×2% | B02/S345/F2/K12458/L0256


27с. x2, 237×237, 200×10% | B1/S345678/F1234578/K245678/L0123



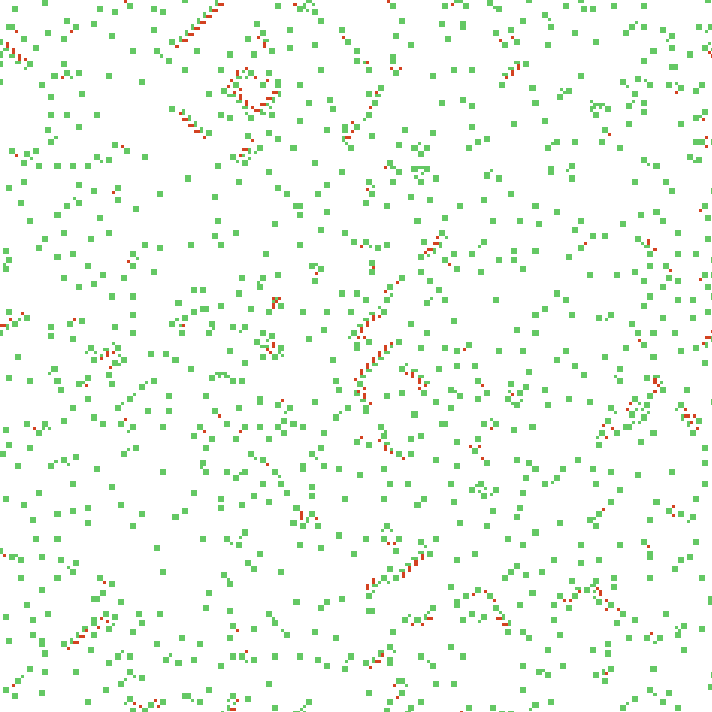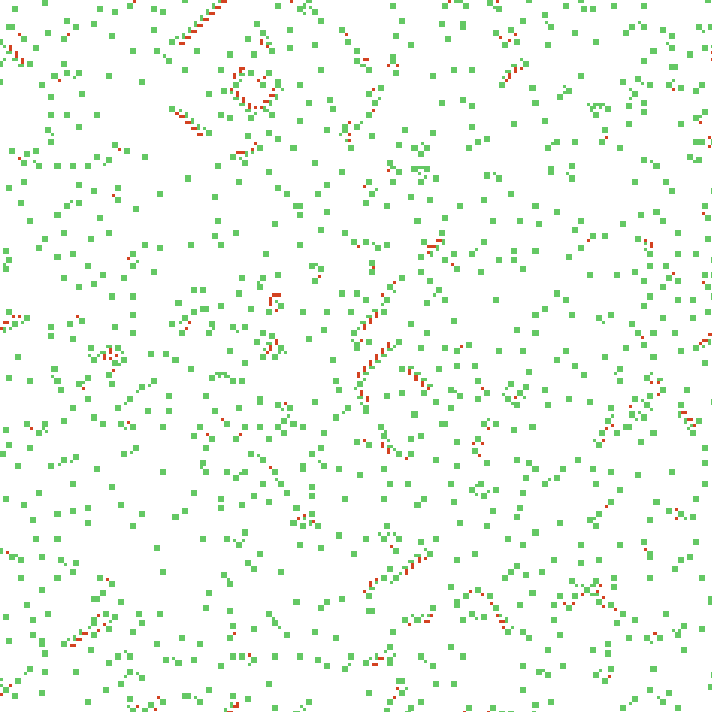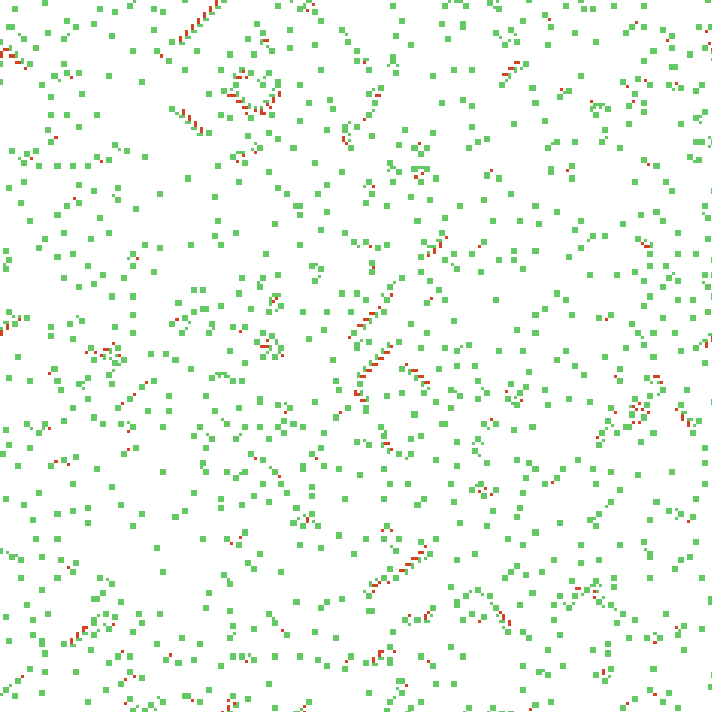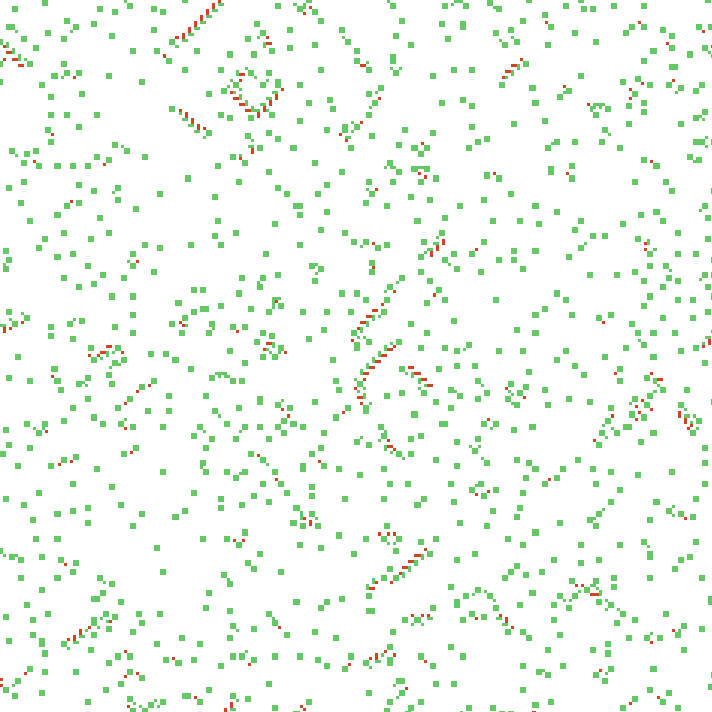
44с. x1.5, 237×237, 150×20% | B347/S3456/F038/K234567/L0346</sup>

Ненаправленные структуры с последнего примера напоминают жуков с LtL, но здесь у них, не считая пары простейших кораблей, даже не находится варианта устойчивого движения. Занятно, учитывая, насколько разными условиями они образованы.

❯ «Заборы»

Ещё в одну группу видов можно выделить правила с более устойчивыми клетками, в которых корабли оставляют за собой однородные хвосты, часто сохраняющиеся и после разрушения самих кораблей.

Пока не отошли далеко от B2/F0, посмотрим на примеры с этой основой:


<sup>35с. x1.5, 237×237, 50×50% | B26/S3456/F0123458/K457/L0178


50с. x1.5, 237×237, 50×50% | B248/S3456/F038/K234567/L047</sup>

А если внести одно мааленькое изменение


^{54с. x1.5, 237×237, 50×50% | B248/S3456/F038/K234567/L067}

На прочих примерах подобное «строительное» поведение чаще встречается в виде отростков статичных структур, а не хвостов кораблей:


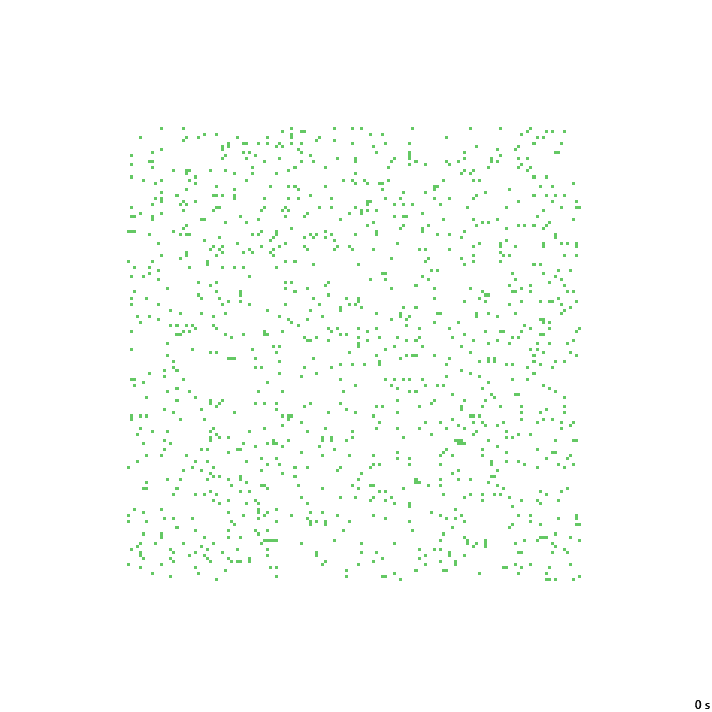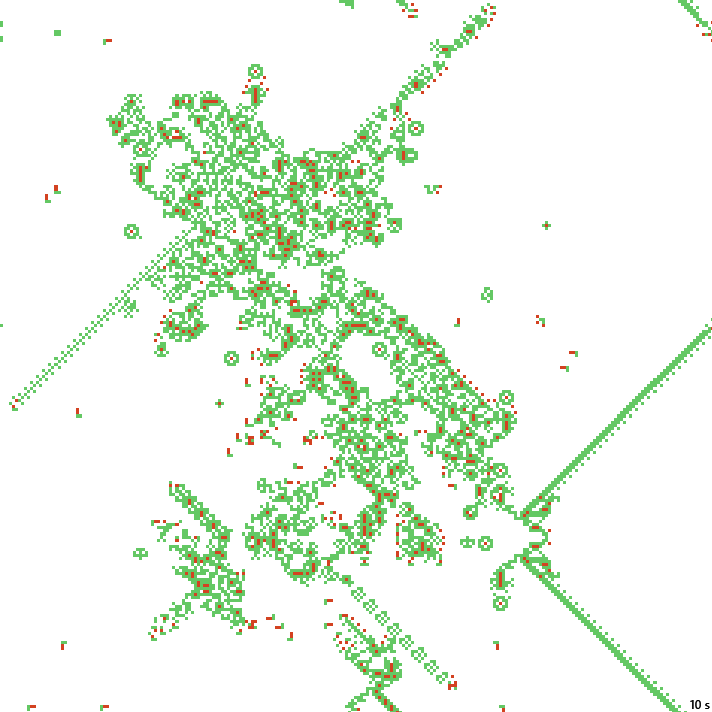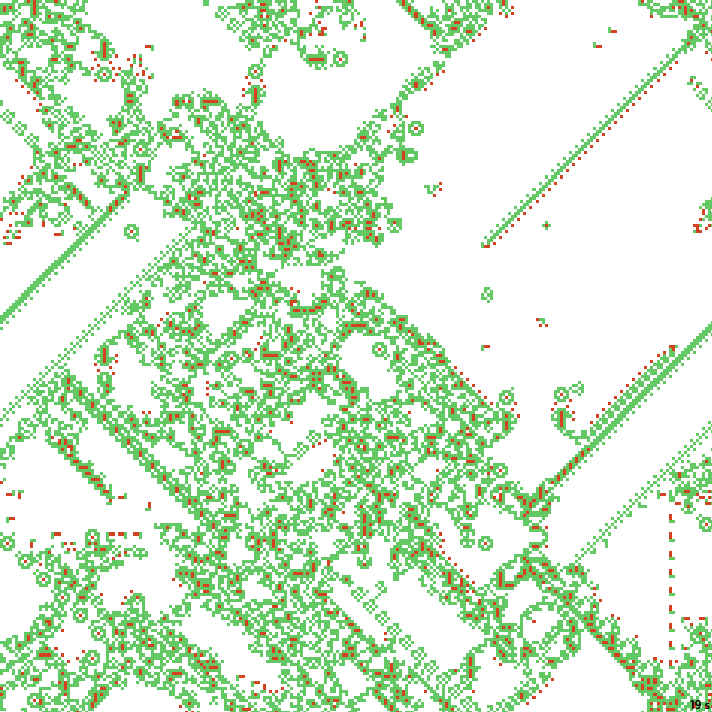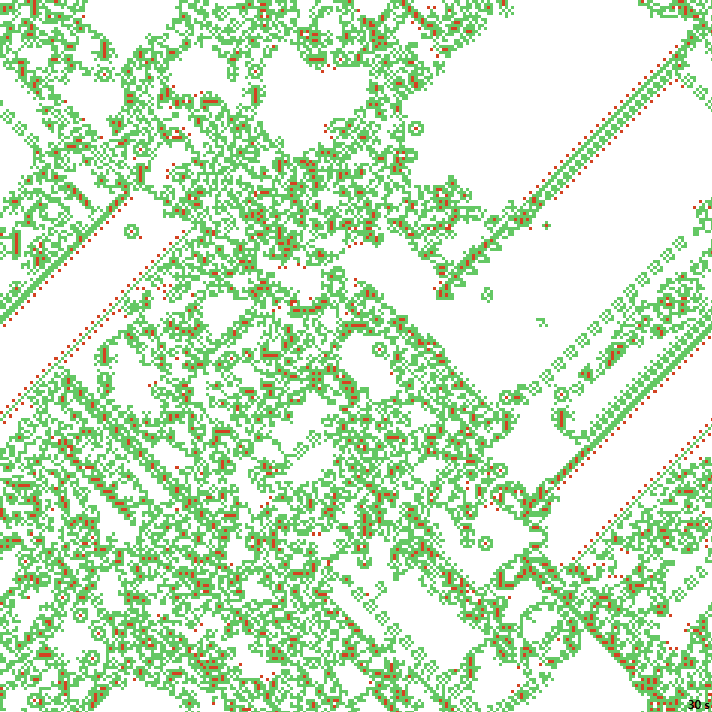
<sup>30с. x1.5, 237×237, 150×5% | B146/S234568/F124578/K57/L01235


20с. x1.5, 237×237, 150×50% | B01378/S2345/F1234567/K36/L01234578


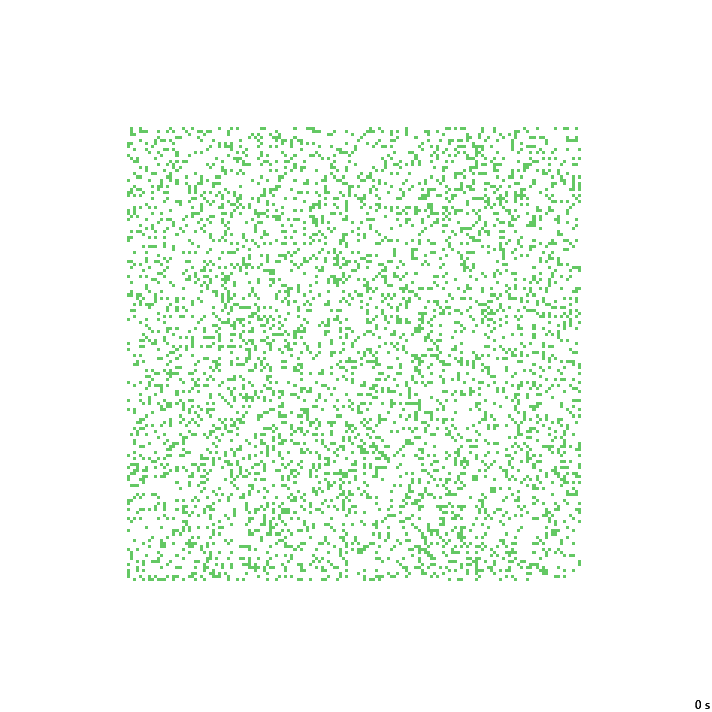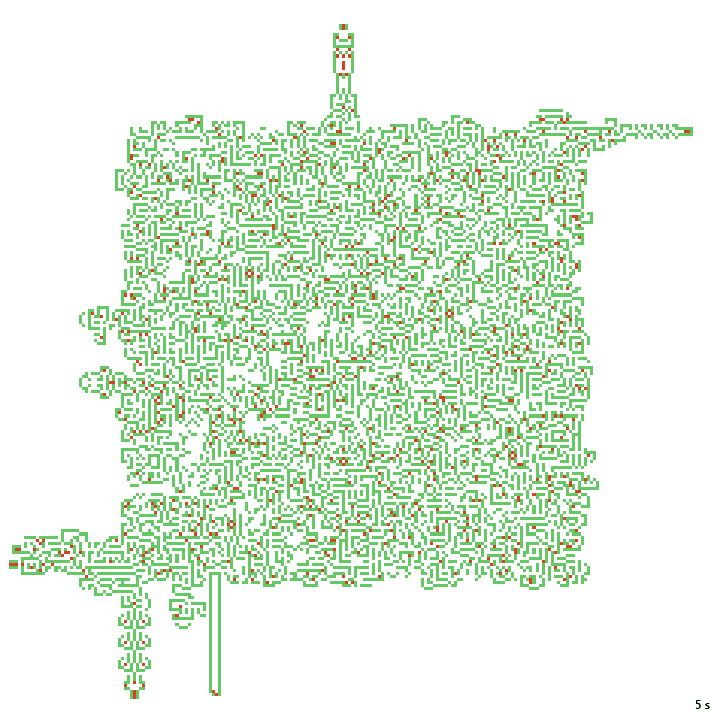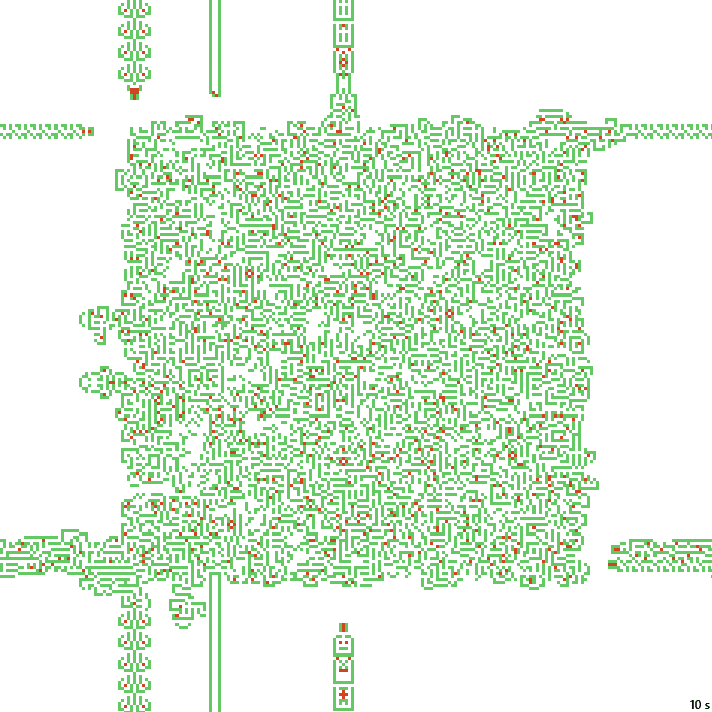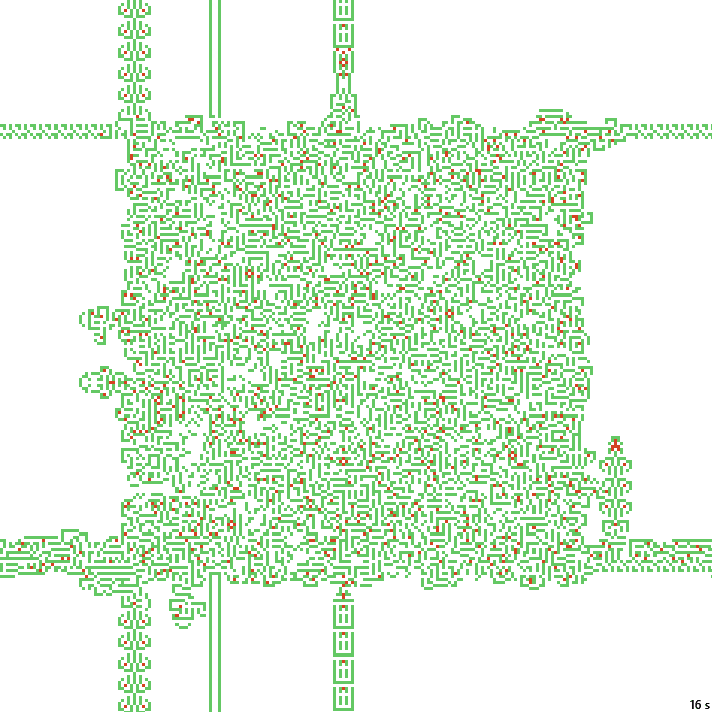
16с. x1.5, 237×237, 150×20% | B01268/S12358/F134/K3467/L0136</sup>

❯ Maze

Последние примеры, возможно, напомнили вам незавершённые лабиринты. В этой группе видов тоже есть несколько известных правил.


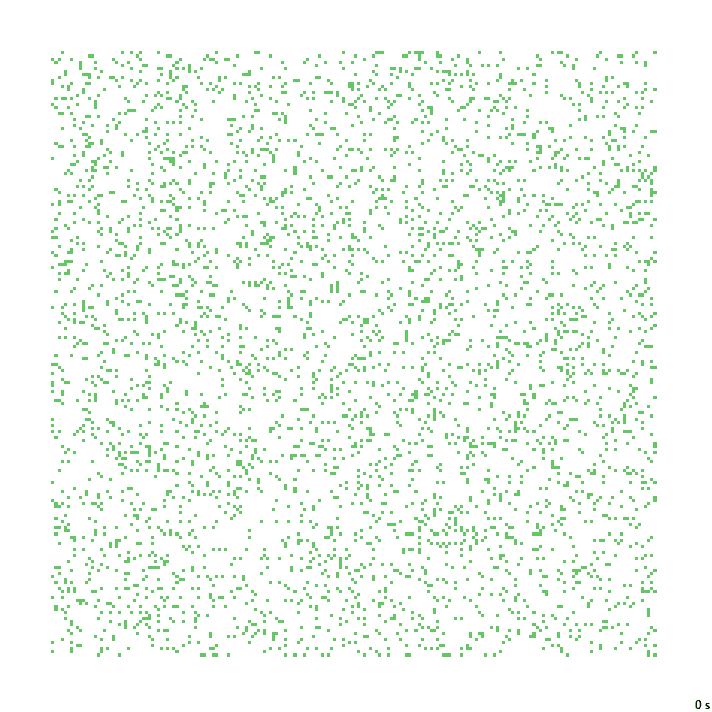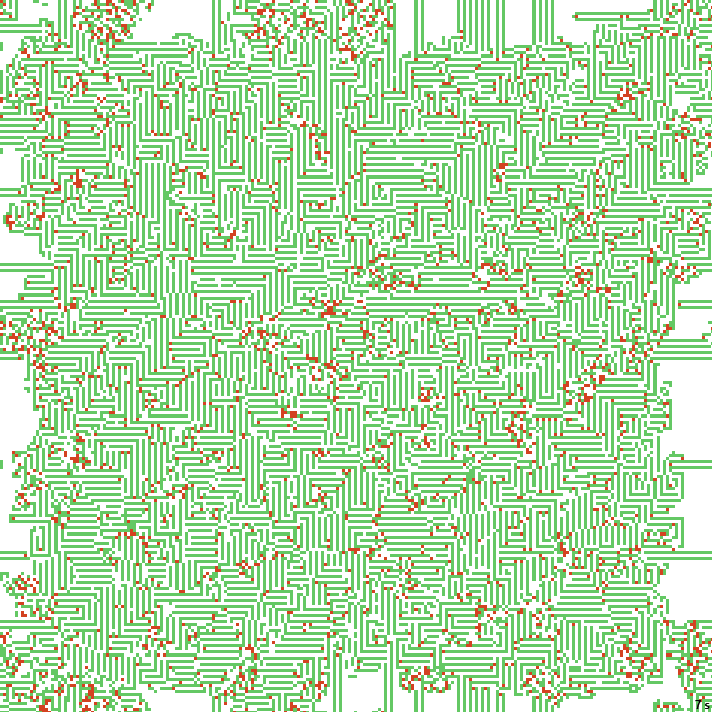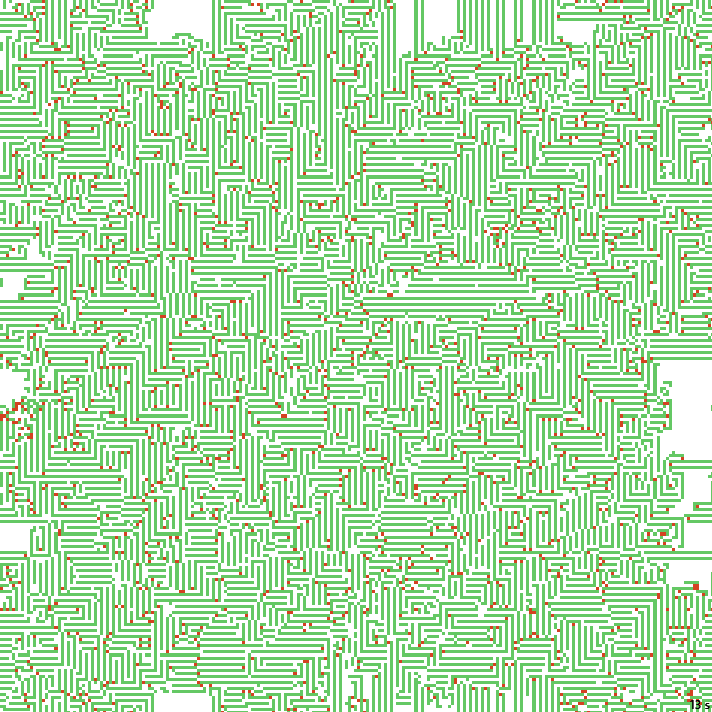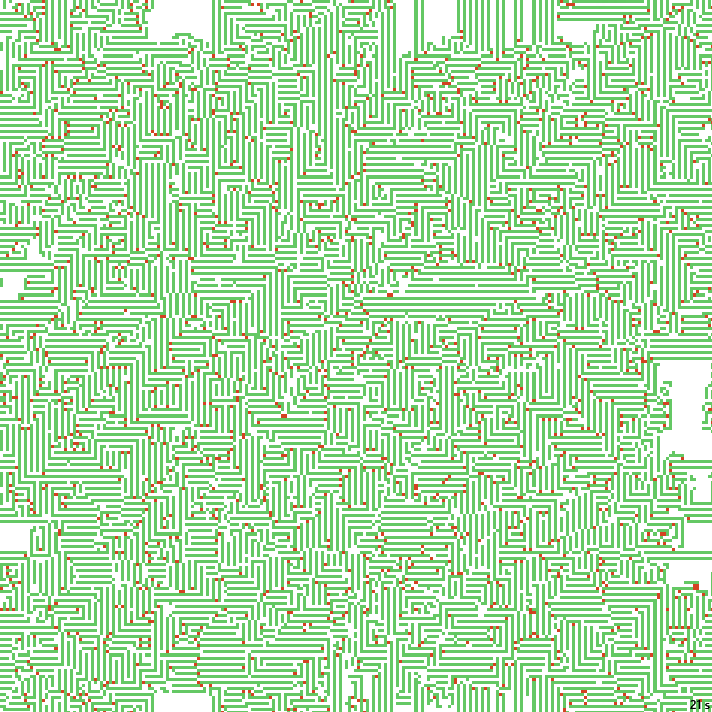
^{21с. x1.5, 237×237, 200×10% | B02378/S12358/F134/K3467/L0136}

При меньшем размере стартового заполнения появится много туннелей, но в этом тоже что-то есть.


^{37с. x2, 237×237, 50×10% | B02378/S12358/F134/K3467/L0136}

Можно поиграться и с заданными симметричными стартами.


<sup>24с. x3, 237×237, 3×77% | B02378/S12358/F134/K3467/L0136


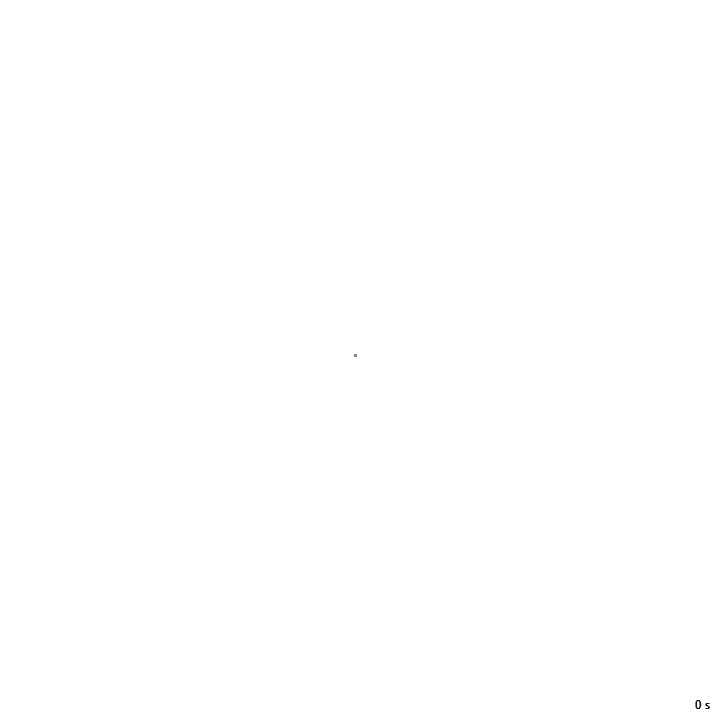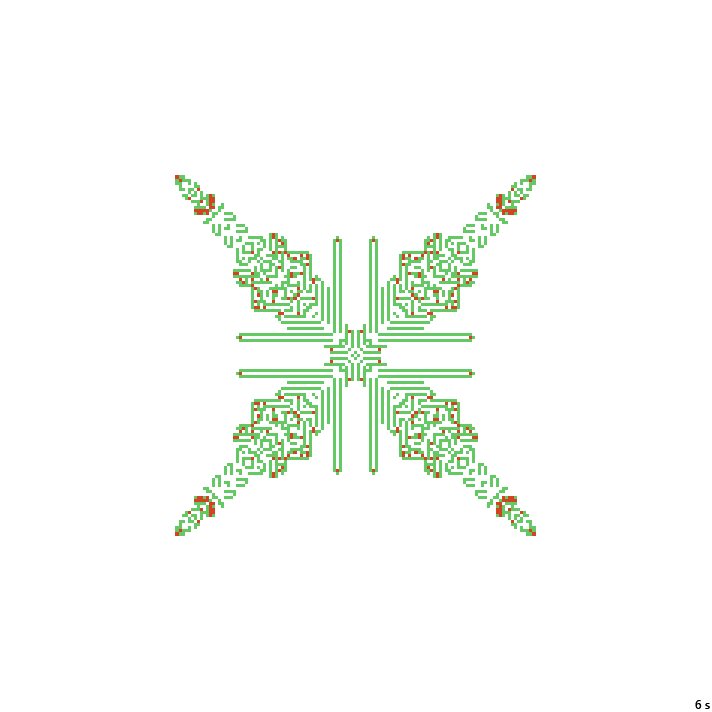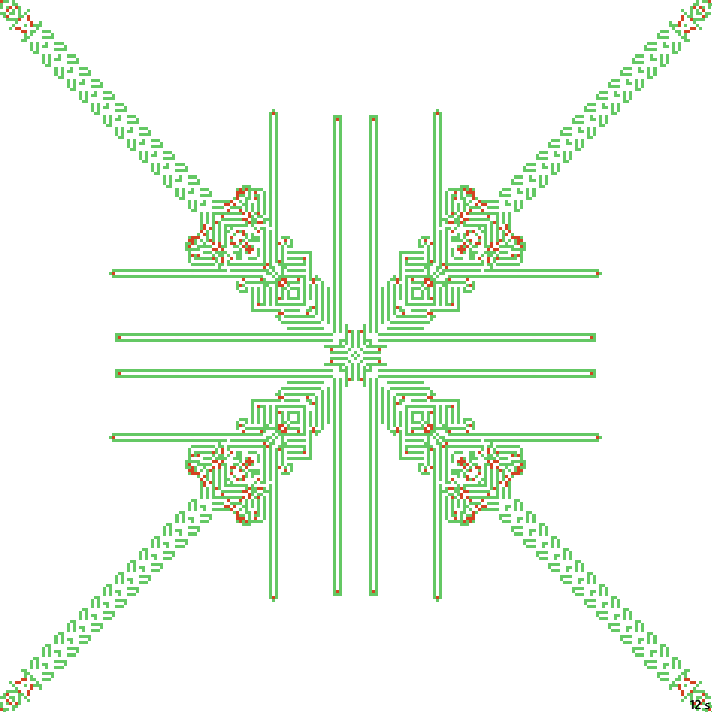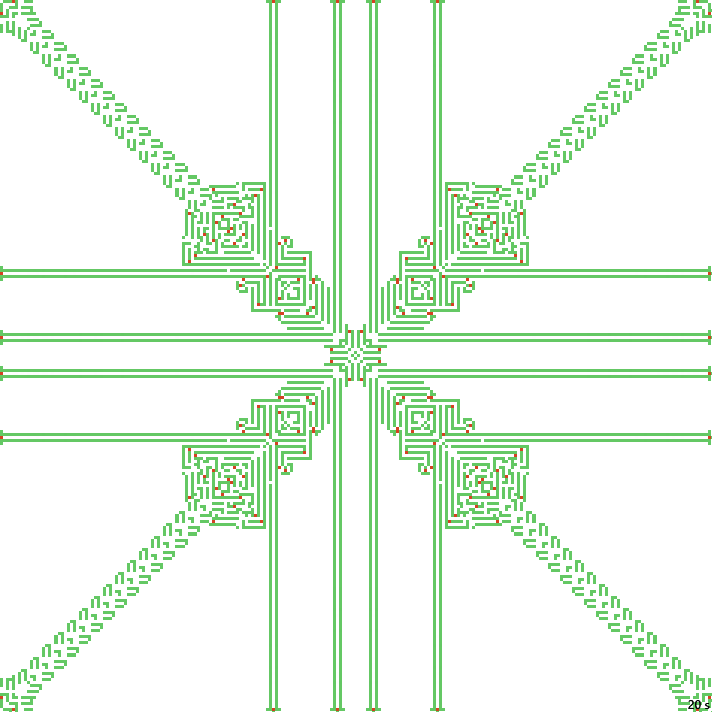
20с. x2, 237×237, 1×100% | B02378/S12358/F134/K3467/L0136</sup>

В следующем примере чуть сгладим мерцание другим цветом киллеров. Здесь уже взрывной рост, без строителей туннелей, но из-за этого может получиться излишняя симметрия при росте, потому начинать тоже стоит с большого размера.


^{17с. x1, 237×237, 200×3% | B13/S1235/F012345/K36/L012345678}

В этих примерах довольно вытянутые коридоры. Попробуем их чуть уменьшить.


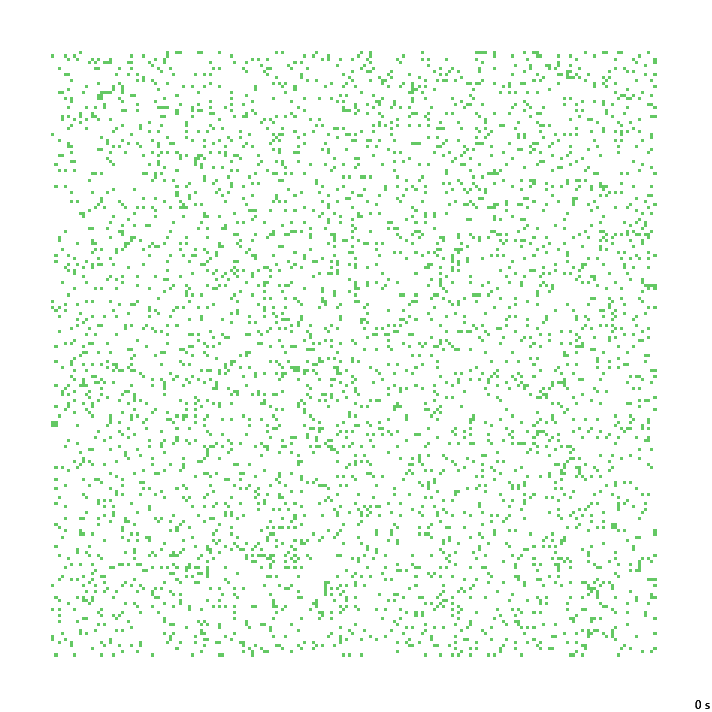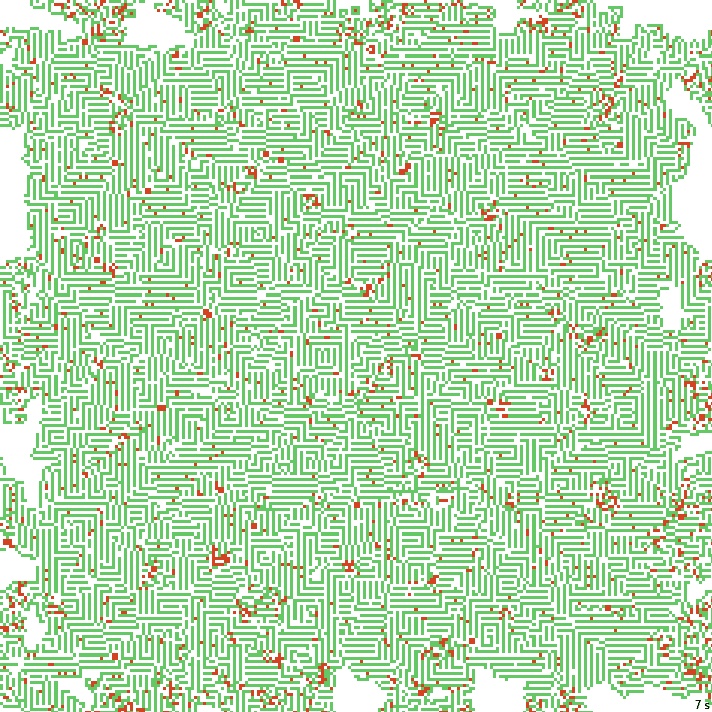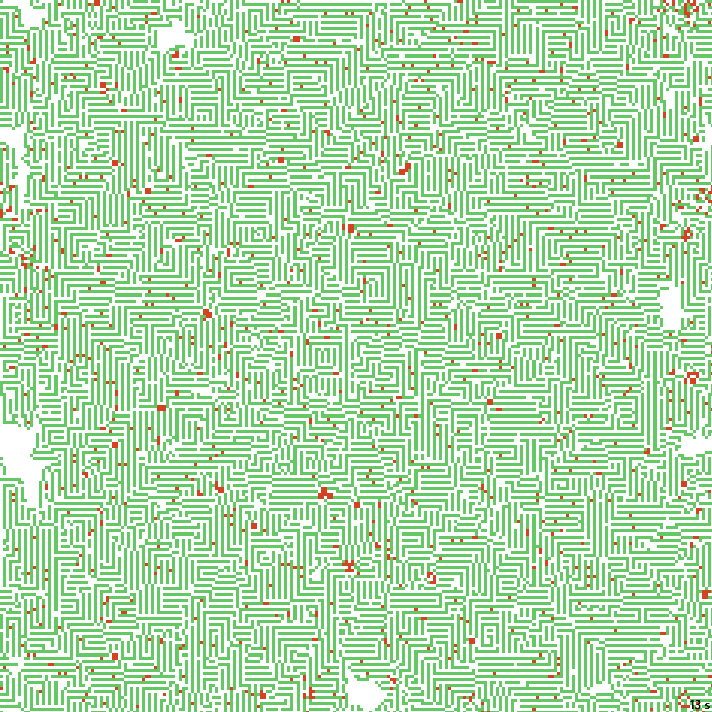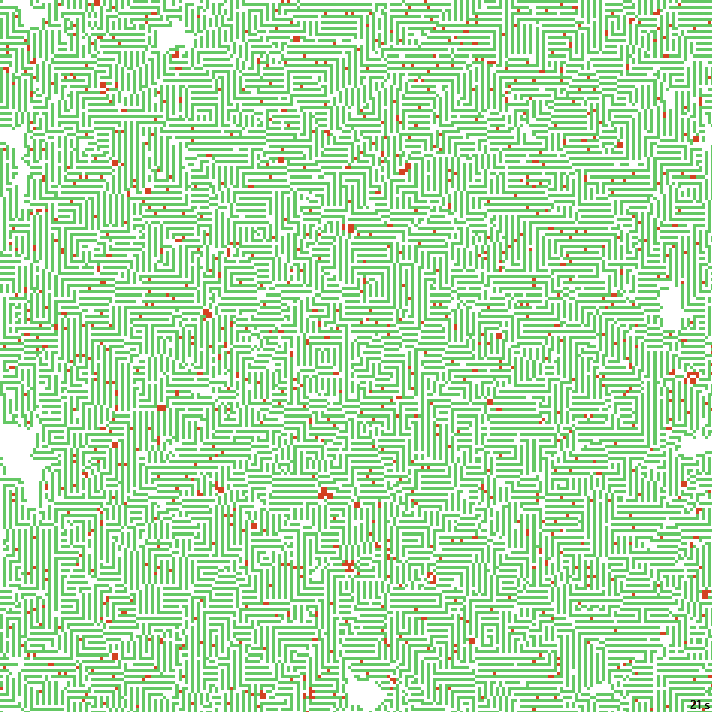
^{21с. x1.5, 237×237, 200×10% | B023/S1235/F134/K3467/L34}

Почти готовая локация для какого-нибудь данжен кроула. Киллеры – мобы, блоки киллеров – боссы. Немного замкнутых коридоров, но это решаемо. Можно в них, например, секретные комнаты делать, со входом через взрыв стены. Забирайте.

---

Что же, закончим на сегодня. Может сложиться ощущение, что вся область клеточных автоматов немного покрыта патиной, но это совсем не так. Объект нашего сегодняшнего внимания появился только в 2014, благодаря всего двум воодушевлённым участникам сообщества, а сегодня это одна из стандартных модификаций классической модели, с десятками интересных правил и заготовок состояний под них. А сколько ещё простора для новых конфигураций, и представить сложно. Любое дело живо, пока есть интересующиеся им.

← Предыдущая часть | Следующая часть (TBA) →