
????, Хабр!
Давно не виделись.
Сегодня мы рассмотрим ещё пару расширений классической модели, которые позволяют достичь ещё большей вариативности поведения правил конфигурации.
В первых статьях цикла мы познакомились с поколениями, одной из базовых и простейших модификаций стандартной конфигурации клеточных автоматов. До этого дополнения наши клетки могли находиться лишь в двух логических состояниях – пустая и живая (0 и 1, соответственно). После же, с новым параметром G, мы добавили третье положение – старение, что значило, что клетка, после выхода из состояния 1, начинала отмирать, доходя до состояния G-1, и только после возвращая состояние к 0. Во время старения клетки не влияют на соседей, не проходят проверки выживания, увеличивая собственный счётчик состояния с каждым шагом, но они и не позволяют новым клеткам рождаться на их месте.
Дополнение поколений является самым популярным, среди всех модификаций стандартной модели, и даже, фактически, оно стало частью правила по умолчанию, наравне с B/S, используясь практически во всех прочих расширениях, хотя использование поколений, конечно, опционально.
Со временем участники сообщества начали предлагать дополнения и к этому варианту конфигурации. На поверхности лежали многие вариации, как ещё возможно изменить или переставить состояния клеток. Одним из них были и обратные поколения, a.k.a. snoitareneG, с которых мы и начнём.
Учёт соседей определяется правилами, которые устанавливаются нами. Вариаций правил существует бесчисленное множество, и они были систематизированы в определённые конфигурации.
Самая популярная конфигурация – «B/S», или «life-like», по названию крайне широко известного клеточного автомата «Game of Life», где B/S обозначает, что в нашем правиле мы описываем всего два параметра – количество соседей необходимых для рождения новой клетки в пустой ячейке, и количество соседей для выживания существующей клетки.
В каждой статье серии мы углубляемся в данную конфигурацию, добавляя новые параметры, либо дополняя существующие. Иногда заглядываем и в прочие конфигурации.
Начало серии здесь, если желаете ознакомиться последовательно.
❯ Обратные поколения
Вы уже наверняка догадались, в чём отличие: вместо «отмирания» после завершённой жизни, клетка «расцветает» до состояния G-1, и только тогда, становясь живой, начинает влиять на соседей и сама проходит проверки выживания.
После описания модификации, участники сообщества первым делом «перевернули» известные именованные правила, открытые на стандартных поколениях, получив несколько интересных видов.
Lava | 60с., 150×20% | G8/B45678/S12345
B – перечисление количества соседей, необходимых для рождения новой клетки. С использованием нотации Хенселя каждому количеству могут быть определены конкретные шаблоны расположения соседей. Пример:
2 = 2 живых соседа в любом положении, 2a = 2 рядом стоящих живых соседа, 2-a = 2 живых соседа в любом положении, кроме a.S – полностью аналогично B, но отвечает за количество/расположения соседей, необходимых для выживания клетки.
Характеристики примера – [ускорение анимации от 100мс. на фрейм, если есть]; длительность анимации; размер и процент центрального заполнения на старте. Поле в примерах всегда 237×237. Границы связаны, если не указано обратное.
Конечно, изменение конфигурации с обычных поколений на обратные не подразумевает, что и вид правила просто станет реверсивным, хотя в некоторых примерах такое ощущение возникает. С подобных мы, собственно, и начнём. В этих правилах легко угадываются их прототипы, и мы взглянем на оба варианта поколений.
Начальные параметры примеров сохранены, где это не мешало наглядности.

Lava | 60с., 150×20% | G8/B45678/S12345
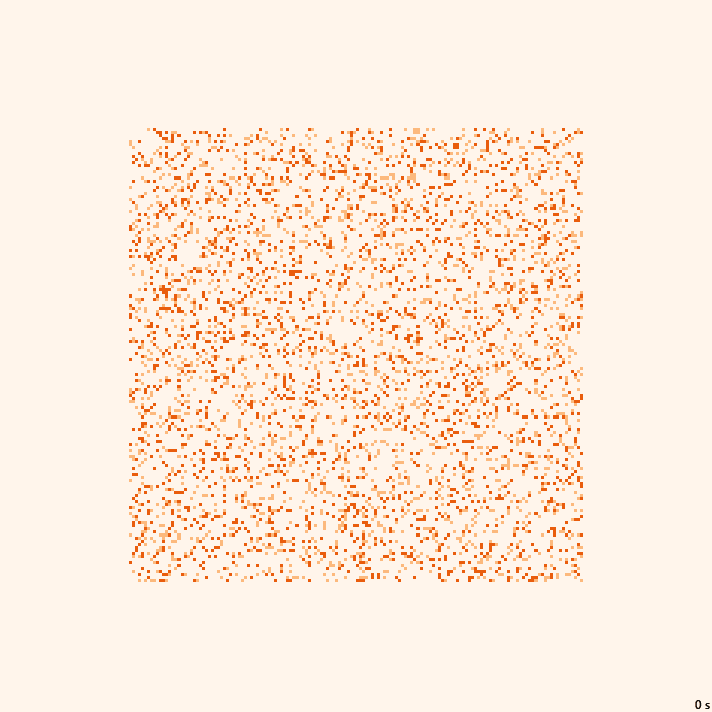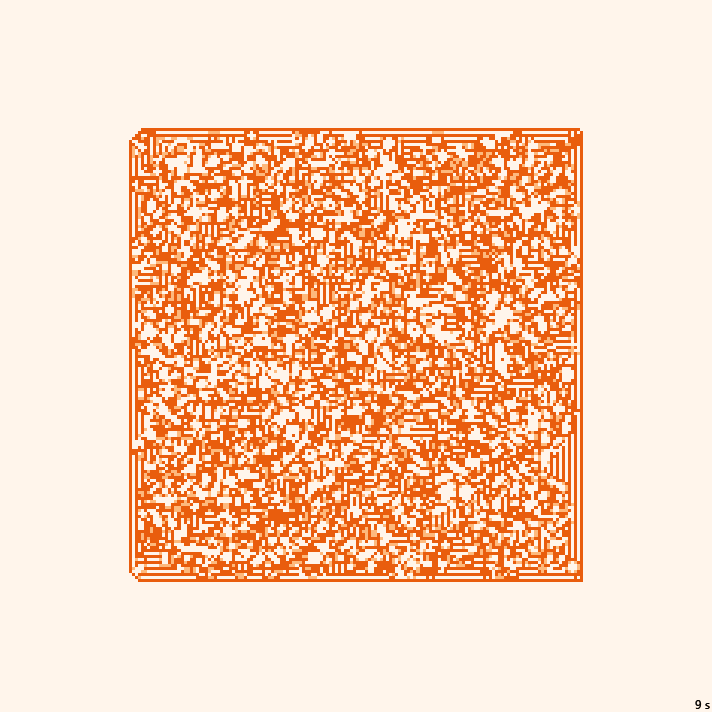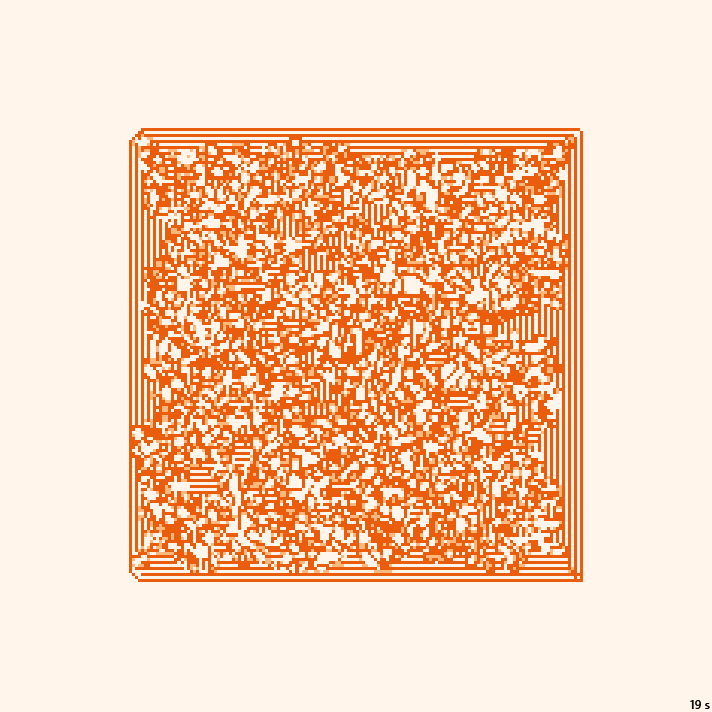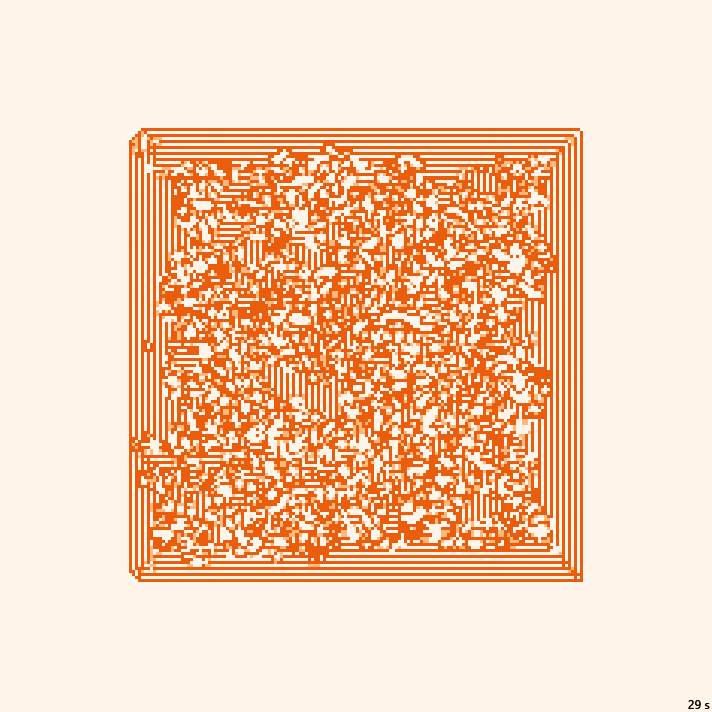
Lines | 29с., 150×20% | G3/B458/S012345

Lines | 10с., 150×20% | G3/B458/S012345

Lines | 40с., 150×20% | G3/B458/S012345

BelZhab Sediment | ×1.25, 40с., 200×0.2% | G8/B23/S145678

BelZhab Sediment | ×1.25, 17с., 200×0.2% | G8/B23/S145678

BelZhab Sediment | ×1.25, 22с., 200×0.2% | G8/B23/S145678
И, всё же, эти примеры скорее исключения, а изменение в виде при обороте поколений может быть кардинальным. За время расцвета клетки состояние окружающих её соседей также вполне вероятно изменится, и структуры, которые работали на правиле с обычными поколениями, будут следовать другим переходам и давать совершенно другие результаты.
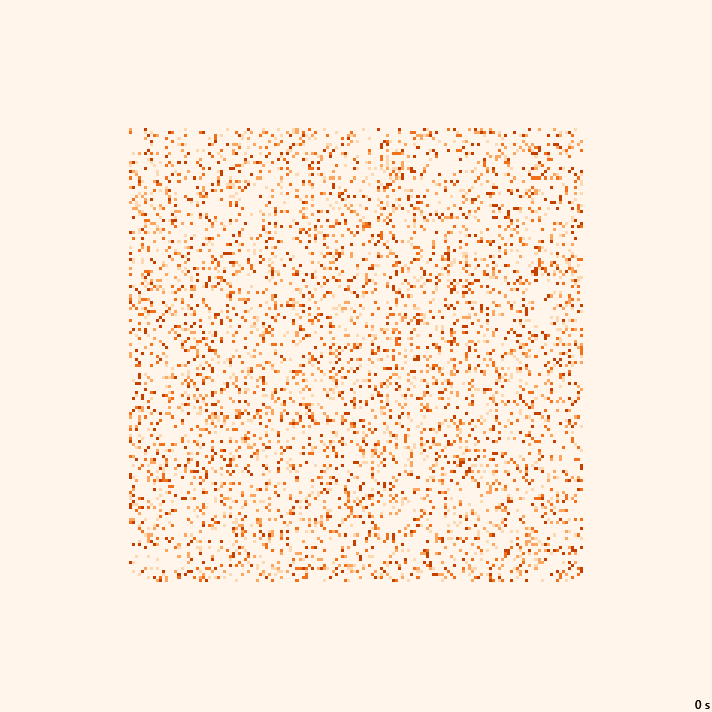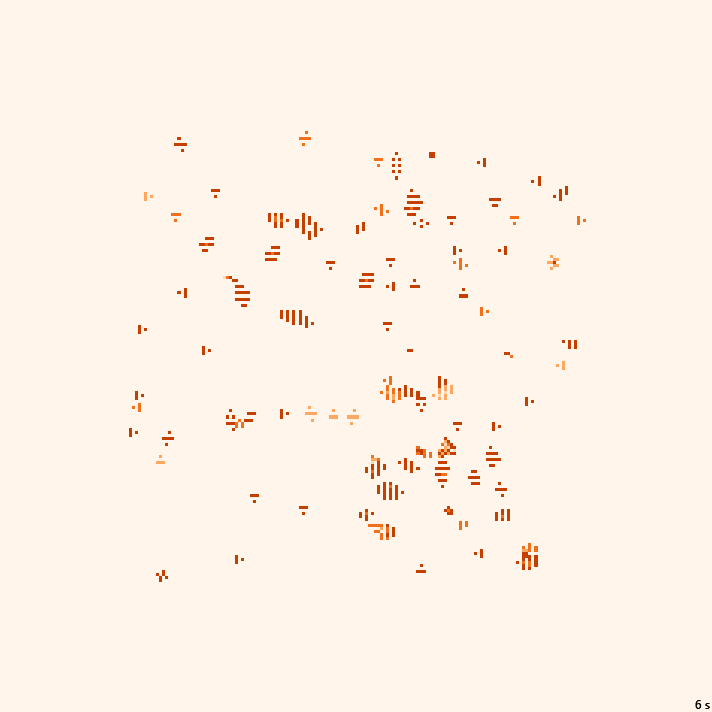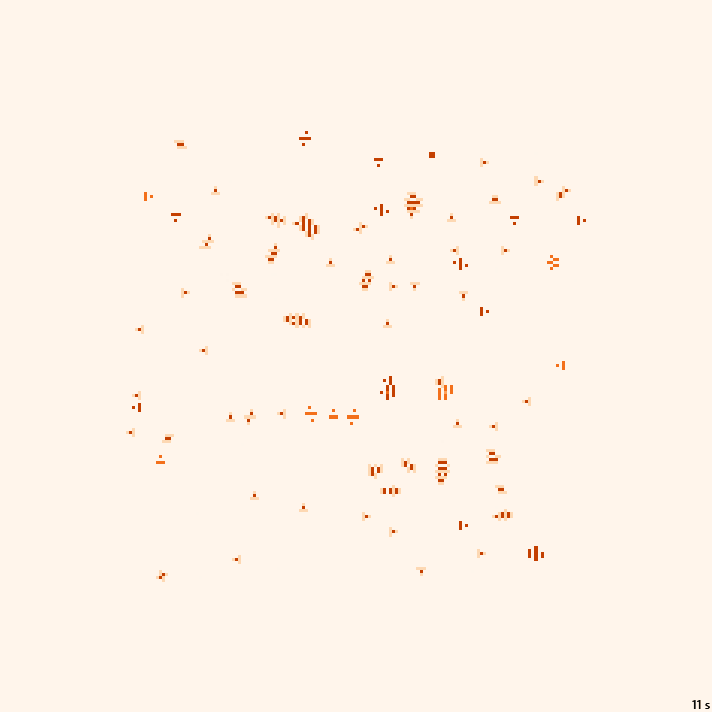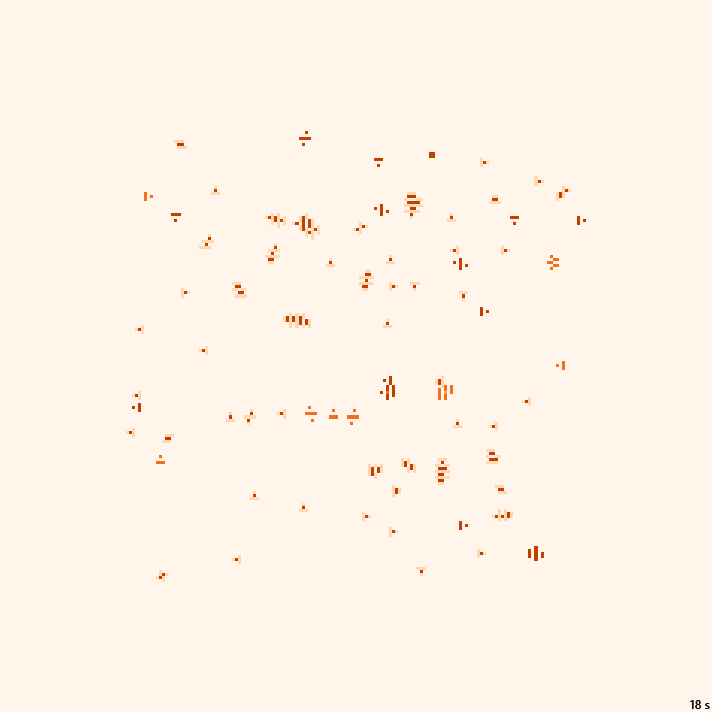
Banners | ×1.25, 18с., 150×20% | G5/B3457/S2367

Banners | ×1.5, 55с., 150×10% | G5/B3457/S2367
Sticks | 28с., 150×20% | G6/B2/S3456
Sticks | ×1.25, 31с., 150×20% | G6/B2/S3456

Meteor guns | 20с., 150×90% | G8/B3/S01245678
Meteor guns | ×1.25, 34с., 150×10% | G8/B3/S01245678

Meteor guns | ×1.25, 16с., 150×10% | G8/B3/S01245678
Можно было бы сказать, что на подобных переворотах, так и не породив новых, собственных правил, и закончился интерес сообщества к данной вариации, но это не совсем так. Данная модификация и разные попытки ещё как-либо изменить поведение поколений, в конечном счёте привели к обобщению всех поколенческих модификаций – расширенным поколениям.
❯ Расширенные поколения
Данная модификация предлагает новую нотацию для соответствующей части, в которой теперь поочерёдно указывается, сколько итераций клетка будет проводить в активном и пассивном состояниях. Количество перечислений не ограничено и мы вольны указывать цепочки любой длины, но начинаем всегда с обозначения активного состояния. Если переложить последний пример, B3/S01245678/G8, с обычными поколениями, на это расширение, мы получим правило B3/S01245678/1-6 1+6≠8?.
То есть при рождении клетка жива, пока один раз не провалит проверку выживания, после чего уходит с поля в течении шести итераций.
Для обратных поколений мы можем использовать 0 в первой части обозначения – B3/S01245678/0-6-1. Таким образом, клетка при рождении сразу входит в пассивное состояние, запуская отсчёт итераций до следующей активной стадии.
Это если говорить о переложениях уже известных нам вариантов поколений. Но ведь цель дополнения не только в их обобщении в единую нотацию, а в том, что мы теперь вольны сами указывать, какие будут состояния на каких итерациях.
В этих переложениях мы использовали 1, при обозначении активной стадии. Теперь же мы можем давать клеткам некоторый запас прочности, указывая бо́льшие значения, и на каждый переход к следующему числовому состоянию активная клетка будет проходить отдельную проверку.
Что же, перейдём к наиболее приглянувшимся примерам. Под спойлерами будут различные вариации правил и стартовых состояний.

×1.5, 15с., 237×0.1% | B1e/S/5-5-5

×2, 14с., симметричный старт | B1e/S/5-5-5

×1.5, 13с., различные стартовые положения | B1e/S/5-5-5

×1.5, 31с., 150×5% | B2-ek/S345678/1-3-1-3

×1.5, 34с., 50×60% | B2-ek/S345678/1-3-1-3

×1.5, 42с., 50×30% | B2-ek/S345678/1-3-1-3

×1.5, 19с., 2×50% | B2-ek/S345/1-3-1-3

×1.5, 9с., 2×50% | B2-ek/S345/1-3-1-3

×1.5, 23с., 100×5% | B345/S/5-5

×1.5, 15с., 100×5% | B345/S/5-5

×1.5, 25с., 150×5% | B345/S5/3-3

×1.5, 47с., 150×100% | B345/S5/3-3
×1.5, 30с., 100×15% | B345/S/2-1
Может возникнуть ощущение, что мы уже видели что-то подобное, и без всех этих расширенных поколений. И для некоторых правил действительно можно подобрать схожие аналоги с других модификаций и конфигураций, но в том-то и прелесть, что образованы такие виды совершенно разной логикой, и ни одна из модификаций не заменяет функциональность другой, если не обобщает её в себе, конечно.
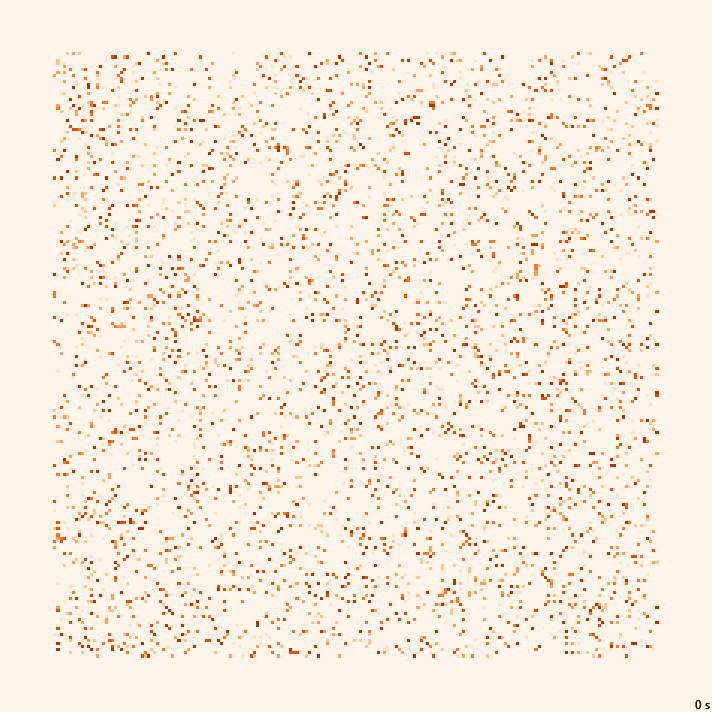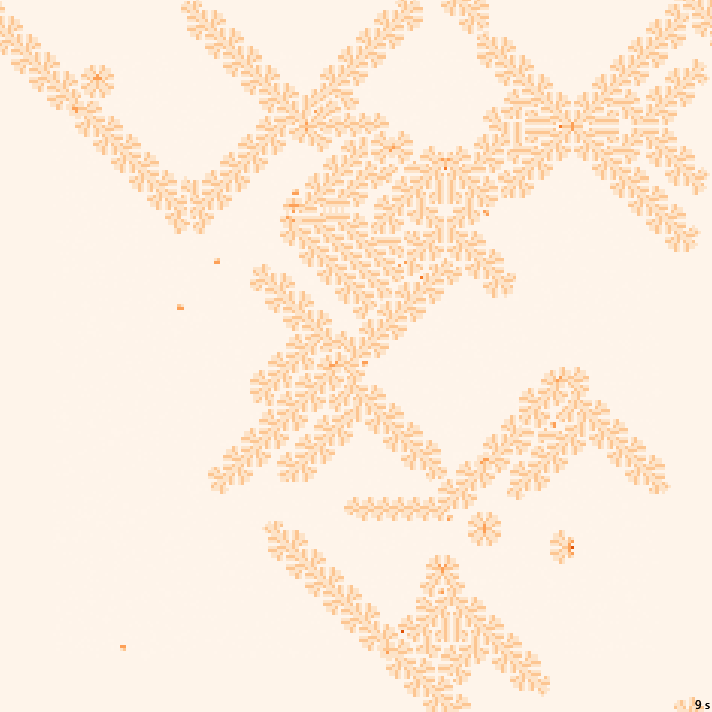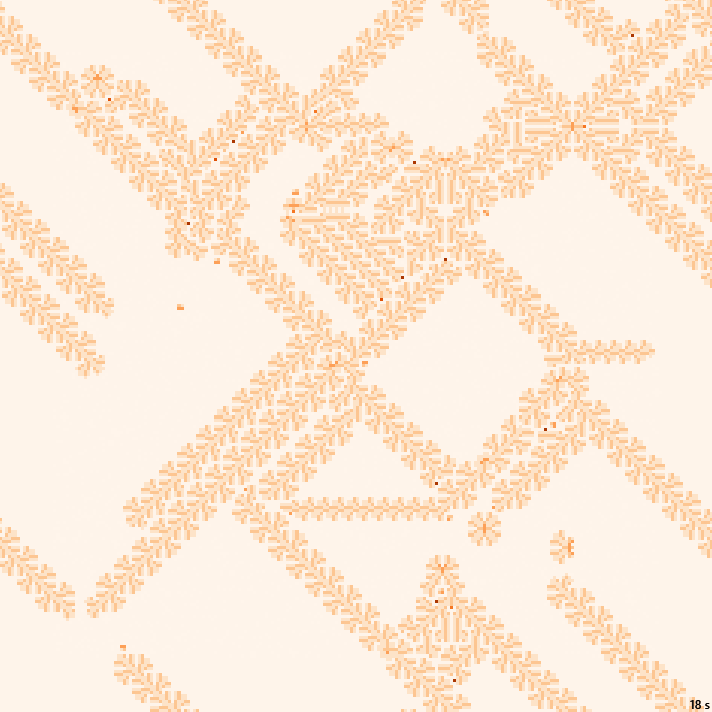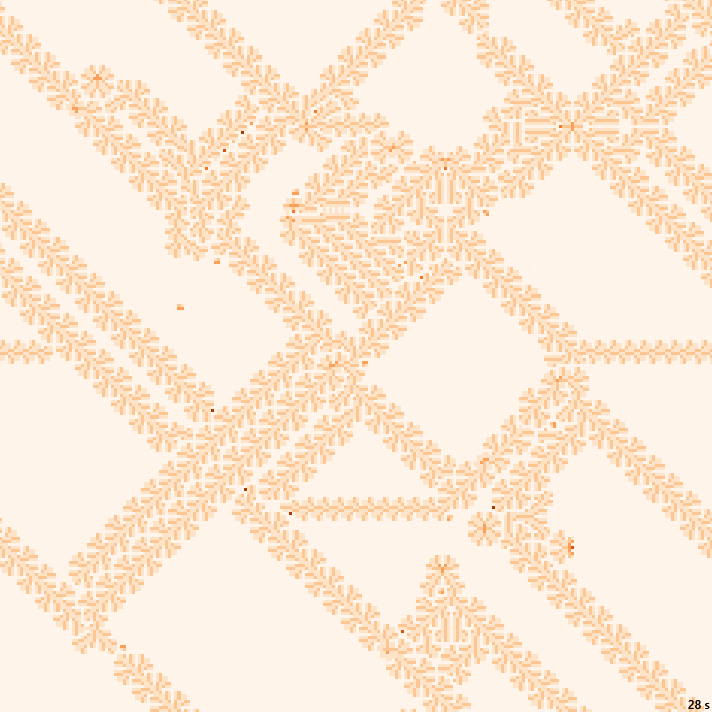
×1.5, 28с., 200×15% | B3kai/S3a45678/3-3
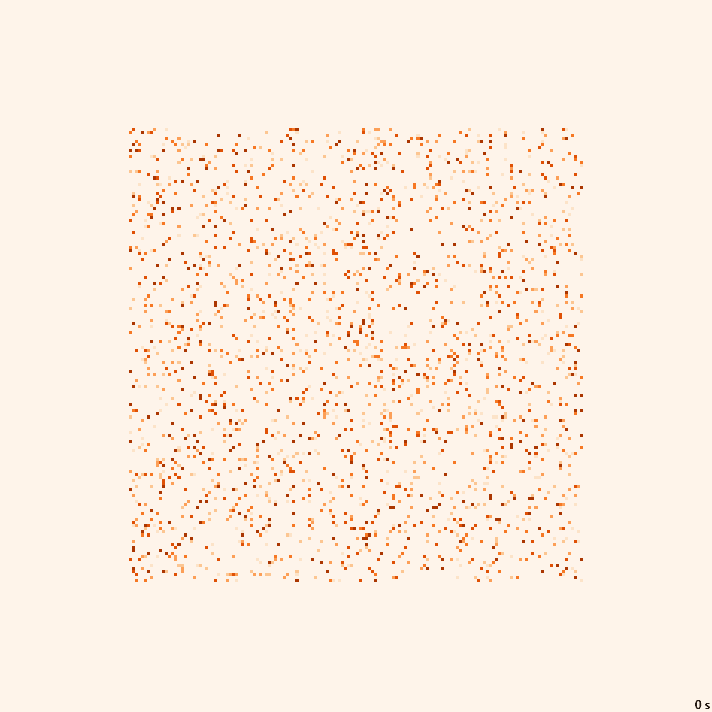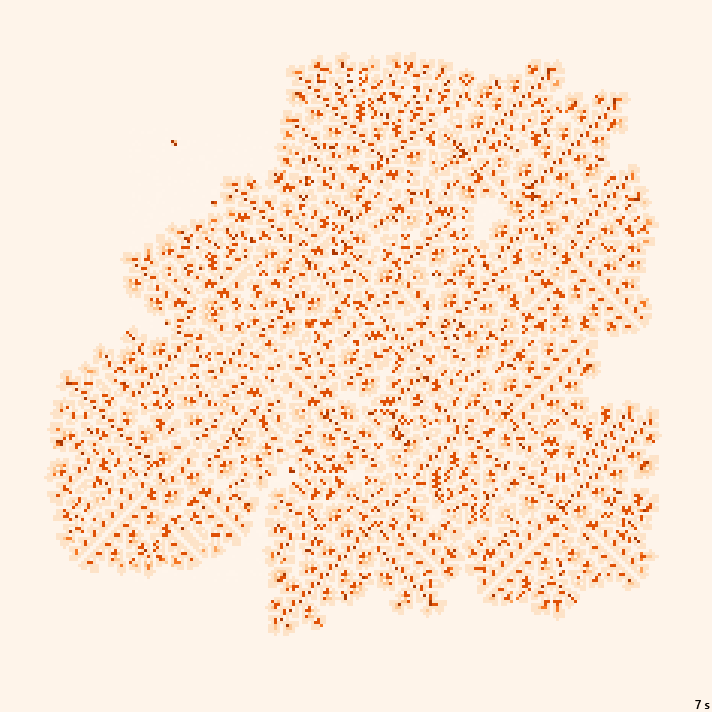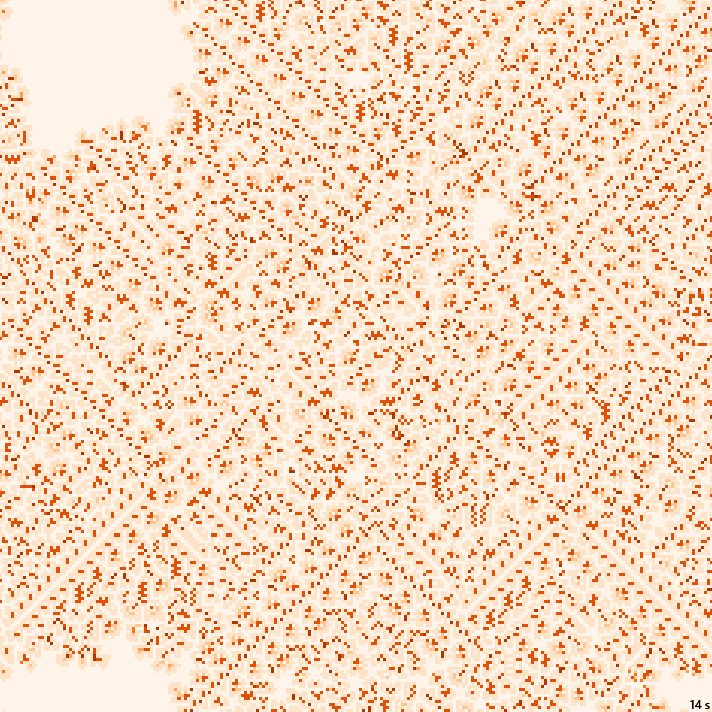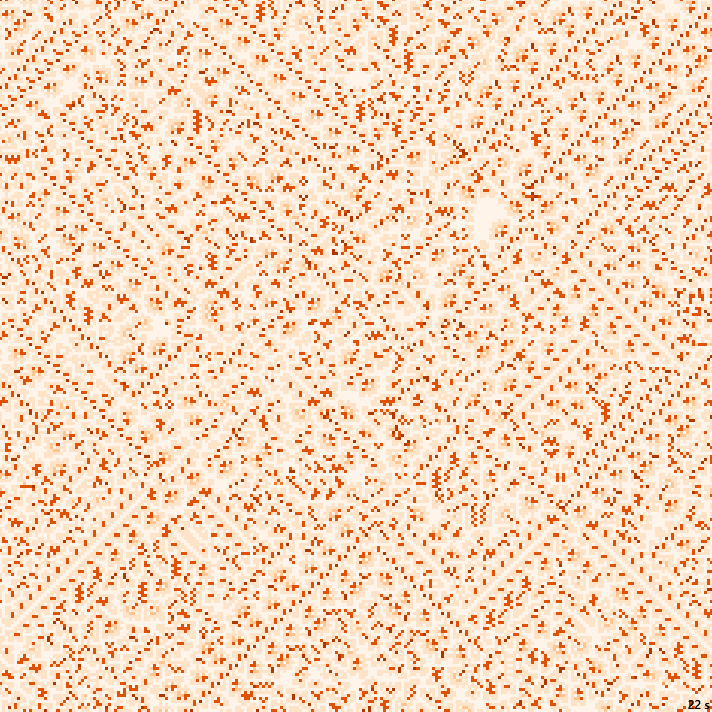
×1.5, 22с., 150×10% | B3kai/S345678/2-2-2
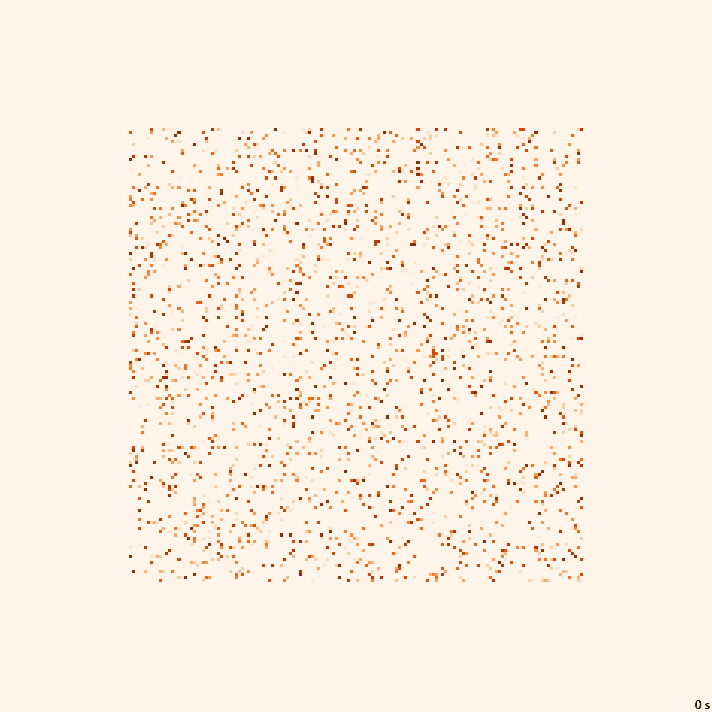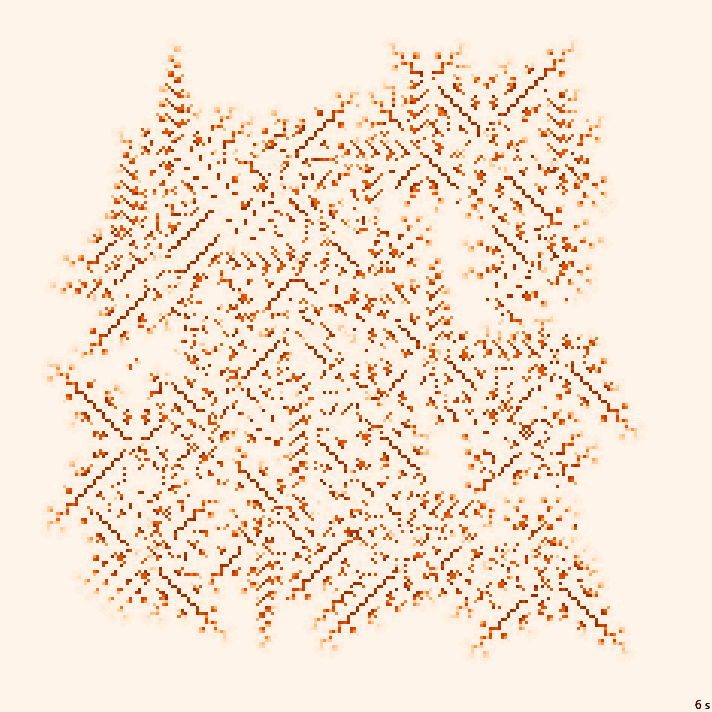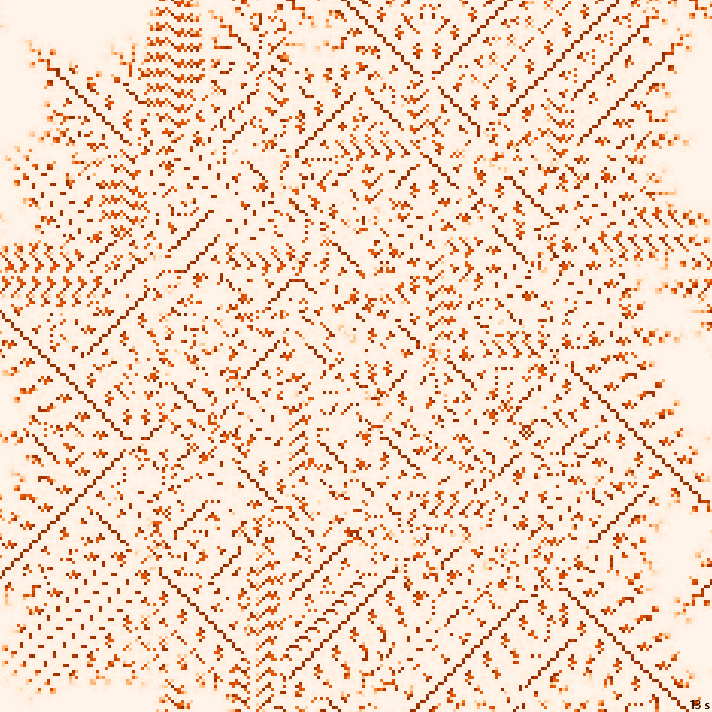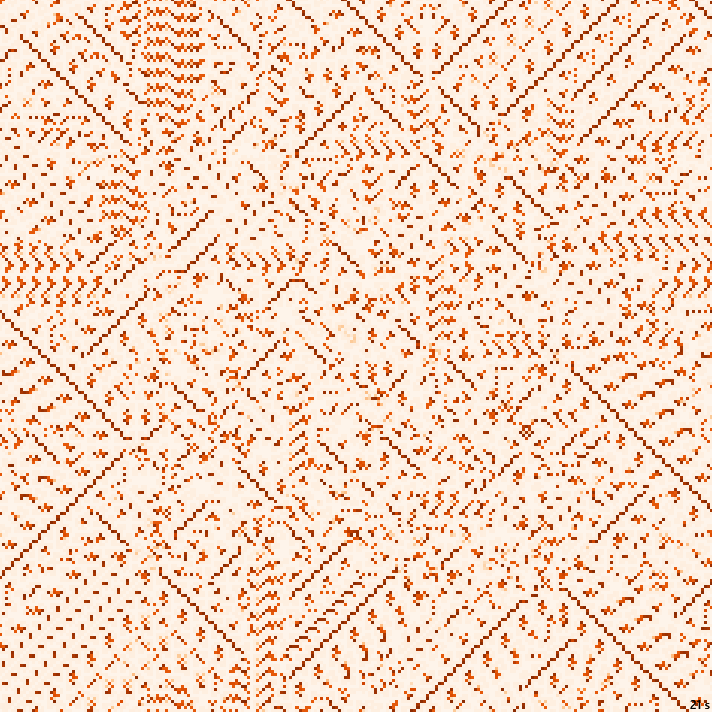
×1.5, 21с., 150×10% | B3kai/S345678/7-7-7

×1.5, 39с., 100×35% | B3kai/S01234567/3-3-3

×1.5, 29с., 150×15% | B3kai/S3a567/3-3

×2, 46с., 3×65% | B2e3-an/S/2-15-10-2

×2, 10с., 3×65% | B2e3-an/S/2-15-10-2

×2, 8с., 3×65% | B2e3-an/S/2-15-10-2
Стоит также упомянуть о значении баланса состояний. Конечно, пассивная клетка по влиянию на соседей полностью эквивалентна пустой, но значение у неё совершенно другое – она, с большой вероятностью, часть структуры, а значит занимает потенциально востребованное место и мешает росту. Чем больше активных состояний мы укажем, тем более насыщенный вид правила может получиться, и наоборот.

14с., 200 итераций, 237×15% | B468/S1357/2-2-2

14с., 200 итераций, 237×15% | B468/S1357/3-2-3

11с., 200? итераций, 237×15% | B468/S1357/2-4-2

×1.5, 22с., 3×55%, закрытые границы | B3/S23e4e567/2-7-7-2

×2, 33с., 50×20%, закрытые границы | B3/S23e4e5678/2-7-7-2

×2, 27с., 50×20% | B3/S235678/2-7-7-2

×2, 67с., 4×90% | B2cek3aej4a7e/S1e2-cn3ery4jz/2-2

×2, 48с., 150×5% | B2cek3aej4a7e/S1e2-cn3ery4jz/2-2

×1.5, 52с., 150×5% | B2cek3aej4a7e/S1e2-cn3ery4jzr5i/2-2

×1.5, 27с., 150×5% | B2cek3aej4a7e/S1e2-cn3ery4jz/1-1-1-1-1-1

×5, 40с., 150×1% | B2cek3aej4a7e/S1e2-cn3ery4jz/20-4

×5, 44с., 3×30% | B2cek3aej4a7e/S1e2-cn3ery4jz/20-4

×5, 22с., 3×30% | B2cek3aej4a7e/S1e2-cn3ery4jz/20-4
❯ Конец
На сегодня всё. В первой статье серии я приводил значение, сколько различных правил возможно на базовой конфигурации (218). После мы как раз рассмотрели стандартные поколения, и с ними подобную цифру уже не представлялось возможным подсчитать, разве что добавить множитель G-1 или же придумать какие-то ограничения/пороги. Но уже там можно было смело говорить о стремлении к бесконечности. О чём бы тогда пришлось говорить сегодня?

4с., 150×95% | B3i/S234567/3-1-3

5с., блоки от 5×5 до 15×15 | B34/S12/0-1-1

×2, 22с., 20×30% | B2ei3aei4e/S12345/3-1-1

×1.5, 23с., 50×30%, закрытые границы | B2aie/S2aie3aie4aie5aie678/1-9-8-4
- Базовая «life-like» конфигурация
- Старение клеток: параметр поколений
- Нотация Хенселя: учёт расположения соседей
- LtL: расширенный радиус поиска соседей
- Циклические клеточные автоматы
- Альтернативные окрестности и HROT
- Блочные КА, окрестность Марголуса
- Взвешенные окрестности, окрестность Гаусса, Far Corners/Edges
- Направленные и пользовательские окрестности
- Клетки-киллеры, BSFK[L]
- Дефицитные правила
- Обратные и расширенные поколения (вы здесь)
- Моделирование лесных пожаров: теория, клеточный автомат на Python
- Сегрегация общества: модель Шеллинга и распределение этнических групп в городах Израиля
Прочее:
- ???? История моделирования лесных пожаров
- ???? REcollapse: фаззинг с использованием unicode-нормализации
- ???? Хватит использовать [a-zа-яё]: правильная работа с символами и категориями Unicode в регулярных выражениях
- ???? Краткая история календаря и фантазии о шестидневной неделе
- ???? Пройти LeetCode за год: экскурсия по сайту и roadmap
← Предыдущая часть | Следующая часть (TBA) →

Комментарии (9)

Krasnoarmeec
11.12.2023 13:36Как гласит народная мудрость, бесконечно можно смотреть на три вещи: как горит огонь, как течет вода и на статьи @TLHE. (Это не сарказм, картинки действительно красивые, замечательно-залипательные. Залип на час.)
Кажется, Вам уже пора делать конкурс на лучшее название. Я, пожалуй, начну:
B345/S/5-5: Реакция Белоусова-Жаботинского:
Вот такая красота:
B2cek3aej4a7e/S1e2-cn3ery4jz/2-2 и B2cek3aej4a7e/S1e2-cn3ery4jzr5i/2-2: Нанороботы травят печатную плату.
B468/S1357/2-4-2: Секретные материалы (Ведь «143» в левом верхнем углу это же не случайно, да?)
B2e3-an/S/2-15-10-2: Бафомет (в конце ожидал увидеть заставку из Дума).
B468/S1357/3-2-3: Мультик из 90х. Тогда авангард был вроде в моде.
B3/S23e4e567/2-7-7-2: Пагода.
B2cek3aej4a7e/S1e2-cn3ery4jz/20-4: Возведение Храма.

TLHE Автор
11.12.2023 13:36Спасибо. Интересный взгляд, особенно с травлением) Реакция Белоусова-Жаботинского нередкий гость на разных конфигурациях, особенно в циклических КА. 143 – воля рандома, да и с отсылкой, признаюсь, не знаком. К B3/S23e4e567/2-7-7-2 ракетные ассоциации были. Для вашей версии особенно хорошо симметрия вида подойдёт, вроде такой:
Пагода


Krasnoarmeec
11.12.2023 13:36Красота!
Отсылка была на сериал "Секретные материалы". Ну а "143" вроде как затравка для конспирологов, так как к картинкам никак не относится и появляется только на одной из них (так что же автор хотел этим сказать?).
В общем, шутка не удалась, посыпаю голову пеплом.

Vlagor
11.12.2023 13:36А не пробовали поиграться с клеточными автоматами на гексогональной сетке? Или вообще в полярных координатах с нулем в центре клетки произвольно задавать сектора в которых может находится/не находится соседняя клетка. А можно плюсом еще динамически менять эти сектора в зависимости от расположения клеток вокруг)

TLHE Автор
11.12.2023 13:36К гексагональной сетке присматриваюсь, но пока визуализация с ней не очень хорошо получается. С полярными координатами свежая идея, спасибо, возьму на заметку.

Wizard_of_light
11.12.2023 13:36еще динамически менять эти сектора в зависимости от расположения клеток вокруг
О, теория относительности в клеточных автоматах! Кстати, свежая идея, предложений менять геометрию поля в зависимости от конфигурации клеток я как-то не припомню.



ivanstor
Если не тайна, в какой программе вы это считали?
TLHE Автор
Никакой тайны, в самописной. В конце серии, надеюсь, решусь представить её на суд общественности.
ivanstor
Ждем :-)