Привет, хабр! Меня зовут Алексей Бойков. Я студент третьего курса факультета компьютерных наук НИУ ВШЭ. В начале весны 2023 года мне удалось попасть на стажировку в Лабораторию искусственного интеллекта Сбера. В ней несколько основных групп, я работал в командах фундаментальных исследований и искусственного интеллекта в медицине. В данной статье я попробую рассказать про часть этой задачи, касающуюся непосредственно применения полной взаимной информации, как меры ассоциации между несколькими случайными величинами.
Введение в тему
Многомерные временные ряды являются важным типом данных, упорядочивающим по времени различные измерения. Такие данные возникают во многих областях, например в задаче прогноза атмосферных осадков и температуры, котировок на финансовых рынках, инцидентов отказа промышленного оборудования и т.п. Подробнее об этом классе задач можно прочитать в статье. Наряду с задачами прогноза часто решается задача классификации, т.е. предсказывается метка для всего многомерного временного ряда.
Для классификации данных такого типа зачастую используют нейросетевые модели на основе сверточных, рекуррентных или трансформенных архитектур. Чтобы добиться высокого качества с помощью таких моделей, обычно требуется большой объём данных, тщательный подбор гиперпараметров обучающего алгоритма (число эпох, learning rate schedule и т.д.) и, конечно, много времени. Кроме того, такие модели обычно сложно интерпретировать – сложно понять, какие ряды повлияли больше на результат, чем другие, учитывались ли их взаимодействия и как именно?
В качестве простой альтернативы есть интересный вариант: посчитать меры взаимосвязи, например коэффициент корреляции, между всемиодномерными временными рядами, а дальше рассмотреть полученные числа как признаки, на которых и обучить простой классификатор. Тем самым, мы получаем признаковое описание многомерного временного ряда не в виде набора признаков индивидуальных рядов, а путем анализа их взаимодействия между собой. Однако взаимосвязи между временными рядами могут быть более сложными чем просто попарными, для их учета нужна мера взаимосвязи сопоставляющая силу взаимодействия более чем двум временным рядам – такая как мера полной взаимной информации, о которой я расскажу далее.
Данные
Помимо уже упомянутых примеров, задача классификации многомерных временных рядов часто встречается в медицине. Например, по данным измерений различных биологических процессов с набора датчиков или носимых устройств хочется уметь определять, есть ли у пациента какое-либо заболевание или нет.
Данные фМРТ
Одним из примеров являются данные функциональной магнитно-резонансной томографии (фМРТ). Говоря простым языком, фМРТ отражает изменение активности мозга в течение некоторого времени, с высоким, относительно других методов, пространственным, но малым временным разрешением. Данные фМРТ имеют вид трехмерных изображений, изменяющихся во времени, таким образом изменение яркости каждого вокселя изображения может быть рассмотрено как временной ряд. Поскольку количество вокселей велико (изображения могут иметь разрешение порядка 1283), их обычно собирают в несколько сотен групп соответствующих определенным участкам мозга, и каждый участок описывают временным рядом-представителем, например полученным путём усреднения рядов в группе.

В своём исследовании во время стажировки я в основном занимался изучением данных фМРТ высокого качества [Allen2022], полученных на аппарате со сверхвысокой мощностью магнитного поля в 7 Тесла (это в 145 000 раз больше мощности магнитного поля Земли). Набор данных был собран путём измерения активности мозга испытуемых во время демонстрации им картинок с вопросами вида "Видели ли вы эту картинку ранее?". Данные были взяты для двух пациентов, всего на двоих получилось 956 временных рядов (картинок было много, пациентам их показывали с перерывами около года) по 226 отсчётов в каждом что в реальном времени соответствовало примерно 5 минутам). В качестве меток классов для данных фМРТ мы задали соответствие измерения первой или второй части эксперимента.
Данные ЭКГ
Другим набором данных с которым я работал были данные электрокардиографии (ЭКГ) измеряющие электрическую активность сердца с помощью электродов, а сами измерения в электрокардиографии называются отведениями. Стандартно ЭКГ состоит из 12 отведений, отведения I, II, III, aVL, aVR, aVF замеряются на конечностях, а отведения V1-V6 на грудной клетке.
Для экспериментов с ЭКГ использовался датасет PTB-XL [Wagner2020]. Это один из лучших открытых датасетов в свободном доступе на сегодня. Он состоит из 21799 десятисекундных записей ЭКГ, в каждой записи 12 отведений. Разметка представлена 71 неэксклюзивным классом (multi-label), которые иерархически сгруппированы сначала в 23 «надкласса», а потом в 5 «суперклассов». В данной работе я классифицирую сигналы только по этим 5 «суперклассам». Так же в работе я использовал не все 21799 записей, а только те, разметка которых прошла валидацию врачами и в которых нет шума и дрейфа изолинии. В репозитории с датасетом есть файл ptbxl_database.csv, в котором имеются соответствующие метки.
Подготовка данных
Любой исследователь занимающийся анализом данных знаком с принципом garbage in, garbage out – на плохо подготовленных данных даже хороший алгоритм будет выдавать плохой результат, а значит, важно уделять должное внимание предобработке входных данных – очистке от артефактов и шума, удалению тренда. В статье “Benchmarking functional connectome-based predictive models for resting-state fMRI” [Dadi2019] как раз описывается, как следует предобрабатывать данные фМРТ, а также описывается простая интерпретируемая модель.
Напомню, что данные ЭКГ – 12-канальные временные ряды, в то время как данные фМРТ – 3D-изображения+время, поэтому предварительно разбиваем изображения на области интереса путем наложения анатомического атласа и выделяем временные ряды-представители каждой из областей. После наложения анатомического атласа AAL было выделено 116 регионов. Из них, для лучшей интерпретируемости и полноты исследования, было выделено 4 подсети головного мозга:
сеть пассивного режима работы мозга (default mode network);
зрительная кора (visual cortex);
сенсомоторная сеть (sensorimotor network);
сеть внимания (attention network).
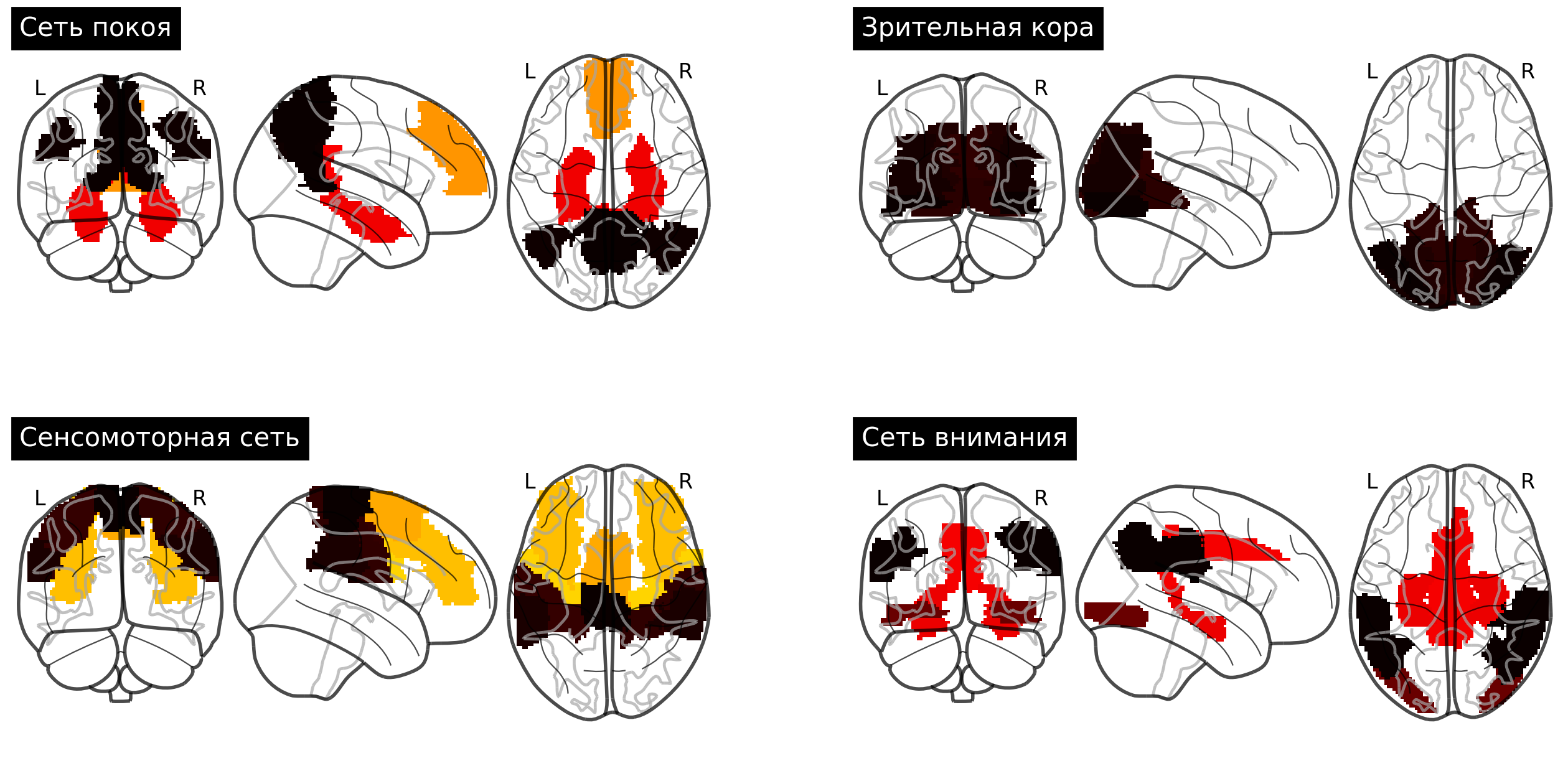
а) сеть покоя, б) зрительная кора, в) сенсомоторная сеть, г) сеть внимания.
Эксперименты
Интерпретируемым подходом, описываемым в данной статье, является подсчёт попарных корреляций между рядами, составляющими один многомерный, и построение по этим признакам-корреляциям модели логистической регрессии.
Подробнее: на входе имеем многомерный временной ряд (например, размерности 12). Мы считаем попарные корреляции между рядами (берём каждые два ряда, мысленно представляем их как реализации случайных величин (да, вот так просто – но это даёт неплохие результаты) и считаем корреляции – в нашем случае получается чисел. Полученные числа считаем признаковым описанием многомерного ряда и строим по этому представлению логистическую регрессию. Для достоверности метод запускался 10 раз в кросс-валидации по пяти разбиениям.
На описанных ранее данных я решал задачу бинарной классификации вида "текущий многомерный временной ряд соответствует эксперименту в первой половине исследования, или во второй". Описанный в предыдущем абзаце подход дал качество (точность) 76-78% (в зависимости от подсети). Также было проведено сравнение с классической моделью LSTM, которая выдала качество около 72%. Это число нужно в качестве бейзлайна, а объектом исследования была проверка гипотезы:
Учёт более чем попарных связей между временными рядами приведет к росту качества решения задачи классификации.
Действительно, в описанном ранее подходе использовались лишь попарные корреляции, но ведь зависимости могут быть более сложными. Поэтому возникает желание рассматривать отношения более, чем на двух объектах. Однако корреляция явным образом не обобщается на несколько объектов, поэтому было решено рассмотреть другой математический объект – взаимную информацию. Обычно она определяется лишь на паре случайных величин, однако существуют несколько обобщений.
Я использовал следующий вариант [Watanabe1960]: взаимная информация нескольких случайных величин есть KL-дивергенция между их совместным распределением и произведением их маргинальных распределений (каждой случайной величины по отдельности) (формула MI1):
Также взаимную информацию нескольких случайных величин можно записать в виде сумм энтропий каждой случайной величины по отдельности за вычетом их совместной энтропии (формула MI2):
Подсчёт взаимной информации для неизвестного распределения – задача не из простых. К слову, выборки с которыми мы работали, как раз относится к такому случаю, т.к. генеральное распределение фМРТ или ЭКГ нам не известно. Для вычисления взаимной информации по формуле MI2 в таких случаях можно использовать различные оценки энтропии.
В работе опробованы различные варианты таких оценок:
гауссовая – при допущении что случайные величины распределены согласно нормальному распределению, формула для оценки энтропии существует в явном виде, ее можно найти например тут [Varley2022, раздел IV.A];
Козаченко-Леоненко – в общем случае применима геометрическая оценка, на основе расстояний до k-ближайшего соседа от каждой точки в совместном распределении [Козаченко1989].
Кроме этого проведено несколько простых экспериментов прямой оценкой взаимной информации при помощи нейросети по формуле MI1 – для этого учим бинарный классификатор [Liao2020] отличать что пример принадлежит совместному распределению либо произведению маргинальных, и по формуле
где – количество точек в выборке, а
– логарифм отношения вероятности принадлежности
совместному распределению (
) к вероятности принадлежности произведению маргинальных (
), оцениваем взаимную информацию.
Кроме того, были рассмотрены обобщения коэффициента корреляции Спирмена и меры зависимости Швейцера-Вульфа на несколько случайных величин [Schmid2010].
Для решения задачи классификации успешно (по сравнению с коэффициентом корреляции Пирсона) себя проявила только гауссовая оценка взаимной информации – наиболее простая из представленных, и, как оказалось, наиболее эффективная. Именно с ней и привожу табличку, в которой можно увидеть подтверждение гипотезы.
k |
Сеть покоя |
Зрительная кора |
Сенсо-моторная сеть |
Сеть внимания |
|
LSTM |
0.722 ± 0.035 |
0.734 ± 0.019 |
0.720 ± 0.025 |
0.732 ± 0.024 |
|
Коэф. корреляции |
2 |
0.781 ± 0.025 |
0.785 ± 0.025 |
0.768 ± 0.026 |
0.771 ± 0.029 |
Взаимная информация |
2 |
0.778 ± 0.026 |
0.763 ± 0.026 |
0.762 ± 0.025 |
0.785 ± 0.025 |
3 |
0.790 ± 0.029 |
0.787 ± 0.027 |
0.772 ± 0.021 |
0.804 ± 0.026 |
|
4 |
0.799 ± 0.030 |
0.792 ± 0.027 |
0.792 ± 0.025 |
0.792 ± 0.025 |
|
5 |
0.800 ± 0.030 |
0.788 ± 0.023 |
0.798 ± 0.027 |
0.798 ± 0.024 |
|
6 |
0.797 ± 0.029 |
0.785 ± 0.023 |
0.799 ± 0.027 |
0.795 ± 0.024 |
Здесь по столбцам расположены подсети головного мозга, по строкам указаны корреляция и взаимная информация, параметр k отвечает за то, какие связи (попарные, по тройкам и т.д.) учитывались в очередном эксперименте. Видно, что лучшими оказываются методы оценки, учитывающие более сложные, чем попарные связи (в разных подсетях оптимальное число элементов в клике разное, но везде больше двух).
Также был проведён ряд экспериментов на данных ЭКГ. Такие данные имеют вид 12-мерных рядов (такие измерения сердечной активности позволяют врачу-кардиологу достоверно определять наличие сердечных патологии). ЭКГ сигналы были размечены пятью видами меток, я решал задачу классификации только для данных помеченных метками заболеваний:
ЭКГ в норме (SUPER_NORM);
нарушение сердечной проводимости (SUPER_CD);
инфаркт миокарда (SUPER_MI);
гипертрофия отделов сердца (SUPER_HYP);
изменение ST/T элементов (SUPER_STTC).
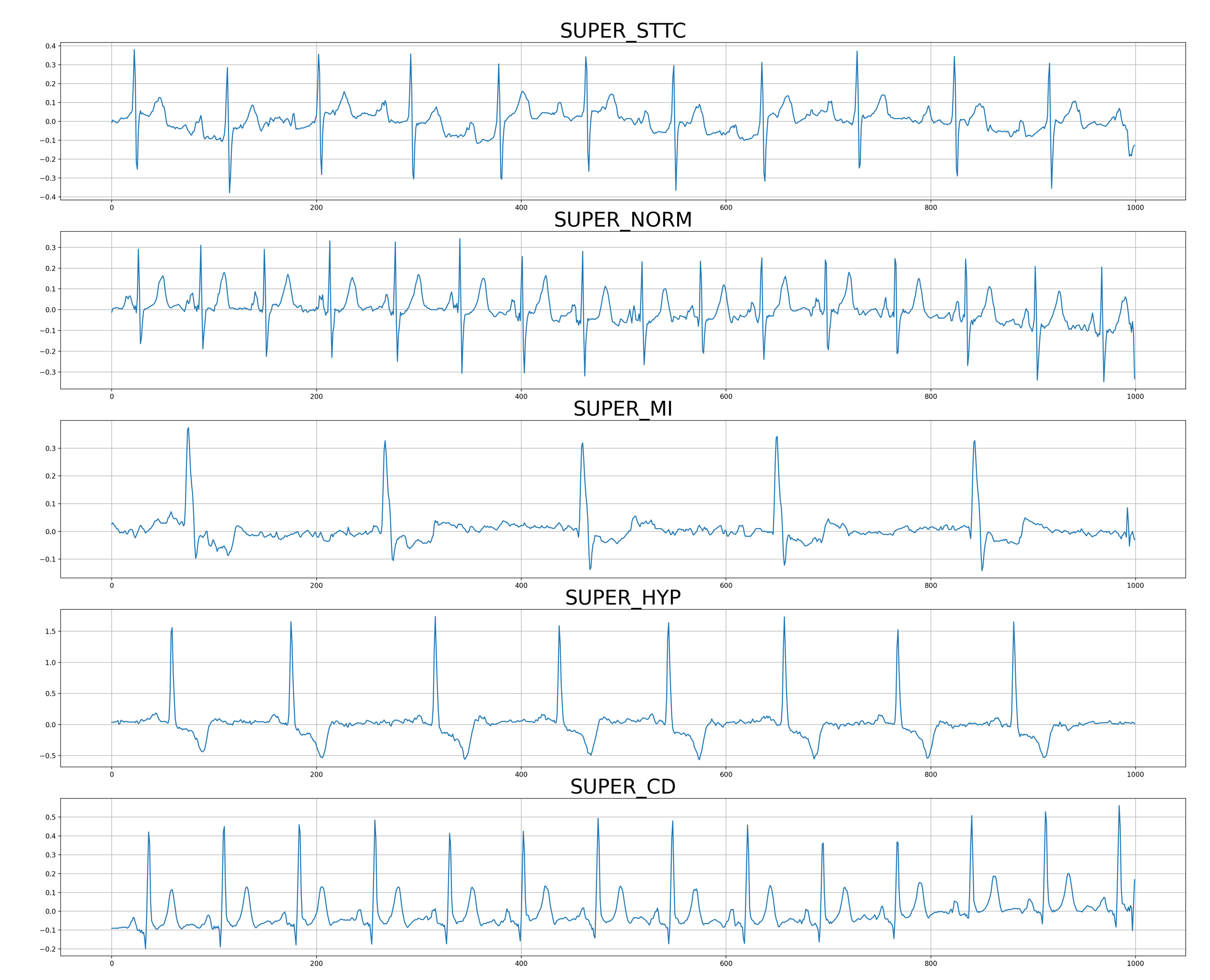
В качестве бейзлайна использовались свёрточные сети – проверенный подход в анализе ЭКГ сигналов. Результаты для коэффициента корреляции обгоняют свёртки по трем из четырех меток заболеваний. Также, на двух из четырех меток заболеваний видим, что, например, на тройках значения лучше, чем на попарных корреляциях. Но эффект учета более чем попарных зависимостей заметно меньше чем для данных фМРТ.
k |
Нарушение проводи-мости |
Инфаркт миокарда |
Гипертрофия отделов сердца |
Изменение ST/T эл-тов |
|
1D CNN |
0.894 ± 0.005 |
0.592 ± 0.046 |
0.357 ± 0.071 |
0.761 ± 0.022 |
|
Коэф. корреляции |
2 |
0.743 ± 0.009 |
0.901 ± 0.004 |
0.947 ± 0.001 |
0.847 ± 0.005 |
Взаимная информация |
2 |
0.739 ± 0.011 |
0.901 ± 0.003 |
0.946 ± 0.001 |
0.850 ± 0.003 |
3 |
0.754 ± 0.007 |
0.901 ± 0.003 |
0.946 ± 0.002 |
0.859 ± 0.005 |
|
4 |
0.752 ± 0.008 |
0.901 ± 0.003 |
0.945 ± 0.003 |
0.858 ± 0.005 |
Заключение
В итоге, исследуемая в работе гипотеза подтвердилась, причём с помощью достаточно простого метода оценки взаимной информации, сравнимого по своей простоте с методом анализа корреляции.
Эксперименты выполненные на медицинских данных показали неплохие результаты. Учитывая свойство интерпретируемости полученных моделей результат может быть интересен для практического применения в сфере здравоохранения. Также признаки на основе взаимной информацией на подмножествах могут быть потенциально использованы в ансамблевых моделях в качестве источника дополнительной информации.
Несмотря на хорошие показатели, данные методы не воспринимают структуру ряда в целом, а это потенциально значимый фактор при классификации рядов. Поэтому в качестве перспектив для дальнейшей работы можно выделить рассмотрение мер оценки близости нескольких временных рядов или использование нейросетевой оценки DEMI на основе не единичных измерений в каждый момент времени, а окон фиксированной ширины.
Ссылки по теме
[Dadi2019] Dadi K. et al. Benchmarking Functional Connectome-based Predictive Models for Resting-state fMRI, NeuroImage (2019)
[Liao2020] Liao et al., DEMI: Discriminative Estimator of Mutual Information. https://arxiv.org/abs/2010.01766 (2020)
[Schmid2010] Copula-Based Measures of Multivariate Association. In: Jaworski, P., Durante, F., Härdle, W., Rychlik, T. (eds) Copula Theory and Its Applications (2010)
[Varley2022] Varley et al., Multivariate Information Theory Uncovers Synergistic Subsystems of the Human Cerebral Cortex. Communications Biology (2022)
[Watanabe1960] Watababe S., Information Theoretical Analysis of Multivariate Correlation, IBM Journal of Research and Development (1960)
[Козаченко1987] Козаченко Л.Ф., Леоненко Н.Н., О статистической оценке энтропии случайного вектора. Проблемы передачи информации (1987)
Датасеты
[Allen2022] Allen E. et al. A Massive 7T fMRI Dataset to Bridge Cognitive Neuroscience and Artificial Intelligence, Nature Neuroscience (2022)
[Wagner2020] Wagner, P., Strodthoff, N., Bousseljot, R.-D., Kreiseler, D., Lunze, F.I., Samek, W., Schaeffter, T., PTB-XL: A Large Publicly Available ECG Dataset. Scientific Data (2020)
Ссылка на код
Комментарии (2)

folal
08.07.2023 07:57Объясните мне пожалуйста вашу фразу, не могу ее понять:
Полученные числа считаем признаковым описанием многомерного ряда и строим по этому представлению логистическую регрессию.
Как можно из 66 чисел получить признаковое пространство, например, для 1000 наблюдений?


S_A
Прочитал с интересом. Как идею могу предложить - посмотреть на dynamic time warping (статистики из него в качестве фич).