В этой статье я расскажу, как, используя недокументированные возможности фреймворка Apache Spark, качественно подобрать гиперпараметры для модели градиентного бустинга всего за один человеко-день вместо обычных пяти.

Как сэкономить время дорогих дата-сайентистов
Как известно, в настоящее время существуют два наиболее мощных метода машинного обучения – нейронные сети и градиентный бустинг. Как правило, нейронные сети доминируют в задачах с пространством непрерывных признаков (таких как изображения). До недавнего времени бустинг показывал лучшие результаты для табличных данных. Теперь и на этом поле нейронные сети показывают такие же или лучшие результаты.
Однако нейронные сети сложнее в обучении и реализации, требуют больших объемов вычислительных ресурсов, поэтому во многих компаниях модели на основе градиентного бустинга в настоящее время де-факто являются стандартом для моделей на табличных данных.
Поскольку градиентный бустинг склонен к переобучению, качество моделей сильно зависит от подбора гиперпараметров. И здесь возникает сложность: для построения модели хорошего качества необходимо как минимум несколько человеко-дней работы дорогого дата-сайентиста.
В этой статье представлена методика, которая позволяет достичь одного из двух результатов: либо сократить время построения модели в 5 раз без ухудшения ее качества, либо за то же время добиться максимально возможного качества модели — с точностью до одного Джини или даже его десятых долей.
В реальных задачах, которые обычно возникают в бизнесе, количество объектов наблюдения составляет от нескольких десятков тысяч до нескольких миллионов. Число доступных переменных (признаков) достигает нескольких тысяч. При этом обычно только немногие независимые переменные оказывают значительное влияние на результирующую переменную.
Несколько тысяч признаков серьезно удлиняют расчеты, поэтому на практике первоначальный набор переменных сокращают до нескольких сотен, отбросив наименее релевантные переменные. Для этого существуют некоторые эвристики. Например, можно построить модель для единичного решающего дерева, узнать важность каждой из переменных и отбросить переменные с нулевой важностью. Либо построить несколько тысяч однофакторных моделей и отбросить те из них, которые дают слишком низкое качество результата.
Использование таких эвристик несет риски вылить с грязной водой и ребенка. На начальном этапе построения модели с высокой степенью вероятности будет отброшена переменная, которая дает в целом плохой результат, но содержит в себе важную информацию для улучшения качества модели в нескольких десятках сложных для классификации случаев. Но без этих эвристик время подбора гиперпараметров устремляется в бесконечность.
После того как набор переменных сокращен до нескольких сотен, характерное время расчета значений модели для одного набора гиперпараметров составляет от нескольких десятков секунд до нескольких минут. Кросс-валидация увеличивает это время в 3–5 раз. Можно грубо принять, что расчет для одной комбинации гиперпараметров занимает 5 минут.
В модель градиентного бустинга, в зависимости от библиотеки, в которой она реализована, входит порядка 10 основных гиперпараметров. Даже если мы проведем расчеты для 3 вариантов каждого из гиперпараметров, нам потребуется 5 * 310 / 60 ≈ 5 000 часов. Разумеется, такие затраты времени чрезвычайно велики.
Поэтому аналитики прибегают к алгоритмам, сокращающим количество комбинаций признаков. Например, к поиску на случайной сетке или к байесовской оптимизации. Обычно считается разумным перебрать 500 комбинаций, что займет всего 42 часа. Если оставлять машину включенной на ночь, приближенное решение — комбинацию гиперпараметров, близкую к оптимальной — можно получить всего за двое суток.
Для нахождения действительно хорошего решения полученная комбинация, как правило, требует дополнительного тюнинга. При тюнинге гиперпараметры уже варьируют в узких пределах, добиваясь лучших результатов. Причем обычно такую подгонку выполняют не для всех гиперпараметров, а только для тех, которые максимально влияют на качество результирующей модели. Обычно у опытного аналитика на тщательный подбор гиперпараметров уходит примерно неделя рабочего времени.
В статье мы покажем, как можно сделать то же самое, но в 5 раз быстрее.
Это потребует значительных вычислительных ресурсов, представленных вычислительным кластером Apache Spark. Однако игра стоит свеч, потому что стоимость вычислительных ресурсов каждый год снижается, а их доступный объем растет. Количество же квалифицированных дата-сайентистов растет не быстрее, а может быть и медленнее, чем количество задач, которые перед ними ставят. Поэтому стоимость их труда пока не снижается.
Таким образом, компаниям выгодно сокращать трудоемкость задач подбора гиперпараметров за счет увеличения их ресурсоемкости. Сокращается и такой важнейший для новой экономики параметр как time-to-market: время от начала работы над моделью до ее внедрения в продакшен. Для дата-сайентиста использование подобных технологий означает сокращение рутинных процедур и возможность посвятить больше времени интересным и творческим задачам.
Учебная модель
Поскольку реальные наборы данных являются собственностью компаний, мы разберем пример на хорошо знакомом всем специалистам наборе MNIST. Поставим задачу о верной классификации рукописной цифры 7 против всех остальных цифр. Тогда задача будет характеризоваться следующими параметрами:
Задача классификации неравновесных классов, в которой целевой класс составляет 10% выборки.
60 000 наблюдений в тренировочной выборке и 10 000 наблюдений в тестовой выборке.
784 признака (рисунок 28*28 точек), из которых значительное число (точки на краях рисунка) не имеют значения для решения задачи;
В качестве критерия качества мы будем использовать коэффициент Джини, который вычисляется по формуле:
Gini = 2 * ROCAUC - 1.
Специфика коэффициента Джини в том, что он принимает значения в диапазоне [0, 1], где 0 означает, что предсказания модели случайны, а 1 — что предсказания модели полностью совпадают с целевой переменной.
Эта задача в целом похожа на значительное количество задач, возникающих в реальных бизнес-кейсах.
Исходный файл с набором MNIST можно скачать по ссылкам:
Код трансформации исходного набора во входные данные для поставленной задачи (для файлов, скачанных и распакованных в директорию /mnist)
# импортируем необходимые модули
import numpy as np
import pandas as pd
import os
import idx2numpy
import matplotlib.pyplot as plt
# настраиваем параметры изображений
%matplotlib inline
plt.rcParams['figure.figsize'] = (18,10)
plt.rcParams['axes.grid']=True
# читаем тренировочный набор изображений
image_file = 'mnist/train-images-idx3-ubyte'
train_array = idx2numpy.convert_from_file(image_file)
# читаем тестовый набор изображений
image_file = 'mnist/t10k-images-idx3-ubyte'
test_array = idx2numpy.convert_from_file(image_file)
# читаем набор тренировочных меток
label_file = 'mnist/train-labels-idx1-ubyte'
train_labels = idx2numpy.convert_from_file(label_file)
# читаем набор тестовых меток
label_file = 'mnist/t10k-labels-idx1-ubyte'
test_labels = idx2numpy.convert_from_file(label_file)
# конвертируем матрицы изображений из uint8 во
# float и одновременно нормируем их значения в диапазон [0, 1]
train_array = train_array.astype(float) / 255
test_array = test_array.astype(float) / 255
# конвертируем метки из uint8 в int
train_labels = train_labels.astype(int)
test_labels = test_labels.astype(int)
# для тренировочных меток выделяем цифру 7
# как положительный класс, а остальные -
# как отрицательный класс, для этого:
# кодируем цифру 7 как -1
train_labels[train_labels == 7] = -1
# кодируем остальные цифры как 0
train_labels[train_labels > 0] = 0
# изменяем кодировку цифры 7 на 1,
# сохраняя кодировки всех остальных цифр как 0
train_labels = -train_labels
# аналогично для тестовых меток
test_labels[test_labels == 7] = -1
test_labels[test_labels > 0] = 0
test_labels = -test_labels
# преобразовываем массив в массив 60000х784х1
train_array = train_array.reshape(train_array.shape[0], -1, 1)
# удаляем лишнюю ось
train_array = np.squeeze(train_array)
# преобразовываем массив в массив 60000х784х1
test_array = test_array.reshape(test_array.shape[0], -1, 1)
# удаляем лишнюю ось
test_array = np.squeeze(test_array)
# преобразовываем в формат pandas DataFrame
train_array = pd.DataFrame(train_array)
test_array = pd.DataFrame(test_array)
train_labels = pd.DataFrame(train_labels)
test_labels = pd.DataFrame(test_labels)
# сохраняем результаты как файлы csv
train_array.to_csv('mnist/train.csv', index=False)
test_array.to_csv('mnist/test.csv', index=False)
train_labels.to_csv('mnist/train_labels.csv', index=False)
test_labels.to_csv('mnist/test_labels.csv', index=False)Apache Spark экономит ваше время и деньги
Apache Spark — фреймворк с открытым исходным кодом для реализации распределенной обработки данных, входящий в экосистему проектов Hadoop. Он предоставляет пользователю возможность параллельной обработки данных на значительном числе экзекьюторов (executors).
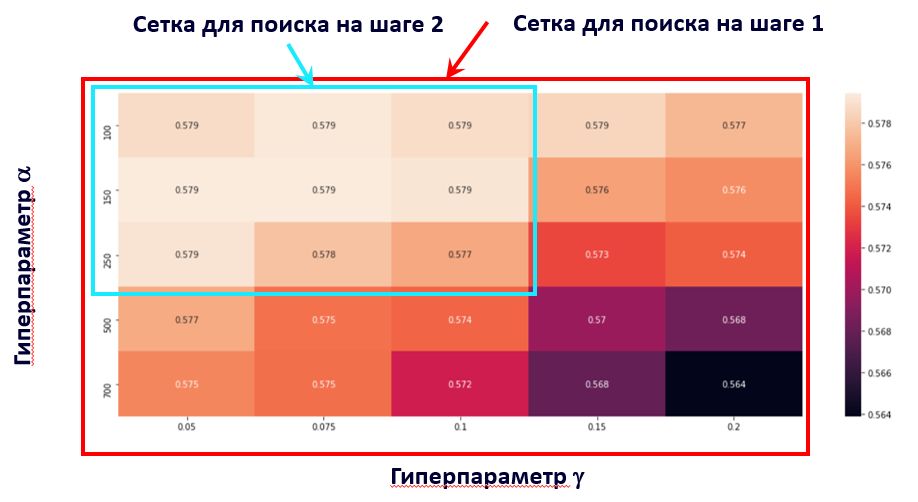
Идея метода такова. Мы формируем двумерную сетку для двух гиперпараметров размера N*N. Каждый узел сетки соответствует уникальной паре гиперпараметров и должен быть обсчитан k раз для k-блочной кросс-валидации. Таким образом, нам нужно произвести N*N*k расчетов целевой функции. Обычно мы производим их последовательно с помощью библиотеки sklearn.
С Apache Spark мы можем произвести расчеты параллельно, запросив у системы N*N*k экзекьюторов. В первом случае общее время расчетов будет равно сумме времени каждого из расчетов, во втором – времени самого длинного расчета. При N и k, равным 5, скорость расчетов может возрасти в 125 раз!
Затем мы усредним полученные значения по k блокам и получим N * N значений функции для каждой пары гиперпараметров. Таким образом усредненные значения функции окажутся результатом кросс-валидации по k блокам!
Поскольку вычислительные ресурсы все равно ограничены, мы должны подобрать для N и k наименьшие разумные значения. Для N таким значением является 5, для k – от 3 до 5.
С помощью двумерной 5-точечной сетки можно легко и быстро найти значения гиперпараметров, которым соответствует значение функции, сколь угодно близкое к ее истинному максимуму.
Как легко и быстро найти максимум функции
В этом разделе мы покажем, как легко и быстро найти приближенный максимум функции на 5-точечной сетке. Сначала представим, что сетка у нас равномерная. Тогда процесс поиска будет выглядеть так:
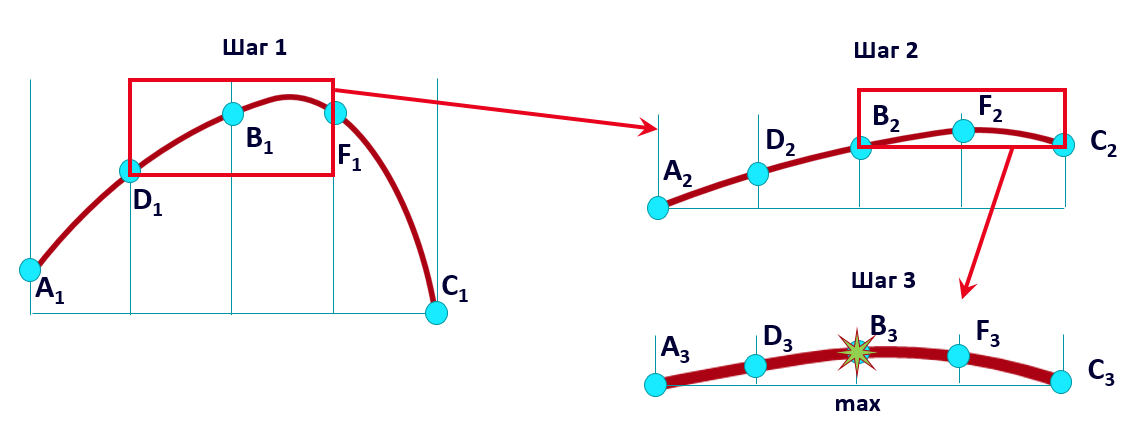
На каждом шаге мы сокращаем размер сетки пополам, выбирая 2 из 4 отрезков. Мы помним, что на каждом шаге нам известны только значения функции в узлах Ai, Di, Bi, Fi, Ci, где i – номер шага. Истинный график функции нам неизвестен и изображен только для удобства. Тем не менее за 3 шага мы очень близко подходим к максимуму функции, используя простое правило ориентирования по сетке: находим три узла с наибольшими значениями и строим на них новую сетку.
Поскольку нам доступны значения функции в узлах сетки, мы всегда можем остановить поиск, когда прирост максимума на очередном шаге становится слишком маленьким.
А что, если у функции на отрезке два максимума? Тогда мы разбиваем наш процесс поиска на два подпроцесса (в данном случае на отрезках A–D–B и B–F–C по отдельности). Находим два локальных максимума и просто выбираем больший из них. Если максимумов больше двух, мы дробим процесс поиска на бо́льшее количество подпроцессов.
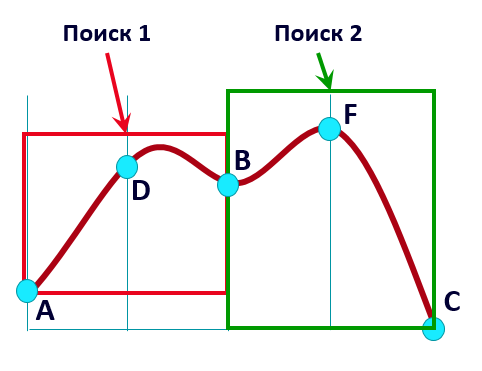
Для пары гиперпараметров мы аналогичным образом ищем максимум на двумерной 25-точечной сетке. При этом мы можем сокращать сетку сразу для обоих параметров, уменьшая ее площадь в 4 раза за один шаг:
Мы рассмотрели поиск на равномерной сетке. Но некоторые гиперпараметры распределены нелинейно. В этом случае мы используем логарифмическую сетку, которую строим по следующим правилам:
Если левый край сетки равен 0, то узлами сетки будет следующий набор чисел: [0, 0.05 * b, 0.1 * b, 0.5 * b, b], где b – правый узел сетки.
Если левый край сетки равен b1, а правый – b2, то узлы сетки имеют значения: [b1, pow(b1 * (b2 / b1), 1/4), pow(b1 * (b2 / b1), 2/4), pow(b1 * (b2 / b1), 3/4), b2], где pow(x, y) означает x в степени y.
В вычислении узлов сетки нам помогает следующая функция, аргументами которой являются координаты левого и правого узла сетки и значение ‘int’ или ‘double’ — в зависимости от того, нужно ли округлять значения до целых (многие гиперпараметры являются целыми числами) или нет. А результатом является список координат узлов сетки.
def calc_grid(alpha_strt, alpha_end, type_res='int'):
"""Рассчитывает узлы сетки для поиска оптимального
значения гиперпараметра. Выдает 5 узлов от
минимального (alpha_strt) до максимального (alpha_end) значения
параметра. Если type_res имеет значение 'int',
то числа будут целые, иначе - типа float
"""
if alpha_strt > 0:
# расчет сетки для случая, если минимальное значение
# больше 0
fctr = (alpha_end / alpha_strt) ** .25
par_vec = alpha_strt * np.array(
[fctr ** i for i in range(5)])
else:
# расчет сетки для случая, если минимальное значение
# равно 0
par_vec = alpha_end * np.array(
[0, .05, .1, .5, 1])
if type_res == 'int':
# округление значений сетки до целых
par_vec = np.round(par_vec, 0).astype(int)
return par_vecНачинаем решать основную задачу
Теперь приступим к решению самой задачи. Будем использовать вычислительный кластер Apache Spark Росбанка.
Существует несколько популярных библиотек, реализующих построение моделей градиентного бустинга: XGBoost, LightGBM и CatBoost. К сожалению, в вычислительном кластере Apache Spark Росбанка они в настоящий момент не реализованы. Поэтому для построения модели использовалась стандартная библиотека sklearn.GradientBoostingClassifier. Ее основным недостатком считается невозможность полноценного распараллеливания вычислений. Но использование системы Apache Spark нивелирует этот недостаток, позволяя библиотеке одновременно проводить расчеты на множестве узлов.
Сначала сделаем необходимые импорты:
# стандартные импорты
import pickle
import numpy as np
import pandas as pd
from tqdm import tqdm
# импорты для SPARK
import os
import sys
import subprocess
# специфические импорты для модели
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
from sklearn.ensemble import GradientBoostingClassifier
# импорт matplotlib и параметры изображения
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (18,7)
plt.rcParams['axes.grid']=True
# персональные данные
MY_OFFICE_ID = 'XXXXXX_confidential_information'Мы будем проводить 5-блочную кросс-валидацию. Определим соответствующую константу.
N_FOLDS = 5Теперь подготовим данные для процедуры.
ВНИМАНИЕ!!! Данные ОБЯЗАТЕЛЬНО преобразовать в формат матриц/векторов numpy, иначе данные в формате pandas DataFrame вызовут сложно отслеживаемую ошибку!
# загружаем изображения
train_df = pd.read_csv('mnist/train.csv')
test_df = pd.read_csv('mnist/test.csv')
# загружаем метки
y_train = pd.read_csv('mnist/train_labels.csv')
y_test = pd.read_csv('mnist/test_labels.csv')
# список переменных
var_list = list(train_df.columns)
# ВНИМАНИЕ!!! Данные ОБЯЗАТЕЛЬНО преобразовать в формат
# матриц/векторов numpy, данные в формате pandas
# DataFrame вызовут сложно отслеживаемую ошибку
train1 = train_df.values
test1 = test_df.values
train_labels = y_train.values
train_labels = train_labels.ravel()
test_labels = y_test.values
test_labels = test_labels.ravel()К сожалению, не все данные поместятся в память (про распараллеливание данных для каждого экзекьютора мы скажем ниже). Поэтому пока мы сократим количество наблюдений в тренировочной и тестовой выборках в 10 раз.
train_features = train1[::10,:]
test_features = test1[::10,:]
train_labels = train_labels[::10]
test_labels = test_labels[::10]Устанавливаем параметры и запускаем Apache Spark.
# настройки перед запуском SPARK - зависят от вашего вычислительного кластера
p = subprocess.Popen(f"/usr/bin/id {MY_OFFICE_ID} -u",
shell=True,
stdout=subprocess.PIPE,
stderr=subprocess.STDOUT)
id_str = p.stdout.readline().decode("utf-8").replace("\n", "")
os.environ["JAVA_TOOL_OPTIONS"] = "-Djava.security.krb5.conf=/etc/krb5.conf.d/krb5.conf"
os.environ["KRB5_CONFIG"] = "/etc/krb5.conf.d/krb5.conf"
os.environ["KRB5CCNAME"] = f"/tmp/krb5cc_{id_str}_{id_str}"
os.environ['ARROW_LIBHDFS_DIR'] = '/usr/hdp/3.1.4.0-315/hadoop/lib/native/'
# настройки SPARK - зависят от вашего вычислительного кластера
spark_home = "/opt/odpp/spark_3.2.0/"
SHELL_PATH = os.path.join(spark_home,'python/pyspark/shell.py')
os.environ ['SPARK_HOME'] = spark_home
sys.path.insert(0, os.path.join(spark_home, 'python'))
sys.path.insert(0, os.path.join(spark_home, 'python/lib/py4j-0.10.7-src.zip'))
os.environ ['PYSPARK_PYTHON'] = '/usr/local/basement/Python-3.7.4/bin/python3.7'
os.environ ['HADOOP_CONF_DIR'] = '/usr/hdp/current/hadoop-client/conf/'
os.environ ['PYTHONPATH'] = '/opt/odpp/spark_3.2.0/python/lib/py4j-0.10.9.2-src.zip:/opt/odpp/spark_3.2.0/python'
os.environ ['PYTHONSTARTUP'] = '/opt/odpp/spark_3.2.0/python/pyspark/shell.py'
# важно: запрашиваем количество экзекьюторов, равное числу узлов сетки (5х5),
# умноженному на число блоков (N_FOLDS), запрашиваем на каждый узел
# по 12 Гбайт памяти
os.environ ['PYSPARK_SUBMIT_ARGS'] = f" --master yarn --deploy-mode client --num-executors {25 * N_FOLDS} --executor-cores 1 --executor-memory 12G pyspark-shell"
# запускаем SPARK
exec(open(SHELL_PATH).read())Здесь важно обратить внимание на то, что мы запрашиваем у системы количество экзекьюторов, равное числу узлов сетки (5 * 5), умноженному на число блоков (N_FOLDS), т.е. 25 * N_FOLDS. На каждый узел запрашиваем по 12 Гбайт памяти.
Проверяем параметры сессии Apache Spark и устанавливаем переменную, отвечающую за SparkContext.
# параметры сессии SPARK
spark
# присваиваем значение SPARK контекста
sc = spark.sparkContextРазбивай и решай!
Вот теперь начинается магия. Сначала мы разобьем все наблюдения тренировочной выборки случайным образом на N_FOLDS блоков. Для каждого из разбиений мы получим 4 блока, что объединим для тренировки модели. А на пятом блоке будем рассчитывать качество получившейся модели.
Поскольку у нас есть 5 разбиений, и в каждом из разбиений один из блоков по очереди играет роль валидационного, а остальные 4 – тренировочных, то, в общем, мы получаем модель 5-блочной кросс-валидации:

Проверим количество наблюдений в каждом из блоков:
# разбиваем все наблюдения случайным образом
# на N_FOLDS блоков
kf = KFold(n_splits=N_FOLDS)
# проверяем разбиение на блоки и размерность данных
i = 0 # номер блока
for train_id, val_id in kf.split(train_features):
print('Блок {} тренировочный, размерность: {}'.format(i, train_features[train_id].shape))
print('Блок {} валидационный, размерность: {}'.format(i, train_features[val_id].shape))
i += 1Получаем:
Блок 0 тренировочный, размерность: (4800, 784)
Блок 0 валидационный, размерность: (1200, 784)
Блок 1 тренировочный, размерность: (4800, 784)
Блок 1 валидационный, размерность: (1200, 784)
Блок 2 тренировочный, размерность: (4800, 784)
Блок 2 валидационный, размерность: (1200, 784)
Блок 3 тренировочный, размерность: (4800, 784)
Блок 3 валидационный, размерность: (1200, 784)
Блок 4 тренировочный, размерность: (4800, 784)
Блок 4 валидационный, размерность: (1200, 784)Для каждой тройки чисел (значения каждого из гиперпараметров и номер блока) мы получаем значение коэффициента Gini на валидационном блоке. Усреднив значения для всех 5 блоков, мы получаем N * N оценок качества модели для каждой пары значений гиперпараметров. На этой сетке мы найдем пару чисел – значения гиперпараметров, соответствующих максимальному качеству модели.
Подбираем предварительные значения гиперпараметров
Теперь приступим к выбору гиперпараметров для оптимизации. Всего в функции GradientBoostingClassifier мы будем подбирать оптимальные значения для 10 гиперпараметров. Причем будем делать это парами по порядку, в котором эти гиперпараметры приведены в табл. 1. В ней представлено название гиперпараметра, его описание, числовой тип, значение по умолчанию, границы изменения, значения базового пункта, а также стартовая сетка, которую мы рекомендуем использовать на первом шаге подбора гиперпараметра. На следующих шагах сетка изменяется по правилам, рассмотренным выше. Это справедливо для всех параметров, кроме max_depth — для него, возможно, придется расширять сетку вправо. Стартовая сетка для этого гиперпараметра содержит только небольшие значения, так как с увеличением его значений быстро увеличивается длительность расчетов.
Мы рекомендуем проводить поиск гиперпараметра до того момента, пока расстояния между узлами сетки не станет равным базовому пункту, указанному в таблице для каждого гиперпараметра. Когда это произойдет, надо выбрать узел, значение функции в котором будет максимальным, — так мы получим оптимальное значение гиперпараметра.
Сначала оставим всем гиперпараметрам значения по умолчанию, кроме max_depth и max_features. А для этих двух гиперпараметров подберем и зафиксируем оптимальные значения.
Затем для max_depth и max_features подставим найденные оптимальные значения гиперпараметров и зафиксируем их. Подберем оптимальные значения для subsample и min_samples_split, оставив в остальных шести гиперпараметрах значения по умолчанию.
Установим ранее найденные оптимальные значения для первых четырех гиперпараметров и подберем оптимальные значения для min_samples_leaf и min_weight_fraction_leaf, оставив для остальных четырех гиперпараметров значения по умолчанию.
Мы будем действовать таким образом, пока для всех гиперпараметров не будут подобраны оптимальные значения. Это не гарантирует, что мы нашли максимум функции. Однако порядок гиперпараметров в таблице подобран так, что в ходе поиска мы получили хорошее представление о ландшафте максимизируемой функции. Поэтому найденное нами значение находится достаточно близко к максимуму.
Гиперпараметры для оптимизации:
Название |
Описание |
Тип |
Значение по умолчанию |
Границы |
Базовый пункт |
Стартовая сетка |
max_depth |
максимальная глубина дерева |
int or None |
3 |
[1, inf) |
1 |
[1, 2, 3, 5, 7] |
max_features |
количество признаков, учитываемых алгоритмом, при построении расщепления в дереве |
int или float |
None |
[1, n_features) |
1 |
[1, int(b) , int(b2) , int(b3) , n_features], где b = n_features1/4, int(.) – целая часть числа |
subsample |
доля наблюдений из выборки, используемых для построения одного дерева |
float |
1 |
(0.0, 1.0] |
.01 |
[.1, .8, .9, .95, 1] |
min_samples_split |
минимальное число объектов, при котором происходит расщепление |
float or int |
2 |
(0.0, 1.0] |
.01 |
[.01, .1, .3, .5, 1] |
min_samples_leaf |
минимальное число объектов в листе (узле) |
float or int |
1 |
(0.0, 1.0) |
.01 |
[.01, .1, .3, .5, .99] |
|
min_weight_ fraction_leaf |
минимальная доля объектов в листе (узле) с учетом весов объектов |
float |
0 |
[0.0, 0.5] |
.01 |
[0, .05, .1, .2, .5] |
|
min_impurity_ decrease |
узел будет разделен, если такое разделение вызовет уменьшение примеси на величину, большую данного числа |
float |
0 |
[0.0, inf) |
.01 |
[0, .05, .1, .7, 3] |
max_leaf_nodes |
Максимальное число узлов в дереве |
int |
None |
[2, inf) |
20 |
[2, 6, 17, 51, 150] |
learning_rate |
скорость обучения |
float |
0.1 |
[0.0, inf) |
.01 |
[.05, .075, .1, .15, .2] |
n_estimators |
количество деревьев |
int |
100 |
[1, inf) |
25 |
[100, 150, 250, 500, 700] |
Находим точные значения гиперпараметров
Теперь мы снова «размораживаем» гиперпараметры max_depth и max_feature и ищем их оптимальные значения. При этом значения остальных 8 гиперпараметров равны ранее найденным оптимальным значениям. Однако оптимум гиперпараметров max_depth и max_feature мы ищем уже не на всей сетке, а на сокращенной.
В качестве центрального узла сокращенной сетки мы возьмем найденное ранее оптимальное значение этого гиперпараметра. От него отложим два базовых пункта влево и два базовых пункта вправо. Если слева (справа) сетка выйдет за границы гиперпараметра, то надо сместить ее вправо (влево) так, чтобы все узлы располагались в области допустимых значений. Теперь находим значения функции на сокращенной сетке. Если максимум находится с левого (правого) края, нужно сдвинуть сетку на 2 базовых пункта влево (вправо), но не выходя за границы допустимых значений. Повторяем это, пока максимум не будет во внутреннем узле сетки. Этот узел мы объявляем новым оптимальным значением гиперпараметра.
Найдя новые оптимальные значения для гиперпараметров max_depth и max_feature, фиксируем их и приступаем к поиску новых оптимальных значений для subsample и min_samples_split, сохранив остальным 6 гиперпараметрам ранее найденные оптимальные значения. В итоге мы получим новый набор уточненных оптимальных значений для всех гиперпараметров.
После этого мы снова начинаем поиск оптимальных значений для max_depth и max_features, затем для второй пары гиперпараметров, затем для третьей и т. д. Повторяем поиск, пока найденные оптимальные значения не прекратят изменяться. Тогда мы поймем, что нашли глобальный оптимум функции — точнее, что истинный оптимум функции находится не далее одного базового пункта от найденной нами точки по каждому из параметров.
На практике для нахождения оптимума требуется максимум три прохода: первичный на стартовой сетке и два уточняющих на сокращенной сетке. Можно даже ограничиться только одним проходом – если мы строим не финальную модель, а модель для сокращения количества признаков.
Теперь разберем соответствующий код. Мы вручную задаем стартовую сетку для поиска оптимума гиперпараметров и формируем переменную tasks – список кортежей, состоящих из 3 чисел: двух значений гиперпараметров и номера блока.
# задаем сетку для первого параметра вручную
alphas = [1, 2, 3, 5, 7]
# задаем сетку для второго параметра вручную
gammas = [1, 5, 28, 148, 784]
tasks = []
# создаем наборы: (параметр 1, параметр 2, номер блока)
for alpha in alphas:
for gamma in gammas:
for fold in range(N_FOLDS):
tasks.append((alpha, gamma, fold))Количество элементов в списке tasks равно количеству запрошенных у системы экзекьюторов. Каждый кортеж мы передадим своему экзекьютору для проведения параллельных расчетов. Проверим данные, которые мы передадим экзекьюторам.
print(tasks)Вот что мы получим:
[(1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 1, 4), (1, 5, 0), (1, 5, 1), (1, 5, 2), (1, 5, 3), (1, 5, 4), (1, 28, 0), (1, 28, 1), (1, 28, 2), (1, 28, 3), (1, 28, 4), (1, 148, 0), (1, 148, 1), (1, 148, 2), (1, 148, 3), (1, 148, 4), (1, 784, 0), (1, 784, 1), (1, 784, 2), (1, 784, 3), (1, 784, 4), (2, 1, 0), (2, 1, 1), (2, 1, 2), (2, 1, 3), (2, 1, 4), (2, 5, 0), (2, 5, 1), (2, 5, 2), (2, 5, 3), (2, 5, 4), (2, 28, 0), (2, 28, 1), (2, 28, 2), (2, 28, 3), (2, 28, 4), (2, 148, 0), (2, 148, 1), (2, 148, 2), (2, 148, 3), (2, 148, 4), (2, 784, 0), (2, 784, 1), (2, 784, 2), (2, 784, 3), (2, 784, 4), (3, 1, 0), (3, 1, 1), (3, 1, 2), (3, 1, 3), (3, 1, 4), (3, 5, 0), (3, 5, 1), (3, 5, 2), (3, 5, 3), (3, 5, 4), (3, 28, 0), (3, 28, 1), (3, 28, 2), (3, 28, 3), (3, 28, 4), (3, 148, 0), (3, 148, 1), (3, 148, 2), (3, 148, 3), (3, 148, 4), (3, 784, 0), (3, 784, 1), (3, 784, 2), (3, 784, 3), (3, 784, 4), (5, 1, 0), (5, 1, 1), (5, 1, 2), (5, 1, 3), (5, 1, 4), (5, 5, 0), (5, 5, 1), (5, 5, 2), (5, 5, 3), (5, 5, 4), (5, 28, 0), (5, 28, 1), (5, 28, 2), (5, 28, 3), (5, 28, 4), (5, 148, 0), (5, 148, 1), (5, 148, 2), (5, 148, 3), (5, 148, 4), (5, 784, 0), (5, 784, 1), (5, 784, 2), (5, 784, 3), (5, 784, 4), (7, 1, 0), (7, 1, 1), (7, 1, 2), (7, 1, 3), (7, 1, 4), (7, 5, 0), (7, 5, 1), (7, 5, 2), (7, 5, 3), (7, 5, 4), (7, 28, 0), (7, 28, 1), (7, 28, 2), (7, 28, 3), (7, 28, 4), (7, 148, 0), (7, 148, 1), (7, 148, 2), (7, 148, 3), (7, 148, 4), (7, 784, 0), (7, 784, 1), (7, 784, 2), (7, 784, 3), (7, 784, 4)]Теперь мы сформируем эстиматор. Это просто: мы задаем первые два гиперпараметра равными аргументам функции, а остальные пока закомментируем — их значения будут установлены по умолчанию. Также мы определим стартовое значение генератора случайных чисел, чтобы обеспечить повторяемость результатов.
def model_estimator(alpha, gamma):
""" Принимает гиперпараметры, возвращает
оценщик соответствующей модели. Прочие
гиперпараметры вручную вводятся прямо в текст
функции"""
estimator = GradientBoostingClassifier(max_depth=alpha,
max_features=gamma,
#subsample=.95,
#min_samples_split=.01,
#min_samples_leaf=.01,
#min_weight_fraction_leaf=0,
#min_impurity_decrease=0,
#max_leaf_nodes=150,
#learning_rate=gamma,
#n_estimators=alpha,
random_state=84 # фиксируем стартовое
# значение генератора случайных чисел,
# чтобы иметь повторяемые значения
# оценщика функции
)
return estimatorА теперь немного сложнее: мы создаем на Python функцию, которая будет передана каждому экзекьютору. Она выполняет следующие действия:
получает тройку чисел в качестве аргументов (пару значений гиперпараметров и номер блока);
на основе номера блока выделяет из одинаковых данных, которые передаются всем экзекьюторам (broadcast_train_features и broadcast_train_labels), тренировочный и валидационный блоки в зависимости от полученного номера блока;
формирует эстиматор на основе полученной пары значений гиперпараметров (остальные значения гиперпараметров фиксированы);
тренирует этот эстиматор на тренировочном блоке;
оценивает качество модели, применяя эстиматор на валидационном блоке и сравнивая предсказанные и истинные значения;
возвращает четверку значений — рассчитанную оценку качества и три входных параметра.
На последнем пункте остановимся особо. В обычном цикле Python нам не нужно включать входные аргументы в выход функции. Мы и так можем понять, какие аргументы получила функция. Но в Apache Spark «под капотом» обрабатываются наборы RDD (наборы ключ-значение). Каждый экзекьютор обрабатывает свою часть набора и возвращает результат. Мы не знаем, что получил на входе конкретный экзекьютор; нам доступен только результат его вычислений. Поэтому единственный способ сопоставить входные и выходные данные — прямо включить входные данные в состав выходных.
def train_model(alpha_par, gamma_par, fold):
"""
Принимает значения двух гиперпараметров и индекс
валидационного блока. Тренирует модель с этими
гиперпараметрами, используя указанный блок для
валидации, а прочие блоки - как тренировочные.
Возвращает значение индекса Джини для валидационного
блока, а также входные параметры.
"""
# читаем набор данных, передаваемый всем узлам SPARK
loc_train_features = broadcast_train_features.value
loc_train_labels = broadcast_train_labels.value
# первоначально - пустые значения
train_idx = []
val_idx = []
fld = 0
# определяем, какие наблюдения попадают в тренировочные блоки,
# а какие - в валидационный блок (индекс этого блока является
# входным параметром функции)
for train_id, val_id in kf.split(loc_train_features):
# перебираем все разбиения подряд
if fld == fold: # если номер блока равен входящему параметру
# разделяем индексы на тренировочный и валидационный наборы
# и выходим из цикла
train_idx = train_id
val_idx = val_id
break
# если еще в цикле, увеличиваем номер блока
fld += 1
# формируем тренировочный и валидационный наборы на основе
# созданных в цикле индексов
X_train = loc_train_features[train_idx]
X_val = loc_train_features[val_idx]
y_train = loc_train_labels[train_idx]
y_val = loc_train_labels[val_idx]
# получаем оценщик модели с данными гиперпараметрами
model_est = model_estimator(alpha_par, gamma_par)
try:
# тренируем модель и рассчитываем индекс Джини на
# валидационном блоке
model_est.fit(X_train, y_train)
predict = model_est.predict_proba(X_val)[:, 1]
score = 2 * roc_auc_score(y_val, predict) - 1
except:
# если не можем натренировать модель, обнуляем score
score = 0
return score, alpha_par, gamma_par, foldТеперь сформируем тот самый RDD-набор из троек чисел и распараллелим его для вычисления на 125 узлах.
# на основе наборов (параметры - номер блока) создаем набор RDD
tasksRDD = sc.parallelize(tasks, numSlices=len(tasks))
print(f"Количество партиций в наборе RDD: {tasksRDD.getNumPartitions()}")Получаем:
Количество партиций в наборе RDD: 125Объявим, что тренировочный набор данных должен быть передан на каждый из 125 узлов перед началом вычислений.
# передаем всем вычислительным узлам SPARK
# одинаковый набор данных (тренировочный набор независимых переменных
# и тренировочные метки)
broadcast_train_features = sc.broadcast(train_features)
broadcast_train_labels = sc.broadcast(train_labels)Стартуем основной блок вычислений. Вот она, магия Apache Spark: мы используем нашу функцию, чтобы обработать каждую тройку чисел из набора RDD и получить для этой тройки результат. Каждую тройку обрабатывает свой экзекьютор. В ходе обработки мы привлекаем набор данных, переданный каждому экзекьютору. Обработка тройки чисел означает построение для них отдельной модели и оценку качества построенной модели.
Еще одной спецификой Apache Spark являются так называемые отложенные вычисления. Вычисления не производятся сразу при поступлении команды, а накапливаются, формируясь в цепочку, в рамках которой происходит внутренняя оптимизация. Команда .cache() дает старт вычислениям.
# на каждом вычислительном узле рассчитываем итоговую функцию
# для одного значения гиперпараметра alpha, одного значения гиперпараметра gamma
# и одного номера тестового блока (4 остальных блока составляют тренировочное множество)
# для этого используем RDD.map, параметры передаем через лямбда-функцию
score_params = tasksRDD.map(lambda alpha_fold: train_model(
alpha_fold[0], alpha_fold[1], alpha_fold[2]))
# кэшируем результат
score_params.cache()
# считаем число результатов: оно должно быть равно
# числу узлов
print(f"Количество результатов: {score_params.count()}")Получаем:
Количество результатов: 125Только что пройденный нами путь формирования данных и расчетов в виде схемы:
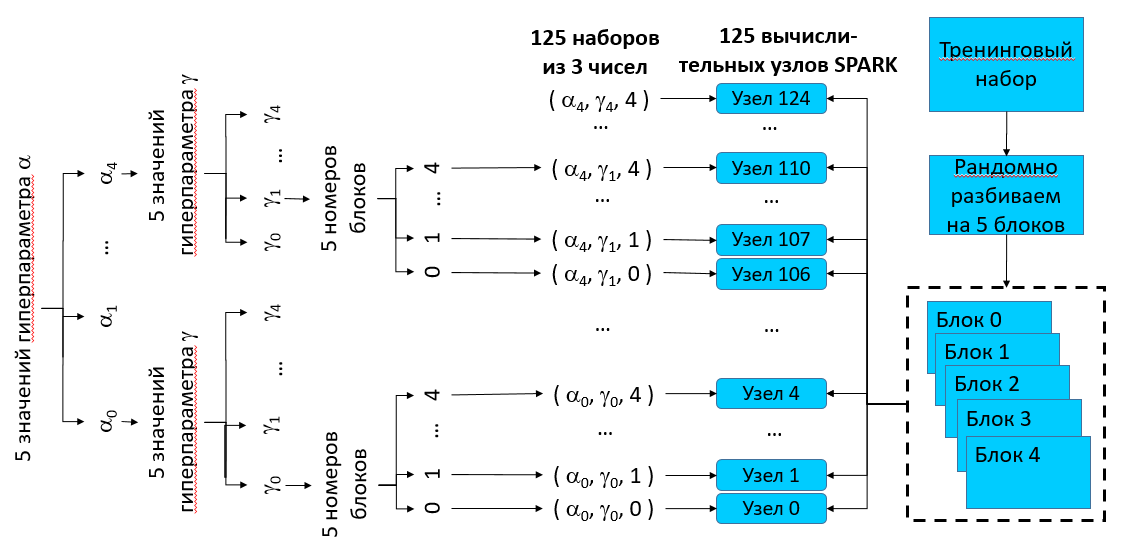
Итак, расчет закончен. Теперь необходимо очистить память от набора данных, переданных всем экзекьюторам.
broadcast_train_features.unpersist()
broadcast_train_labels.unpersist()Собираем данные со всех узлов в список кортежей.
# выделяем компоненты кортежа, который является результатом
# итоговой функции.
# собираем результаты вычислений, используя map.
# собираем данные от всех исполнителей
all_scores = score_params.map(lambda x: (
x[0], x[1], x[2], x[3])).collect()Формируем на его основе объект pandas DataFrame.
# преобразуем набор результатов в DataFrame
all_scores_df = pd.DataFrame(all_scores,
columns=['score', 'alpha',
'gamma', 'num'])Усредняем результаты по разным валидационным блокам.
# выполняем кросс-валидацию: усредняем результаты
# для одинаковых наборов параметров
# по всем вариантам разбиений на блоки
grouped_scores = all_scores_df.groupby(
['alpha', 'gamma'])['score'].mean()
# трансформируем результат из Series в DataFrame
grouped_scores = grouped_scores.to_frame()Формируем сводную таблицу, в которой названия столбцов – один параметр, индексы строк – второй, а значения в ячейках – оценка качества соответствующей модели.
# формируем сводную таблицу,
# где первый параметр - по столбцам,
# а второй - по строкам
pvt_tbl = grouped_scores.pivot_table(values='score',
index='alpha',
columns='gamma')Визуализируем таблицу с помощью библиотеки sns.
# визуализация помогает находить максимум
corr_matr = plt.figure( figsize=(18, 7) );
sns.heatmap(pvt_tbl, annot=True, fmt='.3g');Иногда для поиска оптимальных параметров помогает усреднение значений по одному из параметров.
pvt_tbl.mean()
pvt_tbl.T.mean()Действия по сбору параметров и последующей визуализации в виде схемы:
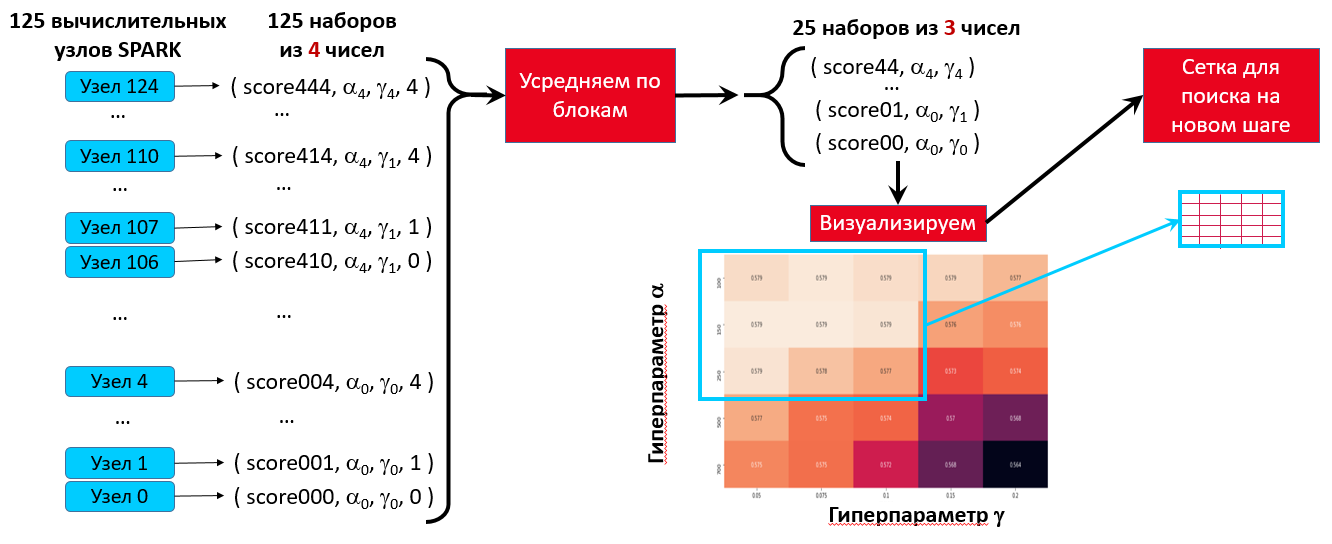
Вот и весь цикл для поиска оптимальных значений гиперпараметров.
Как это выглядит на практике
По шагам рассмотрим поиск значений гиперпараметров max_depth и max_features.
Шаг 1. После поиска на стандартной стартовой сетке получим результат:

Шаг 2. Поскольку максимум расположен на нижнем краю сетки, передвинем ее вниз и получим:

Шаг 3. Еще раз смещаем сетку вниз:

Шаг 4. Теперь по вертикали максимум попадает в сетку. Сократим сетку по горизонтали:

Шаг 5. Снова сокращаем сетку по горизонтали и получаем:

Шаг 6. Еще раз сокращаем сетку по горизонтали:

Шаг 7. В последний раз сокращаем сетку по горизонтали:

Теперь по горизонтали величина сетки составляет 1 базовый пункт. Мы достигли максимального уровня уточнения сетки и еще более мелкой делать ее уже не будем (в данном случае и не смогли бы – параметр max_features является целым числом).

Шаг 8. Максимум снова оказался на краю сетки – смещаем ее вниз и получаем финальные оптимальные значения гиперпараметров: max_depth = 12, max_features = 13.
Действуя по описанной выше схеме, мы осуществим поиск оптимальных значений для всех гиперпараметров и в итоге получим следующий набор: max_depth=12, max_features=13, subsample=.95, min_samples_split=.01, min_samples_leaf=.01, min_weight_fraction_leaf=0, min_impurity_decrease=0, max_leaf_nodes=150, learning_rate=.2, n_estimators=418.
Раньше мы использовали оценки качества модели, сформированные на валидационных блоках. Проверим наши расчеты на тестовой выборке.
# устанавливаем лучшие значения двух последних гиперпараметров
est = model_estimator(418, .2)
# подгоняем на всем тренировочном наборе
est.fit(train_features, train_labels)
# предсказываем на тренировочном и тестовом наборах
predict_tr = est.predict_proba(train_features)[:, 1]
predict_ts = est.predict_proba(test_features)[:, 1]
# счет в Джини на тренировочном и тестовом наборах
score_tr = 2 * roc_auc_score(train_labels, predict_tr) - 1
score_ts = 2 * roc_auc_score(test_labels, predict_ts) – 1
print(f"Счет на тренировочном наборе: {score_tr}, счет на тестовом наборе: {score_ts}")Получаем:
Счет на тренировочном наборе: 1.0, счет на тестовом наборе: 0.9898255961248086Сокращаем число признаков
Напомним, что в начале нашего расчета, чтобы данные уместились в памяти, мы сократили тренировочную выборку в 10 раз. Пришло время увеличить ее обратно. Для этого нужно пропорционально сократить число признаков. Итак, найдем признаки, нерелевантные для нашей задачи, и отбросим их. Искать будем с помощью встроенной процедуры feature_importances_.
# важность признаков
feat_imp = est.feature_importances_Визуализируем важность признаков.
# визуализируем важность признаков
feat_image = feat_imp.copy()
feat_image.resize(28, 28)
plt.imshow(feat_image, cmap='magma')
# два признака доминируют, визуализация бледная
# визуализируем все признаки, важность которых
# превышает 0.1%
feat_image1 = feat_image.copy()
feat_image1[feat_image1 < .001] = 0
feat_image1[feat_image1 > 0] = 1
plt.imshow(feat_image1)Получаем:


Отсортируем переменные по убыванию важности признаков и сохраним результаты.
# создаем DataFrame на основе списка переменных
feat_imp_df = pd.DataFrame(var_list, columns=['feature'])
# важность каждой переменной (признака) в процентах
feat_imp_df['importance'] = 100 * feat_imp
# сортируем по убыванию важности
feat_imp_df = feat_imp_df.sort_values(
by='importance', ascending=False)
# 20 самых важных признаков
feat_imp_df.head(20)
# падение важности от номера признака
plt.plot(feat_imp_df.importance.values, linewidth=3);
plt.xlabel('Номер признака (отсортированного по убыванию важности)', fontsize=16);
plt.ylabel('Важность признака', fontsize=16);
plt.tick_params(labelsize=16)
# сохраняем важности признаков
feat_imp_df.to_csv(f"feature_importance_{feat_imp_df.shape[0]}.csv",
index=False)Получаем:
feature |
importance |
|
738 |
738 |
4.913447426 |
744 |
744 |
4.374967678 |
376 |
376 |
3.719616905 |
713 |
713 |
3.0610702 |
238 |
238 |
2.766689731 |
156 |
156 |
2.555693129 |
519 |
519 |
2.321398591 |
399 |
399 |
2.190660314 |
229 |
229 |
2.174695007 |
260 |
260 |
2.107684541 |
204 |
204 |
2.093190894 |
268 |
268 |
2.058593335 |
152 |
152 |
2.040364041 |
598 |
598 |
2.015834468 |
430 |
430 |
1.917614728 |
378 |
378 |
1.897595208 |
179 |
179 |
1.741610272 |
345 |
345 |
1.607934333 |
297 |
297 |
1.544449307 |
461 |
461 |
1.538421529 |

Не забываем завершить сеанс Apache Spark:
spark.stop()Окончательный подбор признаков
Теперь нам надо открыть новый сеанс Apache Spark, загрузить полученные на предыдущем шаге результаты, удалить из выборки все признаки, важность которых равна 0, увеличить тренировочную выборку — рассматривать не каждое десятое, а, например, каждое второе наблюдение — и вновь проделать описанный выше цикл.
На третьем цикле мы еще больше сокращаем количество признаков, отбрасывая те их них, важность которых больше 0, но очень мала. Наша цель — добиться того, чтобы вся тренировочная выборка вошла в память. Найденные для этого случая оптимальные значения гиперпараметров можно считать финальной моделью.
На этом пути нас поджидает большая неприятность: набор данных никак не хочет помещаться в память системы, и Apache Spark падает, не предоставив результат вычислений.
Если Apache Spark упал один раз, рекомендуется просто повторить цикл вычислений — обычно в следующий раз все будет в порядке. Если Apache Spark падает несколько раз подряд, надо сохранить текущие данные, остановить сеанс Spark, перезагрузить ядро и выполнить вычисления снова. Если это не помогает, придется перейти к поиску значений гиперпараметров на одномерной сетке. Это потребует от нас всего 25 экзекьюторов, но зато каждому можно выделить 60 Гбайт памяти.
Подбор значений гиперпараметров на одномерной сетке осуществляется точно так же, как и на двумерной, только за один шаг ищется оптимальное значение одного гиперпараметра.
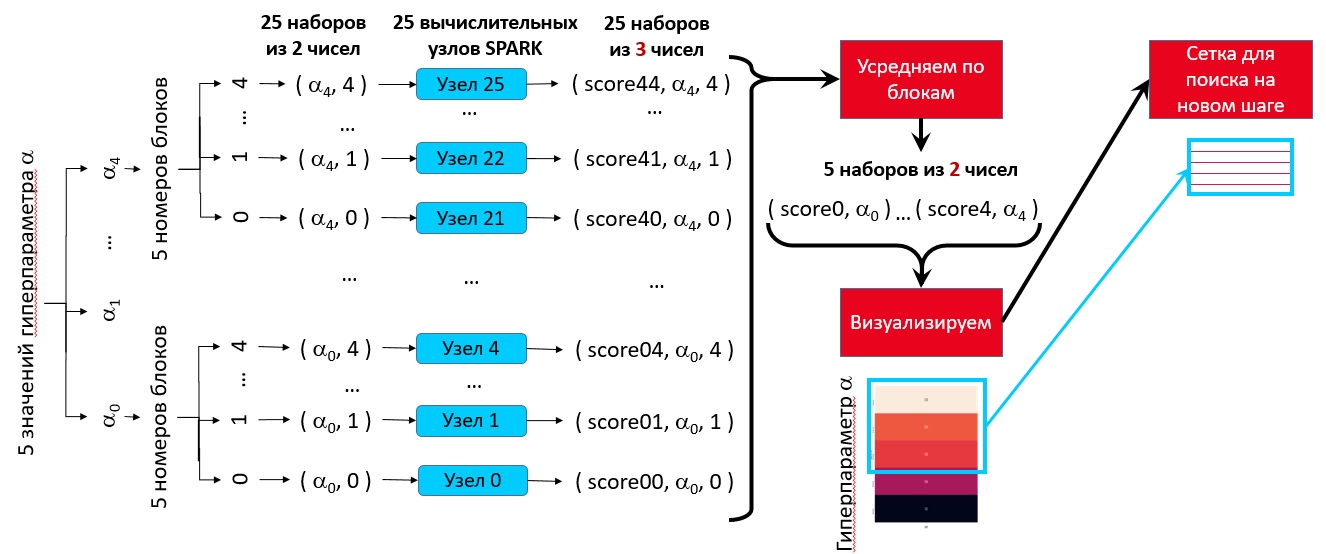
Полный код поиска гиперпараметров для одномерного варианта
# стандартные импорты
import pickle
import numpy as np
import pandas as pd
from tqdm import tqdm
# импорты для SPARK
import os
import sys
import subprocess
# специфические импорты для модели
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
from sklearn.ensemble import GradientBoostingClassifier
# импорт matplotlib и параметры изображения
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (18,7)
plt.rcParams['axes.grid']=True
# персональные данные
MY_OFFICE_ID = 'XXXXXX_confidential_information'
# будем проводить 5-блочную кросс-валидацию
N_FOLDS = 5
## Вспомогательные функции
def calc_grid(alpha_strt, alpha_end, type_res='int'):
"""Рассчитывает узлы сетки для поиска оптимального
значения гиперпараметра. Выдает 5 узлов от
минимального (alpha_strt) до максимального (alpha_end) значения
параметра. Если type_res имеет значение 'int',
то числа будут целые, иначе - типа float
"""
if alpha_strt > 0:
# расчет сетки для случая, если минимальное значение
# больше 0
fctr = (alpha_end / alpha_strt) ** .25
par_vec = alpha_strt * np.array(
[fctr ** i for i in range(5)])
else:
# расчет сетки для случая, если минимальное значение
# равно 0
par_vec = alpha_end * np.array(
[0, .05, .1, .5, 1])
if type_res == 'int':
# округление значений сетки до целых
par_vec = np.round(par_vec, 0).astype(int)
return par_vec
## Подготовка данных для процедуры
# загружаем изображения
train_df = pd.read_csv('mnist/train.csv')
test_df = pd.read_csv('mnist/test.csv')
# загружаем метки
y_train = pd.read_csv('mnist/train_labels.csv')
y_test = pd.read_csv('mnist/test_labels.csv')
# размерность данных
print(train_df.shape, test_df.shape, y_train.shape, y_test.shape)
# читаем файл с важностью признаков,
# подготовленный на прошлом шаге
feature_importance_df = pd.read_csv(
'feature_importance_120.csv')
# формируем список признаков, важность которых превосходит 0.4%
feature_importance_lst = feature_importance_df.loc[
feature_importance_df.importance > .4, 'feature'].to_list()
feature_importance_lst = [
str(f_i_l) for f_i_l in feature_importance_lst]
# ВНИМАНИЕ!!! Данные ОБЯЗАТЕЛЬНО преобразовать в формат
# матриц/векторов numpy, данные в формате pandas
# DataFrame вызовут сложно отслеживаемую ошибку
# отбираем только те признаки, которые входят в список
train1 = train_df[feature_importance_lst].values
test1 = test_df[feature_importance_lst].values
train_labels = y_train.values
train_labels = train_labels.ravel()
test_labels = y_test.values
test_labels = test_labels.ravel()
# размерность данных
print(train1.shape, test1.shape, train_labels.shape, test_labels.shape)
# сокращаем количество наблюдений,
# но в 2 раза (а не в 10 как в прошлый раз),
# мы можем себе это позволить, т.к. мы сократили
# число переменных в 6 раз
train_features = train1[:,:]
test_features = test1[:,:]
train_labels = train_labels[:]
test_labels = test_labels[:]
# размерность данных
print(train_features.shape, test_features.shape, train_labels.shape, test_labels.shape)
# настройки перед запуском SPARK - зависят от вашего вычислительного кластера
p = subprocess.Popen(f"/usr/bin/id {MY_OFFICE_ID} -u",
shell=True,
stdout=subprocess.PIPE,
stderr=subprocess.STDOUT)
id_str = p.stdout.readline().decode("utf-8").replace("\n", "")
os.environ["JAVA_TOOL_OPTIONS"] = "-Djava.security.krb5.conf=/etc/krb5.conf.d/krb5.conf"
os.environ["KRB5_CONFIG"] = "/etc/krb5.conf.d/krb5.conf"
os.environ["KRB5CCNAME"] = f"/tmp/krb5cc_{id_str}_{id_str}"
os.environ['ARROW_LIBHDFS_DIR'] = '/usr/hdp/3.1.4.0-315/hadoop/lib/native/'
# настройки перед запуском SPARK - зависят от вашего вычислительного кластера
spark_home = "/opt/odpp/spark_3.2.0/"
SHELL_PATH = os.path.join(spark_home,'python/pyspark/shell.py')
os.environ ['SPARK_HOME'] = spark_home
sys.path.insert(0, os.path.join(spark_home, 'python'))
sys.path.insert(0, os.path.join(spark_home, 'python/lib/py4j-0.10.7-src.zip'))
os.environ ['PYSPARK_PYTHON'] = '/usr/local/basement/Python-3.7.4/bin/python3.7'
os.environ ['HADOOP_CONF_DIR'] = '/usr/hdp/current/hadoop-client/conf/'
os.environ ['PYTHONPATH'] = '/opt/odpp/spark_3.2.0/python/lib/py4j-0.10.9.2-src.zip:/opt/odpp/spark_3.2.0/python'
os.environ ['PYTHONSTARTUP'] = '/opt/odpp/spark_3.2.0/python/pyspark/shell.py'
# важно: запрашиваем количество экзекьюторов, равное числу узлов сетки (5),
# умноженному на число блоков (N_FOLDS), запрашиваем на каждый узел
# по 60 Гбайт памяти против 12 Гбайт в прошлый раз, т.к. количество узлов
# сократилось в 5 раз за счет перехода на одномерную сетку
os.environ ['PYSPARK_SUBMIT_ARGS'] = f" --master yarn --deploy-mode client --num-executors {5 * N_FOLDS} --executor-cores 1 --executor-memory 60G pyspark-shell"
%%time
# запускаем SPARK
exec(open(SHELL_PATH).read())
# параметры сессии SPARK
spark
# присваиваем значение SPARK контекста
sc = spark.sparkContext
## Основной цикл подбора параметров
### Разбиваем набор на блоки
# разбиваема все наблюдения случайным образом
# на N_FOLDS блоков
kf = KFold(n_splits=N_FOLDS)
# проверяем разбиение на блоки и размерность данных
i = 0 # номер блока
for train_id, val_id in kf.split(train_features):
print('Блок {} тренировочный, размерность: {}'.format(i, train_features[train_id].shape))
print('Блок {} валидационный, размерность: {}'.format(i, train_features[val_id].shape))
i += 1
### Формируем наборы параметров
# РЕКОМЕНДУЕМ!!!
# стартовые значения сеток при подборе
# гиперпараметров для GradientBoostingClassifier:
#--------------------------+---------------+-------------+-----------------+-------------------------------------
# Гиперпараметр | Тип данных | Значение по | Границы | Рекомендуемая
# | | умолчанию | изменения | стартовая сетка
#--------------------------+---------------+-------------+-----------------+-------------------------------------
# max_depth | int | 3 | [1, inf) | [1, 2, 3, 5, 7]
# max_features | int or float | None | [1, n_features) | calc_grid(1, n_features, 'int')
# subsample | float | 1.0 | (0.0, 1.0] | [.1, .8, .9, .95, 1]
# min_samples_split | float | | (0.0, 1.0] | [.01, .1, .3, .5, 1]
# min_samples_leaf | float | | (0.0, 1.0) | [.01, .1, .3, .5, .99]
# min_weight_fraction_leaf | float | 0.0 | [0.0, 0.5] | [0, .05, .1, .2, .5]
# min_impurity_decrease | float | 0.0 | [0.0, inf) | [0, .05, .1, .7, 3]
# max_leaf_nodes | int | None | [2, inf) | [2, 6, 17, 51, 150]
# learning_rate | float | 0.1 | [0.0, inf) | [.05, .075, .1, .15, .2]
# n_estimators | int | 100 | [1, inf) | [100, 150, 250, 500, 700]
#--------------------------+---------------+-------------+-----------------+-------------------------------------
# используем функцию для расчета сетки
# подбора гиперпараметров
calc_grid(19, 49, 'int')
# задаем сетку для ЕДИНСТВЕННОГО параметра вручную
alphas = [750, 775, 800, 825, 850]
tasks = []
# создаем наборы: (параметр, номер блока)
for alpha in alphas:
for fold in range(N_FOLDS):
tasks.append((alpha, fold))
# проверяем наборы (параметр - номер блока)
print(tasks)
### Готовим модель
def model_estimator(alpha):
""" Принимает гиперпараметры, возвращает
оценщик соответствующей модели. Прочие
гиперпараметры вручную вводятся прямо в текст
функции"""
estimator = GradientBoostingClassifier(max_depth=9, #7
max_features=20, #19,
subsample=1,#1
min_samples_split=.01,#.01,
min_samples_leaf=.01,#.01,
min_weight_fraction_leaf=0,#0,
min_impurity_decrease=0,#0
max_leaf_nodes=61, #51,
learning_rate=.26, #.26,
n_estimators=alpha,#800,
random_state=84
)
return estimator
def train_model(alpha_par, fold):
"""
Принимает значение гиперпараметра и индекс
валидационного блока. Тренирует модель с этими
гиперпараметрами, используя указанный блок для
валидации, а прочие блоки - как тренировочные.
Возвращает значение индекса Джини для валидационного
блока, а также входные параметры.
"""
# читаем набор данных, передаваемый всем узлам SPARK
loc_train_features = broadcast_train_features.value
loc_train_labels = broadcast_train_labels.value
# первоначально - пустые значения
train_idx = []
val_idx = []
fld = 0
# определяем, какие наблюдения попадают в тренировочные блоки,
# а какие - в валидационный блок (индекс этого блока является
# входным параметром функции)
for train_id, val_id in kf.split(loc_train_features):
# перебираем все разбиения подряд
if fld == fold: # если номер блока равен входящему параметру
# разделяем индексы на тренировочный и валидационный наборы
# и выходим из цикла
train_idx = train_id
val_idx = val_id
break
# если еще в цикле, увеличиваем номер блока
fld += 1
# создаем тренировочный и валидационный наборы
X_train = loc_train_features[train_idx]
X_val = loc_train_features[val_idx]
y_train = loc_train_labels[train_idx]
y_val = loc_train_labels[val_idx]
# получаем оценщик модели с данными гиперпараметрами
model_est = model_estimator(alpha_par)
try:
# тренируем модель и рассчитываем индекс Джини на
# валидационном блоке
model_est.fit(X_train, y_train)
predict = model_est.predict_proba(X_val)[:, 1]
score = 2 * roc_auc_score(y_val, predict) - 1
except:
# если не можем натренировать модель, обнуляем скор
score = 0
return score, alpha_par, fold
### Готовим набор RDD
print(f"Количество узлов: {len(tasks)}")
# на основе наборов (параметр - номер блока) создаем набор RDD
tasksRDD = sc.parallelize(tasks, numSlices = len(tasks))
print(f"Количество партиций в наборе RDD: {tasksRDD.getNumPartitions()}")
### Разделяем набор для всех узлов
# передаем всем вычислительным узлам SPARK
# одинаковый набор данных (тренировочный набор независимых переменных
# и тренировочные метки)
broadcast_train_features = sc.broadcast(train_features)
broadcast_train_labels = sc.broadcast(train_labels)
### Основной расчет
%%time
# на каждом вычислительном узле рассчитываем итоговую функцию
# для одного значения гиперпараметра alpha
# и одного номера тестового блока (4 остальных блока составляют тренировочное множество)
# для этого используем RDD.map, параметры передаем через лямбда-функцию
score_params = tasksRDD.map(lambda alpha_fold: train_model(
alpha_fold[0], alpha_fold[1]))
# кешируем результат
score_params.cache()
# считаем число результатов: оно должно быть равно
# числу узлов
print(f"Количество результатов: {score_params.count()}")
### Очищаем набор данных, передаваемых всем узлам
broadcast_train_features.unpersist()
broadcast_train_labels.unpersist()
### Собираем результаты со всех узлов
%%time
# выделяем компоненты кортежа, который является результатом
# итоговой функции.
# собираем результаты вычислений, используя map.
# собираем данные от всех исполнителей
all_scores = score_params.map(lambda x: (
x[0], x[1], x[2])).collect()
### Проверяем наличие результатов
# SPARK склонен падать, проверяем, что все рассчиталось
all_scores
### Формируем сводную таблицу
# преобразуем набор результатов в DataFrame
all_scores_df = pd.DataFrame(all_scores,
columns=['score', 'alpha', 'num'])
# выполняем кросс-валидацию: усредняем результаты
# для одинаковых наборов параметров
# по всем вариантам разбиений на блоки
grouped_scores = all_scores_df.groupby(
['alpha'])['score'].mean()
# трансформируем результат из Series в DataFrame
grouped_scores = grouped_scores.to_frame()
# формируем сводную таблицу,
# где первый параметр - по столбцам,
# а второй - по строкам
pvt_tbl = grouped_scores.pivot_table(values='score',
index='alpha')
### Сводная таблица
pvt_tbl
### Визуализируем сводную таблицу
# визуализация помогает находить максимум
corr_matr = plt.figure( figsize=(18, 7) )
sns.heatmap(pvt_tbl, annot=True, fmt='.3g')
### Дополнительно - среднее по всей таблице
pvt_tbl.mean()
### Обучаем финальную модель с лучшим набором гиперпараметров
# поскольку это 1 задача, не требующая параллельных
# вычислений, обучаем ее без SPARK
%%time
# устанавливаем лучшие значения последнего гиперпараметра
est = model_estimator(800)
# подгоняем на всем тренировочном наборе
est.fit(train_features, train_labels)
# предсказываем на тренировочном и тестовом наборах
predict_tr = est.predict_proba(train_features)[:, 1]
predict_ts = est.predict_proba(test_features)[:, 1]
# счет в Джини на тренировочном и тестовом наборах
score_tr = 2 * roc_auc_score(train_labels, predict_tr) - 1
score_ts = 2 * roc_auc_score(test_labels, predict_ts) - 1
print(f"Счет на тренировочном наборе: {score_tr}, счет на тестовом наборе: {score_ts}")
### Рассчитаем важность признаков для сокращения количества переменных в модели
# важность признаков
feat_imp = est.feature_importances_
### Отсортируем переменные по падению уровня значимости
# создаем DataFrame на основе списка важности признаков
feat_imp_df = pd.DataFrame(feature_importance_lst, columns=['feature'])
# важность каждой переменной (признака) в процентах
feat_imp_df['importance'] = 100 * feat_imp
# сортируем по убыванию важности
feat_imp_df = feat_imp_df.sort_values(
by='importance', ascending=False)
# 20 самых важных признаков
feat_imp_df.head(20)
# падение важности от номера признака
plt.plot(feat_imp_df.importance.values, linewidth=3);
plt.xlabel('Номер признака (отсортированного по убыванию важности)', fontsize=16);
plt.ylabel('Важность признака', fontsize=16);
plt.tick_params(labelsize=16)
# падение важности от номера признака
plt.plot(feat_imp_df.importance.values, linewidth=3);
plt.xlabel('Номер признака (отсортированного по убыванию важности)', fontsize=16);
plt.ylabel('Важность признака', fontsize=16);
plt.tick_params(labelsize=16)
plt.ylim(0,1)
plt.xlim(40, 60)
# сохраняем важности признаков
feat_imp_df.to_csv(f"feature_importance_{feat_imp_df.shape[0]}.csv",
index=False)
# не забываем закрыть сеанс SPARK
spark.stop()
# проверяем, что сеанс SPARK закрыт
sparkИтак, реализовав одномерный поиск для 120 признаков, в итоге мы приходим к следующему оптимальному набору гиперпараметров: max_depth=7, max_features=41, subsample=1, min_samples_split=.01, min_samples_leaf=.01, min_weight_fraction_leaf=0, min_impurity_decrease=.01, max_leaf_nodes=150, learning_rate=.14, n_estimators=150.
После этого мы сокращаем число признаков до 49. Теперь мы можем использовать тренировочную выборку в полном объеме — она умещается в памяти. Осуществляем поиск оптимальных значений гиперпараметров для этого случая и после первого прохода получаем следующий набор: max_depth=7, max_features=19, subsample=1, min_samples_split=.01, min_samples_leaf=.01, min_weight_fraction_leaf=0, min_impurity_decrease=0, max_leaf_nodes=51, learning_rate=.26, n_estimators=800.
Теперь уточним подобранные гиперпараметры на сокращенной сетке. Получим следующий набор: max_depth=9, max_features=20, subsample=1, min_samples_split=.01, min_samples_leaf=.01, min_weight_fraction_leaf=0, min_impurity_decrease=0, max_leaf_nodes=61, learning_rate=.26, n_estimators=800.
Попытка еще одного прохода по сокращенной сетке показывает, что оптимальные значения гиперпараметров больше не изменяются. Значит, это финальная модель. Она содержит следующие переменные в порядке убывания важности (имя переменной – это номер точки на картинке):
['742', '405', '713', '709', '433', '712', '155', '744', '457', '402', '376', '404', '514', '183',
'428', '401', '297', '378', '154', '374', '373', '430', '569', '511', '377', '345', '483', '206',
'298', '182', '348', '458', '714', '266', '463', '540', '400', '234', '257', '232', '546', '296',
'258', '233', '580', '239', '487', '432', '715']Проверим, какое качество модели мы получили:
print(f"Счет на тренировочном наборе: {score_tr}, счет на тестовом наборе: {score_ts}")Получаем:
Счет на тренировочном наборе: 1.0, счет на тестовом наборе: 0.994431226591679Результат весьма достойный – качество модели на тестовой выборке составляет 99,4 Джини. Неправильно классифицированными оказались 108 объектов из 10 000. Таким образом, точность модели равна 98,92%.
Чему мы научились
В данной статье мы научились подбирать гиперпараметры для модели градиентного бустинга с использованием системы Apache Spark. Результат достигается в несколько раз быстрее, чем при подборе гиперпараметров обычным способом. Для закрепления материала представим общую схему подбора оптимальных гиперпараметров в графическом виде:

Теперь вы всегда можете подобрать гиперпараметры бустинговой модели за один день. Если, конечно, у вас достаточно вычислительных ресурсов.
Что еще можно сделать
Кстати, если ресурсов не хватает или число объектов очень велико, то можно перейти к поиску оптимума на 0-мерной сетке. Тогда подбор гиперпараметров нужно проводить внутри цикла, на каждой итерации цикла рассчитывая качество модели для единственного значения гиперпараметра. Кросс-валидация осуществляется внутри тела цикла с помощью Apache Spark параллельно на 5 узлах (если ресурсов совсем не хватает, то можно на 3).
Такая схема по-прежнему дает значительную экономию времени, более чем в пять раз. Когда вычисления осуществляются для разных значений гиперпараметра, для одного значения они могут занимать значительно больше времени, чем для другого. А общее время вычислений, выполняемых параллельно, определяется самым медленным узлом.
Если параллельно рассчитываются значения для одного и того же параметра на разных разбиениях тренировочной выборки, то время всех вычислений будет примерно одинаковым. Обозначим ti – длительность i-ой итерации цикла. Тогда для общей длины цикла всегда будет выполняться неравенство:
t1 + t2 + t3 + t4 + t5 ≤ 5 * tmax, где tmax = max(t1, t2, t3, t4, t5)
В частности, если t1 < t2 < t3 < t4 < t5, то t1 + t2 + t3 + t4 + t5 < 5 * t5 , то есть вычисления ускоряются более, чем в 5 раз.
Что касается программной реализации поиска на 0-мерной сетке, предлагаем ее читателям в качестве самостоятельного упражнения.


python_man_1993
Так вот же catboost для PySpark: https://catboost.ai/en/docs/installation/spark-installation-pyspark
Зачем реализовывать самому?