Создались условия, чтобы подвести некий итог. Дело в том, что автоматы в SimInTech могут быть инерционными. И это определенно знаменательный факт. Более того, он даже радует своей неожиданностью, опровергая то фактическое неверие, которое к среде было до этого. Но давайте подробнее о том, как это все таки случилось...
В предыдущей статье (см. [1]) была допущена ошибка. С одной стороны, как говорится, это минус, но, как ни странно, это плюс, т.к. ее все же обнаружили. Нет, не те кто, как я полагаю, ставит минусы, а те, кто вникает в прочитанное. И за это хочется сказать последним огромное спасибо. Пусть даже потом они поставят минус. Это их законное право. Но тут хотя бы можно обсудить за что и сделать какие-то выводы. Хотя, как я их называю "минусеры", подобно "санитарам леса" тоже вносят свой посильный вклад в общее дело. Но все же честнее ... глаза в глаза.
Но, однако, в сторону эмоции и разберемся, в чем была проблема, что привело к ошибке и почему от всего этого плюс. Но плюс уже для тех, кто программирует в SimInTech и использует в своей работе автоматы.
Повторим код из предыдущей статьи, содержащий ошибку. Он приведен на рис. 1. Анализируя его, сосредоточимся на коде текущего состояния автомата. Просто потому, что код остальных состояний на текущем шаге среды будет нерабочим.
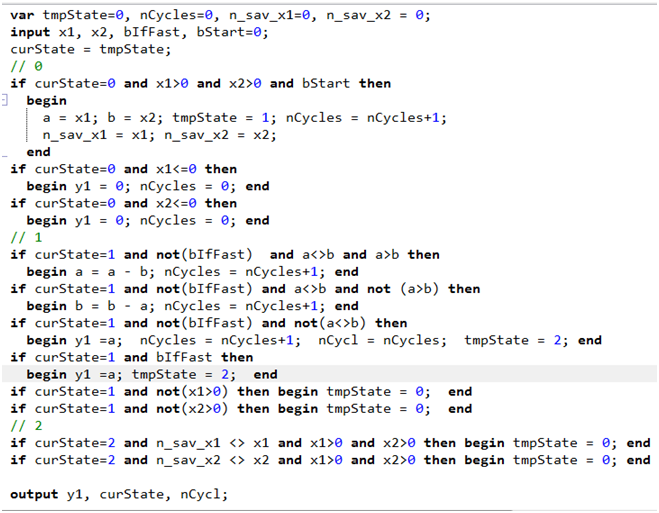
Когда сработал переход из текущего исходного состояния 0 в состояние 1, то изменяется "теневая переменная" состояния автомата - tmpState. Заметим, что только на следующем шаге ее значение будет переписано в переменную текущего состояния curState. Именно такая процедура блокирует код для нового текущего состояния на текущем шаге. Но, как оказалось, это справедливо только по отношению к состоянию, имя которого отличается от имени текущего. И вот тут начинается самое интересное...
Предположим, для текущих значений переменных a и b сработал первый переход a>b. В соответствии с алгоритмом НОД значение большей переменной уменьшается, а к значению счетчика циклов добавится 1. Но если это приведет к тому, что значение переменной a станет меньше b, то следом сработает переход, который уменьшит b, а значение счетчика увеличит еще на 1. Но если так уж случится, что после этого a сравняется с b, то это тут же приведет к срабатыванию еще одного перехода, что приведет к завершению алгоритма. Но при этом значение счетчика увеличится еще раз, а новое текущее состояние (переменная tmpState) станет равным 2. Далее уже в состоянии 2 автомат останется до тех пор, пока не изменится значение входов блока...
Таким образом, в текущем состоянии 1 при определенном соотношении входных параметров за один дискретный шаг может сработать до трех переходов автомата, что, конечно, форменное безобразие, т.к. в теории должен быть только один и только один переход. Тем не менее, эта и подобные ей ситуации могут быть разрешены раз и навсегда очень просто - вставкой оператора exit в конец каждого действия автомата. Проделав подобное, получим следующий код (рис. 2):
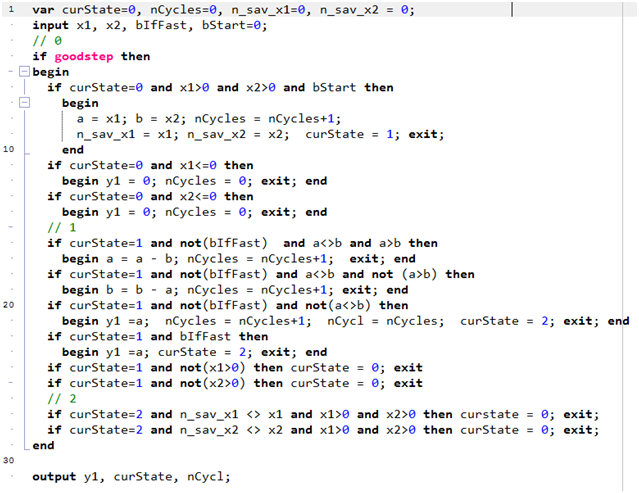
Уф! - проблема решена. Причем легко, просто и весьма надежно. Более того, этот же оператор exit позволяет упростить код автомата, исключив теневую переменную состояния tmpState. Если ранее, как это было выше описано, она была необходима, то теперь в ней нет нужды, т.к. код, который может сработать в случае той же ошибки, "отрезается" естественным образом за счет выхода из блока.
Результат работы схемы, состоящей из трех блоков НОД с входными данными из предыдущей статьи показан на рис. 3.
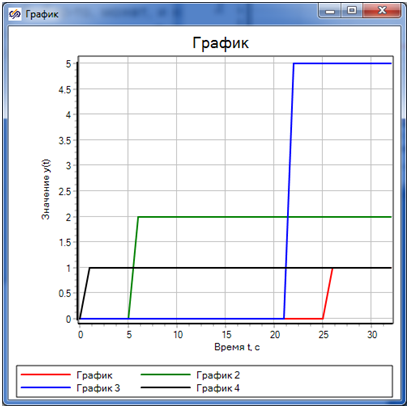
И это уже весьма близко к истине. Но осталась все же еще одна проблема - несоответствие числа исполненных шагов блоков времени их работы (см. ось времени). Эта разница составляет один дискретный шаг для отдельного блока, что составило в конечном итоге привело к опережению на два шага при индикации результата (время работы блоков составляет число шагов среды, равное значению выходной переменной nCycles, помноженное на длительность шага). Сдвиг, что наиболее вероятно, результат отражения графическим блоком текущих значений переменных в начале дискретного шага. Так по замыслу авторов SimInTech, среда "изображает" мгновенность своих вычислений. В реальности такое блокам не под силу. Вычисления по замыслу "создателя" инерционны, а потому в реальной жизни на них всегда тратится то или иное не равное нулю время. Поэтому естественным было бы отображать новые значения переменных по истечении дискретного шага. Но способна ли на это условно "мгновенная" среда SimInTech?
Оказалось - способна. Инерционную задержку можно организовать с помощью стандартного блока среды - "Задержка на шаг интегрирования" из закладки "Нелинейные". С учетом этого можно предложить процедуру создания любого автомата в SimInTech, которая состоит из следующих действий:
1) Представить каждый автомат в форме субмодели;
2) Реализовать отдельно логику автомата (лучше это сделать на внутреннем языке программирования и по описанному шаблону), включив этот блок в субмодель;
3) В рамках субмодели создать порты входа и выхода для соответствующих каналов автомата;
4) Входные каналы автомата напрямую соединить с входными портами субмодели, а между выходными каналами автомата и выходными портами субмодели вставить по одному элементу задержки на шаг.
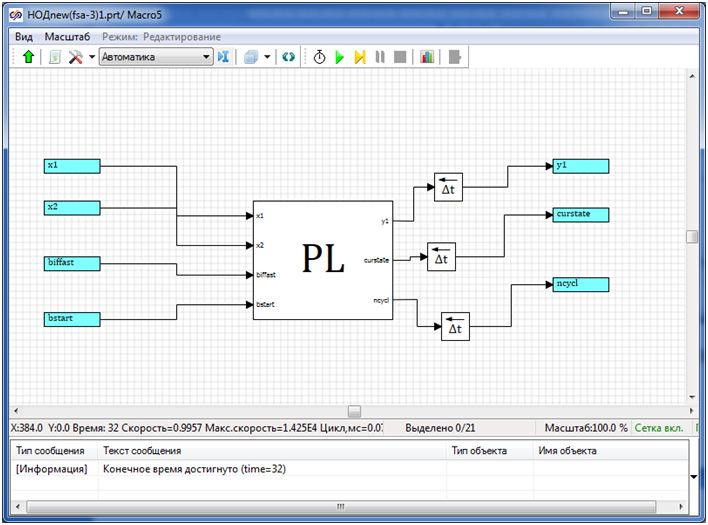
Отвечая описанным выше правилам, исходное решение примет уже несколько иной вид. На структурном уровне оно будет таким, как это показано на рис. 4. Здесь каждый блок НОД представлен субмоделью, каждая из которых имеет вид, представленный на рис. 5.
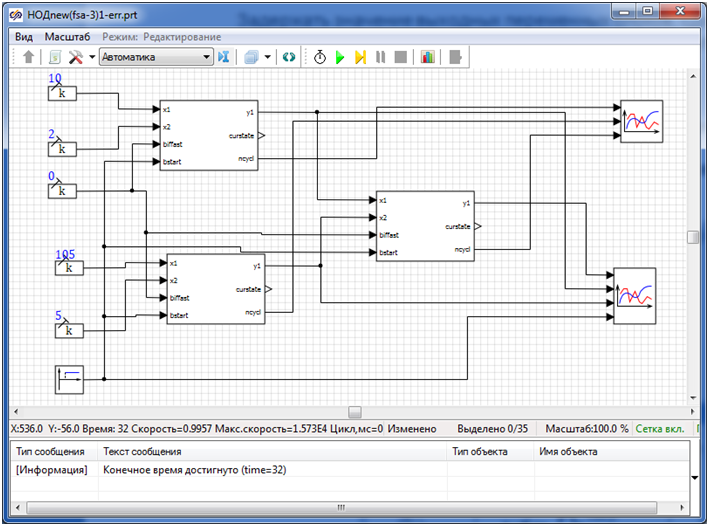
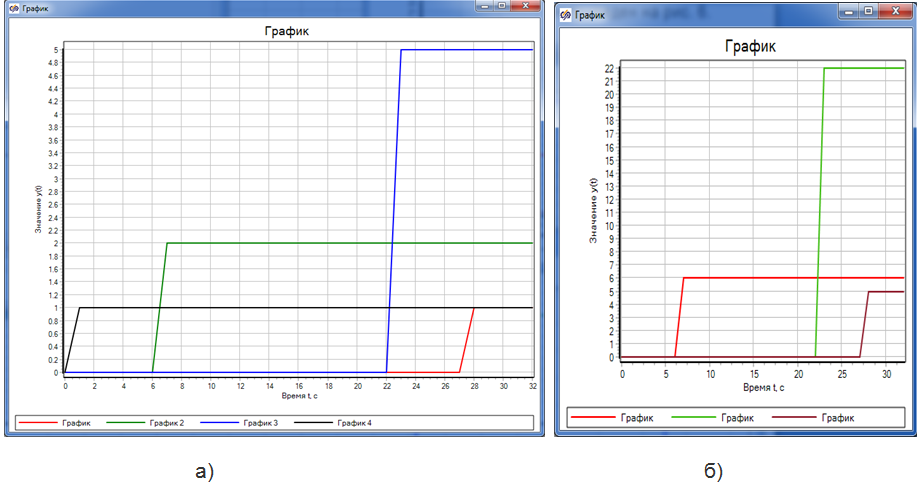
Тестирование уже новой схемы привело к результату, который приведен на рис. 6. Здесь рис. 6а отражает времена вычисления блоков, а рис. 6б - число их рабочих циклов. И вот теперь наконец-то к графикам претензий нет, т.к. значение циклов совпадает с временами работы блоков (сравните с графиками на рис. 4 в [1]). А это все потому, что в этот раз у нас автоматы правильные, т.е. инерционные (подробнее об инерционной модели автомата см в [2]).
Итоги
Выше мы сформулировали правила создания любых автоматов, а на примере алгоритма НОД описали шаблон их кодирования на внутреннем языке SimInTech. Все это в рамках данной среды повышает надежность программирования и увеличивает доверие к результатам работы программ. Если бы раньше им следовать, то столь досадных ошибок допущено бы не было. Как их не было при реализации этого же автомата и этой же схемы в среде ВКПа...
Ну, а я уже чувствую, как, несмотря ни на что, дрожащие от нетерпения ручки моих друзей-минусеров уже тянутся к клавиатуре... Удачи вам, други мои...
Литература
1. Кулинарные шедевры параллелизма. Или что бывает, когда утеряны вкус и обоняние. [Электронный ресурс], Режим доступа: https://habr.com/ru/articles/750244/ свободный. Яз. рус. (дата обращения 30.07.2023).
2. Автоматное программирование: определение, модель, реализация. [Электронный ресурс], Режим доступа: https://habr.com/ru/articles/682422/ свободный. Яз. рус. (дата обращения 30.07.2023).

