Введение
В этой статье я хочу рассказать, как построить матрицу перехода для генератора псевдослучайной последовательности (PRBS - pseudorandom binary sequence). Данная задача особенно актуальная для реализации генератора на ПЛИС, где требуется за минимальное время (один такт) рассчитать как можно больше значений. Также данный метод позволит сократить время перехода на нужное состояние генератора в случае, если расчет производится на процессоре (микроконтроллере).
В этой статье я буду опираться на книгу «on-chip self-test circuit blocks for high-speed applications. ekaterina laskin, 2006» глава «2.3. Parallel PRBS Generators», поэтому данную статью можно считать вольным переводом-пересказом.
Описание задачи
Уже много существует различных статей про генераторы псевдослучайных последовательностей, но в целом все сводится к тому, что дают полином и описывают, как рассчитать следующий бит последовательности. Например, есть полином f(x) = x5 ⊕ x3 ⊕ 1, и его структура расчета (x1-x5 – регистры полинома; out1 – выходной бит последовательности; также нужно понимать что х1-х5 является сдвиговым регистром, от х1 к х5):
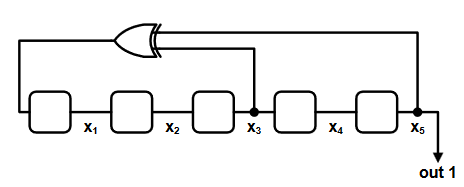
В целом структура есть и из нее можно получить требуемые биты последовательности, но есть одно но(!) - это большое время вычисления (для процессора), либо большие комбинаторные связи для ПЛИС (в том случае, если захочется получать по несколько бит за раз).
И, собственно, задача состоит в том чтобы использовать такой механизм расчета последовательности для того, чтобы она решала проблему времени расчета и таймингов на ПЛИС. Один из вариантов перейти к вычислению в матричном представлении.
Матричный способ
В книге говорится, что можно вычислить следующее состояние полинома (например х1-х5 на рисунке 1), умножив их значения на матрицу перехода:
где U(j + 1) - следующее состояние сдвигового регистра(матрица-столбец размер n, например n=5), U(j) — текущее состояние сдвигового регистра(матрица-строка размер n), T — матрица перехода(размер n на n).
Остается небольшая загвоздка, где взять или как построить эту матрицу перехода? В этой же книге на 13-14 странице описывается алгоритм построения этой матрицы. В ней рассматривается вариант построения матрицы не только для получения 1 бита данных, но и для числа бит равной длине полинома(существует много разных полиномов и в этой книге они так же описываются; как правило их длинна нечетная, на рисунке 1 длина полинома равна пяти). Но давайте пойдем немного другим путем. Сначала построим матрицу перехода для получения 1 бита данных.
Согласно книге в первой строке записывается полином, а в остальных строках записывается единичная матрица со смещением главной диагонали вниз на 1. Либо есть другой вариант описания: в первой строке полином, в последнем столбце нули (кроме первой строки), а все остальное единичная матрица, в любом случае это выглядит так:

Теперь давайте поговорим про полином, а именно про значения Qn(они же tn), ведь это не значение полинома. Если коротко, то Qn (которые tn) показывает используется ли данный бит значения полинома в расчете следующего бита последовательности. Опять обратимся к рисунку 1, в нем видно что 3 и 5 бит используется для расчета нового бита последовательности. (И вот тут первая путаница связана с индексацией элементов, с нуля или с единицы. При реализации этого алгоритма в коде можно нарваться на нее. В данном месте индексация идет с единицы.) Поэтому полином будет в виде:
Естественно зная полином можно построить схему генератора на сдвиговом регистре.
Таким образом, в данном примере из функции полинома f(x) = x5 ⊕ x3 ⊕ 1, получаем полином Р = {0,0,1,0,1}, а, зная полином, можно построить матрицу:
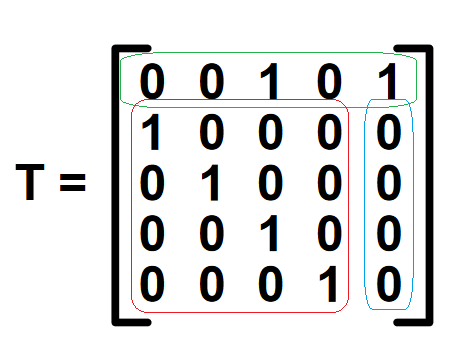
Первая строка обведена зеленым - это значение полинома, единичная матрица обведена красным, оставшиеся нули - синим.
И по сути на этом месте можно остановиться. Так как в этой же книге говорится, что если возвести матрицу в степень k, то можно перевести состояние генератора (не полинома, а сдвигового регистра х1-х5) на k отсчетов. Вот формула:
где U(j + 1) - следующее состояние сдвигового регистра (матрица-столбец размер n, например n=5), U(j) — текущее состояние сдвигового регистра (матрица-строка размер n), T — матрица перехода(размер n на n), k – степень, которая отражает насколько будет выполнен сдвига регистра.
На этом моменте как бы все, но есть нюансы. Про них я сейчас и расскажу.
Нюансы…(некоторые могут показаться очевидными).
Все умножения заменяются на элемент И(and), все сложения заменяются на ИСКЛЮЧАЮЩЕЕ ИЛИ(xor).
Возведение матрицы в степень. Как перемножать матрицы? T * T^(k-1) или T^(k-1) * T ? Как оказалось оба варианта подходят. Где-то в математике есть определение по данному поводу называется Коммутативность матриц.
Нужно понимать, что применение матрицы в единичной степени по сути дает сдвиг регистра на 1 бит. Если матрица во второй степени, то сдвиг регистра происходит на 2 бита, если матрица в третьей степени то сдвиг будет на 3 бита, и так далее… Таким образом (в данном примере), если возвести ее во 2 степень, и выполнять вычисления уже со степенной матрицей (которая всегда будет постоянная), то сдвиговый регистр будет сдвигаться по 2 бита, а это значит, что генератор будет выдавать сразу по 2 бита последовательности, где х5 - младший бит, х4 — старший бит.
У данных полиномов существует длина псевдослучайной последовательности, это значит, что через М тактов последовательность бит начнет повторяться. Длина последовательности рассчитывается как 2^n-1, где n – размер полинома (в приведенном примере длина последовательности 31 бит).
Из пунктов 3 и 4, можно получить замечательное свойство. Как из приведенного полинома получить больше 5 бит последовательности за раз(в случае с ПЛИС)? Все просто. Нужно использовать две разных степенных матрицы. Например, для получения 8 бит: первая матрица в степени 5 (забираем 5 бит из сдвигового регистра, затем умножаем на матрицу в 5 степени); вторая матрица в степени 3 ( из результата перемножения на матрицу в степени 5 забираем 3 бита, а затем умножаем на матрицу в степени 3), а в текущее состояние записываем последний результат умножения на степенную матрицу, для следующей итерации. Вот схема алгоритма:
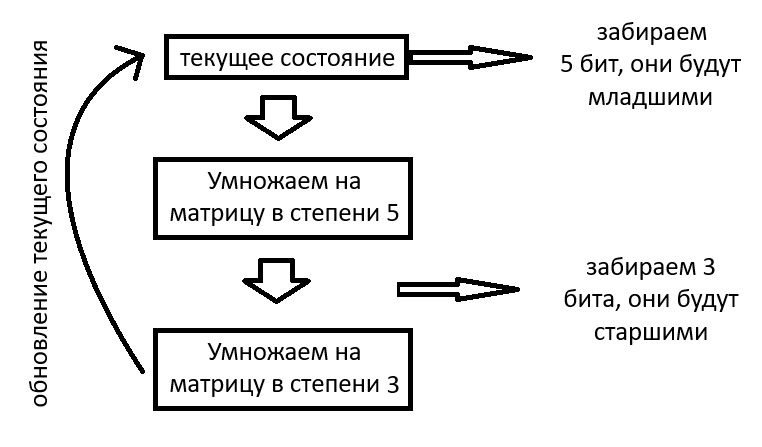
Начальное состояние сдвигового регистра не должно быть равно нулю.
А что если не хочется останавливаться на матрице перехода на 1 бит?
В этой книге также рассказывается, как построить матрицу перехода для сдвига регистра состояния на k-бит. По-сути, результат будет таким же, как при возведение матрицы в степень. В то же время дополнительный вариант построения матрицы отлично подойдет для самопроверки.
И так алгоритм следующий:
Записываем значение полинома не в первую строчку (как это было в первый раз), а в k-ую строчку.
Выше k-ой строки записывается полином со сдвигом влево (справа дополняется ноль), и вот тут внимание! Сдвиг выполняется на одно значение от предыдущей строки (не от k-ой). Если при сдвиге улетает единица, то полученную сдвинутую строку нужно объединить побитово с полиномом по xor.
Ниже k-ой строки записывается единичная матрица и нули, так же, как и выше для матрицы перехода на 1 бит.
Теперь давайте, используя этот алгоритм, построим переходную матрицу для перехода на 4 бита (она должна получиться такой же, как если бы первую матрицу возвели в 4 степень).
И так, полином Р = {0,0,1,0,1}, записываем его в четвертую строчку и формируем строки выше. Пока сформируем вторую и третью строчку, за счет элементарного сдвига, в итоге имеем:

На следующей стадии видно, что в результате сдвига теряется единица, учтем это, и вычислим первую строчку матрицы:

Теперь добавляем единичную матрицу и нули. Так как внизу матрицы осталась одна строчка, то единичная матрица будет из одного элемента — единицы.

Заключение
В этой статье я пошагово описал (и показал) как построить переходную матрицу генератора случайных чисел (он же PRBS). Это замечательная альтернатива расчету на сдвиговом регистре по одному биту. В статье показан пример небольшого генератора(31 бит), но вот в той же книге приведены полиномы длинной 31 бит (длинна последовательности 2^31 – 1). Так же я рассчитываю, что произведение матриц читатель понимает и практикует (в любом случае задавайте вопросы). В результате изучения материала я написал программу в срезе QT Creator, для построение матриц, возведения в степень, и генерации кода для Verilog.
P.S. к сожалению результат на ПЛИС продемонстрировать не могу, а так же код. Так как я делал эту задачу в рамках программирования модуля для ПЛИС, то эта статья оказалась тут.
самописная программа

Список литературы
Комментарии (4)

mpa4b
28.08.2023 16:38+1Действительно, если не хочется останавливаться на матрице перехода на 1 бит -- нужно просто возвести матрицу в нужную степень (умножить саму на себя). Для удобства можно проводить вычисления в https://www.sagemath.org/ . Точно так же можно рассчитать обратную матрицу (переход назад на 1 состояние, возведение матрицы в степень -1). А т.к. LFSR и например CRC одно и то же -- при помощи такой обратной матрицы (отмотка на n бит назад -- матрица в степени -n) можно элементарно "подделывать" нужное значение CRC, если в сообщении есть последовательно k бит (k -- размер CRC), куда можно записать что угодно.

yamifa_1234 Автор
28.08.2023 16:38по подробнее про подделку контрольной суммы, пожалуйста)
p.s. про отрицательную степень не думал

mpa4b
28.08.2023 16:38по подробнее про подделку контрольной суммы, пожалуйста)
Не "контрольной суммы" а CRC.
посчитать xor между получившейся и желаемой CRC
Отмотать получившееся значение на N бит назад соотвествующей матрицей (умножить вектор на матрицу)
Вксорить результат в сообщение в нужном месте.
Есть конечно нюансы типа в каком порядке обрабатываются биты сообщения, инвертируется ли CRC перед записью в конец сообщения, в каком порядке идут биты CRC и т.д.


sci_nov
Матрицы это, конечно, хорошо, но в настоящее время оптимальнее использовать недвоичные регистры. Я делал регистр из 4х ячеек с простым основанием 251. Это укладывается в simd регистры CPU. https://github.com/nawww83/lfsr