В предыдущей статье мы рассмотрели модель Френкеля-Конторовой (1939), которая приводит к уравнению Синус-Гордона (СГ) и достаточно просто моделирует солитоны с положительным и отрицательным зарядом, подчиняющиеся преобразованиям Лоренца. Однако эта модель имеет некоторые недостатки: для небольших волн присутствует дисперсия, то есть зависимость скорости "световых волн" от частоты, которая не наблюдается для реальных электромагнитных волн в вакууме. Кроме того, модель является одномерной, и было бы полезно расширить ее на объемную модель. В принципе, переход к трехмерному пространству, возможно, позволит решить и первую проблему. В этой части мы рассмотрим одну из моделей в трехмерном пространстве, которую в 1958-1962 годах разработал Тони Скирм в попытке моделировать барионные частицы.
Предисловие
Исходя из одномерного уравнения СГ,
можно попробовать создать его многомерные варианты различными способами. Например, к дифференциальному оператору по оси x (в данном случае вторая производная) можно добавить аналогичные дифференциальные операторы по остальным пространственным осям, получив оператор Лапласа. Или можно рассмотреть в пределе разностную модель на кубической решетке или на других многогранниках.
Такой способ расширения успешно работает для волнового уравнения, но волны с устойчивой формой, подчиняющиеся такому уравнению, в двумерном пространстве имеют вид прямых, то есть выглядят как обычные морские волны, а в трехмерном пространстве усточивые волны распространяются в виде плоскости. Таким образом, расширением уравнения СГ мы получим устойчивые волны в виде плоскости бесконечного размера (с положительным и отрицательным зарядом), но вряд ли сможем получить частицы конечного размера и, следовательно, конечной энергии и массы. Кроме того, даже если предположить что конечные какие-то частицы конечного размера существуют, возникает так называемая проблема "3/4", когда отношение кинетической энергии к массе покоя отличается от наблюдаемого.
Мы также можем использовать векторное или другое многокомпонентное поле вместо скалярного. Или варьировать нелинейную функцию вместо синуса, которая для векторного объекта может быть очень разнообразной. Или применить комбинацию этих подходов. Однако нам нужно сохранить свойство "солитонности" и, желательно, чтобы преобразования Лоренца продолжали работать. Несмотря на многие десятилетия исследований и новые компьютерные возможности, задача нахождения полностью удовлетворительного трехмерного расширения уравнения СГ до сих пор не решена. Поэтому полезно знать о уже известных подходах, а также о некоторых "подводных камнях" на пути такого расширения.
В этой статье мы расскажем о двух таких "подводных камнях": теореме Хобарта-Деррика об энергетической устойчивости и о топологическом заряде. Что касается модели Скирма, он начинал разрабатывать трехмерную модель барионов независимо, не зная об уравнении СГ.
Мотивация
Тони Скирм работал в главном британском центре исследований и разработок в области атомной энергии и возглавлял там группу теоретической ядерной физики. В 1958-1962 годах в серии работ он предложил подход, который опирался на необычные для физиков топологические идеи. Более двух десятилетий это направление развивалось лишь группой Скирма, а также Финкейштейном (1968), Рубинштейном (1970) о геометрический характер солитонов) и Вильямсом (1970) (развитие их спинорной структуры).
Прежде чем мы окунемся в подробности модели Скирма, давайте погрузимся в обстановку того времени и опишем фон на котором она развивалась. В то время, пока модель Скирма «дозревала на полке» более двадцати лет, ученые открыли кварки - составные части адронов. В 1965 году, после создания модели Скирма, была разработана квантовая хромодинамика (КХД) - фундаментальная теория сильного взаимодействия, в которой кварки имеют «цветовой заряд» или просто «цвет». КХД является чистой калибровочной теорией Янга-Миллса, без полей Хиггса, связанных с полями фермионных кварков.
Теория Янга-Милса, предложенная в 1954 году Чжэньином Янгом и Робертом Миллсом, основана на неабелевой калибровочной группе. Изначально она рассматривалась как математический поиск, не связанный с реальностью. Однако в 1972 году Герард 'т Хоофт разработал перенормировку для теории Янга-Миллса, что привело к ее всеобщему признанию в физическом сообществе.
На основе теорий Янга-Миллса в 1960-1970-х годах были созданы две основополагающие теории стандартной модели в физике элементарных частиц: квантовая хромодинамика (теория сильных взаимодействий) на базе группы и теория электрослабых взаимодействий на основе групп
.
В 1983 году опубликованные две статьи Эда Виттена (1983), посвященные "алгебре токов", барионам и удержанию кварков, вызвали большой интерес к работам Скирма. В этих статьях автор использовал ранее полученные результаты т'Хофта (1974) и Виттеном (1979), которые независимо друг от друга исследовали обобщение КХД (квантовой хромодинамики). Оказалось, что модель Скирма может быть рассмотрена как приближенный случай КХД в пределе большого числа цветов.
К середине 1980-х годов Тони Скирм, увлекавшийся огородничеством и собравший своими руками Hi-Fi стерео и телевизор, уже не слишком охотно публиковался или проводил семинары. Однако, так как интерес к его работам возрос, и тема активно развивалась, в 1984 году он был приглашен на семинар по скирмионам в конференц-центре Козенер'С Хаус Совета по науке и технике. Там он провел увлекательный разговор и рассказал о своей личной мотивации для создания модели.
В 1987 году в Оксфорде состоялся симпозиум, и было естественно надеяться, что Тони Скирм выступит с подобным докладом, как и в Козенер’С Хаус. Он согласился это сделать. Но за два дня до начала симпозиума Тони Скирм скончался из-за осложнений после неожиданной операции. Частично в качестве памятника Тони Скирму было принято решение попытаться восстановить его беседу в Козенер’С Хаус, используя некоторые заметки, найденные в его офисе, и записи с семинара 1984 года. Реконструкция была включена в Симпозиум Пейерлса 1988 года как его посмертная работа. В ней он изложил четыре основных мотива своей работы. Первым из этих мотивов было, конечно, объединение.
Объединение. Скирм стремился построить всё из единой сущности, но это не означало поиск какой-то великой группы симметрии. Так как традиционно существует два типа фундаментальных полей - бозоны и фермионы, то было бы неплохо, если бы можно было обойтись только одним из них. Он упомянул нелинейную теорию спинорного поля Гейзенберга 1958 года, основанную на самовзаимодействующем фермионном поле, но предпочитал бозоны и решил исследовать возможность создания теории на основе самовзаимодействующих бозонных полей.
Избавление от бесконечной перенормировки. Скирм связывал эту проблему моделями элементарных частиц, в которых они представлялись в виде точек, и хотел представить "частицу" как протяженный объект с конечной собственной энергией. Точечность частиц казалась ему неестественной, так как в квантовой теории поля она приводит к бесконечностям, которые процессом перенормировки только "заметаются под ковер". Было бы хорошо получить протяженный объект обладающей конечной энергией и свойством частиц.
"Проблема фермионов". Скирм был обеспокоен квантово-механическими концепциями без ясных классических аналогов и считал, что использование переменных Грассмана для фермионов и интегралы по траекториям, разработанные Ричардом Фейнманом в 1948 году, были неестественной математической конструкцией. Он надеялся показать, что использование фермионных полей окажется идеализированным способом описания определенной полуклассической конфигурации поля.
Увлечение теорией вихрей атомов Кельвина. Скирм был очарован этой теорией, в которой происхождение сохраняемой величины определялось структурным свойством объекта, а не просто принципом симметрии. Это увлечение в итоге привело к одному из главных вкладов Скирма - топологическому квантовому числу.
Отличия бозонов и фермионов
Бозоны
Частицы или квазичастицы с целым значением спина.
Подчиняются статистике Бозе-Эйнштейна.
Подчиняются каноническим коммутационным соотношениям.
Квантовая система, состоящая из произвольного числа бозонов и чётного числа фермионов, также является бозоном. Например, атом гелия.
Бозонное поле - это квантовое поле, квантами которого являются бозоны.
Примерами бозонных полей являются скалярные поля, описывающие частицы со спином 0 (бозон Хиггса), и калибровочные поля, описывающие частицы со спином 1 (фотон).
Фермионы
Частица или квазичастица с полуцелым значением спина.
Термодинамически равновесное состояние такой системы описывается статистикой Ферми — Дирака.
Подчиняются каноническим антикоммутационным соотношениям.
Подчиняются принципу запрета Паули.
Примеры фермионов: кварки (они образуют протоны и нейтроны, которые также являются фермионами), лептоны (электроны, мюоны, тау-лептоны, нейтрино), дырки (квазичастицы в полупроводнике).
Фермионами являются также квантовомеханические системы, состоящие из нечётного числа фермионов (и произвольного числа бозонов).
Общей нитью в этих мотивах является сильное предпочтение описания с точки зрения областей, которые имеют классические пределы, что выражается в стремлении к "механическим" моделям. Как подчеркнул Скирм, на него большое влияние оказал: Уильям Томсон, ставший известным позже как лорд Кельвин. Скирм привел цитату лорда Кельвина 1884 года, произнесенную в университете Джона Хопкинса, о теории электромагнетизма Джеймса Максвелла опубликованной ранее (1861-1865):
«Я не смогу успокоиться, пока не создам механическую модель явления. Если я смогу создать полностью механическую модель, я смогу это понять. Пока я не могу сделать полную механическую модель, я не могу понять. И именно поэтому я не могу вникнуть в теорию электромагнетизма»
— Уильям Томсон (лорд Кельвин)
Довольно удивительно, что Кельвин так высказался о теории Максвелла. На промежуточном этапе разработки своих уравнений электромагнитного поля в 1865 году, Максвелл опубликовал серию статей в 1861-1862 годах под названием "О физических линиях силы" в трех частях. Во второй части, "Теория молекулярных вихрей, применяемых к электрическим токам", приводилась эта знаменитая диаграмма, демонстрирующая, как согласованное движение соседних вихрей в эфире требует разделения вихрей с помощью "реальных колес", движение которых генерирует так называемый ток смещения.
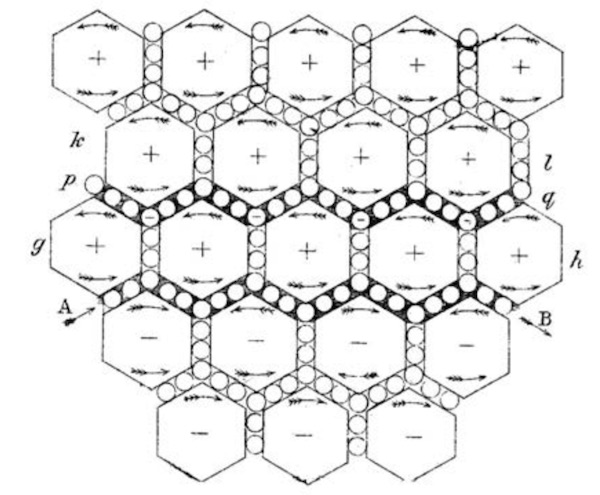
Видео анимация на youtube
Однако отметим, что как показывает история науки, абстрактная модель может описывать реальную картину мира лучше, чем примитивные механистические модели "хрустальных сфер".
Интересно отметить, что Скирм имел прямую семейную связь с Томсоном. Его прадед по материнской линии, Эдвард Робертс, в 1872-73 годах был ответственен за строительство одного из первых аналоговых компьютеров для предсказателя приливов и отливов, который был спроектирован Уильямом Томсоном.

И такая машина находилась в доме дедушки Тони Скирма! На семинаре он рассказал, что "изобретательность ее механизма, с помощью которого она могла создавать такую сложную схему приливов, оказала на меня значительное влияние".
О первых аналоговых компьютерах
Такие машины имели жизненно важное значение для британского адмиралтейства во время Второй Мировой Войны при прогнозировании приливов и отливов для высадки в день «D».
Их также использовало и германское адмиралтейство: очень продуманную версию можно увидеть в немецком музее в Гамбурге.
Более поздняя модель экспонируется в Национальном океанографическом центре.
Статьи на хабре:
Это что касается предпосылок механистического представления. А как принципиально можно моделировать протяженные частицы?
Начиная с 1867 года Томсон, вместе с Питером Гатри Таитом , разрабатывал свою модель "дымового кольца" или "вихря" атома, основанную на работах Германа фон Гельмгольца. В этой модели представляется концепция пространственно-распределенного (не точечного) объекта, обладающего сохраняемым качеством. Они обнаружили, что дымовые кольца могут отскакивать друг от друга, колебаться, но не терять своей существенной целостности.
Это привело их к мысли, что "все тела состоят из вихревых атомов в идеальной однородной жидкости", причем объяснение различий между атомами основываются на разном числе узлов у замкнутых вихревых линий, то есть на топологическом соображении.
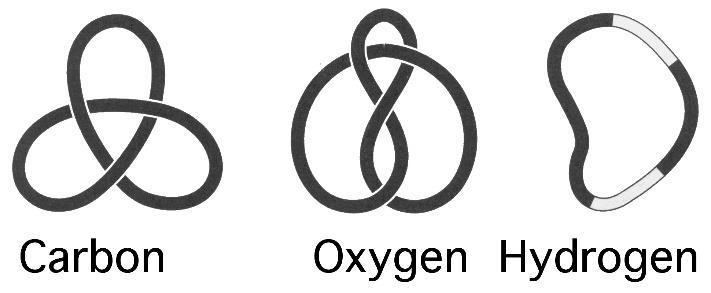
Вихревая теория атомов в виде "кренделей" ушла в прошлое после открытия электрона. Однако Тайт заложил основы теории узлов.
Стоит также отметить, что математические работы Тэйта были посвящены и теории кватернионов. Будучи учеником и последователем открывшего кватернионы Уильяма Гамильтона, Таит развивал кватернионный анализ как математический аппарат для физики, стал лидером в этом направлении и опубликовал "Элементарный трактат о кватернионах". Этот трактат успешно использовался Максвеллом в работе над теорией электромагнитного поля. Идеи Томсона о вихревых атомах тесно связаны с четвертым принципом Скирма – обоснованием закона сохранения в структурных свойствах классической конфигурации поля.
Еще одним важным источником вдохновения для Скирма, о котором он упоминал в своем выступлении на семинаре, была нелинейная теория электромагнетизма, предложенная Максом Борном и Леопольдом Инфельдом в 1934 году.
Эта теория объединяет первые два принципа Скирма: унификацию и отсутствие точечных частиц с их неизбежной бесконечностью. Борн и Инфельд представили свою теорию, отстаивая "унитаристскую" точку зрения, которая предполагает существование только одной физической сущности – электромагнитного поля, соответствующую первому принципу Скирма. В этом подходе частицы материи, включая электрон, не рассматриваются как сущности, полностью отличные от поля (как в "дуалистической" точке зрения), а возникают в теории как сингулярности поля, то есть как особые точки со значением поля, стремящимся к бесконечности. В действительности, сингулярности присутствуют только в идеализированном пределе: в реальном мире плотность заряда частицы распределена, а ее электромагнитная масса конечна, что удовлетворяет второму принципу Скирма.
Вот такие исторические предпосылки идей Скирма. Вкратце, он стремился разработать теорию, в которой фермионные источники барионного числа могли бы возникать как сингулярности (в определенном пределе) нелинейной мезонной теории поля.
Помимо собственной мотивации Скирма, важно рассмотреть общий фон научной обстановки, окружающей его идеи, так как существовало множество других физиков и точек зрения.
В 1897 команда Джозефа Томсона (другой Томсон, не Кельвин и не его брат) открыла электрон. Позже были открыты протон (1917) и нейтрон (1932), составляющие ядра атомов. Возникла проблема в понимании субатомных частиц. Классически точечный электрон имеет бесконечную кулоновскую энергию. Абрахам и Лоренц (1915), а позднее Борн и Инфельд (1934), предпринимали различные попытки придать электрону конечную структуру. Модель Абрахама-Лоренца предполагает электрон с распределенной плотностью заряда, и для стабилизации внутреннего электростатического отталкивания использует уравновешивание скалярных взаимодействий ближнего действия. Модель Борна-Инфельда представляет собой нелинейный вариант электродинамики Максвелла. В этой модели, точечный электрически заряженный источник приводит к конечным значениям напряженности поля и конечной полной энергии. Однако поля не являются гладкими, а имеют прерывистый градиент в источнике. В обоих типах моделей масштабом длины является "классический радиус электрона", который выбирается таким образом, чтобы энергия электростатического поля вне этого радиуса для кулоновского поля была порядка массы электрона.
В 1935 году Хидэки Юкава, первый японский ученый, удостоенный Нобелевской премии, предложил гипотезу о существовании нового типа частиц - мезонов. Эти частицы обладали массой, промежуточной между массами электрона и протона.
По его модели, ядерное взаимодействие между нуклонами (протонами и нейтронами) осуществлялось через обмен мезонами, какое-то поле, аналогичное взаимодействию электрических зарядов через электромагнитное поле. Вместо кулоновского потенциала Юкава предложил использовать потенциал, значение которого убывает с расстоянием по экспоненциальному закону. В данной модели нуклоны представлены как фундаментальные фермионные поля, а пионные поля с нулевым спином выступают в роли "клея", связывающего протоны и нейтроны в ядре.
Мезонное поле описывалось потенциалом Юкавы, который удовлетворяет уравнению
Здесь - плотность вещества,
- потенциал, а
- константа, масштабирующая величину.
Это уравнение напоминает уравнение Пуассона в электростатике . А также линейное уравнение Клейна — Гордона, которое в релятивистской квантовой механике описывает волновую функцию бозона.
Уравнение Клейна-Гордона
Уравнение Клейна-Гордона правильно описывает бесспиновые релятивистские составные частицы, такие как пион. 4 июля 2012 года Европейская организация ядерных исследований ЦЕРН объявила об открытии бозона Хиггса. Поскольку бозон Хиггса является частицей с нулевым спином, это первая наблюдаемая якобы элементарная частица, описываемая уравнением Клейна – Гордона. Требуются дальнейшие эксперименты и анализ, чтобы определить, является ли наблюдаемый бозон Хиггса бозоном Стандартной модели или более экзотической, возможно, сложной формой.
К концу 1940-х годов теория Юкавы былполучила подтверждение благодаря открытию трех видов пионов принадлежащих к группе мезонов. Теория успешно объяснила ряд фундаментальных фактов, например, наличие тензорных сил и квадрупольного момента у дейтрона. Однако, впоследствии возникли сложности в описании ядра и ядерных процессов. Таким образом исследование Хидэки Юкава представляет собой важный шаг в понимании ядерных взаимодействий и структуры атомных ядер. В то время когда Скирм разрабатывал свою модель (1958-1962), теория Юкавы доминировала.
Еще одним предшественником была концепция монополя Дирака, как сингулярное решение обычных электромагнитных уравнений с суммарным магнитным зарядом. Несмотря на то, что модель предполагает бесконечную энергию (что в реальном мире невозможно), поля на фиксированном расстоянии от источника обладают топологическим интересом, связанным с магнитным зарядом, который может возникать только в целых кратных квантам , где
— основная единица электрического заряда.
Были попытки рассмотреть элементарные частицы на основе теории нелинейных фермионных полей, такой как нелинейной теорией спинорного поля Гейзенберга 1958 года, основанная на идеях де Бройля и спинорного поля Дирака. Бозонные поля предлагалось строить из фермионных полей с помощью гипотезы слияния.
В другом направлении, не связанным напрямую со строением атома, развивались квантовые теории конденсированного состояния. Был разработан ряд феноменологических подходов, базирующихся на классической теории поля. Основное поле обычно представляет собой плотность фермионов и предполагает медленное изменение в пространстве и времени. Это поле несет достаточно информации о квантовом состоянии, чтобы можно было записать энергетическую функцию для поля. Это подход Гинзбурга-Ландау (ГЛ). В 1957 году Абрикосовым было обнаружено, что энергетическая функция ГЛ имеет топологические солитоны. Солитоны существуют только в варианте теории с двумя пространственными измерениями и называются вихрями магнитного потока или просто вихрями. Эти вихри магнитного потока сохраняются в релятивистской теории, как показали Нильсен и Олесен, и могут быть интерпретированы либо как частицы в двух измерениях, либо как массивные релятивистские струны в трех измерениях. Теория ГЛ является примером калибровочной теории со спонтанно нарушенной калибровочной симметрией. Калибровочная группа — это абелева группа U (1). В конце 1960-х в таких моделях с неабелевой калибровочной симметрией было предложено объединить электромагнитное и слабое взаимодействия.Двумерные вихри Гинзбурга-Ландау сейчас наблюдаются как солитоны в тонких сверхпроводниках и как протяженные вихри в трехмерных сверхпроводниках. Много позже, уже в нашем веке, были обнаружены магнитные скримионы.
Таким образом, кажется, что мотивы Скирма не были теми, которые в настоящее время используются для оправдания его модели. Очевидная «мораль» этой исторической дискуссии заключается в том, что интересные идеи обладают удивительным способом оказаться полезными и верными.
Конструирование модели Скирма
Еще в 1960-х годах в мире физики существовал интерес к гипотетической частице, называемой -частица. В 1960 г. М. Гелл-Манн и М. Леви представили теорию скалярного поля, "сигма-модель", в которой поле принимало значения в векторном пространстве. Затем была придумана усовершенствованная версия сигма-модели, в которой поле принимает значения в каком-то другом многообразии, и эту версию назвали «нелинейной сигма-моделью» (НСМ).
Эта эффективная теория поля является хорошим приближением к КХД при моделировании физики, в которой кварковая структура не играет роли и ей можно пренебречь. Поэтому НСМ можно рассматривать как базовую адронную теорию поля с основным полем, состоящим из трех легчайших адронов - пионов. Эта теория изменила взгляды физиков на структуру атома и даже предшествовала открытию кварков.
Она также является и предшественником модели Скирма. На ее примере можно ввести основные понятия и свойства, в том числе топологически заряд, а так же определить имеет ли модель условия для существования устойчивых решений. Модель Скирма получается из НСМ путем добавлением одной поправки. Поэтому и рассмотрим ее основания подробно.
Вместо рассмотрения фундаментальных частиц как точек, мы можем представлять их в виде скалярных полей. В НСМ эти скалярные поля соответствуют трем пионам: .
Как и в случае с полной картиной КХД, мы потребуем, чтобы теория имела глобальную группу симметрии , где индексы
и
вводятся чтоб не путать между собой составляющие. В этом случае она может представлять адроны, состоящие из двух ароматов кварков.
Специальная унитарная группа. Обозначения. Индексы.
- специальная унитарная группа, состоит из всех унитарных матриц размером 2х2, то есть из антиэрмитовых матриц, и детерминант которых равен единице. Локально идентична группе вращений в 3-х мерном пространстве, группе
Обе эти группы различаются глобально, то есть для вращений, не являющихся бесконечно малыми. Представима через генераторы вида матрицы Паули. Для более высокой размерности аналогом матриц Паули в группе SU(3) являются матрицы Гелл-Манна.
- хиральная симметрия (левая и правая)
Знаком обозначается "прямое произведение групп.
В реальном мире из-за ненулевых и различающихся масс кварков это только приближенная симметрия, и, следовательно, пионы не безмассовы, но имеют массы небольшие: это псевдо-голдстоуновские бозоны.
Индексы
Обычно (по распространенному соглашению) греческие индексы будут иметь значения от нуля до трех , латинские от одного до трех
В выражениях c индексами используется метрика
. Верхние и нижние индексы в 4-векторах следует различать:
Скалярное произведение двух 4-векторов определяется как:
При написании лагранжианов часто используется символы частных производных, которые определяются следующим образом:
Пусть будет полем
, то есть в каждой точке пространства
(включая время) мы через функцию
присваиваем значение в виде 2x2 матрицы, которая представляет элемент специальной унитарной группы.
Обратим внимание, что в общем случае мы должны рассматривать поля , где
- это количество ароматов кварка. Однако здесь мы моделируем поле пионов, и поэтому имеем только два типа кварков, соответствующие верхним (u) и нижним (d) кваркам.
Так как является полем
, состоящим из трех пионных полей
, оно может быть записано таким образом:
где пионный коэффициент имеющий размерность массы, чтоб аргумент экспоненты был безмассовым,
- мнимая единица, а
- матрицы Паули:
Это является стандартным результатом для любого -значного поля.
Мы можем разложить выражение в ряд Тейлора и сгруппировать степени по четным и нечетным степеням. Затем, используя тождества матриц Паули, получим (4)
где - нормированный до единичного вектор
,
- единичная матрица 2x2, в более общем случае, тождественный оператор. Точка обозначает аналогично скалярному умножению сумму перемножения соответствующих компонент, векторов Паули
.
Отметим также, что мы использовать представление (5) в базисе единичной матрицы вместе с матрицами Паули через 4 скалярных поля , которые подчинены условию
и таким образом лежат на сфере в четырехмерном пространстве.
Простейший лагранжиан, инвариантный относительно с точностью до одного постоянного коэффициента, выглядит следующим образом:
где знаком обозначается эрмитово сопряжение матрицы.
Что касается симметрий, глобальная симметрия подразумевает, что наш лагранжиан симметричен (инвариантен) относительно преобразования
где .
Однако, учитывая что , мы можем выбрать конкретное вакуумное состояние без потери общности, например
. Такой выбор приводит к нарушению симметрии до диагональной (векторной) группы
.
С детерминированным вакуумным состоянием наш лагранжиан теперь инвариантен по преобразованию
Следовательно, симметрия нарушена до
Теперь рассмотрим, могут ли в подобной модели существовать сохраняющиеся величины.
Тайны сохранения: Топологический заряд
В природе мы обнаруживаем удивительные явления, такие как сохранение определенных величин, вроде электрического заряда, барионного числа и лептонного числа. Их сохранение наблюдается во всех известных физических процессах, несмотря на то, что существуют теории, предполагающие возможное нарушение этого сохранения при очень высоких энергиях. Устойчивость и неизменность этих сохраняемых величин заставляют нас предполагать, что они играют фундаментальную роль в структуре физического мира.
Но как можно математически описать сущность, которая не поддается уничтожению и связана с частицами? В одномерной модели дислокаций ФК, описываемой уравнением СГ, сохранение сгущений ("дырок") интуитивно понятно. Аналогично игре "пятнашки", где мы перемещаем 15 фишек в коробке, дислокация в виде пустого места не исчезает, пока мы следуем правилам игры, и новая дислокация не появится. То же самое происходит и в модели ФК: если мы уберем один шарик из впадины, интегральная плотность системы останется неизменной. Мы можем попытаться расширить эту модель на многомерные решетки разными способами. Если мы удалим атом из решетки, то очевидно, что в дальнейших внутренних процессах суммарное количество пустых мест будет сохранятся. Учитывая разнообразие видов дислокаций, которые наблюдаются в природе, не обязательно ограничиваться только кубическими решетками.
Однако в решетчатых моделях есть некоторые сложности, связанные с анизотропностью, так как законы природы не выделяют какие-либо особые направления. В конечном итоге, мы должны прийти к математической модели, и в этом контексте полезно обратить внимание на топологию. С ее помощью мы можем рассмотреть сохранение заряда с новой точки зрения и применить топологические концепции. И, с точки зрения топологии, мы можем изучить, какие виды топологических солитонов могут существовать в разных вариантах и в каких случаях они запрещены.
В простом случае, когда мы рассмотрим несколько решений одномерного уравнения СГ в фиксированный момент времени, их сохранение можно связать с числом "наматываний" кривой вокруг точки. На рисунке слева в верхней части изображена функция решения, соответствующая связанному кинку и антикинку с суммарным зарядом равным нулю. В середине решение соответствует положительно заряженному кинку, внизу двум кинкам, суммарный заряд которых равен двум.
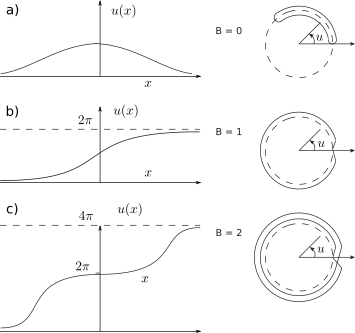
Если проследить за изменением значения функции и представить его в виде угла (на рисунке справа), то в первом случае (a) угол сначала увеличивается, но потом возвращается к вакуумному состоянию. Во втором случае (b) вектор, связанный с углом, совершает полный оборот. В третьем случае (c) вектор совершает два полных оборота вокруг окружности.
Таким образом через функцию мы отобразили окружность связанную с пространством в окружность связанную с полем.
Изображение справа инвариантно относительно сдвига функции по оси х. Например, если мы рассмотрим кинк смещенный на некоторое расстояние влево или вправо от центра (что также является решением уравнения СГ), то вектор будет совершать те же самые действия, хоть и с запаздыванием во времени.
При этом мы предполагаем, что состояние модели (конфигурация поля) имеет конечную энергию. В механической модели ФК плотность нелинейной части энергии, связанная с периодической силой подложки , равна
, соответствует высоте грузика на синусоиде. Поэтому значение поля в вакуумном состоянии должно быть кратно
, как и значения поля на бесконечно удаленных границах, иначе полная интегральная энергия оказалась бы равна бесконечности.
Изменения полей во времени, будь то под действием уравнений поля или воздействием локализованных внешних источников (если они не вызывают возникновение конфигураций с бесконечной энергией), не затрагивают значения полей на бесконечности. То есть отображение, заданное выше, остается неизменным, и оно является топологической характеристикой полевой конфигурации.
Таким образом отображение окружности в окружность можно охарактеризовать числом наматываний кривой вокруг точки. Это понятие связано с "индексом точки" или порядком точки относительно кривой, и играет большую роль в теории комплексного переменного, теореме о вычетах, интегральной теореме Коши и принципе аргумента.

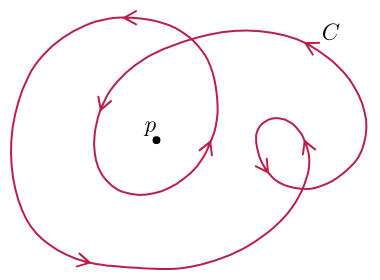
Число наматываний дискретно и не может меняться при непрерывном изменении кривой. Значит, множество всех полей с конечной энергией разбивается на непересекающиеся множества, называемые секторами. Число таких секторов для модели Сайн-Гордон является бесконечным множеством и характеризуется целым числом наматываний . (А, например в модели фи-4, где тоже могут быть кинки, но распадающиеся, количество таких секторов 4, обозначается
)
Теперь полезно будет получить формулу, по которой можно вычислить заряд в виде целого числа для любой функции, задающей состояние поля в одномерном варианте. При отслеживании значения поля во время движения по пространственной оси на величину , оно меняется на величину
, а суммарно, то есть интегрально на величину
После тривиального интегрирования дает , то есть разницу между значениями поля на удаленных границах.
Теперь, чтобы в данной модели получить целое число оборотов, введем нормирующий коэффициент равный длине единичной окружности или, что тоже самое, углу целого поворота , и определим плотность заряда как
Интегральный заряд, то есть заряд всей системы, определяется как интеграл плотности
Мы рассмотрели отображения окружности на пространство параметров поля через функцию состояния поля
. Два разных таких отображения, например, с зарядами B=0 и B=1, невозможно непрерывным образом, то есть без разрыва, перевести друг в друга. С одинаковым же числом оборотов отображения непрерывно деформировать друг в друга можно. Два таких образа называются эквивалентными, принадлежащими одному и тому же классу. Этим как раз и занимается раздел топологии, называемый гомотопией.
Эти простые и тривиальные результаты в простейшем одномерном случае задают базис для перехода на многомерные случаи, для которых мы будем использовать некоторые результаты топологии, в частности гомотопические группы сфер . В данном случае рассматриваются именно сферы, как простейшая выпуклая форма, так как очевидно, что поверхность, например, куба можно натянуть на сферу непрерывным образом.
Гомотопические группы сфер классифицируют отображения между многомерными сферами с точностью до непрерывной деформации и определяют возможные классы (не переходящие друг на друга) отображений и их количество.
Сферы размерности обозначаются
.


Например, множество точек на двумерной плоскости равноудаленных от центра (обычная окружность), обозначается как . Обычная сфера в трехмерном пространстве обозначается как
. И для общности можно определить "сферу" на прямой, она состоит из двух точек удаленных от центра на одинаковое расстояние.
Мы на интуитивном уровне обнаружили, что отображения из окружности в окружность однозначно задаются числом оборотов с точностью до гомотопии, то есть непрерывных отображений, переход между которыми задается через непрерывный параметр от 0 (в исходном пространстве) до 1 (в целевом пространстве). Можно представить это как ползунок (slider), который принимает значения от 0 до 1 и позволяет трансформировать одно пространство в другое. Можно также установить, что при композиции путей числа оборотов складываются, что позволяет применять групповую операцию сложения. То есть можем применять групповую операцию типа сложения, а отображения как элементы бесконечной циклической группы . Так, группа гомотопических отображений окружности на окружность является бесконечной циклической группой и обозначается как
Теперь рассмотрим более сложный случай. Предположим, что у нас есть многомерная сфера и пространство
, в котором изменяется параметр поля. Топология определяет возможные не пересекающиеся классы отображений. Гомотопическая группа отображения n-сферы на топологическое пространство обозначается как
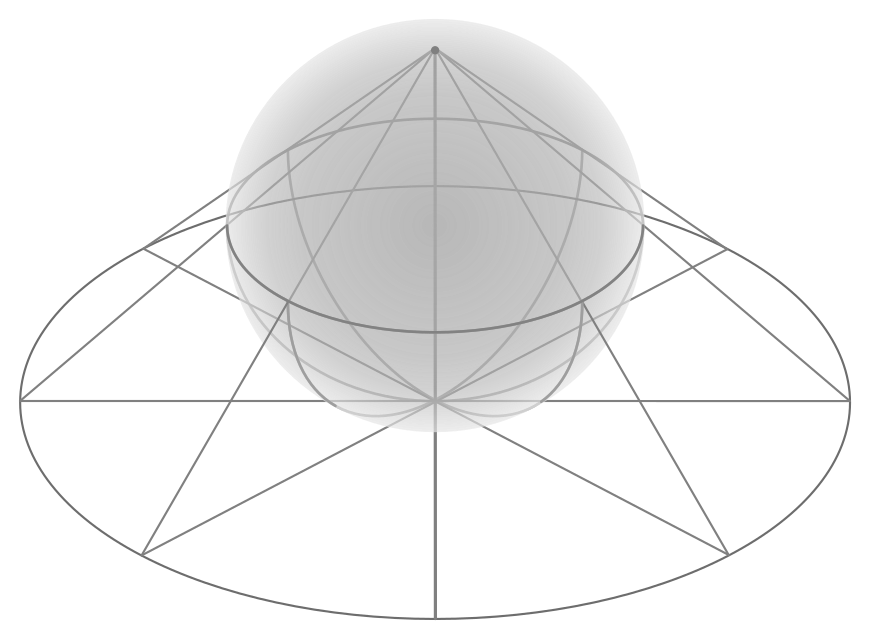
Не все гомотопические группы имеют бесконечное число элементов. Например, любую окружность на сфере можно непрерывным образом стянуть в точку, как показано на рисунке:

На торе существуют замкнутые петли с несколькими оборотами, которые не удастся стянуть в точку путем непрерывной деформации. При этом существуют разные классы петель, которые нельзя преобразовать одну в другую. Это обозначается как
. Следовательно, тор не гомеоморфен сфере.
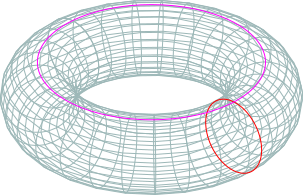
Несмотря на то, что точная структура гомотопических групп сфер пока не полностью изучена, мы можем использовать результаты для некоторых случаев. Например, точно известно, что гомотопическая группа отображений из n-мерной сферы в себя является бесконечной цикличной , аналогично одномерному случаю.Любое отображение сферы меньшей размерности на сферу большей размерности можно сжать в точку, как и окружность на сфере:
, при положительных k.
Устройство группы уже не так очевидно, оно вычисляется через расслоение Хопфа. А, например,
.
В следующих таблицам представлены значения гомотопических групп сфер для некоторых примеров, а также некоторых многообразий классических групп Ли:
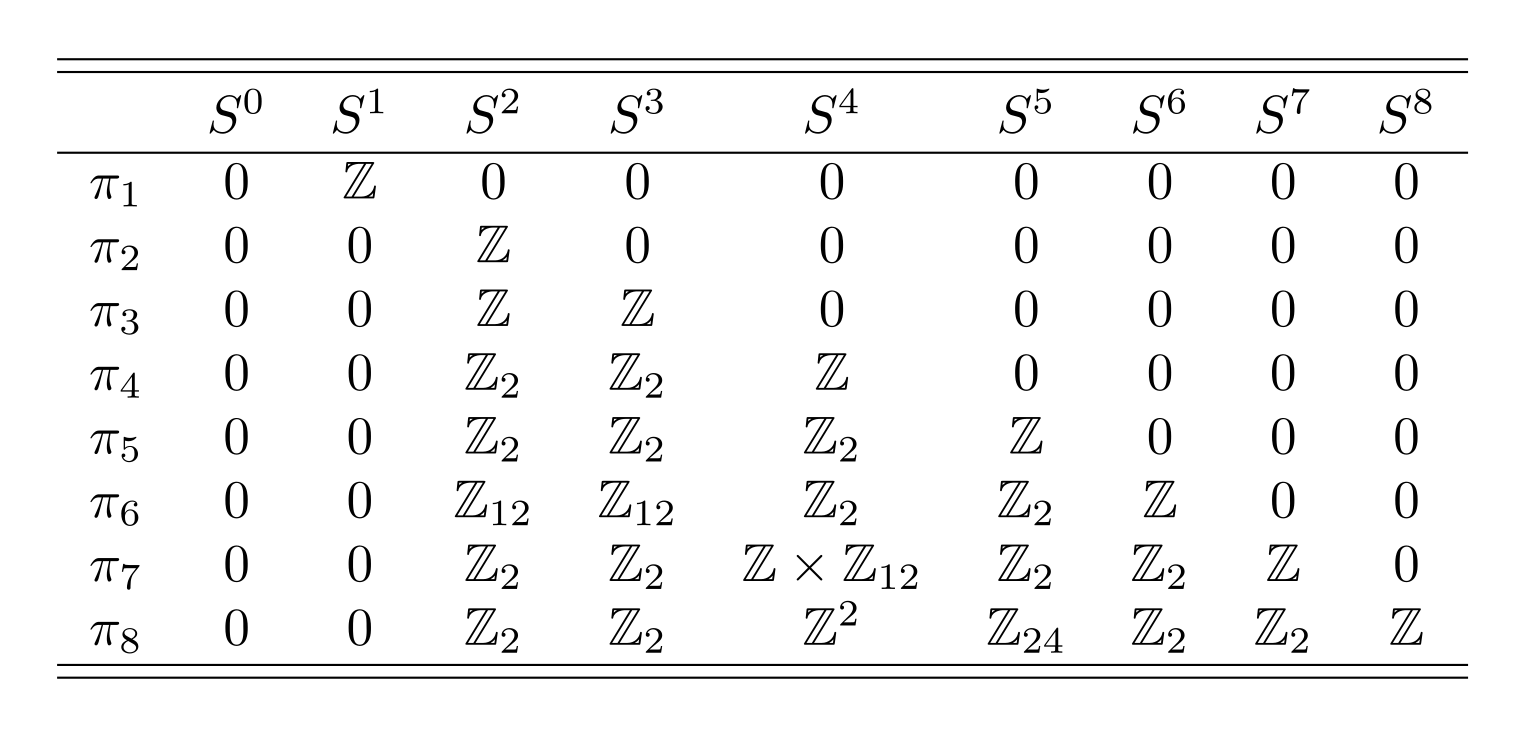
Элементами являются: 0 - тривиальная группа, - бесконечная циклическая группа или группа целых чисел по сложению.
- конечные циклические группы порядка n, например группа
состоит из двух элементов 0 и 1.
Прямые произведения таких групп записываются через или

Теперь перед нами встает задача связать сферы с евклидовым прямоугольным пространством .
Рассмотрим в двумерном пространстве локальное поле параметров (
), связанных условием
. Тройку параметров
можно понимать как вектор, условие как сохранения длины вектора (нормы). То есть вектор параметров
может двигаться только по единичной сфере
.
Возникает вопрос: как подсчитать количество оборотов при отслеживании по всему пространству?
Отобразим наше двумерное пространство на сферу с помощью стереографической проекции. Представим обычную сферу, расположенную в трехмерном пространстве, над плоскостью пространства так, чтоб они соприкасались между собой. Для определенности примем радиус сферы за единицу и центр сферы расположим в точке трехмерного пространства с координатами (0, 0, 1). Таким образом, самая верхняя точка сферы имеет координаты (0, 0, 2), и её можно называть северным полюсом.

Стереографическая проекция
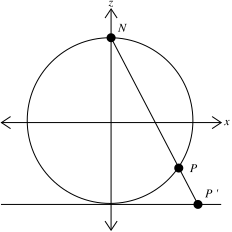
Каждую пару точек, принадлежащих соответственно сфере и пространству плоскости, можно однозначно связать друг с другом через отображение. При прямой стереографической проекции на плоскость, через каждую точку на сфере можно провести прямую, проходящую через нее и через северный полюс, которая пересечет плоскость в единственной точке. Обратная стереографическая проекция отображает точки плоскости на точки сферы, аналогично, как место пересечения сферы и прямой, проходящей через северный полюс и точку плоскости.
Таким образом, мы сделали топологически эквивалентными плоскость и сферу, но при одном дополнительном условии, по которому все точки, расположенные в евклидовом пространстве на бесконечности, переходят в северный полюс сферы и считаются одинаковыми. Здесь интуитивно учитываем, что на удалении в бесконечность поле с конечной энергией имеет одно и то же значение, соответствующее вакуумному состоянию с нулевой плотностью энергии. (В качестве альтернативы можно рассмотреть отображение без северного полюса, то есть исключив его из рассмотрения, но при этом потребуются дополнительные оговорки.)
Мы имеем две сферы, и в связи с этим пространство параметров можно рассматривать как элемент, принадлежащий второй гомотопической группе (отображение из обычной сферы). Из теории гомотопий мы знаем, что эта группа эквивалентна группе целых чисел:
Гомотопическая группа сферы - это множество отображений из сферы
в
, рассмотренное с точностью до гомотопий, то есть непрерывных шевелений, которые к тому же должны сохранять отмеченную точку.

Основной результат, который мы получили из довольно поверхностного рассмотрения и опуская некоторые нюансы, что аналогично числу наматыванию кривой вокруг точки, мы можем рассматривать число наматываний сферы на сферу и это число целое.
Теперь давайте рассмотрим, как подсчитать число оборотов сфер для заданной конфигурации поля, то есть как посчитать топологический заряд. Для одномерного случая, который мы подсчитали ранее, было все более менее тривиально, а для двумерного сложней.
При отслеживании движения в пространстве вдоль пространственной оси x из точки в точку
, вектор будет описывать на этой сфере кривую AB. Аналогично, при отслеживании вдоль другой оси будет описана другая кривая AC. Причем при разных путях A'C'D' и A'B'D', вектор в пространстве параметров, очевидно, тоже придет в одну точку D.

Площадь площадки ABCD вычисляется через определение векторного произведения векторов AB и AC, выделенных на рисунке красным цветом.

Модуль векторного произведения, обозначим его как , равен площади параллелепипеда образованного векторами. Вектора AB и AC выражаются через соответствующие частные производные:
Теперь нужно учесть знак площади. Площадь элемента следует брать со знаком плюс, если ориентация векторов АB и AC в пространстве параметров поля такая же как у у векторов А'B' и A'C' в пространственных переменных. В противоположном случае (именно он изображен на рисунке) знак должен быть минус. Единичный вектор , двигающийся по сфере, ортогонален к ее поверхности. Вектор
тоже перпендикулярен площадке, но он может быть направлен либо втом же направлении, что и
, либо в противоположенном. Знак получится правильным, если учесть его через скалярное произведение на единичный вектор:
Полная площадь поверхности обычной сферы равна , поэтому чтоб получить целое число обмоток мы вводим плотность топологического заряда с соответствующим множителем:
при интегрировании которого получается целочисленный заряд
Полный телесный угол сферы , а наша площадка связана с телесным углом, образованным векторами в пространстве параметров. Удвоенным, так как вектора образуют треугольник ABC, а площадка - параллелепипед ABCD. В тоже время, когда мы отслеживали пространство параметров, площадка в евклидовом пространстве с помощью стереографической проекции отображается на сферу, и заметает ее только один раз.
Скалярное произведение одного вектора на векторное произведение двух других называется смешанным произведением, которое можно выразить через детерминант матрицы размером и образованной строками состоящих из компонент векторов . Мы можем его записать, отойдя от векторов и работая только с компонентами через правило свертки и cимвол Леви-Чивиты, переобозначая при этом
Дополнительное деление на 2 появилось из-за повторения элементов при свертке, которые получаются при замене индексов на
синхронно с заменой индексов
на
. Оба символа Леви-Чивита при этом меняют знак, но произведение двух знаков при этом остается неизменным.
Исследуя двумерное координатное пространство с параметрами на сфере, мы изучили топологический заряд, характерный для таких моделей, включая двумерную нелинейную сигма-модель. Этот заряд можно использовать в двумерной модели Скрима (так называемые "детские скримионы", магнитные скирмионы).
Теперь распространим еще более сложный случай нелинейной сигма-модели с полем праметров и трехмерном пространстве и выведем для нее формулу топологического заряда из других соображений.

Наша цель - построить топологический инвариант в трех измерениях, для чего потребуется использовать трехкомпонентный тензор Леви-Чивиты. Кроме того, нам нужно использовать все индексы тензора Леви-Чивиты, а также три производные, . Поскольку наше поле
является унитарным, мы можем иметь только равное количество
и
s, и поскольку мы хотим вывести число (скаляр), мы используем след. Следовательно, единственная топологически инвариантная величина, которую мы можем построить для специального унитарного поля
в трех пространственных измерениях, равна
Ее называют плотностью топологического заряда. А сам топологический заряд получается путем интегрирования его плотности:
Здесь множитель служит нормирующим, чтобы интеграл по объему давал целое число.
Таким образом формулы (10) (20) (30) определяют плотность топологического заряда соответственно для одномерного, двумерного и трехмерного случая. А выражения (11) (21) (31) определяет соответствующие заряды.
Рассмотрим три основных свойства интеграла (31), который определяет топологический заряд для НСМ и ее вариаций.
Топологический заряд антиэрмитов.
Топологический заряд не изменяется при инфинитезимальном преобразовании
Топологический заряд произведения двух конфигураций поля, равен сумме зарядов этих полей.
Первое свойство действительно показывает, что античастицу (обратную по барионному заряду) можно получить эрмитовым сопряжением поля. Это свойство подчеркивает тесную связь между частицами и античастицами в данной теории.
Второе свойство демонстрирует, что при непрерывном преобразовании, как бы мы ни изменяли поле, сохраняя его гладкость, невозможно изменить заряд. Это свойство аналогично ситуации в модели обмоток кривой линии вокруг точки или окружности, где невозможно непрерывным образом модифицировать кривую, чтобы изменить число оборотов. Здесь подчеркивается устойчивость топологического заряда к непрерывным преобразованиям, что делает его ключевым параметром для классификации различных конфигураций поля.
Третье свойство демонстрирует, что при "наложении" двух решений их заряд суммируется (хотя это не обязательно формирует точное статическое решение поля). Под наложением для унитарного поля понимается умножение. В случае модели Френкеля-Конторовой (ФК) из предыдущей статьи, поле выражено через угол, и углы складываются при умножении соответствующих комплексных чисел или экспонент.
Мы получили мощный результат: если мы сконфигурируем поле с гладким переходом, то как бы не развивалась система (сама, под воздействием внешних полей, вручную) при условии сохранения непрерывности поля, мы можем установить, что топологический заряд не исчезнет. В случаях локальной конфигурации, когда на удаленности плотность энергии нулевая (есть другие варианты моделей с бесконечной энергией), мы можем оценить границу минимальной статической энергии топологического солитона.
Условие сохранения заряда дает потенциальную возможность существования топологических солитонов, но не является достаточным. Дело в том, что в моделях, в которых существует топологический заряд, решения могут разрушаться по другим причинам. Они должны быть также энергетически устойчивыми, чтобы обеспечить долгосрочное сохранение структуры солитона и его свойств.
Столкновение с ограничениями: Теорема Хобарта-Деррика
Одномерное уравнение СГ имеет особую структуру и свойства, которые определяют его специфическое поведение, лоренц-ковариантность, устойчивые частицеподобные волны, существование положительных и отрицательных зарядов. Это делает его интересным объектом исследования, как в теоретической, так и в экспериментальной физике. И, как мы уже упоминали выше, простейшим путем расширения уравнения СГ на трехмерный и двумерные случаи могло быть добавление соответствующих пространственных производных. Для исследования еще более сложных вариантов можно вместо скалярного поля использовать набор скаляров (вектор), а вместо периодической функции подставить какую-нибудь более сложную. Но в результате подробного рассмотрения каждого из этих вариантов расширения окажется, что существование устойчивых решений не получится. Можно определить класс тупиковых направлений расширений. В 1963 году Р. Хобарт и в 1964 Г. Деррик установили условия на запрет существования стабильных локализованных решений в различных вариантах теории поля.
Р. Хобарт рассматривал классические модели с унитарным полем, а Г. Деррик начал с расширения на многомерный случай уравнения СГ, которое тогда снова всплыло совсем из другой области: при описании движения доменных стенок в магнитном кристалле. Высказывалось предположение, что у частиц могут быть аналогичные свойства и поэтому можно попытаться расширить уравнение.
Основная идея проверки существования устойчивых решений состоит в сравнении энергии стационарного решения по сравнению с энергией преобразованного масштабированием того же решения, то есть с уменьшенной или увеличенной его копией. Если энергия преобразованного решения ниже чем энергия исходного, то это означает, что исходное решение неустойчиво с энергетической точки зрения. На графике это выглядит так:
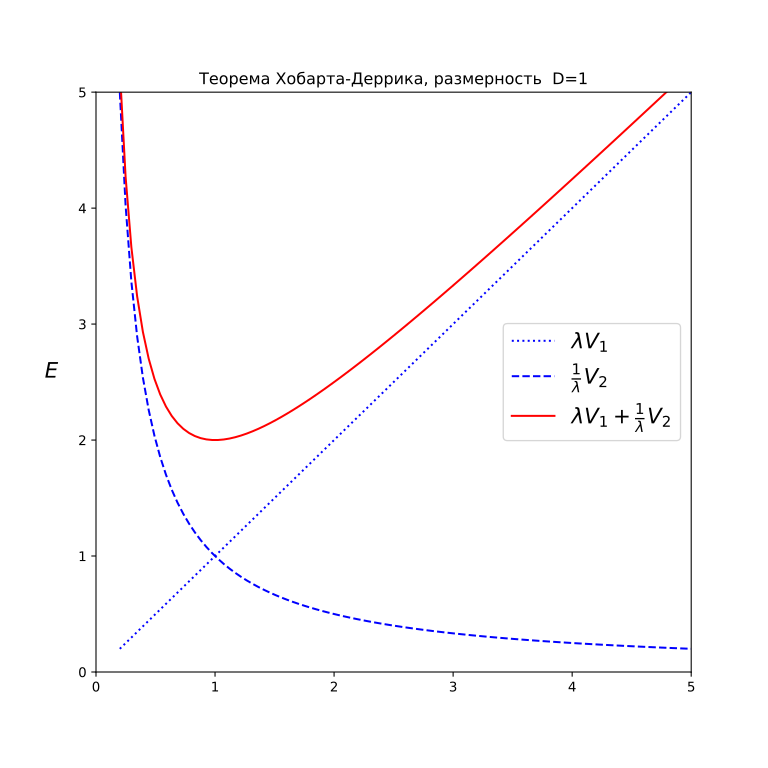
Синими линиями обозначены составляющие энергии: точками так часть энергии, которая зависит от второй степени производных. В одномерном случае она прямо пропорциональна масштабному коэффициенту: при масштабирования энергия вторых производных увеличивается квадратичным образом , как и энергия сжимаемых пружин в модели ФК, в тоже время интеграл берется в уменьшенном пространстве и его значение изменится в
раз. Для одномерного случая общий показатель степени станет равен
. Штриховым пунктиром обозначена часть энергии связанной с потенциальной функций (массовому члену), само ее значение не изменяется в соответствующих точках, но из-за уменьшения объема интегральное значение изменится в
раз. Для одномерного случая общий показатель степени второй части энергии станет равен -1. Таким образом полная энергия, обозначенная на графике красной линией, являющейся суммой двух частей, будет иметь минимум.
В двумерном же расширении уравнения полная энергия не имеет минимума в ограниченном объеме:
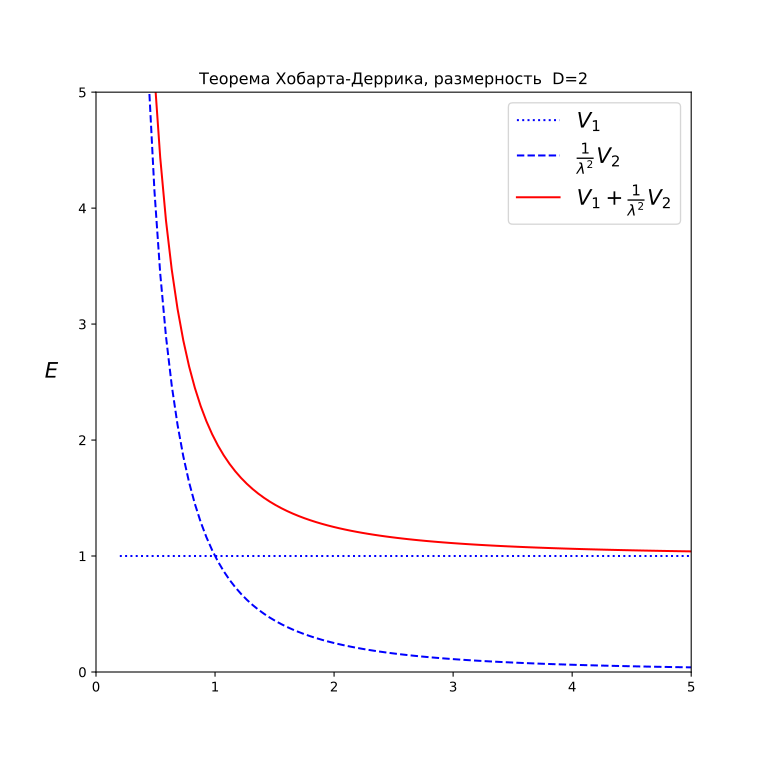
Неустойчивость решения, даже и обладающее топологическим зарядом, но имеющие зависящими от масштабного фактора разные составляющие энергии, можно представить на вымышленном примере ("сферического коня в вакууме") мыльного пузыря, представив, что внутри и снаружи него нет воздуха. Энергия поверхностного натяжения пропорциональна площади поверхности $ ~ r^2$ и сожмет его в точку. Если же рассматривать энергии для обычного мыльного пузыря в воздухе, то добавляется энергия сжатого воздуха заключенного в пузырь, которая имеет уже обратную зависимость от радиуса, поэтому полная энергия имеет минимум при некотором радиусе, что обеспечивает энергетическую устойчивость мыльного пузыря.
Однако заметим, что теорема Хобарта-Деррика касается стационарных и локализованных решений, ею не запрещены пульсирующие решения и она не ограничивает существования решений в виде бесконечных линий в двухмерном пространстве, стенок в трехмерном или глобальных струн.
Обзор различных случаев обхода
Заметим, что вакуумное решение обходит теорему Хобарта-Деррика во всех измерениях, потому что по определению вакуум — это постоянное в пространстве поле, в котором потенциал принимает минимальное значение, поэтому .
Существует возможность обойти теорему в двух измерениях, если , если потенциальный член
отсутствует. В этом случае
не зависит от
и таким возникают локальные решения сигма-модели (sigma model lumps)
Другой способ обойти теорему в скалярной теории поля состоит в том, чтобы включить члены в лагранжиан и энергию, включающие более высокие порядки производных или более высокие их степени. Это приводит к двумерным скирмионам и к скирмионам в трехмерном случае. Мы это сделаем в следующем разделе.
Глобальные вихри обходят теорему, потому что они имеют бесконечную энергию.
В калибровочной теории со скалярным полем общий функционала энергии (с упрощением алгебраической структуры и без учета числовых коэффициентов) после масштабирования имеет вид . Если
или
, то
имеет минимум в некотором диапазоне. Это связано с тем, что получается непрерывная функция, ограниченная снизу нулем, стремящаяся к бесконечности как при
так и при
. Таким образом, решения не исключены в двух или трех пространственных измерениях, и действительно существуют калиброванные вихри в двух измерениях и калиброванные монополи в трех измерениях. Рассматривая случай
можно также установить, что четырехмерном евклидовом пространстве-времени калибровочная теория со скалярами нетривиальных решений не имеет.
В чистой калибровочной теории Янга-Миллса члены, отсутствуют и
и
. В размерности отличной от 4, у функции нет стационарной точки поэтому существует только вакуумное решение. Однако в четырехмерном евклидовом пространстве,
не зависит от масштаба, и возможны решения чистой теории Янга-Миллса типа инстантонов.
Добавление терма Скирма.
В предыдущем разделе мы выяснили, что в размерности (3+1) теорема Хобарта-Деррика запрещает существование стационарных решений для модели с плотностью лагранжиана
поэтому нам нужно модифицировать модель, чтобы оно включало или более высокие порядки производных или более высокие их степени. Причем так, чтобы (для моделирования пионов сохранялась симметрия .
Одна из таких модификаций связана с добавлением дополнительного члена в действие системы. Этот член называется топологическим термом и представляет собой подходящую комбинацию топологических инвариантов, зависящую от конфигурации поля и позволяющую компенсировать энергию, связанную с топологическим зарядом.
Существуют четыре варианта четвертого порядка, которые удовлетворяют требуемой глобальной симметрии:
Однако из них линейно независимы только 1-й и 2-й.
И Скирм выбрал особую их комбинацию, вычтя из второго варианта первый:
После некоторых преобразований эту комбинацию можно записать через коммутаторы
Теперь модификация нелинейной сигма модели путем добавления дополнительного члена (называемым дополнение Скирма ) приводит к лагранжину модели Скирма:
где безразмерный параметр связи Скирма, а 1/16 коэффициент нормализации.
Рассмотрев теорему Хобарта-Дерика применительно к нашей модели, мы получим такую зависимость энергии от масштабного фактора .
где составляющая энергии статического решения зависящая от второй степени производных, связана с частью лагранжиана нелинейной сигма модели, а
, связанной со скирмовской поправкой, зависит от четвертой степени производных.
Отсюда выходит, что локальный минимум существует для всех пространственных измерений с размерностью
В принципе мы уже имеем достаточную информацию, чтоб рассчитать нижнюю границу энергии статического решения. Сейчас ее называют границей Богомольного - Прасада - Соммерфилда (1975), хотя в частном случае для своей модели Скирм определил ее раньше.
Например, для одного скирмиона с зарядом граница массы получается такая:
Используя экспериментальные оценки значений и
, мы находим, что
. На всякий случай отметим, что существует несколько соглашений, которые различаются коэффициентами
. В одних источниках используется значение 184 МэВ, в других 93 МэВ.
Простейший скирмион. Ежовый анзац.
Уравнение модели Скирма, которое следует из лагранжиана модели, существенно нелинейное и его невозможно аналитически решать в общем случае, поэтому можно попробовать рассмотреть простые симметричные конфигурации, чтобы представить как выглядит поле скирмиона, Скирм предложил самую максимальную симметрию в виде "сферически симметричного" статического анзаца.
где искомая функция от радиуса
, а
радиальный единичный вектор в сферически полярных координатах. Сравнивая с (2), мы видим этот анзац соответствует пионному полю
Следовательно пионное поле сферически симметрично, как показано на рисунке. Такая структура известна как "ежовый анзац".
При этому сам анзац не гарантирует что решение будет энергетически устойчивое, лишь много позже, в 1986 году M. Эстебан доказал существование скирмиона B = 1, т. е. функционала минимизирующего энергию, следуя более ранней работе Л.В. Капитанского и О.А. Ладыженской (1983), в которой было доказано, что существует экстремум в семействе сферически-симметричных 1-зарядовых полей Скирма. Считается верным, хотя и не доказанным, что эти два экстремума одинаковы, то есть что скирмион с минимальной энергией в секторе B = 1 сферически симметричен.
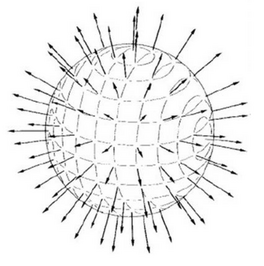
Другие графические представления ежового анзаца.

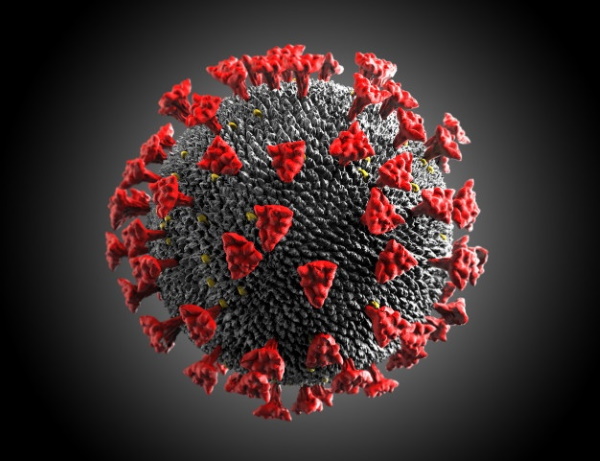
Рассмотрим граничные условия которые необходимо наложить на функцию пионного поля. Во первых энергия должна быть конечна, поэтому на бесконечности оно должно стремиться к вакуумному состоянию, которое мы для определенности выбрали как . В терминах ежового анзаца это приводит к
Во вторых, поле должно быть везде непрерывным. В основном непрерывность достигается непрерывностью радиальной функции f(r), но оно должно быть непрерывным и в центре при что накладывает дополнительное условие на нашу функцию. Перепишем поле ежового анзаца в виде, аналогичного тому (2), как мы делали ранее для пионного поля:
Заметим, что фактически полярный угол в групповом пространстве. Из-за непрерывности в начальной точке поле не может иметь компоненты "направленные наружу", следовательно граничное условие налагает
, что приводит к
Теперь попробуем для случая определить условие для функции которое минимизирует энергию, подставив ежовый анзац в функционал энергии
Получим:
которое не решаемо аналитически при граничных условиях , однако решаемо численно.
Теперь запишем уравнение Эйлера-Лагранжа
используя тождество синуса двойного угла и после некоторых преобразований мы получим обыкновенное дифференциальное уравнение второго порядка.
К сожалению это уравнение опять не решаемо аналитически, с полагаемыми граничными условиями, однако может быть решено численно.
Численное решение, изображенное на рисунке, дает оценку массы , что примерно на 23% больше чем дает оценка Богомольного.
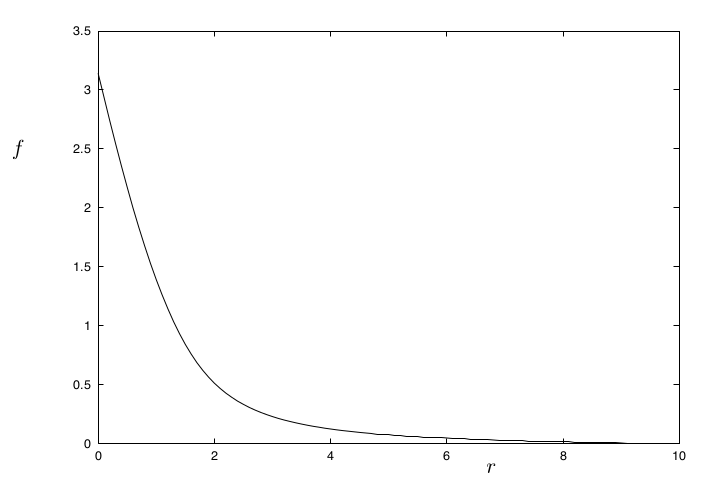
Вид функции похож, как и в одномерном случае уравнения СГ, на половину сигмоида, а также напоминает половину трактрисы, одной из кривой погони, вращение которой образует поверхность с постоянной отрицательной кривизной, также называемой псевдосферой.
Можно оценить среднеквадратичный радиус по формуле:
Рассматривая как волновой пакет с учетом среднеквадратичный радиус получится порядка одного фентометра (
метра).
И мы пока что рассматривали не массивную модель, в которой пионное поле само по себе не дает энергетики, кроме как через производные. Для более реалистичных моделей нужно добавить массивный член
где коэффициент пионной массы.
В одномерном уравнении СГ массовый член соответствует потенциалу периодической функции.
И мы здесь пропустим другие уточнения такие как член Весса-Зумино (1971), который к модели Скирма добавил Виттен (1983) и объяснил связь модели Скирма с КХД.
При квантовании появляются спины и изоспины, и разделение нейтронов и протонов.
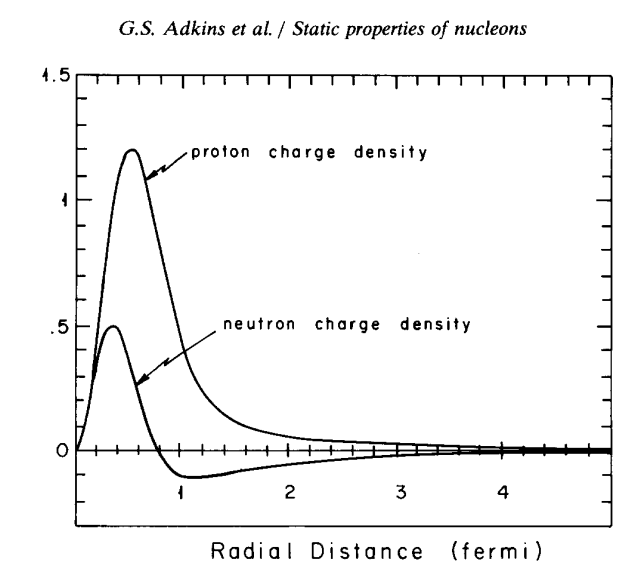
Моделирование более сложных нуклонов
В наиболее простом случае сферически-симметричного скирмиона с зарядом B=1 можно было использовать "ежевый анзац" для конфигурации поля и вычисления минимизации энергии лагранжиана Скирма, однако он не подходит для более сложных случаев.
В 1988 году Эрик Браатен и Ларри Карсон установили тороидальную структуру скирмиона как модель дейтрона с барионным зарядом B=2.
В 1990 Браатен, Таунсенд и Карсон предприняли интенсивный численный поиск скирмионов, и были найдены решения с минимальной энергией вплоть до B=5. (Их решение для B=6 оказалось довольно неточным.)
В 1997 Ричард Бэтти и Пол Сатклифф нашли все скирмионы вплоть до B=8. Затем с применением новых методов они нашли решения-кандидаты до B=22
В тоже время Конор Хоутон, Николас Мэнтон и Пол Сатклифф продемонстрировали, что структуру известных скирмионов можно понять с точки зрения анзаца, используя рациональные отображения, поэтому для скирмионнов с более высоким барионным зарядом было предложено использовать "анзац рационального отображения" [Бэтти (2001), Feist (2013)] и "анзац двойного рационального отображения" [Мэнтон (2000)]
В терминах отображений между сферами Римана рациональное отображение - это голоморфная функция . На первой сфере
координаты
, тогда рациональное отображение степени
задается функцией
через отношение полиномов
где и
полиномы степени не выше
и по крайней мере один их них имеет степень в точность равной
. При этом они не должны иметь общих корней (то есть общих множителей вида
, то есть нет сокращения). Слово "рациональное" показывает, что используется отношение (ratio) подобно определению рациональных чисел. Случай "ежового анзаца" соответствует
.
Рациональные отображения
И изначально рациональные отображения были применены для монополей [Donaldson (1984)], и была установлено однозначное соответствие между N-монополями и отображениями степени N. Но этот подход основывался на направлении в трехмерном пространстве, и не применим в данном контексте. Позже Стюартом Джарвисом (2000), по совету Майкла Атья, был установлен другой подход взаимосвязи. Он требует выбора начала координат и гораздо лучше подходит для изучения полей, инвариантных относительно подгруппы группы вращений вокруг начала координат.
Там для остается одна неоднозначность. Если провести калибровочное преобразование, то R(z) заменяется его преобразованием Мёбиуса на
матрицу
где .
Здесь SU(2) матрица является матрицей калибровочного преобразования, оцениваемой в начале координат, и она действует глобально на R (z), то есть одна и та же матрица встречается для всех z.
Заметим, что SU(2) преобразование Мёбиуса на двумерной сфере соответствует вращению единичного вектора и, следовательно, изоспиновому вращению поля Скирма.
С рациональным отображением связана важная величина "вронскиан"
или, точнее, нули , являющиеся точками ветвления отображения. Иногда вронскиан обладает большей симметрией, чем рациональное отображение
Рациональные отображения — это отображения сфер (обычных двумерных сфер, в трехмерном пространстве), в то время как Скирмионы — это отображения
, есть отображение между трехмерным евклидовым пространством и "объемной" сферой в четырехмерном. Довольно наивная идея состоит в том, чтобы отождествить сферу
с концентрическими сферами на
, а целевую
со сферами "широты" на трехмерной
. Это приводит к новому анзацу для полей Скирма. И можно полагать, что такие отображения помогут понять некоторые решения скирмионов. При этом в отличии от ежового анзаца, где численно искалась одномерная функция, анзац рационального отображения не дает существенных вычислительных упрощений.
Обратим также внимание, что это изменение в классической трактовке скирмиона, и поэтому оно вносится до того, как происходит какое-либо квантование.
Чтобы теперь показать результаты вычислений скирмионов как объемных структур пионного поля, как и визиулизации томографии можно использовать изоповерхности пионного поля и некоторую раскраску кодирующую информацию о его компонентах.
Для скирмиона с B=1 мы показали, что конфигурация безмассового пионного поля уменьшается сферически-симметричным образом при удалении от начала координат. (см. рисунки "ежевый анзац" и "функция F(r)"). Следовательно, если бы мы построили изоповерхность пионного поля, мы бы описали сферу. Поскольку для моделирования одиночного бариона используется триплет пионного поля, эта изоповерхность пионного поля непосредственно соответствует изоповерхности барионной плотности. Выбранная нами конфигурация поля всегда будет минимизировать функционал энергии по отношению к выбранному зарядовому/барионному числу, и, следовательно, это соответствие в общем случае верно.
Изображения изоповерхностей для первых восьми барионных зарядов выглядят так:

Также для визуализации информации о пионном поле на изоповерхностях барионной плотности, мы можем использовать цветовую схему Ф. О. Рунге ( 1810 г.) . Эта схема включает в себя сферу с полным цветовым спектром вокруг экватора и равномерный переход от 100% яркости на северном полюсе (белый) к 0% на южном (черный). Это кодирование цвета впервые было использовано в искусстве, но полезно и для иллюстрации скирмионов, так как может кодировать больше информации. К примеру, в этой схеме белые и черные области соответствуют значениям нормализованного пионного поля , где
соответственно, а
. Экваториальный цветовой круг находится там, где
близко к нулю, а основные цвета плавно переходят друг в друга с изменением компонент поля
.
Из-за того, что скирмион B = 1 имеет симметричную ежовую природу, раскраска воспроизводит саму цветовую сферу. В пределе пренебрегая переходами цветов, если вокруг сферы описать куб и раскрасить шесть его граней в соответствующие цвета, то цвет на сфере будет соответствовать цвету грани куба, на которую укажет вектор пионного поля.
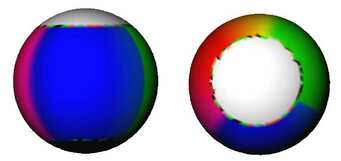
Другой вариант визуализации B=1

Изображения изоповерхностей в цветовой раскраске для первых восьми барионных зарядов:

Ежовый анзац B = 1 соответствует одному бариону и поэтому имеет самую низкую энергию из всех конфигураций, что объясняет, почему он является наиболее симметричным. Данное скирмионное решение было проквантовано с использованием гипотезы о том, что число оборотов мезонной теории поля можно интерпретировать как барионное число, и, следовательно, скирмион с B = 1 соответствует одному бариону. Это теоретическое упражнение оказалось успешным, поскольку оно предсказало разумные значения квантовых чисел и позволило Скирму идентифицировать барион как протон или нейтрон. Однако без каких-либо доказательств, подтверждающих эту гипотезу, логическое развитие скирмионов более высокого порядка оставалось неисследованным в течение многих лет.
В 1988 г. Э. Браатен и Л. Карсон опубликовали основополагающую работу о скирмионе с B = 2, который они обнаружили обладающим тороидальной симметрией и при квантовании отождествили с дейтроном (протон-нейтронной парой). Дейтрон состоит из протон-нейтронной пары, поэтому можно было бы ожидать, что барионная плотность будет иметь знакомую форму гантели. Однако более необычный тороидальный скирмион с B = 2 также имеет некоторую феноменологическую поддержку. Когда компонента спина вдоль оси z равна нулю, пространственная волновая функция дейтрона (или любой нуклон-нуклонной пары) будет сосредоточена в торе с осью z в качестве оси симметрии, что подтверждается вычислительными расчетами. Однако если составляющая вращения по оси z равна , то плотность частиц действительно будет иметь форму гантели, как и ожидалось. Это можно интерпретировать как тор с осью симметрии в плоскости x - y, вращающийся вокруг оси z; и поэтому наш скирмион с B = 2 также имеет последовательную физическую интерпретацию. Ссылка на статьи [Braaten (1988), Forest (1996), Battye (2006), Manko (2007), Brown (2010)] могут предложить дополнительные подробности этого вопроса.
Состояния с зарядом B = 3 и B = 4 проявляют соответственно тетраэдрическую и кубическую симметрию. Если мы рассмотрим квантование скаймрионов при B = 4, то можно связать их с ядром гелия, также известным как альфа-частица. Альфа-частица состоит из двух нейтронов и двух протонов.
Заметим, что изоповерхность B=4 "альфа частицы" можно сконструировать используя две "баранки" (торы) соединенные между собой одна над другой вдоль их общей оси, при этом подгоняя определенным образом "цвета" соответствующие пионному полю.
Аналогично B=6 можно создать с помощью трех "баранок" типа , при этом перевернув среднюю. Этот принцип предоставляет нам простой способ визуализации конструирования скирмионов более высокого порядка: мы можем объединить меньшие скирмионы, соотнося цвета на их стыках, а потом запуская расчет для уточнения.
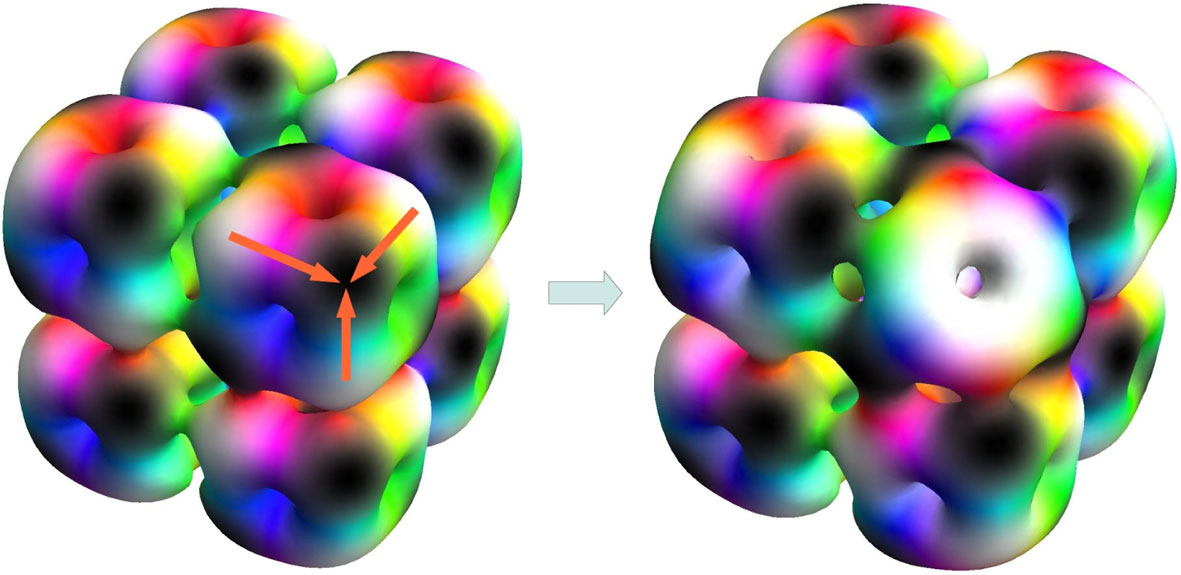
Однако использование одного простого рационального отображения для описания более высоких зарядов приводит к интересному явлению: все изоповерхности с более высокими барионными числами формируют полые многогранники, которые напоминают структуру углеродных фуллеренов. Причем отверстия расположены в направлениях, в которых вронскиан преобразования имеет нули, а количество таких отверстий .

В центре этих полых многогранников барионная плотность очень низкая, и полое ядро окружено оболочкой примерно постоянной толщины. Однако это не соответствует тому, что мы наблюдаем в реальных ядрах с барионными числами больше 6. Мы знаем, что барионная плотность должна быть примерно однородной по всему ядру. Кроме того варианте с массивным членом внутри полости значение поля дает большую значение энергию, и разрастание полости ее повышение и энергетическую неустойчивость.
Полое внутреннее устройство моделей, основанных на рациональных отображениях, - это не единственная сложность. Вторая проблема связана со спином и четностью. Когда мы приступаем к квантованию скирмиона с барионным числом B = 1, мы получаем квантовые состояния, которые соответствуют реальным частицам с B = 1. Такая ситуация успешно распространяется и на скирмион B = 2, а также на другие малые скирмионы. Однако стоит отметить, что эти квантовые числа в общем случае несовместимы. Например, давайте рассмотрим скирмион B = 7. Этот скирмион обладает додекаэдрической симметрией и кажется естественным продолжением структур скирмионов более низкого порядка. Тем не менее, при нулевом квантовании мы обнаруживаем, что низшее спиновое состояние для изоспина 1/2 соответствует спину 7/2, что не соответствует экспериментально наблюдаемым значениям спина 3/2 в основном состоянии некоторых B = 7 частиц, таких как литий и бериллий. Это говорит о том, что структура скирмиона B = 7, хотя и имеет высокую симметрию, может быть слишком симметричной для основного состояния. [Irwin (2000), Krusch (2003)]
Масса пиона также представляет собой значительную проблему. До сих пор мы часто пренебрегали массовым членом пиона, чтобы использовать большую симметрию безмассовой теории поля пиона. Для низких барионных чисел это оказывается довольно приемлемым подходом, так как исследования показывают, что решения относительно устойчивы к уменьшению массы пиона до нуля. Однако для более высоких барионных чисел этот предел уже не применим. Добавление массового члена пиона при больших полых многогранниках приводит к тому, что центр скирмиона имеет значение поля U = -1, противоположное вакуумному значению поля U = 1. Это делает структуру нестабильной, что приводит к ее сплющиванию и разрушению на более мелкие области. В данном контексте текущие исследования [Houghton (2007), Battye (2006a)] показывают, что характеристики скирмионов остаются неизменными по отношению к реальному (положительному и ненулевому) значению массы пиона, поэтому при моделировании скирмионов более высокого порядка часто используется масса, равная 1. [Battye (2005, 2006a), Houghton (2007), Manton (2011), Feist (2013)]
Что касается проблемы массы пиона, она решается простым включением массовый член пиона в наши расчеты.
Для решения проблемы минимизации энергии после квантования, кажется, что нам следует избегать ограничивающегося использованием анзацев одного единственного рационального отображения для построения скирмионов, которые минимизируют классическую энергию. Вместо этого нам, возможно, придется индивидуально рассматривать каждую частицу и использовать имеющиеся знания о ядерной структуре. Этот подход может быть особенно полезным при моделировании скирмионов более высокого порядка. [Feist (2013]
Кроме того, существует другой подход, исследованный Манотоном (2000), который рассматривает многооболочечные рациональные отображения. Этот подход может предоставить альтернативные пути для построения более сложных структур скирмионов, учитывая их поведение при квантовании и минимизации энергии.

Строительный подход
Кроме использования многооболочечных анзацев для моделирования сложных нуклонов со сложной симметрией, можно конструировать их модели путем соединения -частиц.
Еще с 1930-х годов было известно, что некоторые ядра состоят из этих строительных блоков. Например, ядра бериллия-8, углерода-12 и кислорода-16 состоят соответственно из двух, трех и четырех -частиц. Это факт дает нам некоторое представление о том, какие структуры скирмионов мы можем ожидать, когда моделируем эти ядра.
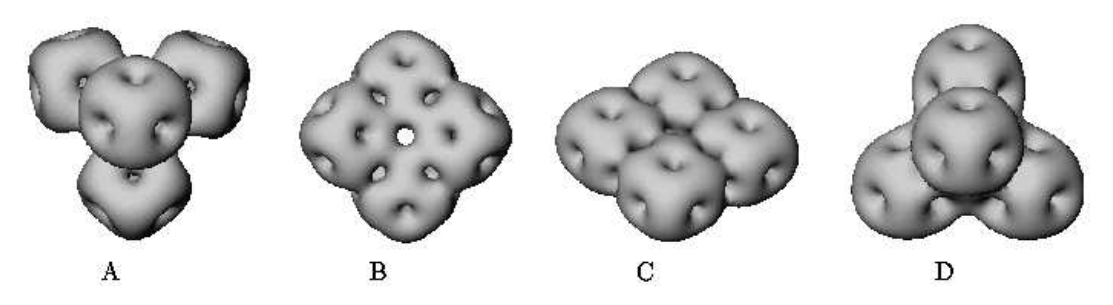
Состояния углерода-12 представляют особый интерес для физиков-ядерщиков, потому что они ясно демонстрируют пробелы в нашем современном понимании структуры ядра. В частности, интенсивные исследования были сосредоточены на особом состоянии углерода-12, известном как состояние Хойла.
Давайте окунемся в детали. В самом начале Большого взрыва были сформированы всего лишь три элемента: водород, гелий и небольшое количество лития. В дальнейшем более тяжелые элементы, такие как углерод, образовывались в звездах благодаря процессу ядерного синтеза. Тем не менее, одной из главных загадок остается вопрос о том, как углерод-12, который состоит из шести протонов и шести нейтронов, образовался. Чтобы произошло соединение трех -частиц, сначала необходимо, чтобы две
-частицы объединились, образуя ядро бериллия-8. И вот здесь возникает сложность.
Ядро бериллия-8 действительно может образоваться путем слияния двух -частиц, но оно обладает крайне коротким временем жизни, составляющим порядка
секунд. Здесь сталкиваемся с проблемой: углерод является важным элементом для жизни на Земле, и у нас наблюдается его значительное изобилие. Однако такое краткое время жизни бериллия подразумевает, что углерод имеет очень маленькую вероятность образования, что может не объяснить наблюдаемое изобилие углерода в настоящее время.
В 1953 году британский астрофизик Ф. Хойл предложил интересное решение этой проблемы. Он предположил, что существует короткоживущее возбужденное состояние углерода-12, известное теперь как состояние Хойла. Это возбужденное состояние может служить резонансом и ускорить образование углерода на многие порядки. Согласно его теории, это возбужденное состояние имеет энергию возбуждения около 7 МэВ. Позже эксперименты подтвердили существование этого состояния.
Таким образом теория, предложенная Хойлом, объясняет относительное изобилие углерода, необходимого для жизни на Земле. Однако текущая проблема заключается в том, что модель ядерной оболочки, лучшая модель ядерной структуры, которой мы располагаем в настоящее время, не предсказывает существование такого состояния. На самом деле подобные короткоживущие возбужденные состояния теперь наблюдаются и в других легких ядрах, которые модель также не может предсказать. Это свидетельствует о серьезном недостатке нашего понимания ядра, и эта тема является одной из наиболее активно изучаемых в области ядерной физики. Поэтому интересно посмотреть, что модель Скирма может сказать о состоянии Хойла.
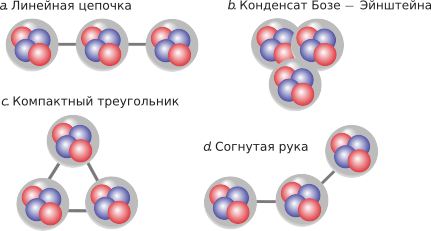
Рис.1. В 2014 г. Лау и Мантон опубликовали статью «Состояния углерода-12 в модели Скирма» для исследования этого вопроса. Они численно нашли скирмионные решения модели Скирма с B = 12, позволив симметричному расположению трех кубических скимионов с B = 4 релаксировать до решения с минимальной энергией. Их результаты привели к двум различным скирмионным конфигурациям, соответствующих компактному треугольному и линейному расположению -частиц. Затем они приступили к квантованию вращательного движения этих скирмионов и сосредоточились на результатах для изоспина 0. Результаты показали, что конфигурация компактного треугольника может быть отождествлена с основным состоянием
углерода-12 (плюс вращательные возбуждения), а конфигурация линейной цепи — с состоянием
Хойла (плюс вращательные возбуждения). Компактное треугольное основное состояние согласуется с результатами КХД, а также в некоторой степени интуитивно понятно. Однако состояние линейной цепи Хойла, по-видимому, не согласуется с текущим консенсусом "согнутых рук". Более того, моделирование скирмионов не смогло подтвердить энергию возбуждения примерно 7 МэВ из-за численных неопределенностей.
Высшие барионные числа
Использование простого анзаца рационального отображения может приводить к неточному масштабированию объема ядра и неверному определению спина/четности для основного состояния. Однако, для преодоления этих проблем и для более точного описания структуры ядра, был предложен метод построения скирмионов с использованием так называемого "кристалла Скирма".
Этот кристалл представляет собой повторяющуюся структуру, состоящую из более мелких фрагментов-скирмионов.
После применения начальной конфигурации кубов B = 4, скирмионы с числом барионов B = 8, 24, 32, могут быть составлены из нескольких таких кубических блоков, объединенных в соответствующей геометрической конфигурации, и затем последующим численным получением минимизирующих энергию конструкций. Более того, если мы не ограничиваемся исходной конфигурацией, состоящей исключительно из кубов, и применяем более общую геометрическую структуру, то мы обнаружим, что скирмионы «естественным образом» имеют тенденцию группироваться в B = 4 субъединицы, а некоторые скирмионы даже могут быть построены. из различных строительных блоков. Например, скирмион B = 25 построен из кластера, включающего в себя три тетраэдра с B = 3 и четыре куба с B = 4.
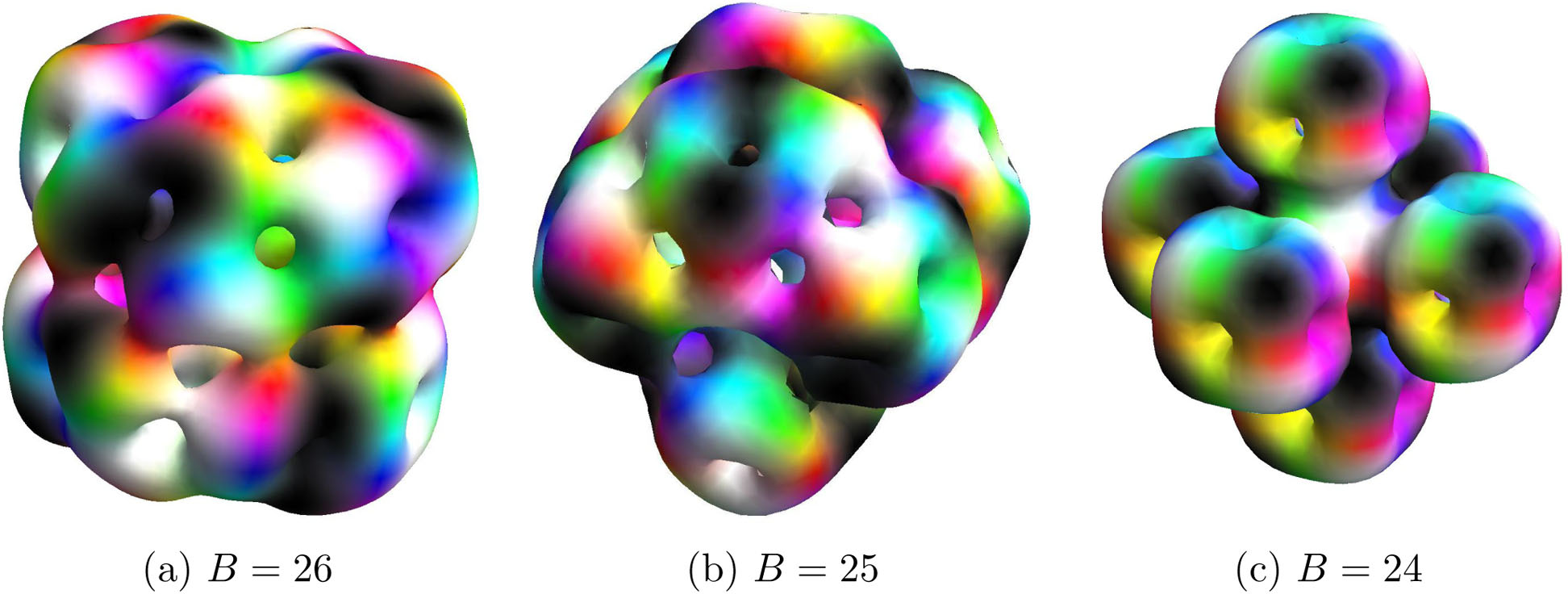
Наибольшей конструкцией скирмиона, показывающей соответствие реальным ядерным энергиям, в настоящее время является скирмион B = 108, состоящий из 27 кубов B = 4 с использованием анзаца трехслойной рациональной карты. Эта структура поистине напоминает кристаллическую решетку.
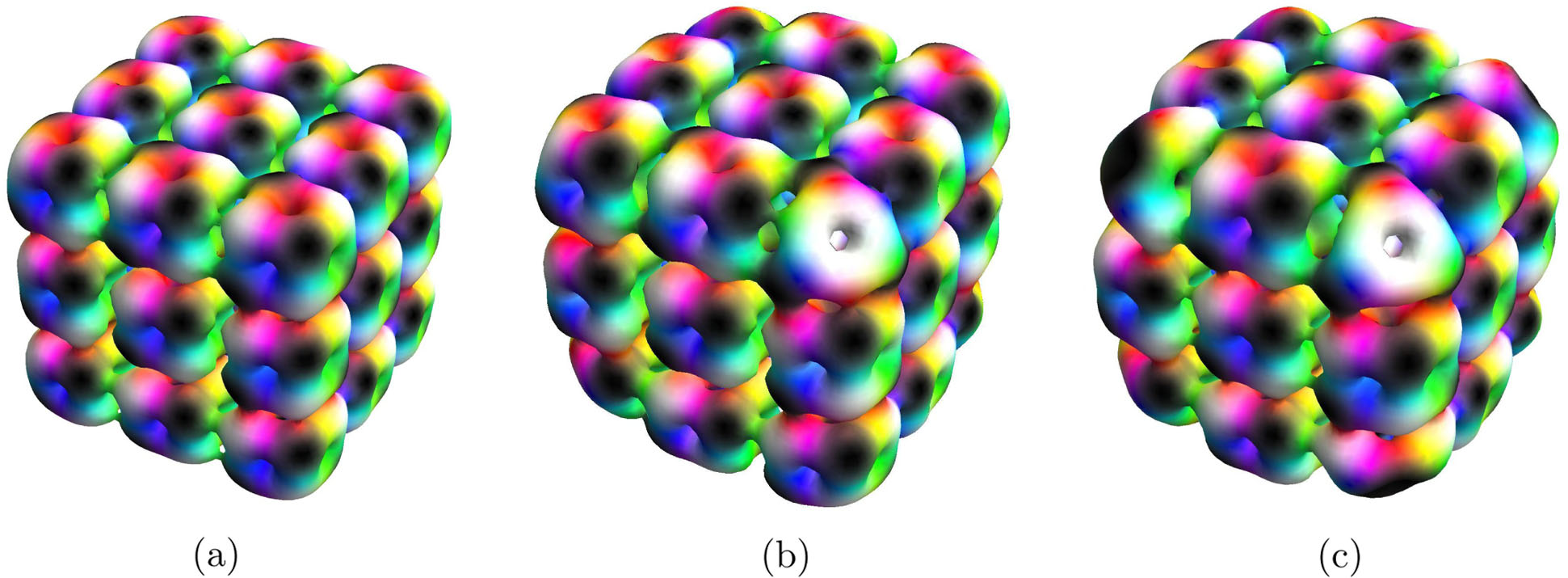
Кроме того, был предложен метод "срезания углов", позволяющий создавать скирмионы меньшего порядка путем удаления угловых барионов из более крупных кубических скирмионов. Напомним, что притяжение цветов на наших диаграммах означает, что белые области будут притягиваться к другим белым областям. Следовательно, в углу наших больших кубических скирмионов энергетически устойчиво переместить три белые области, окружающие угол, в угловую черную область, чтобы создать большую белую область с отверстием. Таким образом, мы можем удалить угловые барионы из более крупных кубических скирмионов, чтобы получить скирмионы более низкого порядка. Например, из скирмиона с числом барионов B = 108 можно удалить восемь угловых барионов и получить скирмион с числом барионов B = 100. Этот метод успешно применяется для множества значений чисел барионов и является эффективным способом решения проблемы масштабирования и структуры ядра в рамках модели Скирма. Метод срезания углов был впервые введен для получения скирмионов B 24-31 из большого куба B = 32 (состоящего из четырех кубов B = 4)
Скирмионы и фермионы
Теперь давайте разберемся, почему скирмионы, построенные из бозонов, могут стать фермионами. Этот удивительный результат был разрешен благодаря работе Эдварда Виттена в 1983 году. Он предложил решение этой загадки, осознав, что скирмион может быть фермионом, если основная теория, лежащая в его основе, имеет нечетное число цветов.
Итак, что это означает? В контексте квантовой хромодинамики (КХД), которая описывает сильные взаимодействия кварков и глюонов, цвет - это заряд, аналогичный электрическому заряду в электромагнетизме. Кварки, из которых состоят барионы, имеют три разных "цвета" - красный, зеленый и синий. Но в отличии от электрического заряда, кварки несущие цветовой заряд соединяются внутри адрона, а цвета смешиваются аналогично, как красный, зеленый и синий свет смешиваются в белый цвет. Термин "цвет" символизирует этот процесс, который называется "смешением цветов" и важен для понимания кварковой конфайнмента - явления, при котором кварки не могут существовать как свободные частицы. Мезоны, с другой стороны, состоят из двух кварков и, следовательно, имеют один цвет и один антицвет.
Теперь, когда мы говорим о нечетном числе цветов, мы имеем в виду, что в основной теории, описывающей скирмионы, число цветов не является кратным двум. Это важное условие, которое делает скирмионы фермионами.
Исследуем энергию: Вычисления B=1 с помощью pytorch
Возвращаясь к простейшему случаю ежового анзаца B=1. Давайте погрузимся в мир вычислений и использования передовых инструментов, чтобы решить сложную задачу минимизации энергии ежового анзаца. В наши дни мы можем воспользоваться мощью библиотек, разработанных в области машинного обучения, чтобы достичь наших целей. Одной из ключевых задач в этом контексте является поиск минимума функции потерь (так называемой лосс-функции ), что является обычным подходом при обучении нейронных сетей. Мы будем использовать библиотеку pytorch, тднако вместо поиска оптимальных весов модели, нашей целью будет поиск оптимальных значений функции , представленных на одномерной сетке вдоль радиуса. Вместо применения дифференцирования, мы будем использовать операцию свертки с фиксированными весами (1, -1). Таким образом, определив "лосс-функцию" как энергию системы, формула которой в зависимости от функции дана выше, мы сможем создать простейшую модель и запустить ее на обучение. Только оптимизация будет не коэффициентов конволюций, а значений сетки.
Основные нестандартные методы модели:
def energy(self):
"""
Потенциальная энергия.
"""
# Получаем текущие значения искомой функции
# вместе с фиксированными границами
f = self.u_with_bounds()
# Вычислим производные.
df = (self.calc_diff(f) / self.hx)
# При вычислении проивзодной число узлов на решетке уменьшено на 1
# поэтому остальные вычисления проивзодим на укороченнной решетке
f = f[:-1]
# вычисление вспомогательных переменных
sinf = torch.sin(f)
r = self.radius_ls
r2 = r ** 2
df2 = df ** 2
sinf2 = sinf ** 2
# вычисление энергии на узлах решетки
e = r2 * df2 + 2 * (1 + df2) * sinf2 + sinf2 ** 2 / r2
# учитываем шаг решетки
e = e * self.hx
# суммирование проивзодится в агррегаторе автоматиччески
# e = e.sum() * self.hx
# общий коээфициент
return e * self.pi2
def u_with_bounds(self):
"""
Добавление граничных условий к функции u.
"""
return torch.cat([self.bound1, self.u, self.bound2])
Полный код прорграммы
import torch
import numpy as np
import datetime
from pathlib import Path
from matplotlib import pyplot as plt
import plotly.graph_objects as go
DIR_OOUTPUT = Path('./output')
class Skyrme_Model_B1(torch.nn.Module):
def __init__(self, N=10, hx=1):
"""
Инициализация модели Skyrme с барионным зарядом B=1.
Параметры:
- N: Количество узлов на одномерной сетке.
- hx: Шаг по радиусу.
"""
super().__init__()
# Задаем параметры модели
# число узлов на решетке
self.N = N
# Оптимизируемые параметры:
# искомая энергия, как функция от радиуса на узлах решетки
self.u = torch.nn.Parameter(torch.zeros(N))
# Необучаемые параметры:
# шаг сетки
self.hx = torch.nn.Parameter(hx * torch.ones(1), requires_grad=False)
# фиксированные границы
self.bound1 = torch.nn.Parameter(torch.ones(1), requires_grad=False)
self.bound2 = torch.nn.Parameter(torch.ones(1), requires_grad=False)
self.hx_numpy = hx
# Создаем сетку на радиусе
self.radius_ls = hx * (1 + torch.arange(N + 1))
self.radius_ls = torch.nn.Parameter(
self.radius_ls,
requires_grad=False)
# Предвычисляем некоторые константы
self.pi4 = torch.nn.Parameter(
torch.tensor(4 * torch.pi),
requires_grad=False)
self.pi2 = torch.nn.Parameter(
torch.tensor(2 * torch.pi),
requires_grad=False)
# Создаем одномерную сверточную операцию
self.conv1 = torch.nn.Conv1d(
in_channels=1, out_channels=1, kernel_size=2,
padding=0, padding_mode='zeros',
bias=False)
with torch.no_grad():
# Дифференцирование можно выразить как свертку с весами (1, -1)
self.conv1.weight.copy_(torch.Tensor([[[1, -1]]]))
# Веса свертки не обучаются
self.conv1.weight.requires_grad = False
def init_state(self, left=0, right=2 * np.pi):
"""
Инициализация начального состояния модели.
Параметры:
- left: Левая граничная условие.
- right: Правая граничная условие.
"""
u = self.u
N = self.u.size()[0]
# Начальное значение зададим как простую ступенчутую функцию от радиуса
n1 = N // 2
u1 = np.ones(n1) * left
u2 = np.ones(N - n1) * right
u0 = np.hstack([u1, u2])
u0 = u0.astype(np.float32)
t_u0 = torch.from_numpy(u0)
# заполняем данные
with torch.no_grad():
u.data = t_u0
# значения на границах
self.bound1.data = torch.ones(1) * left
self.bound2.data = torch.ones(1) * right
def forward(self, x):
"""
Прямой проход модели.
Параметры:
- x: Множитель для энергии.
Возвращает:
- Список, содержащий энергию и функцию u.
"""
energy = self.energy() * x
u = self.u_with_bounds()
# кроме суммарной энергии вовзращаем массив значений функции
return [energy, u]
def energy(self):
"""
Потенциальная энергия.
"""
# Получаем текущие значения искомой функции
# вместе с фиксированными границами
f = self.u_with_bounds()
# Вычислим производные.
df = (self.calc_diff(f) / self.hx)
# При вычислении производной число узлов на решетке уменьшено на 1
# поэтому остальные вычисления проивзодим на укороченнной решетке
f = f[:-1]
# вычисление вспомогательных переменных
sinf = torch.sin(f)
r = self.radius_ls
r2 = r ** 2
df2 = df ** 2
sinf2 = sinf ** 2
# вычисление энергии на узлах решетки
e = r2 * df2 + 2 * (1 + df2) * sinf2 + sinf2 ** 2 / r2
# учитываем шаг решетки
e = e * self.hx
# суммирование проивзодится в агррегаторе автоматиччески
# e = e.sum() * self.hx
# общий коээфициент
return e * self.pi2
def u_with_bounds(self):
"""
Добавление граничных условий к функции u.
"""
return torch.cat([self.bound1, self.u, self.bound2])
def calc_diff(self, a):
"""
Вычисление производной.
В модели реализовано несколько технических вариантов
вычисления производной с соответствующими методами
объекта описанных ниже.
"""
# В данном случае выбран вариант вычисления производной
# с использованием операции свертки (конволюции)
return self._calc_diff_as_conv(a)
def _calc_diff_native(self, a):
"""
Стандартный метод библиотеки torch
"""
return torch.diff(a)
def _calc_diff_onnx(self, a):
"""
Вычисление производной, совместимой с экспортом в ONNX.
"""
a1 = a[1:]
a2 = a[:-1]
return a1 - a2
def _calc_diff_as_conv(self, a):
"""
Вычисление производной с использованием свертки.
"""
res = self.conv1(a.reshape(1, -1))
return res.reshape(-1)
def u_numpy(self):
"""
Преобразование функции в массив NumPy.
"""
uu = self.u_with_bounds()
uu = uu.cpu().detach().numpy()
return uu
class Trainer():
def __init__(self, model):
"""
Инициализация трейнера.
Параметры:
- model: Модель, которую нужно обучать.
"""
self.model = model
def init_criterion(self):
"""
Инициализация критерия функции потерь
"""
self.criterion = torch.nn.modules.loss.L1Loss(reduction='sum')
def init_optimizers(self, **cfg):
"""
Инициализация оптимизатора и планировщика шага обучения.
Параметры:
- cfg: Словарь с конфигурацией оптимизатора и планировщика.
- lr: Скорость обучения (learning rate).
- epochs: Количество эпох обучения.
"""
lr = cfg['lr']
epochs = cfg['epochs']
self.optimizer = torch.optim.Adam(self.model.parameters(), lr=lr)
# шаг обучения будет расти и уменьшаться по циклу вида OneCycleLR
self.scheduler = torch.optim.lr_scheduler.OneCycleLR(
self.optimizer, max_lr=lr,
steps_per_epoch=self.steps_per_epoch,
epochs=epochs)
def init_data_dummy(self):
"""
Инициализация фиктивных данных для обучения.
"""
# фиктивные входные данные для обучения равны единице
# на нее будет умнажаться энергия.
self.x_dummy = torch.ones(1)
# Целевые данные, к которым должна стремиться энергия, зададим нулем.
self.y_target = torch.zeros(self.model.N + 1)
# Число итераций в каждой эпохе
self.steps_per_epoch = 200
def to(self, device):
"""
Перемещение данных и модели на устройство (CPU/GPU).
Параметры:
- device: Устройство, на котором будет производиться обучение.
"""
self.x_dummy = self.x_dummy.to(device)
self.y_target = self.y_target.to(device)
def train(self, epochs=30, lr=1e-2):
"""
Обучение модели.
Параметры:
- epochs: Количество эпох обучения.
- lr: Скорость обучения (learning rate).
"""
self.init_criterion()
self.init_optimizers(epochs=epochs, lr=lr)
t0 = datetime.datetime.now()
for t in range(self.steps_per_epoch * epochs):
x_dummy = self.x_dummy
y_target = self.y_target
# Прямой проход: Вычисление прогноза y, подавая x на вход модели
r = self.model(x_dummy)
y_pred = r[0]
# u_state = r[1]
# Вычисление и вывод результата функции потерь
loss = self.criterion(y_pred, y_target)
if t % 500 == 499:
print(t, self.scheduler.get_last_lr(), loss.item())
# Обнуление градиентов, выполнение обратного прохода
# и обновление весов
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
self.scheduler.step()
t1 = datetime.datetime.now()
print(f"Время обучения: {(t1 - t0)}")
def main():
"""
Основная функция программы: конструирование модели и трейнера
и их инициализация, запуск обучения, вывод результата
в виде графика функции.
"""
# Construct our model by instantiating the class defined above
model = Skyrme_Model_B1(N=2000, hx=0.005)
model.init_state(np.pi, 0)
trainer = Trainer(model)
trainer.init_data_dummy()
device = 'cpu'
# device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
trainer.to(device)
optimizer = 'Adam'
# Первые 50 эпох запустим с максимальным шагом 0,01
lr = 1e-2
trainer.train(epochs=50, lr=lr, optimizer=optimizer)
# Вывод промежуточных результатов полной энергии:
# 499 [0.0010409845525281031] 207593.546875
# 999 [0.002797097538826506] 50292.1796875
# 1499 [0.005197485887954694] 1381.8104248046875
# ...
# 8999 [0.0004951936798652628] 277.37518310546875
# 9499 [0.00012539993764912555] 275.2286376953125
# 9999 [4e-08] 274.85186767578125
# Train time: 0:00:12.745770
# Потом запустим несколько раз по 100 с шагом 0,001
lr = 1e-3
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
trainer.train(epochs=100, lr=lr, optimizer=optimizer)
# Вывод промежуточных результатов полной энергии:
# 499 [5.62960192384632e-05] 265.6378173828125
# 999 [0.00010420310855962904] 253.8949432373047
# 1499 [0.00018045546250708834] 241.1505126953125
# ...
# 18499 [2.8062222612476826e-05] 72.85843658447266
# 18999 [1.2539993764912554e-05] 72.85798645019531
# 19499 [3.1478824777984842e-06] 72.85778045654297
# 19999 [4e-09] 72.85774230957031
# Визуализация результата как график радиальной функции
# Простой график
uu = model.u_numpy()
xx = np.arange(len(uu)) * model.hx_numpy
plt.plot(xx, uu)
# Интерактивный график plotly
fig = go.Figure()
fig.add_trace(go.Scatter(
x=xx, y=uu,
mode='lines',
name='F(r)'))
fig.update_layout(
title='Skyrmion Hedgehog ansatz B=1 numeric solution',
xaxis_title=r'$x = e f_{\pi}r$',
width=800, height=600)
fig.layout["annotations"] = (
{
"x": -0.1, "y": 0.45, "text": "$F(x)$",
"font": {"size": 10},
"textangle": 0,
"showarrow": False, "xref": 'paper', "yref": 'paper',
},
)
fig.show()
fig.write_html(
DIR_OOUTPUT / 'hedgehog_anzatz_plotly.html',
include_mathjax='cdn')
main()
Результат вычислений:
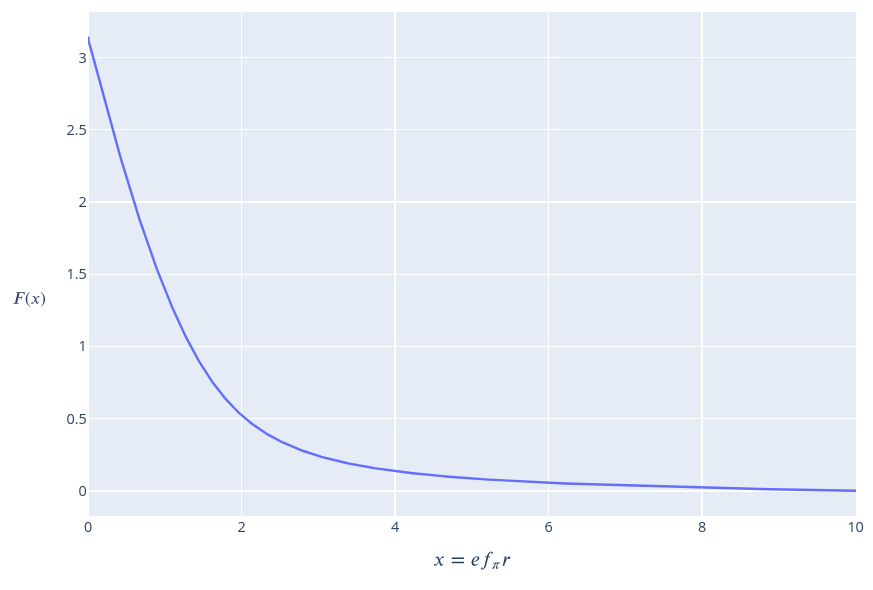
Как видим, результат полностью совпадает с расчетами Мантона (2004), приведенные выше на рисунке 23. Интерактивная версия этого графика выполненная на plotly находится по ссылке.
Для расчета более сложных скирмионов, размерность сетки будет многомерной и время вычисления при той же точности возрастет на несколько порядков. Поэтому имеет смысл использовать, например, адаптивные а не регулярные решотки.
Заключение
Изучая модель синуса-Гордона в измерениях 1+1, мы расширили понимание о том, как теории поля порождают солитонные решения. Солитоны обладают особыми свойствами, которые делают их топологически и энергетически устойчивыми, что ведёт к их выдающейся роли в различных физических системах.
Скирмионы, имеющие свои корни в работах Тони Скирма, являются такими солитонами и показывают, как можно взглянуть на частицы в ядерной физике с новой перспективы. Эти объекты, начиная с их введения в 1960-х годах, стали ключевыми в понимании ядерной структуры и нашли применение в различных областях физики.
Однако, как и любая модель, скирмионная модель имеет свои ограничения. На текущий момент она не может описать все известные частицы, а её применение остается в рамках эффективной теории. Тем не менее, пионы не являются единственными частицами, которые можно рассмотреть в этом контексте. С помощью современных вычислительных методов сейчас активно изучаются модели скирмионов, которые включают в себя не только пионы, но и ро-мезоны, что позволяет более полно описывать различные ядерные системы. Ниже представлена иллюстрация, демонстрирующая между пионами и ро-мезонами.

Что дальше?
В следующей статье мы углубляемся в мир магнитных скирмионов. Их история, значение и применение, например, в нейроморфных компьютерах, будут раскрыты. Кроме того, мы будем освещать разнообразные применения модели синуса-Гордона в различных областях природы.
Список литературы
Работы Скирма и коллег в 1960-х годах:
T. H. R. Skyrme, 1958, A non-linear theory of strong interactions, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 247(1249), pp. 260-278, doi
T. H. R. Skyrme, 1961, A non-linear field theory, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 260(1300), pp. 127-138, doi
J. K. Perring, T. H. R. Skyrme, 1962, A model unified field equation, Nuclear Physics, 31, pp. 550-555, doi
T. H. R. Skyrme, 1962, A unified field theory of mesons and baryons, Nuclear Physics, 31, pp. 556-569, doi
T. H. R. Skyrme, 1988, Origins of Skyrmions, International Journal of Modern Physics A, 03(12), pp. 2745-2751, doi
D. Finkelstein, C. W. Misner, 1959, Some new conservation laws, Annals of Physics, 6(3), pp. 230-243, doi
D. Finkelstein, 1966, Kinks, Journal of Mathematical Physics, 7(7), pp. 1218-1225, doi
D. Finkelstein, J. Rubinstein, 1968, Connection between Spin, Statistics, and Kinks, Journal of Mathematical Physics, 9(11), pp. 1762-1779, doi
-
J. G. Williams, 1970, Topological Analysis of a Nonlinear Field Theory, Journal of Mathematical Physics, 11(8), pp. 2611-2616, doi
Биографические:
R. H. Dalitz, 1988, An outline of the life and work of Tony Hilton Royle Skyrme (1922–1987),, International Journal of Modern Physics A, 03(12), pp. 2719-2744, doi
I. J. R. Aitchison, 2020, Tony Skyrme and the Origins of Skyrmions
О модели Скирма:G. S. Adkins, C. R. Nappi, E. Witten, 1983, Static properties of nucleons in the Skyrme model, Nuclear Physics B, 228(3), pp. 552-566, doi
E. Farhi, 1985, An Introduction to the Skyrmion
I. Zahed, G. E. Brown, 1986, The Skyrme model, Physics Reports, 142(1-2), pp. 1-102, doi
N. S. Manton, 1987, Geometry of Skyrmions, Communications in Mathematical Physics, 111(3), pp. 469-478, doi
E. Braaten, L. Carson, 1988, Deuteron as a toroidal Skyrmion, Physical Review D, 38(11), pp. 3525-3539, doi
E. Braaten, S. Townsend, L. Carson, 1990, Novel structure of static multisoliton solutions in the Skyrme model, Physics Letters B, 235(1-2), pp. 147-152, doi
А. Т. Филиппов, 1990, Многоликий солитон, 2 edition, Издательство: Наука, Физматлит, 1985, Серия: Библиотечка "Квант"
В. Г. Маханьков, Ю. П. Рыбаков, В. И. Санюк, 1992, Модель Скирма и сильные взаимодействия (К 30-летию создания модели Скирма), УФН, 162, pp. 1-61
N. Manton, P. Sutcliffe, 2004, Topological Solitons, Cambridge University Press, doi
В. А. Рубаков, 2005, Классические калибровочные поля: Бозонные теории., 2 edition, Москва: КомКнига
N. S. Manton, 2011, Classical Skyrmions -- Static Solutions and Dynamics, Math. Methods Appl. Sci., 35(10), pp. 1188-1204, doi
V. G. Makhankov, Y. P. Rybakov, V. I. Sanyuk, 2012, Skyrme Model Fundamentals Methods Applications, Springer London, Limited
D. T. J. Feist, P. H. C. Lau, N. S. Manton, 2013, Skyrmions up to baryon number 108, Physical Review D, 87(8), pp. 085034, doi
Эссе о скирмионнахA. Bartholomew, 2015, Skyrmions
Два издания сборника статей "Многогранный скирмион" или можно перевести "Многоликий Скримион" (The multifaceted skyrmion):G. E. Brown, M. Rho, 2010, The Multifaceted Skyrmion, World Scientific, doi
-
M. Rho, I. Zahed, 2015, The Multifaceted Skyrmion, World Scientific, doi
Обширная подборка статей на nLab: nLab authors, 2023, skyrmion
https://ncatlab.org/nlab/show/skyrmion
О нелинейноймодели:
С. В. Кетов, 1992, Нелинейные сигма-модели в квантовой теории поля и теории струн, Новосибирск : Наука : Сиб. отд-ние
-
Y.-L. Ma, M. Harada, 2016, Lecture notes on the Skyrme model
см. также [21], [25]
О топологии и стереографической проекции:
Интерактивное видео о стереографической проекции от 3blue1brown и Ben Eater Р. Додд, Д. Эйлбек, Д. Гиббон, Х. Моррис, 1988, Солитоны и нелинейные волновые уравнения, М.: Мир,
J. Zang, V. Cros, A. Hoffmann, 2018, Topology in Magnetism, Springer International Publishing, doi
см. также [15], [21]
Теорема Хобарта-Деррика, Масштабные преобразования и теоремы об отсутствии солитонов.R. H. Hobart, 1963, On the Instability of a Class of Unitary Field Models, Proceedings of the Physical Society, 82(2), pp. 201-203, doi
G. H. Derrick, 1964, Comments on Nonlinear Wave Equations as Models for Elementary Particles, Journal of Mathematical Physics, 5(9), pp. 1252-1254, doi
Р. Раджараман, 1985, Солитоны и инстантоны в квантовой теории поля, М: Мир
J. Schechter, H. Weigel, 1999, The Skyrme Model for Baryons
См. также [20], [21], [25]
Остальные работы, на которые ссылаемся в статье:J. Rubinstein, 1970, Sine-Gordon Equation, Journal of Mathematical Physics, 11(1), pp. 258-266, doi
E. Witten, 1983, Global aspects of current algebra, Nuclear Physics B, 223(2), pp. 422-432, doi
E. Witten, 1983, Current algebra, baryons, and quark confinement, Nuclear Physics B, 223(2), pp. 433-444, doi
G. Hooft, 1974, A planar diagram theory for strong interactions, Nuclear Physics B, 72(3), pp. 461-473, doi
E. Witten, 1979, Baryons in the 1-N expansion, Nuclear Physics B, 160(1), pp. 57-115, doi
Р. Пенроуз, 2007, Путь к реальности, или Законы, управляющие Вселенной, Институт компьютерных исследований, Регулярная и хаотическая динамика
M. Born, L. Infeld, 1934, Foundations of the new field theory, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 144(852), pp. 425-451, doi
R. A. Battye, N. S. Manton, P. M. Sutcliffe, 2010, Skyrmions and Nuclei, in The Multifaceted Skyrmion, pp. pp. 3-39
H. A. Lorentz, 1952, The Theory Of Electrons, 2 edition, New York: Dover publications, inc
T. H. R. Skyrme, 1971, Kinks and the Dirac Equation, Journal of Mathematical Physics, 12(8), pp. 1735-1743, doi
V. I. Sanyuk, 1992, Genesis and evolution of the Skyrme model from 1954 to the present, International Journal of Modern Physics A, 07(01), pp. 1-40, doi
M. Gell-Mann, M. Levy, 1960, The axial vector current in beta decay, Il Nuovo Cimento, 16(4), pp. 705-726, doi
U. Enz, 1963, Discrete Mass, Elementary Length, and a Topological Invariant as a Consequence of a Relativistic Invariant Variational Principle, Physical Review, 131(3), pp. 1392-1394, doi
H.-J. Lee, B.-Y. Park, D.-P. Min, M. Rho, V. Vento, 2003, A unified approach to high density: pion fluctuations in skyrmion matter, Nuclear Physics A, 723(3-4), pp. 427-446, doi
M. Faber, 2014, Spin and charge from space and time, Journal of Physics: Conference Series, 504, pp. 012010, doi
M. J. Esteban, 1986, A direct variational approach to Skyrme's model for meson fields, Communications in Mathematical Physics, 105(4), pp. 571-591, doi
Л. В. Капитанский, О. А. Ладыженская, 1983, О принципе Коулмэна нахождения стационарных точек инвариантных фунционалов, Записки научных семинаров ЛОМИ, 127, pp. 84-102
N. S. Manton, B. M. A. G. Piette, 2000, Understanding Skyrmions using Rational Maps
R. A. Battye, P. M. Sutcliffe, 1997, Symmetric Skyrmions, Physical Review Letters, 79(3), pp. 363-366, doi
R. Battye, P. Sutcliffe, 2001, Skyrmions, Fullerenes and Rational Maps, Reviews in Mathematical Physics, 14(01), pp. 29-85, doi
C. Houghton, N. Manton, P. Sutcliffe, 1997, Rational Maps, Monopoles and Skyrmions, Nuclear Physics B, 510(3), pp. 507-537, doi
S. K. Donaldson, 1984, Nahm's equations and the classification of monopoles, Communications in Mathematical Physics, 96(3), pp. 387-407, doi
S. Jarvis, 2000, A rational map of Euclidean monopoles via radial scattering, Journal für die reine und angewandte Mathematik (Crelles Journal), 2000(524), doi
O. V. Manko, N. S. Manton, S. W. Wood, 2007, Light nuclei as quantized Skyrmions, Physical Review C, 76(5), pp. 055203, doi
J. L. Forest, V. R. Pandharipande, S. C. Pieper, R. B. Wiringa, R. Schiavilla, A. Arriaga, 1996, Femtometer toroidal structures in nuclei, Physical Review C, 54(2), pp. 646-667, doi
R. A. Battye, N. S. Manton, P. M. Sutcliffe, 2006, Skyrmions and the alpha-particle model of nuclei, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2077), pp. 261-279, doi
S. B. Gudnason, C. Halcrow, 2022, A Smörgåsbord of Skyrmions, Journal of High Energy Physics, doi
J. Cork, C. Halcrow, 2022, ADHM skyrmions, Nonlinearity, 35(8), pp. 3944-3990, doi
Y. Kharkov, O. Sushkov, M. Mostovoy, 2017, Bound States of Skyrmions and Merons near the Lifshitz Point, Physical Review Letters, 119(20), pp. 207201, doi
P. Irwin, 2000, Zero mode quantization of multi-Skyrmions, Physical Review D, 61(11), pp. 114024, doi
S. Krusch, 2003, Homotopy of rational maps and the quantization of Skyrmions, Annals of Physics, 304(2), pp. 103-127, doi
R. A. Battye, P. M. Sutcliffe, 2005, Skyrmions and the pion mass, Nuclear Physics B, 705(1-2), pp. 384-400, doi
C. Houghton, S. Magee, 2007, The effect of pion mass on Skyrme configurations, Europhysics Letters (EPL), 77(1), pp. 11001, doi
R. A. Battye, P. M. Sutcliffe, 2006, Skyrmions with massive pions, Physical Review C, 73(5), pp. 055205, doi
D. Jenkins, O. Kirsebom, 2013, The secret of life, Physics World, 26(02), pp. 23-26, doi
P. Lau, N. Manton, 2014, States of Carbon-12 in the Skyrme Model, Physical Review Letters, 113(23), pp. 232503, doi
С. В. Пикулин, 2019, О задаче Томаса-Ферми и о решениях уравнения Эмдена-Фаулера., Журнал вычислительной математики и математической физики, 59(8), pp. 1358-1380, doi
C. Naya, P. Sutcliffe, 2018, Skyrmions and Clustering in Light Nuclei, Physical Review Letters, 121(23), pp. 232002, doi
С. Адлер, Р. Дашен, 1970, Алгебры токов и их применение в физике чатиц, Москва: Мир

