Представьте, что вам нужно выбрать один из двух баннеров: красный или синий. Разумеется, вам бы хотелось показывать пользователю рекламу с наибольшим откликом.

Но как узнать, какой из баннеров имеет наибольший уровень кликабельности?

Чаще всего для ответа на этот вопрос используется A/B-тестирование. Группа пользователей разделяется пополам, и первой части показывают один баннер, а второй — другой. После этого можно вычислить уровень кликабельности и выбрать лучший из вариантов.

Предположим, что в конце A/B-тестирования у вас получились следующие результаты:

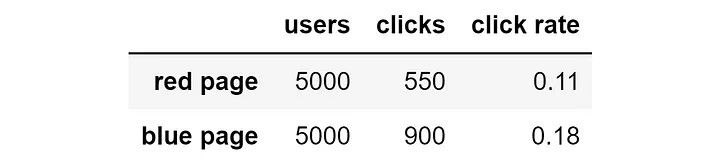
Очевидно, что синяя версия намного лучше красной: кликабельность в 18% против 11%. Но это означает, что мы потеряли множество возможностей: можно было бы показать синий баннер гораздо большему количеству пользователей, получив таким образом гораздо больше кликов.

С другой стороны, что, если бы мы остановили эксперимент очень рано, допустим, всего после двадцати пользователей?

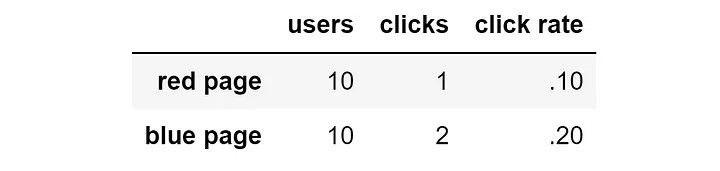
Мы интуитивно понимаем, что после изучения 20 пользователей результаты недостаточно надёжны для того, чтобы показывать всем пользователям вариант с наилучшей характеристикой.

В общем случае проблема A/B-тестирования заключается в следующем:

• если мы выделим слишком большую группу пользователей, то потеряем возможности из-за вариантов с низкими показателями;

• если мы выделим слишком мало пользователей, то тестирование не даст однозначных результатов.

Иными словами, A/B-тестирование неэффективно, потому что слишком статично. В идеале нам необходима умная система, способная динамически учиться с получением новых данных.

Эта система должна:

• исследовать различные альтернативы, когда результаты слишком малы, чтобы быть надёжными;

• использовать результаты, когда они становятся достаточно надёжными, отправляя всё больше трафика варианту с лучшими показателями.

Хорошая новость: такая система существует, она называется сэмплированием Томпсона.

Использование распределений вероятностей вместо чисел

В приведённом выше примере мы пытались оценить каждый из вариантов по одному числу: его кликабельности. Проблема такого подхода заключается в том, что одно число не выражает неопределённость, связанную с самой оценкой.

Для решения этой проблемы сэмплирование Томпсона использует вместо одного числа целое распределение вероятностей.

Задача распределения вероятностей — выразить неопределённость по поводу приблизительной оценки метрики.

Получив распределения (по одному для каждого из вариантов) сэмплирование Томпсона берёт из каждого из них случайное число. Затем пользователю показывается вариант с наибольшим числом.

В чём смысл этого? Смысл в том, что если распределения выражают высокую степень неопределённости, результат сильно зависит от вероятности.

Иными словами, чем меньше у нас уверенности в нашей гипотезе, тем больше система будет исследовать другие варианты. И наоборот: с ростом уверенности система всё чаще будет использовать вариант с наилучшим показателем.

Давайте рассмотрим два распределения вероятностей, которые можно получить из приведённых выше результатов.

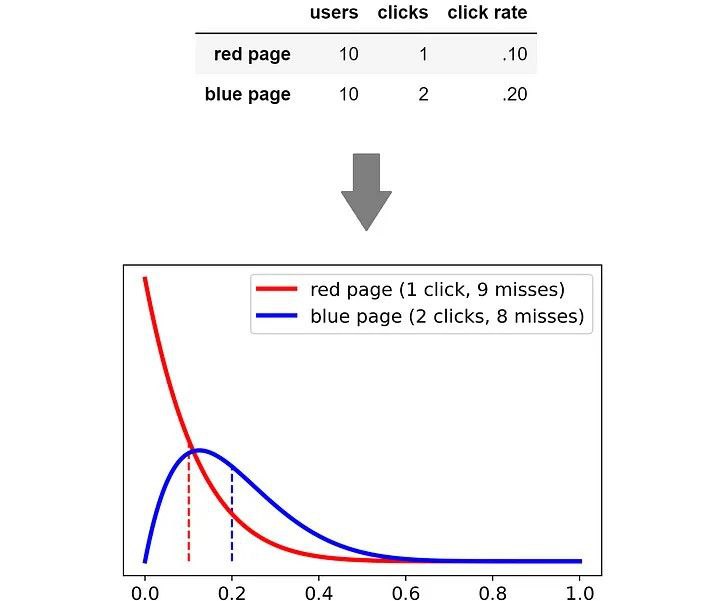
Если попробовать извлекать случайные числа из этих двух распределений, то выяснится, что в 24% случаев извлекаемое из красного распределения число больше, чем извлекаемое из синего. Это численно доказывает, что разница всё ещё статистически незначима.

Но как насчёт ситуации после 10 000 показов?

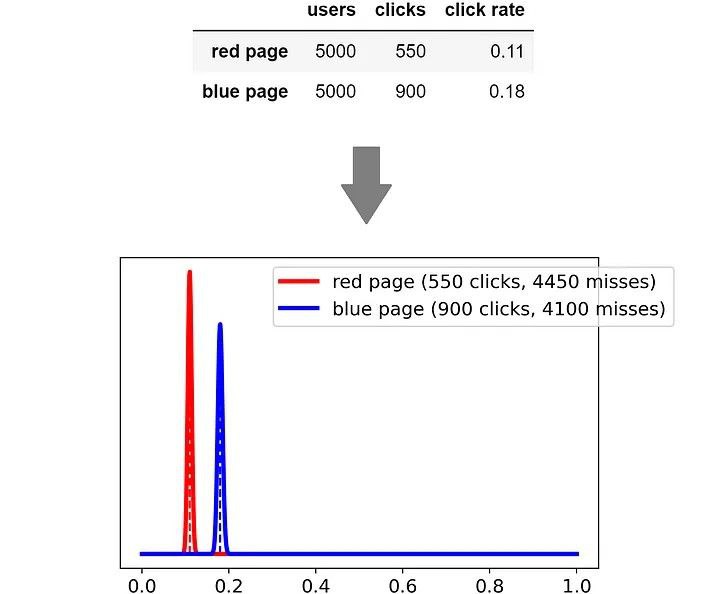
Теперь мы крайне уверены в том, что у синей страницы показатели выше, чем у красной. И на самом деле, практически невозможно извлечь из красного распределения число, которое будет больше, чем извлечённое из синего распределения.

Какое распределение следует использовать?

В нашем примере, поскольку результат двоичен (клик или его отсутствие), лучше всего бета-распределение. Хорошее свойство бета-распределения заключается в том, что оно полностью основано на двух параметрах, a и b, которые можно очень просто интерпретировать:

• a: количество успешных случаев (в нашем случае это количество кликов).

• b: количество безуспешных случаев (в нашем случае это количество отсутствия кликов).

Математическое ожидание распределения равно a / (a + b), а это и есть нужная нам величина: показатель кликабельности (click-through-rate).

Кроме того, бета-распределение есть в Scipy и его очень легко вычислить:

import numpy as np
from scipy import stats
# входные данные: количество кликов и количество отсутствия кликов
clicks = 1
misses = 4
# для создания графика получаем 1000 равномерно распределённых точек от 0 до 1
x = np.linspace(start = 0, stop = 1, num = 1_000)
# вычисляем функцию бета-распределения вероятностей
beta_pdf = stats.beta(a = clicks, b = misses).pdf(x = x)

Давайте составим график нескольких примеров. Возьмём кликабельность в 20%: что произойдёт с бета-распределением при увеличении количества показов?

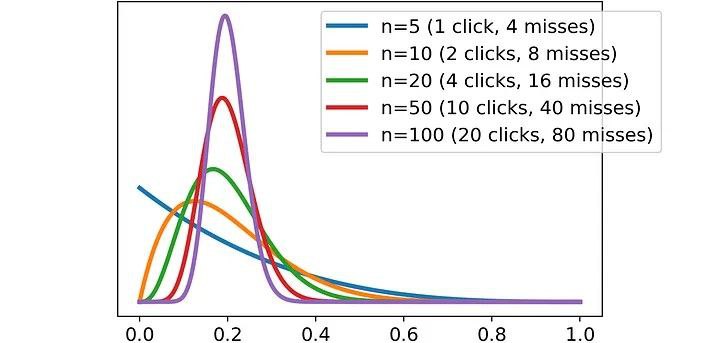
Как мы и ожидали, с увеличением количества пользователей результаты становятся всё более определёнными: это приводит к распределению, которое всё больше концентрируется рядом с ожидаемым значением: 20%.

Иными словами, работа с распределениями вероятностей позволяет нам задать численную меру определённости нашей качественной оценки.

Почему не нормальное распределение?

Если вы изучали статистику, то можете задаться вопросом: «Постойте-ка, согласно центральной предельной теореме, при наличии независимых попыток мы должны использовать нормальное распределение. Так почему же мы используем бета-распределение?»

И в самом деле, это хороший вопрос. Давайте посмотрим, как вычислить функцию распределения вероятностей Beta и Normal на Python.

import numpy as np
from scipy import stats
# входные данные: количество кликов и количество отсутствия кликов
clicks = 1
misses = 4
# вычисляем n и click rate
n = clicks + misses
click_rate = clicks / n
# для создания графика получаем 1000 равномерно распределённых точек от 0 до 1
x = np.linspace(start = 0, stop = 1, num = 1_000)
# вычисляем функцию бета-распределения вероятностей
beta_pdf = stats.beta(a = clicks, b = misses).pdf(x = x)
# вычисляем нормальное распределение вероятностей
normal_pdf = stats.norm(
loc = click_rate,
scale = np.sqrt(click_rate * (1 - click_rate) / n)).pdf(x = x)

Давайте повторим этот процесс для разного количества пользователей и сравним два распределения:

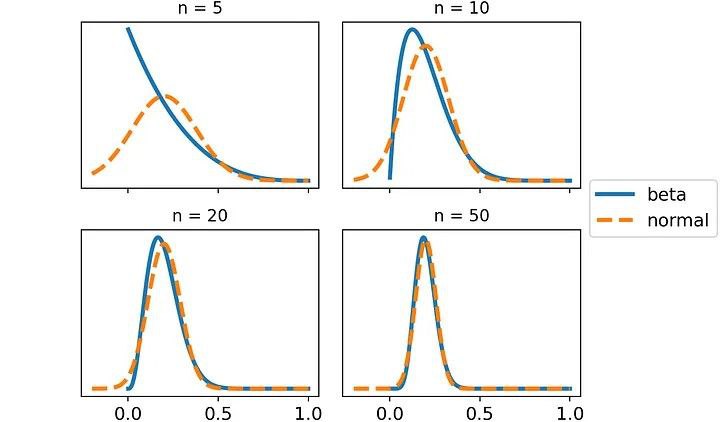
Как видно, с ростом количества показов бета-распределение и нормальное распределение становятся всё более схожими. После 50 итераций они становятся практически одинаковыми.

То есть выбор бета-распределения или нормального распределения не приводит к особой разнице. И это здорово, потому что значит (благодаря центральной предельной теореме), что всегда можно использовать нормальное распределение, вне зависимости от выбранной метрики.

Сэмплирование Томпсона в действии

Давайте создадим пример, чтобы посмотреть на сэмплирование Томпсона в действии.

Мы хотим протестировать четыре варианта рекламы: серый, красный, зелёный и синий. Предположим, что мы также знаем реальный показатель кликабельности для каждой версии.

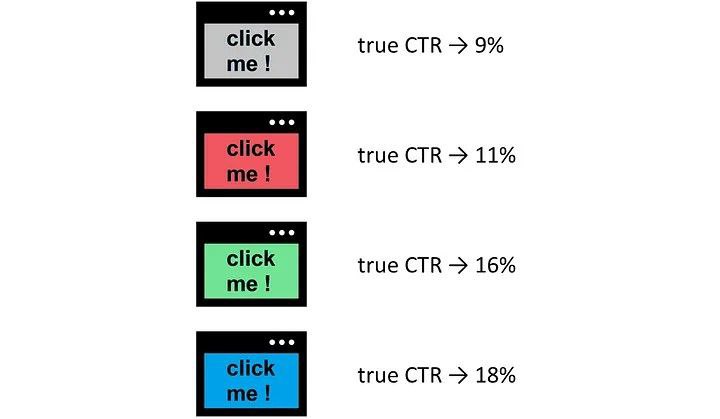
Как и ранее, мы воспользуемся бета-распределением, но нам необходимо внести небольшое изменение. Так как параметры беты (a и b) должны быть строго больше нуля, в случае, если a или b будут равны нулю, мы будем прибавлять к каждому из них 1.

import numpy as np
def draw_from_beta(clicks, misses):
"""Получаем случайное число из беты."""
if min(clicks, misses) == 0:
clicks += 1
misses += 1
return np.random.beta(a=clicks, b=misses)

Для каждого нового пользователя мы должны делать следующее:

1. На основании текущего количества кликов и отсутствия кликов для каждого варианта получать соответстующее бета-распределение.

2. Извлекать число из распределения каждого варианта, полученное в точке 1.

3. Показывать пользователю вариант, соответствующий наивысшему значению.

4. Увеличивать счётчик на результат, полученный для текущего пользователя (клик или его отсутствие).

Давайте посмотрим на графическое представление этого процесса для первой тысячи пользователей:

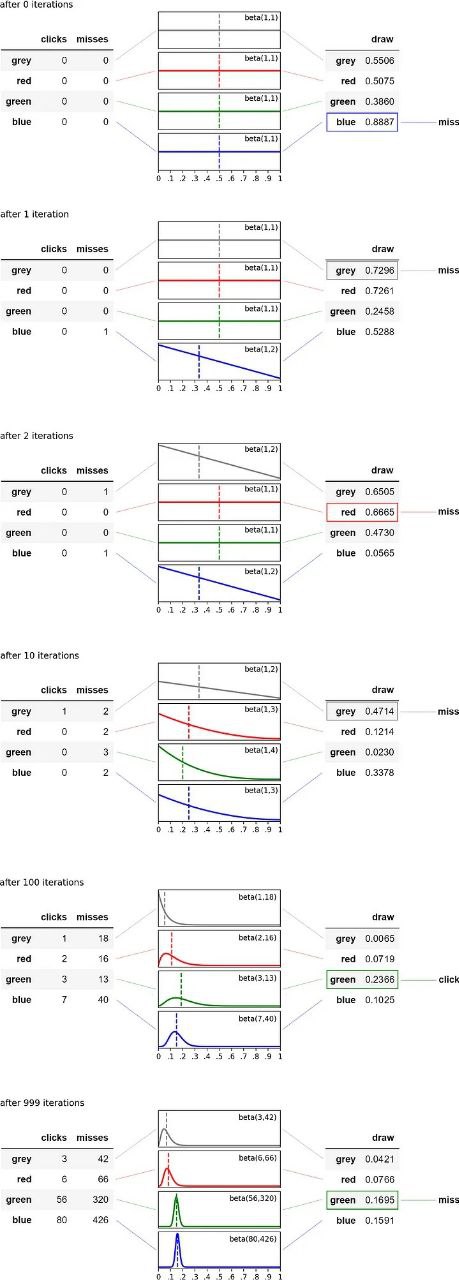
Как мы видим, после 100 итераций наша гипотеза всё ещё не соответствует истине: математическое ожидание зелёного варианта больше, чем синего. Но это связано только с вероятностью. С накоплением опыта наши приблизительные оценки сходятся к истине. Это означает следующее:

• среднее значение распределения будет ближе к истинному показателю кликабельности;

• среднеквадратичное отклонение распределения будет всё ближе и ближе к нулю.

Давайте посмотрим, как изменяются эти две величины на протяжении первых четырёхсот итераций.

Первые 400 итераций алгоритма. Изменение среднеквадратичного отклонения и среднего значения с увеличением количества итераций.

Как мы видим, после тысячи показов результат будет таким:

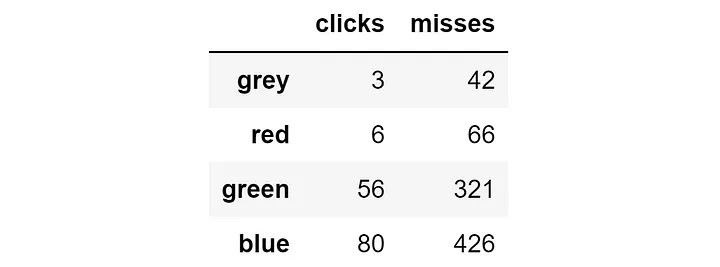
Сэмплирование Томпсона настолько эффективно, что после всего тысячи итераций оно уже концентрировало 50,6% показов на наилучшем варианте (синем) и 37,7% на втором по показателям (зелёном).

И наоборот: что произойдёт, если мы используем A/B-тестирование, отправляя каждый вариант одинаковому количеству пользователей? Показ каждого баннера 250 пользователям даст следующий результат:

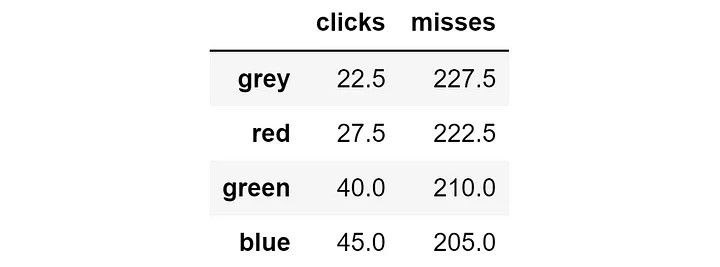
При использовании сэмплирования Томпсона мы получили 145 кликов, а при A/B-тестировании — 135 кликов. Это значит, что благодаря сэмплированию Томпсона мы получили на 7,4% больше кликов! А при увеличении количества итераций разница станет ещё больше.

Заключение

Сэмплирование Томпсона идеально подходит для онлайн-обучения, потому что оно эффективно решает дилемму соотношения исследования и использования.

Это происходит благодаря присвоению каждому тестируемому варианту распределения вероятностей. Распределение используется для выражения неопределённости, связанной с приблизительной оценкой.

То, что сэмплирование Томпсона динамически адаптируется к знаниям, накопленным из предыдущих итераций, делает его более эффективным, чем A/B-тестирование.

Например, мы рассмотрели пример с четырьмя вариантами, и всего при тысяче итераций сэмплирование Томпсона смогло получить на 7% больше кликов, чем A/B-тестирование.