Всем привет! Меня зовут Евгений, я чаптер-лид бэкенда в «Метре квадратном». В этой статье расскажу об алгоритме, который помогает нам решить задачу дедупликации данных без идентификатора, дам контекст решаемой проблемы и словесное описание алгоритма с визуализацией. Реализацию алгоритма можно посмотреть по ссылке в заключении. Любые комментарии, критика кода или этой статьи приветствуются!

Структура статьи

Этот текст состоит из двух основных частей: описания работы алгоритма и применения его на практике. Алгоритму на вход подаются данные и набор правил, по которым происходит обработка этих данных. Работа происходит с персональными данными пользователей. Правила — это «настройка» алгоритма для работы на практике, они устанавливаются на основании специфики данных. 

Статья начинается с бизнес-контекста и подводки к выбору правил как «более человекопонятному и интуитивному действию». А затем приводится рассказ об алгоритме со ссылками на конкретные правила в качестве примера. Они не влияют на алгоритм, но помогают понять его. Правила из примеров могли быть любыми другими. 

Бизнес-контекст

В «Метре квадратном» персональные данные клиентов приходят из разных систем в одну агрегирующую. Экосистема построена так, что в каждом продукте требуется указать разные данные. Например, одна система запрашивает ФИО, email, номер телефона, паспортные данные. Вторая система — ФИО и email. Третья — ФИО и номер телефона. Клиент вносит данные в системы, не обязательно имея учётную запись или любой другой идентификатор. В некоторых случаях за него это делают коллеги из службы клиентской поддержки, также минуя по бизнес-требованиям стадию идентификации пользователя.

Такой подход даёт бизнесу гибкость: для клиента выстраиваются независимые пути на входе через любой продукт. А потом эти пути начинают пересекаться. Возможность их пересечения и объединения — результат работы алгоритма, описанного ниже.

Кстати, поделитесь в комментариях или в личку, какой инструмент или подход используется для дедупликации в вашей компании. 

Слепки данных клиента, которые приходят из продуктов, — это то, над чем производится поиск дубликатов по бизнес-требованиям. Эти данные, по-другому снепшоты, объединяются по набору правил в мастер-записи. Правилом может быть, например, совокупность полей ФИО и email. То есть если среди множества слепков данных от разных систем встречаются два с одинаковыми ФИО и email, то велика вероятность, что они принадлежат одному реальному человеку.

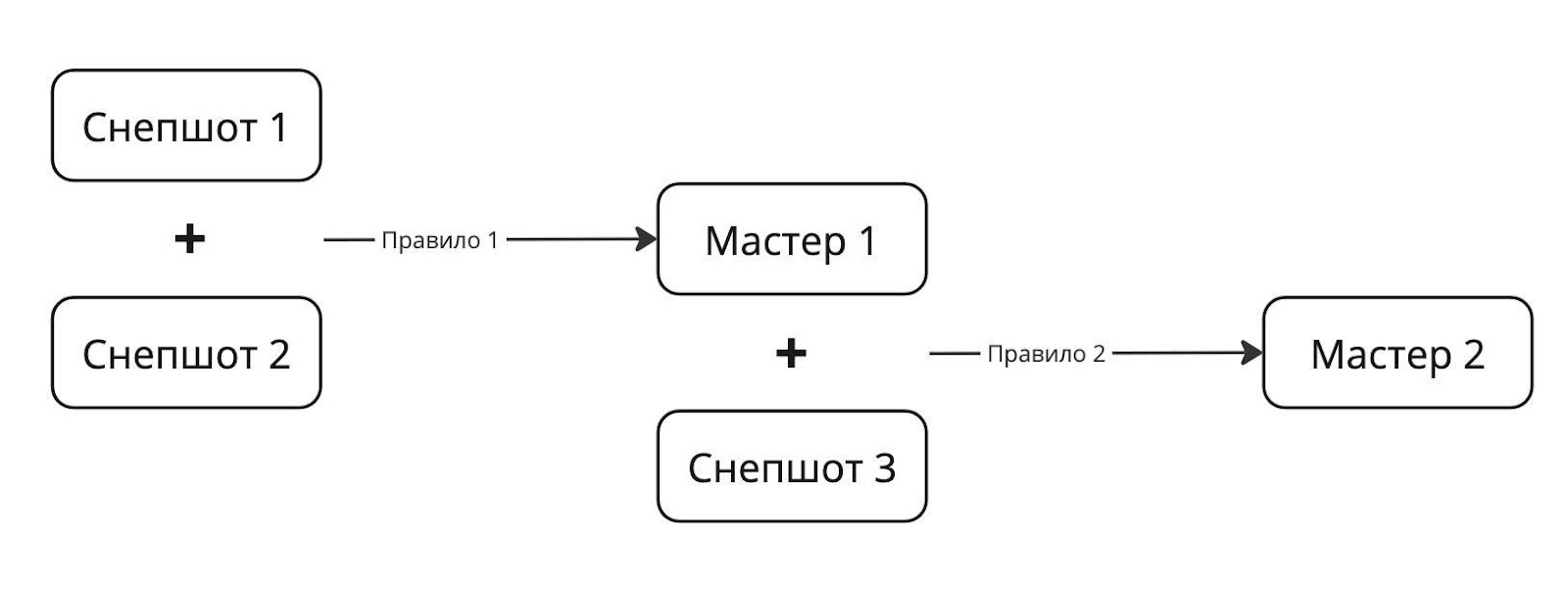
Задача, которую решает алгоритм, — объединение снепшотов. Данные в объединяемых снепшотах принадлежат одному человеку, даже если эта принадлежность неочевидна. Например, данные могут не содержать ФИО. 

Алгоритм, в частности, позволяет справиться с проблемой смены фамилии при сохранении телефона и адреса электронной почты. Это довольно тривиальная задача, которую можно решить просто до тех пор, пока объединение происходит по правилу «телефон+почта» и новая фамилия встречается в снепшотах с парой этих полей («телефон+почта»). Однако она перестаёт быть такой, если новая фамилия приходит в снепшоте, в котором заполнено только одно из полей «телефон» или «почта», но есть другие данные. Об этом подробнее в примере ниже.

Бизнес-постановка задачи оперирует вероятностными характеристиками, потому что даже для уникальных параметров, таких как, например, серия и номер паспорта, есть возможность опечатки при заполнении данных. Для ФИО есть вероятность коллизии, то есть полного совпадения фамилии, имени и отчества. Таким образом, есть ненулевая вероятность совпадения данных у разных людей. И она тем выше, чем меньше этих данных. Например, такая вероятность максимальна, если использовать единичные поля в качестве правила для объединения снепшотов.

Теория

Следующие несколько параграфов будут посвящены логическим проблемам выбора полей, по которым происходит объединение записей в алгоритме. Правило — набор полей; стратегия — набор правил. Стратегия — это то, что подаётся на входе алгоритму наряду с данными.

Интересно, что в теории число записей в базе данных не должно быть большим для высокой вероятности коллизии.

Исходя из парадокса дней рождения следует, что 50% вероятности нахождения людей с одинаковым днём рождения достигается при численности группы в 23 человека. В обобщённом виде закон выглядит так:

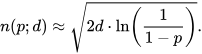
где d — мощность множества (число дней в частном случае), p — вероятность наступления коллизии.

Это значит, что для ФИО из множества самых распространённых (200 имён * 200 отчеств * 250 фамилий), d = 10 000 000, вероятность p = 0.99 достигается на 9597 примерах (записях БД). Почти наверняка при 10 000 записей с ФИО у нас в БД есть коллизия по этому полю. На самом деле — при гораздо меньшем числе, потому что ФИО не обладают свойством равной вероятности появления (реализации случайной величины). Какие-то ФИО гораздо более вероятны.

Имея эту статистику, можно применить закон с учётом неравновероятного распределения. Это нетривиально, если преследовать строгость выкладок. Эффективное число d в этой перспективе становится существенно меньше и, как следствие, n(p; d) тоже снижается. Выше дана наивная оценка, а гораздо более полный метод доступен для ознакомления в статье про парадокс дней рождения, распространённый на неравновероятное распределение на примере японских фамилий.

Главный вывод из этого параграфа — принять разных людей за одного по их ФИО при достаточно большом числе людей очень просто. Поэтому только ФИО в качестве правила использовать наивно. Равно как и другие поля по одному из-за высокой вероятности опечатки. 

Число, порядок правил и цикличность их применения

Объединение по двум и более полям позволяет существенно снизить вероятность полного «ложного» совпадения. Примером такого составного правила может быть ФИО и email или ФИО и паспортные данные.

Рассмотрим наборы правил и их организацию в стратегии.

Если упорядочить правила внутри стратегии, то после срабатывания первого правила может открыться возможность для применения второго (появятся новые сочетания полей в мастерах, мастера по отношению к операциям объединения будут вести себя идентично снепшотам, то есть участвовать в объединениях по правилам). Возможна и обратная ситуация: после применения второго правила может открыться возможность для срабатывания первого. Для простоты можно считать применение набора правил внутри стратегии неделимой операцией. Тогда для применения правила 1 после правила 2 нужно применить второй раз всю стратегию.

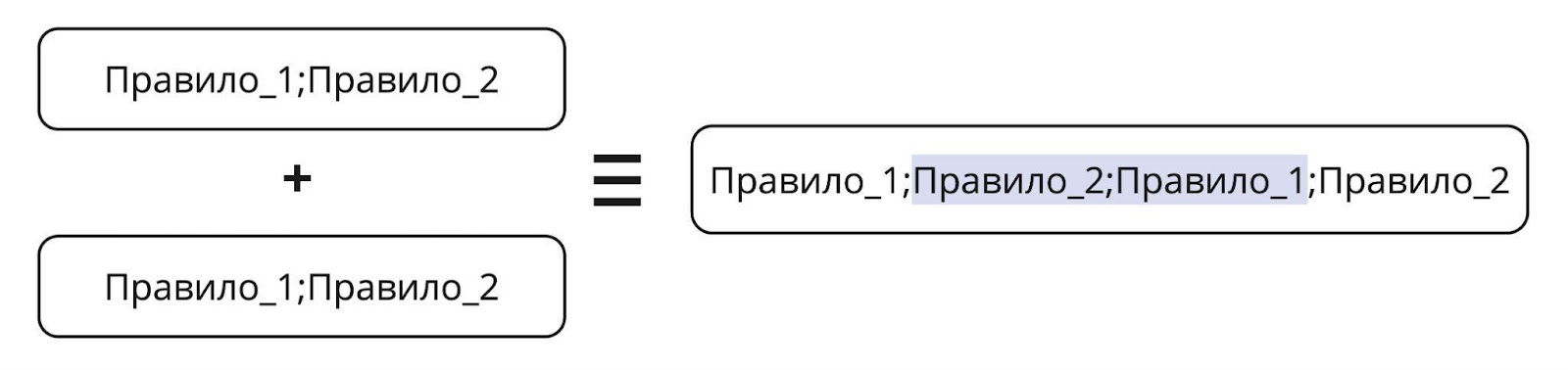
Например, ниже стратегия «ФИО+паспорт; телефон+email» применяется 2 раза. Второе применение части «телефон+email» опущено, но показано применение части «ФИО+паспорт» после «телефон+email». Иллюстрация разделена по вертикали на две для удобства чтения, в процессе участвуют 6 снепшотов.

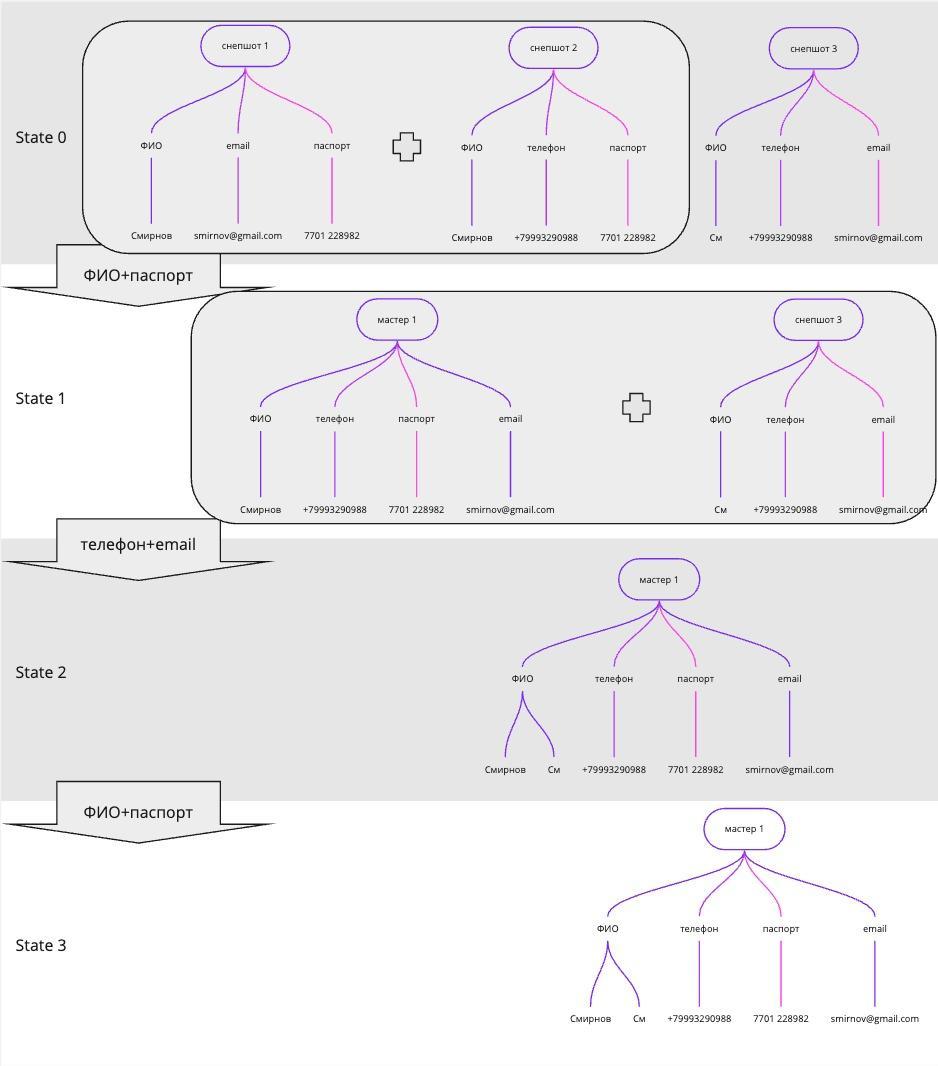
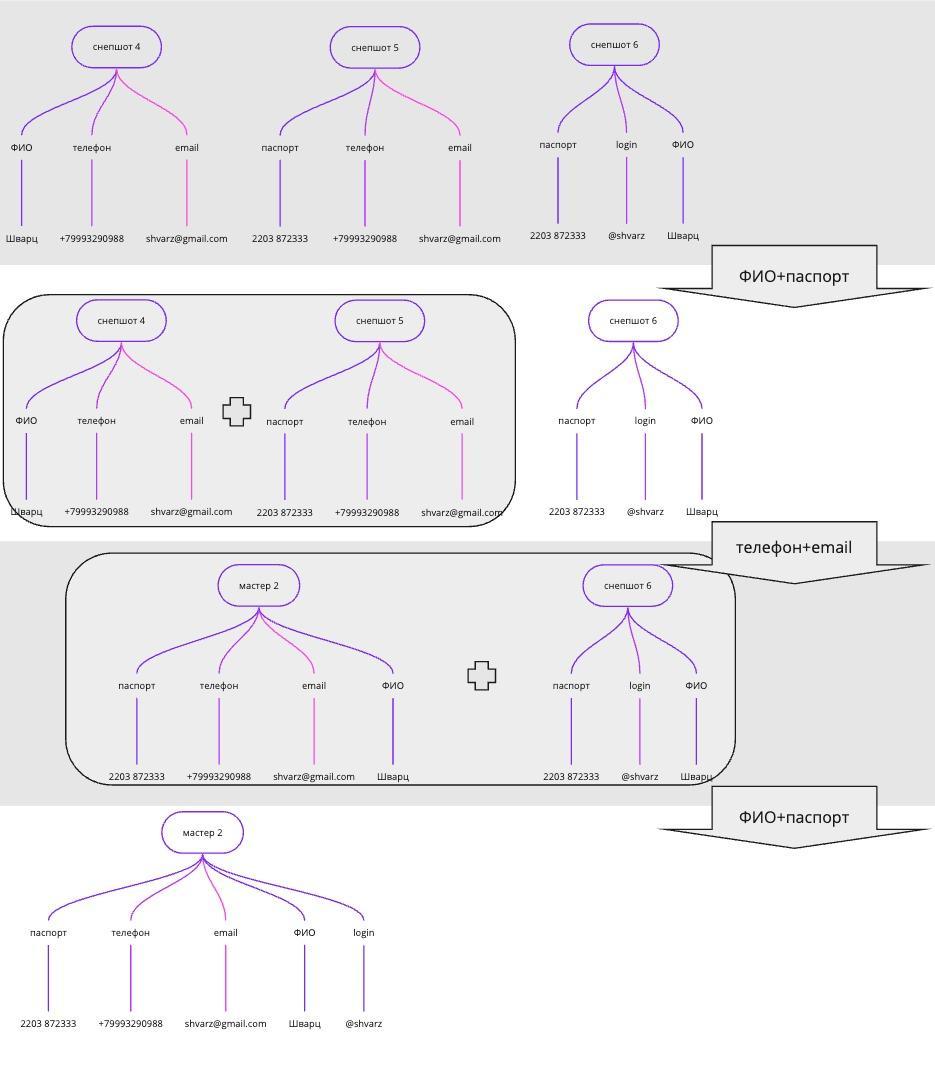
Если бы правило «ФИО+паспорт» не было применено во второй раз, то объединение «мастера 2» со «снепшотом 6» было бы упущено. 

По индукции, чтобы стратегия сработала исчерпывающе, необходимо применять её к набору снепшотов циклично, пока не перестанут происходить объединения.

Как выбрать стратегию?

Для результата крайне важно, из каких правил состоит стратегия. Разные наборы правил дают разные наборы мастеров. С одной стороны, параметром для оптимизации при выборе стратегии является число слияний и обратное к нему — число мастеров. С другой стороны, если будет слишком много слияний, все снепшоты попадут в один или несколько мастеров. И это будет означать, что стратегия выбрана неправильно. 

Например, если в качестве правила выбрать объединение по имени, то мастеров будет ровно столько, сколько в базе данных разных имён. Это бессмыслица, человеческих имён в русском языке не так много. Иван Смирнов будет считаться одним человеком с Иваном Твардовским.

Напомню, эти рассуждения справедливы при условии, что нет данных по точному числу уникальных пользователей. В системе учёта «Метра квадратного» есть данные по зарегистрированным людям, но по незарегистрированным (лишь частично заполнившим данные для продукта) нет. Данных из второй категории в системах великое множество.

Критерий эффективности, или как проверить стратегию?

Одним из понятных критериев качества слияний на относительно большом наборе данных является ФИО. Если у мастера есть несколько ФИО (отличных более чем на опечатку или ошибку в регистре), то это кандидат на неправильное слияние. А также если найдутся разные мастера с одинаковыми ФИО (вплоть до дистанции в несколько букв), то они тоже являются подозрительными. Как показывает практика на данных «Метра квадратного», таких примеров немного даже на больших датасетах. И их все можно проверить вручную.

Если примеров ошибок обоих классов немного или вовсе нет, то стратегию можно считать хорошей. К ней можно добавлять новые правила и следить за деградацией результата. Если качество набора мастеров не упало, а число слияний увеличилось, то стратегия улучшилась.

Структура данных

В базе данных «Метра квадратного» миллионы снепшотов, и это число стремительно растёт. Чтобы обеспечить возможность масштабирования решения, в алгоритме используется абстрактная структура данных граф. Снепшоты и мастера — это вершины в этом графе.

Мастер и снепшот эквивалентны с точки зрения производимых операций над ними. А также они неразличимы в структуре данных. Разделение между ними идеалогическое: снепшот приходит на вход алгоритму. После работы алгоритма, если он не вошёл в состав другого мастера, он сам становится мастером.

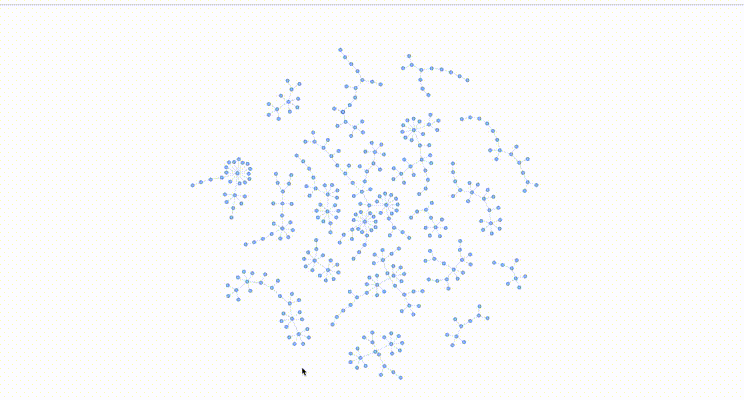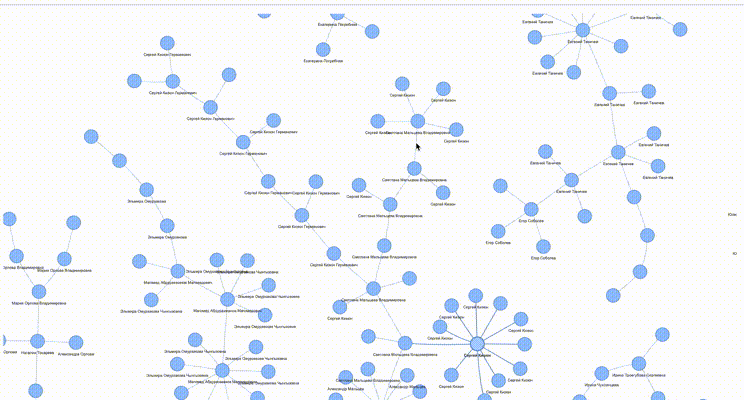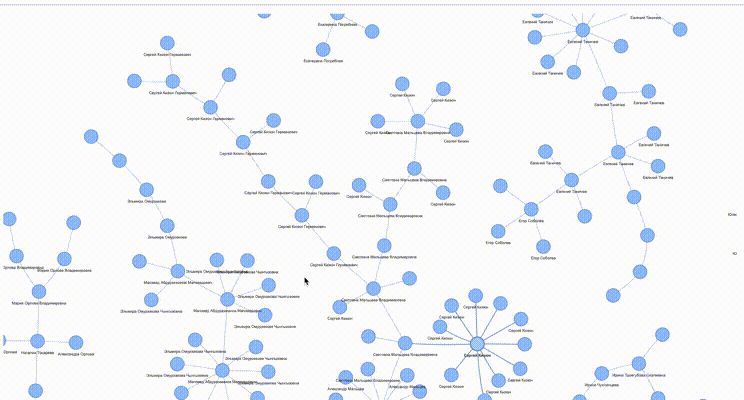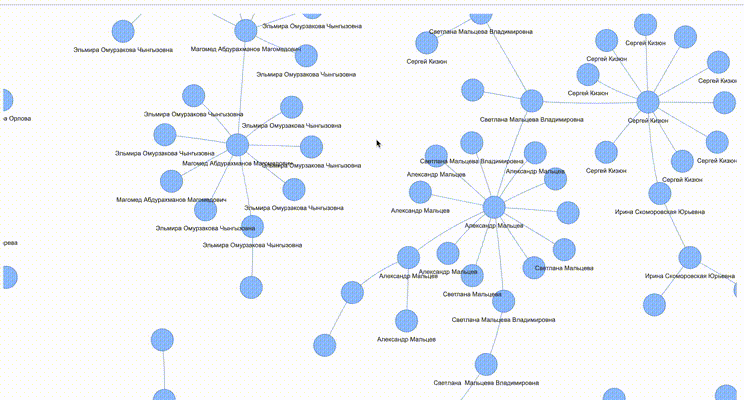
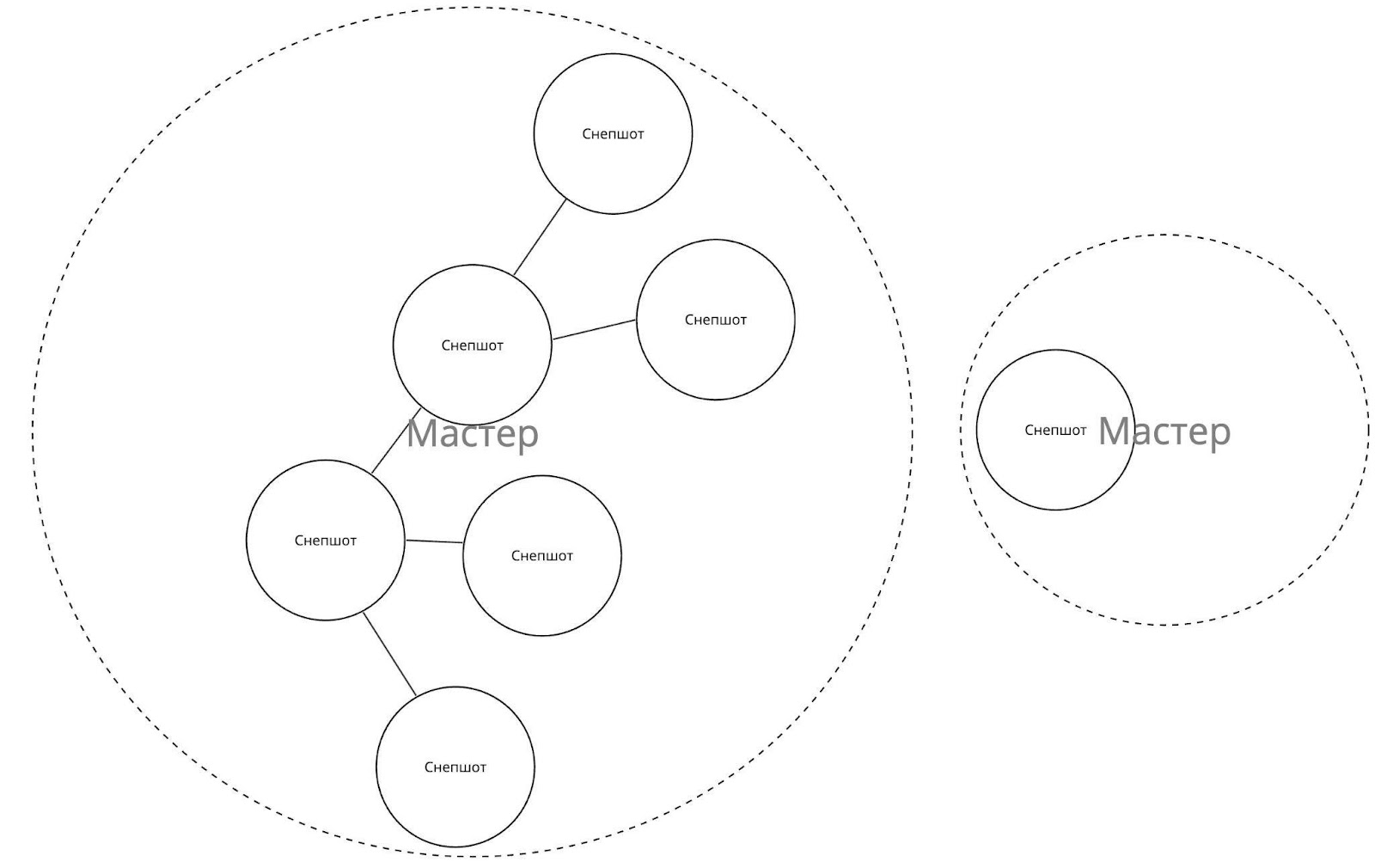
На анимации выше представлен граф мастер-записей. Множество всех мастеров — это несвязный граф. Каждый мастер — это отдельный связный граф, состоящий из вершин-снепшотов. Снепшоты присоединяются к мастеру по правилу. Правило-связь — это грань. Мастер имеет вершину — снепшот-прародитель, к которому присоединяются все другие снепшоты. С точки зрения данных этот снепшот является носителем всей информации о его «детях». Он аккумулирует в себе все ссылки на снепшоты, которые к нему присоединились, а также все значения из полей этих снепшотов-«детей». Он «знает» всё о своих «отпрысках», в том числе опосредованных.

Алгоритм

Предлагаю вам рассмотреть алгоритм подробнее. Для более лёгкого восприятия рекомендую делать это параллельно с чтением кода. Словесное описание скорее служит комментариями к коду. Основная ценность этого параграфа — в попытке оценить вычислительную сложность.

Каждый раз, когда в систему приходит новый снепшот, алгоритм пытается по значениям полей найти ему мастер для присоединения на основании правил стратегии. Если хотя бы по одному из правил произошло слияние, то нужно попробовать применить все правила уже ко всем существующим мастерам, так как мог появиться недостающий соединительный элемент для слияния какой-то пары или нескольких. Так, добавление одного снепшота может породить лавинообразное изменение всего сета мастеров. Каждое следующее слияние может быть логическим мостом для ещё одного или нескольких. Однако на практике происходит не более 10 последовательных слияний.

Ниже на иллюстрации поля снепшотов представлены цветными маркерами. Для простоты, но без ограничения общности, любое поле имеет лишь одно возможное значение (кроме отсутствия значения вовсе, что эквивалентно отсутствию поля-маркера). В рамках такой бинарной логики слияние происходит при наличии у кандидатов набора полей из правила. В алгоритме логика n-арная, то есть для слияния необходимо не только наличие полей, но и совпадение значений в них.

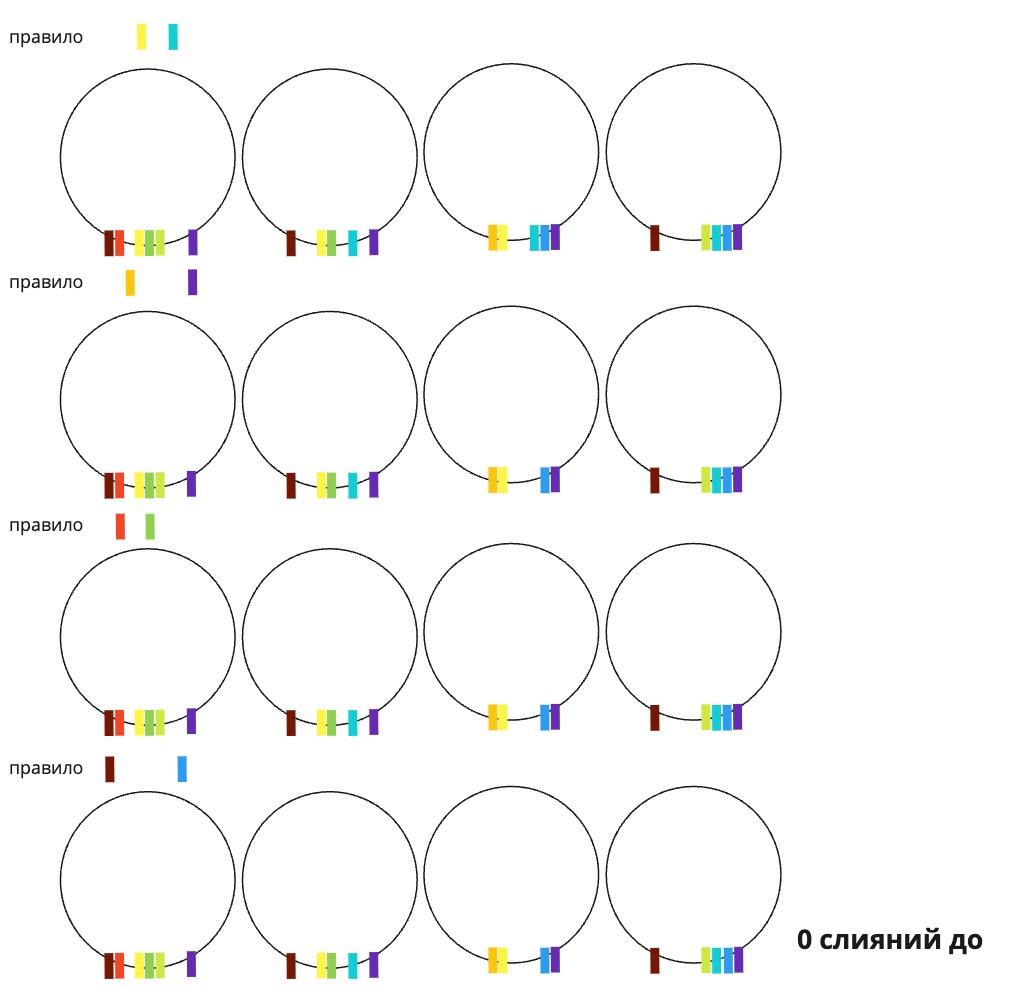
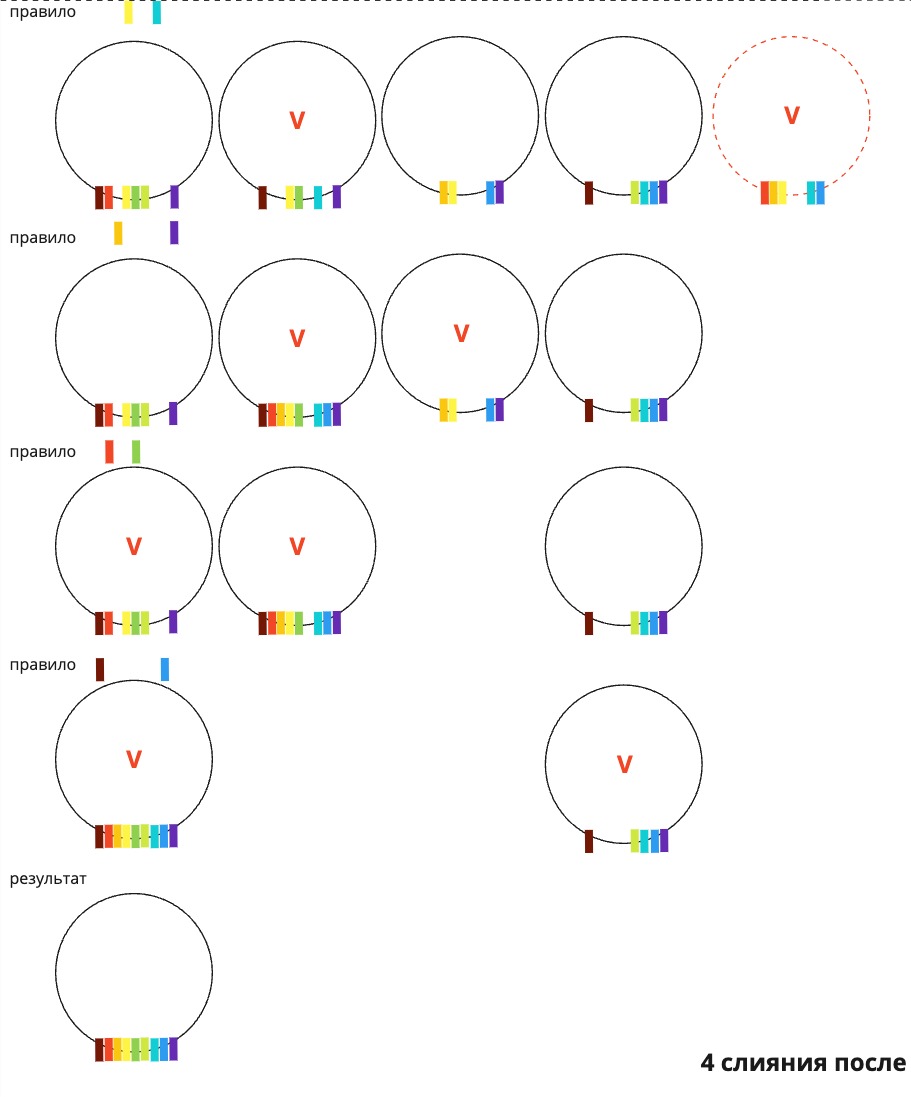
Для поиска того связного графа, к которому нужно присоединить новый снепшот, алгоритм проходится по всем существующим мастерам. Это долгий процесс со сложностью по времени O(n), где n — число несвязных графов, или число мастеров.

Улучшение вычислительной сложности

Этот хардкорный параграф можно пропустить без потери контекста статьи.

Для улучшения вычислительной сложности есть возможность воспользоваться распространённой в базах данных структурой данных — индексами. Алгоритм составляет индекс по каждому правилу стратегии. При появлении нового снепшота ещё перед попыткой объединения алгоритм создаёт ссылки на него в каждом индексе. Так снепшот становится готов к поиску кандидатов для объединения.

Вставка в индекс стоит O(log(n)), о чём мы поговорим ниже. Число индексов - константа I. Сложность поиска подходящего кандидата на объединение составит O(1) из-за группировки в индексе схожих записей (это следствие сортировки). Искать нужно будет тоже в нескольких индексах (I). Итого сложность поиска кандидатов для слияния с учётом вставки ссылок в индексы — O(I * log(n)). Плата за это улучшение — ещё ряд вставок, на каждом слиянии алгоритм должен будет вставлять одну или несколько ссылок в каждый индекс. Число таких ссылок определяется числом комбинаций значений в наборе полей (на каждое правило свой набор полей). У мастера при слиянии меняется состав полей, поэтому каждое слияние вызывает добавление ссылок на этот мастер в индексы. 

Например, если мастер содержит поля «ФИО» и «email» со значениями «Иванов Иван Иванович» и «ivanov@mail.ru», то до слияния в индексе «ФИО, email» на него будет показывать ссылка «Иванов Иван Иванович, ivanov@mail.ru». Если при слиянии с вновь пришедшим снепшотом к мастеру добавится новый email, то в индекс нужно будет добавить ссылку, например «Иванов Иван Иванович, ivanovii@yandex.ru».

Обе ссылки будут показывать на один мастер. Количество новых ссылок мы обсудим ниже, пусть оно будет X, не зависящее от n. А пока оценим сложность вставки в отсортированный связный список. Это O(log(n)), потому что бинарным поиском найти место для вставки — это O(log(n)). А сама вставка — O(1), так как индекс можно имплементировать как двусвязный список. Общая сложность одного слияния — O(X * I * log(n) * I * log(n)) = O(X * I² * log²(n)), X и I - константы. Произведение алгоритмов получаем из необходимости сделать индексы для снепшота на входе, а потом после слияния. Такая сложность лучше, чем O(n).

На этом этапе оценки есть важный момент. Каждое слияние может породить другое слияние, и так далее. Сторого говоря, можно подойти к дальнейшей оценке двумя способами. Можно продолжать оценивать каждое слияние в изоляции от спровоцированных слияний. И тогда оценка одного слияния остановится на значении O(X * I² * log²(n)). В этом случае нужно оценивать число порождённых слияний отдельно, и это приведёт к суммированию таких сложностей O(X * I² * log²(n)), что в итоге приведёт к O(M * X * I² * log²(n)), M - число порождённых слияний, константа. Это неточно.

Либо можно подойти к этому вопросу с точки зрения оценки влияния, привнесённого каждым добавленным в систему снепшотом. Это тоже жизнеспособная позиция, и она точнее. Вызванные слияния зависимы от первого слияния, поэтому оценка превратится в произведение. Результат будет следующим O(X * I² * log²(n) * I * log(n) * I * log(n) * ... m раз) = O(X * I^m * log^m(n)), где m - число порождённых слияний, точнее, раундов порождённых слияний. Внутри одного раунда сложности складываются, малую константу от сложения здесь опустим. Это всё ещё лучше, чем O(n), но с существенными ограничениями. Пятая степень логарифма обгонит по росту линейную функцию на 350 тысячах. Шестая степень будет обгонять с 0. Ниже я приведу рассуждения, что в худшем случае m = n.

Другими словами, улучшение с индексами имеет смысл только на данных, где число спровоцированных слияний не больше 4 (5 - 1 на изначальное составление индекса). Такую гарантию непревышения 4 в терминах асимптотической оценки сверху я привести затрудняюсь. Однако в терминах оценки средней сложности, и как показывает практика, m можно считать равной 2, так как почти каждое слияние не порождает ни одного другого слияния.

После слияния снепшота с каким-то мастером нужно проверить, не появились ли новые возможности для объединения существующих мастеров. Если подходить к этой задаче наивно (без учёта того, какой мастер был изменён последним слиянием), то вычислительная сложность окажется зашкаливающей. Нужно проверить все попарные сочетания мастеров на предмет возможности их слияния. Число сочетаний из n по 2 равно n! / (2 * (n - 2)!) = n * (n - 1) / 2 = (n² - n) / 2, что при устремлении n к бесконечности оказывается O(n²). В нашем случае для многих миллионов снепшотов, которые по (сложно формализуемому) закону превращаются в мастера, возведение в квадрат даёт число операций на процессоре порядка 10¹² с неопределённым, но конечным (и относительно небольшим) коэффициентом K. При частоте современного процессора порядка 10⁹ операций в секунду на каждый пришедший снепшот только перебор всех возможных пар для слияния вызовет паузу в тысячи секунд. Что, конечно, абсурд. В наших реалиях rps достигает десятков в секунду, и любое промедление приведёт к накоплению очереди необработанных снепшотов.

Введение параллелизма в этом алгоритме исключено, так как каждый следующий снепшот нуждается в знании результатов всех предыдущих слияний. Нет возможности запустить процесс поиска кандидатов для слияния для следующего снепшота, пока не закончится процесс обработки предыдущего снепшота.

Использование индексов даёт возможность существенно улучшить сложность по времени. Для отсортированных ссылок одинаковые записи в одном индексе формируют группу. Например, «Иванов Иван Иванович, ivanov@mail.ru»-1 и «Иванов Иван Иванович, ivanov@mail.ru»-2, указывающие на разные снепшоты/мастера, находятся рядом. Достаточно пройтись по всему индексу, чтобы найти всех кандидатов для слияния. Элементы каждой группы сливаются в её «лидера», первую запись. Сложность одного такого прохода — константное. Стоит отметить, что размер группы зависит от того, сколько записей в него было добавлено на предыдущем проходе при слияниях. И, как мы условились раньше, число новых ссылок X не зависит от n.

Число проходов по группам (или спровоцированных слияний) зависит от масштаба «эффекта бабочки». Одно слияние может породить несколько на следующем проходе, или, как ещё можно выразиться, на следующем применении стратегии. Каждое применение, пока в нём есть хотя бы одно слияние, будет порождать следующий проход. На практике число применений стратегии исчисляется единицами. Однако для чистоты верхней оценки представим худший случай, когда каждое слияние порождает ровно одно новое слияние. Тогда число проходов будет n, равное (в смысле функций) количеству снепшотов. Итого, возвращаясь к формуле из абзаца выше O(X * I^m * log^m(n)), получаем подстановкой n на место m O(X * Iⁿ * logⁿ(n)). Это лог-эксоненциальная сложность. Текущая оценка — результат анализа на абстрактном наборе данных, пока без ограничений бизнеса.

Попробуем улучшить эту оценку и зайдём со стороны анализа данных. Что такое слияние? Это попытка объединить все данные, принадлежащие одному человеку. Зависит ли число снепшотов, принадлежащих одному человеку, от числа этих снепшотов? Нет, ведь один человек порождает в системах такое число снепшотов, какое число действий он совершил. Оно не связано с общим числом действий всех клиентов. Это наводит на простую мысль, что в конкретной имплементации алгоритма мы можем считать число проходов (раундов) константой. Итого сложность одного слияния, порождающего цепочку других, равна O(X * I^m * log^m(n)), где m — константа, не зависящая от n.

Продолжение оценки

И теперь самый важный этап. Оценим X — число создаваемых ссылок на новый объединённый мастер. Строго говоря, X — это X^m, где m - число раундов порождённых слияний. На каждом раунде создаётся какое-то число ссылок. Если у нас A правил в стратегии, каждое правило состоит из B полей, каждое поле имеет C значений после слияния, то получаем следующее. Каждое объединение происходит по какому-то правилу, поэтому ссылки будут создаваться в индексы только по A - 1 правилам. Число размещений с повторениями для B полей c С значениями в каждом будет равно C^B. Итого для всех правил в худшем случае число созданных ссылок равно (A - 1) * C^B. Например, для 5 правил по 3 полям с 10 значениями в каждом общее число ссылок будет 4 * 10³ = 4000.

Каждую ссылку нужно вставить в нужное место бинарным поиском со сложностью O(log(n)). Итого одно объединение вызывает создание и размещение ссылок в индексы сложностью O((A - 1) * C^B * log(n)) — без учёта порождаемых слияний. На нашей практике число значений в одном поле в среднем не превышает 3. А стратегии обычно состоят из 7–10 правил, каждое — из 2 полей. Так мы получаем оценку коэффициента (A - 1) * C^B в 9 * 3² = 81.

Общая оценка сложности алгоритма составляет O(Z * (A - 1)^m * C^Bm * I^m * n * log^m(n)), где Z — кумулятивная константа на все неоптимальности верхнеуровневого языка программирования, m - число раундов порождённых слияний. А n здесь отражает тот факт, что алгоритм прогоняется на всех снепшотах в числе n. Этот алгоритм по оценке работает лучше, чем квадратичный на m < 5, так как O(n * log⁴(n)) лучше, чем O(n²). Эта оценка дана без детального анализа констант. Однако на практике константы очень важны, потому что их порядок влияет на реальную длительность работы алгоритма.

Оценка сложности в среднем выглядит ещё более многообещающей θ(Z * (A - 1)² * C^2B * I² * n * log²(n)) = θ(n * log²(n)).

Как бы то ни было, на миллионах значений алгоритм отрабатывает на виртуальной машине последнего поколения за десятки минут при старте (когда создаются все структуры данных и прогоняются все накопленные к текущему времени снепшоты). А потом в транзакционном режиме каждый вновь пришедший снепшот обрабатывается достаточно быстро, чтобы держать десятки rps.

Изменение снепшота

Иногда в снепшот требуется внести изменение, и тогда связный граф этого снепшота распадается. Это происходит потому, что снепшот мог до изменения связывать два или больше других снепшотов за счёт какого-то своего поля. Если изменение придётся на это поле, то текущая структура мастера станет неактуальной. Для нивелирования этого эффекта нужно отменить все предыдущие слияния в этом мастере, а значит, нужно разобрать мастер на исходные составляющие. Затем происходит обработка «осколков» в обычном порядке, так же, как когда они были снепшотами. То есть запускается процесс слияния.

С точки зрения определения абстрактного понятия «слепок» кажется неправильным, что его можно изменять. Но из-за практических особенностей бизнеса было решено сохранить такую возможность. Например, сотрудники службы поддержки, указывая персональные данные клиента, могут допускать ошибки. Чтобы их можно было исправить, в течение короткого срока доступно редактирование карточки. 

Альтернативы предложенному алгоритму

На просторах интернета мне не удалось найти аналоги предложенному алгоритму. В известных мне библиотеках нет ключевой функции — сбора из множества частей (снепшотов) большого мастера. Самые близкие по функциональности проекты с открытым кодом включают в себя: recordlinkage, dedup, data-lineage.

Архитектурное решение

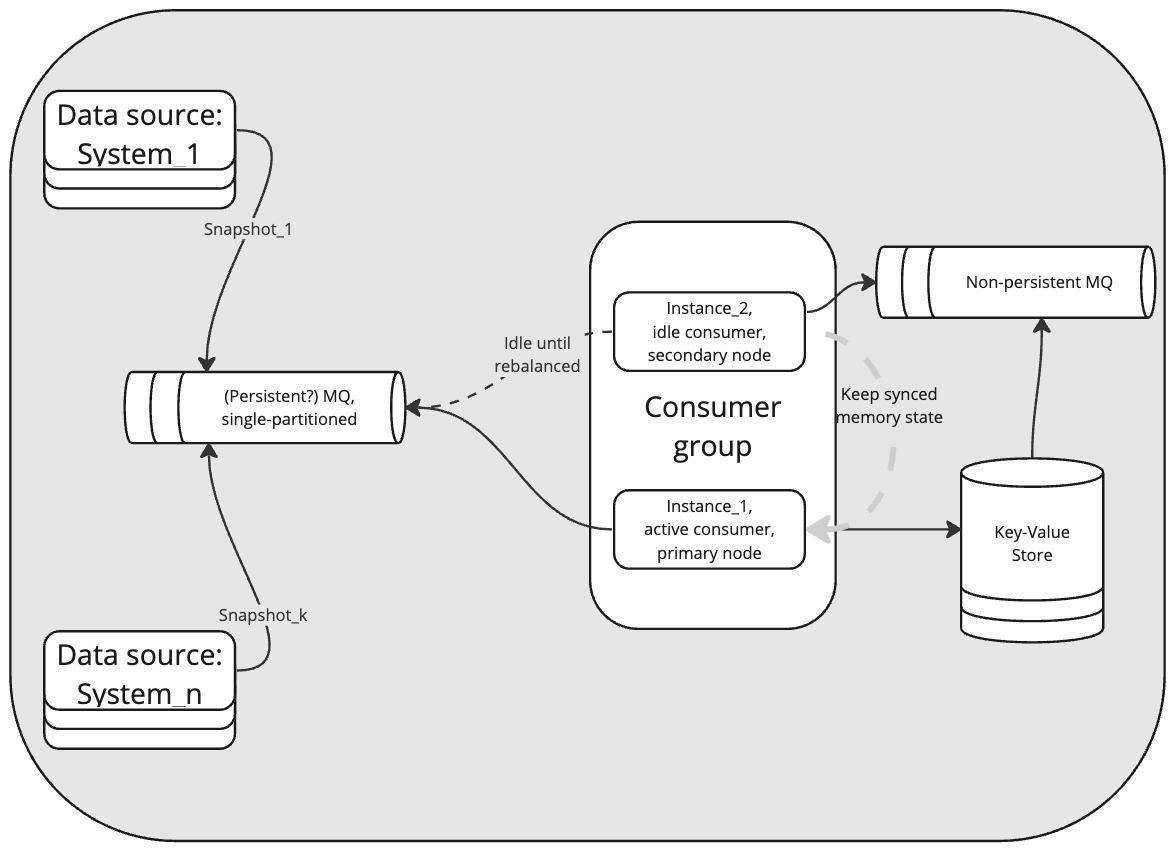
Этот алгоритм получил дальнейшее развитие в качестве сервиса дедупликации и ядра mdm-системы. В качестве заметки по имплементации на наших данных важно отметить, что алгоритм работает в памяти кластера на виртуальных машинах по 128 GB ОЗУ. Машины синхронизируют между собой стейт, рассылая друг другу события по изменению состояния через Redis notifications. Никакие два процесса слияния не происходят одновременно, несмотря на наличие нескольких машин в кластере. Избыточность служит лишь цели повышения доступности, но не преследует ускорение обработки. Persistence достигается за счёт сохранения в Redis-кластер.

Заключение и ссылка

Таким образом, для решения задачи, продиктованной бизнесом, был предложен алгоритм с высокой теоретической сложностью. Однако за счёт профиля данных удалось снизить практическую вычислительную сложность до приемлемой. Алгоритм обрабатывает миллионы записей за 20 минут на запуске, а потом с достаточной эффективностью справляется с десятками запросов в секунду в транзакционном режиме.

Код алгоритма с комментариями доступен по ссылке. Любые замечания, предложения, критика приветствуются. 

P.S. Есть перевод этого алгоритма на джаву, пишите в комментариях, если нужно его выложить в OSS.