Все любители кодокопания заканчивают либо хорошо, либо плохо. Мне повезло. Поэтому я решила написать свою первую статью на Хабре.

Как всё начиналось
Мой друг игрался со вставкой в unordered_map и заметил странную закономерность в изменении параметра bucket_count с ростом числа элементов в таблице.
Немного матчасти
Unordered map в C++ представляет собой хэш-таблицу. Хэш-таблица даёт околоконстантное время операций за счёт того, что каждый элемент хранится по своему уникальному индексу, вычисляемому через хэш-функцию. При вычислении индекса значение хэш-функции (коротко - хэш) масштабируется на размер таблицы, поэтому он не должен меняться при выполнении операций. Совпадение индексов называется коллизией. Есть несколько стратегий обработки коллизий. В std::unordered_map используется bucket hashing.
Заключается она в том, что элементы с одинаковым хэшем кладутся в соответствующий этому хэшу сегмент (bucket). При возрастании числа коллизий скорость операций с таблицей падает, поэтому необходимо производить рехэширование (rehashing) - увеличивать число сегментов и пересчитывать все хэши элементов, соответственно перевыделять память для таблицы и вставлять их заново. Это дорогостоящая по времени и памяти операция, поэтому приходится искать компромисс между числом коллизий и частотой рехэширования.
Эксперимент показал, что рехэширование происходит при вставке соответственно 14го, 30го, 60го, 128го, 258го, 542го, 1110го, 2358го и так далее. Это дал следующий код:
#include <unordered_map>
#include <iostream>
int main () {
std::unordered_map <int, int> umap;
// заполняем таблицу 2000 элементами - парами чисел
for (int i = 0; i < 2000; i++) {
// выводим число элементов и число сегментов на каждой итерации
std::cout << umap.size() << " " << umap.bucket_count() << std::endl;
umap.insert({i, i+1});
}
}
Получается, размеры таблицы образуют последовательность 13, 29, 59, 127, 257, 541, 1109, 2357, ... Но откуда берутся эти числа?
(Здесь сразу стоит оговориться, что кто знает, тому очевидно. Интерес представляет внутренняя структура того, как это реализовано.)
Начинаем копать
Первая часть изысканий делается через встроенную в IDE возможность перехода к определениям функций. insert нам даёт:

Отлично. Мы обнаружили, что unordered_map ссылается на _M_h. Следующие пара шагов нам дают:
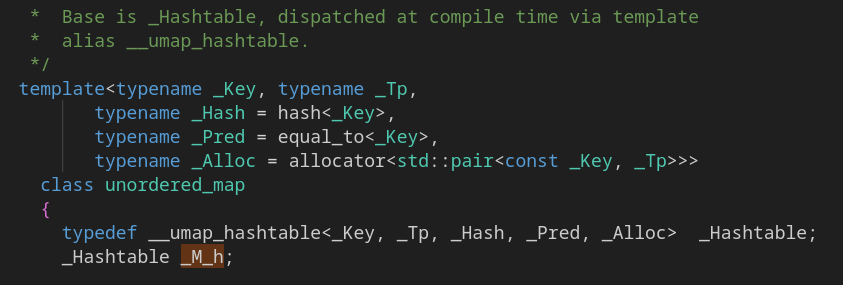
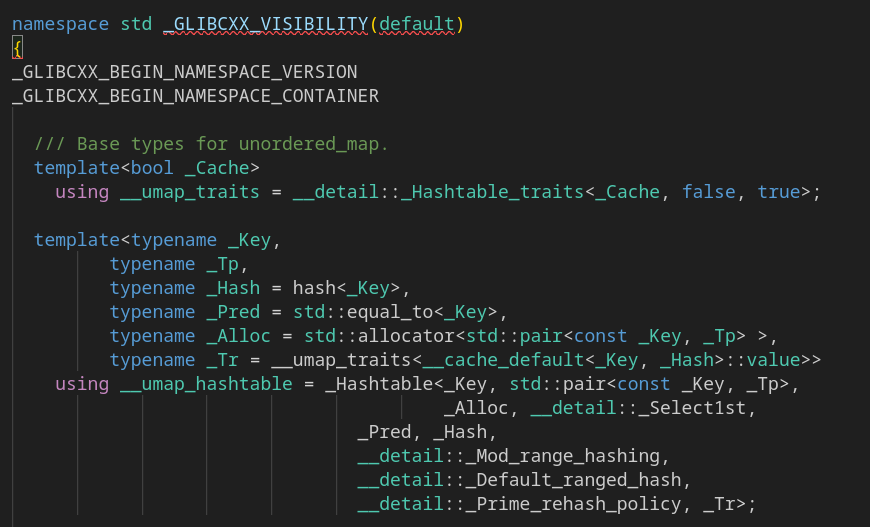
Это шаблон базового типа unordered_map. Там есть параметр, кончающийся на rehash_policy. Звучит как то, что нас интересует! Видно, что параметр определён в std::_detail. Объявим
std::__detail::_Prime_rehash_policy p;Перейдём к определению (используя "Go to definition"). Оно в файле под именем hashtable_policy.h. Лишний раз подтверждает связь хэш-таблицы и unordered_map.
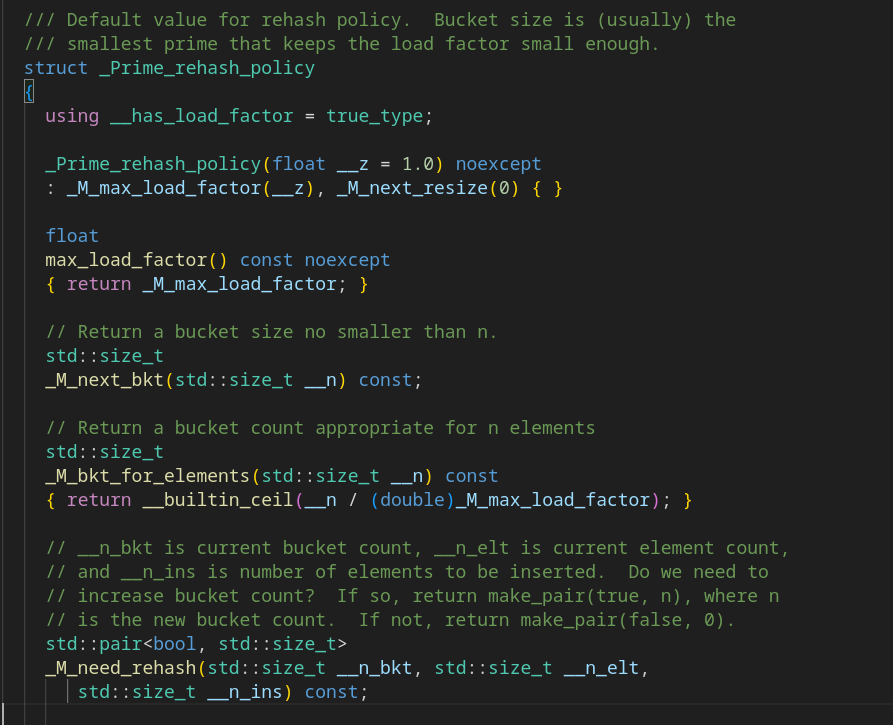
Теперь мы знаем, какие функции дают наши "магические числа". К сожалению, определений в этом файле не нашлось.
Долгожданная реализация
Гугл выдаёт следующее: хэдер с аналогичным названием, но из TR1 (проект-расширение C++ между C++03 и C++11, ставший частью последнего): https://gcc.gnu.org/onlinedocs/libstdc++/libstdc++-html-USERS-4.2/hashtable__policy_8h-source.html
Рассмотрим функцию need_rehash, которая определяет новое количество сегментов (а закон его расчёта мы и ищём):
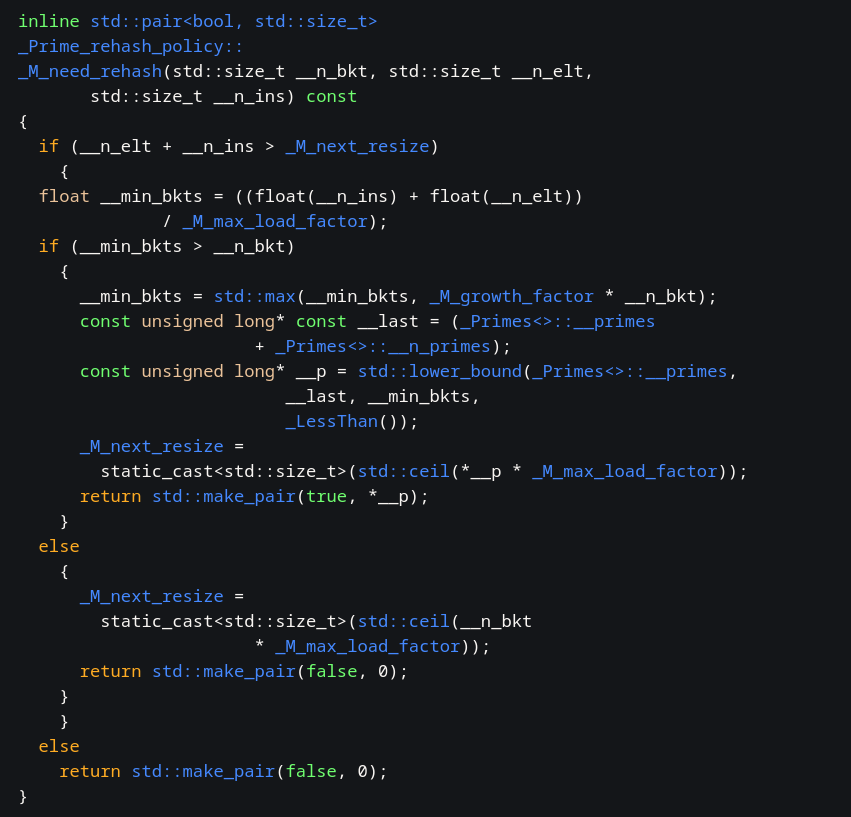
Наш случай - когда функция возвращает true (произойдёт rehashing). Параметр _M_growth_factor, он же _S_growth_factor в новой версии, по дефолту равен 2 (находится поиском по файлу), т.е. размер предварительно удваивается. _M_max_load_factor в дефолтном конструкторе равен 1. Шаблонный класс unordered_map использует именно дефолтные параметры, проверяется это эмпирически с помощью дебаггера.
Двоичный поиск по некоторому массиву _Primes<>::__primes нам даёт первое простое, большее удвоенного размера массива + числа вставленных элементов (1), и устанавливает в него параметр _M_next_resize, определяющий новое число сегментов.
Для первых 6 членов ряда всё ок: (13+1)*2 = 28 -> 29, аналогично 59 и 127. Но (257+1)*2+1 = 517, ближайшее простое - 521, а у нас - 541... Аналогично 1109 и 2357 не соответствуют расчётам.
На этом моменте я конкретно задумалась, но к счастью, моё внимание привлёк огромный массив чисел в начале файла. Это и есть тот самый _Primes<>::__primes:
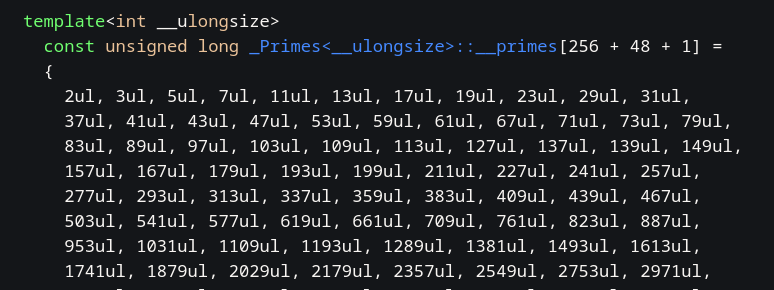
Согласно этому массиву, всё работает верно (это легко проверить). Ура. Мы нашли разгадку.
Заключение
Мы получили, что искомая последовательность формируется по принципу "ближайшее простое, большее 2(n+1), где n - предыдущий член последовательности". С оговоркой на то, что простые числа берутся из некоторого заданного массива. Почему он именно такой - неизвестно. Предположу, что часть простых пропущена из соображений памяти.
Также, невыясненным остался вопрос, почему при вставке одного элемента число сегментов возрастает сразу до 13. Может быть, вы знаете?
Жду замечаний и предложений в комментариях :)
P.S. Судя по тому, что новая библиотека работает как код из tr1, tr1 действительно был внесён в новый стандарт.
Комментарии (13)

AC130
06.10.2023 10:07+1Теперь мы знаем, какие функции дают наши "магические числа". К сожалению, определений в этом файле не нашлось.
Но у вас же прямо в картинке есть комментарий:
Hidden text
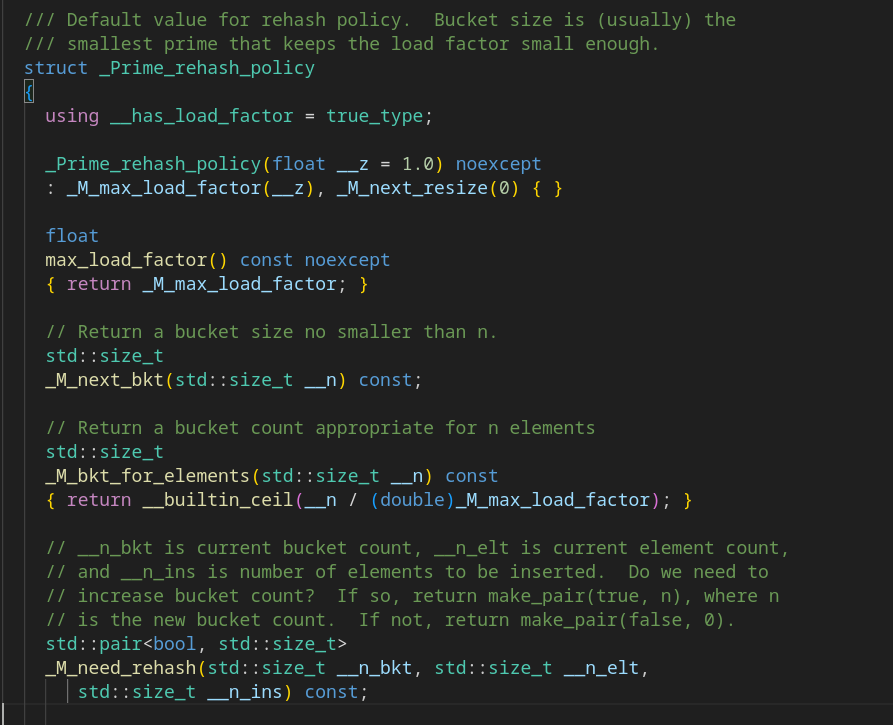
"Default value for rehash policy. Bucket size is (usually) the smallest prime that keeps the load factor small enough."
Ну а причина, по которой умножается на два, примерно такая же как и для std::vector - чтобы амортизированная сложность копирования данных при перехешировании была O(1) на каждую вставку элемента.

x6x4 Автор
06.10.2023 10:07Под определениями имелись в виду определения функций. Их в своей системе я не нашла. Например, для той же _Power2_rehash_policy объявления идут вместе с определениями.

iliazeus
06.10.2023 10:07Насколько я понимаю, простые модули для хеш-таблиц выбирают для того, чтобы было меньше коллизий при использовании определенных алгоритмов хеширования. Условие, насколько помню, даже более слабое - модуль в хеш-таблице должен быть взаимно простым с неким параметром, который используется в алгоритме хеширования. Это легче всего организовать, если либо оба будут простыми числами, либо если одно будет просым больше двух, а второе - степенью двух.
Мои знания алгоритмов уже не те, что раньше, но вот тут есть более подробный разбор (на английском, правда). Там, насколько вижу, и алгоритм из GCC вскользь упоминается.
А конкретная последовательность простых такая для того, чтобы они росли примерно как степени двойки. Это позволяет иметь, в среднем, константное время на переаллокацию и перехеширование таблицы.

wataru
06.10.2023 10:07+4Хеши беруться по модулю размера таблицы. Простые модули используются, потому что хеши по не простым модулям часто распределены хуже.
Потому что, например, операция умножения по не простому модулю не обратима. Поэтому операции над разными входными данными могут совпадать чаще. Например, в таблице умножения по модулю 5, все числа, кроме 0, встречаются по 4 раза. В таблице умножения по модулю 6 же: 1 встречается 2 раза, 2 — 6 раз, 3 — 5 раз, 4 — 6 раз, 5 — 2 раза. Похожие свойства вычисления по модулям сказываются на многих агоритмах вычисления хешей.
Умножение же размера контейнера на какое-то число каждый раз — это известный трюк, гаранитирующий, что каждое число в таблице будет рехешированно O(1) раз в среднем.
Это так потому что сумма 1 + 1/2 + 1/4 + 1/8 +… сходится. Если у вас в таблице оказалось n чисел, то все они были туда один раз добавлены. Половина, возможно была там до прошлого рехеширования. Т.е. было еще n/2 лишних хеширований. Половина от половины могла быть там 2 рехеширования назад — поэтому добавляется еще n/4. и т.д. В итоге не более чем 2n раз были подсчитаны хеши элементов.Рехеширование как бы размазывается во времени равномерно.

maleksware
06.10.2023 10:07Вероятно, поведение при добавлении элемента похоже на автоматический .reserve() вектора на условные 16 элементов при его создании. То есть понятно, что если юзер сделал umap, то туда будут добавляться еще элементы, и было выбрано небольшое число для условного .reserve().

x6x4 Автор
06.10.2023 10:07А у вектора разве есть автоматический reserve при его создании?

maleksware
06.10.2023 10:07Где-то рассказывали, что при создании очень маленьких векторов с изначально заданным размером он резервируется на ~16 элементов некоторыми компиляторами. Может быть, неверно понял.



murkin-kot
Значение по простому модулю (а именно так вычисляется попадание хэша в массив) должно лежать в диапазоне, равном длине массива. Для составных чисел это требование не соблюдается. Поэтому массив длиной [составное число] может быть заполнен лишь частично.
iliazeus
То, что вы говорите, не похоже на правду.
M % Nдля положительного целогоNи неотрицательного целогоMвсегда лежит в[0; N-1]. Даже распределение, насколько понимаю, должно быть равномерным для равномерно распределенногоM.Apoheliy
Согласен с iliazeus.
Также добавлю, что штатная реализация hash table в ядре linux-а оперирует с количеством корзин, равным степени двойки (2, 4, 8, ...). Простыми числами там и не пахнет.
mentin
Думаю при известной хорошей хеш функции - степени двойки быстрее, а в stl вынуждены готовиться к чему угодно, и простые числа надёжнее.
murkin-kot
Степень двойки (как легко вычисляемая сдвигом) по модулю простого числа даёт именно наибольшую относительную "ширину" таблицы только для простых чисел. Для составных размер таблицы будет в разы меньше составного числа.
В википедии степень двойки фигурирует в разделе "Variable range". Текст на английском, но обычно слева есть возможность выбрать язык. Хотя на русском обычно тексты менее полные.