
Под катом три разных варианта решения из разных эпох, от древнего Самарканда до США времён холодной войны.
Простое решение
Первое, что приходит в голову — вот такое заклинание:
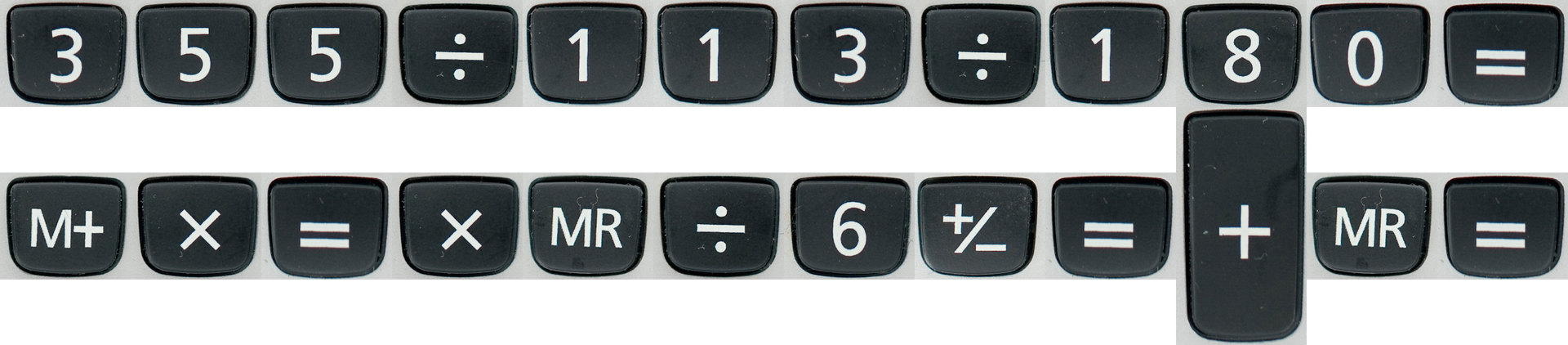
Переведём эту путаную партитуру для калькулятора на более понятный язык bc. Он часто используется как калькулятор в командной строке UNIX-подобных операционных систем. Увидим примерно следующее:
scale = 7
x = 355/113/180
x-x^3/6
.0174524
sin(x) ? x — x3/6
Перед подстановкой градус придётся перевести в радианы умножением на
π и делением на 180°.Отдельный приз полагается заметившим странные цифры 355 и 113. Их нашёл в наш китайский товарищ Цзу Чунчжи (???) ещё во времена династии Ци (479—502). Отношение 355/113 — это единственное приближение числа
π рациональной дробью, которое короче десятичного представления аналогичной точности.Интересное решение
Описанный выше общеизвестный трюк появился только в 1715 году. Тем не менее значения тригонометрических функций были известны намного раньше, и с заметно большей точностью.
Заведующий Самаркандской обсерваторией Гияс-ад-дин Джамшид ибн Масуд аль-Каши (???? ????? ????? ????????) составил таблицы тригонометрических функций с точностью до 16-го знака ещё до 1429 года. В переводе с персидского на bc его заклинание применительно к нашей задаче выглядело примерно так:
scale = 16
sin30 = .5
cos30 = sqrt(3)/2
sin45 = sqrt(2)/2
cos45 = sin45
sin75 = sin30*cos45+cos30*sin45
cos75 = sqrt(1-sin75^2)
cos36 = (1+sqrt(5))/4
sin36 = sqrt(1-cos36^2)
sin72 = 2*sin36*cos36
cos72 = sqrt(1-sin72^2)
(sin3 = sin75*cos72-cos75*sin72)
.0523359562429430
(x = sin3/3)
.0174453187476476
(x = (sin3+4*x^3)/3)
.0174523978055315
(x = (sin3+4*x^3)/3)
.0174524064267667
(x = (sin3+4*x^3)/3)
.0174524064372703
(x = (sin3+4*x^3)/3)
.0174524064372831
(x = (sin3+4*x^3)/3)
.0174524064372831
Обратите внимание на то, что мы по-прежнему используем только сложение, вычитание, умножение, деление и квадратный корень. При желании все эти операции можно выполнить вообще на бумажке в столбик. Cчитать квадратный корень в столбик раньше даже учили в школе. Это занудно, но не очень сложно.
sin30 = .5
cos30 = sqrt(3)/2
sin45 = sqrt(2)/2
cos45 = sin45
Синус и косинус 30° и 45° были известны ещё древним грекам.
sin75 = sin30*cos45+cos30*sin45
Налицо синус суммы углов 30° и 45°. Ещё до аль-Каши эту формулу вывел другой персидский астроном, Абуль-Вафа Мухаммад ибн Мухаммад ибн Яхья ибн Исмаил ибн Аббас аль-Бузджани.
cos75 = sqrt(1-sin75^2)
Пифагоровы штаны во все стороны равны.
cos36 = (1+sqrt(5))/4
sin36 = sqrt(1-cos36^2)
Это из правильного пятиугольника, известного ещё древним грекам.
sin72 = 2*sin36*cos36
cos72 = sqrt(1-sin72^2)
Опять синус суммы и теорема Пифагора.
(sin3 = sin75*cos72-cos75*sin72)
.0523359562429430
Считаем синус разности 75° и 72° и получаем синус 3°.
Теперь можно разложить 3° на сумму трёх углов по 1°, но возникает заминка — получаем кубическое уравнение:
sin 3° = 3 x — 4 x3
где x = sin 1°. Решать кубические уравнения аналитически тогда ещё никто не умел.
Мудрый аль-Каши заметил, что можно выразить это уравнение в следующей форме:
f(x) = (sin 3° + 4 x3) / 3
и потом применить к f(x) метод простой итерации. Напоминаю, что в то время ни Ньютон, ни Рафсон ещё не родились.
(x = sin3/3)
Первое приближение.
.0174453187476476
(x = (sin3+4*x^3)/3)
.0174523978055315
(x = (sin3+4*x^3)/3)
.0174524064267667
(x = (sin3+4*x^3)/3)
.0174524064372703
(x = (sin3+4*x^3)/3)
.0174524064372831
(x = (sin3+4*x^3)/3)
.0174524064372831
Получаем 16 знаков после пяти итераций.
Как считает сам калькулятор
У пытливого читателя может возникнуть законный вопрос: как же считает значение синуса калькулятор, у которого есть такая кнопка?
Оказывается, что большинство калькуляторов используют совершенно третий способ — «цифра за цифрой», родившийся в недрах военно-промышленного комплекса США во время холодной войны.
Главное преимущество метода «цифра за цифрой» в том, что он использует только операции сложения и деления на два (которое легко реализовать сдвигом вправо).
Кроме того, алгоритм можно заставить работать прямо в двоично-десятичном коде, который используется в большинстве калькуляторов, но в приведённом ниже примере мы в эти дебри не полезем.
Алгоритм итеративный и использует таблицу арктангенсов, по одному на итерацию. Таблицу нужно посчитать заранее:
#include <stdio.h>
#include <math.h>
int main(int argc, char **argv)
{
int bits = 32;
int cordic_one = 1 << (bits - 2);
printf("// Число с фиксированной точкой, соответствующее единице с плавающей точкой\n");
printf("static const int cordic_one = 0x%08x;\n", cordic_one);
printf("static const int cordic_table[] = {\n");
double k = 1;
for (int i = 0; i < bits; i++) {
printf("0x%08x, // 0x%08x * atan(1/%.0f) \n", (int)(atan(pow(2, -i)) * cordic_one), cordic_one, pow(2, i));
k /= sqrt(1 + pow(2, -2 * i));
}
printf("};\n");
printf("static const int cordic_k = 0x%08x; // %.16f * 0x%08x\n", (int)(k * cordic_one), k, cordic_one);
}
Заодно считается масштабирующий коэффициент
cordic_k.После этого посчитать пресловутый sin 1° можно так:
#include <stdio.h>
#include <math.h>
// Число с фиксированной точкой, соответствующее единице с плавающей точкой
static const int cordic_one = 0x40000000;
static const int cordic_table[] = {
0x3243f6a8, // 0x40000000 * atan(1/1)
0x1dac6705, // 0x40000000 * atan(1/2)
0x0fadbafc, // 0x40000000 * atan(1/4)
0x07f56ea6, // 0x40000000 * atan(1/8)
0x03feab76, // 0x40000000 * atan(1/16)
0x01ffd55b, // 0x40000000 * atan(1/32)
0x00fffaaa, // 0x40000000 * atan(1/64)
0x007fff55, // 0x40000000 * atan(1/128)
0x003fffea, // 0x40000000 * atan(1/256)
0x001ffffd, // 0x40000000 * atan(1/512)
0x000fffff, // 0x40000000 * atan(1/1024)
0x0007ffff, // 0x40000000 * atan(1/2048)
0x0003ffff, // 0x40000000 * atan(1/4096)
0x0001ffff, // 0x40000000 * atan(1/8192)
0x0000ffff, // 0x40000000 * atan(1/16384)
0x00007fff, // 0x40000000 * atan(1/32768)
0x00003fff, // 0x40000000 * atan(1/65536)
0x00001fff, // 0x40000000 * atan(1/131072)
0x00000fff, // 0x40000000 * atan(1/262144)
0x000007ff, // 0x40000000 * atan(1/524288)
0x000003ff, // 0x40000000 * atan(1/1048576)
0x000001ff, // 0x40000000 * atan(1/2097152)
0x000000ff, // 0x40000000 * atan(1/4194304)
0x0000007f, // 0x40000000 * atan(1/8388608)
0x0000003f, // 0x40000000 * atan(1/16777216)
0x0000001f, // 0x40000000 * atan(1/33554432)
0x0000000f, // 0x40000000 * atan(1/67108864)
0x00000008, // 0x40000000 * atan(1/134217728)
0x00000004, // 0x40000000 * atan(1/268435456)
0x00000002, // 0x40000000 * atan(1/536870912)
0x00000001, // 0x40000000 * atan(1/1073741824)
0x00000000, // 0x40000000 * atan(1/2147483648)
};
static const int cordic_k = 0x26dd3b6a; // 0.6072529350088813 * 0x40000000
void cordic(int theta, int& s, int& c)
{
c = cordic_k;
s = 0;
for (int k = 0; k < 32; ++k) {
int d = (theta >= 0) ? 0 : -1;
int tx = c - (((s >> k) ^ d) - d);
int ty = s + (((c >> k) ^ d) - d);
c = tx; s = ty;
theta -= ((cordic_table[k] ^ d) - d);
}
}
int main(void)
{
double alpha = M_PI / 180;
int sine, cosine;
cordic(alpha * cordic_one, sine, cosine);
printf("CORDIC: %.8f\nExpected: %.8f\n", (double)sine / cordic_one, sin(alpha));
}
Результат:
CORDIC: 0.01745240
Expected: 0.01745241
Тут 32 итерации, поэтому осталась небольшая ошибка. Калькуляторы обычно используют 40 итераций.
Комментарии (44)

a_batyr
30.11.2015 17:36+8Экскурс в античную тригонометрию. Текст до хабраката мне показался слишком скудным для такой интересной статьи.

dimview
30.11.2015 17:53Спасибо за обратную связь, добавил параграф до ката. Исходно хотел сделать условие задачи как можно короче, чтобы можно было понять, не вчитываясь.

PaulZi
30.11.2015 18:23За 355/113 спасибо, правда не знаю, что проще запомнить, учитывая то, что 3.14 точно уже у всех отскакивает от зубов.

ivvi
30.11.2015 19:33+3Но вот 3,1415926 отскакивает далеко не у всех.

AndrewN
30.11.2015 19:45+4Это я знаю и помню прекрасно, пи многие знаки мне лишни напрасны = 3,14159265358
Помню класса с пятого
ruikarikun
30.11.2015 20:08+12How I want a drink, alchoholic of course, after the heavy lectures involving quantuum mechanics = 3,14159265358979

Maccimo
03.12.2015 10:52+3IMHO запомнить «3, 14, 159, 26, 53, 58» намного проще, чем сначала выучить стишок, а потом ещё и считать количество букв в словах.
Для меня, во всяком случае.

Muzzy0
01.12.2015 11:33+2у меня до 6 знака (3.141592) отскакивает. У жены — почти до двадцатого :) Для тренировки она себе пи до какого-то там знака на пароль поставила :)

miwa
01.12.2015 11:38+3Чтобы нам не ошибиться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Вполне себе от зубов :)

vanxant
30.11.2015 18:56+3Есть мнение, что
а) иногда синус аппаратно считают через таблицы (аля Брадиса) с поправками до 3-ей степени. Для машинной точности типа double таблицы получаются не такие уж и большие по размеру, зато очень быстро — пара умножений и сложений;
б) иногда синус считают аппаратно разложением в ряд, в котором коэффициенты посчитаны заранее. Тоже остаётся только сложение и умножение.
dimview
30.11.2015 19:07+1a) Верно, именно так, например, считается синус в библиотеке C когда нет поддержки плавающей точки. Но на калькуляторах так делают редко. Умножение на калькуляторе — дорогая операция, а в CORDIC используются только сложение и сдвиги.
б) Я раньше тоже так думал, но на практике ни разу не встречал. Подозреваю, что это весьма редкое явление.

indalive
30.11.2015 19:32берём первые члены ряда Фурье для синуса, упрощаем/сокращаем и получаем простую формулу для синуса любого угла

dimview
30.11.2015 19:40+12Вы наверное имели в виду ряд Тейлора. Это как раз и есть первое из описанных решений.
Ряд Фурье для синуса будет очень коротким (все коэффициенты, кроме одного, равны нулю).
POGlicier
30.11.2015 23:08-4Член какой придётся в пору, чтоб заправить в зад Тейлору?
Оба члена хороши: и Лагранжа, и Коши!
stepik777
30.11.2015 20:57+1Описанный выше общеизвестный трюк появился только в 1715 году.
Ну ряды для конкретных функций были известны и раньше.

KvanTTT
30.11.2015 21:04+2По первой картинке я уж подумал, что вычисление синуса будет с использованием ряда Тейлора с помощью Arduino, который будет сам кнопочки нажимать…

Mrrl
30.11.2015 22:40+1Я в одной из библиотек видел такой алгоритм — сначала по формулам приведения сводим аргумент к отрезку [0,pi/4], потом применяем к нему синус или косинус (в зависимости от того, какая функция получилась), заданный в виде аппроксимирующего многочлена (8-й или 9-й степени, в зависимости от требуемой точности).

alexpp
30.11.2015 23:31+8Хабр — торт. Простой математический пример в статье, и множество комментариев с методами, алгоритмами, и т.п.

cjfynjy
01.12.2015 02:21+1> Отношение 355/113 — это единственное приближение числа ? рациональной дробью, которое короче десятичного представления аналогичной точности.
Ну, не единственное. В десятичной системе счисления ничего уникального нет. Но «единственное такое, что одновременно короткое и с отличной точностью» — это да.

dimview
01.12.2015 02:29+1Вот тут товарищ Jon McLoone специально искал и не нашёл ничего лучше: All Rational Approximations of Pi Are Useless.

Mrrl
01.12.2015 08:09+1Если брать относительный выигрыш — то может быть, других и нет. Странно, что в этом тексте нет упоминания о разложении в цепную (непрерывную) дробь. Казалось бы, чем больше член разложения, который мы отбрасываем, тем больше должен быть выигрыш в цифрах. Если 355/113 (отбросили 292) даёт 1 знак выигрыша, то приближение первыми 453293 членами разложения (отброшен член 12996958) должно дать 5, а то и 6 знаков.
Ещё странно сравнение sqrt(2) и «e». У sqrt(2) цепная дробь ограничена, поэтому выигрыша больше, чем в 1 цифру, мы не получим никогда, но у «e» её члены неограниченно растут (хотя и довольно медленно — линейно), и, грубо говоря, удлинение записи в 10 раз всегда будет давать лишнюю цифру выигрыша.
dimview
01.12.2015 15:36В комментариях пишут то же самое, про convergents of continued fractions. Их можно посчитать через WolframAlpha, например, Last[Convergents[Pi, 6]] = 104348/33215. Но выигрыша нет — надо запоминать 11 цифр, чтобы получить ? с точностью 10 цифр.
В любом случае много цифр запоминать смысла нет, так что это уже искусство для искусства.

sergku1213
01.12.2015 10:23+3Ждём продолжения — как посчитать это же на камушках и римскими цифрами 8)).

Mrrl
01.12.2015 11:00Интересно, почему в вычислении синуса «по цифрам» не делалось округления при сдвиге:
вместо
int tx = c - (((s >> k) ^ d) - d);
было бы лучше (при k>0, конечно),
int tx = c - (((((s >> (k - 1)) + 1) >> 1) ^ d) - d);
Да и таблица арктангенсов в конце могла бы быть точнее. Выбросить 2/3 её, к сожалению, нельзя — поправочный коэффициент перестанет быть предсказуемым — но заменить вторую половину на обычное умножение (которое наверняка реализовано очень эффективно) было бы и быстрее, и точнее.
Впрочем, военным виднее. Они высоко летают.
dimview
01.12.2015 14:10почему в вычислении синуса «по цифрам» не делалось округления при сдвиге
Думаю, что для простоты. Попробовал предложенный вариант, получил тот же результат.
заменить вторую половину на обычное умножение
Умножение на калькуляторе — дорогая операция. В частности именно поэтому не используются приближения многочленами или рядами.

andy_p
01.12.2015 11:57А аппроксимация полиномами Чебышева не подойдет?

dimview
01.12.2015 14:12Умножение на калькуляторе — дорогая операция, реализуется программно. А сложение и сдвиг — дешёвые, реализованы аппаратно. Поэтому и не используются приближения многочленами или рядами.

il--ya
01.12.2015 14:36-1Умножение реализуется через сложение и сдвиги, так что ваше утверждение не очевидно. Функция умножения в любом калькуляторе уже реализована, скорость вычисления в пределах миллисекунд — удовлетворительно, т.к. операции всё равно вводятся вручную. Не вижу смысла отказываться от рядов, если алгоритм будет проще — аппаратная реализация будет в итоге проще и дешевле.

dimview
01.12.2015 14:58+2Посмотрите на картинку в начале статьи. Этот калькулятор питается от маленькой солнечной батареи, и даже солнца ему не надо — достаточно настольной лампы. Тактовая частота меряется не в гигагерцах и даже не в мегагерцах, а в килогерцах. Для него одно умножение занимает миллисекунды, а чтобы многочлен посчитать уже секунды уйдут, неприемлемо.
Разработчики калькуляторов это ещё в семидесятые годы прикинули и вышло, что CORDIC лучше. Разумеется, на более привычном процессоре помощнее всё может оказаться наоборот.

MichaelBorisov
06.12.2015 01:12+3В бейсике «Спектрум» и во многих других бейсиках того времени для вычисления синусов использовалось именно разложение в ряд Чебышева. Думаю, дело в том, что в литературе по численным методам 80-х годов (всякие книги типа МакКракен и Дорн и т.д.) разложение в ряд Чебышева было самым продвинутым методом аппроксимации, которые рассматривались. Программисты подобного софта по большей части просто не знали, какие еще бывают методы.
CORDIC более перспективен для аппаратной реализации, т.к. не требуется умножение. На самом деле умножение — очень затратная операция по времени либо аппаратным ресурсам. Если разрабатывать микросхему, вычисляющую синус — то лучше отказаться от умножителя и реализовать CORDIC, чем использовать умножитель и аппроксимацию, основанную на умножении. То же касается ассемблерного кода для процессоров, не имеющих аппаратного умножителя.
Если есть умножитель, то несколько лучше, чем разложение в ряд Чебышева, применить аппроксимацию минимакс-полиномом. Коэффициенты такого полинома вычислить сложнее, чем Чебышева, но стоит только освоить алгоритм Ремеза — как трудности исчезнут. Аппроксимация же рядом Тейлора (Маклорена) — это очень неэффективный подход.
Если имеется много памяти — то лучше всего хранить в ней таблицу значений синуса и применять линейную интерполяцию для промежуточных углов. Линейная интерполяция по сути сводится к одному умножению.
При вычислении синусов еще важно то, в какой последовательности надо их вычислять. Скажем, если нужно вычислить синусы многих углов, равноотстоящих друг от друга — то есть рекуррентные соотношения. y[i] = -y[i-2] + 2*b*y[i-1], константа b задает шаг. Одно умножение и два сложения — и это при том, что данная формула дает точные ответы. Конечно, при ее использовании будет накапливаться ошибка округления, поэтому представление чисел должно иметь много бит, и самые младшие из них будут постепенно зашумляться. Есть и другие рекуррентные формулы, вычисляющие одновременно синус и косинус многих углов, где влияние ошибок округления уменьшено.


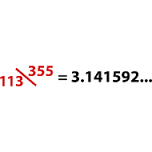
PapaBubaDiop
В принципе, в этой постановке задача решается в уме, поскольку синус малого угла равен углу.
31415/180 = 15707/9.
То есть в уме надо разделить 157075 на 9, что не вызывает сомнений, равно 174527 и совпадает с Вашим ответом до 7 знака.
dimview
Верно. Это то же самое разложение в ряд, только ряд короче.