Мой первый софт и астрономия / forpes.ru

19.11.2023 07:14

ArduinoMiniProjects 1 1900 Источник

Здравствуйте, уважаемые хабровчане! Расскажу о своём небольшом опыте работы в проекте, который был посвящён астрономии, и о математике, с которой пришлось повозиться.

Дело было так - учился я в универе, изучал электронику, и после окончания курса по азам С++ , мне предложили подработку в одном проекте, где нужно было написать небольшую программу для моделирования рассеивания света звёздной пылью. Пришёл я на собеседование, которое проводили два доктора астрофизика, поспрашивали про математику и астрономию, поняли что не математик и уж тем более не астроном, но на работу взяли.

Первым моим заданием было подтянуть математику и боль-мень освоить фортран, так как на фортране был софт одного известного учёного М.И.Мищенко (Michael I. Mishchenko). Этот софт определял оптические свойства пыли в зависимости от её концентрации, формы пыли, длины волны и индекса преломления света.

Далее мне нужно было написать свою программу, которая моделирует рассеивание света. Модель простая - звезда, вокруг неё пылевое облако (параметры оптических свойств пылевого облака можно было рассчитать программой М.И.Мищенко), вдали от облака находится оптический телескоп. Моя программа моделирует полученное изображение на CCD матрице телескопа, а именно значение четырёх векторов Стокса, для каждого пикселя CCD матрицы. Метод, который использовался для моделирования рассеивания света - Монте-Карло. Я уговорил начальника - доктора астрофизики использовать C++, т.к. я не хотел писать её на фортране.

Задача была не сложной, начальник выводил формулы и уравнения, я решал их численными методами и ваял программу.

Упрощённая блок-схема программы, к которой я пришёл интуитивно, а после сравнил с одной публикацией (Three Monte Carlo programs of polarized light transport into scattering media: part I (Jessica C. Ramella-Roman, Scott A. Prahl, and Steve L. Jacques) ) о разных методах Монте-Карло для рассеивания света. И понял что моя совпадает с классическим методом Монте-Карло для поляризованного излучения.

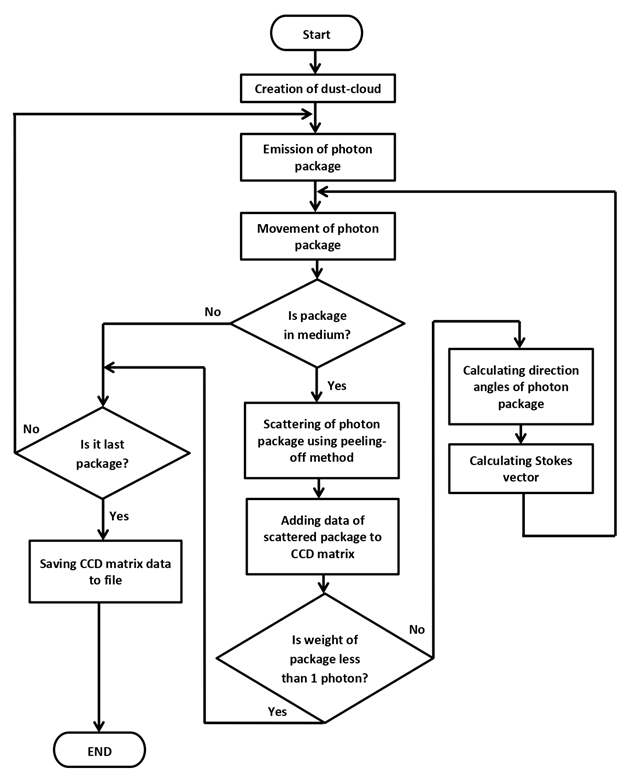
Из звезды вылетают пакеты фотонов (каждый пакет фотонов состоит из 1000 фотонов), которые летят в случайном направлении, после часть энергии рассеивается, в зависимости от направления пакета фотонов и оптических свойств пыли рассчитывается дальнейшее направление пакета фотонов. Каждое рассеивание фиксируется на CCD матрицу телескопа. И так много миллионов раз. Чем больше пакетов фотонов рассеяно, тем точнее изображение.

Часть математики я вывел сам - это моделирование излучения пакетов фотонов из сферического источника света и моделирование проекции пылевого облака на плоскость телескопа.

Моделирование сферического источника света:

Звезда и испускание пакета фотонов из точки её поверхности

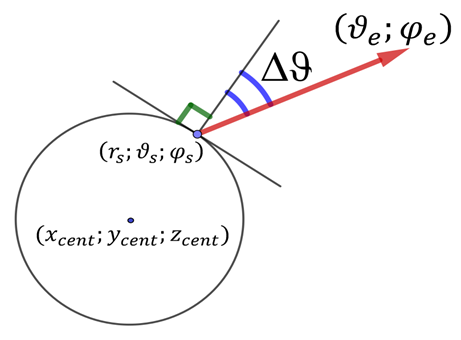
$\left ( x_{cent};y_{cent};z_{cent} \right )$ - Декартовы координаты центра звезды.

$\left ( r_{s};\vartheta_{s};\varphi_{s} \right )$ - сферические координаты точки, на поверхности звезды, из которой будет испускаться пакет фотонов.

$\Delta\vartheta$ - угол между нормалью к поверхности звезды и вектором эмиссии (испускания) пакета фотонов.

$\left (\vartheta_{e};\varphi_{e} \right )$ - полярный и азимутальный углы эмиссии пакета фотонов.

Программа генерирует углы $\varphi_{s}\in \left [ 0;2\pi \right )$ и $\cos \left ( \vartheta_{s} \right ) \in \left [ -1;1 \right ]$ , радиус звезды $r_{s}$ - константа. Декартовы координаты точки эмиссии пакета фотонов рассчитываются по формуле (1.1)

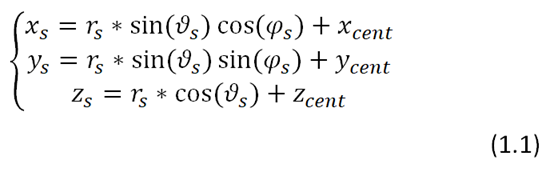
Единичный вектор $\mathbf{n}=\left (x_{n};y_{n};z_{n} \right )$ рассчитывается по формуле (1.2)

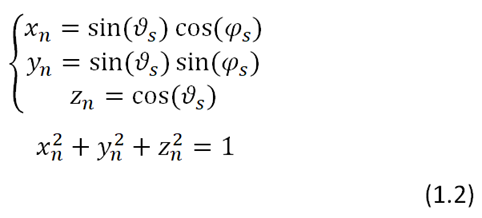
Угол между нормалью к поверхности звезды и вектором эмиссии $\cos \left (\Delta\vartheta \right ) \in \left [ 0;1 \right ]$ .

Программа рассчитывает вектор эмиссии $\mathbf{e_{0}}=\left (x_{e0};y_{e0};z_{e0} \right )$ по формуле (1.3).

Поворачиваем вектор эмиссии вокруг вектора нормали к поверхности звезды $\mathbf{n}$ на угол $\alpha \in \left [ 0;2\pi \right )$ .

Используем матрицу поворота , чтобы рассчитать вектор эмиссии $\mathbf{e_{1}}$ после поворота.

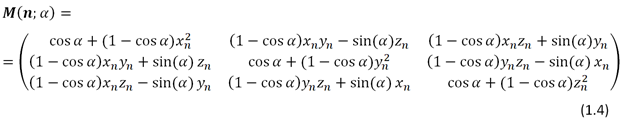
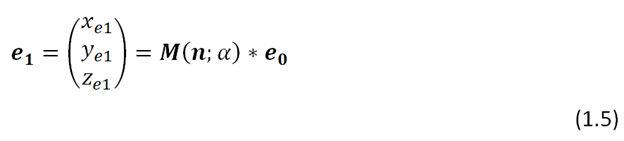
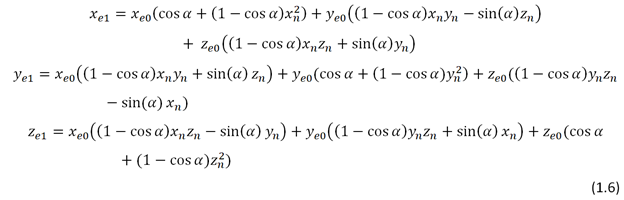
Когда вектор получен,

рассчитываются полярный и азимутальный углы эмиссии $\left (\vartheta_{e};\varphi_{e} \right )$

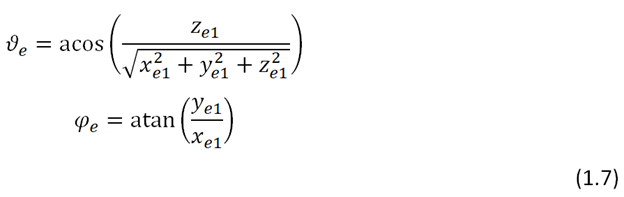
В результате мы получили пакет фотонов, который испускается из точки поверхности звезды с координатами $\left ( x_{s};y_{s};z_{s} \right )$ и летит в направлении которое задают полярный и азимутальный углы $\left (\vartheta_{e};\varphi_{e} \right )$ .

Моделирование проекции пылевого облака на плоскость телескопа:

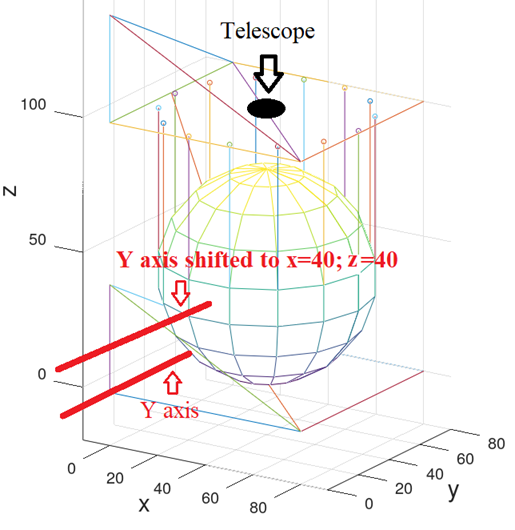
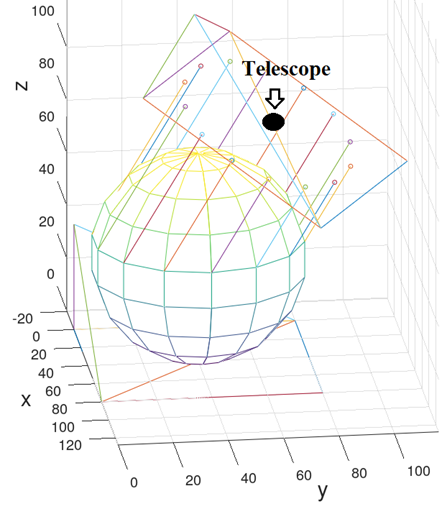
Сферическое облако и позиция телескопа до поворотов в программно заданную точку.

Центр системы координат , центр сферического облака $\left (x_{sph0};y_{sph0};z_{sph0} \right ) = \left (40;40;40 \right )$ , радиус сферического облака 39. (Это описание математической модели, в программе соответственно используются астрономические расстояния).

Координаты телескопа до поворотов:

Первый поворот осуществляется вокруг оси которая параллельна Y оси ,

Телескоп поворачивается на угол $\vartheta_{tel.pos.}$ (полярный угол позиции телескопа):

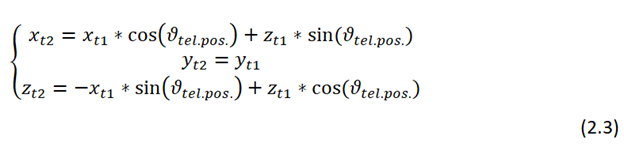
Первый поворот телескопа на угол $\vartheta_{tel.pos.}$ совершён.

Позиция телескопа после первого поворота

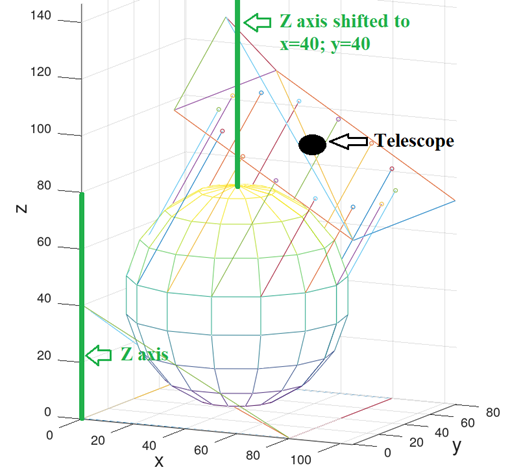
Далее будет произведён поворот вокруг оси параллельной Z оси , на угол $\varphi_{tel.pos.}$ (азимутальный угол позиции телескопа).

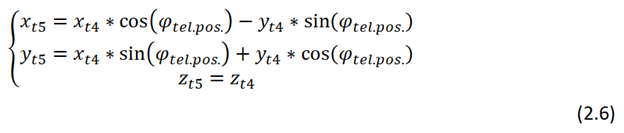
Второй поворот телескопа на угол $\varphi_{tel.pos.}$ совершён.

Позиция телескопа после второго поворота

Далее необходимо рассчитать единичный вектор для плоскости телескопа (для проекции облака на плоскость телескопа):

Необходимо рассчитать константу для уравнения плоскости телескопа:

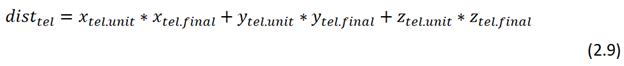
Уравнение плоскости телескопа:

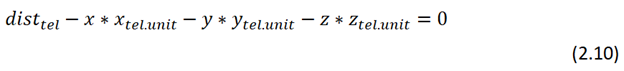
Необходимо рассчитать рассчитать расстояния от точки облака до плоскости телескопа, $\left (x_{sph};y_{sph};z_{sph} \right )$ - точки облака

Далее получаем точки проекции облака на плоскость телескопа:

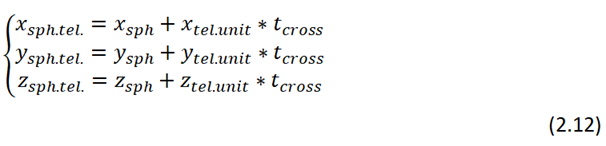
Для того чтобы правильно отобразить все точки облака и векторы Стокса на CCD матрице телескопе, необходимо выполнить обратные повороты.

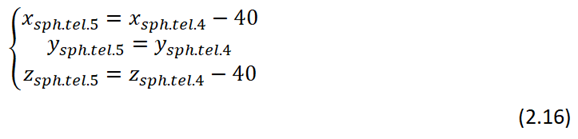
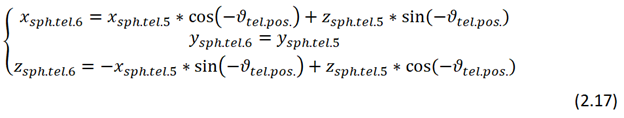
С математикой, которую выводил самостоятельно усё.

Написал я программу , которая рассчитана под линукс, используется C++11 concurency, распараллеливание на ядра процессора (сколько ядер, столько одновременно пакетов фотонов рассеиваются), запускал на кластере суперкомпьютера, у которого было 24 ядра. Получил результаты, но нужно было их как-то проверить.

Начальник принял решение - написать другую программу, которая решит систему интегральных уравнений Фредгольма для простой модели со звездой, сферическим облаком вокруг неё и Рэлеевским рассеиванием света. Для этой задачи я решил использовать питон, из-за удобства библиотек (да и интересно было что-то на питоне написать).

Далее была необходима нормализация параметров, т.к. разные программы давали результаты в разных величинах измерения. Результаты совпали, но для большей убедительности результаты сравнили также с программой известного учёного Cornelis Dullemond RADMC3D. Там результаты тоже совпали.

Были конференции, прикладываю презентацию одной.

А также видео другой (выступает мой бывший начальник) :

И также написана научная публикация (это уже после окончания моей работы, её к сожалению выложить не могу).

Ну вот - как-то так, поработал, написал свой первый софт, подтянул математику, мне понравилось :)

Комментарии (1)

vkams
20.11.2023 19:21
#26179572
Навеяло трогательные воспоминания о начале моей работы в теоротделе ИВТ РАН: тоже писал на С программу, которая рассчитывала рассеяние методом Монте-Карло, и даже уравнения Фредгольма изучил, хотя не пригодились. Компьютеры тогда были - не чета нынешним: 386DX 25 МГц, а больше 286 16 МГц 1 Мб оперативки.

Мой первый софт и астрономия +7

Комментарии (1)

vkams