Существует ли частотная область в реальности? / forpes.ru

Главная
Существует ли частотная область в реальности?

Существует ли частотная область в реальности?

09.04.2024 15:00

veseluha 26 8200 Источник

Частотная область — волшебное математическое пространство, которое трансформирует комплексные сигналы в амплитуды и фазы синусоид. Она открывает нам возможность применять разнообразные методы обработки сигналов, казавшиеся почти недостижимыми при их анализе в наиболее очевидной форме, а именно — во временной области.

Изображение волнового рисунка (выше) и визуализация частотного спектра (ниже) композиции "Girl in Blue"

Однако насколько материально частотное пространство? Дискретное преобразование Фурье (DFT) имеет ключевое значение в сферах связи и анализа сигналов, но не раскрывает ли оно более глубокие, скрытые аспекты реальности? Рассмотрим, к примеру, квадратные волны. Действительно ли они существуют, если преобразование Фурье разлагает их на ряд нечетных гармоник синусоид, которые, в свою очередь, эффективно предсказывают поведение электронных схем в реальном мире?

Сегодня я хочу немного уменьшить роль преобразования Фурье, сняв его с постамента. Несомненно, синусоидальные волны являются повсеместными в природе и служат мощным аналитическим инструментом для множества задач. Однако возможно создание иных частотных областей с хорошими свойствами, которые подчиняются другим принципам. К таким областям можно отнести ту, где реальностью являются исключительно квадратные волны, а все остальное представляет собой лишь гармонические составляющие.

Дискретное косинусное преобразование (DCT)

Для начала давайте обратимся к дискретному косинусному преобразованию — это упрощенный вариант дискретного преобразования Фурье, который задействует только реальные числа. Вспомним формулу DCT-II:

$F_k = \sum^{\substack{ N - 1 }}_{\substack{ n = 0 }} s_n \cdot cos(\pi k \frac{n+\frac12 }{N} )$

Этот процесс заключается в поочередном взятии ряда входных данных (например, аудиосемплов sn), умножении их на определенные значения косинусной функции и последующем суммировании полученных результатов для определения амплитуды на конкретной частоте ().

Основа данного алгоритма представляет собой функцию , создающую синусоиду с частотой, соответствующей индексу текущего частотного бина DCT. Эта функция называется базисной функцией. Мы можем отвлечься от конкретной формы и переформулировать выражение следующим образом:

$F_k = \sum \limits_{n=0}^{N-1} s_n \cdot B(k,n)$

В этой универсальной формулировке для перехода к частотному представлению, определяет некий коэффициент, зависящий от значений и . Программисты могут воспринимать как таблицу для быстрого поиска значений. Предлагаю вычислить эту таблицу — или матрицу в математическом смысле — для N равного 16:

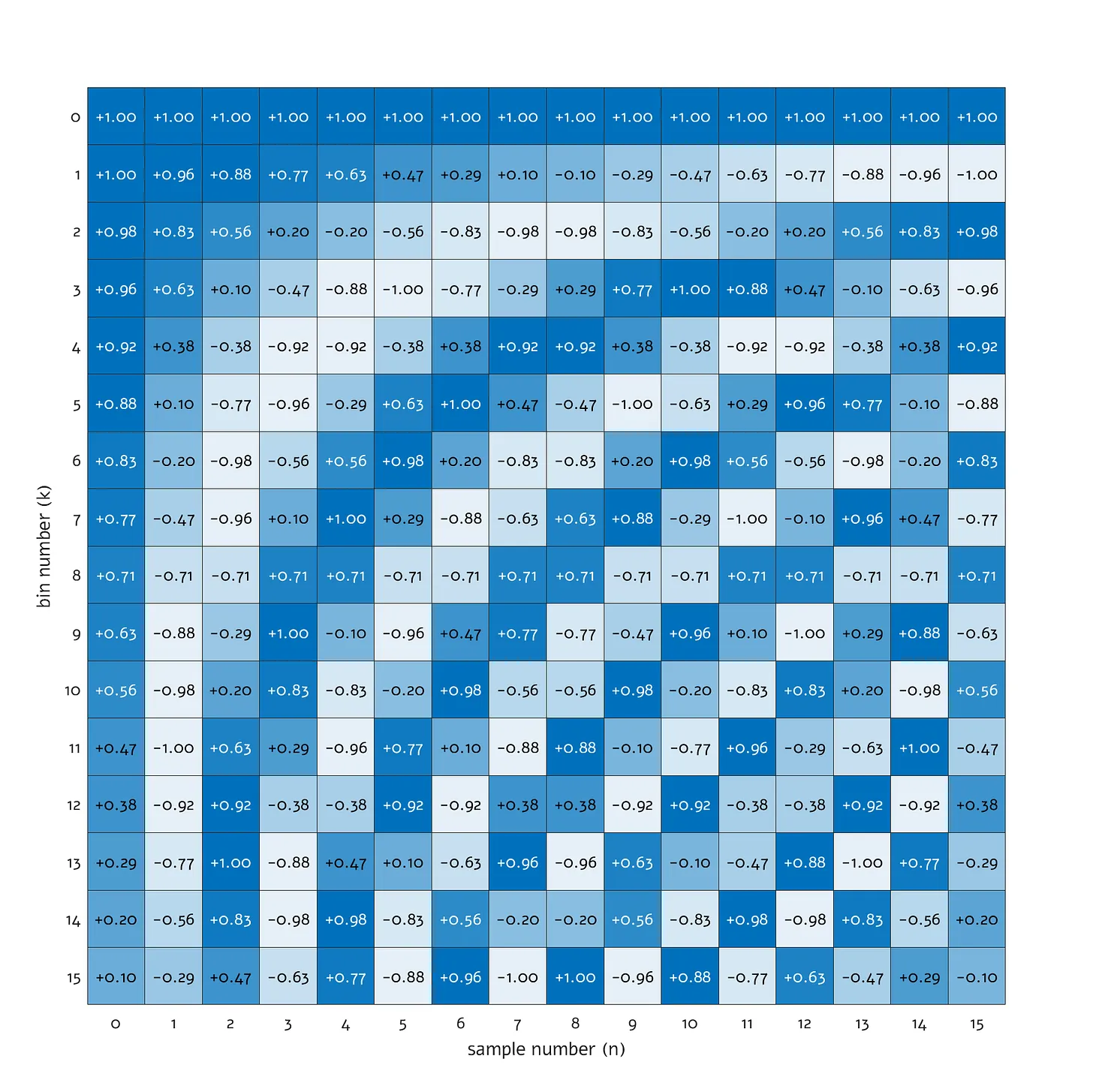
Первая строка () соответствует постоянной составляющей (DC) — это косинус с нулевой частотой, который постоянно равен +1.00. Следующая строка представляет косинус, проходящий через половину своего периода от +1.00 до -1.00; далее идет строка для полного цикла косинуса при , затем цикл и половина при и так далее.

Вселенная квадратных волн

Каким образом можно создать новую базисную функцию, которая вместо разложения сигналов на синусоидальные частоты будет разделять их на квадратные волны? Заглядывая немного вперед, ответ удивительно прост:

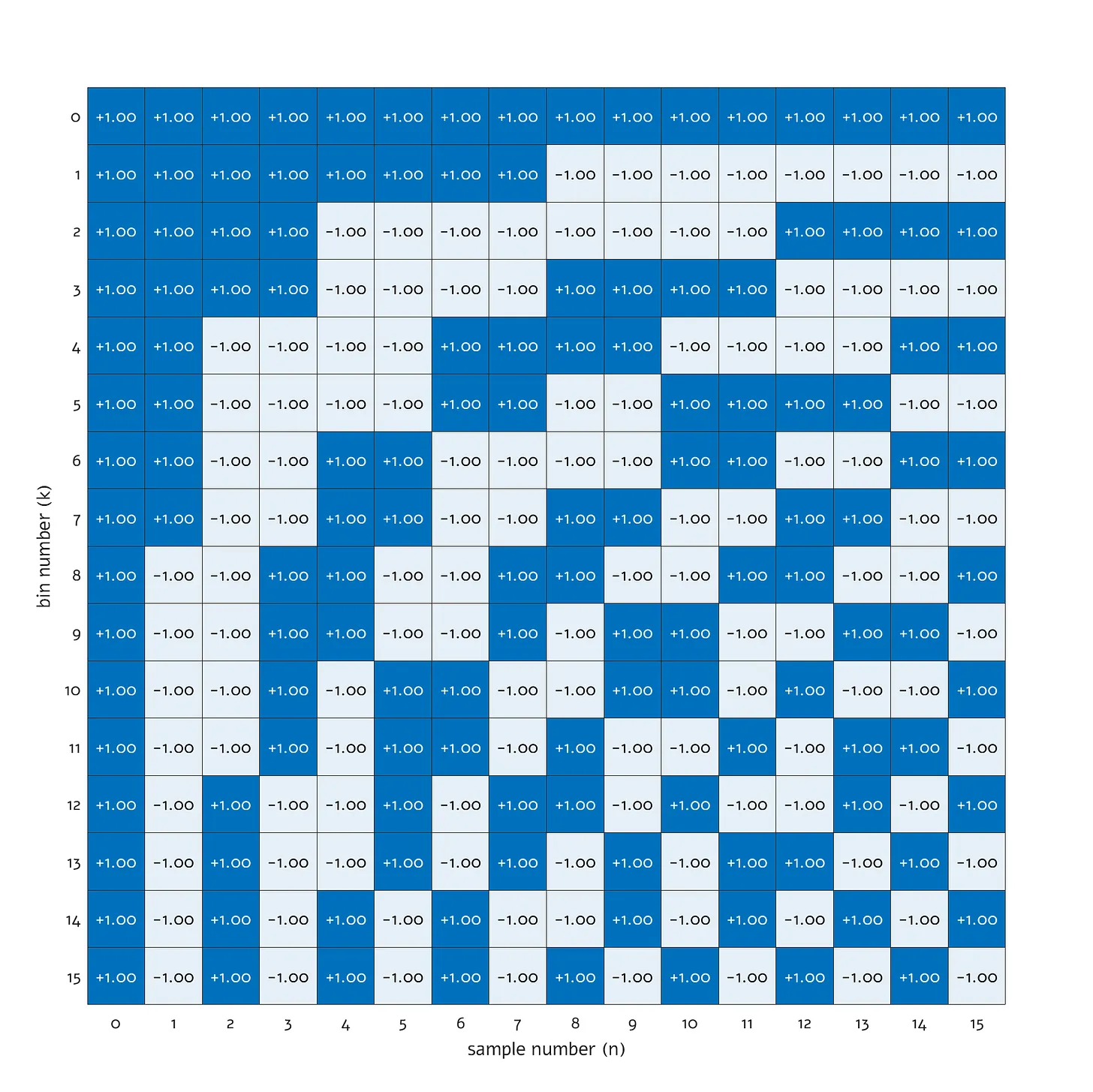
Эта конструкция известна как матрица Уолша. Она составлена из квадратных волн, которые изменяют свою частоту, и содержит в себе определенные сложные симметрии. Каждый элемент матрицы представляет собой либо +1, либо -1, что делает вычисления относительно простыми — достаточно изменить знаки входных данных и выполнить их суммирование.

На первый взгляд, матрица может показаться простой, но разработка ее структуры требует времени. Чтобы охватить всю информацию о частоте и фазе, строки располагаются в порядке увеличения количества изменений знака — каждая последующая строка содержит на один переменный знак больше, чем предыдущая. Кроме того, узор матрицы тщательно сконструирован так, чтобы обеспечивать ортогональность — это особый вид симметрии между входом и выходом, который позволяет безошибочно выполнять преобразования между частотным представлением и временными данными.

Учитывая сложность структуры матрицы Уолша, одним из наиболее эффективных методов ее создания является начало с формирования так называемой матрицы Адамара. Для размерности N=16 эта промежуточная структура выглядит следующим образом:

Матрица Хадамара для N=16 — Матрица Адамара для N=16

Введение в мир Адамара

На первый взгляд, таблица может показаться беспорядочной, но на деле это всего лишь вариация распределения Уолша. К примеру, строки #1 и #8 меняются местами; аналогичная ситуация происходит между строками #1 и #15. В отличие от Уолша, эта структура, которая напоминает фрактал, на удивление проста для создания с нуля.

Начнем с основного одномерного массива размером 1×1:

$H_0 = \begin{bmatrix} +1 \end{bmatrix}$

Исходя из этого, мы последовательно увеличиваем размер массива, используя массив, созданный на предыдущем этапе ( $H_{n-1}$ ). Мы размещаем четыре его копии на решетке, которая вдвое превышает исходные размеры. Первые три копии оставляем без изменений, а четвертую — расположенную в нижнем правом углу — инвертируем по знаку. Математическое выражение для этого процесса расширения выглядит следующим образом:

$H_n = N_{n-1} \otimes \begin{bmatrix} +1 & +1 \\ +1 & -1\end{bmatrix}$

Этот оператор ⊗ называется кронекеровым произведением, хотя в действительности он представляет собой лишь способ копирования и вставки. Первое увеличение массива выглядит так:

$H_1 = \begin{bmatrix} \begin{array}{c|c} +1 & +1 \\ \hline +1 & -1\end{array}\end{bmatrix}$

Еще одна итерация дает нам:

$H_2 = \begin{bmatrix} \begin{array}{c c| c c} +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 \\ \hline+1 &+1 &-1 &-1 \\ +1 &-1 &-1 &+1 \end{array} \end{bmatrix}$

Этот процесс идет дальше. Размер конечной матрицы Адамара всегда составляет $2^n \times 2^n$ , где обозначает число выполненных этапов построения.

Хотя на компьютере можно вычислить матрицу, следуя указанному алгоритму компоновки, существует элегантный метод с использованием битовых операций, который может служить альтернативой: оказывается, чтобы определить значение функции Адамара для любой конкретной ячейки, достаточно вычислить побитовое И (x & y) координат этой ячейки и определить, четным или нечетным является количество установленных битов в полученном результате. Ниже представлен код на языке C, который выполняет эту задачу и выводит на экран матрицу Адамара размером 8×8:

#include <stdint.h>
#include <stdio.h>

#define HD_LEN_POW2 3
#define HD_LEN      (1 << HD_LEN_POW2)

int8_t hadamard(uint32_t x, uint32_t y) {  
  return (__builtin_popcount(x & y) % 2) ? -1 : 1;
}

int main() {
  for (uint32_t y = 0; y < HD_LEN; y++) {
    for (uint32_t x = 0; x < HD_LEN; x++) printf("%+d ", hadamard(x, y));
    putchar('\n');
  }
}

В основном, данная матрица обеспечивает все необходимое для создания преобразования в частотную область. Тем не менее, расположение частотных интервалов в ней является неупорядоченным. Давайте попытаемся упорядочить их, прежде чем завершить.

Войдите, господин Уолш

Для того чтобы преобразовать матрицу Адамара в упорядоченную форму, как было показано ранее, нам необходимо отсортировать строки согласно их частотному порядку.

Самый простой метод, который можно встретить в большинстве стандартных реализаций, заключается в подсчете количества смен знаков в каждой строке. Однако пользователь на платформе Mastodon предложил еще один остроумный подход, использующий битовую арифметику: для матрицы с строками соответствие строк Адамара может быть найдено путем выполнения операции XOR между номерами строк Уолша и их же значением, сдвинутым на один бит вправо, а затем реверсированием последних n бит.

Ниже представлена реализация, которая выполняет именно это и выводит на экран отсортированную матрицу размером 8×8:

#include <stdint.h>
#include <stdio.h>

#define HD_LEN_POW2 3
#define HD_LEN      (1 << HD_LEN_POW2)

int8_t hadamard(uint32_t x, uint32_t y) {
  return (__builtin_popcount(x & y) % 2) ? -1 : 1;
}

uint32_t to_graycode(uint32_t val) {
  return val ^ (val >> 1);
}

uint32_t reverse_bits(uint32_t val, uint8_t bit_cnt) {
  uint32_t res = 0;
  while (bit_cnt--) { res <<= 1; res |= (val & 1); val >>= 1; }
  return res;
}

int8_t walsh_array[HD_LEN][HD_LEN];

void precompute_walsh() {
  for (uint32_t y = 0; y < HD_LEN; y++) {
    uint32_t hd_y = reverse_bits(to_graycode(y), HD_LEN_POW2);
    for (int x = 0; x < HD_LEN; x++) walsh_array[y][x] = hadamard(x, hd_y);
  }
}

int main() {
  precompute_walsh();
  for (uint32_t y = 0; y < HD_LEN; y++) {
    for (uint32_t x = 0; x < HD_LEN; x++) printf("%+d ", walsh_array[y][x]);
    putchar('\n');
  }
}

С этими знаниями в распоряжении, мы в состоянии переосмыслить реализацию дискретного косинусного преобразования (DCT) и разработать "дискретное преобразование Адамара" вместе с его инверсией:

...previous code here, sans main()...

void sqft(double* out_buf, double* in_buf, uint32_t len) {

  for (uint32_t bin_no = 0; bin_no < len; bin_no++) {
    double sum = 0;
    for (uint32_t s_no = 0; s_no < len; s_no++)
      sum += in_buf[s_no] * walsh_array[s_no][bin_no];
    out_buf[bin_no] = sum;
  }

}

void isqft(double* out_buf, double* in_buf, uint32_t len) {

  for (int s_no = 0; s_no < len; s_no++) {
    double sum = 0;
    for (int bin_no = 0; bin_no < len; bin_no++)
      sum += in_buf[bin_no] * walsh_array[bin_no][s_no];
    out_buf[s_no] = sum / len;
  }

}

Формально это преобразование именуется как Уолша-Адамара (WHT), однако название не столь важно. Главное — удостовериться в его функционировании:

...continuing from the previous snippet...

void print_buf(const char* prefix, double* buf, uint32_t len) {
  printf("%s", prefix);
  for (uint32_t i = 0; i < len; i++) printf(" %+.2f", buf[i]);
  putchar('\n');
}

int main() {

  double in[HD_LEN] = { 1, 1, 1, 1, 5, 5, 5, 5 };
  double sq_freq[HD_LEN], out[HD_LEN];

  precompute_walsh();
  sqft(sq_freq, in, HD_LEN);
  isqft(out, sq_freq, HD_LEN);

  print_buf("Input :", in, HD_LEN);
  print_buf("SQFT  :", sq_freq, HD_LEN);
  print_buf("ISQFT :", out, HD_LEN);

  return 0;
}

В качестве входных данных мы используем последовательность чисел, имитирующую квадратную волну: 1 1 1 1 5 5 5 5. Результат применения дискретного преобразования Фурье (ДПФ) или дискретного косинусного преобразования (ДКП) будет представлять собой набор гармоник, распределенных по различным частотным интервалам:

DCT : +24.00 -10.25 -0.00 +3.60 +0.00 -2.41 -0.00 +2.04

В противоположность этому, частотный профиль, сгенерированный программой, демонстрирует ненулевые значения исключительно для (постоянная составляющая) и , что подтверждает наличие алгоритма, способного декомпозировать сигнал на чистые квадратные волны:

SQFT : +24.00 -16.00 +0.00 +0.00 +0.00 +0.00 +0.00 +0.00

В заключение, мы можем удостовериться в том, что функция обратного преобразования — isqft() — корректно конвертирует частотный спектр обратно в исходную последовательность данных:

ISQFT : +1.00 +1.00 +1.00 +1.00 +5.00 +5.00 +5.00 +5.00

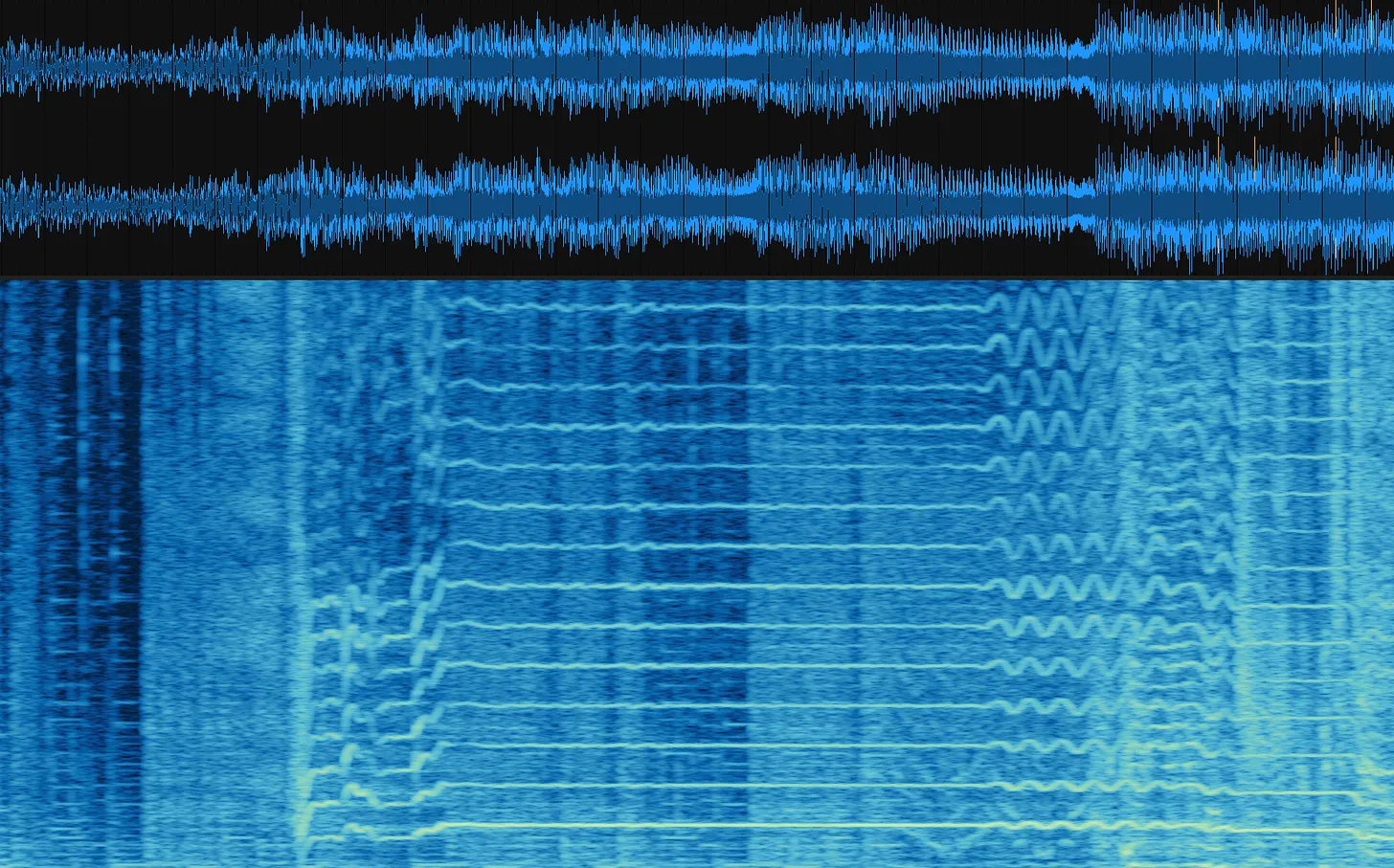
Мне не удалось обнаружить визуальные сопоставления результатов работы алгоритмов, поэтому я решил создать их самостоятельно. Привожу к вашему вниманию квази-стандартную спектрограмму дискретного косинусного преобразования (ДКП) для 11-секундного фрагмента песни "DARE" группы Gorillaz:

Классическая спектрограмма синусоидального сигнала

И в качестве сравнения, вот изящная эквивалентная спектрограмма, выполненная с использованием преобразования Уолша-Адамара:

Преобразование Уолша-Адамара, благодаря своей вычислительной эффективности и хорошей пригодности для определенных типов данных, находит применение в нескольких узких областях. Не в том дело, что его нужно использовать больше; просто дискретное преобразование Фурье не является единственным истинным методом.

Комментарии (26)

ivanstor
09.04.2024 15:38
#26705453
+4
Частотного представление функции в реальности не существует, это математическая абстракция. Поскольку, базисные функции: синусоиды/косинусоиды и их многочисленные аналоги физически не реализуемы. Впрочем, это утверждение относится и к прямой линии. Пользоваться этим инструментом в практических целях эта нереализуемость ничуть не мешает, поскольку всегда можно сделать приближение с любой точностью.
Статья, конечно, полезная.
1. GospodinKolhoznik
  09.04.2024 15:38
  #26706421
  +2
  Математическая абстракция, которая описывает реальное явление так же реальна, как и само явление.
  1. smart_alex
    09.04.2024 15:38
    #26707111
    +3
    Математическая абстракция может (и почти всегда так и делает) описывать только часть существующего в реальности явления, неправильно его интерпретировать, работать только на ограниченном интервале условий или с ограниченной точностью и вообще только вводить в заблуждение относительно природы самого явления и истинных (внутренних) принципов его функционирования.
    
    Так что не нужно ставить телегу впереди лошади — сначала разбираемся с физическим устройством окружающего мира, а потом натягиваем (сову на глобус) математические абстракции, описывающие реальное физическое устройство мира (а никак не наоборот).
    
    Yami-no-Ryuu
    09.04.2024 15:38
    #26710953
    То есть, по вашему, фотонов не существует? Они могут быть представлены как волновой цуг, вполне себе идеальный.
    
    smart_alex
    09.04.2024 15:38
    #26710985
    +2
    По моему, объективно существует некое явление, которое мы называем "фотоном", а вот наши представления о природе этого явления и его внутренних механизмах - это, как минимум, весьма дискуссионный вопрос (какое бы умное лицо при этом не делала наука и как бы она не надувала щёки).
    
    Artyomcool
    09.04.2024 15:38
    #26713215
    +1
    Ну казалось бы современная наука в данном конкретном вопросе щёчки надувать перестала и очень активно чешет репу.
    
    gres_84
    09.04.2024 15:38
    #26712687
    +1
    В студенческие годы у меня был преподаватель, имеющий дипломы МФТИ и мехмата МГУ. Он утверждал, что электронов не существует, это всего лишь решения наших уравнений.
    
    Еще он утверждал, что "математика - это тупик мысли", но это совсем другая история.
    
    engine9
    09.04.2024 15:38
    #26715807
    +1
    Удивительно, как легко люди подвергают сомнению реальность, и как неохотно сам способ мыслить.
    
    Ведь если взглянуть чуть иначе, проблем у мира нет никаких он просто существуют. Проблемы у людей в их мышлении и в категориальных схемах (и ярлыках, которые они вешают на реальные явления, называя их и описывая).
  1. Colorbit
    09.04.2024 15:38
    #26709027
    Вместо разложения по синусам и косинусам (преобразование Фурье) сигнал (функция от времени) можно раскладывать по бесконечно большому количеству базисов.
    
    Например очень удобными являются компактные во времени базисы (вейвлет преобразование)
    
    P.S.: Существует ли мнимая единица в реальности?)
    
    GospodinKolhoznik
    09.04.2024 15:38
    #26710277
    +3
    Ключевой вопрос существует ли натуральная единица в реальности.
1. y_mur
  09.04.2024 15:38
  #26710845
  +2
  Очень даже существует.
  
  Наиболее известный материальный прибор - эквалайзер на LC или RC фильтрах.
  
  Также запросто можно смешать сигналы от реальных LC/RC генераторов и получить реальный сигнал произвольной формы. Это легко увидеть на осциллографе.
  
  Оптический спектрограф реально выдает распределение энергии по спектру и это активно используется для выявления состава и структуры реального вещества.
  
  В общем заголовок провокационный, но сама статья интересная хоть и не соответствует заголовку.
1. Yami-no-Ryuu
  09.04.2024 15:38
  #26710935
  Если среда линейна, то частотное представление вполне себе физически реально. А если нелинейна, то в нём и смысла нет (привет Попперу).
  
  ПС.
  
  Автор излагает с таким пафосом, как будто только что открыл для себя операцию свёртки.

e-zig
09.04.2024 15:38
#26705795
+1
Вообще спектр можно визуализировать вообще не прибегая к цифровому представлению сигнала и математическим преобразованиям.
1. engine9
  09.04.2024 15:38
  #26710171
  Стопкой полосовых фильтров и столбчатыми индикаторами?

murkin-kot
09.04.2024 15:38
#26705811
+4
В русскоязычной литературе автора промежуточного преобразования пишут так - Адамар.

На западе так же лидирующую букву не выговаривают.

Refridgerator
09.04.2024 15:38
#26706893
+2
Упрощенный вариант как дискретного, так и непрерывного преобразования Фурье, который задействует только реальные числа - это преобразование Хартли. Принципиальная разница в теореме о свёртке, которая в Хартли-домене работает, а в косинусном - уже нет.
1. iShrimp
  09.04.2024 15:38
  #26709499
  Интересно, а вообще какие линейные преобразования можно использовать для вычисления свёртки?
  1. Refridgerator
    09.04.2024 15:38
    #26711381
    Мне тоже интересно, но пока что ничего другого не попадалось. Есть специализированные алгоритмы конкретно для свёртки, заточенный под особенности - размер или вид ядра свёртки. Например, свёртку с прямоугольной функцией (скользящее среднее) можно посчитать за O(1) (на итерацию) используя линию задержки. Свёртку с треугольной функцией - просто повторив предыдущую операцию ещё раз. И т.д.

Vytian
09.04.2024 15:38
#26708757
+1
Можно бы добавить, что спектры Адамара - пожалуй, наиболее естественное отображение динамики в квантовых вычислениях, и что по-хорошему надо бы это дело в стандартные курсы высшей математики для всех инженерно-компьютерных специальностей вводить -- наряду с преобразованием Фурье.

tminnigaliev
09.04.2024 15:38
#26709799
+1
Мне кажется, тот факт, что кроме синусов/косинусов есть другие базисы ортогональных функций - не снимает синусы/косинусы с постамента.

Их заслуга перед человечеством в том, что через них выражается e^{i \phi}, которая, в свою очередь, задаёт базисные решения многих диффуров.

Грубо говоря, почему-то волны в море не квадратные. И у радиоволн E и H синусоидальные, а не квадратные. И функции Бесселя тоже не имеют угловатостей, а, наоборот, выражаются через наши любимые синусы и косинусы. Может в какой-нибудь другой вселенной с манхеттенской или ещё какой метрикой они и будут квадратные, но в нашей жизни они описываются синусами и косинусами.

Но статья, безусловно, преинтересная.

phenik
09.04.2024 15:38
#26711499
+1
Существует ли частотная область в реальности?

Если этот вопрос рассмотреть с методологической точки зрения и посмотреть как он решает в философских теориях познания и современных когнитивных исследованиях, то достаточно убедительный ответ можно найти в теории познания И. Канта и исследованиях в русле этих представлений. С позиций физики динамические распределения давления воздуха воздействуют на ушные мембраны, вызывая в конечном итоге звуковые ощущения, или световых волн (фотонов) воздействуют на сетчатку глаз, вызывая соответственно световые ощущения. В самих же сенсорных системах в восходящих путях фактически идет многоуровневый частотный анализ паттернов нейронной активности, как последовательный, так и параллельный. Одновременно в нисходящих путях этих систем по результатам этого анализа происходит синтез целостных ментальных образов слухового и зрительного восприятия. Взаимоотношение этих путей и процессов на всех уровнях в норме оптимизируется с помощью байесовского предсказательного механизма на основе внутренних модельных представлений. В случае воображения или депривации любого рода органов чувств баланс активности смещается в сторону нисходящих путей и в последнем случае могут возникать сновидения и галлюцинации. Как и утверждал Кант мы не знаем, что находится за пределами органов чувств (знаменитые кантовские "вещи в себе"), и можем только строить правдоподобные предположения о их природе исходя из научных представлений, часто из личных предпочтений, заполняя пустоту незнания. В сенсорных путях происходит некоторый аналог частотного анализа, параллельно синтез на его основе ментальных образов обладающих пространственными и временными характеристиками. То, что Кант называл априорными пространственными и временными форма познания, которые развились эволюционно. Резюмируя, весьма упрощенно, можно предположить, что протообъекты, как устойчивые формы реальности, обладают некоторыми масштабными свойствами, которые в сенсорных системах подвергаются частотному анализу, разложению (грубо говоря происходит аналог прямого преобразования Фурье). Его результаты (грубо - коэффициенты преобразования) корректируются в соответствии с внутренними моделями, а в нисходящих путях происходит синтез (грубо - обратное преобразование Фурье). При этом возникает пространственно-временное представление образов устойчивых объектов реальности, их явление нам. Похоже на многоуровневые процессы, в общем случае, нелинейной фильтрации информации, только в мозге, так и есть. По этой теме имеется море нейрофизиологических исследований, которые в общих чертах подтверждают изложенное.
1. evtomax
  09.04.2024 15:38
  #26711815
  Как и утверждал Кант мы не знаем, что находится за пределами органов чувств (знаменитые кантовские "вещи в себе"), и можем только строить правдоподобные предположения о их природе исходя из научных представлений
  
  Истинность предположений проверяема практической деятельностью. У кого предположения неадекватные, тот получает премию Дарвина, например. Если вы развились до способности оставлять комментарии в интернете, то либо вы знаете, что находится за пределами ваших органов чувств, либо вас опекает тот, кто знает, либо вы обладаете сказочным везением. И неполное знание - это тоже знание. В целом адекватные предположения могут быть ошибочны в несущественных для конкретного результата моментах.
  1. phenik
    09.04.2024 15:38
    #26712009
    И неполное знание - это тоже знание.
    
    Так и написал с точки зрения физики там "динамические распределения давления воздуха воздействуют на ушные мембраны, вызывая в конечном итоге звуковые ощущения, или световых волн (фотонов) воздействуют на сетчатку глаз, вызывая соответственно световые ощущения." В следующем приближении может быть не фотоны, а струны, хотя ТС квелая какая-то теория. Потом еще что-то обнаружат более фундаментальное. Но что там в конце концов вряд ли узнаем, как и утверждал Кант) А математики склонны считать, что там платоновкий рай, короче, у всех свои предпочтения.
    
    Истинность предположений проверяема практической деятельностью.
    
    К сожалению такой уровень не проверяется практикой. Вспомните бесконечную грызню про интерпретации КМ, споры о природе ТМ и ТЭ. Случайно найдут дыры в КМ в экспериментах или наблюдениях, разработают новую фундаментальную теорию и споры отпадут. Как было, например, с неожиданными результатами опытов Майкельсона-Морли, или обнаружением аномального смещение перигелия Меркурия, которые привели к новым фундаментальным теориям, объяснивших эти отклонения. Так устроена реальность.

Sdima1357
09.04.2024 15:38
#26711601
Синусы и косинусы связаны с непрерывностью и инвариантностью физики описываемой диффурами. А впрочем.. И круглые и квадратные... Все сходятся к гауссиану .(:

dmiche
09.04.2024 15:38
#26712823
Частотная область в реальности существует.

Во-первых, таковым является пространство внутреннего слоя нейросети. С точки зрения смысла его содержимого, у нас обычные алгоритмы оперируют понятиями пространства и энергии (время в них рассматривается только как обычная пространственная координата), а нейросеть хранит вероятности и связи, что, по сути, является "выворачиванием" континуума и представлением его через время и информацию. Частотное представление - это тоже представление времени в более естественной его форме, как суммы переодичностей.

Другим примером частотной области может быть пространство качеств. Качество (в отличие от свойства) либо есть, либо его нет, что адресует нас к дискретности. Качества кодируют существенные параметры процесса гораздо более компактно, чем дифуры и, по сути, также являются овеществлением волновых процессов. Но, к сожалению, естественное исчисление этой области, как мне кажется, находится вне математики - это в чистом виде нумерология, когда единицы разных качеств не складываются. Собственно, очень похоже на то, как и разные гармоники не складываются.

О некоторых особенностях этого пространства в реальных системах у меня есть заметка в блоге.

polar_winter
09.04.2024 15:38
#26715085
У автора 2 несвязанных темы.
1-ая тема заявлена в тезисе. И ответ на неё весьма банален и описан в станадартных курсах философии для технических специальностей. Звучит примерно так: и временная и частотная область я вляют математическим абстракциями. Но почему временная область интуивно является более материальной? Или почему одни абстракции более реальны чем другие? Данные вопросы сводятся к одному единому, что такое реальность, её достижимость, или в нашем случаии, что такое быть реальным? Ответ на этот вопрос в явном систематизирует ваще предстваление о реальности и даст возможность вас классифицировать с точки зрения философских школ. И решит для вас подобные вопросы заранее.
По 2 конечно преобразование Фурье может быть обощенно, по другим функция-мать. Интересная обзорная статья.