При анализе данных и построении моделей машинного обучения часто возникает необходимость аппроксимировать сложные функции. PyTorch предоставляет удобные инструменты для создания и обучения нейронных сетей, которые могут быть эффективно использованы для этой цели. В этом посте мы рассмотрим простой пример аппроксимации функции с использованием PyTorch.

Шаг 1: Подготовка данных

На этом шаге мы будем генерировать данные, поэтому можно без потери понимания дальнейших рассуждений перейти к следующему шагу, если вам не интересно почитать про диффуры.

Давайте начнем с простого примера из теории управления и решим его сначала аналитически, а затем с использованием PyTorch. Рассмотрим функцию

Это линейное неоднородное дифференциальное уравнение, гдепредставляет собой выход системы, - входной сигнал, а ​ и ​ обозначают, соответственно, первую и вторую производные по времени .

Тогда характеристический полином будет выглядеть

После нахождения корней характеристического уравнения мы можем записать общее решение дифференциального уравнения в виде комбинации экспоненциальных функций. Поскольку корни комплексные, мы можем использовать формулу Эйлера, чтобы выразить решение в терминах косинусов и синусов

где ​ и ​ - произвольные постоянные, которые определяются начальными условиями задачи. Давайте выберем их в нашей задаче и . Тогда можно полностью определить решение нашей задачи

Давайте промоделируем отклик системы для начальных условий помощью библиотеки control

init_state = [1, 2]
dt = 0.001
time = np.linspace(0, 10, int(time/dt))

# create transfer function
numerator = [1]
denominator = [1, 1, 1]
system = ctrl.tf(numerator, denominator)

# get respomse from the TF
response = ctrl.initial_response(system, time, init_state).outputs
plt.plot(time, response, label="Impulse response of the system")

Именно time, response мы позже будем использовать как обучающий датасет. Также заодно изобразим аналитическое решение задачи.

class Analytic:
    def __init__(self, alpha, beta, c_1, c_2):
        self.alpha = alpha
        self.beta = beta

        self.c_1 = c_1
        self.c_2 = c_2 
    
    def calculate(self, t: float) -> float:
        return self.c_1 * np.exp(self.alpha * t) * np.sin(self.beta * t) \
             + self.c_2 * np.exp(self.alpha * t) * np.cos(self.beta * t)
    
    def __call__(self, t: list[float]) -> list[float]:
        return np.vectorize(self.calculate)(t)

analytic = Analytic(
    alpha = -0.5,
    beta = np.sqrt(3)/2,
    c_1 = 4/np.sqrt(3),
    c_2 = 2
)

plt.plot(time, analytic(time), linestyle="--", 
         label="Analityc solution")

Шаг 2: Определение модели

Теперь надо определиться с архитектурой модели. Для нас это будет обычной функцией вида

где

• α: обучаемый параметр, представляющий собой коэффициент экспоненциального роста.

• β: Фиксированное значение (установлено на ): представляющее собой частоту осцилляции. Позже расскажу почему фиксированное.

• и : Обучаемые параметры, представляющие коэффициенты для синусоидальных и косинусоидальных членов соответственно.

Теперь давайте напишем нашу модель с использованием PyTorch. Ниже приведен пример кода для создания модели:

class Model(nn.Module):
    """Our class that will be trained"""

    def __init__(self):
        super().__init__()
        self.alpha = nn.Parameter(torch.zeros(1))
        self.beta = np.sqrt(3)/2
            

        self.c_1 = nn.Parameter(torch.zeros(1))
        self.c_2 = nn.Parameter(torch.zeros(1))
        
    def forward(self, t):
        return self.c_1 * torch.exp(self.alpha * t) * torch.sin(self.beta * t) \
             + self.c_2 * torch.exp(self.alpha * t) * torch.cos(self.beta * t)

Этот код определяет класс Model, который наследуется от класса nn.Module в PyTorch. В методе init мы определяем обучаемые параметры alpha, C1 и C2, а также фиксированную частоту beta. В методе forward определяется прямой проход модели, где мы вычисляем выходное значение output в зависимости от входной переменной t с использованием заданных параметров.

Для обучения модели нам нужно написать класс датасет, наследник класса torch.utils.data.Dataset.

class TimeResponseDataset(Dataset):
    """Torch Dataset for x=time and y=response"""
    def __init__(self, time, response):
        self.time = torch.Tensor(time)
        self.response = torch.Tensor(response)
        
    def __len__(self):
        return len(self.time)
    
    def __getitem__(self, idx):
        return {'time': self.time[idx], 'response': self.response[idx]}

Он нам нужен, чтобы позже закинуть его в torch.utils.data.DataLoader. Он то и будет нам выдавать батчи данных во время обучения.

dataset = TimeResponseDataset(time, response)
dataloader = DataLoader(dataset, batch_size=512, shuffle=True)

Шаг 3: Обучение

Давайте посмотрим количество обучаемых параметров в модели.

model = Model()
print(f"trainable params: {len(model.parameters())}")

Результат, как мы и задумывали, равен 3.

Проинициализируем лосс функцию и оптимизатор. Лосс функция будет говорить нам как далеко нам до оптимума, а оптимизатор будет определять как быстро и в каком направлении менять веса, чтобы добраться до него.

lr = 0.01
betas = (0.9, 0.999)
history = []

criterion = nn.MSELoss() 
optimizer = torch.optim.Adam(model.parameters(), lr=lr, betas=betas, eps=1e-8)

Теперь обучим модель на 150 эпохах, сохраняя при этом историю лосс функции.

epochs = 150
for epoch in tqdm(range(epochs)):
    for data in dataloader:
        optimizer.zero_grad()
        pred = model(data['time'])
        loss = criterion(pred, data['response'])
        loss.backward()
        optimizer.step()
        
        history.append(loss.detach().numpy())

Здесь мы итерируемся epochs раз по всему датасету. Класс DataLoader выдает нам стопку (батч) данных . После чего мы подсчитаем, что выдаст нам наша модель, и найдем ошибку между реальными данными и предсказанными. В нашем случае мы выбрали среднеквадратичное отклонение

Но чтобы сделать оптимизационный шаг optimizer.step(), нам надо сначала обнулить градиенты optimizer.zero_grad() и вычислить их вновь по параметрам модели loss.backward().

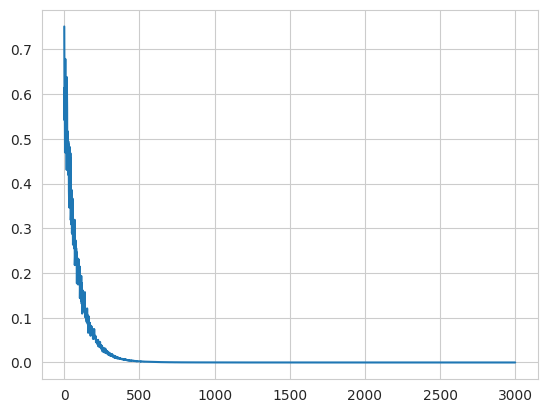
Здесь приведен график лосс функции от количества батчей обучения. Как видно из графика модель сошлась еще на 500 шаге. Давайте посмотрим на обученные параметры и на аналитическое решение.

А зачем нам вообще torch.autograd? Давайте сами найдем выражения для градиентов.

И правда, давайте найдем! Однако если вам не интересна математика, то, пропустив этот пункт, ничего страшного не произойдет.

Но сначала вспомним зачем нам нужен это ваш градиент? Объясняю. Градиент - это вектор состоящий из частных производных функции. И каждая компонента градиента показывает в каком направлении функция растет в разрезе этой компоненты. И если собрать все эти производные в один вектор, мы получим вектор наибыстрейшего роста. Умножим на минус и получим направление куда бы нам хотелсь пойти, чтобы достичь минимума.

Минимум лосс функции - это минимум ошибки нашей модели. То есть чем меньше лосс функция, тем меньше наша модель ошибается.

Вспомним еще раз как выглядит наша модель

И мы хотим найти

А сами частные производные равны

Теперь мы можем определить градиент в каждой точке тренировочного датасета. Можно заметить, что в формулах стоит сумма от 1 до N, однако в реальных задачах бывает сложно за раз подсчитать градиент по всему датасету, поэтому обычно берут случайную выборку (батч) из датасета и усредняют градиент по нему.

Теперь как сделать оптимизационный шаг? Это уже вопрос к оптимизатору. Самый простой из них это стохастический градиентый спуск (SGD)

где это скорость обучения, более известный как learning rate. Однако в нашем случае мы используем адаптивный алгоритм оптимизации Adam.

Шаг 4: Сравнение

analytic.alpha, analytic.c_1, analytic.c_2

estimation = [float(param.data) for param in model.parameters()]
estimation

Ошибка меньше . Давайте посмотрим на то, как хорошо легла наша модель под реальные данные.

approx = Analytic(
    alpha=estimation[0],
    beta=model.beta, 
    c_1=estimation[1],
    c_2=estimation[2]
)

# Analytic, we defined earlier
plt.plot(time, analytic(time), color[0], 
        label="$y=4/\sqrt{3} \cdot e^{-t/2} sin(\sqrt{3}t/2) - 2 e^{-t/2} cos(\sqrt{3}t/2)$.")

# Approximation
plt.plot(time, approx(time), color[2], linestyle='--', label='Approximation')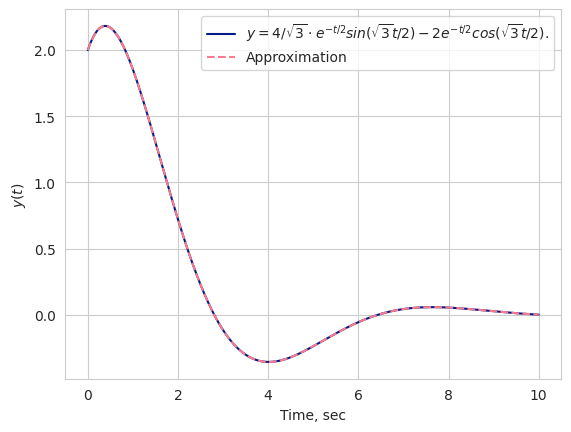

Чтобы осознать как быстро сходится модель на этой задаче, можно посмотреть на графики ниже. Это сравнение аналитического решения и нашей модели на эпохах 0, 10, 20 .

Дополнительно

Как вы могли заметить, у нас не все параметры в модели были обучаемыми. Коэффициент , что должен был стоять в периодических функциях, был сразу же зафиксирован. Зачем это было сделано? Показываю.

Объясняю. Косинус и синус, которые стоят в нашей аппроксимирующей модели

очень сильно изменяют форму лосс функции над пространством параметров, делая ее более неприятной для методов градиентного спуска (практически всех оптимизаторов). Это связано с их периодическим характером и быстрыми изменениями, которые могут приводить к локальным минимумам и плохой сходимости алгоритмов оптимизации.

Наша модель сошлась к таким значениям

То есть буквально модель приняла вид , что далека от нами задуманной.

Послесловие

Преимуществом торча в данной задаче является модуль autograd, который сам под капотом считает градиенты для оптимизационного шага. Используя дифференцируемые функции в прямом проходе модели, можно не волноваться об обратном распространении ошибки и писать сколь угодно большие архитектуры. Однако недостатком любой модели, конечно, является её ограниченность архитектуры, поэтому возможность "аппроксимации любой функции" ограничена вашим воображением. Смело генерируйте идеи и проверяйте их с помощью гибкой библиотеки PyTorch.

Надеюсь вам было легко читать этот материал. Полный код вы можете найти на кагле, а меня в телеграме. Буду рад поправкам и комментариям.