Всегда было интересно как же рисовать линии напряженности не только на интуитивном уровне - от плюсы к минусу, но и на практике. Как на самом деле они выглядят в каждой точке на нашем условном поле? Сейчас и разберемся по ходу дела рассматривать и более сложные системы точек, используя силу языка python.

Теория

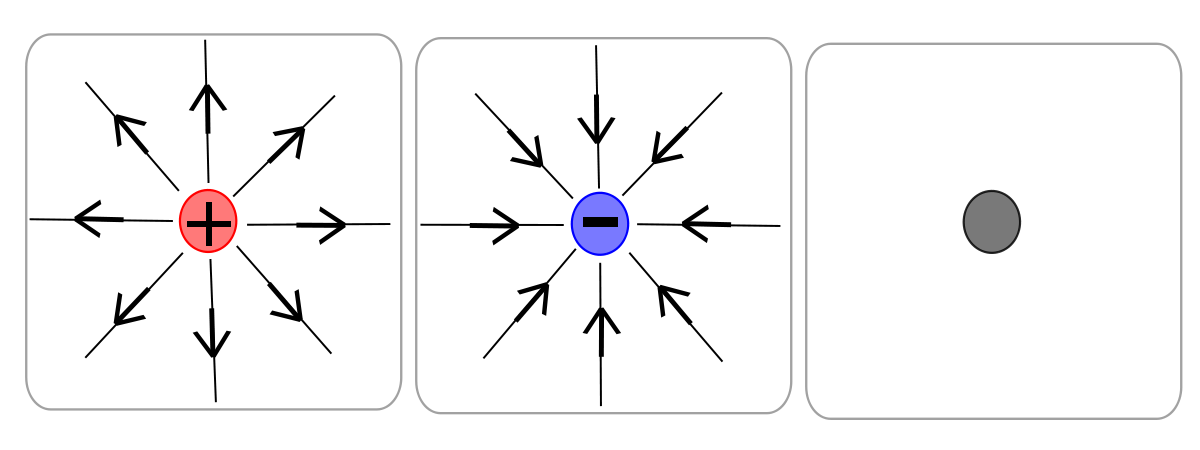
Любой заряд создает вокруг себя поле, которое влияет на другие заряды - электрическое поле.

Также в сумме некоторое количество зарядов создает вокруг себя поле, с различным влиянием в каждой точке. Поэтому для обнаружения и исследования электрического поля нам нужен заряд, который называют пробным. Этот заряд мы берем, чтобы «попробовать», существует ли в той или иной точке пространства электрическое поле: если в какой-то точке на этот заряд действует электрическая сила.

Сила с которой взаимодействуют два заряда описывается законом Кулона.

Пусть у нас есть два неподвижных заряда, тогда силой Кулона называется силы, выражаемой формулой:

где радиус векторы первого и второго заряда, а диэлектрическая постоянная. Формула на самом деле очень похожа на формулу гравитационного взаимодействия. Можно сделать такую же аналогию - сила зависит от величины двух объектов и расстояния между ними, помноженную на какую-то константу.

Обобщение на случай распределенного заряда:

Здесь у нас не просто заряд, а какое-то тело. Не вдаваясь в подробности, мы пользуемся аддитивностью силы () и высчитываем силу от заряда до маленькой части тела . Уменьшив размеры части тела и сложив все такие силы, мы получим интеграл.

С помощью пробного заряда можно оценить “силу влияния” какого-то поля - этой величиной называется напряженность электрического поля.

Напряженность в точке пробного заряда пропорциональна силе и обратно пропорциональна заряду —

Соответственно напряженность поля в точке заряда :

Так же как и сила , напряженность электрического поля аддитивна

также это свойство называется принципом суперпозиции. То есть в рассматриваемой нами статье напряженность точки - точка пространства, можно получить сложив напряженность относительно и плоскости:

Моделирование

Для некоторого упрощения понимания результата работы было принято решение смотреть на плоскость - срез - проходящий через две точки и пересекающий перпендикулярно плоскость.

Для моделирования силовых линий электрического поля был использован язык python. В основе реализации лежит класс ElectricField описывающий электрическое поле с конструктором, принимающий на вход все объекты, имеющие заряд.

А именно две точкиPoint(number charge, number x, number y)

и прямую Line(number charge, number[] firstPoint, number[] secondPoint).

Сигнатуру методов указана для упрощения понимания =)

class ElectricField:
    dt0 = 0.01  # The time step for integrations
    def __init__(self, charges):
        #Инициализация поля по вводным объектам
        self.charges = charges

    def vector(self, x):
        #Возвращает все вектора поля
        return np.sum([charge.E(x) for charge in self.charges], axis=0)

    def magnitude(self, x):
        #Возвращает длину вектора
        return norm(self.vector(x))

    def angle(self, x):
        #Возвращает угол от оси абцисс до вектора в радианах
        return np.arctan2(*(self.vector(x).T[::-1])) 

Каждый из этих объектов имеет метод, который вычисляет напряженность в какой-то пробной точке по своей специфичной для своего рода объекта формуле.

Например, для класса Point это .

Что примечательно мы не просто так опускаем коэффициент пропорциональности . Дело в том, что этот скаляр влияет лишь на длину всех векторов в поле, поэтому опустив, его мы не упустим наглядности результата. Весь код вы можете найти в дополнительных материалах.

Соответственно, наши объекты будут обладать начальными условиями: Point зарядом и координатами на плоскости, Line зарядом и двумя точками, на длине которой этот заряд определен.

# Создадим объекты и засунем их в поле 
charges = [Line(1, [0, -10], [0, 10]),
        Point(-1, [-1, 0]), 
           Point(1, [1, 0])]
field = ElectricField(charges)

Инициализируем дополнительно наши размеры, массивы размеров ширины и высоты, а далее пройдемся по выделенными нами точкам.

x, y = np.meshgrid(np.linspace(XMIN/ZOOM+XOFFSET, XMAX/ZOOM+XOFFSET, 41),
                      np.linspace(YMIN/ZOOM, YMAX/ZOOM, 31))
u, v = np.zeros_like(x), np.zeros_like(y)
n, m = x.shape
# Вот тут проходим по точкам
for i in range(n):
    for j in range(m):
				# Если точка лежит на прямой Е = 0
        if any(charge.is_close([x[i, j], y[i, j]]) for charge in charges):
            u[i, j] = v[i, j] = None
        else:
						# Находим длину и корректируем ее немного 
            mag = field.magnitude([x[i,j], y[i,j]])**(1/5)
						# Находим угол и суем компоненты вектора в u v массивы
            a = field.angle([x[i,j], y[i,j]])
            u[i, j], v[i, j] = mag*np.cos(a), mag*np.sin(a)

После чего нам остается кое-что поправить в графике и вывести его функцией pyplot.show()

Примеры

Пусть у нас даны начальные условия двух точек и прямой.

charges = [Line(1, [0, -10], [0, 10]),
        Point(-1, [-1, 0]), 
           Point(1, [1, 0])]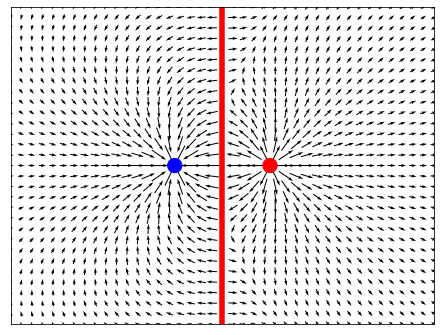

Довольно ожидаемая картина - линии напряженности выходят из положительно заряженных объектов и входят в отрицательно заряженные.

Тогда если изменить заряды на одинаковые:

Отличие лишь в направлении каждого вектора - они поменяли направление из-за знака.

Что если изменить величину зарядов:

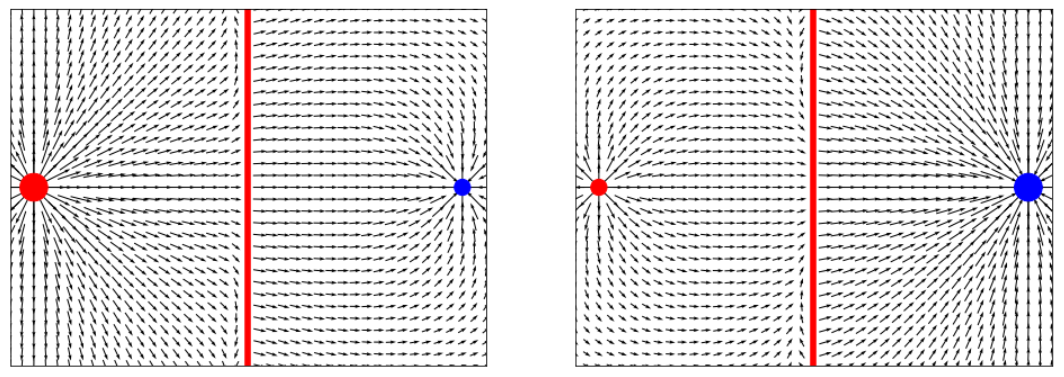
Как и ожидалось - более заряженные объекты искривляют электрическое поле больше. Опять же аналогия с гравитационным полем: чем больше масса там больше тело изменяет пространство вокруг себя.

Однако все ли здесь хорошо?

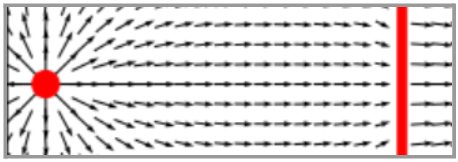
Что происходит? Мне в школе говорили, что одинаково заряженные объекты отталкиваются, а тут получается, что не совсем?

Однако если посмотреть на всю картину, то станет ясно, кто во всем виноват:

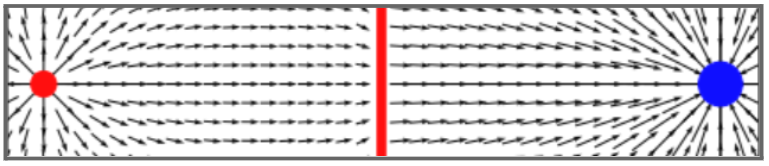
Построим более наглядную картину, увеличив отрицательный заряд.

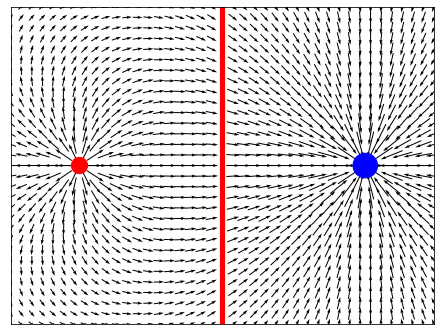
Очень сильно отрицательно заряженная точка искривляет поле так, что влияние этой положительно заряженной линии Line просто подавляется, но если посмотреть более пристально, то можно увидеть, что длина линий напряженности после прохождения Line немного увеличивается.

При огромном желании эти графики построить можно самому. Этот код я частично позаимствовал у tomduck. Кстати, у него еще больше показательных примеров не только 2-D, но и 3-D графиков. Очень рекомендую посмотреть хотя бы описание библиотеки.

Спасибо, что посмотрели этот пост, который был лишь для защиты проектной лабораторной по физике с моделированием.