Введение

Есть короткий анекдот - «Вы умеете играть на скрипке? – Не знаю, не пробовал!»

Даже если человеку дать в руки скрипку Страдивари и даже если человек обладает абсолютным слухом, но не владеет элементарной техникой извлечения звуков из скрипки при помощи смычка он так и не сумеет определить наличие возможно скрытого в нем таланта.

Этот текст написан для владеющих минимальными навыками игры на скрипке работы в Матлаб и желающими углубить свои навыки и убедиться в наличии у себя таланта инженера-исследователя. Конечно можно шаг за шагом изучать функции Матлаб отвлеченно от конкретного их применения. Но это скучно. Мы же сразу начнем создавать программу шаг за шагом наблюдая за работой каждой функции при решении конкретных задач. Мы попытаемся совместно написать программу векторизации некоторых изображений. Зачем нужна векторизация изображений? Какое изображение мы бы не исследовали - будь то микрофотография крошечной амебы или фотография огромного амебообразного озера или ледника, полученная из спутника мы получим изображение, составленное из отдельных точек (пикселей). Например, на рисунке ниже фотография прямой линии (зеленая линия) будет представлена пикселями (черные квадратики).

Если исследователю необходимо вычислить длину этой линии, то ему доступна для вычислений будет только ломанная линия, соединяющая центры пикселей (красная ломаная линия). Известно, что кратчайшая линия, соединяющая две точки это прямая. Даже без вычислений видно насколько отличается длина зеленой линии от красной. Во многих случаях исследователю требуется вычислить длину как можно точнее. Векторизация как раз и дает возможность заменить искаженную дискретизованную фотокамерой красную линию на зеленую линию, выраженную с помощью математической формулы.

Те же проблемы возникают при необходимости точного измерения не только периметра, но и площади изображения. Например, у геофизиков, исследующих динамику таяния льдов или изучающих динамику изменения площади и периметра водоемов в зависимости от климатических условий. Или у биологов, исследующих влияние различных факторов на микроорганизмы или анализирующих форму различных кровяных телец или у медиков анализирующих динамику роста новообразований и т.д. и т.п.

На рисунке ниже видно какая набегает ошибка при измерении периметра замкнутой фигуры.

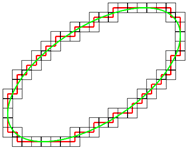
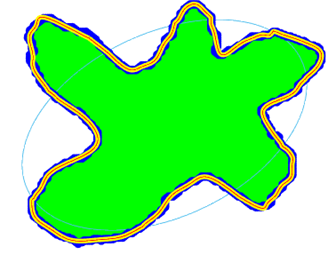
Здесь мы рассмотрели искажения изображения возникающие из-за дискретизации изображения фотокамерой. Но в реальности могут быть искажения вызванные и другими факторами. Например, какие-то посторонние микрочастицы, попавшие в исследуемый препарат наложатся на изображение контура амебы. И в этом случае векторизация изображения позволит исправить ситуацию хотя точность измерения периметра или площади возможно уменьшиться.

Мы наметим пути векторизации некоторых выпуклых и не выпуклых фигур, некоторых замкнутых и не замкнутых фигур и фигур с самопересечением. Мы познакомимся с эвристическим программированием. Понятно, что это будут только программы-эксперименты для проверки пригодности тех или иных методов для решения конкретных задач.

Из математики нам потребуются некоторые материалы из учебников по Информатике для 10 и 11 классов (ссылки будут позже по тексту). Вообще все материалы, которые нам понадобятся Вы сможете скачать по ссылкам, приведенным в этом тексте.

Ответы на многие вопросы Вы сможете найти в книге - "Р.Гонсалес, Р.Вудс. Цифровая обработка изображений в среде MATLAB (2006, PDF)". Соответствующие ссылки на эту книгу будут такими: Гонсалес-стр. ххх. Для загрузки этой книги на Ваш компьютер надо скопировать ссылку (ниже), вставить в адресную строку браузера и загрузить файл:

https://disk.yandex.ru/i/g4Iq8J3n0dlQeQ

Очень надеюсь, что нижеизложенный текст будет интересен и понятен для любознательных школьников (балы по ОГЭ и ЕГЭ в этом случае абсолютно не играют никакой роли!!!).

1. Предварительная обработка.

Мы будем векторизовать вот это изображение амебы:

Если мы хотим не просто рассматривать комиксы (весь текст ниже такой: картинка - описание действия- измененная картинка - описание нового действия – новая измененная картинка – и т.д.) а хотим обучаться непосредственно участвуя в работе, то Вам необходимо загрузить именно это изображение на Ваш компьютер. Почему именно это, а не реальное фото амебы из интернета? На то есть две причины. Во-первых, на реальном фото Вам придется выделить края (границы) контура амебы. А это часто не такая простая задача, требующая отдельного Туториала. А во-вторых, в процессе работы мы будем получать конкретные результаты относящиеся именно к этому изображению, и Вы сможете контролировать правильность выполнения уже Вашей программы посылая запросы через командную строку и сравнивая результаты. Для загрузки этого изображения на Ваш компьютер надо скопировать ссылку (ниже), в браузере вставить ссылку в адресную строку, перейти по этой ссылке и в открывшейся вкладке кликнуть "Скачать":

https://disk.yandex.ru/i/JDyX3mvQNuSRxQ

Скачанный файл ameba0.jpg перенесите в любую папку на Вашем компьютере и запишите путь к файлу. Например, на моем компьютере он по адресу - 'd:\MATLAB_NEW\kot23\ameba0.jpg'. Т.е. файл ameba0.jpg хранится в папке kot23 которая находится в папке MATLAB_NEW которая в свою очередь находится на диске d:

Начнем. Загрузим цветную RGB картинку амебы, преобразуем ее в серое изображение (grey), затем серое в бинарное (bw) и с помощью морфологических операций bwmorph очистим от мусора и наконец получим скелет контура амебы для дальнейшей работы. Вот программа, которая выполняет всю эту работу:

%__Амеба____
clear all;clf;clc;close all
name='d:\MATLAB_NEW\kot23\ameba0.jpg';
RGB=imread(name);
RGB = im2double(RGB);
gray=rgb2gray(RGB);
bw1=(gray<.9);
bw2 = bwmorph(bw1,'thin',inf);
bw3 = bwmorph(bw2, 'shrink',inf);
bw4 = bwmorph(bw3,'skel',inf);
bw5 = bwmorph(bw4,'clean',inf);

Скопируйте программу, перенесите ее в редактор Матлаб, скорректируйте в переменной name путь доступа на Вашем компьютере к файлу ameba0.jpg,присвойте ей имя ameba.m и запустите выполнение программы:

Если что-то пошло не так – появилось сообщение об ошибке, то попросите Учителя Информатики помочь Вам или задавайте вопросы в комментариях. Если все прошло успешно, то никаких изменений Вы не увидите. Просто программа выполнена и в переменных RGB, gray, bw1 – bw5 записана информация о соответствующих изображениях.

Начнем с первой переменной RGB. Наберите в командной строке Матлаб команду: imshow(RGB). Должна появиться картинка:

Чтобы получить информацию о переменной RGB наберите в командной строке – whos RGB.

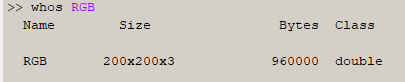
В первой матрице записана яркость «красного цвета» каждого пикселя, во второй яркость зеленого цвета и в третьей соответственно синего. Как из этих трех матриц получается цветное изображение? Наберите в командной строке Матлаб команду: imshow(RGB). Наведите курсор мышкой на изображение. Над изображением в правом верхнем углу появится всплывающее меню.

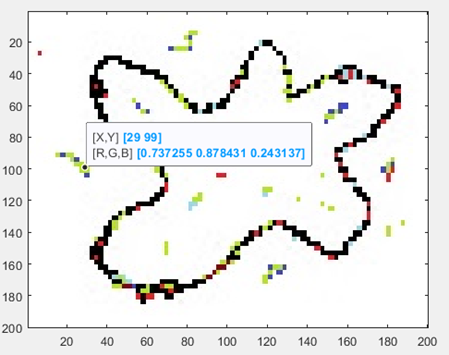
Как бы художник получил краску нужного оттенка имея в наличии только красную, зеленую и синюю краску? Он смешал бы их в нужной пропорции, тщательно перемешал и нанес на холст в нужное место. Так вот если мы смешаем красную, зеленую и синюю краски в пропорции 0.737 : 0.878 : 0.243 и окрасим пиксель с координатами x=29, y=99 то получим как раз то что требовалось. А давайте проверим. Нарисуем рядом квадратик и смешаем цвета в той же пропорции. Для этого в командной строке введем команды –hold on; rectangle('Position',[20,120,10,10],'FaceColor',[0.737 0.878 0.243]) и получим картинку:

Чтобы получше рассмотреть снова вызовем всплывающее меню и кликнем «плюс в кружочке» (Zoom in) и выделим интересующий нас участок изображения.

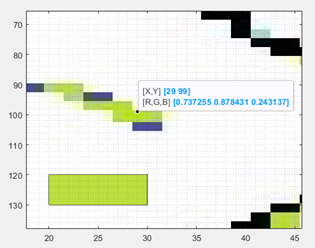
Вот поэтому я и предложил Вам работать именно с ameba0.jpg. Вы можете сравнивать Ваши результаты с моими чтобы контролировать правильность выполнения действий. Понятно, что все эти операции Вы можете выполнять с любой точкой изображения. Мы можем также непосредственно обратится, например, к первой матрице (R) и узнать какое число находится в 29 колонке и 99 строке:

Строка 6 нашей программы – переводим RGB в gray (цветное в серое). В командной строке вводим – imshow(gray), colorbar, whos gray

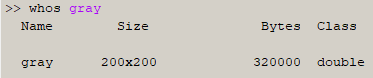
Строка 7 нашей программы. Что означает для программы команда - gray < .9? Число 0.9 – это порог. Программа сканирует каждый элемент матрицы gray и устанавливает в этом месте логическую «1» если яркость gray в этой точке <0.9 или логический «0» если яркость gray в этой точке > или = 0.9. Изменяем порог в диапазоне от 0 до 1 и устанавливаем его значение, при котором контур фигуры не разорван и уровень шумов приемлемый.

Ну вот теперь у нас все готово чтобы подключить к работе мощную функцию морфологической обработки бинарных изображений bw2 = bwmorph(bw1,operation,n). С описанием этой функции и с примерами ее применения можно ознакомиться в ранее скачанной Вами книге "Р.Гонсалес, Р.Вудс. Цифровая обработка изображений в среде MATLAB (2006, PDF)".   Ссылка на нужный материал будет выглядеть так - Гонсалес-стр. 373.

Строка 8 – выполняет команду bw2 = bwmorph(bw1,'thin',inf);

imshow(bw2)

Строка 9 - bw3 = bwmorph(bw2, 'shrink',inf);

imshow(bw3)

Строка 10 -  bw4 = bwmorph(bw3,'skel',inf);

imshow(bw4)

Проверим. Наведите курсор мышкой на изображение. Над изображением в правом верхнем углу появится всплывающее меню.

Нажимаем на иконку всплывающего меню «Zoom in» (отмечена красной стрелкой) и с помощью мышки выделяем интересующий нас участок. Вращая колесико мышки меняем масштаб.

Строка 11 - bw5 = bwmorph(bw4,'clean',inf);

imshow(bw5)

Ну вот мы и разобрали результаты выполнения первых 11 строк нашей программы. Поехали дальше.

2. Извлечение координат точек контура амебы и их упорядочение.

Найдем координаты точек контура амебы с помощью функции - [row col]=find(bw5==1). Функция find сканирует нашу картинку-матрицу bw5 начиная с крайней верхней точки в левом углу (там у нас начало координат) двигаясь вниз. Достигнув самой нижней точки в первой колонке, она начинает сканировать вторую колонку матрицы начиная с ее самой верхней точки и т.д. пока не просканирует всю матрицу. Во время сканирования она сравнивает число (в нашем случае там только логические 0 или 1) которое находится в колонке col и в строчке row и, если там «1» она заносит значения row и col в массив [row col]. Если там «0» в массив ничего не заносится. Вот так выглядит начало массива координат точек контура амебы:

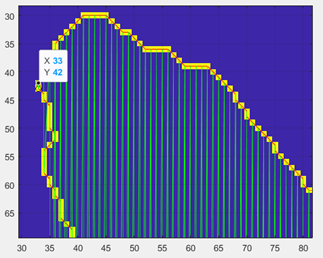
Поэтому координаты в массиве хранятся не упорядочено. Нам желательно расположить их в последовательности друг за другом как бы оббегая контур точка за точкой. Т.е. соседние точки на контуре должны быть соседними и в массиве. Прибегнем к помощи графов. Кому интересно побольше узнать о графах прочитайте страницы 219-229 из прекрасного учебника: «Информатика и ИКТ. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / А. Г. Гейн, А. И. Сенокосов. 2-е изд. _ М.: Просвещение, 2009.». Для загрузки этой книги на Ваш компьютер надо скопировать ссылку (ниже), в браузере вставить ссылку в адресную строку, перейти по этой ссылке и в открывшейся вкладке кликнуть "Скачать":

https://disk.yandex.ru/i/ntdIYmXITNqazQ

Мы же не будем углубляться в теорию, а попытаемся на практике с помощью Матлаб оценить пригодность графов для решения нашей задачи. Но все же если Вы хотя бы пробежитесь по тексту о графах я буду безмерно рад.

Вот какую визуальную интерпретацию графов я нашел в интернете:

«Представьте себе, что у вас есть большая пространственная молекула, которая состоит из жестких шариков, неважно, из чего сделанных (из картона, из металла). И эти шарики между собой перелинкованы, то есть соединены проволочками, прямолинейными отрезками. Получается жесткая конструкция, которую в математике принято называть графом. Это чисто наглядная интерпретация – в виде молекулы. Хотя мне думается, она кажется удобной всякому, кто пытается представить, что такое граф.» (https://www.pvsm.ru/matematika/47881)

В нашем случае шарики — это пиксели, а проволочки — это соединения пикселя с его ближайшими соседями. Для создания графа мы воспользуемся функцией:

graf=graph(dist([col  row]') <= sqrt(2), 'omitselfloops')

Условие dist([col  row]')<=sqrt(2) означает что к графу добавляется точка если она отстоит от хотя бы одной точки графа на расстояние, не превышающее кв. корня из 2. Т.е. каждый граф будет состоять из связного множества точек. Точка, отстоящая от любой точки данного графа на большее расстояние будет уже включена в другой граф. Переменная 'omitselfloops' не позволяет добавлять самоциклы к графу. Т.е. расстояние точки к самой себе равное нулю игнорируется.

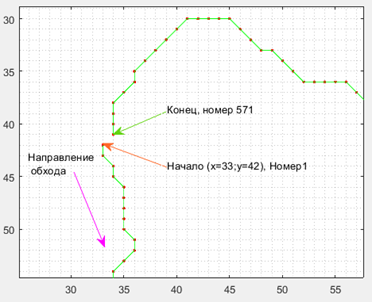
Теперь мы уже можем расположить в массиве [row col] координаты точек в последовательности друг за другом как бы оббегая контур точка за точкой. Т.е. соседние точки на контуре будут соседними и в массиве. В этом нам поможет функция v = dfsearch(graf,1) осуществляющая поиск графа в глубину. Эта функция начинает движение против часовой стрелки от первой точки в нашем массиве (цифра «1» указанная в позиции последнего аргумента функции) к соседней точке контура, заносит в массив «V» номер (индекс) координат из массива [row col] этой соседней точки. Затем переходит к следующей точке занося в массив «V» ее номер и т.д. пока оббежав весь контур не достигнет 1-й точки.

Как нам перетасовать наш массив чтобы координаты точек приобрели новые номера в порядке как в переменной V? Очень просто – наш массив надо записать в таком виде: [col(v) row(v)]. Тогда получится так:

Введем новые обозначения: x = col(v); y = row(v); xy = [x y];

Теперь у нас соседние точки на контуре стали соседями и в массивах x, y и xy.

В командной строке выполним:

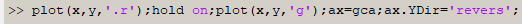
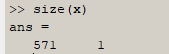
Замыкаем наш контур путем добавления к массиву еще одного 572 – го элемента: x(572) = x(1); y(572) = y(1); xy = [x y].

(В общем случае можно записать так - x(end+1)=x(1); y(end+1)=y(1); xy=[x y]).

Контур замкнулся – можете проверить.

Давайте дополним нашу программу вычислениями, выполненными выше. Скопируйте программу (ниже) и добавьте ее к записанной ранее в редактор Матлаб программе ameba.m.

%__Координаты точек контура и их упорядочение_______________ 
[row, col]=find(bw5==1);
graf=graph(dist([col  row]') <= sqrt(2), 'omitselfloops');
v = dfsearch(graf,1);
x = col(v); y = row(v); 
x(end+1)=x(1); y(end+1)=y(1); xy=[x y];

Вы, наверное, уже заметили, что мы работаем с двумя объектами – изображениями и массивами координат. Изображения для наших глаз – мы рассматриваем изображения, анализируем их. Мы уже научились увеличивать участки изображений, получать информацию о каждом интересующем нас пикселе (его координаты, цвет) и информацию о картинке в целом (размеры, цветное или серое, или бинарное). Мы поняли, как изображения можно представлять в виде матрицы. Научились извлекать массивы координат из матрицы. А вот массивы координат нужны уже для работы нашей программы. Мы научились извлекать из массива координаты пикселя зная его «номер» в массиве и можем извлечь из массива координаты точек кусочка контура амебы задав только номера координат начала и конца этого кусочка, научились перетасовывать координаты в массиве. Кстати, Матлаб (Матричная Лаборатория) тем и удобен для работы с изображениями что он имеет очень удобный графический интерфейс и огромный набор функций для работы с матрицами. А мы уже поняли, как изображения можно представлять в виде матрицы.

Мы уже научились извлекать отдельные звуки из нашей скрипки. Пришла пора попытаться исполнить хотя бы простенькую мелодию используя наши навыки.

2. Векторизация с помощью метода наименьших квадратов (МНК).

Сохраните вашу программу ameba.m и откройте новую вкладку в редакторе Матлаб. Скопируйте следующий код и вставьте его в открытую вкладку. Сохраните его с именем ameba_test.m и запустите выполнение программы.

clear All;clf;clc;close all;warning off;
t=(0:1/100:1)*2*pi;
r1=10;r2=10;x=r1*cos(t);y=r2*sin(t);
xh=round(x);yh=round(y);
a = [xh'.^2 xh'.*yh' yh'.^2 xh' yh']; b=ones(size(xh,2),1);
s=a\b;
A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;
h=fimplicit(@(x,y)(s(1)*x.^2)+s(2)*x.*y+s(3)*y.^2+s(4)*x+s(5)*y-1,...
     [-16 16 -16 16],MeshDensity=100,Visible='off');
xx=h.XData;yy=h.YData;
%__Визуализация результатов______________________________
hold on
plot(x,y,'.r');plot(x,y,'-r','LineWidth',4)
plot(xx',yy','g','LineWidth',2);
plot(xh,yh,'k');plot(xh,yh,'.k')
axis equal; grid minor; hold off
%__Оценка точности приближения___________________________
radius_MNK=1./sqrt(s([1 3]))
polyin = polyshape([x],[y]);
per_real = perimeter(polyin) 
polyin = polyshape([xh],[yh]);
per_deskr = perimeter(polyin) 
polyin = polyshape([xx],[yy]);
per_MNK = perimeter(polyin) 

err_MNK=abs(per_real-per_MNK)/per_real*100
err_deskr=abs(per_real-per_deskr)/per_real*100
%__Дисперсия___________________________________
dst=dist([xh' yh'],[xx' yy']');
[mdst q ]=min(dst');
disper=sum(mdst.^2)/(max(size(mdst))-1);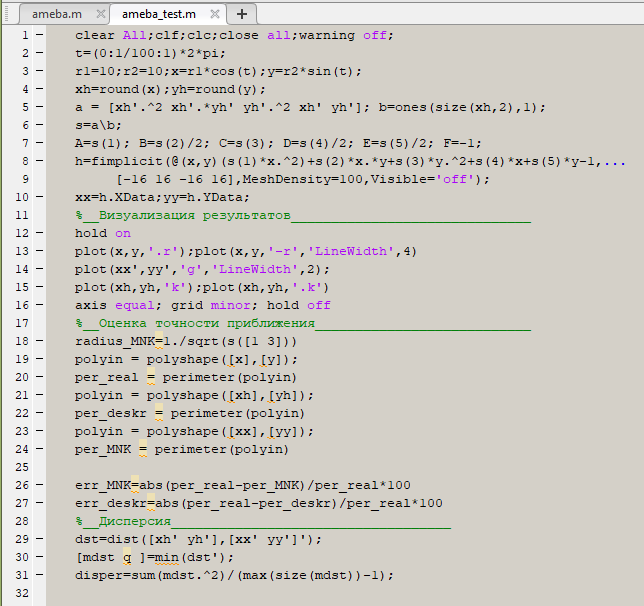

Анализируем программу и результаты ее выполнения. Мы получили вот такую картинку и такие результаты вычислений:

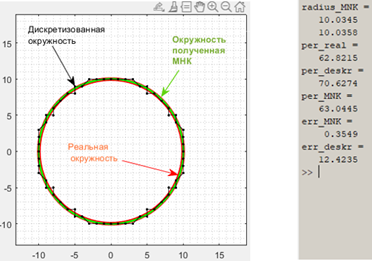
Мы программно как бы повысили разрешающую способность камеры. Как мы увидим ниже повышение точности зависит от многих факторов (размер, положение точек эллипса относительно светочувствительных элементов матрицы фотокамеры) и повышение может быть как выше, так и ниже указанной.

Разбираемся с программой ameba_test.m.

2-3 строчки - задаем массив [х y], содержащий 101 координату «реальной» окружности радиусом 10 и с центром в начале координат.

4 строка – округляем x и y до ближайшего целого числа тем самым получаем массив [xh yh] дискретизованных координат той же окружности. Мы имитируем искажение «реальной» окружности фотокамерой.

5 и 6 строки – с помощью метода наименьших квадратов (МНК) используя дискретизованные координаты xh и yh вычисляем константы уравнения эллипса наилучшим образом приближенного к нашему «реальному» эллипсу (наша «реальная» окружность – частный случай эллипса с одинаковыми полуосями: r1=r2=10).

Кому интересно побольше узнать о МНК прочитайте страницы 66-71 из другого прекрасного учебника тех же авторов: «Информатика и ИКТ. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / А. Г. Гейн, А. И. Сенокосов. 2-е изд. _ М.: Просвещение, 2009.». Чтобы переместить файл на свой компьютер, скопируйте ссылку ниже и вставьте в адресную строку браузера. Перейдите по ней и нажмите «Скачать» в появившейся вкладке.

https://disk.yandex.ru/i/x1X2vS6Pf0h56g

Мы же не будем углубляться в теорию, а попытаемся объяснить «на пальцах» суть МНК и пригодность этого метода для решения нашей задачи. Но все же если Вы хотя бы пробежитесь по тексту о МНК я буду безмерно рад.

Уравнение кривой второго порядка (эллипс, парабола, гипербола):

Константы A, B, C, D, E полностью определяют размеры эллипса, его «сплющенность», положение его в системе координат, угол поворота его осей относительно системы координат. Если у нас есть массив координат 5-ти точек, принадлежащих конкретному эллипсу мы можем составить систему из 5 уравнений с 5 неизвестными нам константами. Решив эту систему, мы найдем константы A, B, C, D, E и воспользовавшись уравнением сможем вычислить координаты всех точек эллипса.Но как быть если у нас есть массив координат больше чем 5 точек и к тому же эти точки не совсем точно лежат на эллипсе, а разбросаны в его окрестности? Через эти точки можно с некоторым приближением провести бесконечно много эллипсов. Но как нам найти координаты единственного и в некотором смысле «оптимального» эллипса? Метод наименьших квадратов помогает найти такой эллипс.

Его «оптимальность» в том, что сумма квадратов минимальных расстояний всех экспериментальных точек к эллипсу будет наименьшей из множества соответствующих сумм всевозможных эллипсов. Великий Гаусс, использовал МНК для анализа орбиты карликовой планеты Паллада, которая была открыта в 1802 году. Затем он использовал этот подход для прогнозирования местоположения другого объекта на той же орбите, которым оказалась Церера. Это позволило ему точно обнаружить и отследить орбиту Цереры. Для вычисления точных параметров орбиты он воспользовался несколькими не совсем точными измерениями положения планеты в разные моменты времени. Мы же сейчас пытаемся решить очень похожую задачу с помощью Матлаб.

Как реализовать МНК на Матлаб в нашем случае? Составим матрицу а так: в первой колонке у нас будет столбик значений хh² – (xh'.^2), во втором столбике xh*yh – (xh'.*yh'), далее yh² – (yh'.^2), xh – (xh'), yh – (yh'). У нас xh и yh – строки, а символ «'» превращает их в столбцы xh' и yh'.

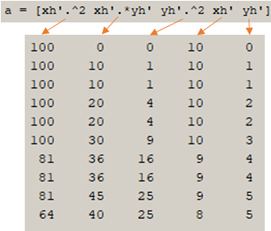
Теперь нам необходимо получить колонку из единиц длиной 101 элемент: b=ones(size(xh,2),1). У нас все готово для решения системы из 101 линейного уравнения содержащих 5 неизвестных. Решение этой системы находим при помощи оператора «\»: Строка 6 – s = a\b; Теперь в s содержатся вычисленные коэффициенты нашего уравнения – Строка 7:

A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;

Теперь нам необходимо вычислить координаты приближающего эллипса. Нам поможет функция fimplicit которая занимает две строчки 8 и 9 программы. Для продолжения функции на следующую строку примените три точки в конце предыдущей. @(x,y)- указываем переменные x и y. (s(1)*x.^2)+s(2)*x.*y+s(3)*y.^2+s(4)*x+s(5)*y-1 – здесь записано наше уравнение кривой второго порядка и указанно что коэффициенты уравнения надо брать из переменной s. Расчет координат точек и их визуализацию проводить в прямоугольнике с координатами вершин [Хmin Xmax Ymin Ymax]. MeshDensity=100 это количество вычисленных точек на единицу площади. Более высокая плотность обычно дает более точные результаты анализа, но анализ занимает больше времени. Использование сетки с более высокой плотностью для важных объектов обычно обеспечивает более точные результаты. Visible='on' – выводить изображение вычисленных точек, Visible='off' – только вычисления.

Строка 10 – вычисленные координаты эллипса присваиваются переменным xx и yy.

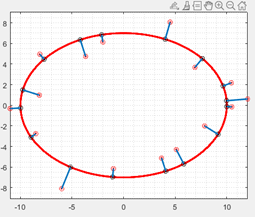
Строки 11 – 16 – визуализация результатов. [x y] – координаты «реальной» окружности, [xh yh] - дискретизованные координаты той же окружности, [xx yy] – координаты окружности, вычисленной МНК.

Строки 17 – 27 - оценка точности приближения: radius_MNK – полуоси вычисленного эллипса. В нашем случае «реальной» окружности они обе равны 10, а вычисленные равны – 10.0345 и 10.0358. Т.е. МНК вычислил их с точностью 0.35%.

per_real, per_deskr и per_MNK – периметры «реальной окружности», дискретизованной окружности и окружности вычисленной МНК.   

err_MNK и err_deskr – относительные ошибки вычисления периметра с помощью МНК и непосредственно по дискретизованной окружности соответственно.

Строки 29 – 31 – вычисление дисперсии. Дисперсия является показателем точности приближения точек изображения линиями, вычисленными МНК. Любой участок контура амебы мы сможем приблизить МНК к эллипсу, прямой линии, полиному любой степени и т.д. «На глаз» мы легко сможем выбрать самый удачный метод приближения. Но у программы нет глаз и поэтому нужен этот показатель для выбора программой самого удачного приближения. В конкурсе выигрывает приближающая линия с самой низкой дисперсией.

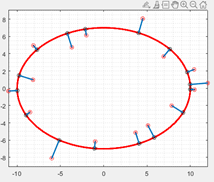
Мы можем поэкспериментировать. Например, в строчке 3 изменим длины полуосей эллипса: r1=15; r2=7.5 и запустим программу.

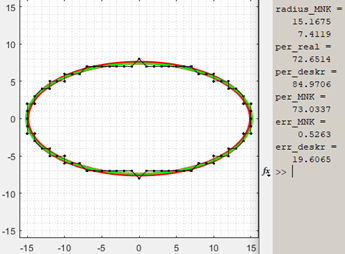
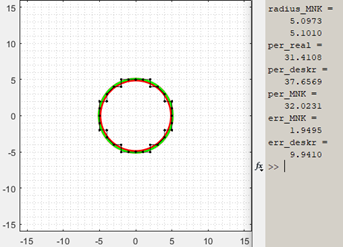
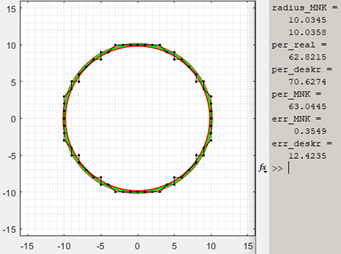
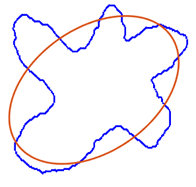
Любой замкнутый контур будет приближаться эллипсом хотя контур может быть совсем не похожим на эллипс. Например, попробуем приблизить контур нашей совсем не эллипсообразной амебы:

Продолжим эксперименты. Вернее, продолжу я, не анализируя программы целиком (при желании Вы наверняка уже сами сможете проделать то же самое). Я хочу, чтобы Вы ухватили суть и не увязли в деталях. Выделим какой ни будь участок контура амебы, например, между номерами координат 32 и 106 (xh=x(32:106)'; yh=y (32:106)';) и найдем приближение МНК этого участка контура:

a = [xh'.^2 xh'.*yh' yh'.^2 xh' yh']; b=ones(size(xh,2),1);
s=a\b;
A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;
h=fimplicit(@(x,y)(s(1)*x.^2)+s(2)*x.*y+s(3)*y.^2+s(4)*x+s(5)*y-1,...
     [0 200 0 200],MeshDensity=100,Visible='on');
xx=h.XData;yy=h.YData;

Выведем на экран результат:

hold on
plot(x,y,'r','LineWidth',2)
plot(xh,yh,'g','LineWidth',2)
plot(xh(1),yh(1),'ok')
plot(xh(end),yh(end),'ok')
plot(xx,yy,'b')
axis equal
ax=gca; ax.YDir= 'revers';

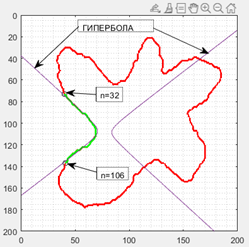
У нас получилось решение нашей системы уравнений в квадрате [0 200 0 200] – мы наблюдаем две красивые ветви гиперболы и нам теперь необходимо выделить участок гиперболы, который приближает выделенный нами участок контура амебы (зеленая линия). Есть предложение переместить зеленую линию так чтобы ее крайние точки n=32 и n=106 легли на ось 0Х и мы смогли бы легко выделить нужный нам участок гиперболы. Но лучше один раз увидеть, чем сто раз услышать:

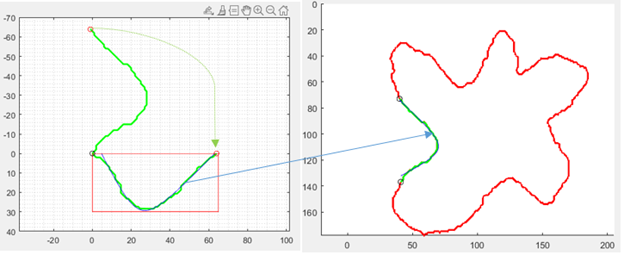
Вид кривой заданной нашим уравнением зависит от трех инвариантов. Например, если мы хотим обрабатывать только кривые похожие на эллипс, то нам необходимо вычислить инварианты и записать соответствующие условия.

A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;
%__Инварианты_____________
I1=A+C;
I2=det([A B; B C]);
I3=det([A B D; B C E; D E F]);
%__Условия для эллипса______
%__if I2 > 0 & I1 * I3 < 0 …………end

Так как нам придется выполнять эти вычисления для каждого участка контура то необходимо создать свою функцию, к которой мы могли бы обращаться как к обычным функциям Матлаб – из любой программы и даже из командной строки. Ниже приведена функция my_ellips. В редакторе Матлаб откройте новую вкладку и поместите в нее скопированную функцию.

function [xx,yy,disper]=my_ellips(xh,yh)

%__Перенос в начало координат___________
xr=xh-xh(end); yr=yh-yh(end); %__Перенос____
%__Поворот____________________________
fi=atan2(-yr(1),xr(1)); %__Угол поворота__
rot=[cos(fi) -sin(fi); sin(fi) cos(fi)];
er=(rot*[xr' yr']')'; %__Поворот___________

%__решение МНК для фрагмента_______________________________
xm=er(:,1)';ym=er(:,2)';
a = [xm'.^2 xm'.*ym' ym'.^2 xm' ym']; b=ones(size(xm,2),1);
s=a\b; %__МНК__
%__Параметры области решения_______________________________
  if max(ym)==0,
      y1=min(ym)-10; y2=0;
  else
      y1=0; y2=max(ym)+10; %__10 добалено чтобы избежать потерь
  end
%__МНК_______________________________________________________________
h=fimplicit(@(x,y)(s(1)*x.^2)+s(2)*x.*y+s(3)*y.^2+s(4)*x+s(5)*y-1,...
     [0 max(xm) y1 y2],MeshDensity=100,Visible='off');
xe=h.XData;ye=h.YData;
%__Обратный Поворот и перенос________________________________________
fi=-fi;
rot=[cos(fi) -sin(fi);sin(fi) cos(fi)];
xypr=(rot*[xe' ye']')';
xpr=xypr(:,1);ypr=xypr(:,2);
xx=xpr+xh(end); yy=ypr+yh(end);
%__Дисперсия_______________________________________
dst=dist([xh' yh'],[xx yy]');
[mdst q ]=min(dst');
disper=sum(mdst.^2)/(max(size(mdst))-1);

%__Инварианты______________________________________
A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;
I1=A+C;
I2=det([A B; B C]);
I3=det([A B D; B C E; D E F]);
%__Условия для эллипса________
  if (I2 > 0)&(I1 * I3 < 0)==0
     xx=[];yy=[];disper=inf; %__Если не эллипс____
  end
end

Запомните эту функцию с именем my_ellips.m в той же папке где находится файл ameba.m.

Создадим еще одну функцию приближения данных [x y] полиномами по методу наименьших квадратов. Для этого воспользуемся функцией p=polyfit(x,y,n) которая возвращает вектор коэффициентов полинома p(x) степени n, который с наименьшей среднеквадратичной погрешностью приближает данные и функцией y = polyval(p,xint) которая вычисляет многочлен p в каждой точке интервала xint. Ниже приведена функция my_polinom. В редакторе Матлаб откройте новую вкладку и поместите в нее скопированную функцию.

function [xpr,ypr,disper]=my_polinom(xy)

%__Перенос и Поворот______________________
xl=xy(:,1)-xy(1,1);yl=xy(:,2)-xy(1,2);
fi=atan2(-yl(end),xl(end));
rot=[cos(fi) -sin(fi); sin(fi) cos(fi)];
er=(rot*[xl yl]')';
%__Полином_________________________________________________
xp=er(:,1)';yp=er(:,2)';
p = polyfit(xp,yp,8);%__находим 8 кэфф. полинома___________ 
xpol=0:max(xp)/100:max(xp); %__область решения 100 точек___
ypol = polyval(p,xpol);     %__вычисление в обл. реш.______
 
%__Обратный Поворот___________________
fi=-fi;
rot=[cos(fi) -sin(fi);sin(fi) cos(fi)];
xypr=(rot*[xpol' ypol']')';
%__Обратный Перенос___________________
xpr=xypr(:,1);ypr=xypr(:,2);
xpr=xpr+xy(1,1);
ypr=ypr+xy(1,2);

%__Дисперсия_______________________________________
dst=dist([xpol' ypol'],[xp' yp']');
[mdst q ]=min(dst');
disper=sum(mdst.^2)/(max(size(mdst))-1);

end

Сохраните эту функцию с именем my_polinom.m в той же папке где находится ameba.m

Нам осталось создать еще одну функцию - функцию дефрагментации контура. При попытке приблизить эллипсом контур нашей совсем не эллипсообразной амебы мы получили такую картинку :

Оптимальна ли такая дефрагментация? Трудно сказать – нет теоретического обоснования. Но «на глаз» вроде получилось не плохо – почти одинаковые фрагменты не сложной формы и вполне доступные для приближения теми функциями, которые у нас уже есть. Как он сработает в случаях отличных от нашего тоже мы ничего сказать не можем. Интуитивно надеемся, что он будет полезен и в других случаях просто потребуется дополнительная проверка. Википедия подсказывает: «Эвристический алгоритм — алгоритм решения задачи, включающий практический метод, не являющийся гарантированно точным или оптимальным, но достаточный для решения поставленной задачи. Позволяет ускорить решение задачи в тех случаях, когда точное решение не может быть найдено». Вот цитата Ю.И.Журавлева из сборника «Мехматяне вспоминают: 3»:

«И тут мне пришла в голову некая эвристика. Алгоритм, который был более или менее обоснован лет, так, через тридцать пять, а тогда он был совершенно не обоснован. Виктор Михайлович Глушков его называл «шаманским алгоритмом». Но он работал! И давал ответ! Много позже выяснилось, что этот алгоритм я просто угадал. Ну, угадал!»

Нам ничего не остается кроме как тоже воспользоваться своим «шаманским алгоритмом» дефрагментации – контур приблизим эллипсом, который разобьет контур на внутренние и внешние фрагменты доступные для приближения теми функциями, которые у нас уже есть. Для извлечения координат внутренних и внешних фрагментов воспользуемся функцией… Возможно у Вас сложилось впечатление что в нужный момент я как фокусник достаю из рукава нужную функцию и затем рассказываю о том, как она работает. Но функций в Матлаб сотни и сотни, и я не фокусник. Просто в Яндекс поисковике я задаю вопрос: «Внутренние точки многоугольника в Матлаб». Чаще всего подходящий ответ я нахожу на сайте обозначаемом в поисковике вот такой иконкой:

Открываем страницу и находим: «inpolygon - обнаружение точек, расположенных внутри или на краю полигональной области» и далее описание функции и примеры ее применения.

Продолжим - для извлечения координат внутренних и внешних фрагментов воспользуемся функцией in = inpolygon(x,y,xx,yy) где x, y – координаты точек контура, xx, yy – координаты точек приближающего эллипса, in – номера координат точек контура лежащих внутри эллипса. Соответственно ~in - номера координат точек контура лежащих вне
эллипса. in – массив, состоящий из 0 и 1 – 1 если точка внутри эллипса 0 – если точка вне эллипса. Логический оператор ~ меняет в массиве 1 на 0 и 0 на 1. xin=x(in), yin=y(in) – получили массив координат всех внутренних точек и xout=x(~in), yout(~in) массив всех внешних точек. Теперь из этих массивов нужно выделить отдельные фрагменты и рассортировать их так чтобы они были легко доступны для МНК обработки и сшивания в окончательно векторизованный контур. Построим граф из массива внешних точек.

Выделим координаты связных компонент графа. Набираем в поисковике: «связные компоненты графа Матлаб». Находим: «conncomp - Компоненты связного графа». bins = conncomp(graf) – переменная bins – массив, состоящий из номеров 1,2, 3, 4, 5. Теперь мы сможем отдельно выделить координаты каждого внешнего фрагмента. Например, координаты 3-го внешнего фрагмента [xout(bins==3) yout(bins==3)]. 

Последнее что нам необходимо для этой функции — это поправить расположение координат в фрагменте, в котором изначально находились первая и последняя точки нашего контура. Координаты этих точек находятся где-то внутри массива, а нам необходимо циклически передвинуть координаты в массиве так чтобы первая точка находилась на одном конце фрагмента, а последняя на другом конце. Сначала найдем координаты, которые находятся на концах фрагмента. Учтем, что разница между соседними х-координатами внутри фрагмента может быть -1, 0, 1. То же самое для y-координаты.  На концах фрагмента абсолютное значение этой разницы больше 1.

Номер К массива координат где наблюдается разрыв абсолютных значений координат более 1: K=find(abs(diff(xfr(i)))>1|abs(diff(yfr(i)))>1). Если разрыв обнаружен, то циклическое передвижение координат осуществляется с помощью функции circshift:  if K~=0, xym = circshift(xym,-K); end.

Нам еще понадобиться «ящик», в который мы будем складывать внешние и внутренние фрагменты так чтобы их потом было легко поочередно извлекать для векторизации и затем помещать туда векторизованные фрагменты для последующего сшивания в векторизованный контур. Используем массив структур, который является типом данных, который группирует связанные данные с помощью полей. Звучит это грозно, но на самом деле все просто. Создаем структуру с именем str: str=struct. Пусть xyout(3) – третий внешний фрагмент. Помещаем этот фрагмент в структуру: str(3).out= xyout(3). Второй внутренний фрагмент xyin(2) помещаем в структуру: str(2).in= xyin(2). Извлечения соответствующих координат в переменные: Per=str(3).out и Per=str(2).in.

Ниже приведена функция my_sekator. В редакторе
Матлаб откройте новую вкладку и поместите в нее скопированную функцию:

function [str]=my_sekator(x,y)
%__Рассекаем контур эллипсом________________________
 
xh=x';yh=y';
% xh=xyout(:,1)';yh=xyout(:,2)';
a = [xh'.^2 xh'.*yh' yh'.^2 xh' yh']; b=ones(size(xh,2),1);
s = pinv(a)*b;% s=a\b;
A=s(1); B=s(2)/2; C=s(3); D=s(4)/2; E=s(5)/2; F=-1;
h=fimplicit(@(x,y)(s(1)*x.^2)+s(2)*x.*y+s(3)*y.^2+s(4)*x+s(5)*y-1,...
[0 200 0 200],MeshDensity=100,Visible='off',MarkerEdgeColor='g',LineWidth=1);
xx=h.XData;yy=h.YData;
%________________________________________________________________
%__Отделяем внутренние и внешние точки_______________
in = inpolygon(x,y,xx,yy);
str=struct;
%__Внешние точки______
yii=y(~in);xii=x(~in);
graf=graph(dist([xii  yii]') <= sqrt(2), 'omitselfloops');
bins = conncomp(graf);
hold on
for i=1:max(bins)
    xym=[xii(bins==i) yii(bins==i)];%plot(xym(:,1),xym(:,2),'g')
    K=find(abs(diff(xym(:,1)))>1|abs(diff(xym(:,2)))>1);
    if K~=0, xym = circshift(xym,-K);end
    str(i).out=xym;
end
%__Внутренние точки___
yii=y(in);xii=x(in);
graf=graph(dist([xii  yii]') <= sqrt(2), 'omitselfloops');
bins = conncomp(graf);
hold on
for i=1:max(bins)
    xym=[xii(bins==i) yii(bins==i)];%plot(xym(:,1),xym(:,2),'r')
    str(i).in=xym;
end

Сохраните эту функцию с именем my_sekator.m в той же папке где находится ameba.m

Нам осталось применить МНК к каждому фрагменту и затем сшить все векторизованные фрагменты в векторизованный контур амебы. Этим мы займемся в основной программе ameba.m:

Ниже приведено продолжение программы ameba.m. Скопируйте код и поместите его начиная со строчки 18 и сохраните файл.

%__Дефрагментация контура__
str=my_sekator(x,y);
%__Обрабатываем фрагменты МНК и формируем структуру_________
for i=1:size(str,2)
  xyo= str(i).out;%__внешние фрагменты_____
  [xpr,ypr]=my_polinom(xyo);
  str(i).op=[xpr,ypr];
  xyin= str(i).in;%__внутренние фрагменты__
  [xpr,ypr]=my_polinom(xyin);
  str(i).ip=[xpr,ypr];
end
%__Сшиваем вычисленние МНК фрагменты_________________________
xyam=[]; %__В этот массив будем поочерено загружать фрагменты
for i=1:max(size(str))
    xyam=[xyam;str(i).op]; %__внешний
    xyam=[xyam;str(i).ip]; %__внутренний
end
%__Координаты векторизованного контура____________
 xyam(end+1,:)=xyam(1,:); %__Замыкаем контур 
 
%__Визуализация результата_________________ 
 hold on
 plot(x,y,'g',LineWidth=2)      %__Исходный контур
 plot(xyam(:,1),xyam(:,2),'r')%__векторизованный контур
 ax=gca; ax.YDir= 'revers';
 
%__Периметр и площадь векторизованного контура 
xy= polyshape(xyam); 
P = perimeter(xy)
S = area(xy)

Запускаем программу. Должно появиться изображение:

Для анализа программы полезно рассмотреть эту картинку:

Напомню содержание структуры str: str(i).out – i-й внешний фрагмент контура, str(i).in – i-й внутренний фрагмент контура, str(i).op – i й внешний обработанный МНК фрагмент контура, str(i).ip – i-й внутренний обработанный МНК фрагмент контура.

polyshape - функция создает многоугольник, заданный координатами вершин для вычисления периметра и площади.

Вы можете самостоятельно в графическом редакторе нарисовать любой контур и векторизовать его с помощью нашей программы подобрав нужную степень приближающего полинома (строка 10 функции my_polinom):

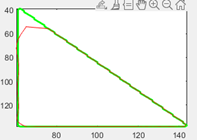
По-видимому, придется изобретать новую приближающую функцию.

ЗАКЛЮЧЕНИЕ

Ну вот Вы и научились извлекать звуки из Вашей скрипки и даже исполнили незамысловатую мелодию. Тренируйтесь, попробуйте исполнить более сложную мелодию, и я надеюсь Вы сможете стать виртуозом!