Избавление изображения от шума – одна из фундаментальных операций компьютерного зрения. Алгоритмы сглаживания применяются почти везде: они могут быть как самостоятельной процедурой для улучшения фотографии, так и первым шагом для более сложной процедуры, например, для распознавания объектов на изображении. Поэтому существует огромное множество способов сглаживания, и я бы хотел рассказать об одном из них, отличающемся от остальных хорошей применимостью на текстурах и изображениях с большим количеством одинаковых деталей.

Под катом много картинок, аккуратнее с траффиком.

Предварительная информация

Вкратце о поставленной задаче. Предполагается, что в некотором идеальном мире мы можем получить идеальное изображение (матрица или вектор элементов), которое идеально передаёт информацию о внешнем мире. К сожалению, мы живём не в столь прекрасном месте, и поэтому по разным причинам нам приходится оперировать изображениями , где – матрица или вектор шума. Существует много моделей шума, но в этой статье мы будем предполагать, что – белый гауссов шум. По имеющейся информации мы пытаемся восстановить изображение , которое будет максимально близко к идеальному изображению . К сожалению, это почти всегда невозможно, так как при зашумлении часть данных неизбежно теряется. Кроме того, сама постановка задачи предполагает бесконечное множество решений.

Как правило, обычные сглаживающие фильтры устанавливают новое значение для каждого пикселя, используя информацию о его соседях. Дешёвый и сердитый гауссов фильтр, например, сворачивает матрицу изображения с матрицей гауссианы. В результате, в новом изображении каждый пиксель является взвешенной суммой пикселя с тем же номером исходной картинки и его соседей. Немного другой подход использует медианный фильтр: он заменяет каждый пиксель медианой среди всех близлежащих пикселей. Развитием идей этих способов сглаживания является билатеральный фильтр. Эта процедура берёт взвешенную сумму вокруг, опираясь как на расстояние до выбранного пикселя, так и на близость пикселей по цвету.

Идея фильтра

Тем не менее, все вышеперечисленные фильтры используют только информацию о близлежащих пикселях. Основная же идея нелокального сглаживающего фильтра состоит в том, чтобы использовать всю информацию на изображении, а не только пиксели соседние с обрабатываемым. Как же это работает, ведь зачастую значения в отдалённых точках никак не зависят друг от друга?

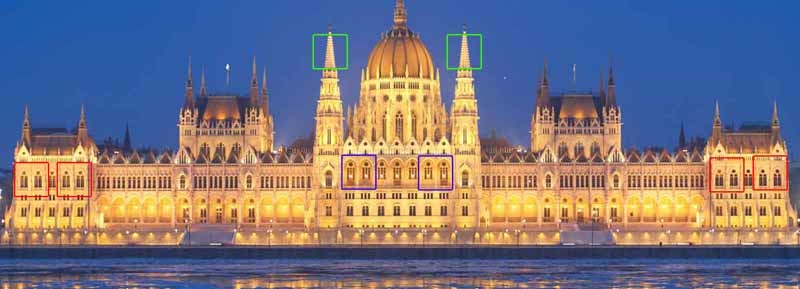
Совершенно очевидно, что если у нас есть несколько изображений одного и того же объекта с разным уровнем шума, то мы можем скомпоновать их в одну картинку без шума. Если эти несколько объектов помещены в разные места одного изображения, то мы всё равно можем воспользоваться этой дополнительной информацией (дело за малым – сначала отыскать эти объекты). И даже если эти объекты выглядят немного по-разному или частично перекрыты, то у нас всё равно есть избыточные данные, которыми можно воспользоваться. Нелокальный сглаживающий фильтр использует эту идею: находит похожие области изображения и применяет информацию из них для взаимного усреднения. Разумеется, что части изображения похожи, не означает, что они принадлежат одним и тем же объектам, но, как правило, приближение оказывается достаточно хорошим. Посмотрите на рисунок с линиями. Очевидно, что окна 2 и 3 похожи на окно 1, а окна 4, 5 и 6 — нет. На фотографии венгерского парламента, также можно заметить большое число одинаковых элементов.




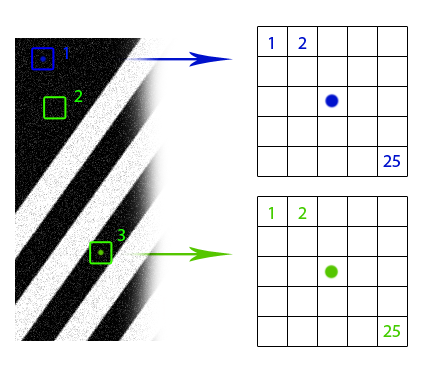
Предположим, что если окрестность пикселя в одном окне похожа на окрестность соответствующего пикселя в другом окне, то значения этих пикселей можно использовать для взаимного усреднения (синяя и зелёная точки на рисунке). Но как найти эти похожие окна? Как поставить им в соответствие веса, с какой силой они влияют друг на друга? Формализуем понятие «похожести» кусков изображения. Во-первых, нам понадобится функция различия двух пикселей. Здесь всё просто: для чёрно-белых изображений обычно используется просто модуль разности значений пикселей. Если имеется какая-то дополнительная информация об изображении, возможны варианты. Например, если известно, что чистое изображение состоит из объектов абсолютно чёрного цвета на полностью белом фоне, хорошей идеей будет использовать метрику, которая сопоставляет нулевое расстояние пикселям, не сильно отличающимся по цвету. В случае цветных изображений опять-таки возможны варианты. Можно использовать евклидову метрику в формате RGB или что-нибудь похитрее в формате HSV. «Непохожесть» окон изображения это всего лишь сумма различий их пикселей.

Теперь хорошо бы преобразовать полученную величину в более привычный формат веса . Передадим вычисленное на предыдущем шаге различие окон в какую-нибудь убывающую (или хотя бы невозрастающую) функцию и нормируем полученный результат суммой значений этой функции на всех возможных окнах. Обычно в роли такой функции выступает знакомая всем до зубовного скрежета , где – расстояние, а – параметр разброса весов. Чем больше , тем меньше влияет различие между окнами на сглаживание. При , все окна вне зависимости от различия между ними в равной мере вносят вклад в каждый пиксель, и изображение получится идеально серым, при , значимый вес будет только у окна, соответствующего самому себе, и сглаживания не получится.

Таким образом, наивная математическая модель нелокального усредняющего фильтра выглядит так:


-тый пиксель результирующего изображения равен сумме всех пикселей исходного изображения, взятых с весами , где вес это


а нормирующий делитель


Альтернативная метрика, предложенная выше:


Во всех случаях обозначает поэлементную разницу между окнами, как описано выше.

Если внимательно присмотреться, то итоговая формула получается почти такой же, как и у билатерального фильтра, только в экспоненте вместо геометрического расстояния между пикселями и цветовой разницы находится разница между лоскутами картинки, а также суммирование проводится по всем пикселям изображения.

Рассуждения об эффективности и реализация

Очевидно, что сложность предложенного алгоритма , где – радиус окна, по которому вычисляется похожесть частей изображения, а – полное количество пикселей, ведь мы для каждого пикселя сравниваем его окрестность размера с окрестностью каждого другого пикселя. Это не слишком хорошо, потому что наивная реализация алгоритма достаточно медленно работает даже на изображениях 300x300. Обычно предлагаются следующие улучшения:

• Очевидно, что необязательно пересчитывать все веса всё время, ведь вес пикселя для пикселя и наоборот – равны. Если сохранять вычисленные веса, время выполнения сокращается вдвое, но требуется памяти для хранения весов.
• Для большинства реальных изображений веса между большей частью пикселей будут равны нулю. Так почему бы не обнулить их вовсе? Можно использовать эвристику на основе сегментации изображения, которая будет подсказывать, где считать вес попиксельно бессмысленно.
• Экспоненту при вычислении весов можно заменить на более дешёвую для вычисления функцию. Хотя бы кусочную интерполяцию той же экспоненты.

Обычный вопрос, который возникает при рассмотрении этого алгоритма: почему мы используем только значения центрального пикселя в области? Вообще говоря, ничего не мешает поставить в основную формулу суммирование по всей области, как в билатеральном сглаживании, и это даже несильно повлияет на сложность, но результат изменённого алгоритма, скорее всего, получится слишком размытым. Не забывайте, что в реальных изображениях даже одинаковые объекты редко бывают абсолютно идентичными, а такая модификация алгоритма усреднит их. Чтобы воспользоваться информацией с соседних элементов изображения, можно предварительно выполнить обычное билатеральное сглаживание. Хотя если известно, что исходные объекты были или должны в итоге получиться абсолютно одинаковыми (сглаживание текста), то подобное изменение как раз пойдёт на пользу.

Наивная реализация алгоритма (С + OpenCV 2.4.11):

#include "targetver.h"

#include <stdio.h>
#include <math.h>

#include <opencv2/opencv.hpp>
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/imgproc/imgproc_c.h"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/core/core.hpp"
#include "opencv2/features2d/features2d.hpp"
#include "opencv2/calib3d/calib3d.hpp"
#include "opencv2/nonfree/nonfree.hpp"
#include "opencv2/contrib/contrib.hpp"
#include <opencv2/legacy/legacy.hpp>

#include <stdlib.h>
#include <stdio.h>

using namespace cv;


/*
	Returns measure of diversity between two pixels. The more pixels are different the bigger output number.
	Usually it's a good idea to use Euclidean distance but there are variations.
*/
double distance_squared(unsigned char x, unsigned char y)
{
	unsigned char zmax = max(x, y);
	unsigned char zmin = min(x, y);
    return (zmax - zmin)*(zmax - zmin);
}

/*
    Returns weight of interaction between regions: the more dissimilar are regions the less resulting influence.
    Usually decaying exponent is used here. If distance is Euclidean, being combined, they form a typical Gaussian function.
*/
double decay_function(double x, double dispersion)
{
	return exp(-x/dispersion);
}

int conform_8bit(double x)
{
	if (x < 0)
		return 0;
	else if (x > 255)
		return 255;
	else
		return static_cast<int>(x);
}


double distance_over_neighbourhood(unsigned char* data, int x00, int y00, int x01, int y01, int radius, int step)
{
    double dispersion = 15000.0; //should be manually adjusted
    double accumulator = 0;
	for(int x = -radius; x < radius + 1; ++x)
	{
		for(int y = -radius; y < radius + 1; ++y)
		{
            accumulator += distance_squared(static_cast<unsigned char>(data[(y00 + y)*step + x00 + x]), static_cast<unsigned char>(data[(y01 + y)*step + x01 + x]));
		}
	}
    return decay_function(accumulator, dispersion);
}


int main(int argc, char* argv[])
{
	int similarity_window_radius = 3; //may vary; 2 is enough for text filtering
	char* imageName = "text_noised_30.png";
    IplImage* image = 0;
	image = cvLoadImage(imageName, CV_LOAD_IMAGE_GRAYSCALE);
	if (image == NULL) {
		printf("Can not load image\n");
		getchar();
		exit(-1);
	}
	
	CvSize currentSize = cvGetSize(image);
	int width = currentSize.width;
	int height = currentSize.height;
	int step = image->widthStep;
	unsigned char *data = reinterpret_cast<unsigned char *>(image->imageData);
	vector<double> processed_data(width*height, 0);
	//External cycle
	for(int x = similarity_window_radius + 1; x < width - similarity_window_radius - 1; ++x) 
	{
		printf("x: %d/%d\n", x, width - similarity_window_radius - 1);
		for(int y = similarity_window_radius + 1; y < height - similarity_window_radius - 1; ++y) 
		{
			//Inner cycle: computing weight map
			vector<double> weight_map(width*height, 0);
			double* weight_data = &weight_map[0];
			double norm = 0;
			for(int xx = similarity_window_radius + 1; xx < width - similarity_window_radius - 1; ++xx)
				for(int yy = similarity_window_radius + 1; yy < height - similarity_window_radius - 1; ++yy)
				{
                    double weight = distance_over_neighbourhood(data, x, y, xx, yy, similarity_window_radius, step);
                    norm += weight;
                    weight_map[yy*step + xx] = weight;
				}
			//After all weights are known, one can compute new value in pixel
			for(int xx = similarity_window_radius + 1; xx < width - similarity_window_radius - 1; ++xx)
				for(int yy = similarity_window_radius + 1; yy < height - similarity_window_radius - 1; ++yy)
                    processed_data[y*step + x] += data[yy*step + xx]*weight_map[yy*step + xx]/norm;
		}
	}
	//Transferring data from buffer to original image
	for(int x = similarity_window_radius + 1; x < width - similarity_window_radius - 1; ++x)
		for(int y = similarity_window_radius + 1; y < height - similarity_window_radius - 1; ++y)
			data[y*step + x] = conform_8bit(processed_data[y*step + x]);
	cvSaveImage("gray_denoised.png", image);
	
	cvReleaseImage(&image);
	return 0;
}

Примеры

Давайте посмотрим на некоторые результаты:



Обратите внимание на практически идеальное сглаживание и чёткие края линий. Чем больше одинаковых квадратных областей на изображении, тем лучше работает алгоритм. Здесь у программы было достаточно примеров для каждого типа окрестности, ведь все квадратные области вдоль линий примерно одинаковые.

Разумеется, всё не так радужно для тех случаев, когда «похожесть» областей нельзя обнаружить простым квадратным окном. Например:



Хоть фон и внутренность круга сгладились хорошо, вдоль окружности остались артефакты. Разумеется, алгоритм не может понять, что правая сторона круга такая же, как и левая, только повёрнута на 180 градусов, и использовать это при сглаживании. Такой очевидный промах можно исправить рассмотрением повёрнутых окон, но тогда время выполнения увеличится во столько раз, сколько поворотов окна рассматривается.

Чтобы не было сомнений, что алгоритм умеет сглаживать не только прямые линии, вот ещё один пример, который заодно иллюстрирует важность выбора сглаживающего параметра:




На втором рисунке видны примерно такие же артефакты, как и в предыдущем случае. Тут дело не в недостатке похожих окон, а в слишком маленьком параметре : даже похожие области получают слишком малые веса. На четвёртой картинке, напротив, был выбран слишком большой , и все области получили примерно одинаковые веса. Третья представляет золотую середину.

Ещё пример работы на тексте. Даже небольшое и сильно зашумлённое изображение обработано достаточно хорошо для последующего использования машиной (после эквализации гистограммы и наведения резкости, разумеется):





Ещё немножко примеров с сайта, на котором можно применить уже оптимизированный нелокальный алгоритм сглаживания:





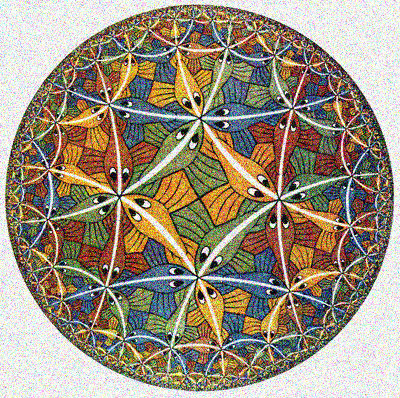
Порядок: исходное, зашумлённое, восстановленное. Заметьте, как хорошо были очищены рисунки Эшера, в которых много подобных элементов. Только чёрные линии стали прозрачнее и сгладилась текстура.

Подсчёт весов при помощи дескрипторов особых точек

К сожалению, высокая вычислительная сложность алгоритма ограничивает его применение на практике, тем не менее, он показывает хорошие результаты на задачах сглаживания изображений с повторяющимися элементами. Главная проблема этого алгоритма кроется в его основной идее вычисления весов. Приходится для каждого пикселя проходить по окрестностям всех других пикселей. Даже если предположить, что двукратный просмотр всех пикселей – это неизбежное зло, то просмотр его соседей кажется лишним, ведь даже для радиуса окна 3 он увеличивает время подсчёта весов в 49 раз. Вернёмся немного назад к первоначальной идее. Мы хотим найти похожие места на изображении, чтобы использовать их для сглаживания друг друга. Но нам необязательно попиксельно сравнивать все возможные окна на картинке, чтобы найти похожие места. У нас уже есть хороший способ для обозначения и сравнивания интересных элементов изображения! Разумеется, я говорю о разнообразных дескрипторах особенностей. Обычно под этим подразумевается SIFT, но в нашем случае лучше использовать что-нибудь менее точное, ведь целью на этом этапе является найти много достаточно похожих областей, а не несколько точно таких же. В случае применения дескрипторов шаг подсчёта весов выглядит так:

• Предварительно считаем дескрипторы в каждой точке изображения
• Проходим по изображения и для каждого пикселя
• o Проходим по каждому другому пикселю
• o Сравниваем дескрипторы
• o Если дескрипторы похожие, то сравниваем окна попиксельно и считаем вес
• o Если разные, обнуляем вес
• Чтобы не проходить по изображению второй раз, посчитанные веса и координаты пикселей заносятся в отдельный список. Когда в списке накопилось достаточное число элементов, можно прекращать поиск.
• Если не получилось найти заданное количество похожих точек (пиксель ничем не примечателен), просто проходим по изображению и считаем веса как обычно

Достоинства такого подхода:

• Улучшается сглаживание в особых точках, которые нам обычно больше всего и интересны
• Если на изображении много похожих особых точек, заметно повышение скорости

Недостатки:

• Не факт, что будет достаточно много похожих точек, чтобы окупить подсчёт дескрипторов
• Результат и ускорение алгоритма сильно зависят от выбора дескриптора

Заключение

Выводы:

• Алгоритм хорошо работает на периодических текстурах
• Алгоритм хорошо сглаживает однородные области
• Чем больше изображение, тем больше похожих областей и тем лучше работает алгоритм. Но безбожно долго.
• Области, для которых не удалось найти подобных, сглаживаются плохо (решается предварительным применением билатерального фильтра или рассмотрением поворотов окон)
• Как и для многих других алгоритмов, приходится подгонять значение сглаживающего параметра

Таким образом, мы рассмотрели алгоритм сглаживания, который использует информацию о похожих объектах на изображении для наилучшего приближения чистого изображения. От такого «псевдораспознавания» недалёк переход к настоящему сглаживанию после выделения похожих объектов. И действительно, современные подходы к восстановлению изображений используют для этой цели нейронные сети и они, как правило, действительно справляются лучше и быстрее. Однако нейронные сети требуют большего мастерства в программировании и тонкой настройки. Даже такой алгоритм, только имитирующий распознавание, может дать сопоставимый, а иногда лучший результат.

Источники

Antoni Buades, Bartomeu Coll A Non-local Algorithm For Image Denoising
Yifei Lou, Paolo Favaro, Stefano Soatto, and Andrea Bertozzi Nonlocal Similarity Image Filtering