Методы оптимизации нейронных сетей / forpes.ru

Главная
Методы оптимизации нейронных сетей

Методы оптимизации нейронных сетей +78

04.01.2017 11:18

Siarshai 66 17200 Источник

В подавляющем большинстве источников информации о нейронных сетях под «а теперь давайте обучим нашу сеть» понимается «скормим целевую функцию оптимизатору» лишь с минимальной настройкой скорости обучения. Иногда говорится, что обновлять веса сети можно не только стохастическим градиентным спуском, но безо всякого объяснения, чем же примечательны другие алгоритмы и что означают загадочные $\inline \beta$ и $\inline \gamma$ в их параметрах. Даже преподаватели на курсах машинного обучения зачастую не заостряют на этом внимание. Я бы хотел исправить недостаток информации в рунете о различных оптимизаторах, которые могут встретиться вам в современных пакетах машинного обучения. Надеюсь, моя статья будет полезна людям, которые хотят углубить своё понимание машинного обучения или даже изобрести что-то своё.

Под катом много картинок, в том числе анимированных gif.

Статья ориентирована на знакомого с нейронными сетями читателя. Предполагается, что вы уже понимаете суть backpropagation и SGD. Я не буду вдаваться в строгое доказательство сходимости представленных ниже алгоритмов, а наоборот, постараюсь донести их идеи простым языком и показать, что формулы открыты для дальнейших экспериментов. В статье перечислены далеко не все сложности машинного обучения и далеко не все способы их преодолевать.

Зачем нужны ухищрения

Напомню, как выглядят формулы для обычного градиентного спуска:

$\Delta \theta = -\eta \nabla_\theta J( \theta)$

$\theta = \theta + \Delta \theta = \theta - \eta \nabla_\theta J( \theta)$

где $\inline \theta$ — параметры сети, $\inline J( \theta)$ — целевая функция или функция потерь в случае машинного обучения, а $\inline \eta$ — скорость обучения. Выглядит удивительно просто, но много магии сокрыто в $\inline \nabla_\theta J( \theta)$ — обновить параметры выходного слоя довольно просто, но чтобы добраться до параметров слоёв за ним, приходится проходить через нелинейности, производные от которых вносят свой вклад. Это знакомый вам принцип обратного распространения ошибки — backpropagation.

Явно расписанные формулы для обновления весов где-нибдуь в середине сети выглядят страшненько, ведь каждый нейрон зависит ото всех нейронов, с которымии он связан, а те — ото всех нейронов, с которыми связаны они, и так далее. При этом даже в «игрушечных» нейронных сетях может быть порядка 10 слоёв, а среди сетей, удерживающих олимп классифицирования современных датасетов — намного, намного больше. Каждый вес — переменная в $\inline J( \theta)$ . Такое невероятное количество степеней свободы позволяет строить очень сложные отображения, но приносит исследователям головную боль:

Застревание в локальных минимумах или седловых точках, коих для функции от $\inline> 10^6$ переменных может быть очень много.
Сложный ландшафт целевой функции: плато чередуются с регионами сильной нелинейности. Производная на плато практически равна нулю, а внезапный обрыв, наоборот, может отправить нас слишком далеко.
Некоторые параметры обновляются значительно реже других, особенно когда в данных встречаются информативные, но редкие признаки, что плохо сказывается на нюансах обобщающего правила сети. С другой стороны, придание слишком большой значимости вообще всем редко встречающимся признакам может привести к переобучению.
Слишком маленькая скорость обучения заставляет алгоритм сходиться очень долго и застревать в локальных минимумах, слишком большая — «пролетать» узкие глобальные минимумы или вовсе расходиться

Вычислительной математике известны продвинутые алгоритмы второго порядка, которым под силу найти хороший минимум и на сложном ландшафте, но тут удар снова наносит количество весов. Чтобы воспользоваться честным методом второго порядка «в лоб», придётся посчитать гессиан $\inline J( \theta)$ — матрицу производных по каждой паре параметров пары параметров (уже плохо) — а, скажем, для метода Ньютона, ещё и обратную к ней. Приходится изобретать всяческие ухищрения, чтобы справиться с проблемами, оставляя задачу вычислительно подъёмной. Рабочие оптимизаторы второго порядка существуют, но пока что давайте сконцентрируемся на том, что мы можем достигнуть, не рассматривая вторые производные.

Nesterov Accelerated Gradient

Сама по себе идея методов с накоплением импульса до очевидности проста: «Если мы некоторое время движемся в определённом направлении, то, вероятно, нам следует туда двигаться некоторое время и в будущем». Для этого нужно уметь обращаться к недавней истории изменений каждого параметра. Можно хранить последние $\inline n$ экземпляров $\inline \Delta \theta$ и на каждом шаге по-честному считать среднее, но такой подход занимает слишком много памяти для больших $\inline n$ . К счастью, нам и не нужно точное среднее, а лишь оценку, поэтому воспользуемся экспоненциальным скользящим средним.

$v_t = \gamma v_{t-1} + (1-\gamma) x$

Чтобы накопить что-нибудь, будем умножать уже накопленное значение на коэффициент сохранения $\inline 0 < \gamma < 1$ и прибавлять очередную величину, умноженную на $\inline 1-\gamma$ . Чем ближе $\inline \gamma$ к единице, тем больше окно накопления и сильнее сглаживание — история $\inline x$ начинает влиять сильнее, чем каждое очередное $\inline x$ . Если $\inline x=0$ c какого-то момента, $\inline v_t$ затухают по геометрической прогрессии, экспоненциально, отсюда и название. Применим экспоненциальное бегущее среднее, чтобы накапливать градиент целевой функции нашей сети:

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)$

$\theta = \theta - v_t$

Где $\inline \gamma$ обычно берётся порядка $\inline 0.9$ . Обратите внимание, что $\inline 1-\gamma$ не пропало, а включилось в $\inline \eta$ ; иногда можно встретить и вариант формулы с явным множителем. Чем меньше $\inline \gamma$ , тем больше алгоритм ведёт себя как обычный SGD. Чтобы получить популярную физическую интерпретацию уравнений, представьте как шарик катится по холмистой поверхности. Если в момент $\inline t$ под шариком был ненулевой уклон ( $\inline \nabla_\theta J( \theta)$ ), а затем он попал на плато, он всё равно продолжит катиться по этому плато. Более того, шарик продолжит двигаться пару обновлений в ту же сторону, даже если уклон изменился на противоположный. Тем не менее, на шарик действует вязкое трение и каждую секунду он теряет $\inline 1-\gamma$ своей скорости. Вот как выглядит накопленный импульс для разных $\inline \gamma$ (здесь и далее по оси X отложены эпохи, а по Y — значение градиента и накопленные значения):

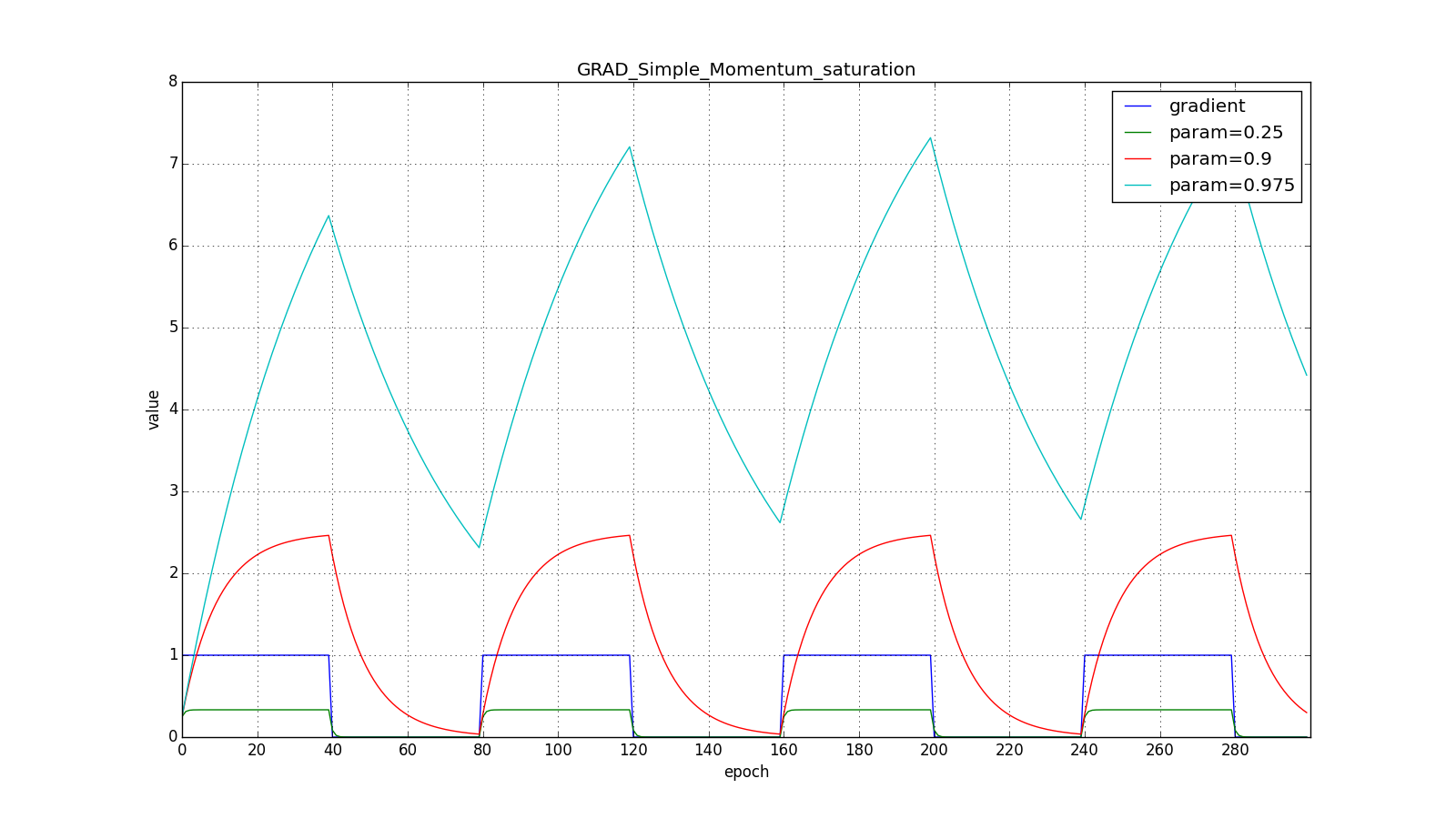
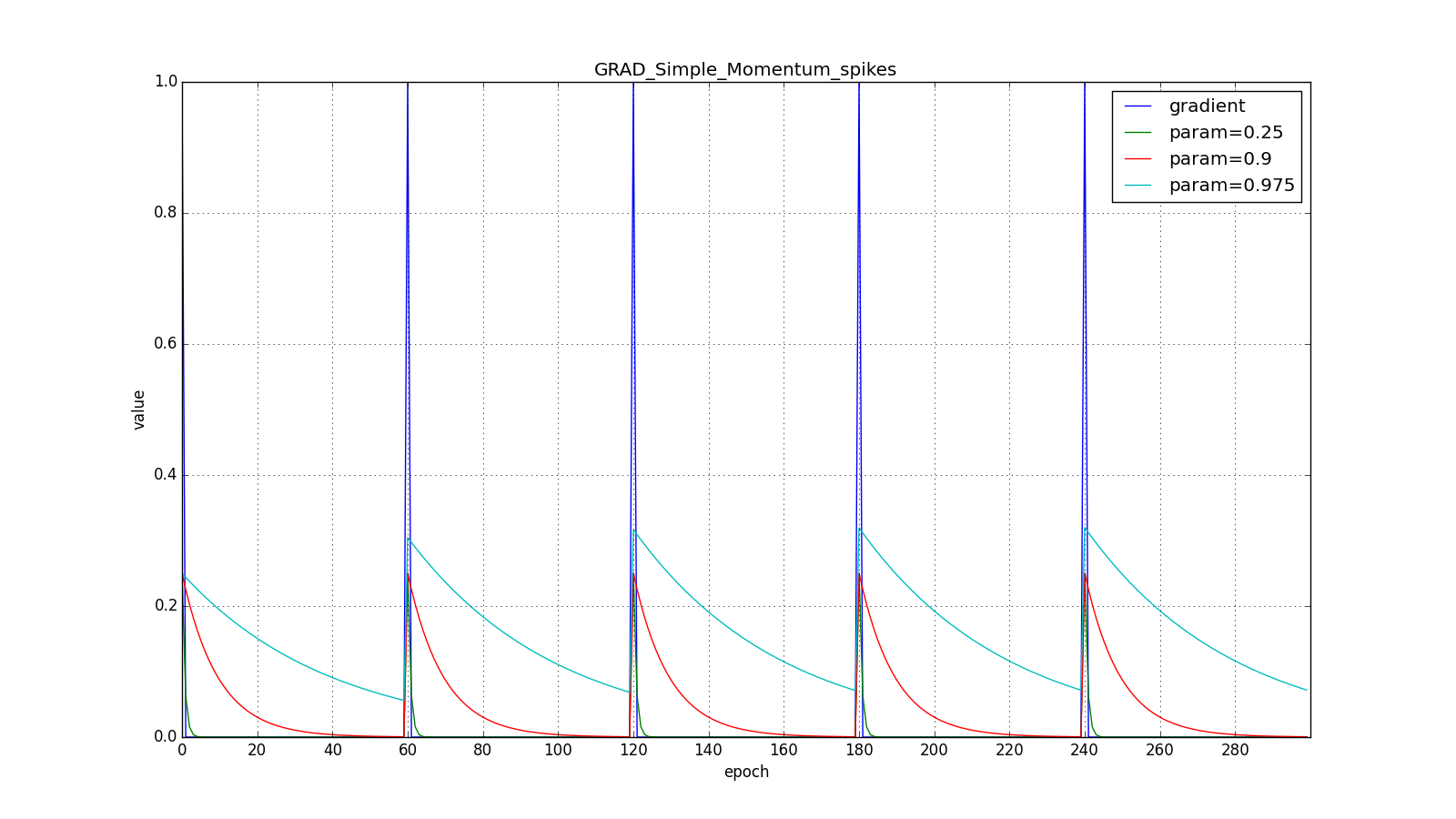
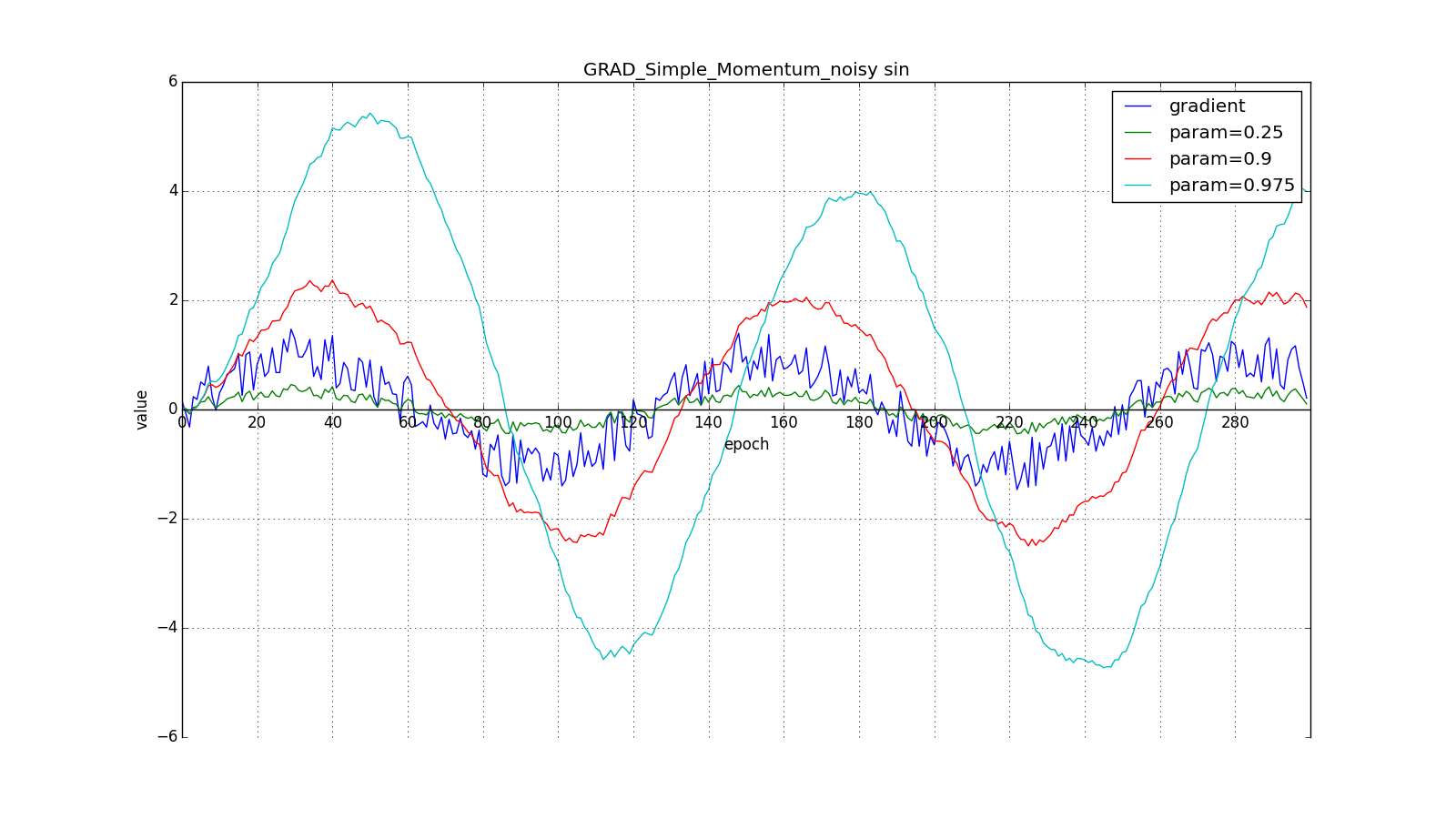
Заметьте, что накопленное в $\inline v_t$ значение может очень сильно превышать значение каждого из $\inline \eta \nabla_\theta J( \theta)$ . Простое накопление импульса уже даёт хороший результат, но Нестеров идёт дальше и применяет хорошо известную в вычислительной математике идею: заглядывание вперёд по вектору обновления. Раз уж мы всё равно собираемся сместиться на $\inline \gamma v_{t-1}$ , то давайте посчитаем градиент функции потерь не в точке $\inline \theta$ , а в $\inline \theta - \gamma v_{t-1}$ . Отсюда:

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1} )$

$\theta = \theta - v_t$

Такое изменение позволяет быстрее «катиться», если в стороне, куда мы направляемся, производная увеличивается, и медленнее, если наоборот. Особенно этого хорошо видно для $\inline \gamma=0.975$ для графика с синусом.

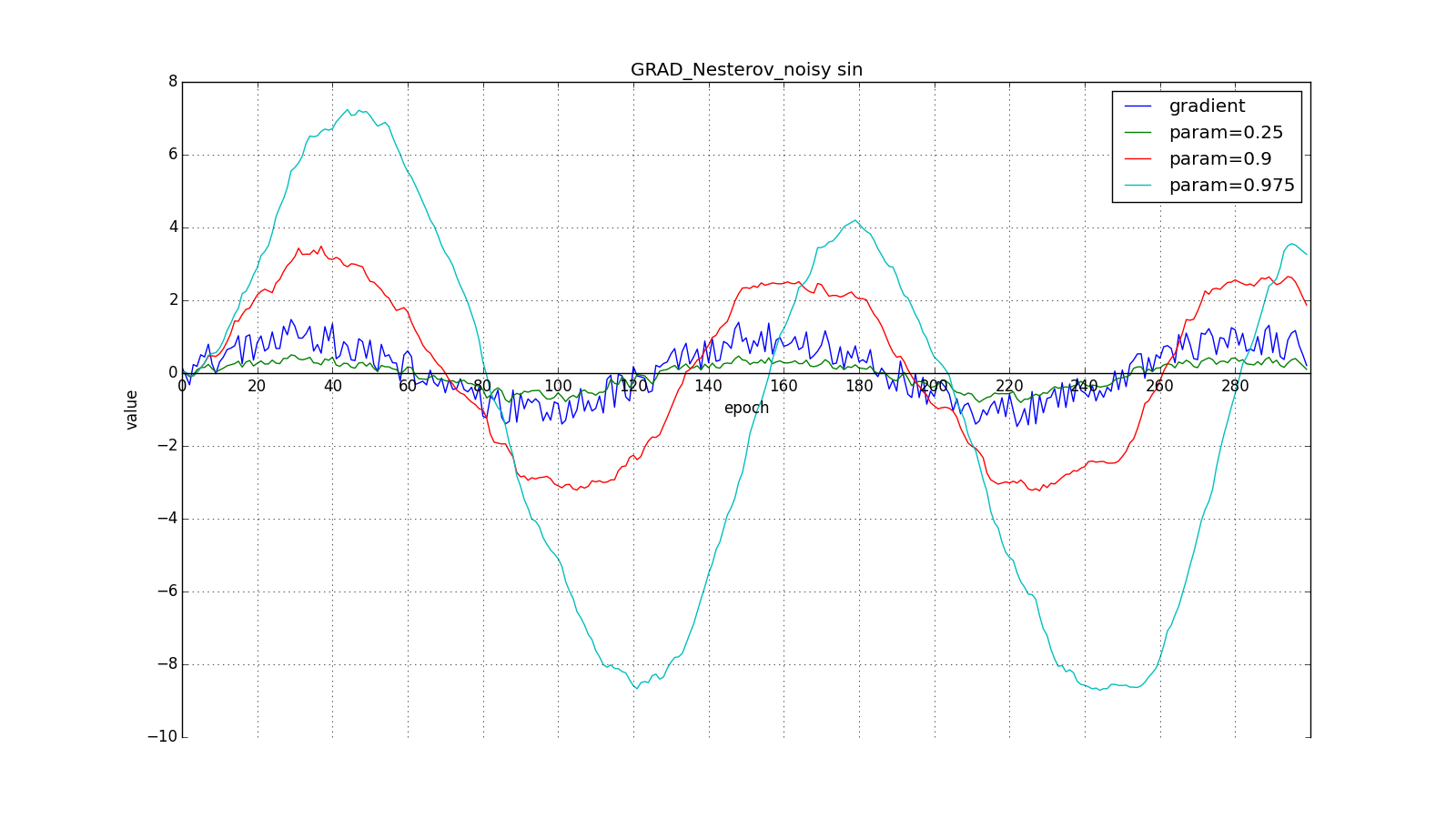
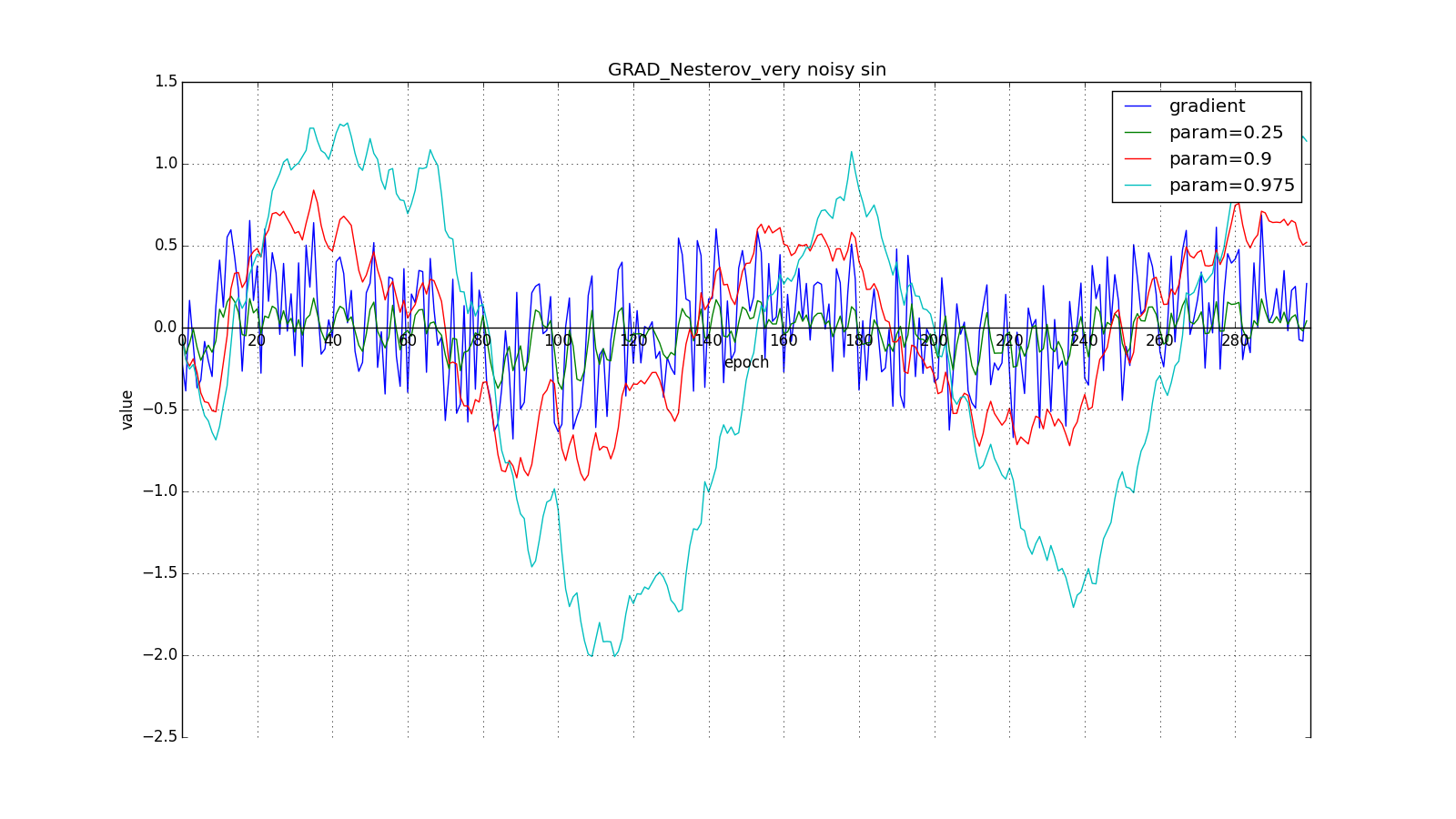
Заглядывание вперёд может сыграть с нами злую шутку, если установлены слишком большие $\inline \gamma$ и $\inline \eta$ : мы заглядываем настолько далеко, что промахиваемся мимо областей с противоположным знаком градиента:

Впрочем, иногда такое поведение может оказаться желательным. Ещё раз обращу ваше внимание на идею — заглядывание вперёд — а не на исполнение. Метод Нестерова (6) — самый очевидный вариант, но не единственный. Например, можно воспользоваться ещё одним приёмом из вычислительной математики — стабилизацией градиента усреднением по нескольким точкам вдоль прямой, по которой мы двигаемся. Скажем, так:

$v_t = \gamma v_{t-1} + \frac{\eta}{3} \big( \nabla_\theta J( \theta - \frac{\gamma v_{t-1}}{3} ) + \nabla_\theta J( \theta - \frac{2\gamma v_{t-1}}{3} ) + \nabla_\theta J( \theta - \gamma v_{t-1} ) \big)$

Или так:

$v_t = \gamma v_{t-1} + \frac{\eta}{7} \big( \nabla_\theta J( \theta - \frac{\gamma v_{t-1}}{2} ) + 2\nabla_\theta J( \theta - \frac{3\gamma v_{t-1}}{4} ) + 4\nabla_\theta J( \theta - \gamma v_{t-1} ) \big)$

Такой приём может помочь в случае шумных целевых функций.

Мы не будем манипулировать аргументом целевой функции в последующих методах (хотя вам, разумеется, никто не мешает поэкспериментировать). Далее для краткости

$g_t \equiv \nabla_\theta J( \theta_t )$

Adagrad

Как работают методы с накоплением импульса представляют себе многие. Перейдём же к более интересным алгоритмам оптимизации. Начём со сравнительно простого Adagrad — adaptive gradient.

Некоторые признаки могут быть крайне информативными, но встречаться редко. Экзотическая высокооплачиваемая профессия, причудливое слово в спам-базе — они запросто потонут в шуме всех остальных обновлений. Речь идёт не только о редко встречающихся входных параметрах. Скажем, вам вполне могут встретиться редкие графические узоры, которые и в признак-то превращаются только после прохождения через несколько слоёв свёрточной сети. Хорошо бы уметь обновлять параметры с оглядкой на то, насколько типичный признак они фиксируют. Достичь этого несложно: давайте будем хранить для каждого параметра сети сумму квадратов его обновлений. Она будет выступать в качестве прокси для типичности: если параметр принадлежит цепочке часто активирующихся нейронов, его постоянно дёргают туда-сюда, а значит сумма быстро накапливается. Перепишем формулу обновления вот так:

$G_{t} = G_{t} + g_{t}^2$

$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{G_{t} + \epsilon}} g_{t}$

Где $\inline G_{t}$ — сумма квадратов обновлений, а $\inline \epsilon$ — сглаживающий параметр, необходимый, чтобы избежать деления на 0. У часто обновлявшегося в прошлом параметра большая $\inline G_t$ , значит большой знаменатель в (12). Параметр изменившийся всего раз или два обновится в полную силу. $\inline \epsilon$ берут порядка $\inline 10^{-6}$ или $\inline 10^{-8}$ для совсем агрессивного обновления, но, как видно из графиков, это играет роль только в начале, ближе к середине обучение начинает перевешивать $\inline G_t$ :

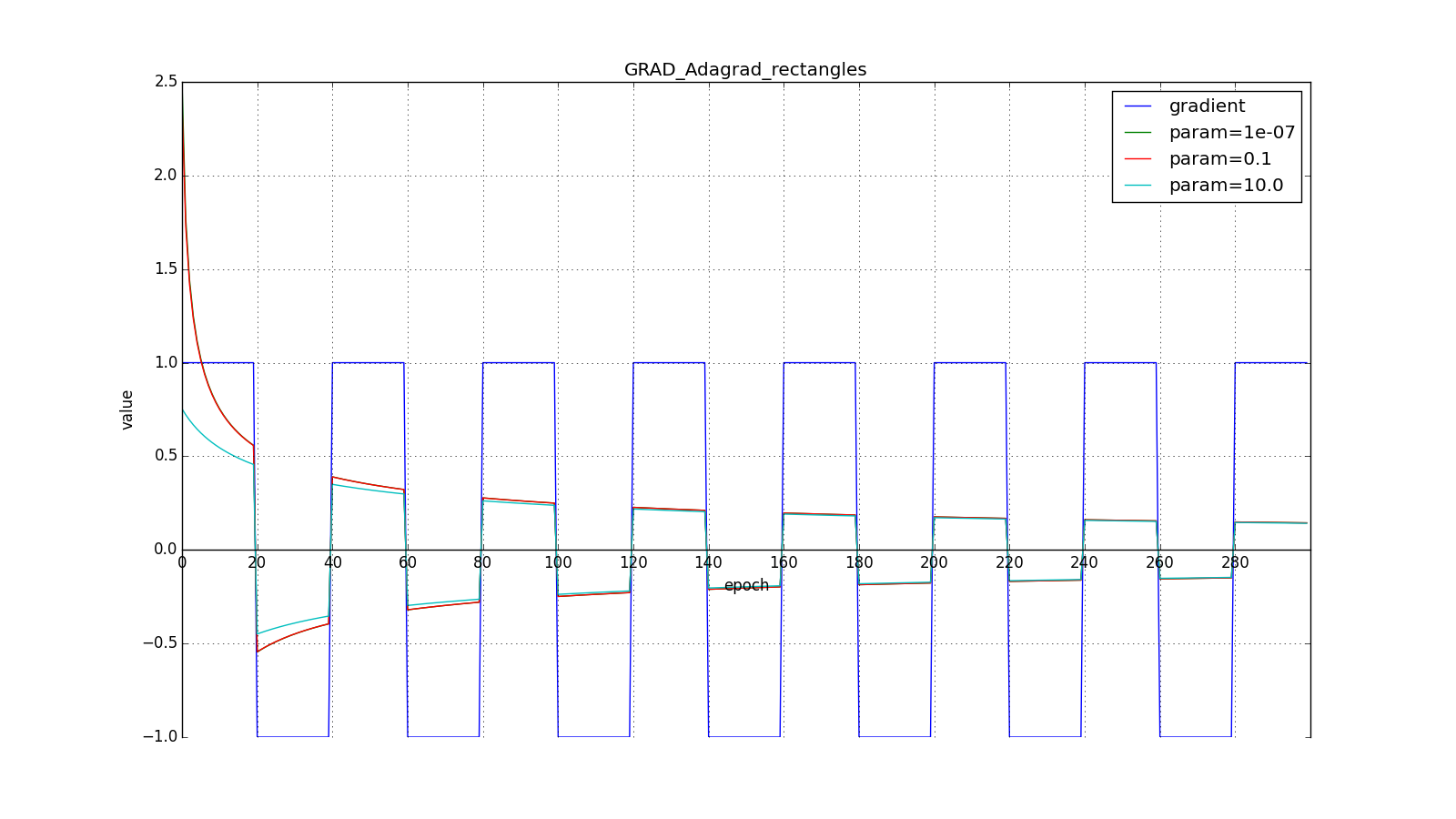
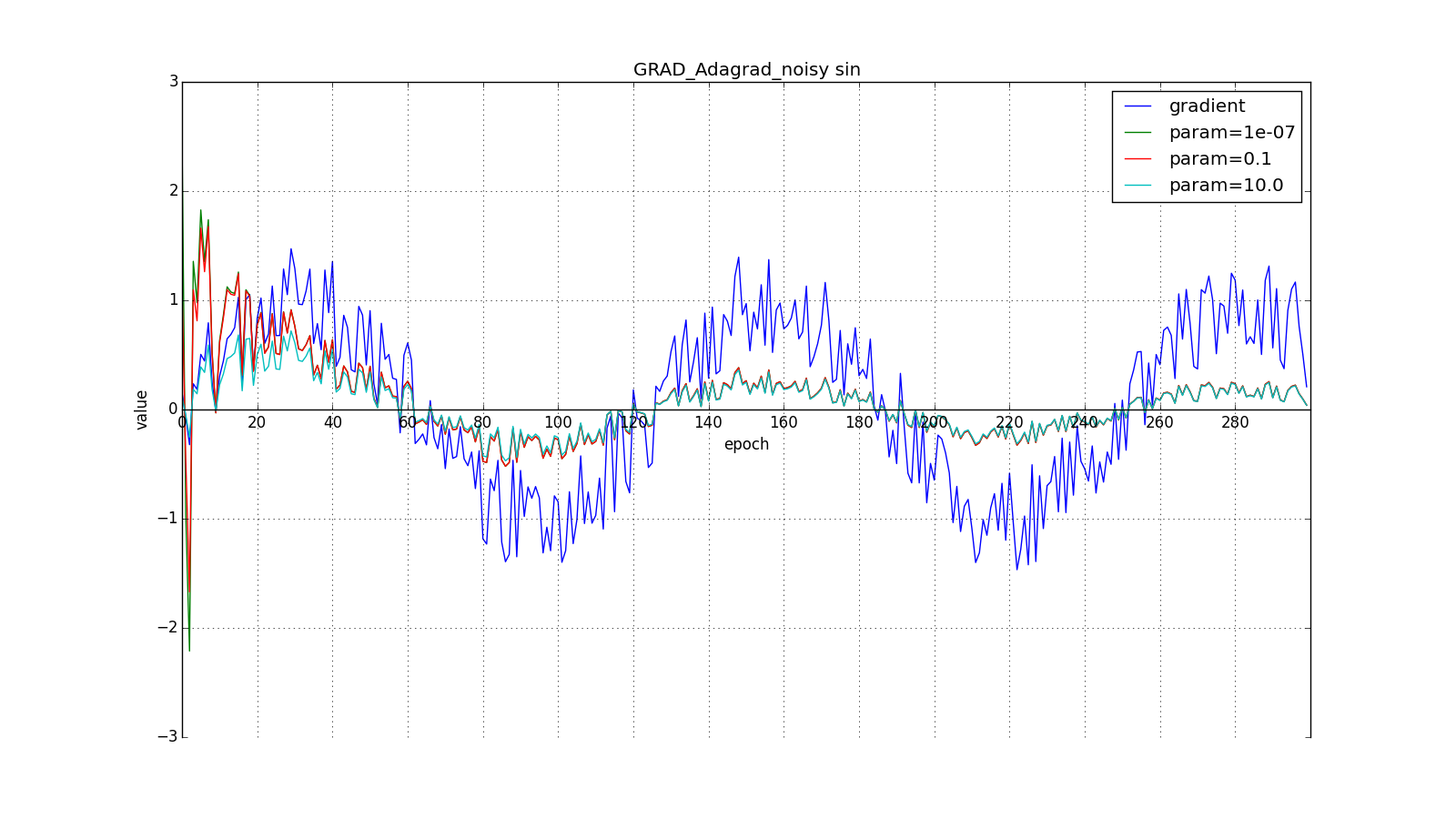
Итак, идея Adagrad в том, чтобы использовать что-нибудь, что бы уменьшало обновления для элементов, которые мы и так часто обновляем. Никто нас не заставляет использовать конкретно эту формулу, поэтому Adagrad иногда называют семейством алгоритмов. Скажем, мы можем убрать корень или накапливать не квадраты обновлений, а их модули, или вовсе заменить множитель на что-нибудь вроде $\inline e^{-G_{t}}$ .

(Другое дело, что это требует экспериментов. Если убрать корень, обновления начнут уменьшаться слишком быстро, и алгоритм ухудшится)

Ещё одно достоинство Adagrad — отсутствие необходимости точно подбирать скорость обучения. Достаточно выставить её в меру большой, чтобы обеспечить хороший запас, но не такой громадной, чтобы алгроритм расходился. По сути мы автоматически получаем затухание скорости обучения (learning rate decay).

RMSProp и Adadelta

Недостаток Adagrad в том, что $\inline G_{t}$ в (12) может увеличиваться сколько угодно, что через некоторое время приводит к слишком маленьким обновлениям и параличу алгоритма. RMSProp и Adadelta призваны исправить этот недостаток.

Модифицируем идею Adagrad: мы всё так же собираемся обновлять меньше веса, которые слишком часто обновляются, но вместо полной суммы обновлений, будем использовать усреднённый по истории квадрат градиента. Снова используем экспоненциально затухающее бегущее среднее
(4). Пусть $\inline E[g^2]_t$ — бегущее среднее в момент $\inline t$

$E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t$

тогда вместо (12) получим

$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}$

Знаменатель есть корень из среднего квадратов градиентов, отсюда RMSProp — root mean square propagation

$RMS[g]_t = \sqrt{E[g^2]_t + \epsilon}$

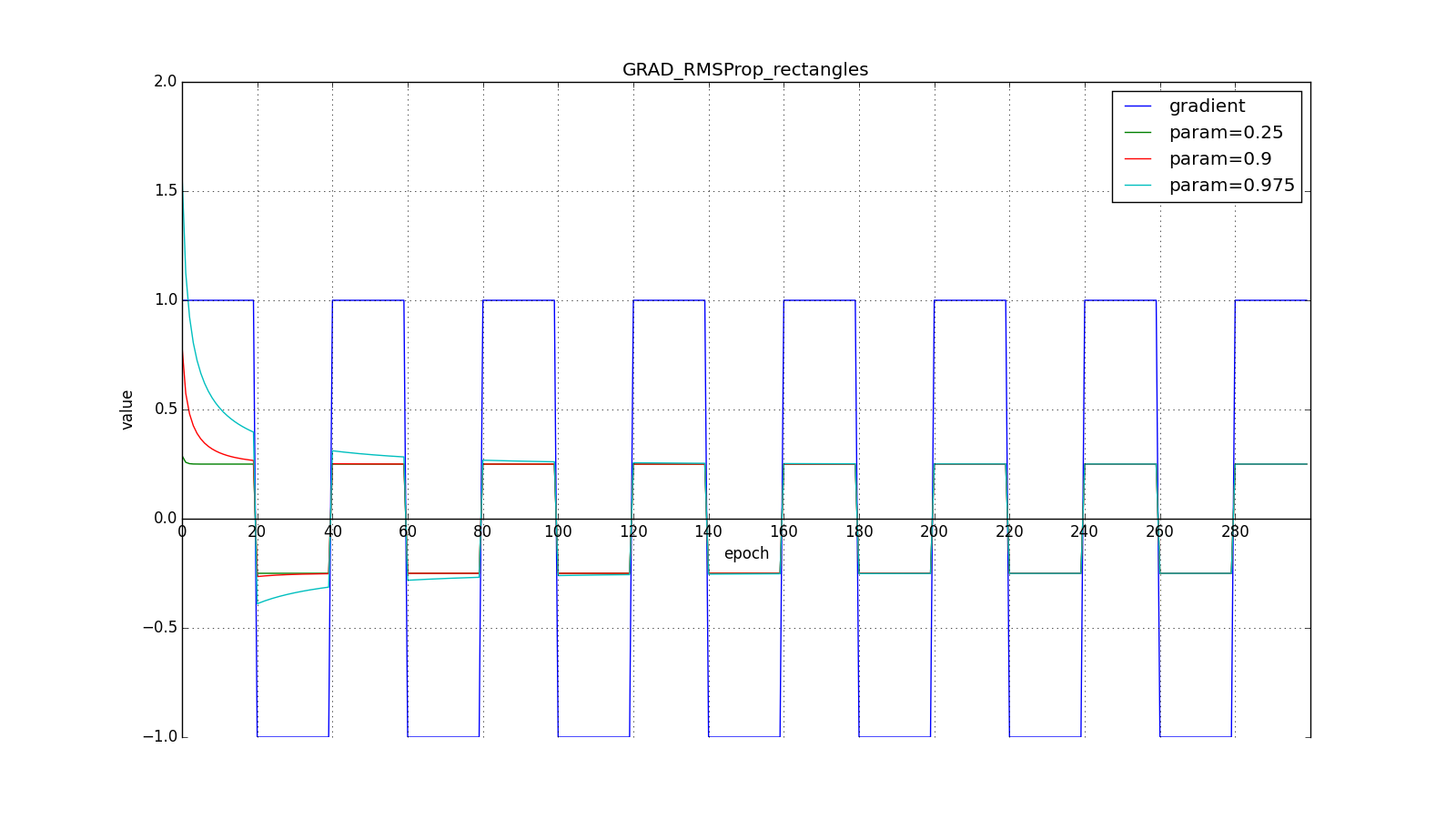
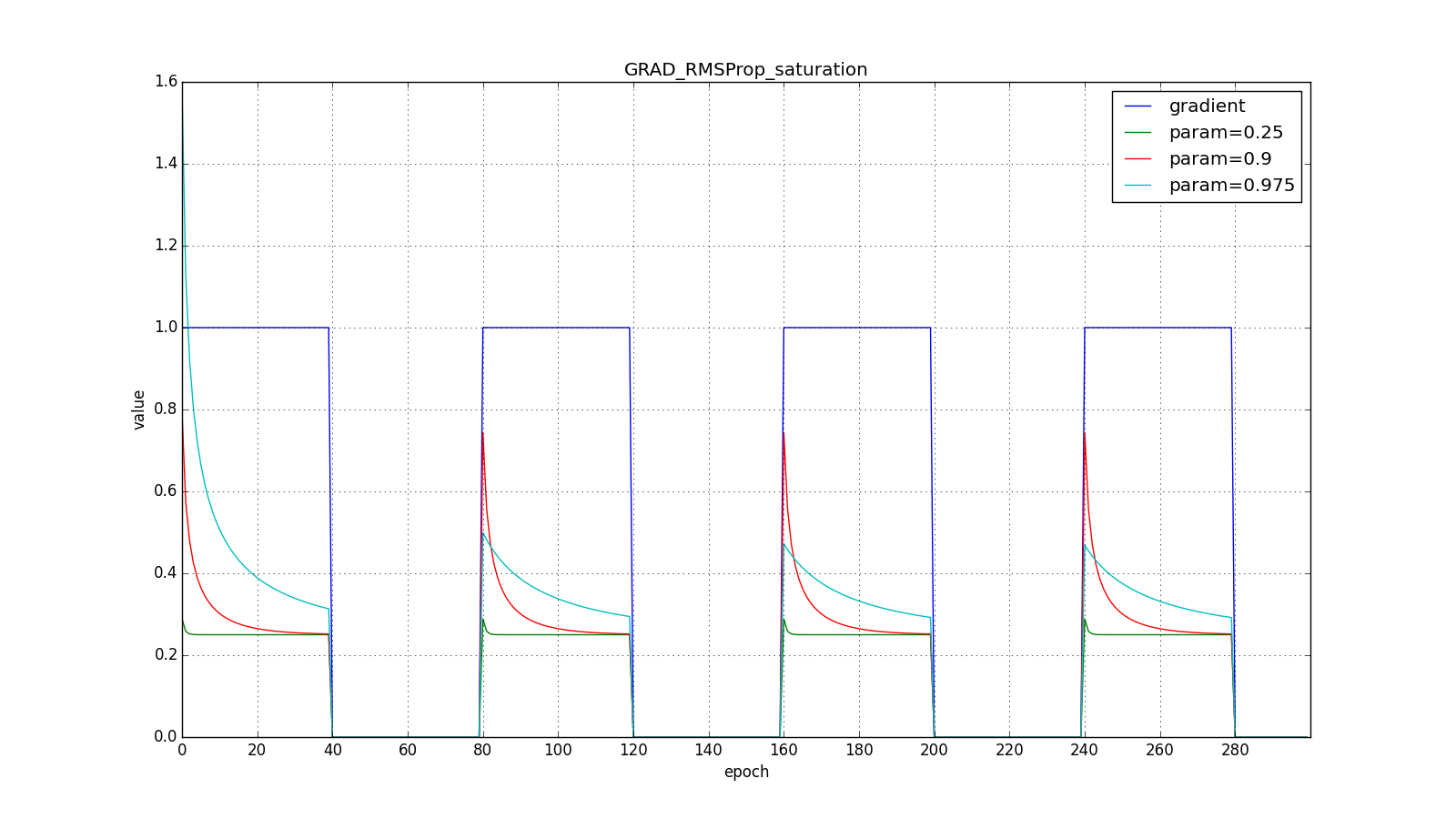
Обратите внимание, как восстанавливается скорость обновления на графике с длинными зубцами для разных $\inline \gamma$ . Также сравните графики с меандром для Adagrad и RMSProp: в первом случае обновления уменьшаются до нуля, а во втором — выходят на определённый уровень.

Вот и весь RMSProp. Adadelta от него отличается тем, что мы добавляем в числитель (14) стабилизирующий член пропорциональный $\inline RMS$ от $\inline \Delta\theta_t$ . На шаге $\inline t$ мы ещё не знаем значение $\inline RMS[\Delta \theta]_{t}$ , поэтому обновление параметров происходит в три этапа, а не в два: сначала накапливаем квадрат градиента, затем обновляем $\inline \theta$ , после чего обновляем $\inline RMS[\Delta \theta]$ .

$\Delta \theta = -\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}}g_{t}$

$\theta_{t+1} = \theta_{t} - \frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}}g_{t}$

$E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t$

$RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon}$

Такое изменение сделано из соображений, что размерности $\inline \theta$ и $\inline \Delta \theta$ должны совпадать. Заметьте, что learning rate не имеет размерности, а значит во всех алгоритмах до этого мы складывали размерную величину с безразмерной. Физики в этом месте ужаснутся, а мы пожмём плечами: работает же.

Заметим, что нам нужен ненулевой $\inline RMS[\Delta \theta]_{-1}$ для первого шага, иначе все последующие $\inline \Delta \theta$ , а значит и $\inline RMS[\Delta \theta]_{t}$ будут равны нулю. Но эту проблему мы решили ещё раньше, добавив в $\inline RMS$ $\inline \epsilon$ . Другое дело, что без явного большого $\inline RMS[\Delta \theta]_{-1}$ мы получим поведение, противоположное Adagrad и RMSProp: мы будем сильнее (до некоторого предела) обновлять веса, которые используются чаще. Ведь теперь чтобы $\inline \Delta \theta$ стал значимым, параметр должен накопить большую сумму в числителе дроби.

Вот графики для нулевого начального $\inline RMS[\Delta \theta]$ :

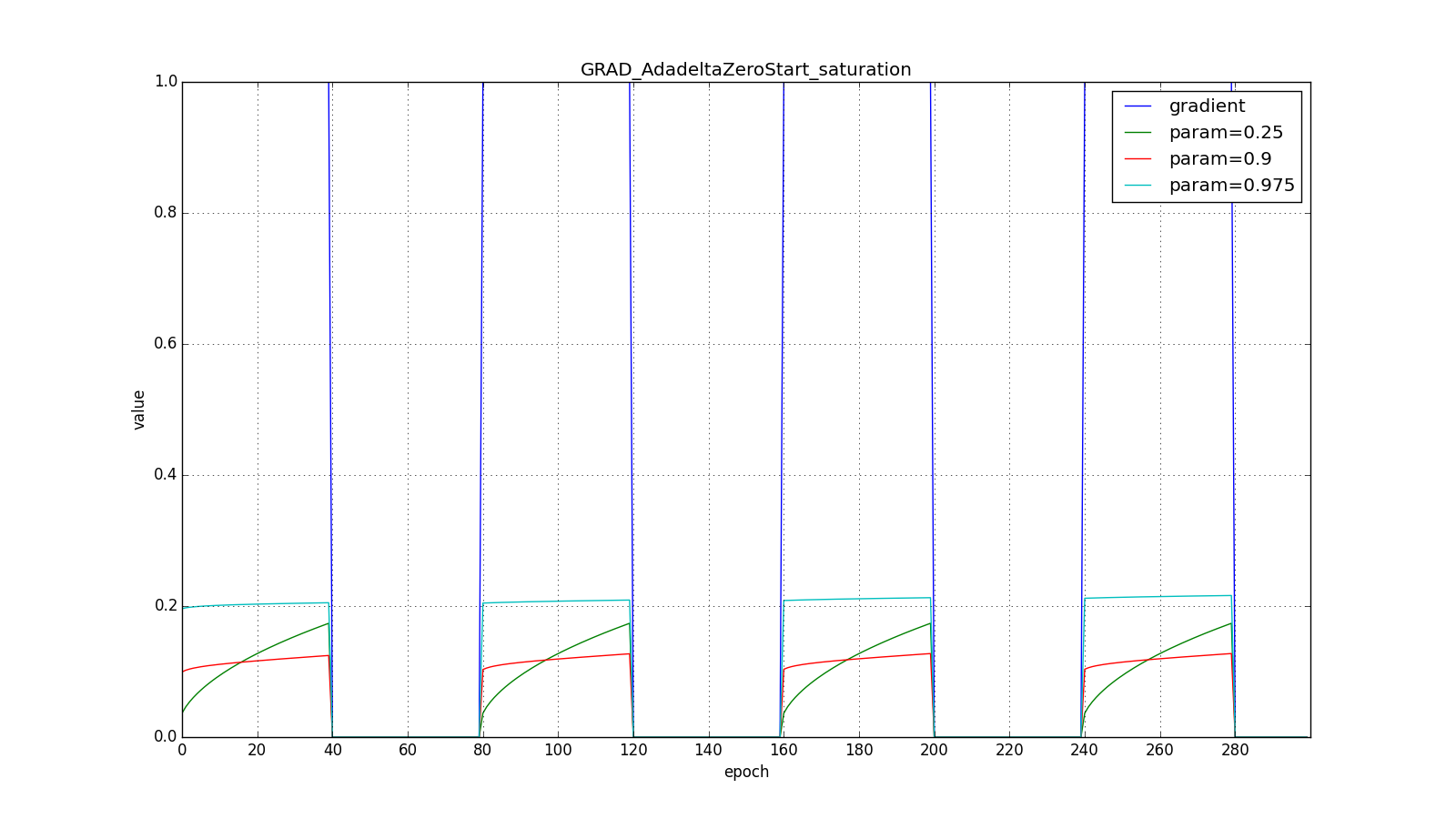
А вот для большого:

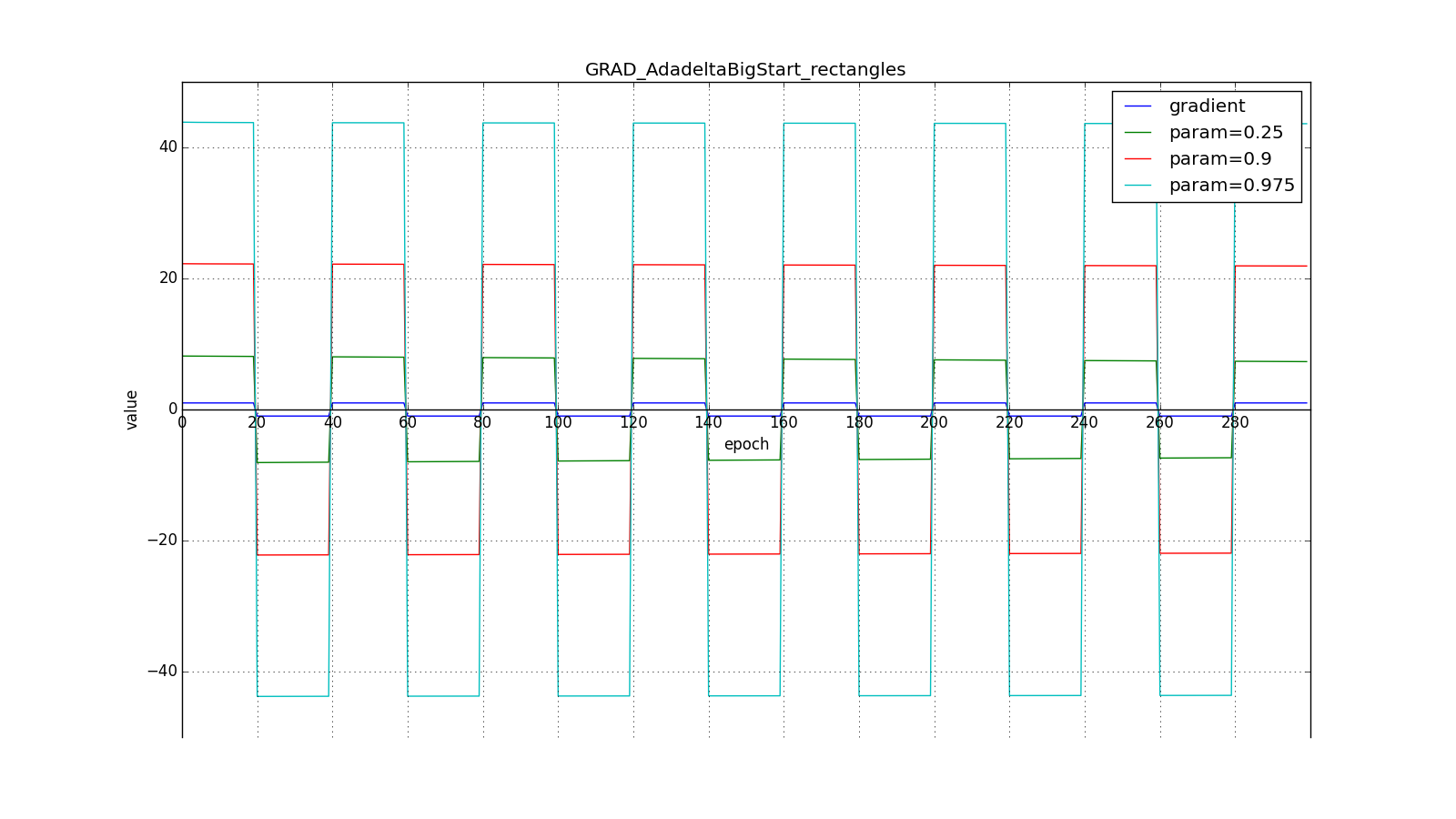
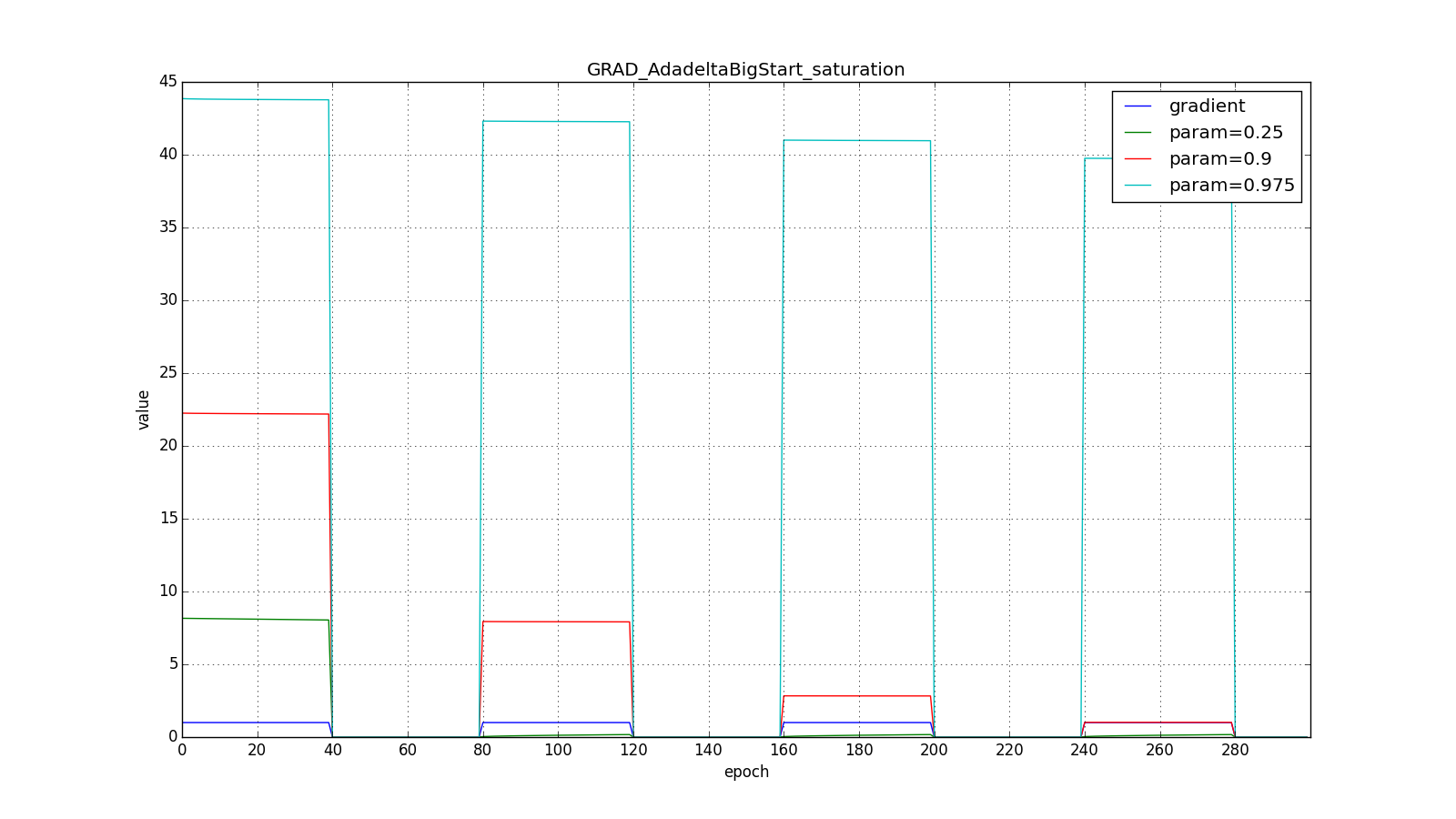
Впрочем, похоже, авторы алгоритма и добивались такого эффекта. Для RMSProp и Adadelta, как и для Adagrad не нужно очень точно подбирать скорость обучения — достаточно прикидочного значения. Обычно советуют начать подгон $\inline \eta$ c $\inline 0.1 - 1$ , a $\inline \gamma$ так и оставить $\inline 0.9$ . Чем ближе $\inline \gamma$ к $\inline 1$ , тем дольше RMSProp и Adadelta с большим $\inline RMS[\Delta \theta]_{-1}$ будут сильно обновлять мало используемые веса. Если же $\inline \gamma \approx 1$ и $\inline RMS[\Delta \theta]_{-1} = 0$ , то Adadelta будет долго «с недоверием» относиться к редко используемым весам. Последнее может привести к параличу алгоритма, а может вызвать намеренно «жадное» поведение, когда алгоритм сначала обновляет нейроны, кодирующие самые лучшие признаки.

Adam

Adam — adaptive moment estimation, ещё один оптимизационный алгоритм. Он сочетает в себе и идею накопления движения и идею более слабого обновления весов для типичных признаков. Снова вспомним (4):

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

От Нестерова Adam отличается тем, что мы накапливаем не $\inline \Delta \theta$ , а значения градиента, хотя это чисто косметическое изменение, см. (23). Кроме того, мы хотим знать, как часто градиент изменяется. Авторы алгоритма предложили для этого оценивать ещё и среднюю нецентрированную дисперсию:

$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

Легко заметить, что это уже знакомый нам $\inline E[g^2]_t$ , так что по сути тут нет отличий от RMSProp.

Важное отличие состоит в начальной калибровке $\inline m_t$ и $\inline v_t$ : они страдают от той же проблемы, что и $\inline E[g^2]_t$ в RMSProp: если задать нулевое начальное значение, то они будут долго накапливаться, особенно при большом окне накопления ( $\inline 0 \ll \beta_1 < 1$ , $\inline 0 \ll \beta_2 < 1$ ), а какие-то изначальные значения — это ещё два гиперпараметра. Никто не хочет ещё два гиперпараметра, так что мы искусственно увеличиваем $\inline m_t$ и $\inline v_t$ на первых шагах (примерно $\inline 0 < t < 10$ для $\inline m_t$ и $\inline 0 < t < 1000$ для $\inline v_t$ )

$\hat{m}_t = \frac{m_t}{1 - \beta^t_1}, \; \hat{v}_t = \frac{v_t}{1 - \beta^t_2}$

В итоге, правило обновления:

$\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \hat{m}_t$

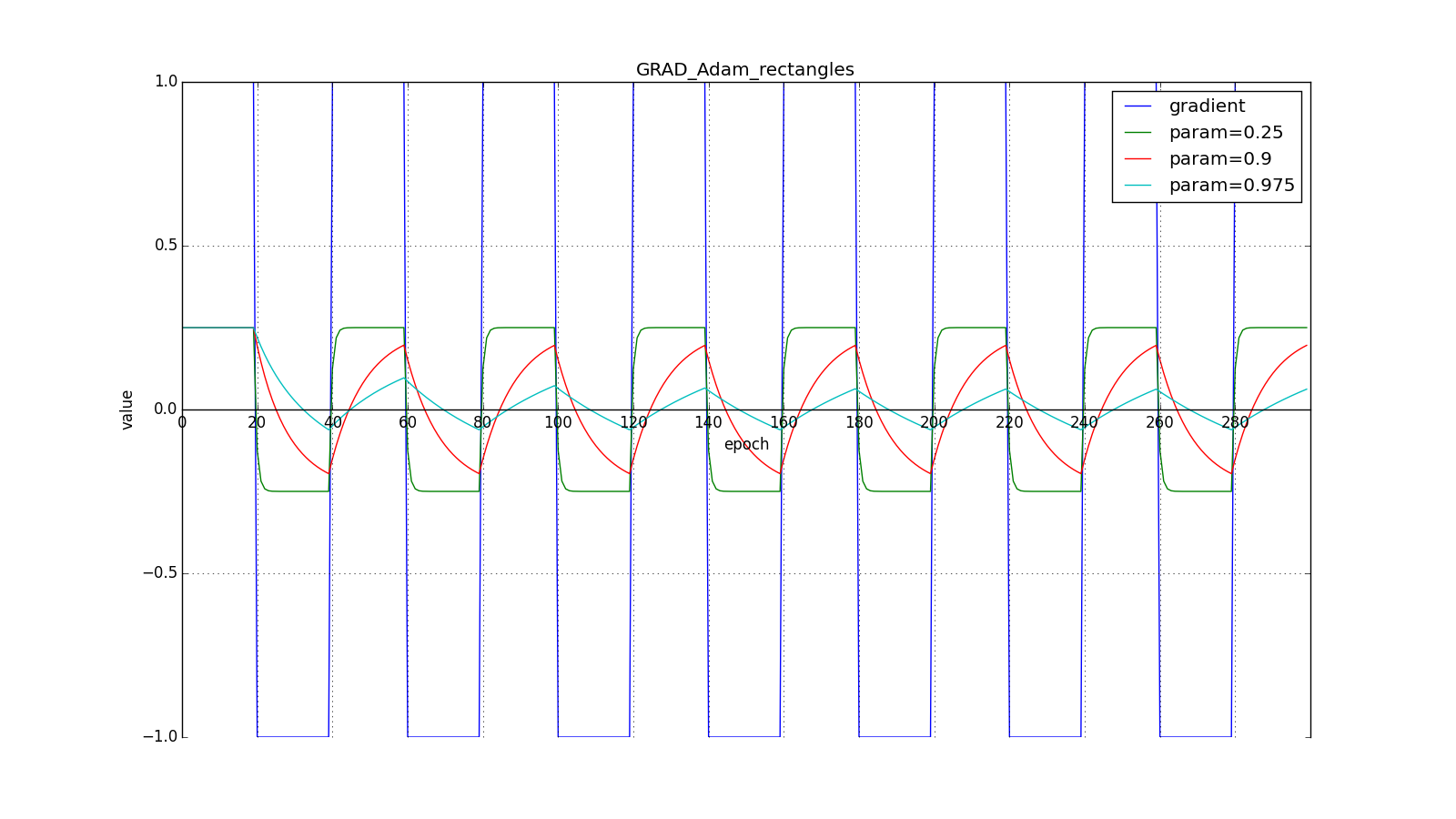
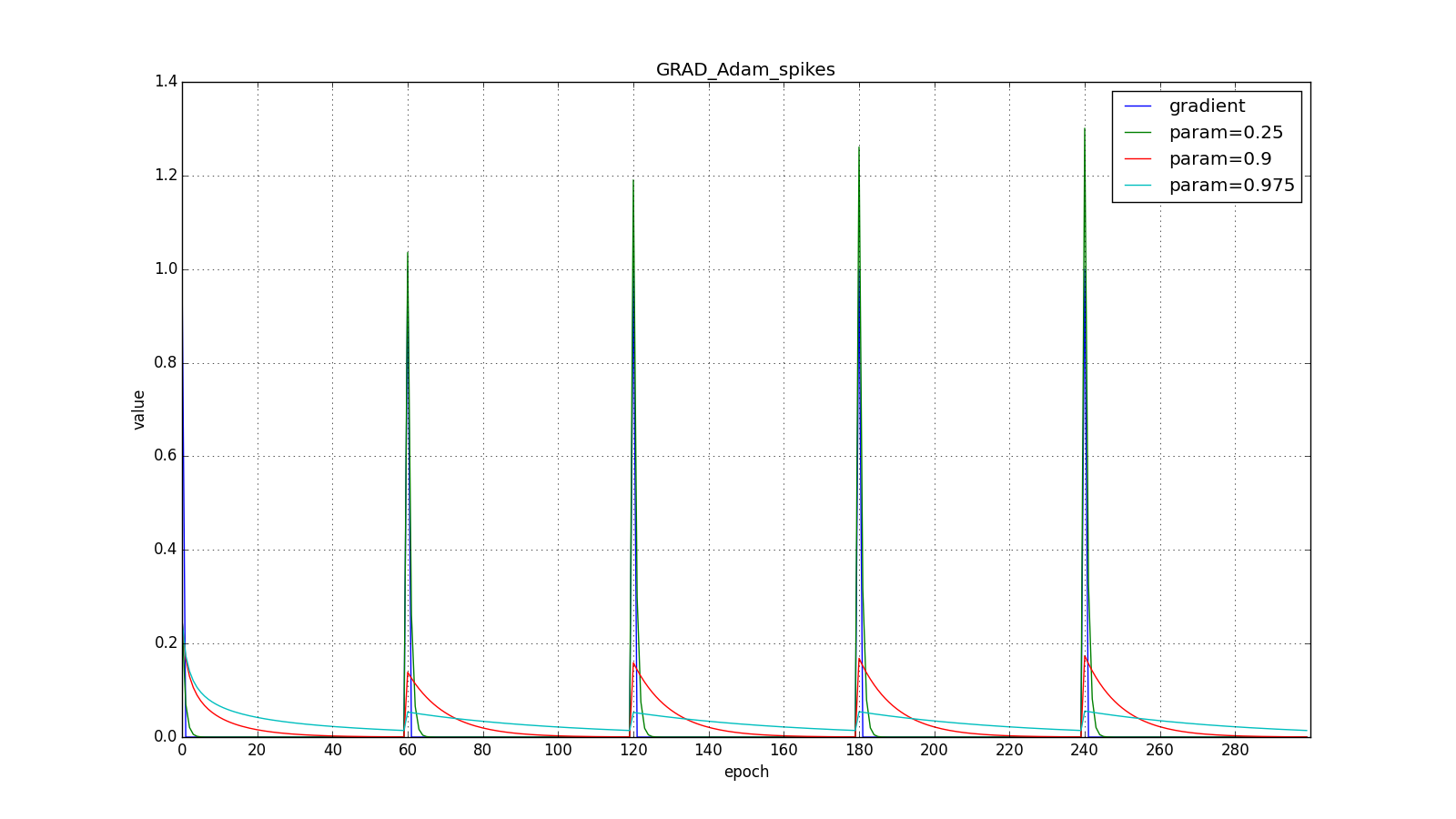
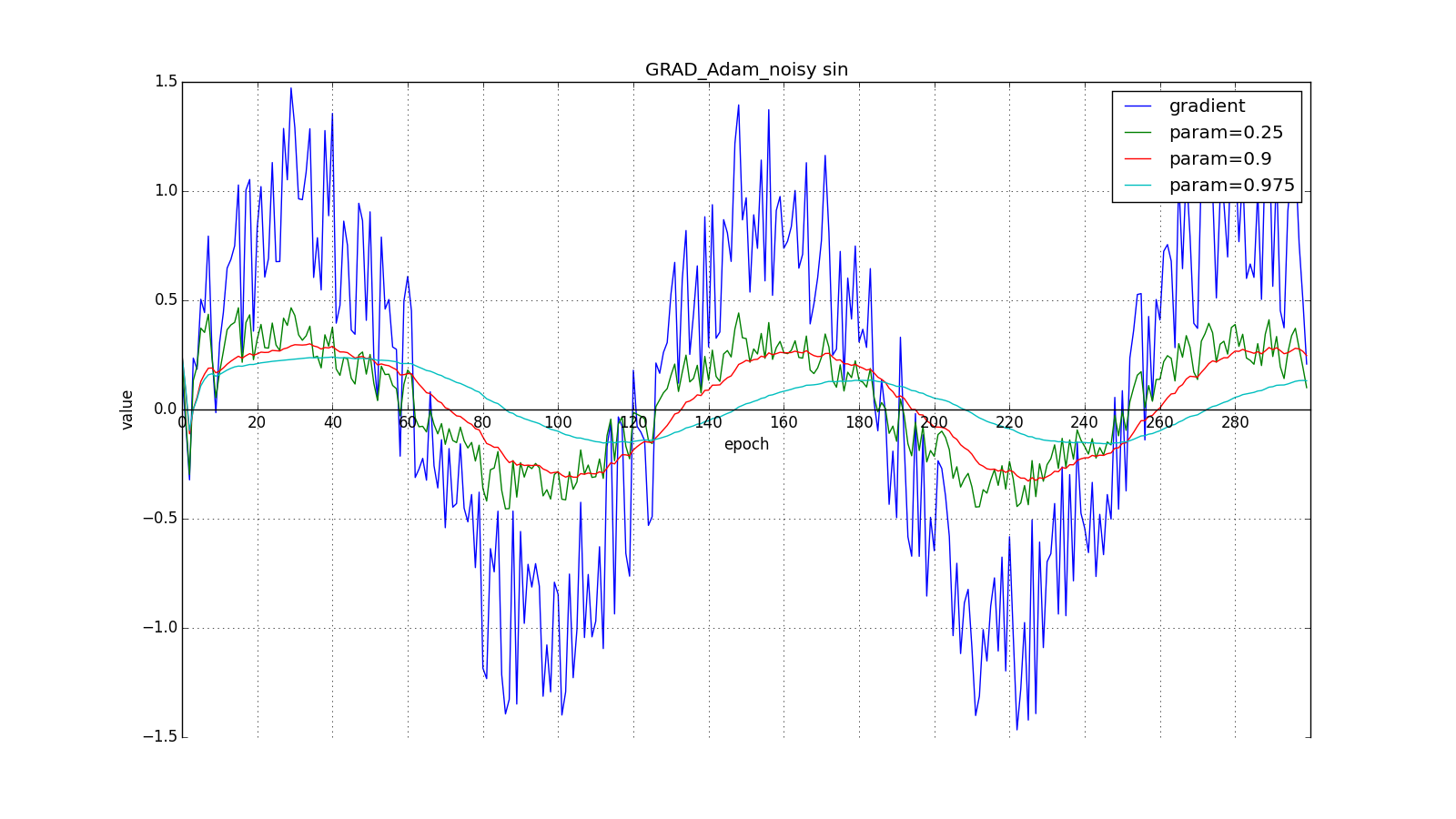
Здесь следует внимательно посмотреть на то, как быстро синхронизировались значения обновлений на первых зубцах графиков с прямоугольниками и на гладкость кривой обновлений на графике с синусом — её мы получили «бесплатно». При рекомендуемом параметре $\inline \beta_1$ на графике с шипами видно, что резкие всплески градиента не вызывает мгновенного отклика в накопленном значении, поэтому хорошо настроенному Adam не нужен gradient clipping.

Авторы алгоритма выводят (22), разворачивая рекурсивные формулы (20) и (21). Например, для $\inline v_t$ :

$E[v_t] &= E\Bigg[ (1 - \beta_2) \sum_{i=1}^{t}{\beta_2^{t-i}g_i^2} \Bigg]$

$= E[g_t^2] (1 - \beta_2) \sum_{i=1}^{t}\beta_2^{t-i} + \zeta$

$= E[g_t^2] (1 - \beta_2) \frac{1 - \beta_2^t}{1 - \beta_2} + \zeta$

$= E[g_t^2](1 - \beta_2^t) + \zeta$

Слагаемое $\inline \zeta$ близко к $\inline 0$ при стационарном распределении $\inline p(g)$ , что неправда в практически интересующих нас случаях. но мы всё равно переносим скобку с $\inline \beta_2^t$ влево. Неформально, можно представить что при $\inline t=0$ у нас бесконечная история одинаковых обновлений:

$\hat{v}_1 = v_{1} + \beta_2 v_{1} + \beta_2^2 v_{1} + \ldots = \frac{v_{1}}{1 - \beta_2}$

Когда же мы получаем более близкое к правильному значение $\inline v$ , мы заставляем «виртуальную» часть ряда затухать быстрее:

$\hat{v}_2 = v_{2} + \beta_2^2 v_{2} + \beta_2^4 v_{2} + \ldots = \frac{v_{2}}{1 - \beta_2^2}$

Авторы Adam предлагают в качестве значений по умолчанию $\inline \beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}$ и утверждают, что алгоритм выступает лучше или примерно так же, как и все предыдущие алгоритмы на широком наборе датасетов за счёт начальной калибровки. Заметьте, что опять-таки, уравнения (22) не высечены в камне. У нас есть некоторое теоретическое обоснование, почему затухание должно выглядеть именно так, но никто не запрещает поэкспериментировать с формулами калибровки. На мой взгляд, здесь просто напрашивается применить заглядывание вперёд, как в методе Нестерова.

Adamax

Adamax как раз и есть такой эксперимент, предложенный в той же статье. Вместо дисперсии в (21) можно считать инерционный момент распределения градиентов произвольной степени $\inline p$ . Это может привести к нестабильности к вычислениям. Однако случай $\inline p$ , стремящейся к бесконечности, работает на удивление хорошо.

$v_t = \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p$

Заметьте, что вместо $\inline \beta_2$ используется подходящий по размерности $\inline \beta_2^p$ . Кроме того, обратите внимание, чтобы использовать в формулах Adam значение, полученное в (27), требуется извлечь из него корень: $\inline u_t = v_t^{\frac{1}{p}}$ . Выведем решающее правило взамен (21), взяв $\inline p \rightarrow \infty$ , развернув под корнем $\inline v_t$ при помощи (27):

$u_t = \lim_{p \rightarrow \infty}{ v_t^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big[ \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p \Big]^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big[ (1 - \beta_2^p) \sum_{i=1}^{t}\beta_2^{p(t-i)} |g_i|^{p} \Big]^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ (1 - \beta_2^p)^{\frac{1}{p}} \Big( \sum_{i=1}^{t}\beta_2^{p(t-i)}|g_i|^{p} \Big)^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big( \sum_{i=1}^{t}\beta_2^{p(t-i)}|g_i|^{p} \Big)^{\frac{1}{p}} }$

$= max(\beta_2^{t-1} |g_1|, \beta_2^{t-2} |g_2|, \ldots , \beta_2|g_{t-1}|, |g_t| )$

Так получилось потому что при $\inline p \rightarrow \infty$ в сумме в (28) будет доминировать наибольший член. Неформально, можно интуитивно понять, почему так происходит, взяв простую сумму и большую $\inline p$ : $\inline \sqrt[100]{10^{100} + 9^{100}} = 10\sqrt[100]{1 + \frac{9}{10}^{100}} = 10\sqrt[10]{1.00002} \approx 10$ . Совсем не страшно.

Остальные шаги алгоритма такие же как и в Adam.

Эксперименты

Теперь давайте посмотрим на разные алгоритмы в деле. Чтобы было нагляднее, посмотрим на траекторию алгоритмов в задаче нахождения минимума функции двух переменных. Напомню, что обучение нейронной сети — это по сути то же самое, но переменных там значительно больше двух и вместо явно заданной функции у нас есть только набор точек, по котором мы хотим эту функцию построить. В нашем же случае функция потерь и есть целевая функция, по которой двигаются оптимизаторы. Конечно, на такой простой задаче невозможно почувствовать всю силу продвинутых алгоритмов, зато интуитивно понятно.

Для начала посмотрим на ускоренный градиент Нестерова с разными значениями $\inline \gamma$ . Поняв, почему выглядят именно так, проще понять и поведение всех остальных алгоритмов с накоплением импульса, включая Adam и Adamax.

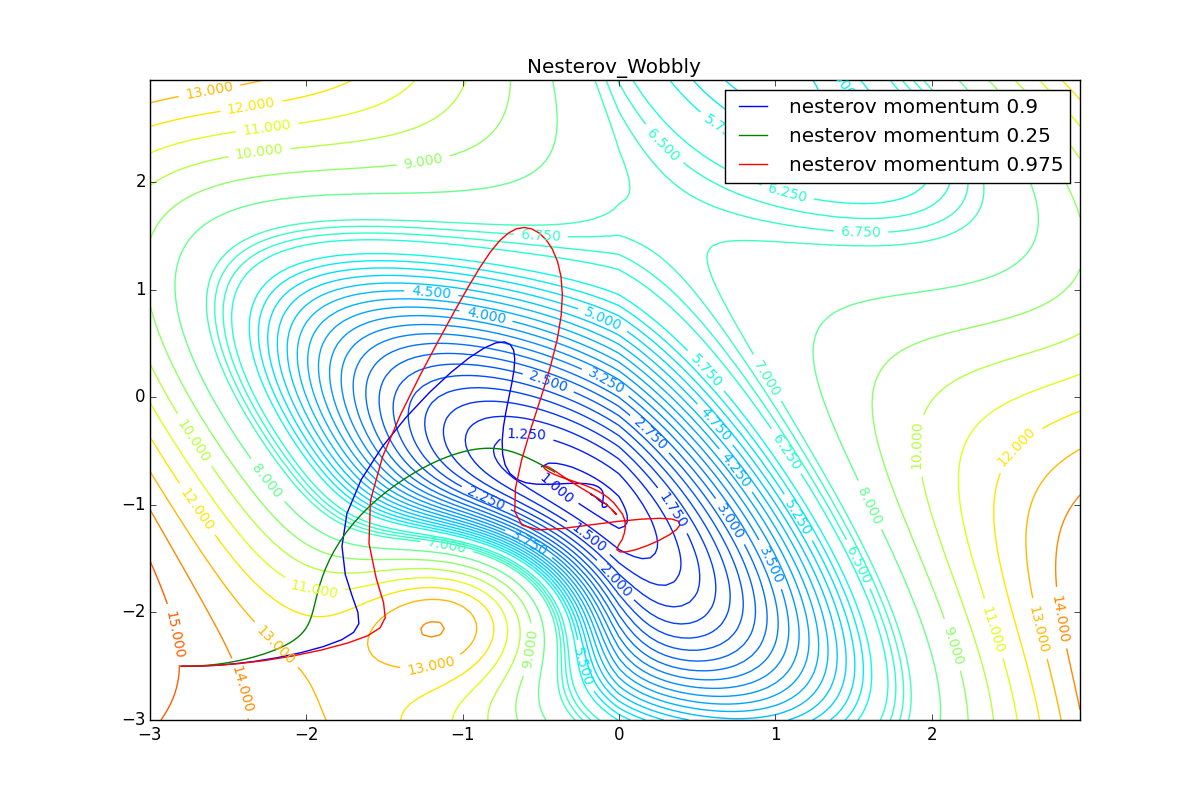
Все траектории оканчиваются в одном и том же бассейне, но делают они это по-разному. С маленьким $\inline \gamma$ алгоритм становится похож на обычный SGD, на каждом шаге спуск идёт в сторону убывающего градиента. Со слишком большим $\inline \gamma$ , начинает сильно влиять предыстория изменений, и траектория может сильно «гулять». Иногда это хорошо: чем больше накопленный импульс, тем проще вырваться из впадин локальных минимумов на пути.

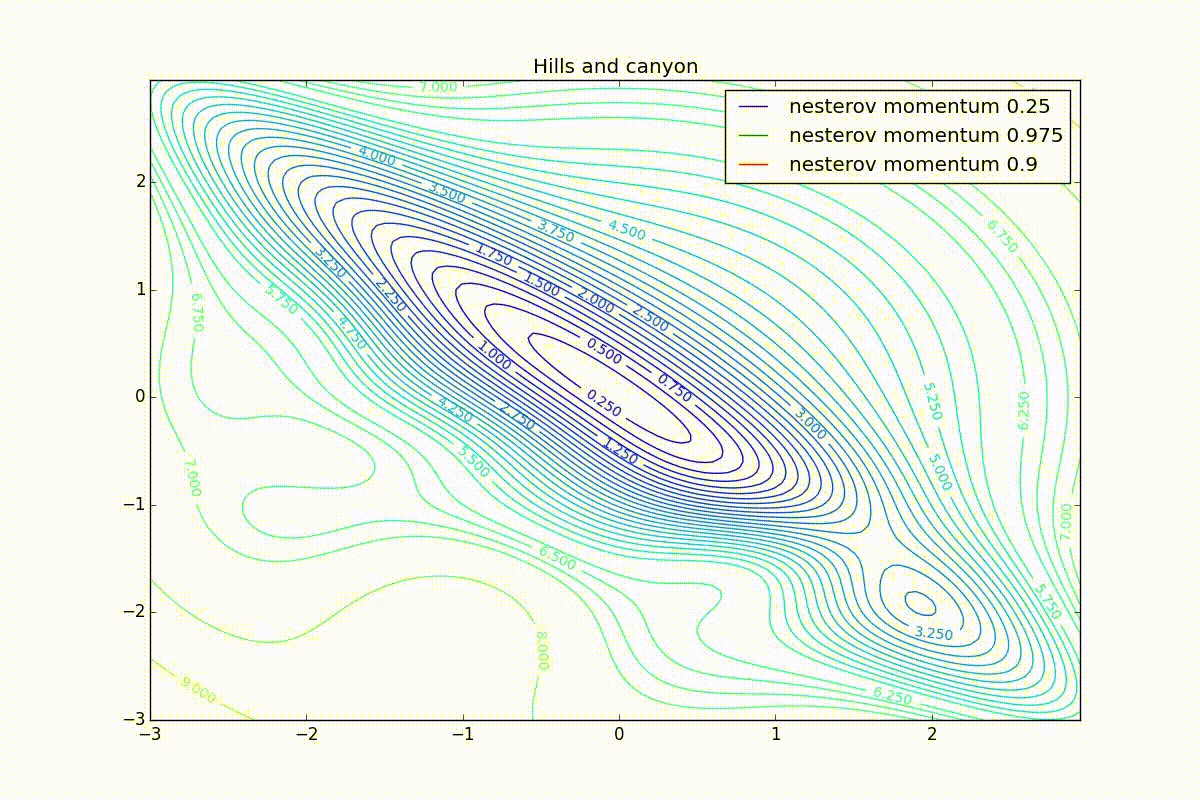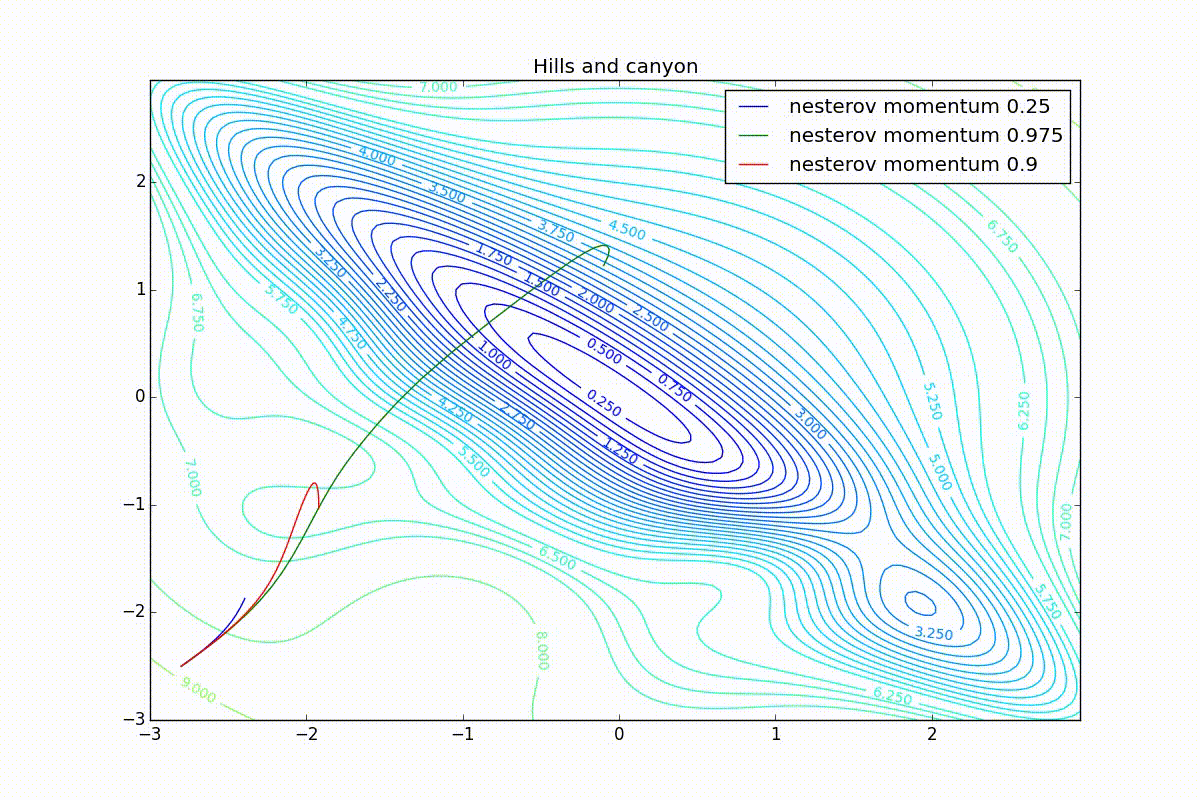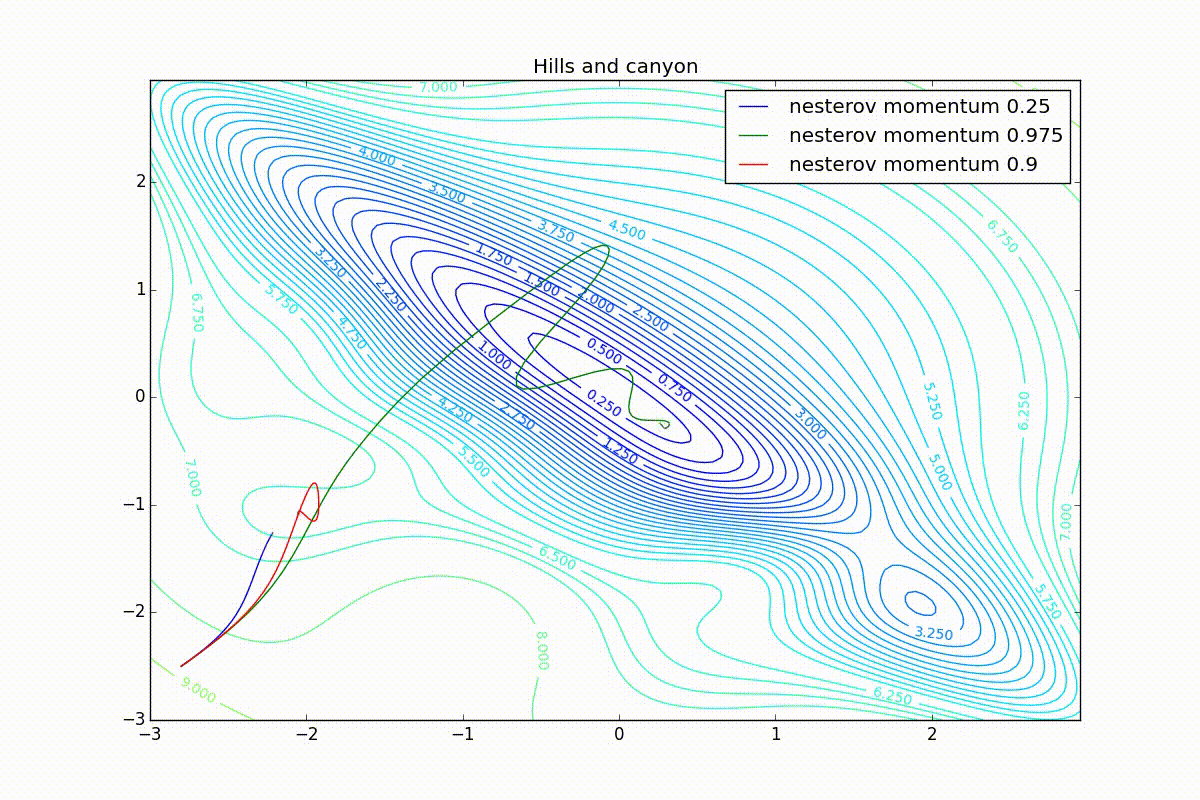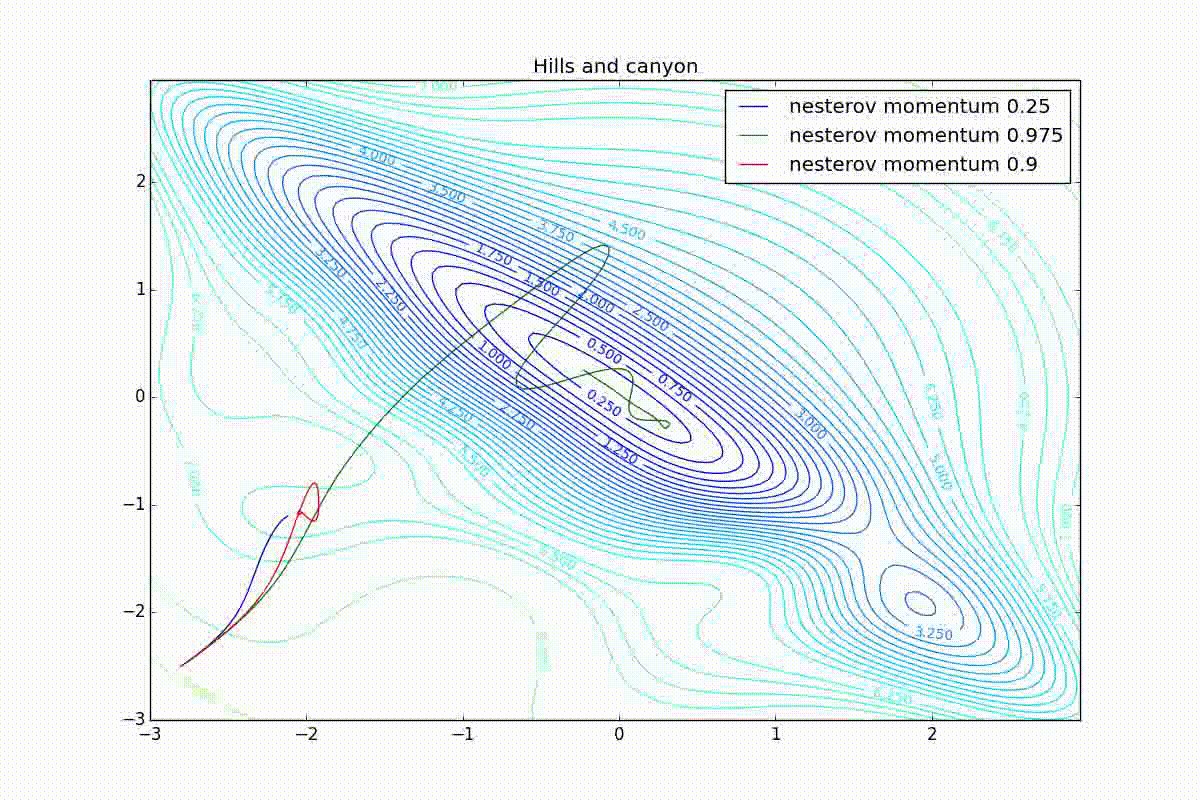
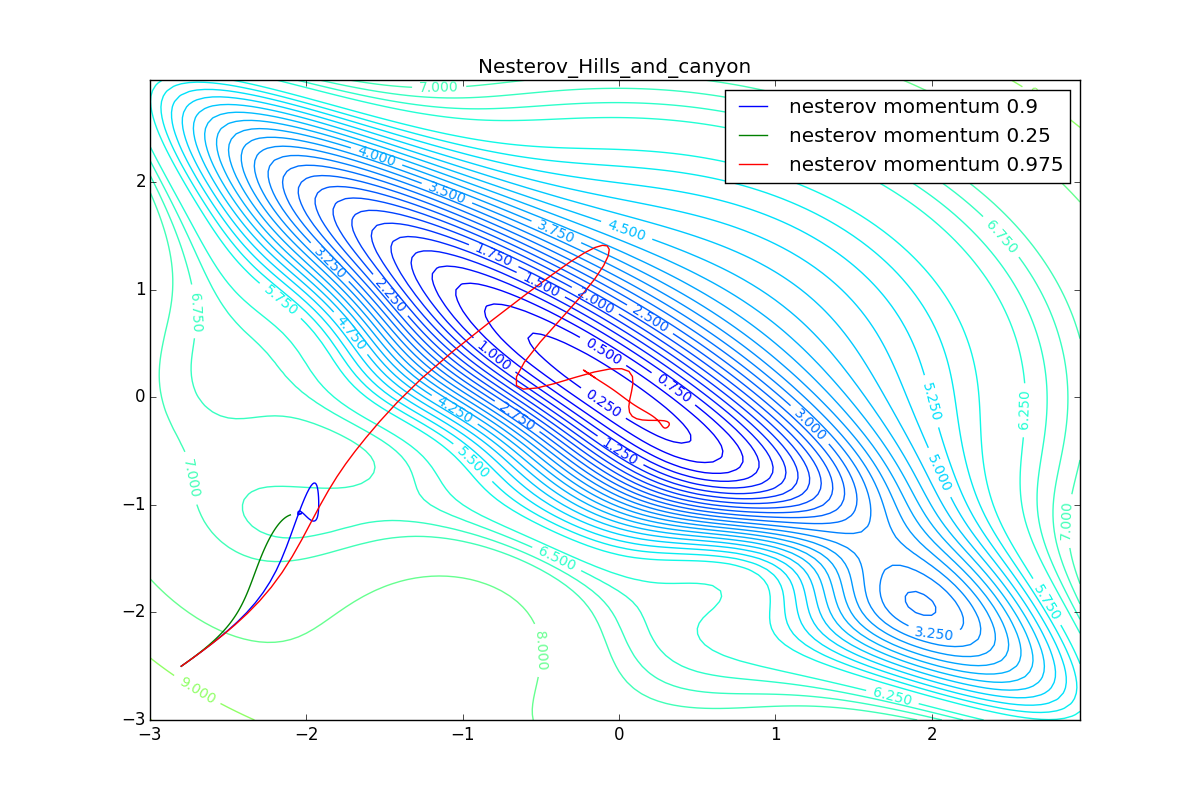
Иногда плохо: можно запросто растерять импульс, проскочив впадину глобального минимума и осесть в локальном. Поэтому при больших $\inline \gamma$ можно иногда увидеть, как потери на тренировочной выборке сначала достигают глобальный минимум, затем сильно возрастают, потом снова начинают опускаться, но так и не возвращаются в прошедший минимум.

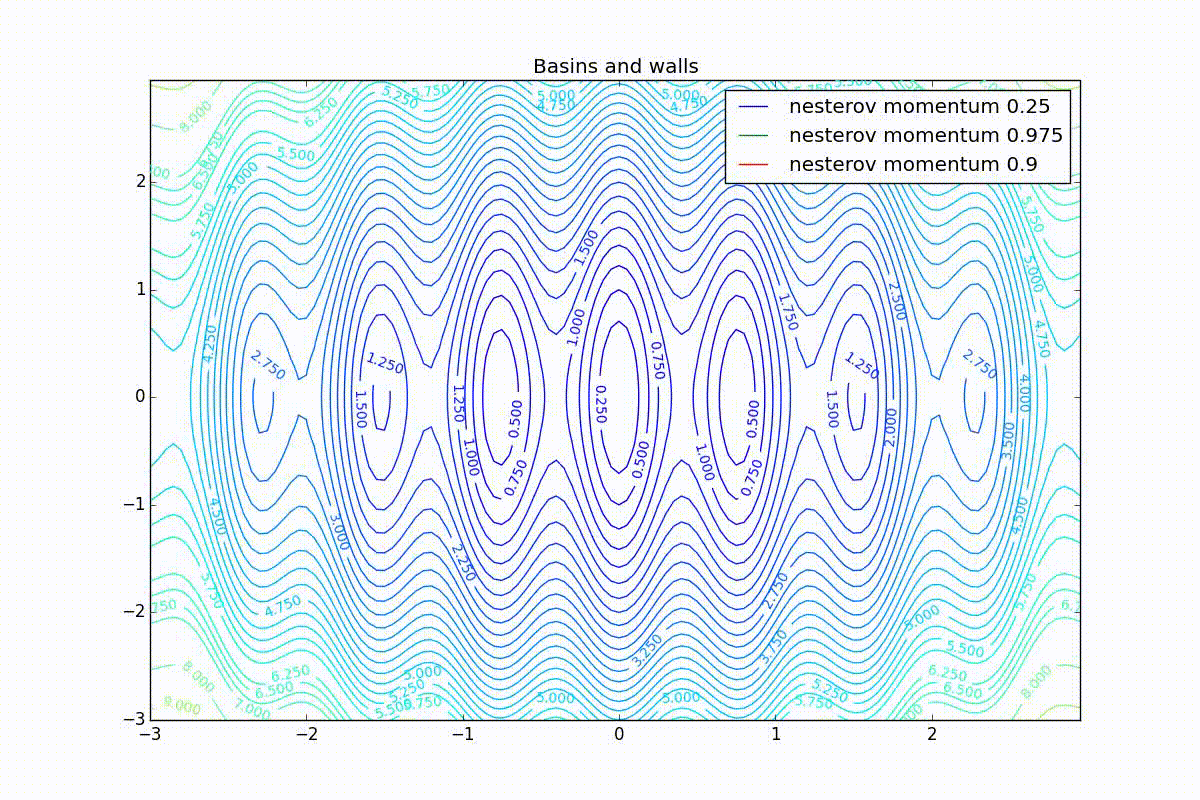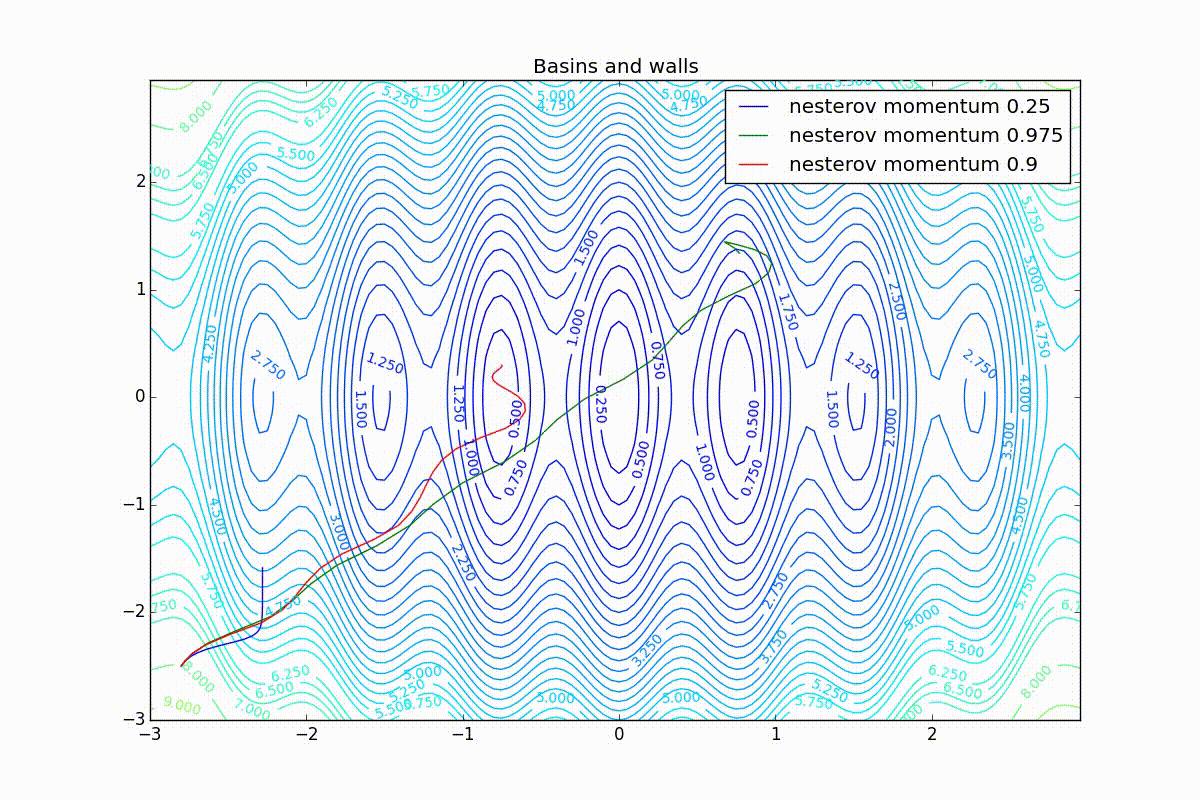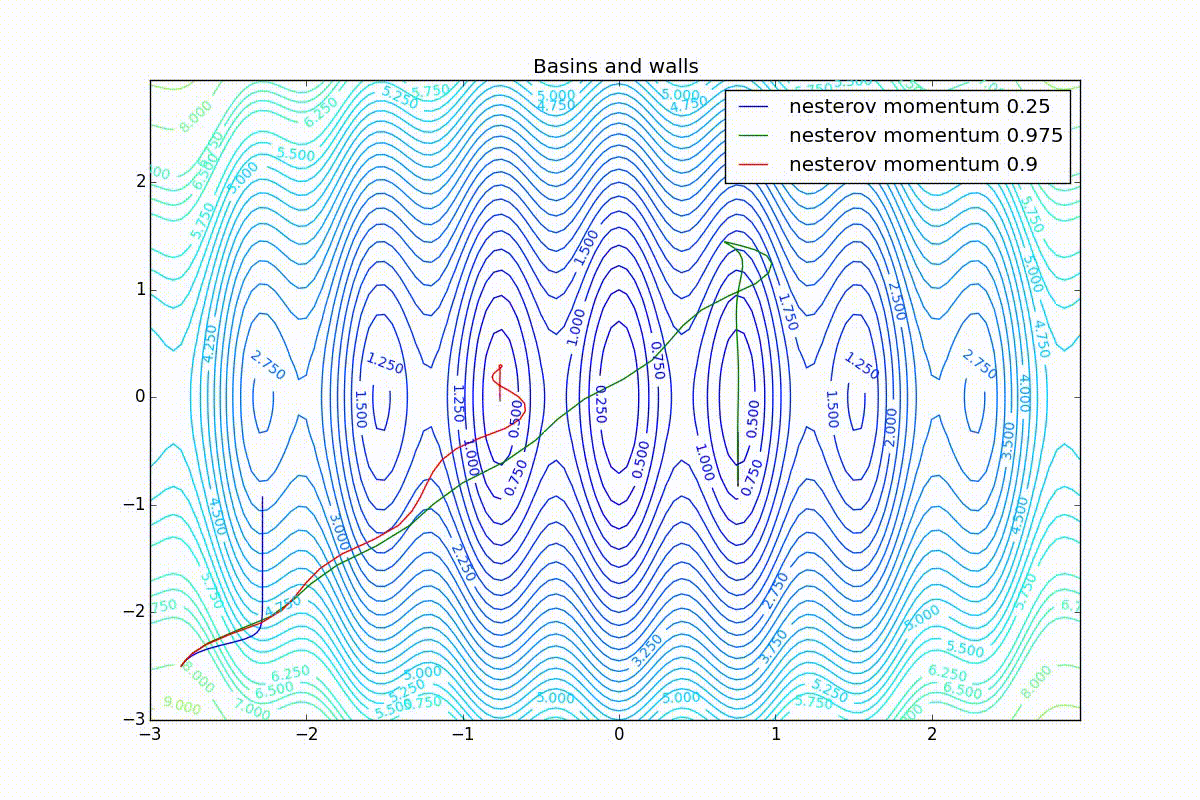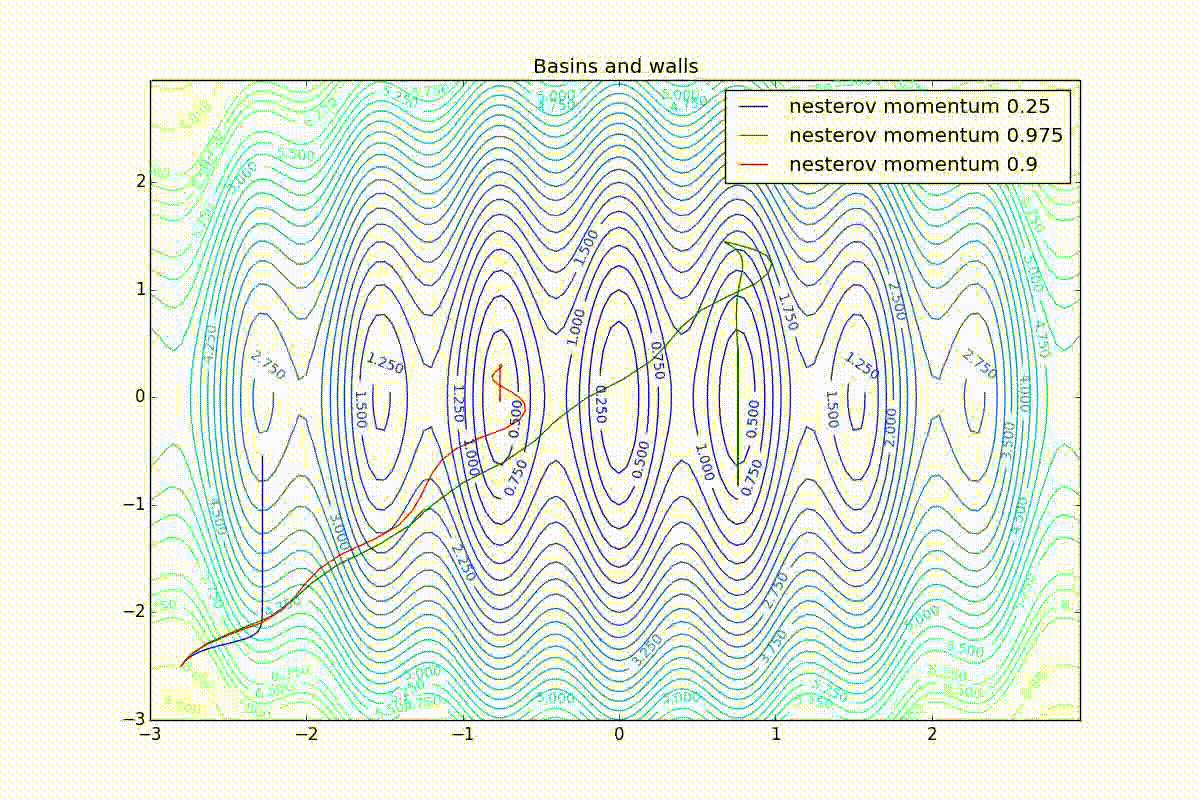
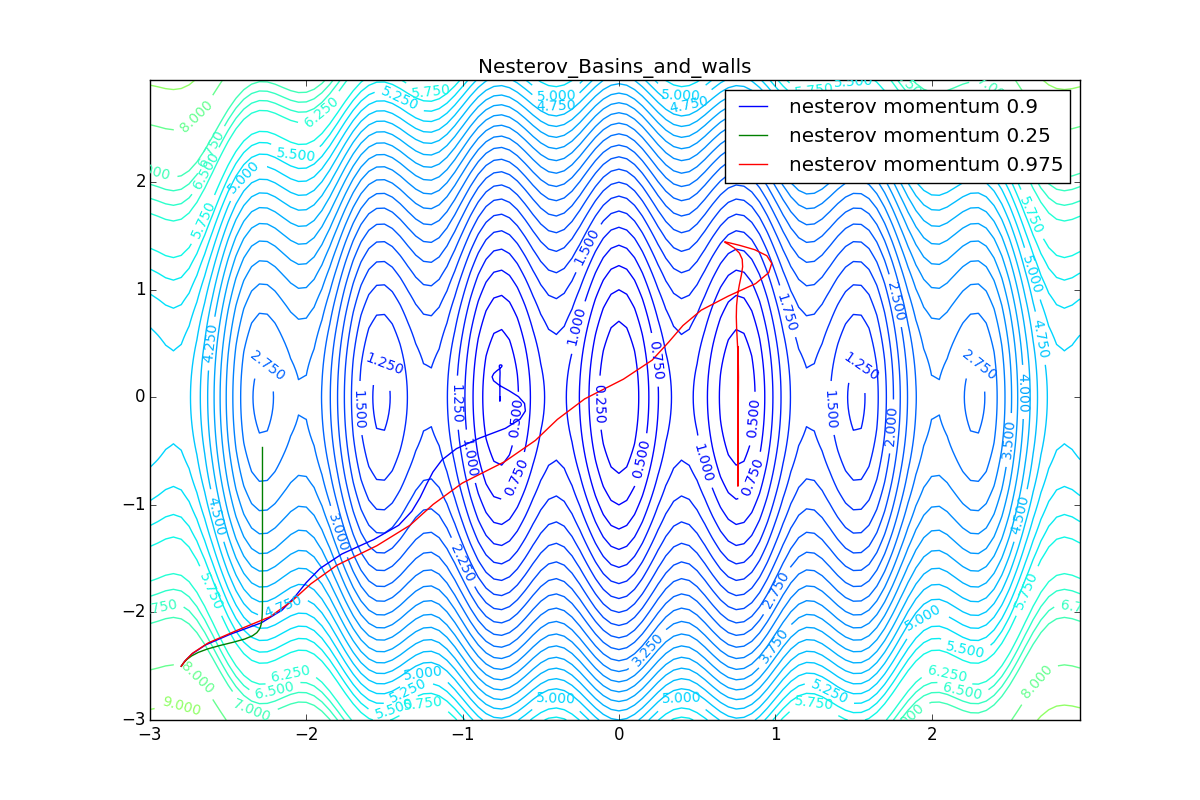
Теперь рассмотрим разные алгоритмы, запущенные из одной точки.

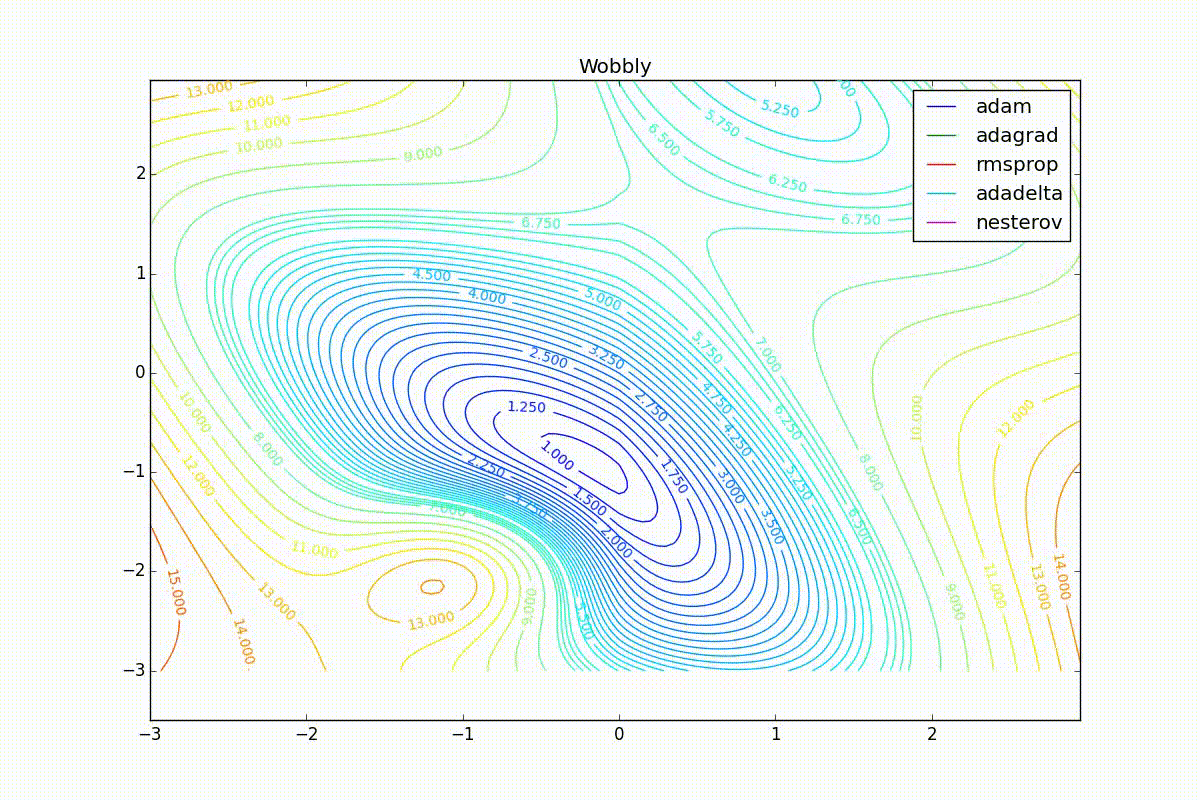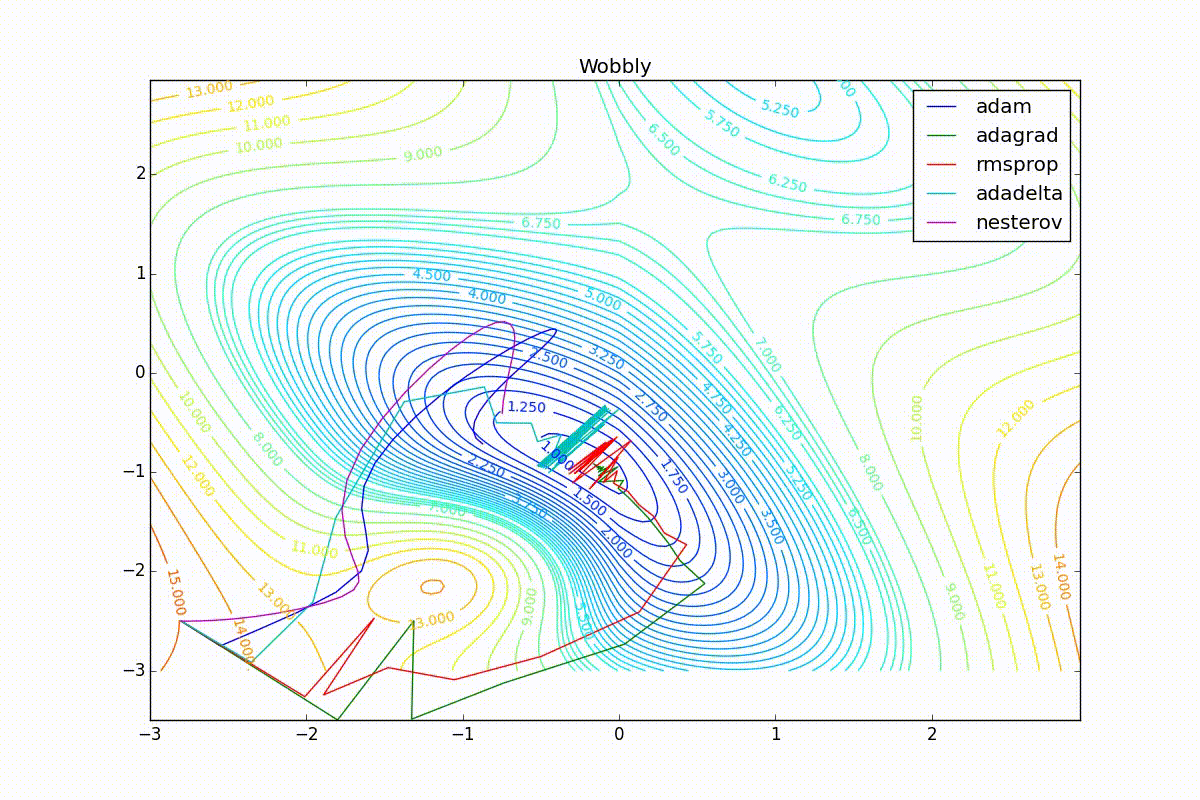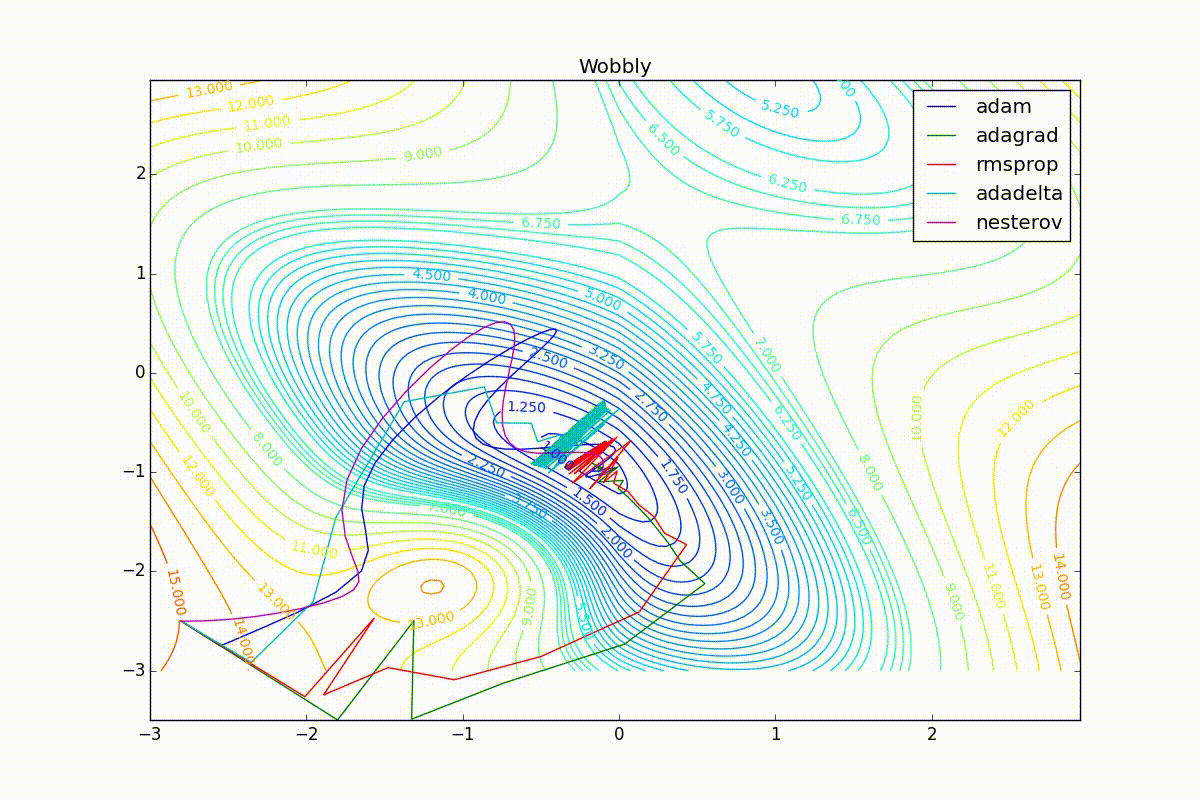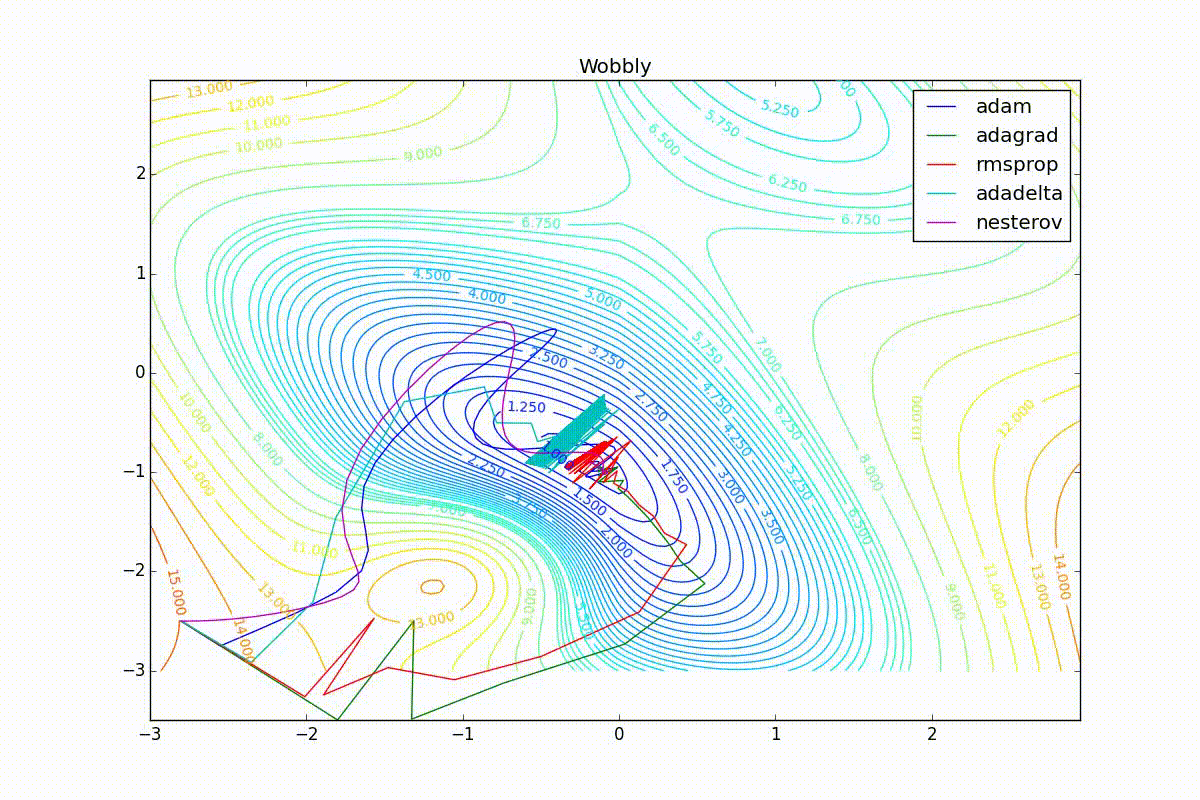
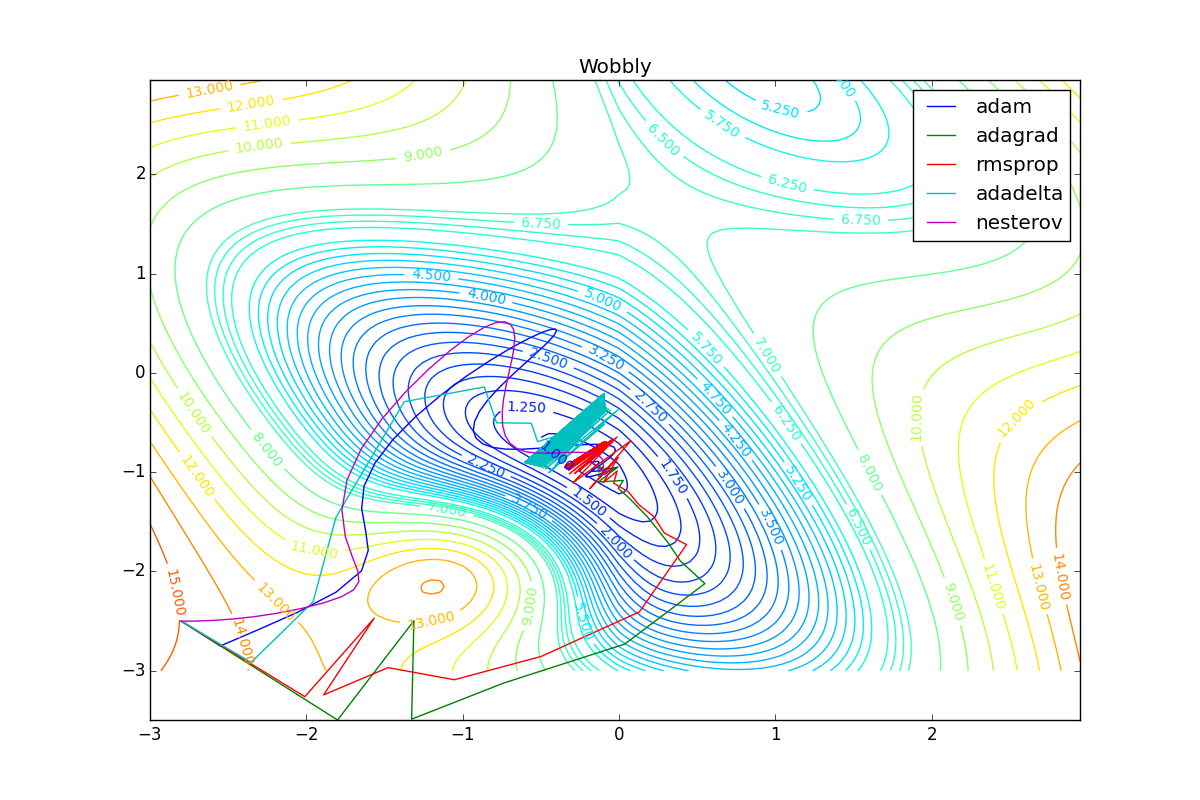
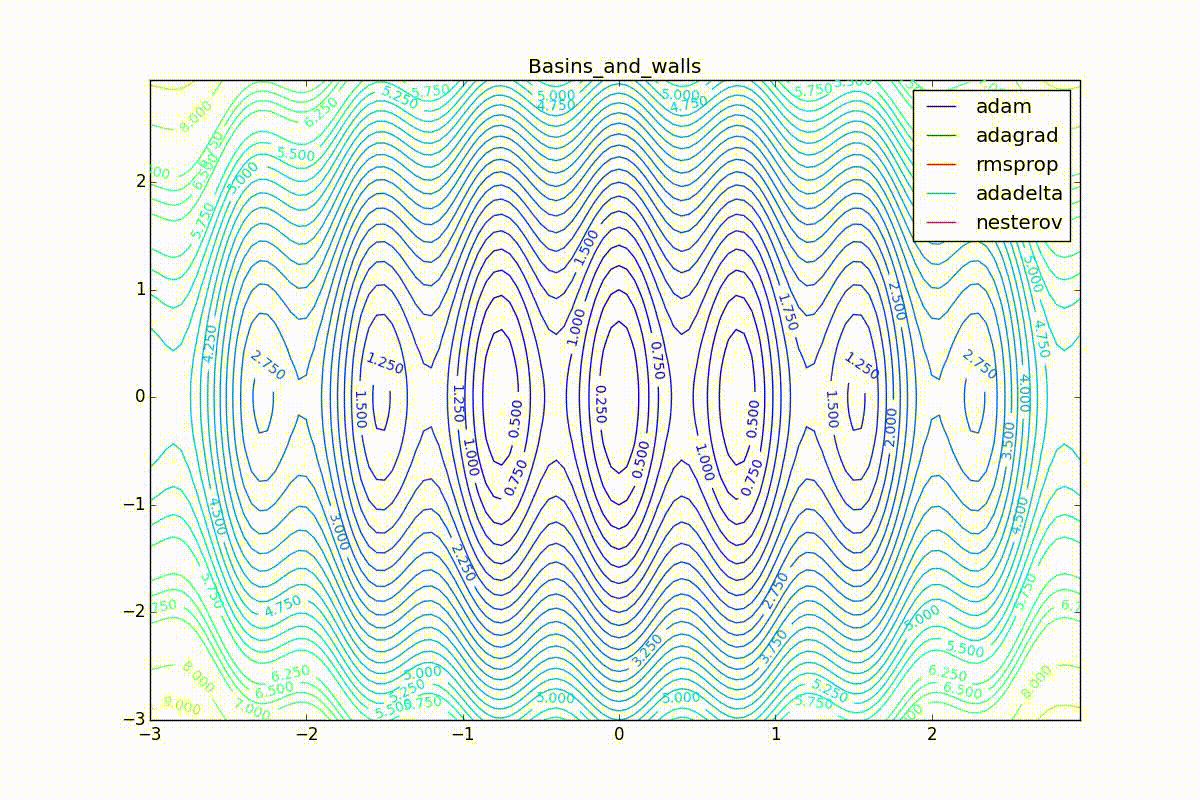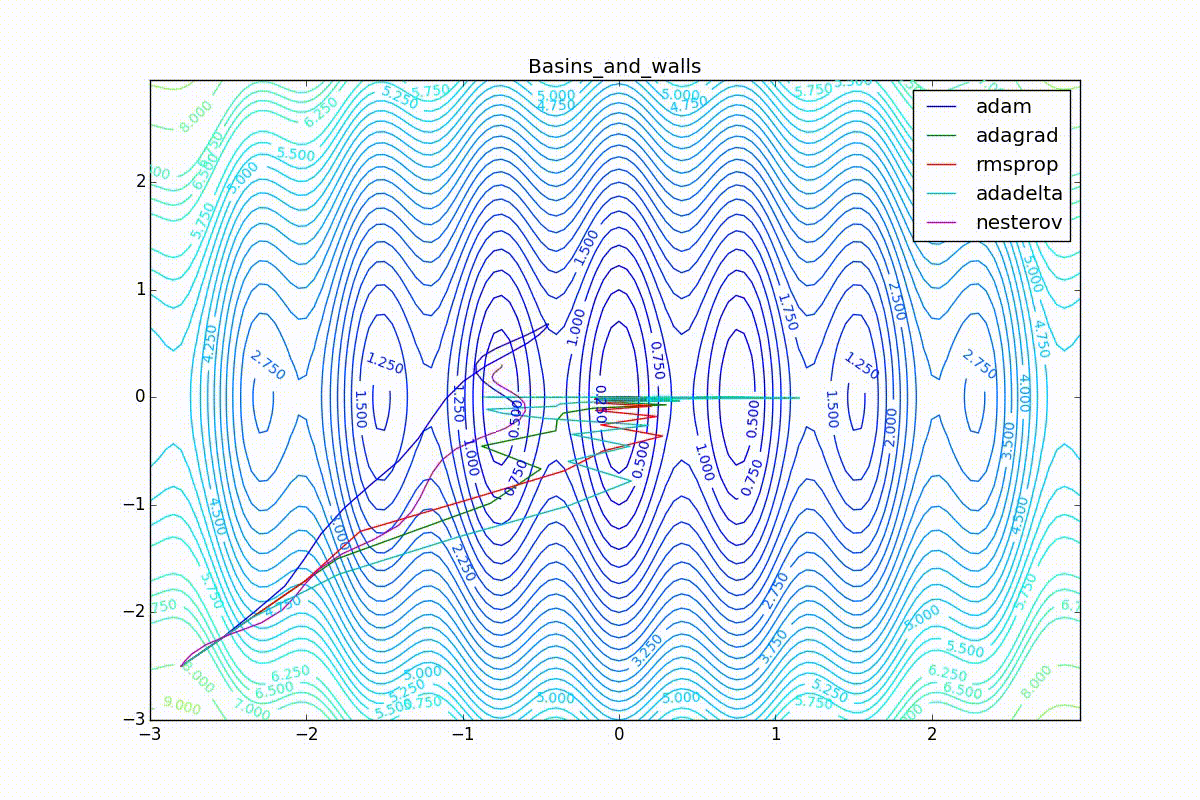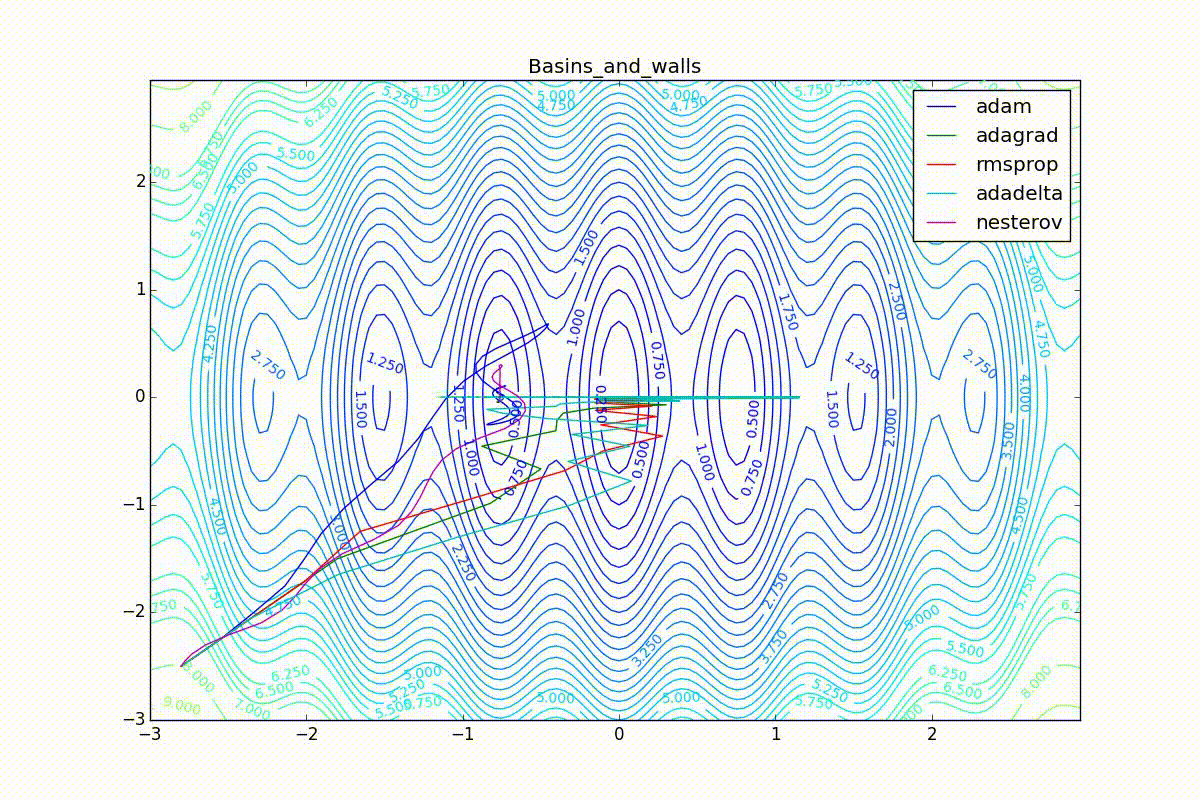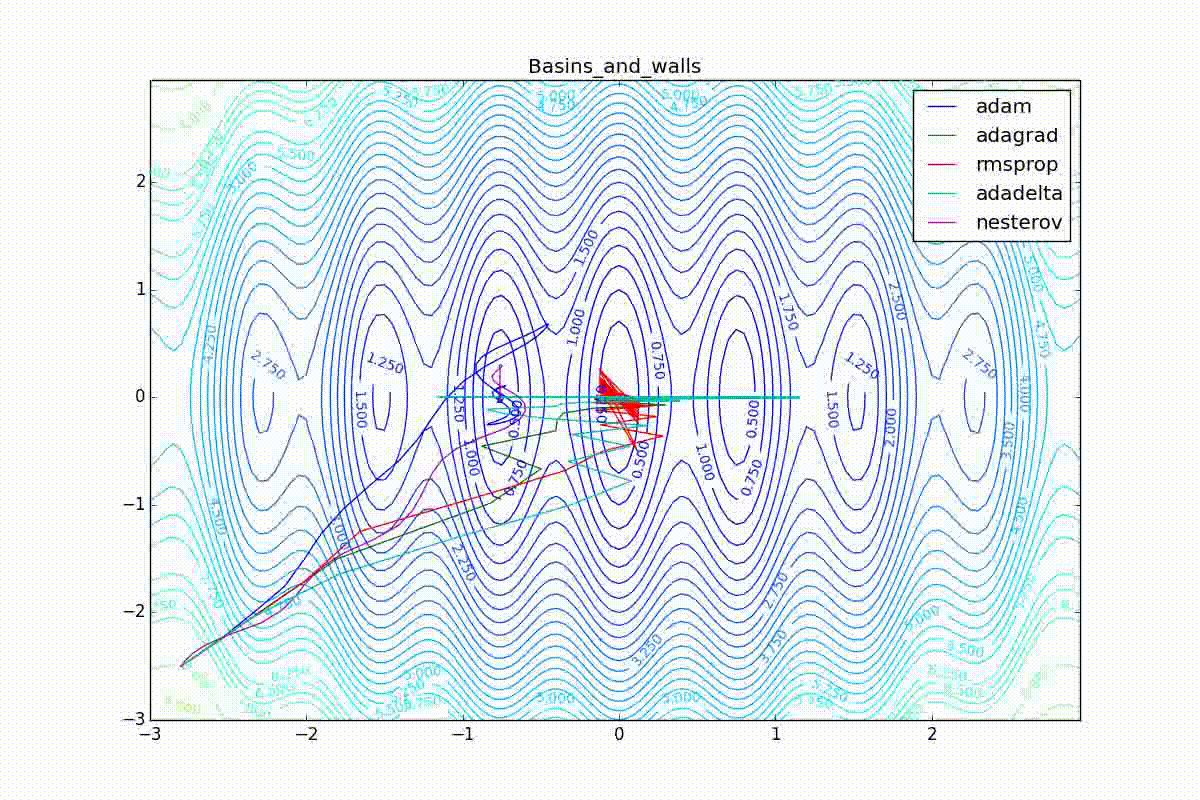
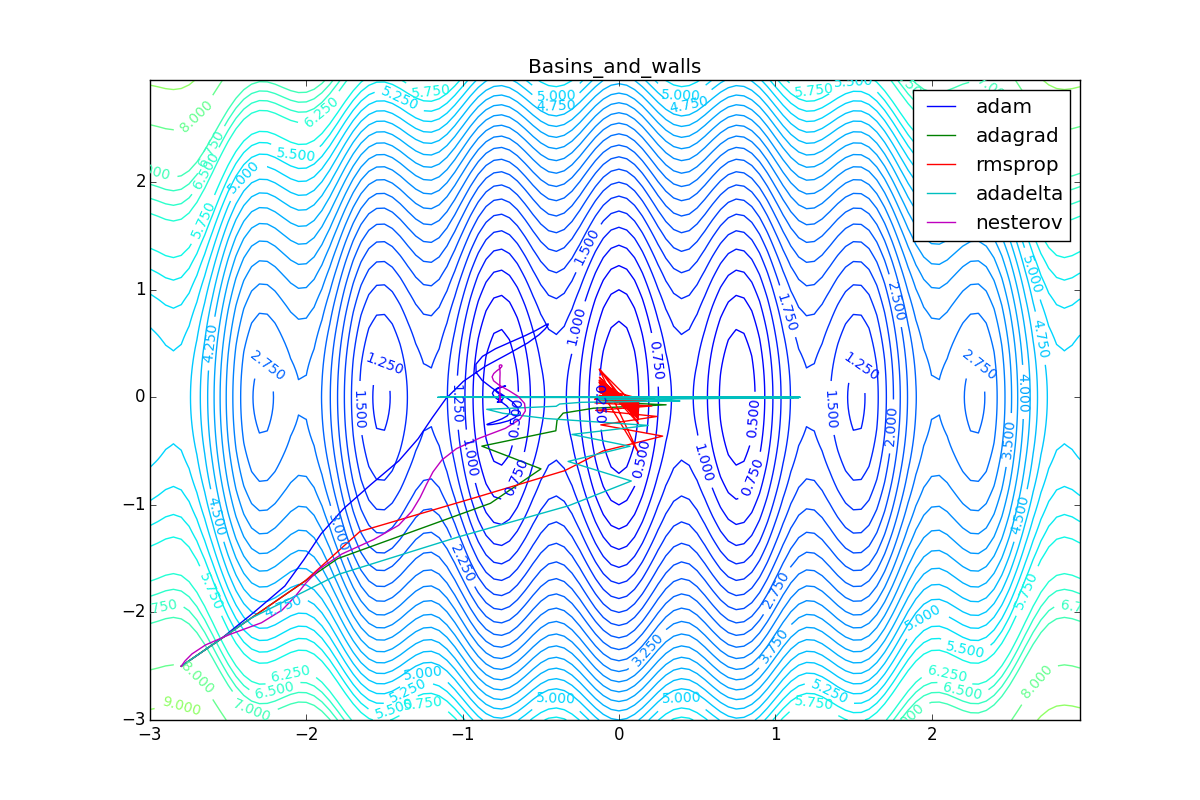
Как видно, все они довольно хорошо сходятся (с минимальным подбором скорости обучения). Обратите внимание на то, какие большие шаги совершают Adam и RMSProp в начале обучения. Так происходит потому что с самого начала не было ниаких изменений ни по одному параметру (ни по одной координате) и суммы в знаменателях (14) и (23) равны нулю. Вот тут ситуация посложнее:

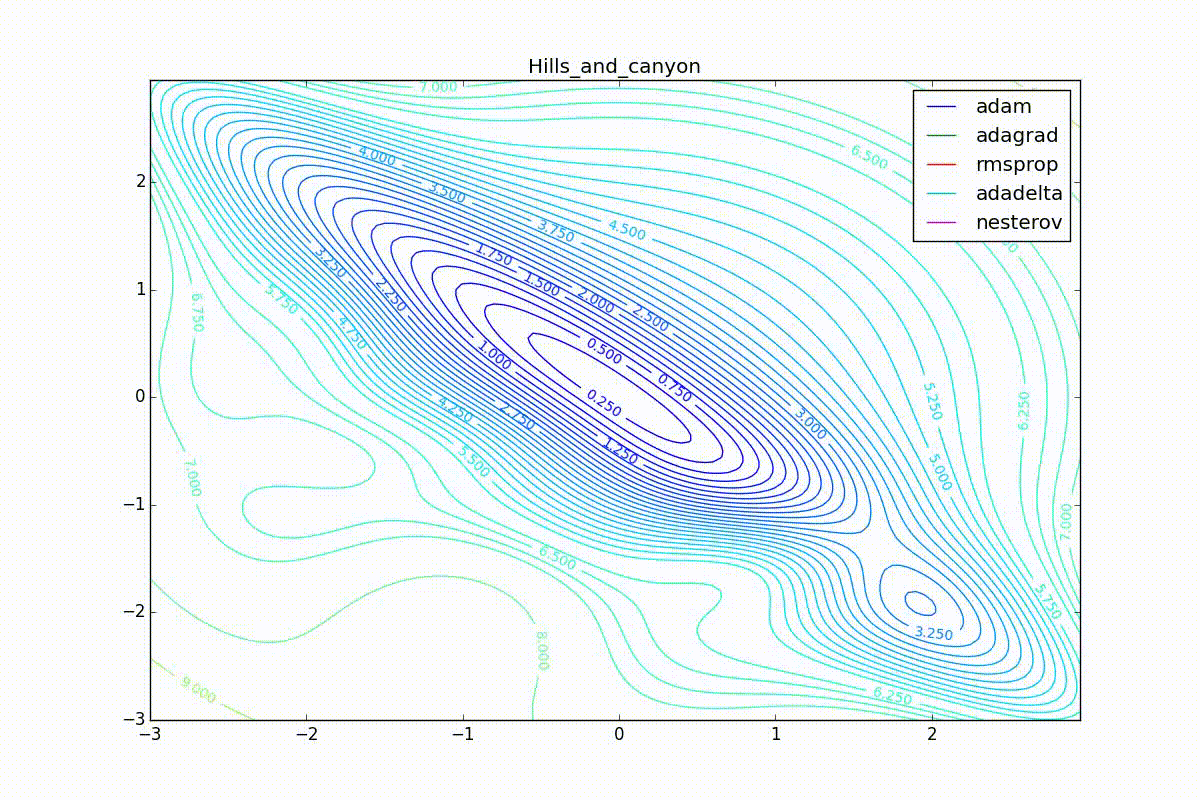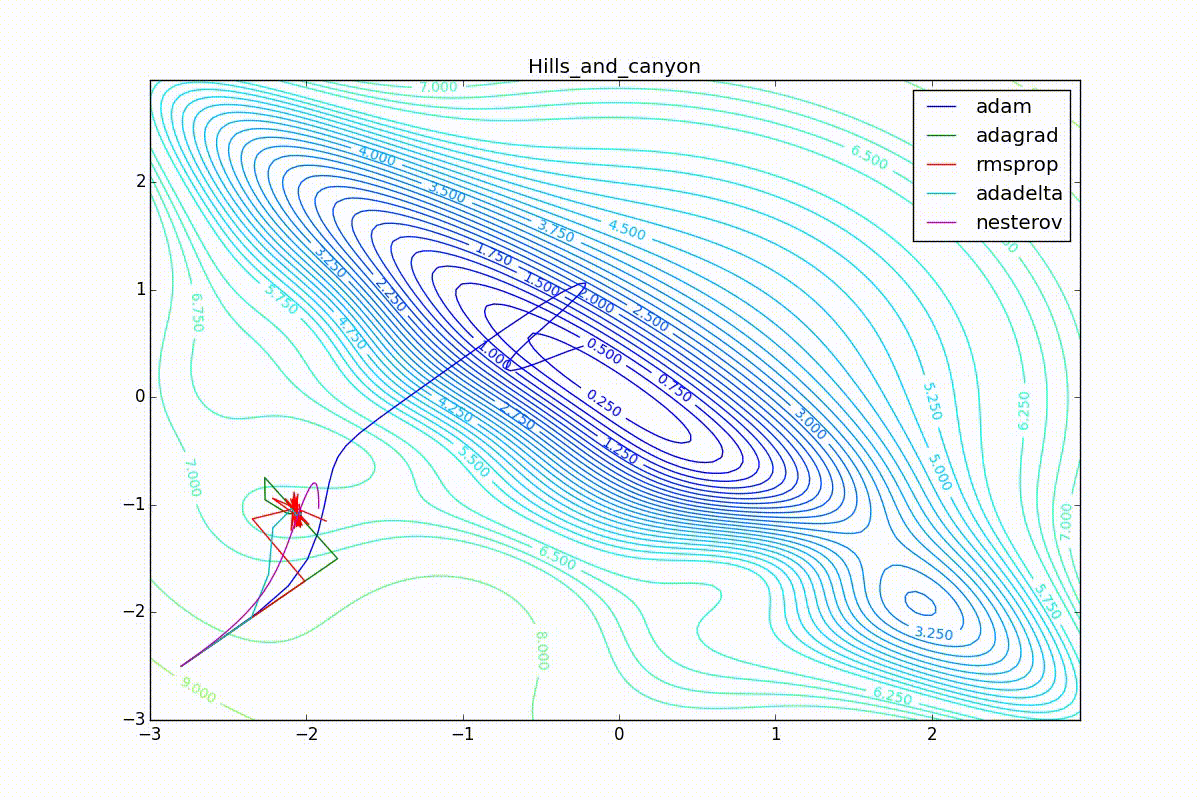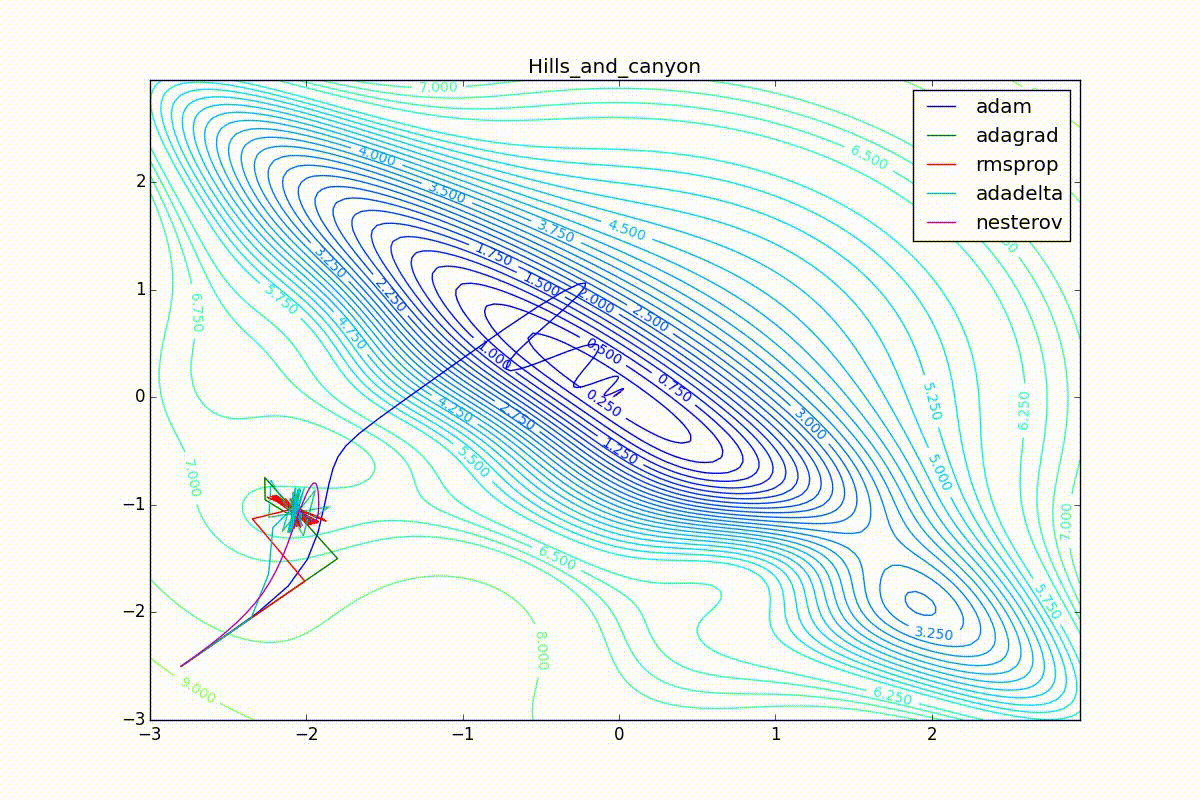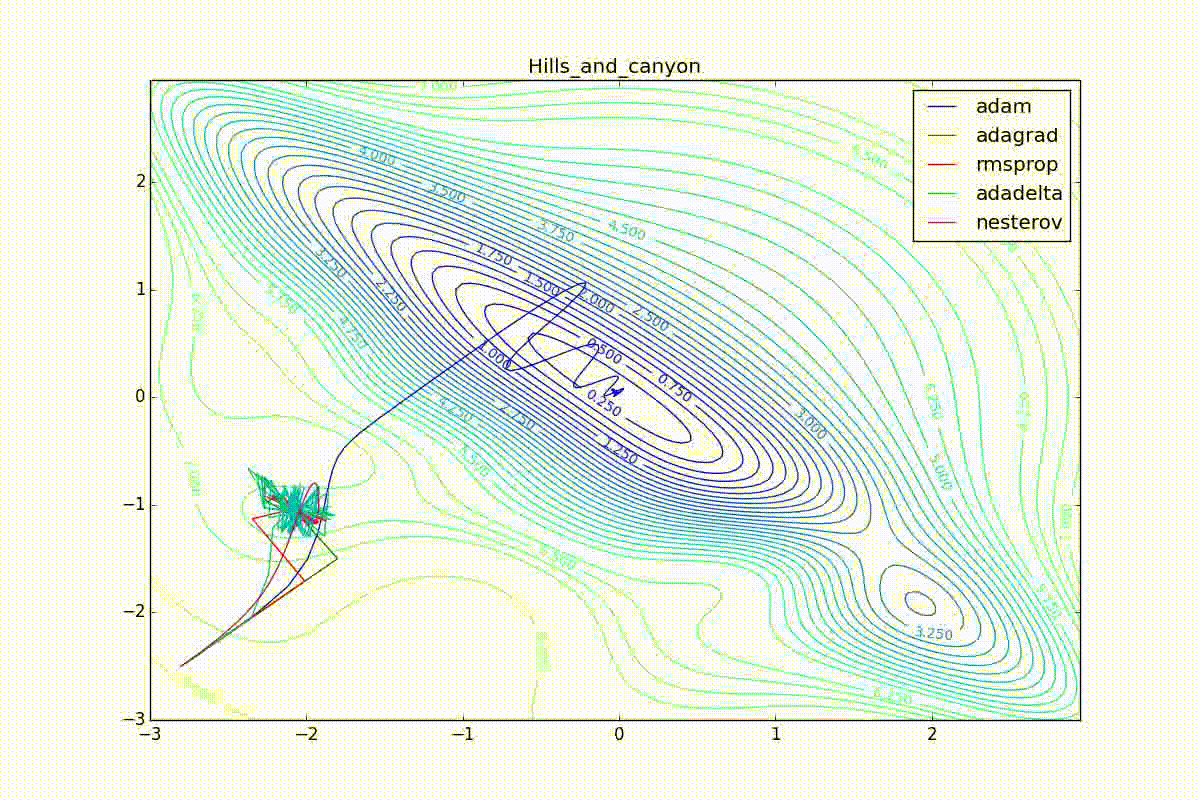
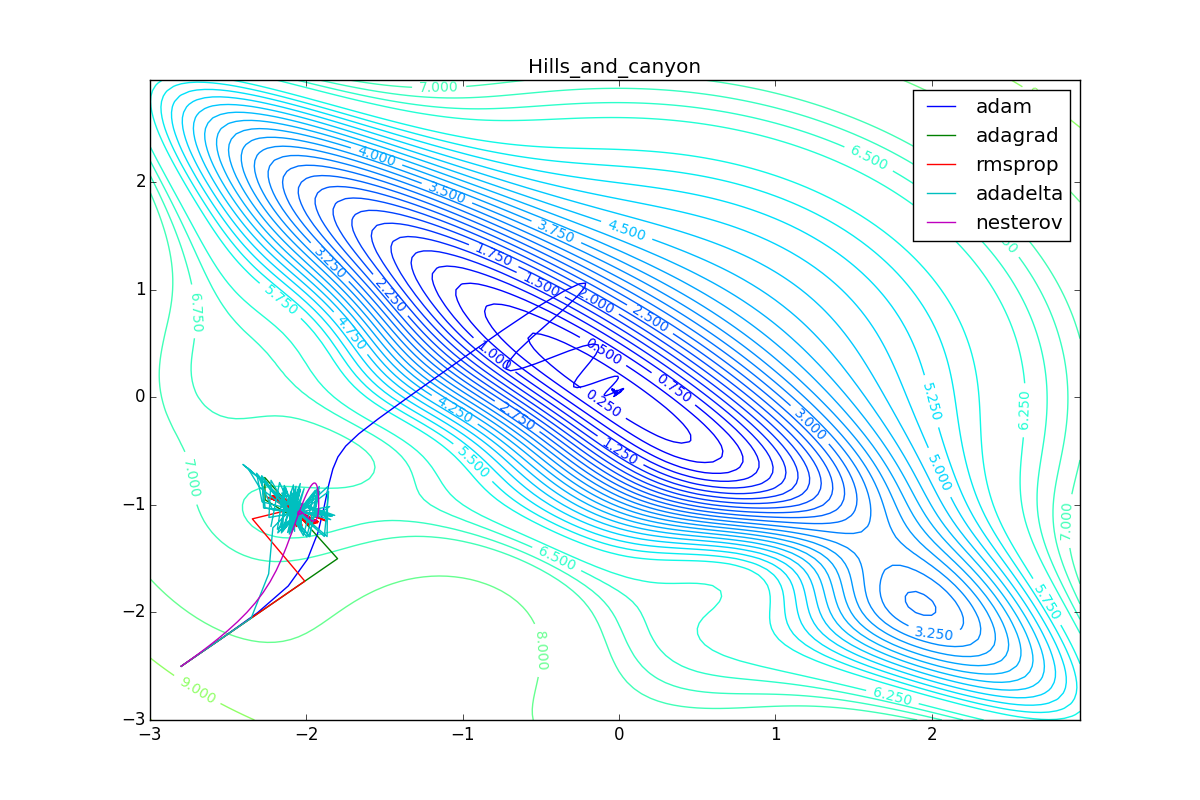
Кроме Adam, все оказались заперты в локальном минимуме. Сравните поведение метода Нестерова и, скажем, RMSProp на этих графиках. Ускоренный градиент Нестерова, с любым $\inline \gamma$ , попав в локальный минимум, некоторое время кружится вокруг, затем теряет импульс и затухает в какой-нибдуь точке. RMSProp же рисует характерных «ёжиков». Это тоже связано с суммой в знаменателе (14) — в ловушке квадраты градиента маленькие и знаменатель снова становится маленьким. На величину скачков влияют ещё, очевидно, скорость обучения (чем больше $\inline \eta$ , тем больше скачки) и $\inline \epsilon$ (чем меньше, тем больше). Adagrad такого поведения не показывает, так как у этого алгоритма сумма по всей истории градиентов, а не по окну. Обычно это желательное поведение, оно позволяет выскакивать из ловушек, но изредка таким образом алгоритм сбегает из глобального минимума, что опять-таки, ведёт к невосполнимому ухудшению работы алгоритма на тренировочной выборке.

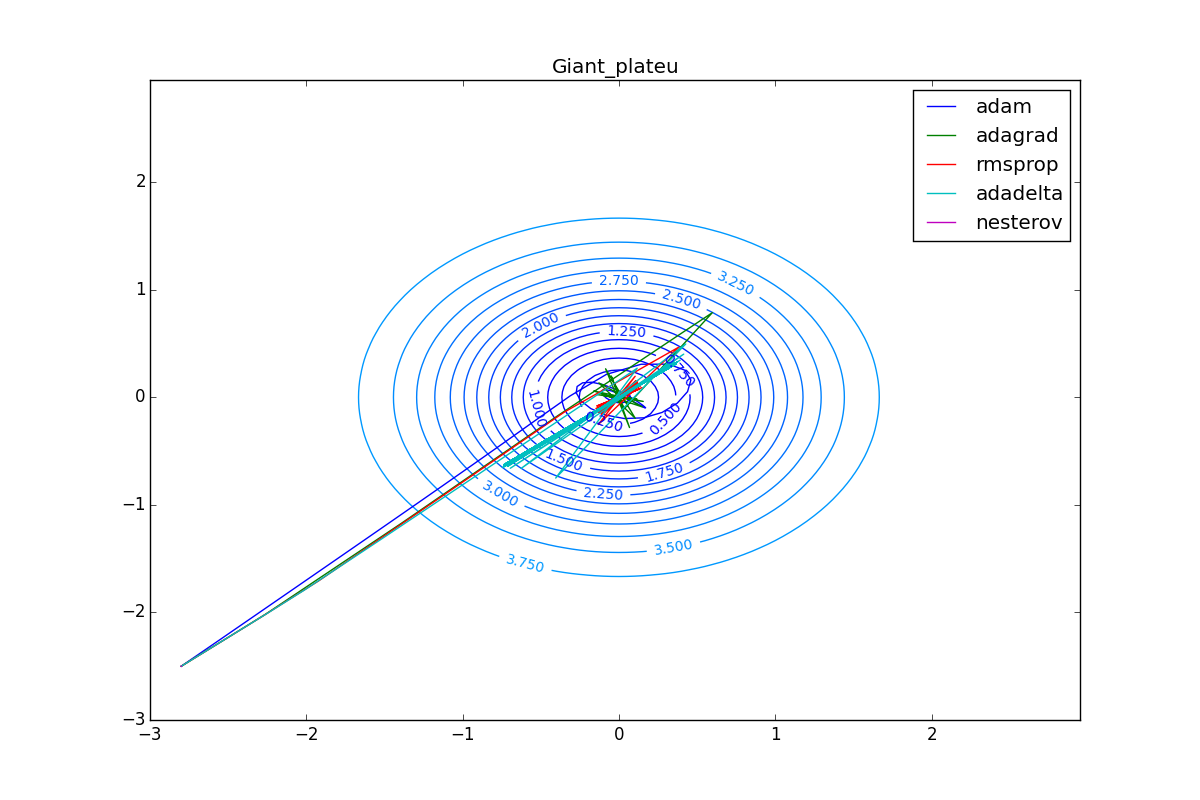
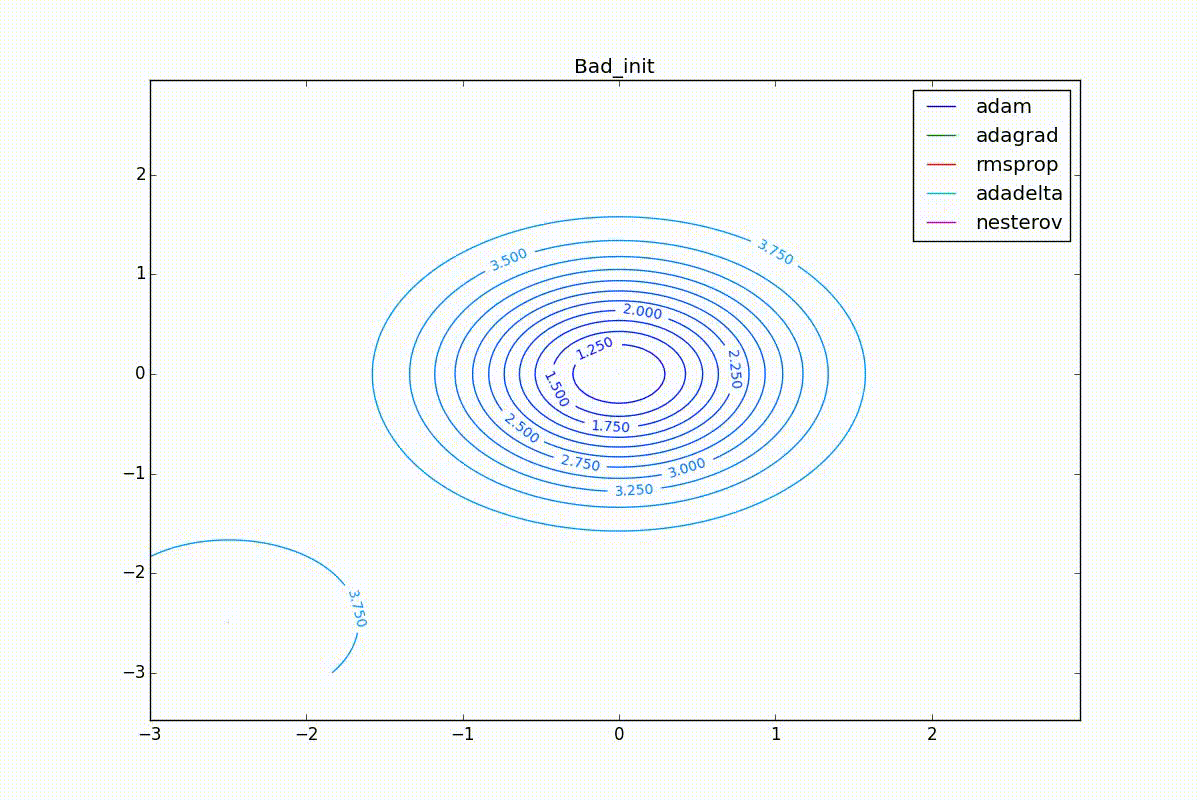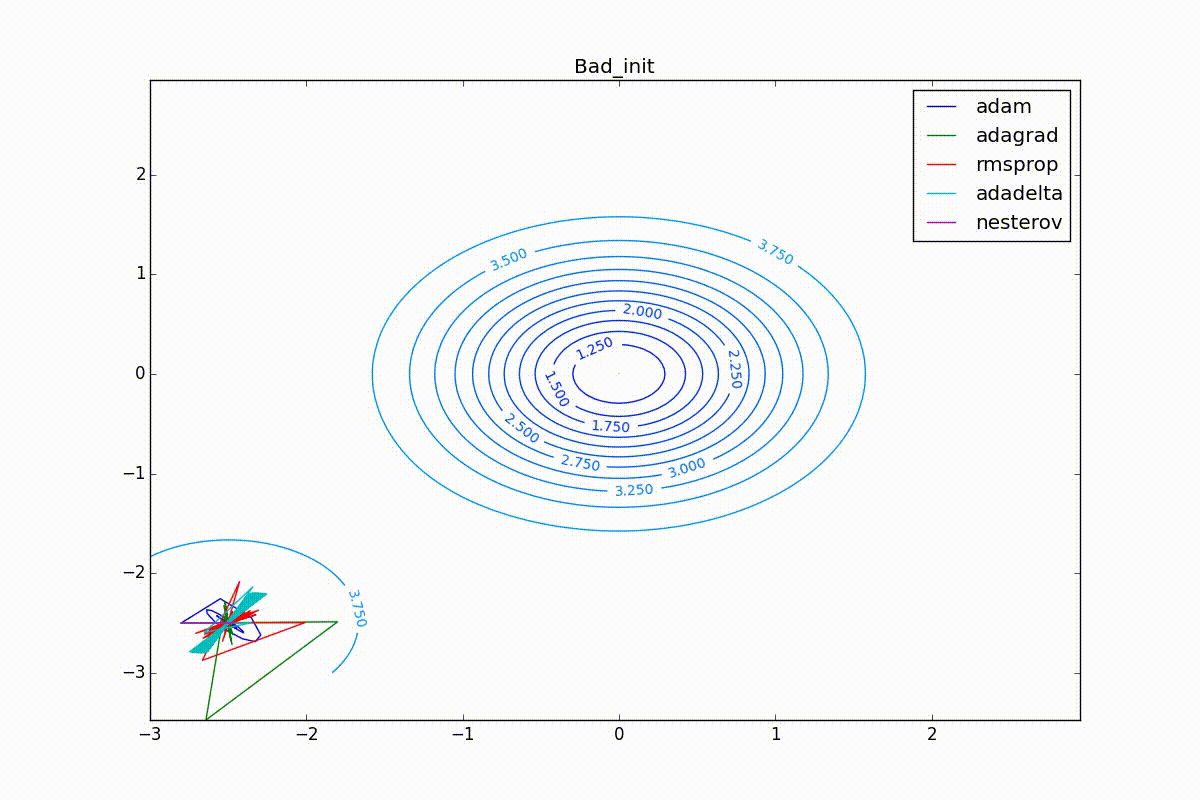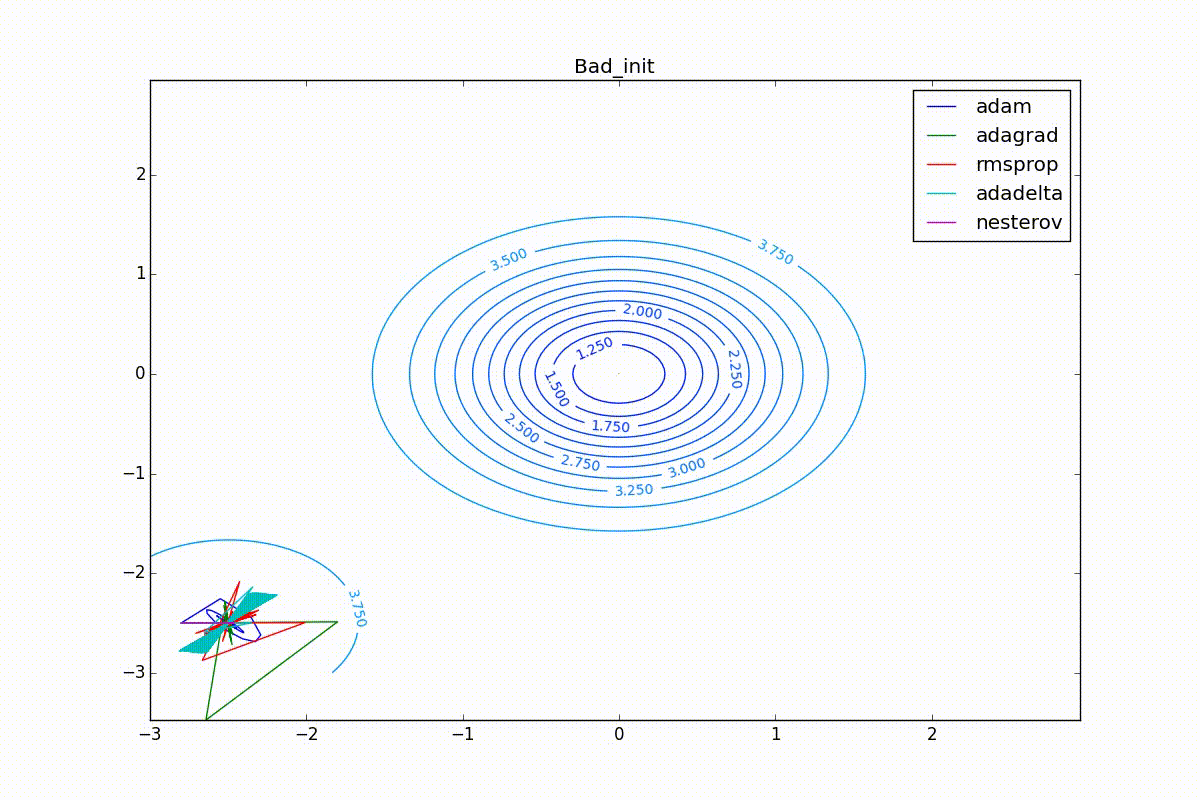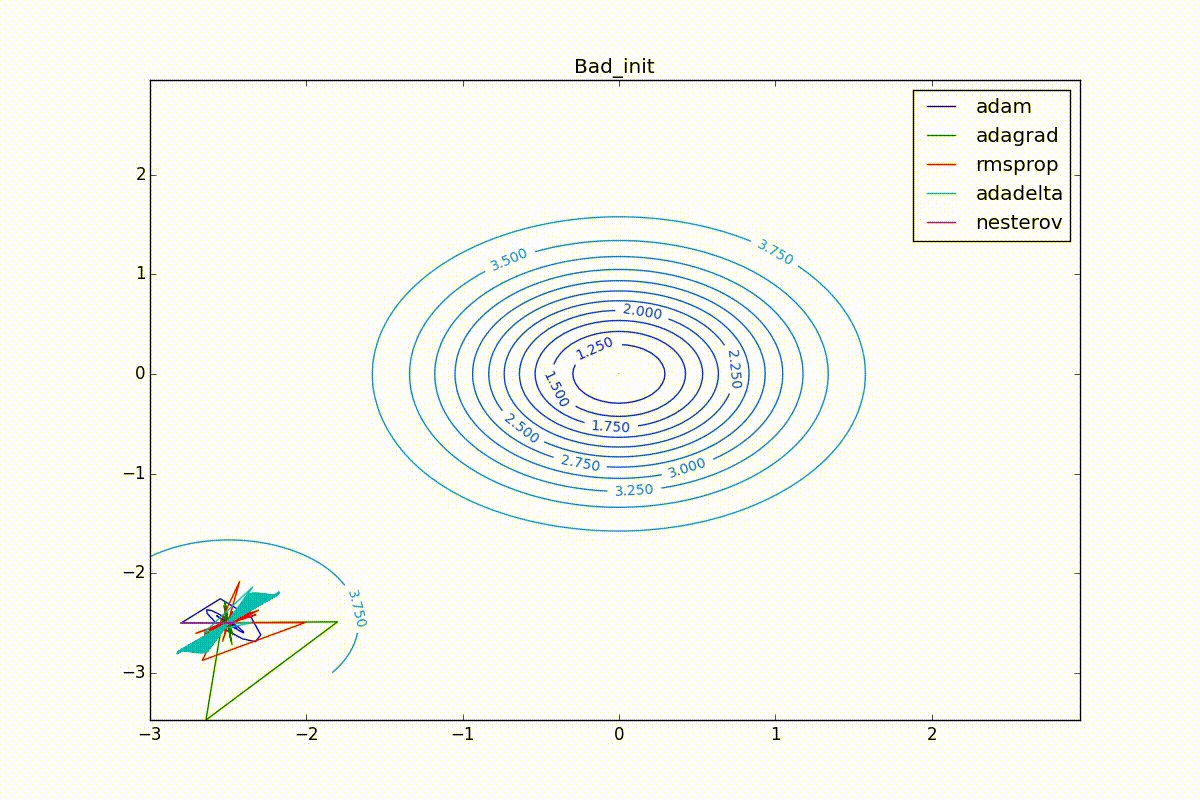
Наконец, заметьте, что хоть все эти оптимизаторы и могут найти путь к минимуму даже по плато с очень маленьким уклоном или сбежать из локального минимума, если до этого они уже набрали импульс, плохая начальная точка не оставляет им шансов:

Заключение

Итак, мы рассмотрели несколько наиболее популярных оптимизаторов нейронных сетей первого порядка. Надеюсь, эти алгоритмы перестали казаться волшебным чёрным ящиком с кучей загадочных параметров, и теперь вы можете принять взвешенное решение, какой из оптимизаторов использовать в своих задачах.

Напоследок, всё же уточню один важный момент: вряд ли смена алгоритма обновления весов одним вжухом решит все ваши проблемы с нейронной сетью. Конечно прирост при переходе от SGD к чему-то другому будет очевиден, но скорее всего история обучения для алгоритмов, описанных в статье, для сравнительно простых датасетов и структур сети будет выглядеть как-то так:

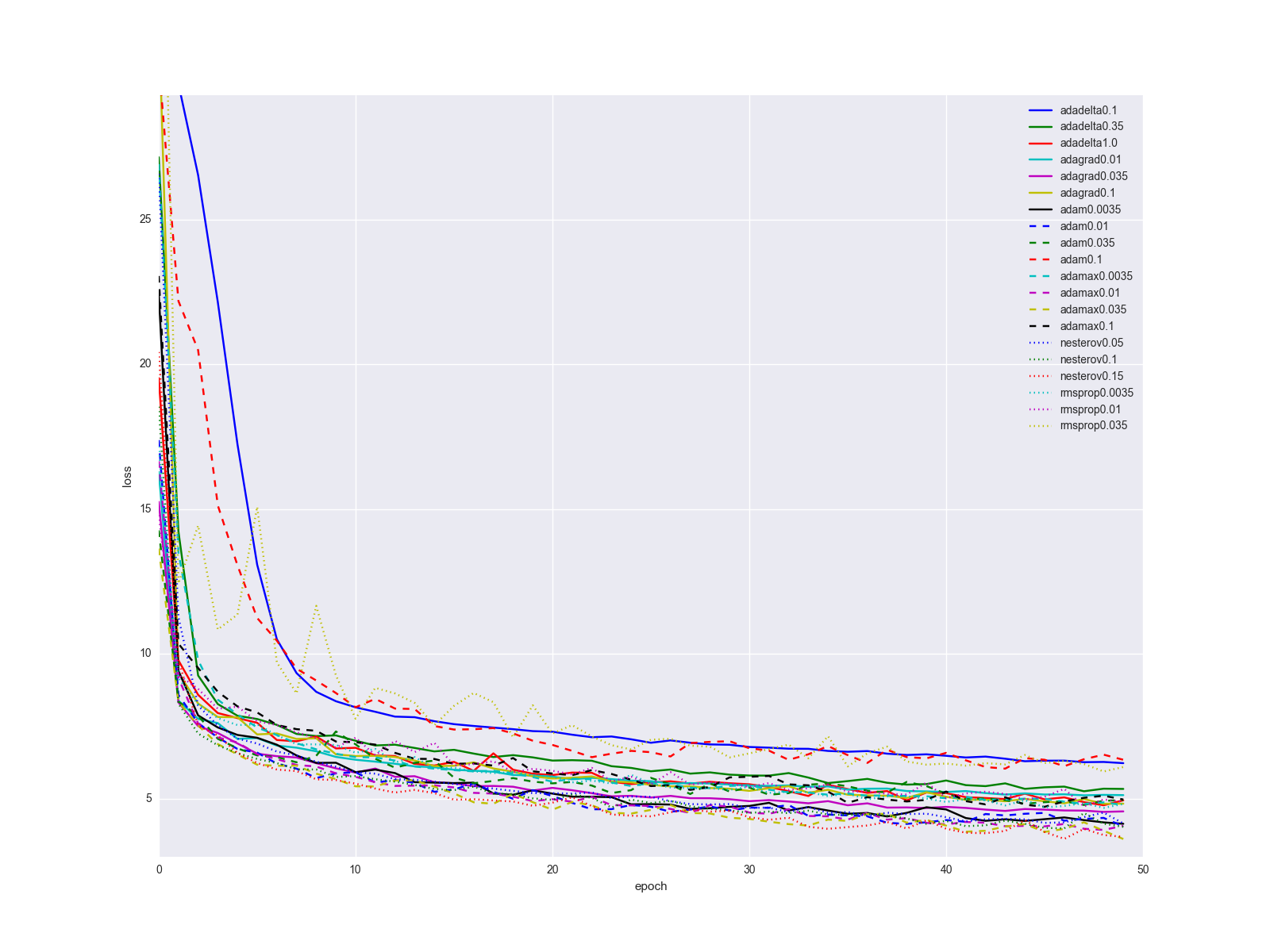
… не слишком впечатляет. Я бы предложил держать качестве «золотого молотка» Adam, так как он выдаёт наилучшие результаты при минимальном подгоне параметров. Когда сеть уже более-менее отлажена, попробуйте метод Нестерова с разными параметрами. Иногда с помощью него можно добиться лучших результатов, но он сравнительно чувствителен к изменениям в сети. Плюс-минус пара слоёв и нужно искать новый оптимальный learning rate. Рассматривайте остальные алгоритмы и их параметры как ещё несколько ручек и тумблеров, которые можно подёргать в каких-то специальных случаях.

Если хотите несколько собственных графиков с градиентами, воспользуйтесь этим скриптом на питоне (требуется python > 3.4, numpy и matplotlib):

Код

from matplotlib import pyplot as plt
import numpy as np
from math import ceil, floor

def linear_interpolation(X, idx):
    idx_min = floor(idx)
    idx_max = ceil(idx)
    if idx_min == idx_max or idx_max >= len(X):
        return X[idx_min]
    elif idx_min < 0:
        return X[idx_max]
    else:
        return X[idx_min] + (idx - idx_min)*X[idx_max]

def EDM(X, gamma, lr=0.25):
    Y = []
    v = 0
    for x in X:
        v = gamma*v + lr*x
        Y.append(v)
    return np.asarray(Y)

def NM(X, gamma, lr=0.25):
    Y = []
    v = 0
    for i in range(len(X)):
        v = gamma*v + lr*(linear_interpolation(X, i+gamma*v) if i+gamma*v < len(X) else 0)
        Y.append(v)
    return np.asarray(Y)

def SmoothedNM(X, gamma, lr=0.25):
    Y = []
    v = 0
    for i in range(len(X)):
        lookahead4 = linear_interpolation(X, i+gamma*v/4)   if i+gamma*v/4      < len(X) else 0
        lookahead3 = linear_interpolation(X, i+gamma*v/2)   if i+gamma*v/2      < len(X) else 0
        lookahead2 = linear_interpolation(X, i+gamma*v*3/4) if i+gamma*v*3/4    < len(X) else 0
        lookahead1 = linear_interpolation(X, i+gamma*v)     if i+gamma*v        < len(X) else 0
        v = gamma*v + lr*(lookahead4 + lookahead3 + lookahead2 + lookahead1)/4
        Y.append(v)
    return np.asarray(Y)

def Adagrad(X, eps, lr=2.5):
    Y = []
    G = 0
    for x in X:
        G += x*x
        v = lr/np.sqrt(G + eps)*x
        Y.append(v)
    return np.asarray(Y)

def RMSProp(X, gamma, lr=0.25, eps=0.00001):
    Y = []
    EG = 0
    for x in X:
        EG = gamma*EG + (1-gamma)*x*x
        v = lr/np.sqrt(EG + eps)*x
        Y.append(v)
    return np.asarray(Y)

def Adadelta(X, gamma, lr=50.0, eps=0.001):
    Y = []
    EG = 0
    EDTheta = lr
    for x in X:
        EG = gamma*EG + (1-gamma)*x*x
        v = np.sqrt(EDTheta + eps)/np.sqrt(EG + eps)*x
        Y.append(v)
        EDTheta = gamma*EDTheta + (1-gamma)*v*v
    return np.asarray(Y)

def AdadeltaZeroStart(X, gamma, eps=0.001):
    return Adadelta(X, gamma, lr=0.0, eps=eps)

def AdadeltaBigStart(X, gamma, eps=0.001):
    return Adadelta(X, gamma, lr=50.0, eps=eps)

def Adam(X, beta1, beta2=0.999, lr=0.25, eps=0.0000001):
    Y = []
    m = 0
    v = 0
    for i, x in enumerate(X):
        m = beta1*m + (1-beta1)*x
        v = beta2*v + (1-beta2)*x*x
        m_hat = m/(1- pow(beta1, i+1) )
        v_hat = v/(1- pow(beta2, i+1) )
        dthetha = lr/np.sqrt(v_hat + eps)*m_hat
        Y.append(dthetha)
    return np.asarray(Y)

np.random.seed(413)
X = np.arange(0, 300)

D_Thetha_spikes = np.asarray( [int(x%60 == 0) for x in X])
D_Thetha_rectangles = np.asarray( [2*int(x%40 < 20) - 1 for x in X])
D_Thetha_noisy_sin = np.asarray( [np.sin(x/20) + np.random.random() - 0.5 for x in X])
D_Thetha_very_noisy_sin = np.asarray( [np.sin(x/20)/5 + np.random.random() - 0.5 for x in X])
D_Thetha_uneven_sawtooth = np.asarray( [ x%20/(15*int(x > 80) + 5) for x in X])
D_Thetha_saturation = np.asarray( [ int(x % 80 < 40) for x in X])

for method_label, method, parameter_step in [
                ("GRAD_Simple_Momentum", EDM, [0.25, 0.9, 0.975]),
                ("GRAD_Nesterov", NM, [0.25, 0.9, 0.975]),
                ("GRAD_Smoothed_Nesterov", SmoothedNM, [0.25, 0.9, 0.975]),
                ("GRAD_Adagrad", Adagrad, [0.0000001, 0.1, 10.0]),
                ("GRAD_RMSProp", RMSProp, [0.25, 0.9, 0.975]),
                ("GRAD_AdadeltaZeroStart", AdadeltaZeroStart, [0.25, 0.9, 0.975]),
                ("GRAD_AdadeltaBigStart", AdadeltaBigStart, [0.25, 0.9, 0.975]),
                ("GRAD_Adam", Adam, [0.25, 0.9, 0.975]),
            ]:
    for label, D_Thetha in [("spikes", D_Thetha_spikes),
                            ("rectangles", D_Thetha_rectangles),
                            ("noisy sin", D_Thetha_noisy_sin),
                            ("very noisy sin", D_Thetha_very_noisy_sin),
                            ("uneven sawtooth", D_Thetha_uneven_sawtooth),
                            ("saturation", D_Thetha_saturation), ]:
        fig = plt.figure(figsize=[16.0, 9.0])
        ax = fig.add_subplot(111)

        ax.plot(X, D_Thetha, label="gradient")
        for gamma in parameter_step:
            Y = method(D_Thetha, gamma)
            ax.plot(X, Y, label="param="+str(gamma))

        ax.spines['bottom'].set_position('zero')
        full_name = method_label + "_" + label

        plt.xticks(np.arange(0, 300, 20))
        plt.grid(True)
        plt.title(full_name)
        plt.xlabel('epoch')
        plt.ylabel('value')
        plt.legend()
        # plt.show(block=True) #Uncoomment and comment next line if you just want to watch
        plt.savefig(full_name)
        plt.close(fig)

Если хотите поэкспериментировать с параметрами алгоритмов и собственными функциями, используйте это, чтобы создать собственную анимацию траектории минимизатора (требуется вдобавок theano/lasagne):

Ещё код

import numpy as np
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import theano
import theano.tensor as T
from lasagne.updates import nesterov_momentum, rmsprop, adadelta, adagrad, adam

#For reproducibility. Comment it out for randomness
np.random.seed(413)

#Uncoomment and comment next line if you want to try random init
# clean_random_weights = scipy.random.standard_normal((2, 1))
clean_random_weights = np.asarray([[-2.8], [-2.5]])
W = theano.shared(clean_random_weights)
Wprobe = T.matrix('weights')

levels = [x/4.0 for x in range(-8, 2*12, 1)] + [6.25, 6.5, 6.75, 7] +          list(range(8, 20, 1))
levels = np.asarray(levels)

O_simple_quad = (W**2).sum()
O_wobbly = (W**2).sum()/3 + T.abs_(W[0][0])*T.sqrt(T.abs_(W[0][0]) + 0.1) + 3*T.sin(W.sum()) + 3.0 + 8*T.exp(-2*((W[0][0] + 1)**2+(W[1][0] + 2)**2))
O_basins_and_walls = (W**2).sum()/2 + T.sin(W[0][0]*4)**2
O_ripple = (W**2).sum()/3 + (T.sin(W[0][0]*20)**2 + T.sin(W[1][0]*20)**2)/15
O_giant_plateu = 4*(1-T.exp(-((W[0][0])**2+(W[1][0])**2)))
O_hills_and_canyon = (W**2).sum()/3 +                      3*T.exp(-((W[0][0] + 1)**2+(W[1][0] + 2)**2)) +                        T.exp(-1.5*(2*(W[0][0] + 2)**2+(W[1][0] -0.5)**2)) +                      3*T.exp(-1.5*((W[0][0] -1)**2+2*(W[1][0] + 1.5)**2)) +                      1.5*T.exp(-((W[0][0] + 1.5)**2+3*(W[1][0] + 0.5)**2)) +                      4*(1 - T.exp(-((W[0][0] + W[1][0])**2)))

O_two_minimums = 4-0.5*T.exp(-((W[0][0] + 2.5)**2+(W[1][0] + 2.5)**2))-3*T.exp(-((W[0][0])**2+(W[1][0])**2))

nesterov_testsuit = [
                (nesterov_momentum, "nesterov momentum 0.25",    {"learning_rate": 0.01, "momentum": 0.25}),
                (nesterov_momentum, "nesterov momentum 0.9",     {"learning_rate": 0.01, "momentum": 0.9}),
                (nesterov_momentum, "nesterov momentum 0.975",   {"learning_rate": 0.01, "momentum": 0.975})
            ]

cross_method_testsuit = [
                (nesterov_momentum, "nesterov",     {"learning_rate": 0.01}),
                (rmsprop,           "rmsprop",      {"learning_rate": 0.25}),
                (adadelta,          "adadelta",     {"learning_rate": 100.0}),
                (adagrad,           "adagrad",      {"learning_rate": 1.0}),
                (adam,              "adam",         {"learning_rate": 0.25})
            ]

for O, plot_label in [
           (O_wobbly, "Wobbly"),
           (O_basins_and_walls, "Basins_and_walls"),
           (O_giant_plateu, "Giant_plateu"),
           (O_hills_and_canyon, "Hills_and_canyon"),
           (O_two_minimums, "Bad_init")
        ]:

    result_probe = theano.function([Wprobe], O, givens=[(W, Wprobe)])

    history = {}
    for method, history_mark, kwargs_to_method in cross_method_testsuit:
        W.set_value(clean_random_weights)
        history[history_mark] = [W.eval().flatten()]

        updates = method(O, [W], **kwargs_to_method)
        train_fnc = theano.function(inputs=[], outputs=O, updates=updates)

        for i in range(125):
            result_val = train_fnc()
            print("Iteration " + str(i) + " result: "+ str(result_val))
            history[history_mark].append(W.eval().flatten())

        print("-------- DONE {}-------".format(history_mark))

    delta = 0.05
    mesh = np.arange(-3.0, 3.0, delta)
    X, Y = np.meshgrid(mesh, mesh)

    Z = []
    for y in mesh:
        z = []
        for x in mesh:
            z.append(result_probe([[x], [y]]))
        Z.append(z)
    Z = np.asarray(Z)

    print("-------- BUILT MESH -------")

    fig, ax = plt.subplots(figsize=[12.0, 8.0])
    CS = ax.contour(X, Y, Z, levels=levels)
    plt.clabel(CS, inline=1, fontsize=10)
    plt.title(plot_label)

    nphistory = []
    for key in history:
        nphistory.append(
                [np.asarray([h[0] for h in history[key]]),
                 np.asarray([h[1] for h in history[key]]),
                 key]
            )

    lines = []
    for nph in nphistory:
        lines += ax.plot(nph[0], nph[1], label=nph[2])
    leg = plt.legend()

    plt.savefig(plot_label + '_final.png')

    def animate(i):
        for line, hist in zip(lines, nphistory):
            line.set_xdata(hist[0][:i])
            line.set_ydata(hist[1][:i])
        return lines

    def init():
        for line, hist in zip(lines, nphistory):
            line.set_ydata(np.ma.array(hist[0], mask=True))
        return lines

    ani = animation.FuncAnimation(fig, animate, np.arange(1, 120), init_func=init,
                                  interval=100, repeat_delay=0, blit=True, repeat=True)

    print("-------- WRITING ANIMATION -------")

    # plt.show(block=True) #Uncoomment and comment next line if you just want to watch
    ani.save(plot_label + '.mp4', writer='ffmpeg_file', fps=5)

    print("-------- DONE {} -------".format(plot_label))

> PDF-версия статьи

Спасибо Роману Парпалак за инструмент, благодаря которому работа с формулами на хабре не так мучительна. Можете посмотреть статью, которую я брал за основу своей статьи — там есть много полезной информации, которую я опустил, чтобы лучше сфокусироваться на алгоритмах оптимизации. Чтобы ещё сильнее углубиться в нейронные сети, рекомендую эту книгу.

Хороших новогодних выходных, Хабр!

Поделиться с друзьями

-->

Комментарии (66)

BelBES
04.01.2017 15:18
#9995952
+3
К статье стоит добавить, что не умея пользоваться методами оптимизации, иначе как черным ящиком, практически не возможно повторить эксперименты с тренировкой таких могучих современных сетей, как VGG, ResNet, Inception, etc. с нуля, да и при умении пользоваться тоже приходится с бубном плясать, чтобы получить статейные циферки точности.
1. DistortNeo
  04.01.2017 16:40
  #9996112
  Да даже гораздо более простые вещи нельзя в лоб оптимизировать, например, вот такой функционал (многокадровое суперразрешение):
  
  А ведь он вообще идеальный: не имеет локальных минимумов, но Нестеров, например, сходится на порядок быстрее, чем обычный субградиент.
  
  Здесь, правда, всё сводится к опыту: смотрим на график, показывающий поведение ошибки и крутим параметры метода. Наилучшие результаты достигаются при динамически изменяющимся коэффициенте перед шагом градиента (learning rate).

begemot_sun
04.01.2017 19:48
#9996308
+2
Актуальная тема. Выбор параметров настройки НС до сих пор «исскусство». Вот когда это дело формализуют, тогда будет прорыв на следующую ступень технологий AI.
1. Siarshai
  04.01.2017 20:00
  #9996322
  Так не формализуется это дело толком. Для этого нужно наложить какие-то ограничения на функцию потерь, а она меняется от задачи к задаче, от сети к сети, от нелинейности к нелинейности.
  Это, конечно, поспособствовало бы прорыву в AI, но есть гораздо более важные вещи.
1. eiennohito
  05.01.2017 13:05
  #9997118
  +2
  Почти по теме: вот как раз вчера читал https://arxiv.org/pdf/1606.04474v2.pdf
  
  Learning to learn by gradient descent by gradient descent (NIPS 2016)
  
  Учат оптимизатор как нейросеть

supersonic_snail
04.01.2017 20:47
#9996374
Отличное ревью, ничего не забыто, все хорошо прокоментировано. Спасибо.

Где-то с полгода назад видел я статью, где люди сказали «а давайте используем еще одну нейросеть, чтобы выбирать размеры шагов sgd». Вроде показывают, что если обучить всю такую мега систему end-to-end, как сейчас модно, то работает неплохо, но жутко вычислительно неэффективно. Было бы любопытно посмотреть, как та сеть себя поведет на разных ваших примерах, особенно том, где все сфейлили, кроме Adam-а.
1. ggrnd0
  04.01.2017 22:26
  #9996444
  В задачах оптимизации не «выпуклых функций» абсолютно любой алгоритм может сфейлиться. то что алгоритм справился, считай чистая случайность…

sim0nsays
04.01.2017 23:30
#9996508
+5
Отличный пост!
Я бы хотел добавить, что дополнительная мотивация увеличивать веса в направлении маленького градиента — это чтобы лучше вылезать из седловых точек, в которых практически всегда застревает отпимизация (настоящий локальный минимум встретить в таком многомерном пространстве — очень маловероятно)
Вот наш кумир Andrej Karpathy в CS231 поясняет - http://cs231n.github.io/neural-networks-3/#ada
1. Siarshai
  05.01.2017 00:19
  #9996542
  Спасибо. Действительно, хорошее замечание насчёт седловых точек.

mephistopheies
05.01.2017 09:19
#9996728
+1
пс, а ты не в курсе про http://opendatascience.ru/? у нас чат в слаке, там есть канал по дип лернингу, тебя там уже ждут
1. varagian
  05.01.2017 14:40
  #9997236
  а что там ещё помимо DL?
  1. mephistopheies
    05.01.2017 14:44
    #9997244
    прочий мотан, но вообще вопрос странный, разве нужно что-то еще кроме дл?
    
    varagian
    05.01.2017 15:02
    #9997260
    Какой-то холиварный вопрос, как бы DL ? DS. А там визуализация или интерпретируемые методы вполне могут быть интересны людям и без DL.
    
    mephistopheies
    05.01.2017 15:24
    #9997306
    ладно ладно, все там есть, около 30 каналов и уже >2к людей
1. Siarshai
  05.01.2017 16:05
  #9997368
  Хм, «Сорян, сайт временно на реконструкции»
  1. mephistopheies
    05.01.2017 16:06
    #9997370
    так бывает, упорство и трут все перетруд
1. kraidiky
  07.01.2017 01:42
  #9998980
  Подписан туда. Быстро обнаружил, что там есть или очень хардкорные товарищи, обсуждающие свои очень специфические темы на птичьем языке, до которых мне ещё тянуться и тянуться, либо датасайнтисты, применяющие всё из коробки и не интересующиеся алгоритмами вообще. Среднее звено между толпой в розовых толстовках и и суровыми баесианцами представлено крайне слабо и на том уровне, на котором эта статья поговорить можно мало с кем.
  Но если автор этой статьи подтянется глядишь станет на одного больше.
  
  >> «Сорян, сайт временно на реконструкции»
  А на сайте кроме формы регистрации в чатике ничего и нет, и по большому счёту и не нужно. Так что он весто останется на реконструкции. :)))
1. BelBES
  07.01.2017 16:39
  #9999360
  Имхо, на данный момент самый живой чат по ML, DL и всему с этим связанному в кружочках.
  1. mephistopheies
    07.01.2017 16:44
    #9999366
    конечно нет, самое большое русскоговорящее это одс, сейчас там 2.5к людей
    
    buriy
    11.01.2017 18:12
    #10006918
    +1
    Увы, самое большое — не значит самое хорошее.
    По соотношению сигнала к шуму ODS сильно проигрывает кружочкам.
    Всё таки древовидный форум намного лучше линейного IRC-style чатика.
    
    mephistopheies
    12.01.2017 11:31
    #10008438
    расскажите мне про отношение сигнала к шуму
    
    buriy
    12.01.2017 15:53
    #10009344
    +1
    Процитирую пару первых попавшихся сообщений из поиска по интернету:
    «When social communities grow past a certain point (Dunbar’s Number?), they start to suck. Be they sororities or IRC channels, there’s a point where they get big enough that nobody knows everybody anymore. The community becomes overwhelmed with noise from various small cliques and floods of obnoxious people and the signal-to-noise ratio eventually drops to near-zero — no signal, just noise. This has happened to every channel I’ve been on that started small and slowly got big.»
    И про плоский формат форума: http://inmotion.live/notes/forums-types/
    «Плоский формат — Минусы:
    — Ответ на вопрос может быть отделен многими страницами флейма.
    — Не всегда легко понять, кто кому и на что отвечает.
    — Уход разговора «в сторону» и, наоборот, возвращение к основному топику невозможно отследить, не прогрузив всю нить целиком (или несколько страниц).
    — Нить – всегда «кот в мешке», на прогрузку и чтение неинтересных дискуссий уходит слишком много времени.»
    
    Добавлю ещё такой нюанс IRC-style формата: если никто не ответил на вопрос хорошо в течение нескольких следующих сообщений, то никто его обсуждать больше не будет. А значит, этот стиль не для сложных вопросов, к которым можно возвращаться через дни или недели.
    Содержательных дискуссий (больше чем на 3 фразы) по DL на ODS я за 3 недели не увидел, зато сообщений не по теме и разнообразных смайликов-реакций — сколько угодно.
    
    BelBES
    13.01.2017 16:52
    #10011806
    Может там сейчас не самая "жара", но активных юзеров там не больше 50 (и даже эта оценка завышена) и большинство обсуждений — это small talks на около-ML тематику. В то время как в кружочках при чуть меньшей аудитории (думаю, что там примерно 10-15 боле-мене активных юзеров) концентрация полезных обсуждений выше.
    
    Ну и как правильно пишет buriy, полезные сообщения там легко теряются в потоке отвлеченных разговоров.
    
    Но как тематический чат, да, намного лучше полудохлых telegram-чатов на схожую тематику)
    
    varagian
    13.01.2017 19:28
    #10012070
    Видимо "жара" спала в январе — кинул заявку дней десять назад и тишина.

pchelintsev_an
05.01.2017 18:30
#9997618
Отличный топик на Хабре! Такое детальное исследование численных методов оптимизации — снимаю шляпу! Когда был студентом, программировал различные методы, тема очень знакома.

P.S. С Новым годом!

ndv79
06.01.2017 12:20
#9998380
Nesterov — это конвексная оптимизация, а так как обучение нейронных сетей — мягко говоря, не конвексная задача, то Nesterov более подвержен застреванию в локальном минимуме, чем SGD.
1. Siarshai
  06.01.2017 12:25
  #9998392
  Nesterov более подвержен застреванию в локальном минимуме, чем SGD.
  
  С чего бы? Действительно, сходимость всех эти оптимизаторов к глобальному минимуму (включая SGD) доказана только в случае выпуклых функций. Но у ванильного SGD вообще нет никаких методов преодолевания «бугров» на пути, на то он и ванильный. Как по мне, так он больше всех подвержен застреванию в локальных минимумах.
  1. ndv79
    06.01.2017 13:17
    #9998424
    SGD — стохастический, поэтому движение происходит не в сторону градиента целевой функции ошибки (которая включает всю обучающую выборку), а в сторону градиента ошибки от случайной подвыборки. Считайте, что вы к настоящему градиенту прибавили нормально распределенный шум. Этот шум и позволяет выбираться из локальных минимумов.
    
    Siarshai
    06.01.2017 20:30
    #9998728
    Все вышеописанные алгоритмы также поддерживают обучение minibatch-обучение
    
    ndv79
    06.01.2017 20:39
    #9998740
    А, ну тогда нет проблем
    
    BelBES
    07.01.2017 16:47
    #9999372
    А разве кто-то вообще учит сетки, считая градиент ошибки сразу по всей выборке? Вроде бы стандарт де факто — это тренировка на минибатчах.
    
    ndv79
    13.01.2017 16:18
    #10011710
    А разве кто-то вообще учит сетки, считая градиент ошибки сразу по всей выборке?
    
    Вообще-то, да. Например, все квазиньютоновские методы оптимизации. Либа netlab для octave/matlab вообще не умеет минибатчи.
    
    Эта статья — про минимизацию функции. Алгоритм Нестерова — про то же. А когда мы обучаем сеть, то на каждом шаге функция разная. Очень разная. Градиентный спуск в этих условиях, очевидно, сходится (в гугле это доказали математически недавно). Квазиньютоновские методы в этих условиях, очевидно, не сходятся, так как оценивают гессианскую матрицу по значениям градиента в соседних точках, используя BFGS. Если они посчитаны на разных батчах, в гессианской матрице будет мусор.
    
    С алгоритмом Нестерова не все так однозначно. В scikit и caffe он идёт опцией, а не по умолчанию.
1. kraidiky
  07.01.2017 01:11
  #9998958
  +1
  Пришлось погуглить что такое конвексная поверхность прежде чем писать развёрнутый комментарий. :)
  На самом деле условие конвексности всей адаптивной поверхности чрезвычайно избыточное. Стоит говорить лишь о достаточной простоте поверхности если она ведёт себя как конвексная на участке, достижимом из текущей точки за несколько (не слишком много) циклов обучения. Это очень важное уточнение, потому что достижимая область для алгоритмов первого порядка, как правило, непосредственно ограничивается скоростью обучения. Уменьшив скорость в 1000 раз вы с удивлением обнаружите, что поверхность, которую изучает ваш алгоритм достаточно простая. Но это не такое важное уточнение.
  
  SGD с моментом (я раньше встречал только такое название Нестерова в неспецифической литературе) действительно подвержен зависанию в локальных минимумах больше чем SGD, но вопрос в том, на сколько более подвержен?
  
  В первом приближении можно сказать, что способность SGD покидать локальные минимумы связана с размерами бросков, которые испытывают веса после каждого изменения, грубо говоря броски должны быть сопоставимы с размерами минимума чтобы алгоритм имел шанс случайно его покинуть. SGD с моментом тоже имеет такие броски, если вдуматься они меньше ровно во столько раз, какое у вас окно округления. Если окно округления 100, то есть параметр 0.99 то броски будут в сто раз меньше. То есть SGD с моментом с скоростью 0.1 будет по способности выходить из локальных минимумов будет аналогичен обычному SGD со скоростью 0.001
  
  Однако реальная функция по которой мы ищем минимум, как правило имеет как участки достаточно простые, так и участки испещрённые локальными минимумами. На простых участках SGD with M от обычного SGD почти не отличается при равной скорости.
  
  Вот и получается, что если вы заранее не знаете рельефа вашей функции или подозреваете, что он может содержать как относительно ровные так и очень зубастые участки, а вы не планируете поправлять параметры вручную очень внимательно следя за сетью, то лучше иметь не SGD v=0.001, а SGD+M v=0.1
  
  Прошу прощения за очень неканонические обозначения.
  1. kraidiky
    07.01.2017 01:47
    #9998982
    Блин!!! Во я тупой! После беглого просмотра не понял суть отличия Нестерова от SGD с моментом. Часть моего коммента про простоту функции в окрестности можно вычёркивать.
1. kraidiky
  07.01.2017 01:20
  #9998972
  +1
  Более подробно посмотреть на примере когда сеть идёт по какому типу рельефа можно вот в этой моей статье на хабре: https://habrahabr.ru/post/221049/ Там описан способ, который я использую чтобы визуализировать это движение не для упрощённой двумерной функции, а для реальной нейросети решающей реальную, хоть и несложную задачу. Кроме выводов, которые я тут уже описал смотрение на такую визуализацию позволяет сделать ещё много интересных наблюдений, так что всем советую пользоваться. Но почти уверен, что никто этим советом не воспользуется. :)
1. kraidiky
  09.01.2017 23:49
  #10002844
  Но, кстати, по поводу неконвексной задачи. Я в своё время в числах посмотрел какая доля синапсов имеет больше двух значимых производных. Брал экспериментально получал первую производную и вторую дважды по одной и той же координате. А потом смотрел, на сколько результат на большом расстоянии будет отличаться от маленького. К моему немалому удивлению поведение процентов 95 всех синапсов хорошо описывались всего двумя производными. Но вот в сторону лучшего градиента ситуациябыла совершенно иная. Вероятно те синапсы, для которых задача неконвексная и есть самые важные.

kraidiky
07.01.2017 00:29
#9998920
+1
Боже ж ты мой! Реально полезная статья про алгоритмы нейросеток на хабре. Так неожиданно, что я даже расчехлил свой комп посреди отпуска чтобы высказать свой респектище и накатать несколько комментариев. Теперь понятно чем заняться в ближайшее время — воспроизводить все описанные алгоритмы в пробирке. А то у меня только самый первый сейчас используется.

Dark_Daiver
07.01.2017 01:04
#9998952
+1
Классная статья!

> Рабочие оптимизаторы второго порядка существуют, но пока что давайте сконцентрируемся на том, что мы можем достигнуть, не рассматривая вторые производные.

Немного позанудствую, Алгоритм Левенберга-Марквардта это все же не совсем метод второго порядка, и он использует первые производные (но не совсем производные от ф-ии ошибки) чтобы аппроксимировать матрицу вторых производных.
1. kraidiky
  07.01.2017 01:34
  #9998978
  +2
  Апроксимирование матрицы вторых производных — дело чрезвычайно неблагодарное. В своё время я её считал для нейросети всякими хитрыми аналитическими способами и даже напрямую измерял «в лоб» для каждого из весов сети попарно. И когда я сталкиваюсь с фразами «а давайте, примем для простоты, что она диагональная» и тому подобным меня больше удивляет, что такие методы работают хоть как-то вообще. Она капец какая не диагональная, и непростая.
  
  Алгоритм Левенберга-Марквардта мне не хватило терпения разобрать по косточкам, но на сколько я успел понять он тоже основан на нектором такого же рода упрощении.
  
  Но что гораздо более важно. все алгоритмы второго порядка намертво застревают в локальных минимумах если к ним не применять жестокое обращение. А применять глубокое обучение обычно имеет смысл только в тех задачах, где этих локальных минимумов милиарды миллионов. В случаях, когда это не так — обычные алгоритмы, гораздо менее капризные чем нейросети дают результат ничуть не хуже.
  1. Dark_Daiver
    07.01.2017 09:22
    #9999084
    меня больше удивляет, что такие методы работают хоть как-то вообще. Она капец какая не диагональная, и непростая.
    
    Меня тоже =)
    Но ведь если наша аппроксимированная матрица позволяет нам достаточно быстро спускаться, так ли важно точная ли она? Тем более (если я не ошибаюсь), реальная матрица может быть не положительно определенной, и тогда мы не сможем уменьшить ошибку.
  1. barmaley_exe
    12.01.2017 15:45
    #10009330
    И когда я сталкиваюсь с фразами «а давайте, примем для простоты, что она диагональная» и тому подобным меня больше удивляет, что такие методы работают хоть как-то вообще. Она капец какая не диагональная, и непростая.
    Всё же лучше, чем считать, что эта же матрица вообще скалярная как в случае простых методов первого порядка.
    
    Но что гораздо более важно. все алгоритмы второго порядка намертво застревают в локальных минимумах если к ним не применять жестокое обращение
    А Вы чего хотели? Нахождение глобального минимума невыпуклой задачи – NP сложная задача, никакой надежды на это нет. Радоваться надо тому, что методы второго порядка добираются до локальных минимумов.
    
    А применять глубокое обучение обычно имеет смысл только в тех задачах, где этих локальных минимумов милиарды миллионов
    Локальные минимумы есть артифакт модели и функции потерь, непонятно, о каких локальных минимумах Вы говорите, не задав сперва оптимизируемую поверхность.
    
    kraidiky
    12.01.2017 23:41
    #10010360
    Локальные минимумы есть артифакт модели и функции потерь, непонятно, о каких локальных минимумах Вы говорите, не задав сперва оптимизируемую поверхность.
    
    Множество локальных минимумов может быть свойством входных данных изучаемой задачи, а не искомой поверхности и метрики которую мы оптимизируем. Приведу простейший пример, с которым когда-то встретился — на входе у вас два действительных числа — координаты, на выходе действительное число — рельеф очень простой функции. В задача почти нет локальных минимумов, сеть учится «в лёт» на нескольких нейронах:
    
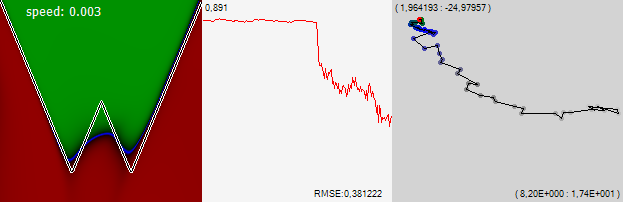
    Потом берём ту же самую функцию, но входные денные — 16 бинарных признаков. Первые 8 — битовое разложение первой координаты, вторые 8 то же самое для второй. Аналитически задачка решается слоем из двух нейронов, первый из которых композитит первые 8 бинарных признаков, а второй вторые 8 после чего задача свелась к предыдущей. Но это если логически подумать. А если просто предложить задачу сети, то для неё эта задача имеет чудовищно сложный рельеф с множеством локальных минимумов. И способность быстро найти первый из них даёт угрюмый результат:
    
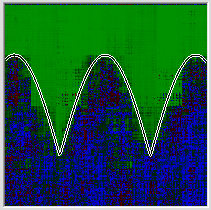
    И это при том, что конечная задача и метрика точно такие же. Я не проверял лично, но я почти уверен, что любая задача, входные данные которой будут обладать высокой дискретностью, например текстовой анализ, если на вход подавать не приведённые бинарные признаки слов, будет обладать теми же свойствами, вне зависимости от того какую оптимизируемую поверхность вы зададите, то есть какой вывод будете ожидать от сети.
    
    Конечно можно сказать, что это артефакт модели и если вместо буквально слов подавать на вход их ворд2векнутое представление минимумов будет меньше, но это уже привлечение априорной информации о данных, то есть по сути переформулировка задачи.
    
    Всё же лучше, чем считать, что эта же матрица вообще скалярная как в случае простых методов первого порядка.
    А вот вопрос лучше ли. Я пока пробовал сравнивать SGD с методами более или менее второго порядка только на узком круге задач, но уже пришёл к мысли, что способность миновать ближайшие локальные минимумы может быть важнее чем способность их быстро найти по крайней мере для задач некоторой сложности. Если поверхность как на иллюстрациях в статье, тогда да, хорошо найти побыстрее какой-нибудь минимум. Но, если вспомнить, что настоящих локальных минимумов в задачах такой размерности почти не бывает, то то что нам касается локальным минимумом на самом деле седловина — один из коридоров лабиринта. Например такого:
    
    И вот теперь вопрос, много ли мне счастья от того что мой алгоритм очень быстро найдёт середину ближайшего от Маши прохода? В такой задаче успех сводится или к умению бодро бегать вдоль туннелей, или скакать через стены.
    
    Конечно открытым остаётся вопрос каков на самом деле рельеф в конкретной задаче. В некоторых самых простых задачах, которые я попробовал результат фактически не зависил от момента, и это свидетельствует, что в них рельеф очень гладкий. Но есть способ проследить за рельефом буквально. Я его в своей статье описывал — присваиваем каждому синапсу произвольный двумерный единичный вектор, и суммируем их все помноженные на веса синапсов. Получается почти произвольная проекция пространства в котором ищет сеть на двумерное пространство, где текущее состояние сети это одна точка. Следя за траекторией этой точки можно предполагать свойства поверхности, по которой она катается в поисках минимума. Я сделал соответствующее видео:
    
    barmaley_exe
    13.01.2017 16:37
    #10011758
    И к чему это полотно текста? Во втором примере Вы специфицировали модель, для которой нашли локальные минимумы. Потрудились бы, что ли, доказать, что нельзя моделью с выпуклой поверхностью задачу решить.
    
    Я не проверял лично, но я почти уверен
    Вера – это про религию, а мы здесь науку / инженерию обсуждаем.
    
    kraidiky
    13.01.2017 16:57
    #10011818
    Вы правы, полотно текста ушло впустую. Жаль.
    
    Вера – это про религию, а мы здесь науку / инженерию обсуждаем.
    
    И если уж на то пошло — большое заблуждение считать что эта область является инженерией. Это гораздо ближе к области блуждающего поиска и описания случайно найденного. Здесь чаще всего не доказывают, а находят и убеждают в применимости. Сколько из 10 последних применённых вами методов имели формально доказанную эфективность?
    
    Если сравнивать DL с наукой, то это скорее география, чем математика.
    
    barmaley_exe
    13.01.2017 17:08
    #10011844
    Жаль
    Краткость – сестра таланта. Чем длиннее ваше описание, тем меньше шанс, что Вам удастся донести свою идею до собеседника. Более того, пространные рассуждения плохи ещё и тем, что если собеседник не согласен с одним из ранних тезисов, вся дальнейшая цепь импликаций бессмысленна.
    
    Не имеет значения, география это или математика. Важно лишь то, что это воспроизводимые наблюдения, а Ваше утверждения основываются на частных примерах и "почти уверенности". Как если бы путник, случайно блуждающий в пустыне, говорил о том, что снега не существует.
    
    В рассуждениях про локальные минимумы Вы противоречите себе:
    
    способность миновать ближайшие локальные минимумы может быть важнее чем способность их быстро найти [...] настоящих локальных минимумов в задачах такой размерности почти не бывает, то то что нам касается локальным минимумом на самом деле седловина
    Так если локальных минимумов почти нет, зачем же их избегать?
    
    kraidiky
    13.01.2017 19:16
    #10012034
    В рассуждениях про локальные минимумы Вы противоречите себе:
    Так если локальных минимумов почти нет, зачем же их избегать?
    
    Ну вообще-то это не я говорю а Карпаты и иже с ними. https://habrahabr.ru/post/318970/#comment_9996508 Там это подробно разобрано, что когда люди говорят «локальный минимум» в применении к нейросетям они обычно сталкиваются с седловыми точками — в виде длинных узких тоннелей, в которых обучение вязнет. Если бы вы потрудились прочитать эту портянку, то узнали бы что я вам предложил простой способ как воспроизвести всё мои наблюдения на любой вашей сети наглядно, причём в две питоньи строки, и ещё много чего, что не имеет смысла тут повторять, потому что всё это уже написано один раз, но вам не понравилась какой-то из из тезисов.
    
    Я не сразу понял, что я должен убеждать и очень умело формулировать мой текст чтобы вы стали интересоваться сутью написанного. Но мне сказали, что вы вдумчивый интересный комментатор на ods, вот я и полез, как дурак, тратить своё и ваше время.
    
    Жаль.
    
    barmaley_exe
    13.01.2017 20:44
    #10012174
    Ну вообще-то это не я говорю а Карпаты и иже с ними
    Это где он такое говорит, можно конкретную ссылку? Хочется избегать седловых точек, да, а вот локальные минимумы нас вполне устраивают (тем более, что их слишком мало, чтобы ими пренебрегать)
    
    когда люди говорят «локальный минимум» в применении к нейросетям они обычно сталкиваются с седловыми точками
    Не надо подменять понятия, седловые точки и локальные минимумы – разные вещи.
    
    kraidiky
    14.01.2017 00:34
    #10012414
    Вас устраивают? Очень хорошо. Мне этого мало — мои проблемы. Зачем вы тратите моё и своё время чтобы пытаться меня переспорить? Чего пытаетесь добиться?
    
    Чтобы я не пытался вам ничего объяснять? Так этого результата вы добились своим первым комментарием. Или я был слишком глуп чтобы начать с вами чем-то поделиться. Или вы слишком умны чтобы мочь воспринимать эти, в общем-то, очень простые вещи если они не написаны наукообразно. Но даже если бы это было не так — попытки придираться к словам не обогатили бы знаниями ни одного из нас.

kraidiky
07.01.2017 02:15
#9999000
+2
Два маленьких комментария по самой статье пока не ушёл в оригинал:
1) Выбор для момента чисел порядка 0.9 исторически сложился, но не имеет под собой рациональных оснований. Если ты понимаешь что ты делаешь можно ставит окна округления на порядки больше. Я, например, свои лучшие сети учил при 0,999, с соответсвующей скоростью, конечно. Более того, когда ты делаешь отжиг, например, ты можешь не уменьшать скорость каждый раз, а оставлять скорость той же, но увеличивать окно округления. Результат по локальным минимумам такой же, а скорость схождения на порядки выше. Объяснение механизма в мегакомменте выше.
2) График ошибки в самом конце статьи — самая дезориентирующая вещь на свете. Я даже когда-то хотел написать статью с названием «Обучение вашей нейросети начинается только после того как она уже сошлась». На самом деле после того, как ошибка уже вышла на полочку внизу если продолжить учить умело играя параметрами сети можно улучшить результат, например, в два раза. И вот то, на сколько её можно ещё после этого улучшить драматическим образом зависит от алгоритма и способа обучения. Обычное обучение полной выборкой без минибатча или методы второго порядка намертво зависают в первых же большого размера локальных минимумах и после выхода на полку дальше уже, практически, не учатся. SGD при постипенно снижающейся скорости даже без ничего больше может нащупать решение, например, в полтора раза лучше, перед этим конечно изрядно пометавшись по округе. А SGD с моментом с постепенно увеличивающимся окном например до 1000 и скоростью уменьшающейся например до 0.001 может найти места близкие по размерам к точности вычисления float в проце.
На сколько хороши или плохи другие упомянутые в статье алгоритмы после «выхода на полочку» — узнаю если найду время с ними поэкспериментировать. За что ещё раз спасибо.

Arqwer
10.01.2017 01:24
#10002956
В статье указано, что при некоторых параметрах оптимизаторы могут выскакивать из глобального минимума, и сказано что это проблема. Почему? Разве нельзя просто запоминать, где был достигнут минимум функции ошибок, и возвращаться туда?
И ещё интересно, применяются ли для обучения НС какие-то методы непохожие на модификацию SGD? Имитации отжига, или ещё какие-нибудь необычные?
1. Siarshai
  10.01.2017 01:33
  #10002966
  В статье указано, что при некоторых параметрах оптимизаторы могут выскакивать из глобального минимума, и сказано что это проблема. Почему? Разве нельзя просто запоминать, где был достигнут минимум функции ошибок, и возвращаться туда?
  
  Разумеется, можно. Так обычно и поступают, это называется обучение с возвратами. К сожалению, это сильно замедляет обучение, т.к. каждую эпоху приходится сохранять всю сеть. Этот приём не относится напрямую к оптимизаторам, его же используют и в других случаях, когда ошибка на валидационной выборке может возрастать.
  
  И ещё интересно, применяются ли для обучения НС какие-то методы непохожие на модификацию SGD? Имитации отжига, или ещё какие-нибудь необычные?
  
  Для имитации отжига слишком много параметров. Из интересного: RBM, но это уже не обычная нейронная сеть прямого распространения.
  1. Dark_Daiver
    10.01.2017 06:47
    #10003110
    >это сильно замедляет обучение, т.к. каждую эпоху приходится сохранять всю сеть
    btw, мне казалось что просто скопировать веса сети в любом случае значительно дешевле чем посчитать градиент. А градиент мы так или иначе считаем каждый раз. Я не прав?
    
    Siarshai
    10.01.2017 16:26
    #10004216
    Просто скопировать веса нейронной сети — действительно просто, наверное, я погорячился, сказав, что это так уж сильно замедляет обучение. Но часто они расположены не в оперативной памяти, а в GPU. Если сеть большая, их хорошо бы сбросить из RAM на диск.
    
    DistortNeo
    10.01.2017 18:12
    #10004492
    В случае свёрточной нейросети количество коэффициентов — от 10 до 100 тысяч.
    А львиная доля памяти расходуется на хранение обучающей выборки (она не меняется) и вычисление градиента (его вообще хранить не нужно).
1. Dark_Daiver
  10.01.2017 06:43
  #10003104
  +1
  Что характерно, попадание прям в самый глобальный минимум нам не то чтобы особо нужно — нередко это может привести к оверфиту. А в реальности мы хотим минимизировать ошибку не для обучающей выборки, а для всех возможных данных (но не можем, т.к. у нас есть только обучающая/валидационная/тестовая выборка =) ). Если я не ошибаюсь
  
  >методы непохожие на модификацию SGD
  Раньше в почете были методы использующие приближенную вторую производную — сопряженные градиенты, BFGS. Сейчас вроде как применяют только SGD. Ибо быстро.
  Использование не градиентных методов, ИМХО, не особо оправданно из-за огромного пространства поиска.
1. kraidiky
  11.01.2017 01:16
  #10005180
  Разве нельзя просто запоминать, где был достигнут минимум функции ошибок, и возвращаться туда?
  и даже не оверфит самая большая проблема. Методы борьбы с ним, в конце концов, уже многочисленны. Дело в том.что чтобы узнать, что вы пришли в глобальный минимум вам нужно посчитать ошибку для всей имеющейся у вас выборки. А если ваша учебная выборка — несколько террабайт текстов из википедии это может быть немножечко затратно.
  
  В процессе обучения обычно следят не за реальной ошибкой, а за скользящей средней ошибкой на обучающих батчах, подсчёт которой оказывается побочным продуктом обучения сети.

dim2r
10.01.2017 13:28
#10003716
А есть применить AI для настройки другого AI?
1. Siarshai
  10.01.2017 16:28
  #10004218
  +2
  Выше есть комментарии про обучение нейронной сети при помощи другой нейронной сети. Если же вы про подбор параметров при помощи другой сети или какого-то алгоритма — это жутко долго.
  1. kraidiky
    11.01.2017 01:19
    #10005182
    А вот подбор метапараметров более простым эволюционным алгоритмом я считаю перспективненьким. Типа есть у меня, например 10 родственных сеток, учащихся одновременно. Даже если без скрещивания раз в поколение худшую выкидываю, а лучшую копирую изменив один метапараметр. Уже должно быть неплохо. Но, блин, с той скоростью, с которой я пишу, до экспериментов с этой темой я может года через два дойду. :(
    
    Siarshai
    11.01.2017 01:45
    #10005202
    +1
    Представьте себе количество параметров:
    
    Размер minibatch
    
    Алгоритм обучения
    
    Параметры, которые входят в алгоритм обучения. Как минимум learning rate: 1-5
    
    Регуляризация L1, L2, шум, ещё что-нибудь: 3-5
    
    Количество слоёв и нейронов в них. Тут можно очень здорово сузить количество вариантов, но всё равно это минимум два параметра: «толщина» и «глубина»
    
    Функции активации
    
    Если обучаем CNN, то размер окон свёртки и пулинга
    
    Если обучаем ансамбль, то размер ансамбля и способы его объединения
    
    Много всякой специфичной фигни
    
    Даже если зафиксировать большую часть параметров (скажем, выкинем параметры отвечающие за архитектуру сети, а не за обучение), то всё равно будет параметров 5-10. Учтите, что сеть при обучении может засесть в плохом или хорошем локальном минимуме, поэтому хорошо бы её обучать хотя бы раза три и брать среднюю точность как fitting factor. Мне кажется, описанному эволюционному алгоритму понадобится итераций 50, чтобы сойтись хоть куда-нибудь (а вообще больше). Если предположить, что NN у нас несложная, и её обучение занимает пять минут, то 3*5*50 = 750 = 12.5 часов. Если же в меру сложная — час — то 3*60*50 = 9000 = 150 часов = 6 дней.
    
    Итог: хорошо для экспериментирования на MNIST, плохо на практике, если у вас совершенно случайно нет вычислительного кластера.
    
    kraidiky
    11.01.2017 02:02
    #10005212
    А вы меня немного неправильно поняли. Я хочу менять только те метапараметры, которые можно поменять налету. То есть я не с 0 учу сеть каждый раз, а учу, например 10 сетей, Через 10 эпох останавливаюсь, самую плохую из 10 сетей, если она хуже среднего на сколько-то, стираю. Лучшую дуплиёцирую и мутирую в ней один параметр. После чего иду дальше. Разница в скорости получется ровно во столько раз сколько сетей в популяции.
    
    Некоторые параметры, которые привычно считают неизменяемыми налету тоже можно менять при должной ловкости. Например, мутацией может быть дропаут или добавление нейрона в случайный слой. Только какую-то кроссвалидацию добавить чтобы алгоритм с добавлением нейронов не перебарщивал. А при остальных мутациях можно даже и без этого.
    
    Siarshai
    11.01.2017 02:13
    #10005224
    +1
    Менять параметры налету — довольно странно. Если сеть уже сошлась в какой-то минимум, а затем мы немного поменяли параметр, скорее всего она так и останется в этом минимуме. См. мои размышления в статье о том, как ведёт себя в минимуме Нестеров. Если у него в минимуме поменять гамму — он так и останется в этой точке, ведь ему неоткуда будет набрать скорость. Да и если обучать сеть с одними параметрами, затем изменить параметры, после чего продолжить обучать сеть — и получить какой-то хороший результат — это совсем не то же самое, что обучать сеть сразу со вторыми параметрами. По-хорошему, придётся повторять всю историю параметров.
    
    kraidiky
    11.01.2017 03:03
    #10005252
    +1
    Если вам это странно — советую начать пробовать. :) Много интересного увидите.
    За нестерова не ручаюсь, а обычный SGD с моментом может много куда уползти после того как алгоритм казалось бы сошёлся. Как я писал в комментариях выше: «После того как ваша сеть сошлась обучение только начинается».
    
    а и если обучать сеть с одними параметрами, затем изменить параметры, после чего продолжить обучать сеть — и получить какой-то хороший результат — это совсем не то же самое, что обучать сеть сразу со вторыми параметрами.
    
    Простой пример. Берём достаточно сложную задачку с кучей минимумов, не ирисы, Учим GD minibatch. Размер пачки 100, скорость 0,05. Сеть куда-то сошлась, ошибка 0.35. Потом меняем параметры, 200/0.02, потом 200/0.01, потом 200/0.005, потом 500/0,005, потом 1000/ 0.001. Получаем сеть с ошибкой 0.22. Вопрос, могли бы мы туда попасть стартовав с параметрами 1000/0.001? Да никогда в жизни, — при таком маленьком уровне стахастики для нас первый же локальный минимум стал бы последним, и не видать нам ошибки 0.4 как своих ушей. Цифры близки к реальным, использовавшимся при обучении сети из моей статьи. Первичное схождение сети минут 20, полное обучение до конца — 8 часов, больше сеть уже не училась — ей синапсов нехватало на большее. Правда это времена на страшно тупо реализованной сетке, так что обращать внимание не на абсолютные значения времени, а только на соотношения.
    
    Более широко известнай пример: того что, никаким обучением сразу с конечными параметрами вы не сможете достигнуть такого же результата, хоть 100 лет учите — современные сети для распознавания изображений:
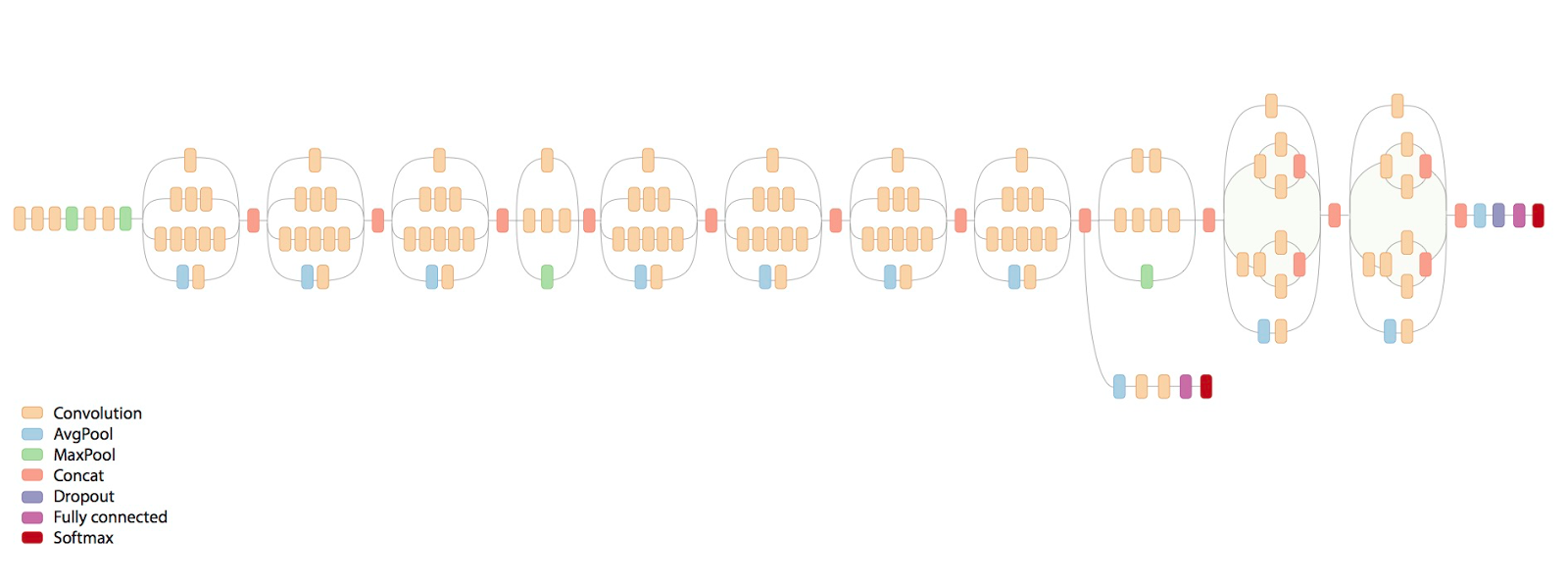    Если сразу учить всю эту гирлянду — эффект будет никакой. Берёте первый повторяющийся блок, к концу прикручиваете фулл-коннектед и софтмакс солои — учите. Потом отрубаете последние два слоя, до конката, вместо них добавляете ещё один повторяющийся блок и к нему фуллконнектед и софтмакс. Опять учите, и так 8 раз пока сеть не разрастётся до такой вот гирлянды. После чего добавляете на конец ещё одну надстройку с картинки и учите уже финально. Профит. Это я уже не конкретно эту сеть описывал, а вообще как учится весь класс сетей с такими архитектурами.
    
    Siarshai
    11.01.2017 08:07
    #10005340
    +1
    C SGD вы описали learning rate decay. Тут я согласен: действительно хороший способ менять параметры сети во время обучения. Но суть прочих алгоритмов в том, что они автоматически настраивают скорость обучения (ещё одна перспектива на то, зачем нужен импульс). Я как то пробовал делать learning rate decay на Нестерове — это никак не сказалось на результатах сети.
    
    Насчёт гирлянд, как на картинке: я, опять таки, согласен с итеративным способом обучения (занимался им и получил хорошие результаты), но не пойму причём тут эволюционные алгоритмы.
    
    Впрочем, чего тут болтать — тут экспериментировать надо. Может, затухание скорости обучения действительно работает и не только на SGD, и мне просто тогда попались неудачные параметры сети или датасет с маленьким количеством минимумов/седловых точек.
    
    kraidiky
    11.01.2017 14:08
    #10006046
    Так для того и говорим, чтобы знать о чём экспериментировать.
    Скорость большинство приведённых тут алгоритмов регулируют. А вот размер окна округления — нет. Про ценность окна округления тут: https://habrahabr.ru/post/318970/#comment_9998958
    Если вы используете SGD с моментом можно менять момент. Если mini-batch — можно менять размер батчей. На самом деле это почти одно и то же.
    
    Кроме того есть куча других параметров, которые можно менять. Параметры регуляризации, параметры дропаута. Параметры добавления нейронов, добавление слоёв, удаление промежуточных аутпутов. Это только из общепринятых параметров.
    
    buriy
    13.01.2017 05:42
    #10010536
    +1
    >Если сразу учить всю эту гирлянду — эффект будет никакой.
    Эмм… С ResNet уже не так, промежуточные выходы блоков больше не нужны.
    До ResNet и BatchNorm (и ReLU) это была скорее общая проблема с vanishing gradient, из-за которой нельзя было учить сильно многослойные сети (а до 2008 года из-за использования sigmoid эта же проблема была и с обучением сетей глубже 2 слоёв!).
    Даже сразу неизменный learning rate в 0.001 достаточен, если каждый следующий слой не теряет большую часть этого градиента.
    Karpathy это неплохо разбирает в
    https://medium.com/@karpathy/yes-you-should-understand-backprop-e2f06eab496b