Недавно мы вместе с компанией Intel проводили небольшое исследование эффективности реализации алгоритма Штрассена для сопроцессора Intel Xeon Phi(TM). Кому интересны тонкости работы с этим устройством и просто любящих параллельное программирование, прошу под кат.
Общее количество операций стандартного алгоритма умножения квадратных матриц размера n (сложений и умножений):
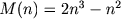
Алгоритм Штрассена (1969), который относится к быстрым алгоритмам умножения матриц требует:
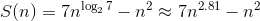
Таким образом, алгоритм Штрассена имеет меньшую асимптотическую сложность и потенциально быстрее на больших размерах матриц. Но рекурсивная природа данного алгоритма представляет определенную сложность для эффективного распараллеливания на современных вычислительных системах и использования данных из памяти.
В данной работе рассматривается комбинированный подход, в котором при достижении порогового значения из алгоритма Штрассена вызывается стандартный алгоритм умножения матриц (в качестве стандартного алгоритма мы использовали Intel MKL DGEMM). Это связано с тем, что при маленьких размерах матриц (десятки или сотни, в зависимости от архитектуры процессора) алгоритм Штрассена начинает проигрывать стандартному алгоритму и по количеству операций, и за счет большего числа кэш-промахов. Теоретические оценки для порогового значения размера матриц для перехода на стандартный алгоритм (без учета кэширования и конвейерной обработки) дает различные оценки — 8 у Хайема и 12 у Хасс-Ледермана, на практике пороговое значение зависит от архитектуры вычислительной системы и должно оцениваться экспериментально. Для нашей системы с Intel Xeon Phi(TM) 7120D наиболее эффективным оказалось значение 1024.
Результаты вычислительных экспериментов сравнивались с функцией DGEMM из библиотеки Intel MKL. Рассматривалось умножение квадратных матриц размера
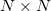, где 
и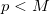 
. Под M здесь понимается пороговое значение размера матриц, после которого вызывается стандартный алгоритм. Умножение двух матриц записывается как 
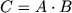, где A, B и C матрицы размера 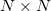. Метод Штрассена для умножения матриц основан на рекурсивном делении каждой перемножаемой матрицы на 4 подматрицы и выполнении операций над ними. Требование к размеру матриц ( и 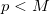) необходимо, чтобы была возможность разбить каждую матрицу на 4 подматрицы на требуемую глубину рекурсии.Метод Штрассена описывается следующей формулой:
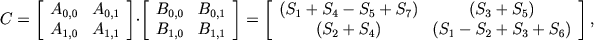
где
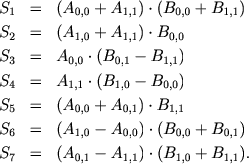
Ниже показано, как можно выделить 4 группы операций, в каждой из них все операции могут быть выполнены параллельно.
В реализации распараллеливания нет ничего сложного. Использовалось OpenMP и механизм задач (omp task), распределение нагрузки между задачами показано на рисунке. Первые группы операций были совмещены в одну, так получается меньше точек синхронизации, так как это очень дорогая операция.
Для замера времени использовался стандартный подход с «разогревающим» запуском и усреднением времени нескольких запусков. В качестве таймера используется функция Intel MKL dsecnd.
double run_method(MatrixMultiplicationMethod mm_method, int n, double *A, double *B, double *C)
{
int runs = 5;
mm_method(n, A, B, C);
double start_time = dsecnd();
for (int i = 0; i < runs; ++i)
mm_method(n, A, B, C);
double end_time = dsecnd();
double elapsed_time = (end_time - start_time) / runs;
return elapsed_time;
}
После реализации распараллеливания мы провели ряд тестов. Тесты проводились в нативном режиме на Intel Xeon Phi(TM) 7120D, 16 Гб.
| Наименование | TDP (WATTS) | Число ядер | Частота (GHz) | Пиковая производительность (GFLOP) | Пиковая пропускная способность (GB/s) | Объем памяти (GB) |
| 3120A | 300 | 57 | 1.1 | 1003 | 240 | 6 |
| 3120P | 300 | 57 | 1.1 | 1003 | 240 | 6 |
| 5110P | 225 | 60 | 1.053 | 1011 | 320 | 8 |
| 5120D | 245 | 60 | 1.053 | 1011 | 352 | 8 |
| 7120P | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120X | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120A | 300 | 61 | 1.238 | 1208 | 352 | 16 |
| 7120D | 270 | 61 | 1.238 | 1208 | 352 | 16 |
 |
 |
 |
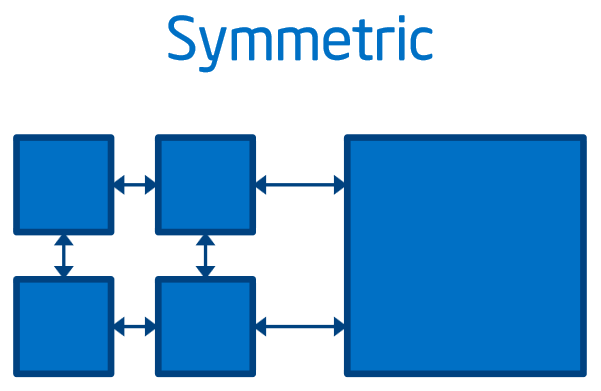| Подходит для высоко-параллельного и векторизуемого кода, последовательный код выполняется медленно | Подходит для последовательного кода с большими параллельными регионами, потенциальная проблема – передача данных по PCIe | Подходит для высоко-параллельного кода, эффективно выполняющегося на обеих платформах, потенциальная проблема – дисбаланс нагрузки |
Чтобы не усложнять статью, все тесты будут проводиться на размере матриц 8192?8192 (данный размер является почти предельным по потреблению памяти для распараллеленного алгоритма Штрассена — около 10GB — и является достаточно большим, чтобы ощутить эффект меньшей асимптотической сложности алгоритма).
| Количество потоков | 1 | 4 | 8 | 16 | 60 | 120 | 180 | 240 |
| Штрассен, с | 114.89 | 29.9 | 15.75 | 8.85 | 3.68 | 3.58 | 4.22 | 8.17 |
| MKL DGEMM, c | 131.79 | 34.38 | 17.27 | 9 | 2.61 | 1.90 | 2.45 | 2.54 |
На небольшом количестве потоков алгоритм Штрассена оказался быстрее Intel MKL DGEMM. Также было замечено, что на большом количестве потоков наблюдается падение производительности (задача почти не масштабируется больше 60 потоков). Для эффективного использования ресурсов Intel Xeon Phi(TM) в многопоточном приложении, рекомендуют использовать число потоков, кратное NP-1, где NP — количество процессоров в устройстве (в нашем случае 61). Подробнее можно почитать здесь.
Возникла мысль, что помочь дальнейшему масштабированию может использование параллелизма внутри вызываемого из Штрассена DGEMM. Для управления количеством потоков в MKL есть несколько функций: mkl_set_num_threads, mkl_set_num_threads_local, mkl_domain_set_num_threads. При попытке использовать mkl_set_num_threads мы обнаружили, что данная функция не влияет на количество потоков в MKL DGEMM, вызываемой из алгоритма Штрассена (на количество потоков в MKL за пределами Штрассена данная функция влияла). Вложенный параллелизм при этом был включен (OMP_NESTED=true).
Как выяснилось, MKL активно сопротивляется вложенному параллелизму. MKL использует переменную окружения MKL_DYNAMIC, которая по умолчанию равна true. Данная переменная позволяет MKL уменьшать количество потоков, которое задает пользователь, в частности при вызове функций MKL из параллельной области будет принудительно установлено количество потоков, равное 1. Чтобы разрешить параллелизм в MKL DGEMM, мы использовали функцию mkl_set_dynamic(0).
mkl_set_dynamic(0);
omp_set_nested(1);
set_num_threads(num_threads);
mkl_set_num_threads(mkl_num_threads);
strassen( … );
…
mkl_set_num_threads(num_threads * mkl_num_threads);
dgemm( … );
| Общее количество потоков | Штрассен, с | MKL DGEMM, с | ||
| Количество потоков в MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 3.68 | 3.89 | 5.19 | 2.61 |
| 120 | 3.58 | 3.50 | 3.82 | 1.90 |
| 240 | 8.17 | 4.23 | 3.59 | 2.54 |
Результаты алгоритма Штрассена для 120 потоков при использовании многопоточного MKL DGEMM стали немного лучше, но серьезного выигрыша мы не получили.
Следующим нашим шагом было изучение привязки программных потоков OpenMP к физическим и логическим ядрам (binding). На Xeon Phi для управления привязкой потоков к ядрам служат переменные окружения KMP_AFFINITY и KMP_PLACE_THREADS. Хорошее описание нашли здесь.
Самым важным среди параметров KMP_AFFINITY является type, который управляет очередностью назначения потоков на ядра (см. рис. ниже).
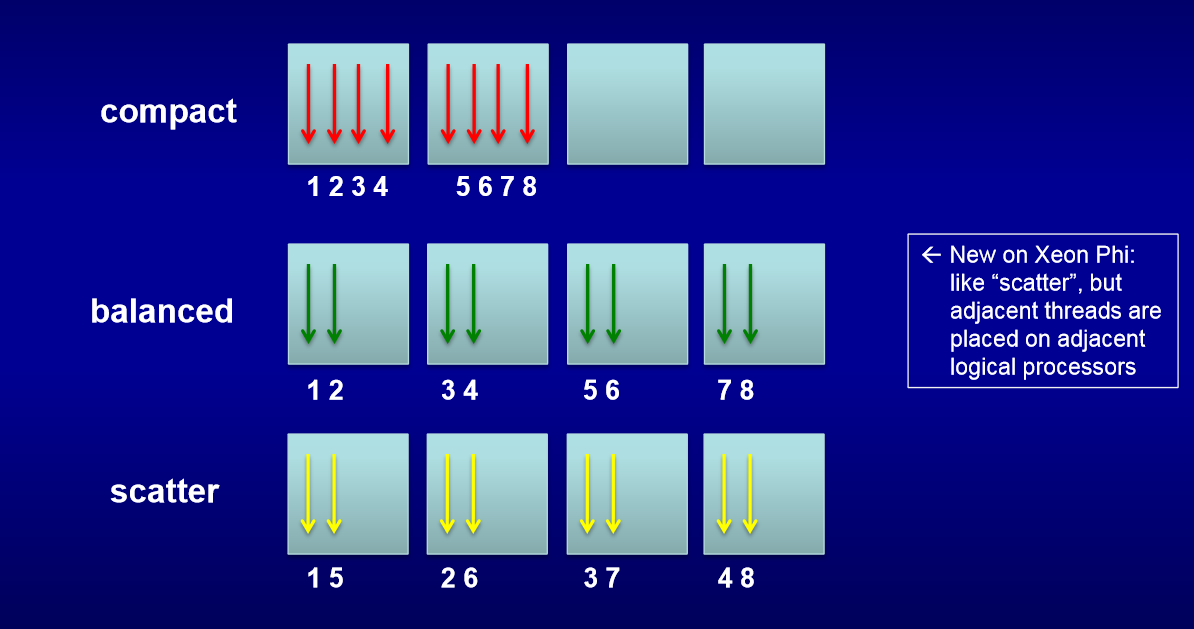
Были использованы следующие значения KMP_AFFINITY:
KMP_AFFINITY = granularity=fine,balanced
| Общее количество потоков | Штрассен, с | MKL DGEMM, с | ||
| Количество потоков в MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 3.67 | 4.07 | 5.53 | 2.64 |
| 120 | 3.54 | 3.51 | 3.95 | 1.51 |
| 240 | 7.11 | 4.33 | 3.41 | 1.15 |
KMP_AFFINITY = granularity=fine,compact
| Общее количество потоков | Штрассен, с | MKL DGEMM, с | ||
| Количество потоков в MKL DGEMM | ||||
| 1 | 2 | 4 | ||
| 60 | 9.29 | 9.96 | 10.27 | 4.58 |
| 120 | 6.23 | 6.79 | 6.04 | 2.31 |
| 240 | 9.32 | 5.21 | 4.21 | 1.15 |
По умолчанию, переменная KMP_AFFINITY= granularity=core,balanced. При тестировании выяснилось, что лучшие параметры для умножения матриц KMP_AFFINITY= granularity=fine,balanced, причем на результаты MKL DGEMM данные параметр влияет не так сильно, как на алгоритм Штрассена, где по сравнению с KMP_AFFINITY= granularity=fine,compact наблюдается двукратное сокращение времени работы. Также заметим, что изменение переменной окружения KMP_AFFINITY с его значения по умолчанию (KMP_AFFINITY= granularity=core,balanced) сократило время работы MKL DGEMM с минимальных 1.90 с до 1.15 с (примерно в 1,5 раза). Результаты MKL DGEMM с compact и balanced отличаются предсказуемым образом, например при 120 потоках вариант с compact использует 30 ядер по 4 потока, а balanced — 60 по 2, за счет большего количества ядер и получается почти двукратное ускорение в варианте balanced.
Еще мы попробовали профилировать программу на Xeon Phi, как это сделать можно почитать здесь. Чтобы профилировать только алгоритм умножения мы использовали возможности VTune API.
В итоге мы не смогли догнать MKL DGEMM на максимальном количестве потоков, но немного больше узнали про программирование такого мощного вычислителя, как Intel Xeon Phi(TM).
Комментарии (15)
andreybotanic
21.12.2015 15:59+3Вот читаю статью, а перед глазами вижу свою работу полуторалетней давности. Тот же Штрассен, тот же Xeon Phi… Сравнение с тем же DGEMM… И даже результат тот же: я тоже так и не смог догнать DGEMM. У меня, правда, все было совсем плохо: моя реализация была быстрее DGEMM на обычном процессоре при, но вот на Xeon Phi оказывалась во много раз медленнее. Уж не знаю, как так вышло. А вообще, если кому интересно, вот.
OShapovalov
21.12.2015 16:10Интел регулярно поднимает тему алгоритма Штрассена, похоже видят какие-то перспективы на этот счет. Помимо вашей работы, например, проводился Intel Threading Challenge 2009, где также была эта задача. Судя по нашему обзору открытых источников наши результаты оказались лучше результатов наших предшественников.
grafmishurov
22.12.2015 02:02+1Так в чем в итоге проблема отставания, в рекурсии и синхронизации?
OShapovalov
22.12.2015 08:50Я бы выделил несколько основных причин отставания. Во-первых, синхронизация, которая вызывается на каждом уровне рекурсии по 3 раза. Затем, древовидная структура распараллеливания (на верхнем уровне создается 7 потоков, на каждом они делятся еще на 7 и т.д.), здесь возникает как минимум 3 проблемы: неравномерная загрузка потоков, не кратное степени 2 число потоков (а значит не оптимальное отображение на архитектуру Xeon Phi), а также вопрос ограничения максимального количества потоков. Мы пробовали создавать различное число потоков на каждом уровне рекурсии, оставить распараллеливание только на 2-3 верхних уровнях, по-разному группировать вычислительные операции по потокам, разный binding, но все равно, результаты распараллеливания нельзя назвать очень хорошими. Отдельно стоит выделить проблему с вложенным параллелизмом, который достаточно сложен в использовании и сам по себе, а эффективно использовать свой параллелизм поверх параллелизма MKL вообще очень сложно, т.к. MKL предоставляет ограниченный API для управления параллелизмом. Также стоит отметить, что в однопоточном варианте наша реализация оказалась существенно быстрее MKL DGEMM (около 1.5-2 раз), то есть мы проиграли именно в распараллеливании.
grafmishurov
22.12.2015 14:07Ну я вот и спрашиваю про параллельный вариант. На одном то юните алгоритм сам по себе быстрее, чем больше юнитов, тем больше разница в абсолютных значениях. Я так понял, что проблема, которая, видимо, общая для всех алгоритмов, которые распараллеливают рекурсию: неравномерность вычислений, которая затормаживает быстрые потоки на моменте синхронизации и несоответствие количества вычислений количеству юнитов. А не пробовали другие методы использовать, что нибудь а ля thread pool для этих задач?
OShapovalov
22.12.2015 14:29Мы пробовали преобразовывать рекурсию в цикл (алгоритм нашли в одной из статей). Но это потребовало определенного препроцессинга и постпроцессинга, которые занимали слишком много времени (эффективность непосредственно умножения подматриц ожидаемо увеличилась). Насчет реализации собственной очереди задач (если вы это имели в виду) мы думали, но решили, что это не даст никакого положительного эффекта.
Mixim333
22.12.2015 10:23Я правильно понимаю, что алгоритм Штрассена (4.21с) ни дал никакого прироста в скорости по сравнению со стандартным алгоритмом, реализованном в Intel MKL (1.15c)? Если да, то очень странно выглядит даже из Ваших же формул: M(n)=2*n^3-n^2; S(n)=7*n^2.81-n^2 или в вашем случае n=8192=> M(8192)=2*8192^3?8192^2?1.099444519*10??; S(8192)=7*8192^2.81?8192^2?0.694515302457*10??, т.е. алгоритм Штрассена требует значительно меньшего количества арифметических операций (~1/3), чем стандартный алгоритм=>должен был исполнится на 30% быстрее или это как раз и вызвано затыками на синхронизацию между потоками?
OShapovalov
22.12.2015 10:31На максимальном количестве потоков не дал. При однопоточном выполнении ускорение было получено, примерно такое, как Вы посчитали, правда формула расчета количества операций для алгоритма Штрассена будет сложнее, т.к. мы использовали комбинированный алгоритм (начиная с определенного значения размера подматриц вызывается стандартный алгоритм). По поводу причин отсутствия ускорения смотрите в комментарии выше.
Vadikus
22.12.2015 12:19+1Вопрос автору, при использонии алгоритма Штрассена, чем/как перемножались малые матрицы?
MKL тем и хорош, что исбользует правильные алгоритм кеш-блокинга/рекурсивное деление матриц, что бы запихнуть правильные плитки (tiles) матриц в разные уровни кешей. Без этого мы говорим не о compute-bound имплементации, а намного замедленном коде, т.к. в нем будет слишком много кеш промохов.
А еще для Xeon Phi 1.2 TFLOP/s — это только максимально возможная производительность на double precision, для FMA инструкций при использовании 512-битных векторных инструкций на всех ядрах. Только одна нить из 4-х на ядро смоежет использовать VPU за цикл. Но это я отвлекся. Т.е нужно еще думать как векторизовать весь код, если он не bandwidth-bound.
Если есть желание побеседовать по этой теме — прошу в личку.OShapovalov
22.12.2015 12:27По первому вопросу:
(в качестве стандартного алгоритма мы использовали Intel MKL DGEMM)
Т.е. в вопросе векторизации умножения подматриц мы как раз на MKL и полагались. Насчет производительности Вы правильно заметили, что это теоретический предел, в статье также про это написано.
grafmishurov
22.12.2015 14:47+1OShapovalov, «векторизация» вот это я подразумевал выше под «попробовать другие способы». Это правильней с терминологической и практической точки зрения. У меня еще возник вопрос по ходу чтения этого комментария с упоминанием про fma-инструкции и кеша. Зачем там x86 архитектура, если устройство предназначено для плавающей точки. Ведь на OpenCL и CUDA можно самому регулировать что в какую память пойдет и на какие вычислительные единицы. Получается, что теряется гибкость и контроль. Есть ли у этого какие-то плюсы, кроме того, что там Линукс?
OShapovalov
22.12.2015 15:48Основное преимущество x86 заключается в более простом программировании (для нативного режима часто достаточно перекомпиляции программы без изменений в исходном коде). А гибкость… я не думаю, что она часто требуется. Вообще у нас не стояла задача выбирать вычислительное устройство. Кстати OpenCL на Xeon Phi поддерживается.
Vadikus
23.12.2015 00:38+1У Интела сейчас задача заставить программистов переписать старый legacy код, который разрабатывался в 80х-90х без учета векторных операций и мульти- и много-ядерности под новые архитектуры. И мы говорим о коде в сотни тысяч строк или даже нескольких миллионов строк. Переписывать все это богатство с нуля отвыжится только сумасшедший. Поэтому стратегически было принято решение поддерживать х86 инструкции и устоявшуюся инфроструктуру, векторизацию спихнуть на компилятор, а параллелизм нитей реализовать с помощью OpenMP стандарта — прагмы проще вставлять, чем переписывать сам код. Это далеко не идеальное решение, но уж какое Интел придумал. MIC первого покаления — это первый шаг в направлении такое системы, где без векторизации и нитей нифига летать не будет. Со вторым поколением (KNL) схожая ситуация, хотя и чуть ускорился одно-поточный код. И плюс в KNL с memkind библиотекой специальными аллокаторами можно будет управлять где выделяется памить: в MCDRAM или DDR4, если чип во flat mode памяти находится.
barkalov
А почему вы не ставите ( R ) после слова Xeon?
OShapovalov
Старался учесть все правила Интел, после слова Xeon символ ( R ) не нужен.