Эта статья посвящается удивительным особенностям в мире хаоса. Я постараюсь рассказать о том, как обуздать такую странную и сложную вещь, как хаотический процесс и научиться создавать собственные простейшие генераторы хаоса. Вместе с вами мы пройдем путь от сухой теории до прекрасной визуализации хаотических процессов в пространстве. В частности, на примере известных хаотических аттракторов, я покажу как создавать динамические системы и использовать их в задачах, связанных с программируемыми логическими интегральными схемами (ПЛИС).

Введение
Теория хаоса – необычная и молодая наука, описывающая поведение нелинейных динамических систем. В процессе своего зарождения теория хаоса просто перевернула современную науку! Она будоражила умы учёных и заставляла их все больше и больше погружаться в исследования хаоса и его свойств. В отличие от шума, который является случайным процессом, хаос – детерминирован. То есть для хаоса существует закон изменения величин, входящих в уравнения описания хаотического процесса. Казалось бы, при таком определении хаос ничем не отличается от любых других колебаний, описываемых в виде функции. Но это не так. Хаотические системы очень чувствительны к начальным условиям, и малейшие их изменения могут привести к колоссальным различиям. Эти различия могут быть настолько сильными, что невозможно будет сказать, одна или несколько систем подвергались исследованию. Из научно-популярных источников лучше всего это свойство хаоса описывает процесс под названием "эффект бабочки". Многие слышали о нем, и даже читали книги и смотрели фильмы, в которых использовался прием с использованием эффекта бабочки. В сущности, эффект бабочки отражает главное свойство хаоса.
Американский ученый Эдвард Лоренц, один из первопроходцев в области хаоса, сказал однажды:
Бабочка, взмахивающая крыльями в Айове, может вызвать лавину эффектов, которые могут достигнуть высшей точки в дождливый сезон в Индонезии.

Итак, окунемся в теорию хаоса и посмотрим, какими подручными средствами можно генерировать хаос.
Теория
Перед изложением основного материала, хотелось бы дать несколько определений, которые помогут понять и прояснить некоторые моменты в статье.
Динамическая система – это некоторое множество элементов, для которого задана функциональная зависимость между временной координатой и положением в фазовом пространстве каждого элемента системы. Проще говоря, динамическая система – это такая система, у которой состояние в пространстве изменяется с течением времени.
Многие физические процессы в природе описываются системами уравнений, представляющими собой динамические системы. Например, это процессы горения, течения жидкости и газов, поведение магнитных полей и электрических колебаний, химические реакции, метеорологические явления, изменение популяций у растений и животных, турбулентности в морских течениях, движение планет и даже галактик. Как видите, многие физические явления можно в той или иной мере описать как хаотический процесс.
Фазовый портрет – это координатная плоскость, в которой каждая точка соответствует состоянию динамической системы в определенный момент времени. Иными словами, это пространственная модель системы (может быть двумерной, трехмерной и даже четырехмерной и более).
Аттрактор – некоторое множество фазового пространства динамической системы, для которого все траектории с течением времени притягиваются к этому множеству. Если совсем простым языком, то это некоторая область, в которой сосредоточено поведение системы в пространстве. Многие хаотические процессы представляют собой аттракторы, т. к. сосредоточены в определенной области пространства.
Реализация
В этой статье я хотел бы рассказать о четырех основных аттракторах – Лоренца, Ресслера, Рикитаке и Нозе-Гувера. Помимо теоретического описания в статье отражены аспекты по созданию динамических систем в среде MATLAB Simulink и дальнейшей их интеграции в FPGA фирмы Xilinx с помощью средства System Generator. Почему не VHDL/Verilog? Можно синтезировать аттракторы и с помощью RTL-языков, но для лучшей визуализации всех процессов MATLAB является идеальным вариантом. Я не буду затрагивать сложные моменты, связанные с расчетом спектра показателей Ляпунова или построения сечений Пуанкаре. И уж тем более никаких громоздких математических формул и выводов не будет. Итак, приступим.
Для создания генераторов хаоса нам потребуется следующий софт:
- MATLAB R2014 с лицензией на Simulink и DSP Toolbox.
- Xilinx ISE Design Suite 14.7 с лицензией на System-Generator (DSP Edition)
Эти программы достаточно тяжелые, поэтому наберитесь терпения при их установке. Установку лучше начать с MATLAB, а уже затем поставить софт Xilinx (при другой последовательности некоторым моим знакомым не удалось интегрировать одно приложение в другое). При установке последнего выскакивает окно, где можно связать Simulink и System Generator. Ничего сложного и необычного в установке нет, поэтому этот процесс опустим.
Аттрактор Лоренца
Аттрактор Лоренца – это, пожалуй, самая известная динамическая система в теории хаоса. Уже несколько десятков лет он привлекает большое внимание многих исследователей для описания тех или иных физических процессов. Первое упоминание аттрактора приводится в 1963 году в работах Э. Лоренца, который занимался моделированием атмосферных явлений. Аттрактор Лоренца – это трехмерная динамическая система нелинейных автономных дифференциальных уравнений первого порядка. Она имеет сложную топологическую структуру, асимптотически устойчива и устойчива по Ляпунову. Аттрактор Лоренца описывается следующей системой дифференциальных уравнений:

В формуле точка над параметром означает взятие производной, которая отражает скорость изменения величины по времени (физический смысл производной).
При значениях параметров ? = 10, r = 28 и b = 8/3 эта простая динамическая система была получена Э. Лоренцом. Он долго не мог понять, что происходит с его вычислительной машиной, пока наконец не осознал, что система проявляет хаотические свойства! Она была получена в ходе экспериментов для задачи о моделировании конвекции жидкости. Кроме того, эта динамическая система описывает поведение следующих физических процессов:
- – модель одномодового лазера,
- – конвекция в замкнутой петле и плоском слое,
- – вращение водяного колеса,
- – гармонический осциллятор с инерционной нелинейностью,
- – завихрения облачных масс и т.д.
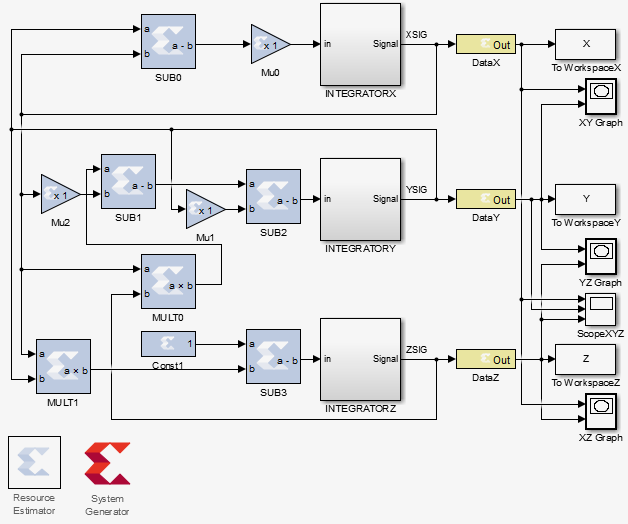
На следующем рисунке приведена система аттрактора Лоренца в среде MATLAB:
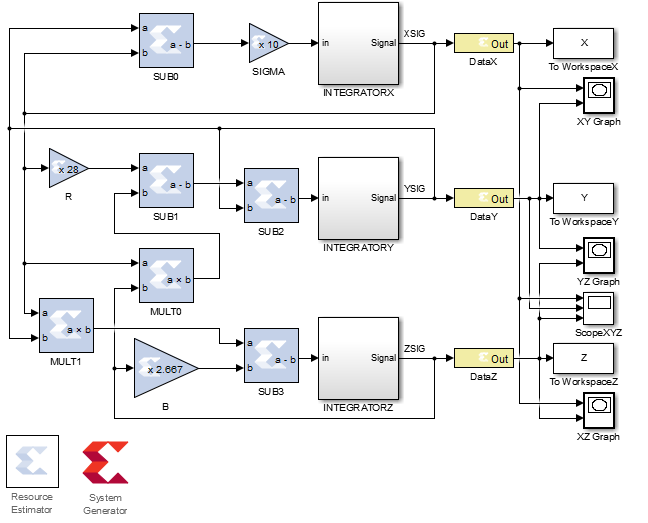
На рисунке используется ряд следующих обозначений:
- вычитатели: SUB0-3;
- умножители на константу: SIGMA, B, R;
- перемножители: MULT0-1;
- интеграторы с ячейкой задания начального условия: INTEGRATOR X,Y,Z;
- выходные порты OUT: DATA X,Y,Z для сигналов XSIG, YSIG, ZSIG;
Кроме того, на схеме представлены вспомогательные инструменты анализа, это:
- сохранение результатов вычисления в файл: To Workspace X,Y,Z;
- построение пространственных графиков: Graph XY, YZ, XZ;
- построение временных графиков: Scope XYZ;
- средства для оценки занимаемых ресурсов кристалла и генерации HDL-кода из модели «Resource Estimator» и «System Generator».
Внутри каждого узла математических операций необходимо указать разрядность промежуточных данных и их тип. К сожалению, в ПЛИС не так-то просто работать с плавающей точкой и в большинстве случаев все операции производятся в формате с фиксированной точкой. Неправильное задание параметров может привести к неверным результатам и огорчить вас при построении своих систем. Я экспериментировал с разными величинами, но остановился на следующем типе данных: 32-битный вектор знаковых чисел в формате с фиксированной точкой. 12 битов отводится на целую часть, 20 битов на дробную часть.
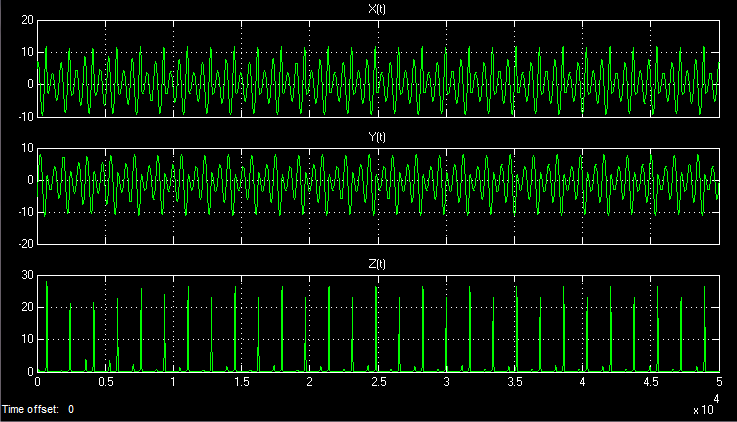
Установив в интеграторах X, Y, Z в блоке триггера начальное значение системы, например, {10, 0, 0}, я запустил модель. Во временной развертке можно наблюдать три следующих сигнала:
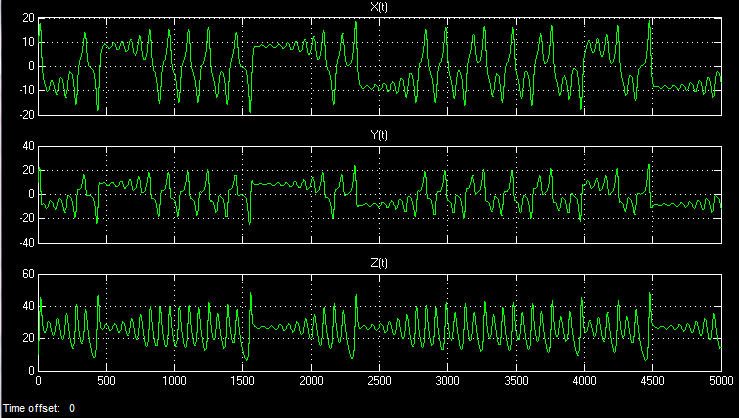
Даже если время моделирования устремить к бесконечности, то реализация во времени никогда не повторится. Хаотические процессы непериодичны.
В трехмерном пространстве аттрактор Лоренца выглядит следующим образом:

Видно, что аттрактор имеет две точки притяжения, вокруг которых происходит весь процесс. При незначительном изменении начальных условий процесс также будет сосредоточен вокруг этих точек, но его траектории будут существенно отличаться от предыдущего варианта.
Аттрактор Рёсслера
Второй по количеству упоминаний в научных статьях и публикациях аттрактор. Для аттрактора Рёсслера характерно наличие граничной точки проявления хаотических или периодических свойств. При определенных параметрах динамической системы колебания перестают быть периодическими, и возникают хаотические колебания. Одно из примечательных свойств аттрактора Рёсслера — фрактальная структура в фазовой плоскости, то есть явление самоподобия. Можно заметить, что и остальные аттракторы, как правило, обладают этим свойством.
Аттрактор Рёсслера наблюдается во многих системах. Например, он применяется для описания потоков жидкости, а также для описания поведения различных химических реакций и молекулярных процессов. Система Рёсслера описывается следующими дифференциальными уравнениями:
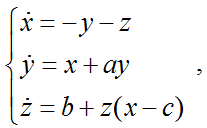
В среде MATLAB аттрактор строится следующим образом:
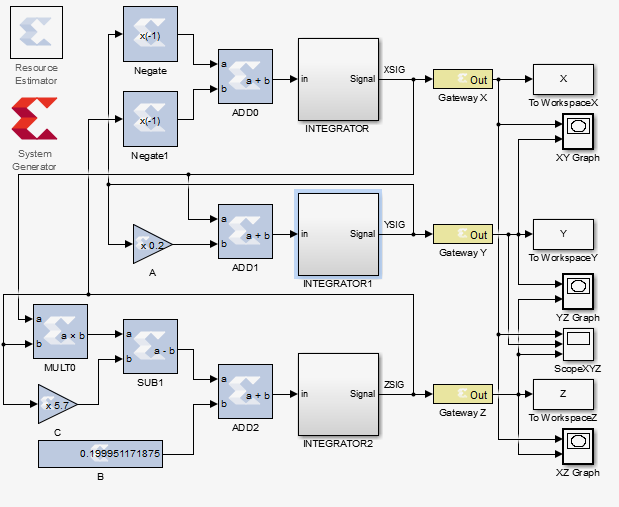
Временная реализация пространственных величин:
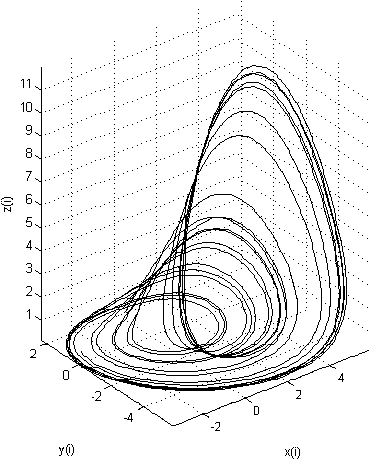
Трехмерная модель аттрактора Рёсслера:
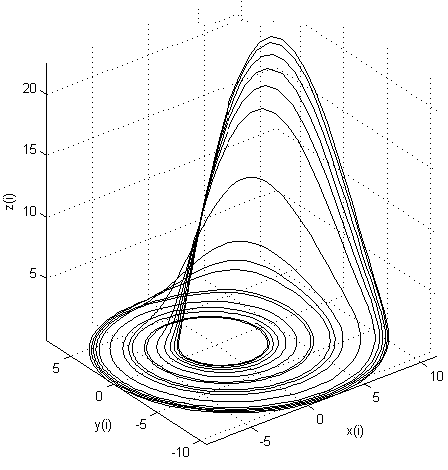
Аттрактор при иных коэффициентах в системе уравнений (хаотический процесс превратился в периодический!)

Сравните картинки трехмерных аттракторов при разных начальных условиях и коэффициентах в системе уравнений. Видите, как резко изменились траектории движения в первом случае? Но так или иначе они сосредоточены вблизи единой области притяжения. Во втором случае аттрактор вообще перестал подавать признаки хаоса, превратившись в замкнутую периодическую петлю (предельный цикл).
Аттрактор Рикитаке
Динамо Рикитаке – одна из известных динамических систем третьего порядка с хаотическим поведением. Представляет собой модель двухдискового динамо и впервые была предложена в задачах о хаотической инверсии геомагнитного поля Земли. Ученый Рикитаке исследовал систему динамо с двумя взаимосвязанными дисками построенную таким образом, что ток из одной катушки диска перетекал в другую и производил возбуждение второго диска, и наоборот. В определенный момент система начала сбоить и показывать непредсказуемые вещи. Активные исследования аттрактора позволили спроецировать динамо Рикитаке на модель связи больших вихрей магнитных полей в ядре Земли.
Динамо Рикитаке описывается следующей системой уравнений:

Модель динамо Рикитаке в MATLAB:
Временная реализация:
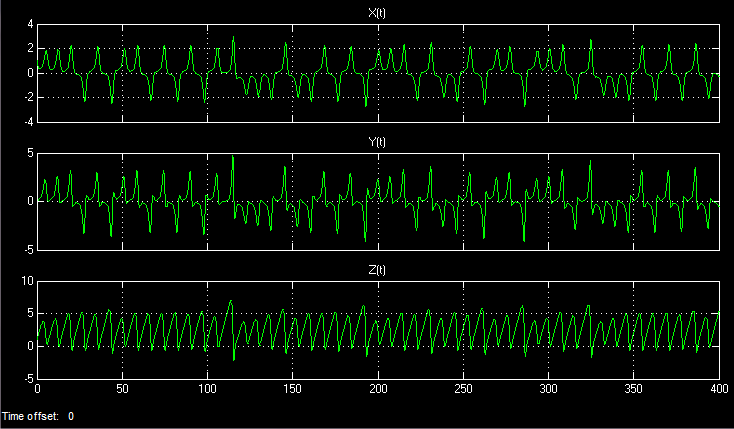
Аттрактор (первая версия):

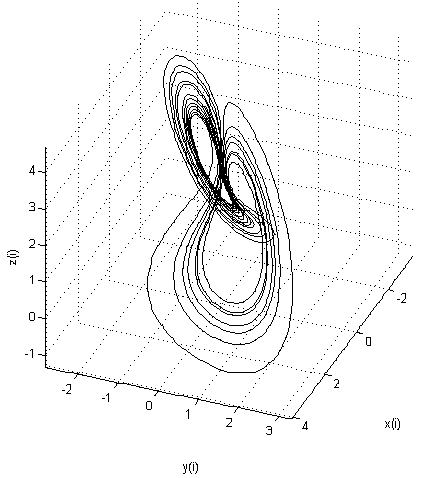
Можно заметить, что динамо Рикитаке в чем-то похоже на аттрактор Лоренца, но это совершенно разные системы и описывают разные физические процессы!
Аттрактор Нозе-Гувера
Менее знаменитая, но не менее важная трехмерная динамическая система – термостат Нозе-Гувера. Используется в молекулярной теории как обратимая во времени термостатическая система. К сожалению, про этот аттрактор я знаю не так много, как про остальные, но мне он показался интересным и я включил его в обзор.
Термостат Нозе-Гувера описывается следующей системой уравнений:
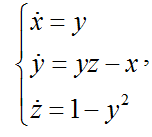
Модель Нозе-Гувера в MATLAB:
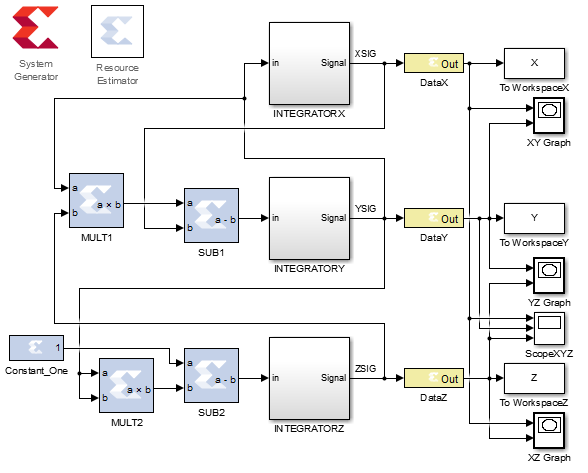
Временная реализация:

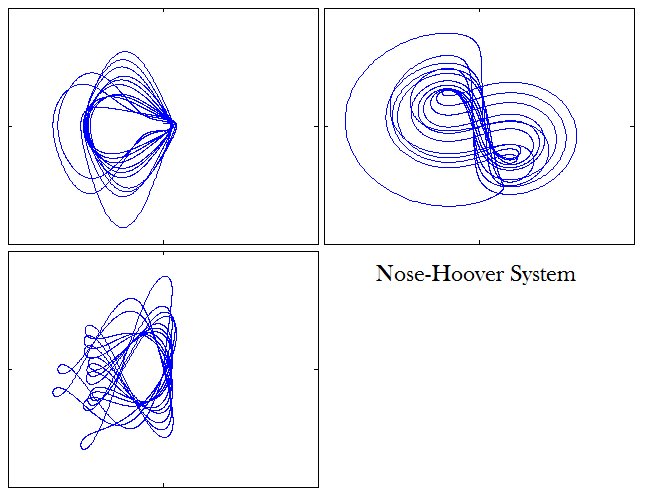
Двумерные проекции аттрактора:
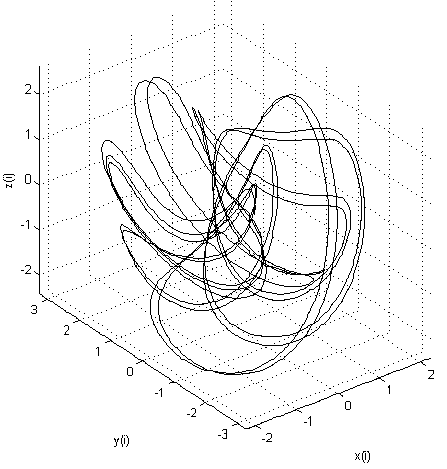
Трехмерная модель термостата Нозе-Гувера:

Синтез проекта
Для синтеза проекта нужно нажать на красненький значок «X», который запустит настройки System Generator. Здесь можно выбрать семейство и тип ПЛИС, результирующий формат файлов (VHDL/Verilog — для создания исходных кодов, NGC — для создания ядра в виде списка соединений), предварительные значения тактовых частот и т. д. Мои типичные настройки представлены на следующем рисунке:

После установки всех настроек — нажимаем «Generate» и на выходе имеем синтезированный проект для ПЛИС. Далее дело за малым — вставить сгенерированное ядро в нужную вам часть проекта. (Как это делается, вы можете найти в других моих статьях, посвященных цифровой обработке сигналов). Все перечисленные аттракторы занимают очень мало ресурсов в современных кристаллах ПЛИС (около 10-20 блоков DSP48 и немного логики).

Система галактик похожая на аттрактор Лоренца:

Заключение
Перечисленные аттракторы находят применение во многих физических процессах в различных областях науки и техники – от физики и химии до механики и метеорологии. В частности, генераторы хаоса используются для создания длинных последовательностей псевдослучайных чисел (ПСП). В задачах радиотехники хаос может применяться для модулирования несущей при создании сверхширокополосных сигналов цифровыми методами (на ПЛИС или процессорах).
Теория хаоса – интересная и удивительная наука. И благодаря современным средствам анализа и моделирования она становится довольно привлекательной для исследования. С помощью этой статьи вы можете самостоятельно смоделировать свои собственные динамические системы, вплоть до гиперхаотических систем порядка выше 3 (например, гиперхаос Лоренца, Росслера и т.д.). Надеюсь, материал моей публикации может кому-то пригодиться, а кто-то найдет для себя новое и полезное.
Исходные файлы аттракторов на Github
Мои статьи по схожей тематике:
Литература
- Хаос на хабре!
- Chaoscope Online
- Хаос. Создание новой науки
- Теория хаоса — Wiki
- Аттрактор Лоренца — Wiki
- Аттрактор Рёсслера — Wiki
- Элегантный хаос (также продается на русском языке)
Ура, хаб FPGA вернулся на хабр. Всех с наступающим новым годом!
Комментарии (13)

leshabirukov
28.12.2015 15:55Идея дёмки придумалась:
— время дёмки = время аттрактора;
— выбрать пару параметров (сигма, b, r в случае Лоренца) и связать их с координатами точки на экране, в каждой точке экрана рисовать свой аттрактор;
— сопоставить тройку переменных аттрактора компонентам цвета rgb, то есть цвет меняется со временем.
Хаотические области параметров будут наглядно отличаться от периодических.

Daffodil
28.12.2015 18:16+2А где видео с осциллографом? Ну или хотя-бы с дисплеем.
…
Подозреваю что количество годных демок для FPGA увеличиться, когда в следующем поколении появится поддержка floating point в DSP юнитах.
capitanov
28.12.2015 18:40+1На дисплей не выводил, хотя задумка была и наработки для VGA-FPGA есть (см. сапёр на плис). Может как-нибудь прикручу, когда свободного времени будет побольше. Самому интересно это попробовать :)
Для Xilinx floating point сейчас только в виде IP-корок, но в Vivado HLS можно работать с плавающей точкой и даже проекты небольшие на выходе можно получить. За серьезные не ручаюсь :) А вот у Альтеры есть DSP ячейки с поддержкой плавающей точки (Arria 10, если мне память не изменяет).

BubaVV
28.12.2015 23:44Интересно, делали ли такое на россыпи микросхем. Оно чудно вписалось бы куда-нибудь в 7400 contest, например

capitanov
28.12.2015 23:54+1На россыпи делал вот здесь товарищ с хабра. Как видите — тоже ничего сложного нет и все теплое «ламповое» аналоговое. :)

BubaVV
29.12.2015 00:00Это все-таки чуть другое, как мне кажется. Статья давным-давно в избранном)

capitanov
29.12.2015 00:23Если уж совсем на рассыпухе серии 7400, то выйдет красиво, но много микросхем. Главное математику (умножители и сумматоры) организовать, больше тут по сути ничего и нет. Тот же умножитель, если делать по алгоритму Бута — еще +20-30 сумматоров, в зависимости от разрядности данных. А сумматоры вообще разбить на логические функции. Рассыпухи станет будь здоров! Уж лучше на самом маленьком spartan3 сделать без извращений :)

Leo5700
30.12.2015 00:21+1Спасибо за статью. Судя по первой картинке, Вы знакомы с программой Chaoscope.
Для тех кто не знаком: Chaoscope шикарно визуализирует Лоренца и ещё некоторые аттракторы. Вот уравнения. Вот картинки.


romanjoe
Железо вернулось на хабр, да здравствует железо и его авторы!