Среди многих исследователей и разработчиков бытует мнение, что инструменты обработки больших данных в области машинного обучения часто избыточны – всегда можно сделать сэмпл, загнать в память и использовать любимые R, Python и Matlab. Но на практике встречаются задачи, когда даже относительно небольшой объем данных, размером в пару гигабайт, обработать в таком стиле затруднительно – и тут-то и могут помочь те самые технологии «больших данных».

Хорошим наглядным примером такой задачи является задача нашего конкурса SNA Hakathon 2016: дан социальный граф одного миллиона пользователей и их демография. Задача — найти скрытые связи в этом графе. Размер предоставленного графа всего два гигабайта в GZip и, казалось бы, применение технологий больших данных здесь не оправданно, но это только на первый взгляд.

Одной из самых важных «фич» в задаче поиска скрытых связей в социальном графе является количество общих друзей. И в расчетном плане это очень тяжелая «фича» — количество узлов, между которыми существуют пути длины 2, на несколько порядков больше, чем количество прямых связей в графе. В результате при расчете граф «взрывается» и из разрежённой матрицы на два гигабайта превращается в плотную терабайтную матрицу.

Казалось бы, для решение этой задачи впору поднимать небольшой кластер, но спешить не стоит: взяв на вооружение принципы обработки больших данных и соответствующие технологии, задачу можно решить и на обычном ноутбуке. Из принципов мы возьмем «разделяй и властвуй» и «руби хвосты сразу», а в качестве инструмента — Apache Spark.

В чем проблема?

Открытый для анализа граф представлен в виде списка смежности (для каждой вершины дан список соседей) и асимметричен (не для всех вершин известны исходящие дуги). Очевидный способ рассчитать количество общих друзей между вершинами в этом графе выглядит следующим образом:

1. Переводим граф в вид списка пар;
2. Join-им список пар сам на себя по «общему другу»;
3. Суммируем число вхождений каждой пары.

К плюсам такого подхода, несомненно, следует отнести простоту — на Spark это решение займет 5 строчек. Но минусов у него гораздо больше. Уже на втором шаге при реализации join-a происходит shuffle (пересылка данных между разными этапами обработки), который очень быстро исчерпает ресурсы локального хранилища. А если вдруг на вашем ноутбуке все-таки хватит под него места, то его уже точно не хватит для shuffle-а на третьем этапе.

Чтобы справиться с задачей, нужно разбить её на части («разделяй и властвуй») и отфильтровать результаты с небольшим количеством общих друзей («руби хвосты сразу»). Но выполнить оба условия сразу проблематично – при расчете числа общих друзей только на части графа мы получим неполную картину и не сможем адекватно применить фильтр…

Где решение?

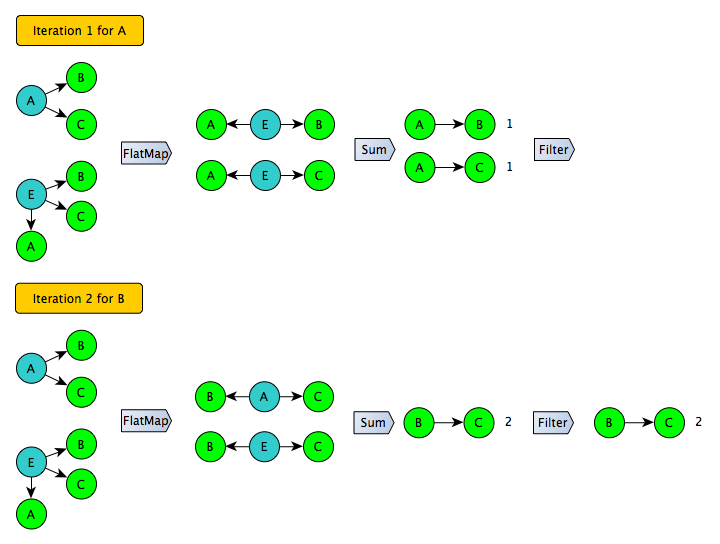
Попробуем взглянуть на проблему с другой стороны. Больше всего неприятностей вызывает join списка пар на втором этапе: сам формат списка пар неэффективен с точки зрения размера, к тому же одну из сторон join-a невозможно отфильтровать, не исказив результат. Можно ли обойтись без конвертации в список пар и join-a? Да, если воспользоваться принципом «я общий друг для двух своих друзей». В этом случае мы итерируемся по списку смежности для каждого из списка друзей и генерируем все пары, а после чего считаем сколько раз каждая из пар появилась в целом по системе – в итоге задача решается с помощью одного shuffle :)

Развивая эту идею, несложно сделать и следующий шаг: вместо того, чтобы генерировать все возможные пары, надо генерировать только пары для определенного подмножества пользователей в левой части (например, с четными идентификаторами). Далее эту процедуру можно повторить несколько раз и получить полное покрытие. При этом на каждой итерации можно смело применять фильтр для отсечения «длинного хвоста» – для пользователей в этом подмножестве цифры получены точно.

Этот подход хорошо работает для симметричного графа, но представленный на SNA Hakathon 2016 граф асимметричен – для некоторых пользователей известны только входящие дуги. Чтобы использовать этот трюк, граф надо сначала развернуть:



Результат конвертации уже можно сохранить и использовать в качестве входа для итеративного алгоритма:

Стоит ли игра свеч?

Именно на этом графе подсчет количества общих друзей «в лоб» занял 1 час на кластере из 100 серверов. Оптимизированный итеративный вариант отработал за 4 с половиной часа на одном двухъядерном ноутбуке. Эти цифры позволяют сделать вывод, что вариант «в лоб» приемлем только для достаточно крупных фирм и/или исследовательских коллективов, тогда как оптимизированный вариант может запустить практически любой желающий. К тому же, весь необходимый код и инструкции опубликованы в открытом доступе на GitHub.

Действительно ли в этой схеме необходимы те самые «технологии больших данных»? Можно ли то же самое повторить на R или Python? Теоретически, нет ничего невозможного. Но на практике при реализации придется решить большое количество проблем и познакомиться со многими весьма специфичными пакетами и функциями. Полученный в результате код будет больше по размеру и явно дороже в разработке и поддержке.

На самом деле, даже если абстрагироваться от данного примера, использование Apache Spark во многих случаях может оказаться предпочтительнее R и Python: для Spark естественной является параллельная обработка данных, что обеспечивает более высокую скорость, практически без изменений код может быть перенесен на кластер в Google Cloud (case study) и применен к значительно большему объему данных. Ну а коллекция поддерживаемых алгоритмов машинного обучения, хотя еще и уступает «прародителям», но уже достаточно внушительна и постоянно пополняется (MLLib).

Время учить Scala :)