Натыкаясь в разных местах на то, как объясняются некоторые моменты: с одной стороны убедительно, с другой сомнительно, с третьей неверно, с четвертой, в принципе и верно… думаю, стоит на всякий случай приглядеться им, а так как начать придется от оснований, то и «самые маленькие» могут поднянуться без боязни формул.
Прежде всего нас будет интересовать, как образуются и распространяются электромагнитные волны от «электрических» и «магнитных» полей, а посему сразу лакмусовая бумажка:

Если эта схема вам прекрасно знакома и не вызывает рефлекса кое-что пояснить и дополнить, чтобы не ввела других в заблуждение, то прошу под кат. Если она вам прекрасно знакома, и вы поняли, что там требуется допояснять, то гуляйте дальше) Пост не для вас.
Если схема не очень знакома или понятна, можете заглянуть.
Чтобы идти по порядку, начнем с далека, а именно — возьмем и рассмотрим окружность. Казалось бы, о чем тут говорить, фигуры проще не бывает. С детства мы привыкли рисовать, взяв точку-центр на бумаге и очертив все точки на одинаковом от центра расстоянии.
Потом мы узнаем другие способы «нарисовать» круг. Казалось бы, совсем разные принципы, а ведут к одному и тому же.
Возьмем один из них, один из полезнейших на мой взгляд:

Что это было? Ничто иное, как дифференциальное уравнение окружности. Смысл которого звучит так:
«Есть две взаимодействующие сущности. Первая прикладывает силы, чтобы усилить вторую. Вторая, по мере сил, пытается ослабить первую.»
Эту динамику мы можем записать в форме самой простой системы дифф. уравнений в мире (не считая экспоненты)

Образно говоря, в любой момент очень короткого периода одинаковой длины «dt», изменение «у» (т.е. «dy») зависит от величины «x».
При этом в этот же момент изменение «x» (т.е. «dx») зависит от величины «y».
Оба уравнения аналогичны уравнению механики макромасштабов — «расстояние = скорость * время». Только в данном случае отрезки «dt» очень малы (а точнее, бесконечно малы, но сути не меняет).

При чем все эти зависимости линейные, и об окружности им ничего не известно. А принцип инь-ян проявляется в противостоящих знаках воздействия одного элемента на другой.
Если система находится не в равновесии, т.е. «x» и «y» не равны нулю, это взаимодействие, складывая все микро-отрезки времени, приведет к бесконечному циклу колебаний.
<html>
<body>
<canvas height='300' width='300' id='cnv' style="border: 1px solid black"></canvas>
<canvas height='300' width='200' id='cnv2' style="border: 1px solid black"></canvas>
<script>
var cnv = document.getElementById("cnv");
var cx = cnv.getContext('2d');
var cnv2 = document.getElementById("cnv2");
var cx2 = cnv2.getContext('2d');
var h = parseInt(cnv.getAttribute("height"));
var w = parseInt(cnv.getAttribute("width"));
var h2 = parseInt(cnv2.getAttribute("height"));
var w2 = parseInt(cnv2.getAttribute("width"));
var id = cx.createImageData(w, h);
var id2 = cx2.createImageData(w2, h);
var rd = Math.round;
var x = 0, y = 1, x1, y1;
var dt = 0.0001;
var t=0;
i=1000000; while (i--) {
dx = -y;
dy = x;
x1 = x + dx*dt;
y1 = y + dy*dt;
t = t + dt;
x = x1; y = y1;
// draw (x, y)
drawOn(id, rd(100*x + 150), rd(100*y + 150), w, h, 0, 0, 0);
// draw x(t), y(t)
drawOn(id2, rd(10*t), rd(100*y + 150), w2, h2, 255, 0, 0);
drawOn(id2, rd(10*t), rd(100*x + 150), w2, h2, 0, 0, 255);
}
drawHorizLine(id, 0, w, h/2, w, h);
drawHorizLine(id2, 0, w2, h2/2, w2, h2);
cx.putImageData(id, 0, 0);
cx2.putImageData(id2, 0, 0);
function drawOn(id, x, y, w, h, red, green, blue) {
if (x < w && y < h && x >=0 && y >=0) {
var idx = 4*(x + y*w);
id.data[idx] = red;
id.data[idx+1] = green;
id.data[idx+2] = blue;
id.data[idx+3] = 255;
}
}
function drawHorizLine(id, xFrom, xTo, y, w, h) {
for (var x = xFrom; x < xTo; x++) {
drawOn(id, x, y, w, h, 0, 0, 0);
}
}
</script>
</body>
</html>
Из этого же представления мы получаем как результат — функции синус и косинус, т.к. «х» и «у» ими соответственно и являются (с точностью до масштаба).
Отсюда же сразу понятно, почему производная синуса — косинус, косинуса — минус синус… и почему цепочка производных зацикливается. И тянется в бесконечность…
Если посмотреть на «x» и «y» (синус и косинус) на одной оси, то они конечно сдвинуты на пи/2

Итак, к чему все это.
Вернемся к электромагнитным волнам. Пустое 3-хмерное пространство. Как известно, два вида полей, электрическое и магнитное, проявляют схожую зависимость между собой.
Грубо говоря, изменение интенсивности магнитного поля порождает разницу электрического потенциала (закон Фарадея). И так же изменение электрического потенциала в точке пространства порождает магнитное поле (закон Ампера).
В уравнениях Максвелла эти зависимости между «E» (электрическое поле) и «B» (магнитное поле) выглядят так

(еще два дополнительных уравнения сводятся к «закону сохранения энергии», и нам не будут интересны)
Прежде чем вникать в детали, следует заметить, что эта система дифф.ур. очень похожа на дифф. ур. инь-яна. Главные элементы здесь — «E», «B» и «t», на остальные параметры можно не обращать внимания, например «J» это внешнее электрическое воздействие, которое не будем рассматривать, а остальное можно принять за константы и забыть.
Кроме этого надо заметить, что и «Е», и «B», это не просто два числа, а поля трехмерных векторов в каждой точке трехмерного пространства. Но это тоже в данном случае ничего кардинально не меняет.
Зато важный элемент — треугольник с крестиком перед «Е» и «B», т.н. «ротор» поля. Из-за него как раз рождаются определенные сомнения и вопросы. К ротору вернемся чуть позже, посмотрим, что за вопросы и неясности вызывает.
Итак, мы видели, что круговая динамика это две связанные величины, которые на одном графике от времени, представляют собой две волны со сдвигом пи/2.
Таким же образом из начального возмущения распространяется электромагнитная волна, через зацикленность интенсивностей и их изменений. Изменение электрического поля порождает магнитное поле, которое, увеличиваясь (=изменяясь), порождает обратное электрическое поле, которое… и т.д. Это классическое (и верное) объяснение, известное наверное каждому.
Но… посмотрим на схему с которой все началось:

Сдвиг… где тут сдвиг? Векторы, обозначающие интенсивности полей, колеблются в одной фазе!
Ошибка? Смотрим на вики. Там то же самое. Ошибка на вики? Смотрим гугл. Что там у нас?
Какие-то непонятные споры… Должен быть сдвиг или нет? Консенсуса нет. Одни говорят «сдвиг должен быть, там везде все неправильно». Другие «доказывают», что правильно. Шок, как так? Идеальная и элегантная теория, которой 300 лет в обед, и еще какие-то неясности?
Например объяснение: www.sciforums.com/threads/luminiferous-ether.57402
Hi BillyT,
From my understanding Vern is correct. Your citation of Maxwell's equation is a good idea, but you are incomplete. In free space you have no currents and no charges so Maxwell's 4 equations simplify down to 2 equations (considering a single spatial dimension):
dE/dx = -dB/dt
dE/dt = -c2 dB/dx
So when the temporal derivative of one is maximal the spatial derivative of the other is minimal (maximally negative). If you consider a simple single-frequency sinusoidal plane wave you find that this happens for E and B in phase. In the above equations:
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt)
Вот, вышло, что должны быть в фазе. И еще в разных местах в интернете другие вариации на эту тему.
Правильно ли? Нет, неправильно.
Почему неправильно? Потому что ротор поля это не его производная по пространству!
dE/dx — так нельзя.В других местах «упрощают» пространство до двумерного другими способами и получают тот же результат. Так тоже нельзя, ротору нужны 3 измерения (не меньше).
Посмотрим, что за это несчастный ротор. Думаю, вещь знакомая со школы.
Дело в том, что изменение электрического поля порождает не абы какое магнитное поле, а «закрученное». Типичный пример, изначальный ток по проводу, порождающий изменение электропотенциала вдоль линии провода, создает закрученное вокруг провода магнитное поле.

То же самое с изменяющимся потенциалом магнитного поля, если изменение имеет векторную направленность, электрическое напряжение будет закручено вокруг него.
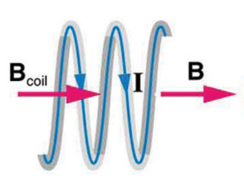
Поэтому ротор поля это не дифференциал, это специальный способ выразить его значение (наподобие смены системы координат), иначе говоря, ротор — это и есть значение поля.
Как в итоге выглядит каскадная зацикленная волна таких закрученностей?
Довольно сложно описать…
Совсем упрощенная схема выглядит так

Но это большое упрощение, такой картинки с колечками вообще не возникает, т.к. все находится во вращении и это скорее спирали, вращающиеся вокруг друг друга. Но при этом и не спирали, т.к. расходятся в пространстве, и взаимосложение даст еще более дивную картину.
Однако в любом случае… сдвиг на пи/2 есть.
Что же насчет классического рисунка? Классический рисунок представляет собой пример однонаправленной волны линейной поляризации… Что-то похожее на лазер. Такую поляризованную волну можно получить, прибавляя к электро- волне круговой поляризации ее зеркальное отражение (стереоизомер). Получится ли после такого сложения волна с колебаниями электропотенциала и магнитной интенсивности в одной фазе?
Следует помнить, что стереоизомеры вращательно-поляризованных волн не симметричны, т.к. векторы сопуствующего магнитного поля всегда повернуты под прямым углом в одну и ту же сторону.
А поэтому… вполне возможно? Или вполне возможно нет?
Комментарии (223)
ivlis
23.02.2016 04:47+4Плоская волна является решением уравнений Максвелла, можете подставить и проверить. Если очень хочется получить именно фотон, то можно дописать вращение поляризаций, чтобы был ненулевой спин. Волна которая идёт в другую сторону будет иметь отрицательную амплитуду одного из полевых векторов, чтобы сохранить "правость" тройки E,H и k. Из такого можно составить такую экзотику как у вас, это не будет плоская распространяющая волна.
И да, электромагнитная волна не LC контур :)
И ротор, это, конечно, производная, только на выходе у неё вектор. Так как пространство изотропно, то nabla \times == \vec{k} \times

Shamrel
23.02.2016 07:20Эм. И в итоге, рисунок, который теребил мне душу с далекого первого курса, верный?
А пока, уважаемый автор, вы мне напомнили моего преподавателя физики (вполне достойный человек). Хочется на конкретный вопрос получить конкретный ответ. Так сказать, для пролетария.
ivlis
23.02.2016 08:15+1Конечно правильная картинка.
Пусть электрическое поле имеет гармонический вид:
,
гденекая амплитуда,
— единичный вектор и
— волновой вектор, так что
. Запишем уравнение Максвелла:
. Поставив в это уравнение
получим:
, где
— скорость света. Как видно, величина магнитного поля прямо пропорционально величине электрического (коэффициент пропорциональности зависит от выбранной системы единиц) и а вектора перпендикулярны.

Shamrel
23.02.2016 09:05+1Тогда получается, существует момент времени и пространства (H и E равны нулю), когда энергии просто нет, она ушла в никуда, а в следующее мгновение, она берется из неоткуда? Наблюдаем рождение вселенной?
Wizard_of_light
23.02.2016 10:30Энергия в этот момент где-то рядом :)

grekmipt
23.02.2016 12:38+4Этот момент часто является предметом споров на форумах "диванных теоретиков". Однако если вспомнить что эм-волна всегда порождается ускорением заряда, а так же вспомнить что поток эм-энергии задается вектором пойнтинга (т.е. векторным произведением электрического и магнитного полей) то вопрос снимается. Ибо есть скажем колеблющийся туда-сюда заряд (гармонически, т.е. по синусу). Покуда он ускоряется в одну или другую сторону — он "сбрасывает" энергию в виде эм-волны (сбрасывает одинаково, независимо от направления ускорения — прямого или обратного). Но в точке своего среднего положения — там где ускорение равно нулю — он ничего не излучает (хотя в этот момент и находится в движении). Вот и получаются эдакие "спайки", толчки излученной эм-энергии. Излучение растет-и падает до нуля. И потом снова растет и падает до нуля. И так в цикле. Так что да, в эм-волне есть точки где энергия эм-поля строго нуль. А затем в эту точку доходит/поступает энергия от следующего полупериода. Т.е. энергия не берется из ниоткуда — она поступает (добегает) в данную точку пространства из следующей "полуволны". Примерно так же как в волне по воде — есть точки где уровень воды не изменился (относительно уровня спокойно воды), а потом этот уровень воды уходит вверх или вниз, и никого это не удивляет ).
0serg
23.02.2016 11:26+1Не-а. Просто бессмысленно говорить о волне как чем-то что можно наблюдать в одной точке. Распространение волны состоит в том что приведенная на рисунке конструкция (с нулями и максимумами) просто целиком движется через пространство. И да, энергия этой волны распределена не равномерно.

Duduka
23.02.2016 11:50Вы в корне неправы, решений однородной системы ур. Максвелла бесконечное множество, это среда без токов, зарядов, источников и стоков, не проподает и не появляется, т.к. не реагирут.
В варианте «длинная линия», есть TM и TE волны, которые больше «стоячие» и ближе к последнему рисунку.0serg
23.02.2016 15:13+1Выше выписано уравнение движущейся волны. Стоячая волна конечно тоже возможна, но там будет другое уравнение и насколько я помню как раз там-то будет тот самый сдвиг между электрической и магнитной компонентами и энергия будет переходить из электрической в магнитную и обратно.

Duduka
23.02.2016 17:02Выше написана система двух волн, не имеющая ни источника, ни стока (Вы встречали такие в природе?), вечных, без переноса энергии, что в принципе возможно, но в нашей вселенной не регистрируемо, т.к. энергетического взаимодействия нет.
ivlis
23.02.2016 17:52+1Вы из XIX века пишите? :) Электромагнитной волне не нужна среда и стоячая волна не будет переносить энергию, на то она и стоячая.

Duduka
24.02.2016 11:48-2А где у меня написано, что для «Электромагнитной волне нужна среда»? У меня написано! "… среда без токов, зарядов, источников и стоков...", система в топике такая, а не у меня, и Вы защищаете позицию что такая система физически реализуема. Я написал: «Вы встречали такие в природе?», приводите пример и как ее детектировать.
Или у Вас проблемы с пониманием текстов? (так и скажите)
Перенос энергии вне материи невозможен (меняется состояние материи, и другого способа зафиксировать передачу энергии нет).
А к Вашему сведению, стоячая волна переносит энергию(вернее волны образующие стоячую волну), со/на стенки, печально, что Вы это не проходили. Я даже не мог представить, что Вы будите приписывать мне свое полную некомпетентность.
Elrond16
24.02.2016 11:57Если отойти от того, что само ЭМ поле является видом материи, ЭМ волны прекрасно распространяются в вакууме и переносят энергию.
Для идеальной стоячей волны (в резонаторе без затухания) тангенциальная компонента электрического поля на стенке в
силу гран условий на металле равна 0, и потока энергии в стенки/из стенок нет ни в какой из моментов времени.
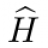
ivlis
24.02.2016 20:20Со стенки или в стенки она переносит, когда стенки с конечной проводимостью. Если стенки идеально проводящие, то тангенциальная компонента ноль и нормальная составляющая вектора Поинтинга равна нулю и никакого потока энергии нет. Видимо вы это где-то проходили, что плохо запомнили и не поняли. Это подтверждает мой тезис на 100% https://geektimes.ru/post/271494/?reply_to=9045774#comment_9045292

Duduka
26.02.2016 06:44Ваш тезис — некомпетентность, незнание, и «сферический конь в векууме». Вас кидает из одной парадигмы в другую. Определитесь вы «эфирник», или все же есть электродинимина с электронами, протонами, и переносчиками заряда?! Как можно создать стоячую волну в длинной линии с терминаторами(если можете сделать идеально проводящие, то делайте), и без подвода энергии. Стоячая волна — сумма волн каждая частотная компонента, которых, взаимосогласованна, источником которых является подводимая энергия и отрожение с разрывов и терминаторов (мало того, что энергия теряется на неидеальных проводниках и излучают разрывы, так еще и не часто всречаются среды с 100% отрожающей способностью, так с отражения «стенка» получает импульс и колеблется). Есть аналогии такого же поведения в во всех «волновых» системах, например, в стакане с водой поробуйте получить стаючую волну и чтобы стакан «не звенел», а потом отключите подачу энергии, даже с учетом потерь, картинка развалится слишком быстро, «со споростью звука», в то время как вы говорите, что энергия не переносится.
Тем более, вы используете только демагогические приемы, отвечаете только на вопросы, на которые знаете ответ, игнорируя «неудобные», приписываете оппоненту фразы и идеи которые он не озвучил, и пытаетесь их опровергнуть. (где у меня сказанно, что только в средах(только не в вакууме распростроняется Elrond16 ?) распростроняются волны? я только сказал, что перенос энергии возможен только между средами! Все!).
Любой датчик — это не ваккум, а состоит из материи, без материи невозможно зафиксировать изменение, и перенос энергии, и более того, сгенерировать «вектор Пойтинга», в среде без материи — невозможно, даже если математически у вас ненулевой вектор, не факт, что это решение имеет место быть в реальности, а не в «сферическом сознании в вакууме».
Воздараюсь к теме ветки: «если вы не верите мне, то возьмите любую систему визуализации, (если система не поддерживает 3D, то возьмите 2D проекции и нагенерируйте мульт от t, и представте, что творится в 4D), и промоделируйте модельные решения из топика, если этот 4D-объект занявший всю вселенную и время — фотон, то я скромно удаляюсь, и посыпаю свою голову пеплом.»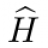
ivlis
26.02.2016 07:21В физике нормально использовать абстракции. Стенки идеально проводящие и бесконечно тяжёлые. Да, отражение 100%. Если волна там существует, то ей никакой подвод энергии не нужен, она там будет вечно существовать. Что тут удивительного?
Скачите как раз вы, видимо из-за пробелов в математике. Топикстартер рассматривает собственное решение уравнений Максвелла, коим является плоская волна, например. Вы же говорите про приёмники, антенны и тп, то есть рассматриваете несобственные решения. Да, они могут быть очень непохожими на плоские волны, но причём тут это?
не факт, что это решение имеет место быть в реальности, а не в «сферическом сознании в вакууме»
Ну уж нет так не пойдёт, если решение есть, значит оно есть в реальности. Иначе можно отбрасывать решения по своему усмотрению какие хочется. Тогда это не наука и чёрт знает что. Другое дело, что решение может быть неустойчивым, не возбуждаться обычными методами, но решением оно не перестаёт быть.
Зачем мне система визуализации, если я всё уже аналитически решил тут: https://geektimes.ru/post/271494/#comment_9043708
И да, никаких электронов и протонов в классической электродинамике, конечно нет. ЭМ волны распространяются без материи, сами по себе, вот такие они забавные.
Duduka
26.02.2016 09:21"… Топикстартер рассматривает собственное решение уравнений Максвелла, коим является плоская волна, например. Вы же говорите про приёмники, антенны и тп, то есть рассматриваете несобственные решения..."
1) Да, для собственного решения — 4D волны, два решения преведены, а также различные линейные суммы волн синусов, и косинусов, прямых и обратных волн, т.е. сказать чему равен вектор Пойтинга, вы не можете, даже констант четыре, у них нет источника(момента их рождения), нет момента поглощения, каждая точка пространтства колеблется во времени; 2) предложите способ измерения энергии, в условиях собственных колебаний, в отсутствии от источников, осциляторов, проводников, антен и других материальных детекторов/генераторов.
«Ну уж нет так не пойдёт, если решение есть, значит оно есть в реальности. Иначе можно отбрасывать решения по своему усмотрению какие хочется. Тогда это не наука и чёрт знает что.»
Не все решения ур. Максвелла реализуемы, система неполна, дополняют лоренцевской калибровной и нормировкой на бесконечности, как и квантуемостью зарядов элементарных частиц, и спина… Вот из-за собственных решений и нельзя использовать конечные разности(которые используются повсеместно), физически могут быть нереализуемы. Только несобственная формулировка уравнений соответсвует опыту, физики не в «сферической иллюзорной лаборатории» ставили эксперименты, им уравнения в основном и удовлетроряют, а не мысленным экспериментам.
Ага решил, поздравляю, только (t,R)-4D объект, непрерывное поле + ikr+wt, тоже решение, и перпендикулярное вашему решению, в любой точке — тоже…
И ничего забавного, в натягивании (совы) реального физического эксперимента, на математические абстракции.
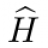
ivlis
23.02.2016 14:04+1Отличный вопрос! Плоская электромагнитная волна движется со скоростью света, в её системе координат нет времени, она существует всегда и во всём пространстве, вот такой вот зверь. Так что энергия никуда не девается.
Другое дело в волноводе или резонаторе, там распределение больше похоже на то что вы нарисовали, но это как минимум две плоские волны вместе.

Neuromantix
23.02.2016 08:53Про нужный для первой картинки сдвиг фазы кажется еще у Перельмана было, или у кого-то из иных популяризаторов науки начала/середины ХХ века.

faiwer
23.02.2016 08:55+18Зашёл прочитать про "электромагнетизм для самых маленьких", а получил производные, системы уравнений, сдвиги волн и пр. Всё таки это статья не для самых маленьких, а для уже подросших ;) Ныне даже квантмех в научпопе и то доступнее объясняется.
Вот скажите, чего вы бы ожидали от статьи? Статья, получается, объясняет про сдвиг Пи/2. А, исходя из названия, я то надеялся увидеть что-нибудь вроде объяснения что такое электрическое поле, что такое магнитное поле, почему их разделяют, и почему их совмещают. Чем они обусловлены, что такое поле вообще. Какое отношение к ним имеют протоны и электроны. Ну и т.д. Вот тогда это был бы "электромагнетизм для самых маленьких".
mkovalevich
23.02.2016 11:22-4Черт, надо было еще "производные" объяснить...
А ваши вопросы слишком сложные. Официальная физика не знает на большинство из них ответов))
faiwer
23.02.2016 11:53+8Черт, надо было еще «производные» объяснить...
Гхм. А зачем? Какую цель вы ставите перед статьёй? Что именно она должна была прояснить в умах страждующих? Вот например тут математики практически нет. Но обсуждаются довольно сложные вещи. После прочтения такой статьи в голове появляется некая картинка, человек начинает понимать как оно там что. И понимает какое отношение всё это имеет к реальной действительности.
А здесь? Положим, я человек, желающий познакомиться с электромагнетизмом. Я вижу в этой статье математику: вектора, графики, уравнения, призводные и пр. Но при этом даже что такое вообще электромагнетизм и с чем его едят не описано. К примеру в статье на вики указывается, что сие есть одно из 4 фундаментальных видов взаимодействия. И многое другое.
Цитата из первого же абзаца вашей статьи:
Потому что ничего сложного там нет.
Но вместо понятных описаний что почём и зачем мы окунаемся в то, почему смещение между кривыми электрического поля и магнитного поля равняется Pi/2. С таким же успехом я могу сказать, что компьютеры это просто, и вместо объяснения что такое ЭВМ, какие задачи решает и пр., сразу начну описывать виды распределённых вычислений. Или опишу, что аэродинамика это просто, и вместо разности давления и пр. штук начну лечить про экранный эффект в формулах или же про обтекание ЛА на сверхзвуковых скоростях.
А вот это вообще обрадовало:
стереоизомеры вращательно-поляризованных волн не симметричны, т.к. векторы сопуствующего магнитного поля всегда повернуты под прямым углом в одну и ту же сторону.
Симметричность стереоизомеров вращательно поляризованых волн! Вот оно что! Для самых маленьких.
Не поймите меня не правильно. Я не считаю, что подача материала слишком сложна. Или что математика зло. Или ещё какую-нибудь глупость. Не в коей мере. Но вам стоило бы хотя бы переписать заголовок, чтобы он соответствовал действительности. Назовите её как-нибудь «Разбираемся со сдвигом между электрическим и магнитным полем».
mkovalevich
23.02.2016 13:19-4Какую цель вы ставите перед статьёй? Что именно она должна была прояснить в умах страждующих?
Цель, обратить внимание, что картинка совсем неадекватна тому, что она якобы поясняет.
Во-первых, любой, понимающий связь между "значением" и "его изменением", услышав объяснение про взаимопорождающиеся поля и получив картинку как "наглядный пример", задаст тот же вопрос. "А где сдвиг?" — полинтернета его задало)
Во-вторых, она дает вам представление, будто поля порождаются в плоскостях, что совсем не так. Линейная поляризация это такой частный случай, что показывать его в качестве "вот так распространяются волны", это вводить в серьезное заблуждение.
Вот например тут
Такой обзор всего может и полезен, чтобы знать, что "существуют электроны", но для меня такая подача больше похожа на забивание головы непонятными, несвязанными вещами. Понимания там нет. Самый наглядный пример, "спин"… "Он бывает и 1/2, и 3/2". Отличная информация, спасибо, буду знать))
grekmipt
23.02.2016 13:29+2Взаимопорождение полей — это стереотипное заблуждение тянущееся еще из школы, равно как и идея об этих вот колечках-полях инициирующих друг друга и вызывающих распространение эм-волны, равно как и то что сдвиг фаз обязательно есть. Фактически в статье Вы как раз привели стандартный набор недопониманий базовых аспектов электродинамики. Т.е. Вы не правы сразу много где — см. ниже. Не сочтите за "наезд", все те заблуждения что есть у Вас в статье они есть более чем у половины студентов, окончивших техвузы, что нормально, ибо вникать в нюансы в вузе часто некогда...

faiwer
23.02.2016 13:43+3Цель, обратить внимание, что картинка совсем неадекватна тому, что она якобы поясняет.
А причём тут тогда электромагнетизм для самых маленьких?
но для меня такая подача больше похожа на забивание головы непонятными, несвязанными вещами.
Приглядитесь к своей статье повнимательнее, разве это не её описание, вы только что случайно выдали? Стереоизомеры для самых маленьких, ага ага :)
Самый наглядный пример, «спин»… «Он бывает и 1/2, и 3/2». Отличная информация, спасибо, буду знать))
Вопрос на засыпку: а если бы там рядом с этим спином привели бы пару тройку формул, из которых этот спин можно вывести, вы бы сказали, что понимания стало больше? :) Большинство людей с вами не согласятся. Понимание мат. аппарата физ. явления это последующий этап, а вовсе не ознакомительный.

Shafikov
23.02.2016 12:06+2Не надо было бы объяснять производные. В статье слишком много слов, но мало смысла.
С самых первых абзацев читатель ожидает, что к концу будет доказано, что самая первая картинка неверна, а вместо неё должна быть такая же, но со сдвигом в pi/2. Этого сделано не было. В итоге совершенно непонятно, о чём вообще статья.
Правильно ли? Нет, неправильно.
Почему неправильно? Потому что ротор поля это не его производная по пространству!
Да, правильно. Попробуйте взять ротор от поля E(x,y,z)=E(x).
Поэтому ротор поля это не дифференциал, это специальный способ выразить его значение (наподобие смены системы координат), иначе говоря, ротор — это и есть значение поля.
Нет, это не значение поля. Если ставите целью объяснить ротор людям, не знающим о нём, хотя бы не запутывайте их. По-простому ротор — это закрученность поля. Если взглянуть на самую первую картинку, то можно заметить, что максимальная закрученность у обоих полей как раз в "узлах" (легко проверить мысленно взяв интеграл по контуру) и, как раз, там же находится максимальная производная по времени (так же легко проверить начав мысленно сдвигать синусоиды в одну из сторон).
Таким образом, на Вашей лакмусовой бумажке поле изображено верно, без сдвига.
А исходя из названия, можно было бы ожидать побольше про сами поля (тем более, ответы на все вопросы выше физика то знает), что-нибудь интересное на уровне школьной физики ("для самых маленьких"), поподробнее про связь полей, про вектор-потенциал что-нибудь (для "и не только").
mkovalevich
23.02.2016 15:40Да, правильно. Попробуйте взять ротор от поля E(x,y,z)=E(x).
Если E(x) = (Ex(x), Ey(x), Ez(x)), тогда rotE = (сюда вставить формулу ротора). И что? Речь шла о неправильности сведения к одномерному полю. Надеюсь, ваше E(x) не R1->R1?
Нет, это не значение поля. Если ставите целью объяснить ротор людям, не знающим о нём, хотя бы не запутывайте их. По-простому ротор — это закрученность поля.
Да, и это же выражает значение, но вместо векторов интенсивности — мера закрученности. То, что там производные — пусть вас не вводит в заблуждение.
Таким образом, на Вашей лакмусовой бумажке поле изображено верно, без сдвига.
Однако это особый случай, который как раз запутывает. Формально все на нем сходится, но "в жизни все не так"! Первичны — закрученные волны, а линейная поляризация — вторичный "продукт", крайне особый случай. На этой картинке очень сложно увидеть взаимодействие ротора и интенсивностей. А говорить "вот смотрите, как одно поле порождает другое" — просто неверно.
Shafikov
23.02.2016 16:13+2Очевидно, речь шла о поле E(r) = (Ex(r), Ey(r), Ez(r))=(Ex cos (kx x — w t)). Формально и по сути это векторное поле трех координат от трёх координат. Если Вас вводит в заблуждение наличие только х компонент в конечном выражении, сделайте произвольную замену координат — получите выражение со всеми компонентами и координатами.
Формально все на нем сходится, но «в жизни все не так»!
Вы, возможно, сейчас удивитесь, но все модели в физике — всего лишь модели, с разной точностью описывающие реальность. Была модельная задача — уравнения Максвелла в бесконечном вакууме. Одним из многих её решений является плоская э/м волна. Вы попытались это опровергнуть, но не вышло. На этом спор можно было бы и завершить.
То, что там производные — пусть вас не вводит в заблуждение.
Как раз меня это не вводит в заблуждение. Заблуждение ведь у Вас: "ротор — это и есть значение поля".
mkovalevich
23.02.2016 17:55Очевидно, речь шла о поле E® = (Ex®, Ey®, Ez®)=(Ex cos (kx x — w t)).
Нет, он сказал "волна плоская, а поэтому ну их, эти "у" и "z"". Будем одномерными. И бац, dE/dx.
Одним из многих её решений является плоская э/м волна. Вы попытались это опровергнуть, но не вышло.
Будьте добры показать, где это я пыталась опровергнуть?)
Как раз меня это не вводит в заблуждение. Заблуждение ведь у Вас: «ротор — это и есть значение поля».
Мощная аргументация, сдаюсь.
Elrond16
23.02.2016 18:04+1Нет, он сказал "волна плоская, а поэтому ну их, эти "у" и "z"". Будем одномерными. И бац, dE/dx.
Ничто не мешает рассматривать поле, у которого в трехмерном пространстве есть только одна пространственная компонента, а остальные равны 0. Тогда, если поле еще и зависит от одной координаты, у ротора будет тоже только одна компонента равная, например, dE/dx.
Будьте добры показать, где это я пыталась опровергнуть?)
Видимо там, где вам не нравится классическая картинка, иллюстрирующая плоскую волну.

Elrond16
23.02.2016 16:36+1Я не понимаю, почему вы обращаете внимание на поляризацию вообще, она тут не при делах. В цилиндрически и эллиптически поляризованной плоской волне разность фаз по-прежнему будет 0.
И это не какая-то искусственная штука, не встречающаяся в жизни. Нулевая (или околонулевая) разность фаз поперечных полей необходима для передачи энергии. К примеру, в распространяющиеся волноводных модах (без учета затухания) это строго выполняется, разность фаз поперечных полей всегда равна 0.
mkovalevich
23.02.2016 18:00цилиндрически и эллиптически поляризованной плоской волне
Это как, круговая, но плоская?
Речь не об искусственности или редкости, конечно, а о том, насколько она годится для демонстрации "взаимно-образующихся полей". На линейной этого не видно.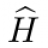
ivlis
23.02.2016 18:09Это называется фотон :)

Elrond16
23.02.2016 18:19Я плохо помню КЭД, но если мне не изменяет память, то в состоянии с фиксированным числом фотонов среднее значение поля обязано быть равно 0 (в отличие от средних квадратов поля), т.к. оператор поля содержит операторы рождения и уничтожения, моменты которого для этого состояния 0. Поэтому мне не очень понятно, как плоская волна (или любой волновой пакет) соотносится с фотоном, в них число фотонов вроде как должно быть неопределенным.

Elrond16
23.02.2016 18:11+1Произвольная плоская монохроматическая волна, распространяющаяся вдоль z:
E = Re [(Ex, i Ey, 0) * exp(i w t — i h z)]
При Ex = 0 или Ey = 0 имеем линейно-поляризованную волну, при Ey = +-Ex циркулярно-поляризованную (в прошлом комментарии я случайно написал "цилиндрически" вместо "циркулярно", прошу прощения), в общем случае эллиптически поляризованную
Плоской называется волна, фазовый фронт которой имеет форму плоскости.
Поляризация волны определяется по поведению проекции вектора электрического поля на плоскость, перпендикулярную направлению распространения.
Поляризация никак не связана с тем, что волна плоская.
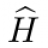
ivlis
23.02.2016 14:06+1Электродинамику принципиально нельзя понять не умея решать уравнения в частных производных. Увы.

faiwer
23.02.2016 14:29+3Ну если "понять", это уметь применить на практике, то, наверное. А если просто удовлетворить своё любопытство поняв основные принципы, то неужели нельзя? Нужно ли знать
 , для того чтобы понять, что мир не стоит на 3-х китах? Нужно ли углубляться в системы уравнений ОТО, чтобы понять то, что гравитация там рассматривается как искривление пространства-времени?
, для того чтобы понять, что мир не стоит на 3-х китах? Нужно ли углубляться в системы уравнений ОТО, чтобы понять то, что гравитация там рассматривается как искривление пространства-времени?
Скажем производные брать учили ещё в 10-ом классе. Интегралы мы брали уже в университете. Так что какое-то беглое понимание написанного я имею, и при желании, мог бы углубиться, вспомнить, что там да как, и понять уже не бегло. НО! Это же ни на грамм не поможет мне понять суть.
Как абстрактные математические причинно-следственные связи в указанных уравнениях помогут человеку понять суть элетричества, магнетизма? Ну вот увижу я, что Y следует из X. Ну а окромя этого оно же мне ни о чём не скажет. Оттого что мат. уравнения сходятся праздному обывателю ни жарко, ни холодно.
Вот скажем взять аэродинамику. Можно взять уравнение Бернулли, долго и муторно с графиками рассуждать о взаимосвязи скорости и давления и прочем. Заморочить человеку голову по самое не могу, взявшись описывать тонкости индуктивного сопротивления. А можно просто дать посмотреть вот такой вот ролик. Вот это и будет аэродинамикой для чайников. А большего ему и не нужно. Самолёты ему не строить, науку вперёд не толкать.
Возвращаясь к цитате. Вы правда считаете, что электродинамика ещё дальше от обывателя нежели механика, квантмех, аэродинамика и прочие разделы физики? Естественно, я имею ввиду самое поверхностное представление.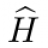
ivlis
23.02.2016 18:08+1Ну мультиков можно сколько угодно нарисовать. Мультики не дают инструмента, если у вас возникает вопрос на который вы в мультике нет ответа, то ответить вы не сможете, примерно как автор поста. Картинку увидел, а откуда она получается — не знает, вот и получаются вопросы. Физика построена на математическом аппарате, не зная аппарата невозможно оперировать физическими величинами. И у каждого "раздела" свой аппарат. Законы Кеплера можно без дифуравнений записать и из этого уже извлечь информацию о движении планет. Не мультик анимационный посмотреть, а прямо посчитать как какие планеты двигаются. Квантовая механика (как её учат на 2-3 курсах института) действительно проще электромагнетизма в плане матаппарата, так как уравнение Шредингера скалярное и первого порядка. А вот уравнения Максвелла они принципиально трёхмерные и нужно оперировать такими понятиями как дивергенция и ротор, которые в школе не учат. Ну или взять какие-нибудь топологические изоляторы, то их теория довольна сложна для обычного физика, потому что используется формализм дифференциальной геометрии, которую обычно не изучают на физических факультетах.
Я считаю, что физика это в первую очередь возможность вычислить предсказанные эффекты, иначе очень легко скатится в метафизику. Shut up and calculate!
faiwer
23.02.2016 18:19+3Мультики не дают инструмента, если у вас возникает вопрос на который вы в мультике нет ответа, то ответить вы не сможете, примерно как автор поста
А должен? Таких задач перед беглым ознакомлением, так сказать, введением, никто и не ставит.
Физика построена на математическом аппарате, не зная аппарата невозможно оперировать физическими величинами
А нужно? Пусть этим занимаются специально обученные люди.
Не мультик анимационный посмотреть, а прямо посчитать как какие планеты двигаются
И зачем, допустим, мне, это нужно? Что за ерунда? Мне достаточно знать, что планеты движутся по эллиптической орбите вокруг светила. Нужно будет узнать как оно там в системах с двумя звёздами или других сложных случаях — ну вот тогда уже полезу в рассчёты. Но ~100% что не полезу, ибо зачем мне это? Я же не астрофизик.
так как уравнение Шредингера скалярное и первого порядка.
А зачем его вообще знать? Разве недостаточно того, что из него вытекает? Мы ведь не про физиков говорим. Тут речь про «самых маленьких».
Я считаю, что физика это в первую очередь возможность вычислить предсказанные эффекты, иначе очень легко скатится в метафизику. Shut up and calculate!
Глупости какие. Зачем мне это нужно? Пусть этим занимаются «прикладные физики». У меня другая профессия. И вот уже по ней я зарываюсь с головой в литературу, документацию и пр…
По вашему получается, что человек либо считает, что живёт на 3 китах, а мир был создан за 7 дней, либо целыми днями высчитывает орбиты планет. А людей, которым просто интересно иметь базовые представления об окружающем мире нужно примкнуть к одному из этих двух лагерей.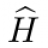
ivlis
24.02.2016 06:50Я могу нарисовать очень убедительный мультик про "трёх китов" и вы никогда не сможете отличить это реального положения вещей.
По моему опыту, пока не пройдешь все выводы сам, пока не решишь несколько модельных задач — понять ничего невозможно. Выучить можно, что делают 85% студентов, поверить можно, но не понять.
mkovalevich
24.02.2016 11:35Интересно, а вот именно это решение, как на первой картинке — реализуемо на деле? Как-то не вижу, каким образом оно может распространяться по прямой (именно прямой, а не плоскости) — и при этом не расходиться в стороны?
По-моему не все формально правильные решения — жизненны. Поэтому "shut up and calculate" недостаточно. Надо еще не забыть про "turn on brain")
Elrond16
24.02.2016 12:02Интересно, а вот именно это решение, как на первой картинке — реализуемо на деле?
Конечно. Любой волновод. Самый простой пример — ТЕ10 мода прямоугольного волновода. В ней электрическое поле всегда направлено по одной поперечной оси, а поперечное магнитное — по другой. И они абсолютно в одних и тех же точках по продольной координате обращаются в ноль.
Если брать открытое пространство, то можно использовать гауссовы пучки. Они, конечно, будут расходиться, но расходимость правится системой линз/зеркал.
mkovalevich
24.02.2016 12:13По прямой. А не по волноводу и не в пучках.
Решение же есть? Покажите реализацию именно этого решения. Пусть даже "прямая" будет не нулевой толщины, но близко.
Elrond16
24.02.2016 12:31Плоская волна — это решение, ничем не ограниченное в пространстве и имеющее бесконечную энергию. По очевидным причинам его реализовать нельзя. При чем тут вообще прямая какой-то толщины, я не понимаю, оно существует во всем пространстве. Любое реалистичное решение — это комбинация хотя бы двух таких плоских волн. Плоская волна тем и хороша, что набор плоских волн удобно рассматривать в качестве базиса.
Но с точки зрения разности фаз, про которую вы говорите в посте, решения с нулевой разностью фаз между E и H реализуются.
mkovalevich
24.02.2016 12:56При чем тут вообще прямая какой-то толщины, я не понимаю, оно существует во всем пространстве.
Ну как же, мы рассматриваем решение именно с картинки, т.е. поле существует лишь вдоль прямой, а тут ivlis показывал решение https://geektimes.ru/post/271494/?reply_to=9045932#comment_9043708
На всякий случаю добавлю, лазер не предлагать, ну разве что с доказательством, что фотоны синусоидальны)
mkovalevich
24.02.2016 13:01Ага, там решение таки для всего пространства… но существует и для одной прямой.
И насчет этого решения — "По очевидным причинам его реализовать нельзя" — а какой смысл в таком решении?
grekmipt
24.02.2016 13:10+1Бррр… не существует никакого решения, задающего поле только на одной прямой. Лазер не исключение — лазерный пучок существует в виде такого вот пучка только если толщина пучка как минимум несколько длин волн, иначе пучка нет — в противном случае лазерный пучок уже не пучок а просто эдакий быстро расходящийся конус. Решения в виде бесконечно тонкой прямой уравнения Максвелла не допускают в принципе. Вы о чем вообще? ) А для ненулевой толщины — да, обычный лазерный луч (т.е. т.е. гауссов пучок, погуглите что это) и задает внутри пучка такую вот волну. На оси пучка — будет как раз строго такая картинка (конечно если рассматривать самую простую моду лазера), а чем ближе к краю пучка — тем сильнее картинка будет отклоняться от указанной (будут появляться продольные компоненты поля, а поперечная компонента будет уменьшаться).

mkovalevich
24.02.2016 13:23Обычный лазерный луч, обычные фотоны) Только при чем тут синусоиды?

Elrond16
24.02.2016 13:24+1При том, что излучение лазера отлично описывается классической электродинамикой без всяких фотонов.

Elrond16
24.02.2016 13:22Смысл я сказал — это очень простое по поведению решение, поэтому плоские волны во многих случаях удобно рассматривать как базис. Часто Фурье-разложение делают именно по плоским волнам. Еще поле в волновых пакетах достаточного размера очень похоже по поведению на плоскую волну.

grekmipt
24.02.2016 13:02мы рассматриваем решение именно с картинки, т.е. поле существует лишь вдоль прямой
Как говорится, "спасибо, поржал" ))).
Картинка же не про поле существующее только на прямой. А про направления и амплитуды векторов полей в точках лежащих на прямой. Рядом же с этой прямой идут другие параллельные прямые — где свои значения полей в точках этих прямых. Т.е. Ваша картинка это фактически одномерный срез поля в какой-то момент времени. А само поле при этом разумеется задано в объеме (вектора полей существуют в любой окрестности от этой прямой), и в указанном случае это поле растянуто на всю бесконечность — и какую параллельную прямую не проведи (к указанной на картинке), всюду вектора полей будут иметь вот такую структуру. Что и означает плоскую пространственную эм- волну. Закрадывается подозрение что Вы вообще не понимаете что нарисовано на Вашей картинке. А?
mkovalevich
24.02.2016 13:06См. коммент выше.
а) Есть решение и для прямой
б) Покажите реализуемость этого решения, а так как невозможно, смысл его использования как наглядного примера.
Иначе говоря, покажите, что это не сферический конь в вакууме)
grekmipt
24.02.2016 13:15+2Для бесконечно тонкой прямой — решения не существует. Для пучка конечной толщины и конечной длины — решение есть, гуглите гауссов пучок. Т.е. вот эти вот самые уравнения Максвелла и дают возможность существовать лазерному пучку (который и есть гауссов пучок), с совершенно классическим электромагнитным полем внутри пучка (не требующим каких-либо понятий о квантовости). Для пучка бесконечной длины — решения так же не существует (лазерный пучок в конечном итоге на определенном расстоянии начинает быстро расходиться, т.е. до какого-то момента это пучок, а потом хлоп — и пучок переходит в быстро расширяющийся конус). Тем не менее, на оси пучка (даже когда он начинает расходиться) поля вот именно такие как на картинке, в фазе друг с другом, и равны по амплитуде.

mkovalevich
24.02.2016 13:19Для бесконечно тонкой прямой — решения не существует.
Конечно существует. Возьмите из решения для всего пространства одну прямую по вектору волны, обнулите все остальные — вот и решение. Ровно как на картинке)
Я же говорила, лазер не предлагать, гауссов пучок не катит.
Elrond16
24.02.2016 13:23+1Это решение очевидно не удовлетворяет УМ.

mkovalevich
24.02.2016 13:26Удовлетворяет, можете проверить.

Elrond16
24.02.2016 13:31+1Для него не выполнено divE = 0, divB = 0 из-за сингулярности на прямой.

mkovalevich
24.02.2016 13:42Что за сингулярность? dEx/dx + dEy/dy + dEz/dz = 0
Что я делаю не так?)
Elrond16
24.02.2016 13:43+1Вы неправильно дифференцируете дельта-функцию.
dEx /dx = E0 delta'(x) delta(y)
mkovalevich
24.02.2016 14:10Непонятная запись (сделайте картинкой), и при чем тут "y"?

Elrond16
24.02.2016 14:16Насколько я понимаю, с нулевой кармой нельзя ставить картинки (если это не изменилось).
Вы задаете поле на прямой, соответственно оно должно представляться в виде дельта-функций по двум поперечным координатам, т.е. по x и y. Пусть само поле направлено по x: E = (E0 delta(x) delta(y), 0, 0) * cos(wt — kz)
Тогда, когда вы берете дивергенцию, вы обязаны взять производную от дельта-функции, которая не равна 0.

grekmipt
24.02.2016 13:32+3Конечно существует. Возьмите из решения для всего пространства одну прямую по вектору волны, обнулите все остальные — вот и решение. Ровно как на картинке)
Ууу… Слушайте… Вы в курсе что такое решение? ) Решение — это такое выражение, которое при подстановке в уравнения — дает тождество. Уравнения наши — это дифференциальные уравнения Максвелла. Если вы зададите поле только на прямой, и нуль поля в любой сколь малой окрестности от прямой, то такое поле невозможно совместить с уравнениями Максвелла. Т.е. уравнения Максвелла для такого поля не будут выполняться. Вообще. Просто потому что содержат пространственные производные полей. А у вас поля заданы только на прямой — т.е. заданы в виде дельта-функции. Такое поле автоматически не имеет ничего общего с уравнениями Максвелла, по той простой причине что уравнения Максвелла описывают кусочно-гладкое поле (т.е. дифференцируемое в любой точке, за исключением отдельных особых точек). А никак не поле в виде дельта-функции — у Вас всё поле это особые точки )))).
У общем я понял, дискуссию надо закрывать — у Вас явно хромают не только базовые представления электродинамики, но и базовые понятия из теории дифференциальных уравнений. С такой хромой базой я не возьмусь прояснить Вам теорпол, это реально надо курс лекций...
mkovalevich
24.02.2016 13:40-2Т.е. уравнения Максвелла для такого поля не будут выполняться. Вообще. Просто потому что содержат пространственные производные полей.
А вы проверьте. Направьте волну вдоль оси для упрощения, например "z". И посчитайте.
grekmipt
24.02.2016 13:51+3Какая разница куда направлять волну. Чему равна div E для такого поля? Напомню, дивергенция это по простому — сумма производных по всем (а не одной) ортам. Т.е. дивергенция поля для вашей прямой — это сумма в которой есть нормальная производная (вдоль прямой), а так же две производные от дельта-функции, (в стороны от прямой), которые по своей сути равны (внезапно) бесконечности, а по форме — не определены в пространстве гладких функций. Ну и как вы будете использовать такую дивергенцию в рамках уравнений Максвелла? То же самое касается и ротора. Уравнений Максвелла они трехмерны. Всегда, везде, и без исключений. Превращать операторы ротора и дивергенции в производные вдоль одной прямой — нельзя. А если так сделать то получившееся не будет иметь к уравнениям Максвелла никакого отношения (потому что не будет иметь никакого отношения к ротору и дивергенции). Если Вам это не очевидно — то проведение дальнейшего ликбеза совершенно бессмысленно, вначале Вам надо подучить курс диффуров да и просто и матана, потом нормально понять теорпол (не в контексте электродинамики, а вообще сам мат аппарат — что такое операторы теорпола и что с ними можно делать а что нельзя), и только потом начинать думать об электродинамике.

mkovalevich
24.02.2016 14:15-3Дело в том, что частные производные по всем осям — нули. Поэтому никакой неопределенности производных тут нет. Вы забыли, что единственная частная производная не нулевая — это dEx/dz (если волна в плоскости xz и в направлении z). И она в дивергенцию не входит.
Матан учить вам))
Elrond16
24.02.2016 14:17+2Вы серьезно не понимаете, чем дельта-функция отличается от 0 или константы с т.з. дифференцирования? Это, конечно, не совсем матан, а функан, но всё же...

grekmipt
24.02.2016 14:23Всё, сил больше нет )), отвечаю крайний раз. Что такое производная по сути? Это скорость изменения функции в точке. То самое буквальное dE арифметически разделенное на dx. Е у вас задано на прямой (не равно нулю), и строго нуль в любой точке около прямой. Чему равно dE? Очевидно, оно просто равно Е: dE = E(на прямой) — Е(бесконечно близко к прямой) = E(на прямой) — 0 = E(на прямой). Чему равно dx? Ну это по определению бесконечно малое приращение по координате. Что получится когда вы конечную величину (dE) разделите на бесконечно малое dx (т.е. возьмете предел отношения dE/dx=Е(на прямой)/dx при dx стремящемся к нулю)? Разумеется, получится бесконечность. Производная от дельта-функции не равна нулю, где вы такую дичь взяли? Так что дивергенция дает сумму нормальной частной производной (вдоль направления по прямой, и эта частная производная как раз не нуль, а тот самый синус/косинус) и плюс двух бесконечностей (производных по направлениям перпендикулярным прямой). Всё. Учите матчасть, мадам. Серьезно.

mkovalevich
24.02.2016 14:49-1Ок, вы правы, dEx/dx меня сбил))
Чтобы исправиться) можем расширить решение по всей оси x. Получим решение волны, запертой в плоскости. Столь же абсурдно, как и по прямой.
Что на это официальная физика? )
Elrond16
24.02.2016 14:55+1На это у вас осталось B, которое перпендикулярно плоскости xz и для которого тоже нужно выполнить div B = 0. Итого, чтобы исправиться с ним, вам придется расширить решение и по координате y и, внезапно, получить обычную плоскую волну.

mkovalevich
24.02.2016 15:03-1Ох ты, ну ладно, уговорили.) Можно конечно сглаживать, чтобы не все пространство, а диапазон...
Тем не менее главного это не меняет — само решение в жизни не встречается!

grekmipt
24.02.2016 13:23Идеальная плоская волна разлитая по всему пространству — это разумеется абстракция. Но очень полезная на практике, т.к. в огромном кол-ве случае реальное поле отличается от этой абстракции настолько ничтожно, что этим отличием просто пренебрегают. Ну т.е. есть там компонента полей у которой скажем есть сдвиг фазы, но это компонента в мильон раз меньше чем компонента полей у которых сдвига фазы нет. В такой ситуации — выкинули лишнее (за малостью) и оперируем идеальной плоской волной.
Хотя можно строго показать, что любая эм-волна не являющаяся плоской (т.е. занимающей всё пространство) обязательно содержит помимо вот таких вот поперечных компонент — еще и продольные компоненты. И чем сильнее отличие фронта волны от плоского — тем сильнее будут по амплитуде продольные компоненты. В случае того же лазера (т.е. гауссова пучка) это очень сильно выражено — строго поперечная компонента есть только на оси пучка, а чем дальше от оси пучка тем сильнее продольная компонента (когда векторы поля направлены вдоль пучка а не поперек). Но это уже технические детали.
Идеальная плоская волна — это по сути ни что иное как просто разложение реального поля в ряд Фурье. Вы же знаете что такое ряд Фурье, и насколько он полезен в мат-анализе? И вас же не смущает что синус определен на всей бесконечности — что никак не мешает пользоваться рядом Фурье для целей мат-анализа и делать вполне корректные выводы в итоге? В случае эм-волны синус заменяется на плоскую волну, вот и вся разница.
mkovalevich
24.02.2016 13:35-1Тут речь о более серьезной вещи. Помните, как в квантовой электродинамике в решениях получались бесконечности? Так вот, если у вас уравнения, и вы нашли какое-то решение — это не значит, что оно будет работать в реальности.
В КЭД ошибочность была очевидна, здесь как видим не очень. Взяли одно из бесконечного числа решений, самое простое, как раз по принципу "shut up and calculate". "Приложим ротор, разделим переменные, о, волновое уравнение. Подставляем синус — все сходится. Ура, товарищи".
А то, что в жизни такая волна вообще никаким боком, на это решили не обращать внимание. "Ну это же физика, тут все приближенно". Только тут даже не приближенно — тут вообще даже близко такое решение не реализуемо. (опять же на всякий случай повторю, фотоны это совсем другое)
grekmipt
24.02.2016 13:44+3Нде. Всё плохо. Перечитайте выше. Поле определенное только на прямой — НЕ является решением уравнений Максвелла, вообще вне зависимости от того какие там поля на этой прямой, хоть в фазе хоть нет, хоть поперек прямой направлены хоть вдоль. Ибо не дифференцируемо такое поле в силу того что ротор и дивергенция не определены (не имеют смысла). А значит уравнения Максвелла так же не имеют смысла для такого поля, ну или наоборот — такое поле не умеет смысла в рамках уравнений Максвелла, что и значит — не стыкуется с Максвеллом (т.е. не описывается им — и не является решением оного). Я честно не понимаю как Вы можете рассуждать что-то про КЭД и при этом не понимать таких простых вещей из области по сути базового матана. )

mkovalevich
24.02.2016 15:06-1Ок, ошибки исправили, но суть поста выше остается. А что там в КЭД было, это рядовой случай в разных ситуациях, когда за вычислениями забываешь о смысле и приложимости к жизни.

Elrond16
24.02.2016 13:44+1Еще раз, широкий гауссов пучок вблизи центра хорошо аппроксимируется плоской волной.

mkovalevich
24.02.2016 14:57-2Вы понимаете, что гауссов пучок возможен лишь благодаря фотонам, или на "языке волн" — благодаря некой локализации волны, вроде солитона или чего-то подобного. То есть, далеко не синус. Натягивать на это плоскую
совуволну — бумага все стерпит конечно...
Elrond16
24.02.2016 15:07+1Мы говорим про классическую электродинамику, в ней никаких фотонов нет.
Разумеется, гауссов пучок локализован. Однако, при достаточных размерах этого пучка его поведение в окресности центра с точностью до членов порядка lambda/d (где lambda — несущая длина волны, а d — характерные продольные и поперечные размеры) совпадает с поведением плоской волны. Типичные несфокусированные пучки бывают достаточно широкими, из-за чего приближение плоской волны для них может работать с замечательной точностью.
И что значит "далеко не синус"? Типичный пучок — это штука с огибающим и заполнением типа "E = E(r,t) sin(wt — kz)", где огибающая E(r,t) имеет пространственный и временной масштабы много большие, чем масштабы колебаний синуса, поэтому локально рассматривается как E sin(wt — kz).

mkovalevich
24.02.2016 15:24-1Приводить лазер, демонстрируя Максвелла, при этом приговаривая "вполне неплохо так аппроксимируется" совсем несуразно. Эта теория ("Максвелла") гораздо лучше, чем такое натягивание…
Она гораздо осмысленнее там, где волны распространяются относительно свободно. В технике например радио и т.п. Поглядите, как выглядят волны там, и сравните с этим сферическим конем натянутым на сову...
grekmipt
24.02.2016 15:33+3Лазер это и есть свободные электромагнитные волны. Никаких натяжек и подгонок тут нет. Лазерное излучение — это определенное распределение векторов Е и Н в пространстве, и это распределение строго описывается Максвеллом, но не является плоской волной. А вот в центре пучка (на оси) — поле распределение полей действительно очень близко к тому что нарисовано на Вашей картинке. Поэтому Вам и говорят что в центре пучка эм-волна отлично аппроксимируется (локально) плоской волной. Ибо часть поля, не совпадающая с плоской волной — пренебрежимо мала. Но это именно в центре пучка. По мере отхода от оси пучка — поле будет всё сильнее несовпадать с полем плоской волны, и будет по прежнему задано в явном виде как определенные зависимости Е(r,t) и H(r,t), и эти зависимости будут строго удовлетворять Максвеллу.
Что у вас за идея что лазерное поле это какое-то особое поле? Это самое обычное электромагнитное поле. Точно такое же как у любой обычной антенны.
Я Вам даже больше скажу. Есть в антеннах вполне себе аналог лазера. Например антенна Уда-Яги, если Вы возьмете её оооочень с большим кол-вом директоров (т.е. сделаете очень длинной в длинах волн), то и получится нечто очень близкое к лазерному пучку. А уж фазированная антенная решетка диаметром в несколько длин волн так и вовсе может создать строго "лазерный" луч, но только для радиодиапазона (поле такой решетки будет вообще ничем не отличаться от поля лазерного пучка по своей структуре). Что собственно и используется на практике в радарах, в чистом виде. Т.е радары как раз и создают "лазерный" пучок, которым и ведут скажем цель (вражеский самолет).
mkovalevich
24.02.2016 16:11-3В моем понимании (можете поправить) "обычные" волны и фотоны, хоть используют то же поле, качественно отличаются из-за их различного происхождения. "Обычные" волны создаст например колеблющийся заряд, и частота волны будет зависеть от частоты колебания заряда. Фотоны излучаются элементарными частицами, например электроном. И частота зависит от разницы уровней энергии при излучении. При этом, если "обычная" волна имеет волновую природу, фотон более странный — в некотором смысле локализованный (корпускулярный). То есть, в некотором смысле имеет траекторию (конечно с поправкой на волновой дуализм), и в некотором смысле его можно зарегистрировать его как частицу.
А например вайфай как частицу зарегистрировать невозможно. И Максвелл касается именно "обычных" волн. А при фотонах он бессмысленен (разве что при проявлениях дуализма, но… все равно это уже не его территория)).
BigBeaver
24.02.2016 16:19Вопрос лишь в масштабах локализации. Дуализм — весьма сомнительная штука с точки зрения современной физики. И если вы выделяете фотоны как нечто особенное, то приведите пожалуйста, длину волны, начиная с которой "зарегистрировать, как частицу" становится не возможным.

Elrond16
24.02.2016 16:30И корпускулярные, и волновые свойства проявляют волны любой длины да и любые объекты вообще (в том числе вы и я). Однако в огромном количестве случаев описания ЭМ-поля корпускулярные свойства не нужны, и классическая электродинамика отлично подходит для того, чтобы описывать это поле в очень широких диапазонах, включая, конечно, и оптику. Классическая теория работает настолько хорошо, что для решения задач широко используется комбинация квантовой механики и классической электродинамики без квантования поля и перехода к КТП.

grekmipt
24.02.2016 16:37+1Понимание не верное. С позиций современной физики, любое классическое эм-поле (в т.ч. поле радиоизлучения антенны) можно одинаково корректно рассматривать и как классическое поле, и как совокупность конечного числа фотонов. Поменяется лишь мат-аппарат и сложность расчетов, а итоговый результат не изменится абсолютно. Т.е. в контексте эм-полей и обычной радиофизики, что Максвелл, что генерируемые антенной фотоны — приведут строго к одному и тому же, разницы в макро-результате (макро-полях) нет вообще.
Далее, с позиций современной физики, корпускулярность фотона не имеет никакого отношения к его локализации. Фотон принципиально не локализован — он существует сразу во всей вселенной (т.е. принципиально ДЕлокализован). Но вот наблюдение фотона возможно только в одной конкретной точке (то самое схлопывание волновой функции и всё такое), и это наблюдение автоматически меняет состояние фотона (точнее фотон исчезает сразу из всей вселенной — и просто поглощается фотодетектором). Корпускула фотона — это именно факт того что он неделим, является квантом энергии. Т.е. может быть наблюден/поглощен фотодетектором только в одной точке (одним атомом/молекулой), и не может быть наполовину поглощен одним атомом, и наполовину — соседним.
Но это не имеет никакого отношения к локализации фотона.
Вайфай, как вообще принципиально любое радиоизлучение на принципиально любых частотах — теоретически можно зарегистрировать как частицу (фотон), разумеется. Колеблющийся заряд (скажем диполь), так же как и любая антенна — создает не что иное как поток фотонов очень высокой плотности, что аппроксимируется (усредняется) макроскопически как раз в виде уравнений Максвелла. Так что фотоны от диполя принципиально можно задетектрировать именно как отдельные фотоны.
Но для диапазона частот вайфая (крайне малая энергия фотона) — для этого нужно чтобы мощность излучения вайфая была мизерной, так чтобы статистический поток фотонов (сливающийся в макроскопическое Максвелловское эм-поле) как-бы "распался" на отдельные акты излучения антенной этих фотонов. Далее нужно как-то умудриться заэкранировать все внешние шумы до полного нуля (т.е. спец камера с температурами близко к нулю кельвинов, и т.п. и т.д.), и далее еще как-то суметь найти "квантовый приёмник" для таких никзочастотных фотонов (ибо отдельный фотон наведет на антенне настолько малые напряжение/ток, что на фоне собственных тепловых шумов антенны, даже при температуре близкой к абсолютному нулю, никакой чувствительности детектора не хватит чтобы зарегистрировать такой слабый по энергии фотон). Тем не менее, какими-то хитрыми косвенными методами наверное такой эксперимент поставить наверняка можно, ну и чем выше частота радиоизлучения тем проще это будет сделать (залезать нужно будет куда-нибудь в терагерцовый диапазон или даже сильно выше, там это уже чисто технически пожалуй будет реально).
mkovalevich
24.02.2016 19:15BigBeaver, Elrond16, grekmipt, отвечу тут сразу. Мда, вопрос сложный и без детальных знаний лучше помолчу на эту тему. Единственное, как вы заметили, у всех есть сомнения насчет "что это такое?". Единственное, что не вызывает сомнений, это опыты и формулы. Но интерпретация...
Например, как Фейнман объяснял отражение света, мол фотон проходит все возможные пути, но только тот с "лучевой" траекторией не аннигилируется другими. Тут сразу возникает дежавю с голограммами, в которых также образ формируется отражением от всей отражающей среды, тем более, зеркало оказывается лишь частным случаем голографического отражения. Казалось бы — отлично, зачем тогда какие-то фиктивные фотоны, если все объясняется волнами. Но потом оказывается, что волнами таки не обойтись. (хотя надеюсь, что в итоге окажется, что можно))
Еще сомнения насчет "фотонов" и "квантов энергии". У фотонов энергии разные, поэтому какие же они кванты. То, что например электроны поглощают или испускают именно такие "порции", т.е. частоты, можно объяснить резонансом. Например, стеклянный бокал можно разбить именно заданной частотой, т.е. такой "квант" он поглощает)) А струна испускает именно такую частоту (тоже квант)) (образная аналогия)
Если эм волны это поток фотонов, то возможность модулирования их частот и амплитуд, ставит под вопрос их "квантовость".
Прошу не принимать всерьез, просто мысли вслух, наверняка на уровне моделей все это схвачено.
Кстати недавно была новость про эксперимент, объясняющий парадокс-дуализм с двойной щелью. Там использовали нелокальность (но не в смысле неопределенности, а в смысле пространственной квантовой спутанности), но в детали не вникала. Написали, что интерпретация Бома, от которой в целом отказались, тут оказывается кстати. То есть, нелокальность, скрытые уровни, возможно детерминизм. Такое решение выглядит интересно.
Тут
https://www.newscientist.com/article/2078251-quantum-weirdness-may-hide-an-orderly-reality-after-all/

Elrond16
24.02.2016 15:59+2И в лазерах, и в терагерцовом излучении, и в СВЧ, и в радио-диапазонах существуют гауссовы пучки. Элекродинамике вообще нет дела до длин волн излучения. В радио-диапазоне гауссовы пучки использовать на практике несколько сложнее по той причине, что там длина волны велика. А в лазерах как раз повсеместно используются именно гауссовы пучки.

grekmipt
24.02.2016 15:14+3гауссов пучок возможен лишь благодаря фотонам, или на «языке волн» — благодаря некой локализации волны, вроде солитона или чего-то подобного.
Если вам кто-то такое рассказал на лекции или семинаре — смело идите в ректорат и увольняйте бедолагу за профнепригодностью.
Лазерное излучение совершенно строго описывается полностью в рамках обычных уравнений Максвелла. Это такое вот электромагнитное поле (волна), существующее в виде двух конусов (развернутых друг к другу острым концом) и соединенных тонким пучком. Волна заходит в конус, сжимается в пучок, идет в виде пучка, и потом снова разжимается обратно в конус. Почему так может быть — потому что поле линейно и есть такая штука как интерференция. Так что если проинтегрировать поле, генерируемое фронтом волны в виде такого конуса (поверхностью конуса) — то на каком-то пространстве получим просто узкий пучок. Никакие фотоны тут не нужны, никакие солитоны тоже, всё строго линейно, строго по Максвеллу, обычная электродинамика, и всё отлично получается просто на принципе гюйгенса-френеля и линейности поля. Такое вот объемное распределение эм-поля. Имеющее в некоторой области пространства — форму пучка, и расходящееся по обе стороны от пучка.
Лазер это по сути половинка такой структуры, т.е. медленно расходящийся пучок — который с какой-то дистанции начинает расходиться быстро. Всё поле внутри пучка и около него — при этом сугубо классическое, т.е. можно в явном виде задать распределение полей в объеме пучка, и убедиться что оно соответствует Максвеллу.
FransuaMaryDelone
24.02.2016 16:42+1У меня возникло подозрение что тут некий ИИ успешно проходит тест Тьюринга.

grekmipt
24.02.2016 16:44Хмм… интересная мысль )))))))

FransuaMaryDelone
24.02.2016 16:58Можно уточняющий вопрос в Вашем высказывании? Почему так принципиально важно, чтобы поля не влияли друг на друга, не вызывали друг друга? Пусть влияют, — кому от этого плохо?

grekmipt
24.02.2016 17:11+2Да ничем особо не плохо — просто поля влияющие друг на друга/вызывающие друг друга поля это некая другая физика, не соответствующая реальности.
Плохо тут скорее то, что еще из школы, как-то автоматически, тащится вот это вот наивное представление о вызывающих друг друга полях — и обычно сознательно не корректируется преподавателями в техвузе. Это и вызывает "брожение в умах" у студентов (как например в данном случае у автора статьи), в силу непонимания того факта что электрическое и магнитное поля это лишь две взаимодополняющие друг друга, но лишь части описания общего объекта (эм-поля), а вовсе не самостоятельные сущности. И это влечет за собой такие вот долговременные затруднения в понимании сути классической электродинамики, рассуждения про сдвиг фазы, про ошибки в плоской эм-волне, и т.п. и т.д…
Если же сразу говорить что формальные электрическое и магнитное поля — это лишь части общего описания эм-поля, то брожения в головах будет намного меньше, и тема станет сильно прозрачнее. Что на мой взгляд — вполне себе хорошо.
mkovalevich
24.02.2016 19:21А есть описания всего Максвелла, но только одним полем? Ведь если это одно и то же, то можно выкинуть скажем магнитное (оно больше всего похоже на фейк) и описать все через электрическое.

grekmipt
24.02.2016 19:32+1Да, оставить только одно векторное поле это разумеется возможно. Помню что например в МГУ один из преподавателей как раз давал электродинамику как связку электрического поля и теории относительности (и в рамках такой трактовки получалось что все эффекты относимые к магнитному полю это не что иное как релятивистские эффекты завязанные на электрическое поле и его эволюции, т.е. магнитного поля нет вообще а есть электрическое поле + релятивизм).
Так же можно расписать Максвелла скажем через 4-вектор (поле векторного потенциала + скалярный потенциал, вектором уже не являющийся). Или можно иные варианты накреативить, если есть желание. Тут вопрос скорее удобства для конкретных расчетов. Потому что, как писал тут, само по себе эм-поле это тензор, а уж формализация этого тензора (т.е. выделение конкретных параметров общей сущности эм-поля) может быть сделана очень большим кол-вом способов (т.е. условно, можно придумать/формализовать самые разные способы математического описания слона — сам слон от этого никак не изменится, и все такие мат-формализмы будут приводить к одинаковым наблюдаемым эффектам/явлениям т.е. наличию у слона 4-х ног и одного хобота :) ).
Соответственно, что удобнее в конкретной ситуации/задаче, то и применяется. Представление в виде 4-вектора удобно ибо позволяет крутить калибровки (что хорошо в ряде задач). Представление в виде двух полей (электрического и магнитного) удобно в смысле бытового понимания, или в задачах близких к электро/магнитостатике (там где полем излучения пренебрегают и рассматривают только реактивное поле). Ну и т.п.
grekmipt
24.02.2016 20:04Еще один (часто применяемый в технической электродинамике) пример ур-ий Максвелла, выраженных через только одно векторное поле — это запись через т.н. вектор Герца. Позволяет описать эм-поле сугубо на одном векторном поле (а не на двух), т.е. пожалуй самая короткая запись Максвелла "полевого характера" это именно запись через вектор Герца. Можете почитать на эту тему скажем Вайнштейна (книжка "электромагнитные волны"), там масса интересного есть по части электродинамики. И вектор Герца, и волноводы, и поле провода, и поверхностные эм-волны, и активные-реактивные поля, и т.п. и т.д., и вроде вполне доступно всё написано.

mkovalevich
25.02.2016 04:14Спасибо, пока глянула "Электромагнитный потенциал", чем-то напоминает расширение 3-хмерных линейных до 4-хмерных = 3-хмерных афинных преобразований. Но полного избавления от В не увидела, но еще посмотрю.

FransuaMaryDelone
24.02.2016 22:23это влечет за собой такие вот долговременные затруднения в понимании сути классической электродинамики, рассуждения про сдвиг фазы, про ошибки в плоской эм-волне, и т.п. и т.д…
Мне доводилось преподавать электродинамику в ВУЗе, — с подобными проблемами не сталкивался. Работа моя накрепко связана с электродинамикой. И несмотря на это, признаться, сам этот угол зрения: «влияет-не влияет» — мне внове и как-то не приживается в голове. Не знаю, может я испорчен уже окончательно «неправильным преподаванием», а может до меня не доходит Ваше объяснение, но я не могу взять в толк — почему мне нельзя надеяться изменить «одну координату», дергая руками «другую координату».
grekmipt
25.02.2016 10:43Ну просто со школы еще идет объяснение что мол электрическое и магнитное поля это отдельные сущности (объекты), и это объяснение дополнительно усиливается (на уровне интуитивного понимания) формальной разбивкой части темы на магнитостатику и электростатику. В итоге возникает в голове четкое — "ну понятно, есть объект под название электрическое поле, и есть другой под названием магнитное поле, и есть их взаимные превращения друг в друга". Нде. А на самом деле — есть объект под названием "тензор электромагнитного поля", и есть совершенно разные но строго равнозначные способы описания этого объекта. И через электрическое/магнитное поля, и через 4-потенциал, и через вектор Герца. И те же, скажем, электрическое и магнитное поля оказываются чем-то вроде "улыбки чеширского кота" — в одной системе координат это одни величины, в другой системе координат (скажем движущейся относительно первой равномерно) это уже другие величины, в третьей системе координат вообще может остаться только одно из полей — а второе занулится. Ну Вы это разумеется знаете ), но тут как… Правильное понимание структуры сущности (полей нет, это конкретный выбранный формально вариант "параметров/координат/описания" общей сущности, а возможны и другие полностью эквивалентные варианты) позволяет легче и с мЕньшим кол-вом ошибок пользоваться этой сущностью при выводах формул, и при осмыслении полученных результатов. Вполне можно и не заморачиваться на эти около-филосовские нюансы, но тогда у малого процента отдельных повышенно-любопытных студентов возникают разного рода вопросы, а поскольку иной раз преподаватели сами эти филосовские нюансы не вполне осознают — то иной раз некоторые вопросы остаются без ответов (у меня например так и было). И зачастую в итоге с этого возникает мысль "ба, да тут явно какая-то ошибка в электродинамике", а с этой мысли некоторые особенно некритичные и не достаточно въедливые (чтобы разобраться самостоятельно) доплывают и до "а придумаю ка я свою конструкцию, правильную и непротиворечивую", ну и всё, готов ещё один альтернативщик-недоучка на форумах, который начинает рассказывать в интернетах про "ошибки у Максвелла и в учебниках". Сталкивался уже не раз… Посему, я все-таки за полную ясность в этом вопросе в головах у людей. Чтобы потом не возникало всякого. Есть модельная сущность, есть её формально выбранные параметры (удобные для той или иной задачи), и есть законченный мат-формализм, который позволяет успешно решать практические задачи, а то что физическая основа сущности объективно не ясна и заменена формальным "объект существующий и распространяющийся сам в себе" — это нормально, это просто мат-модель. Всегда есть предел на котором начинается "это так потому что так устроен мир, бОльшего мы пока не знаем", в электродинамике этот предел отодвигается подальше через КЭД — до понятия виртуальных фотонов и интегралов Фейнмана (что не менее странно/нелогично для осознания нежели "объект распространяющийся сам по себе" в случае эм-поля и по сути снова является границей "это так потому что это так"). А поскольку такой предел есть всегда и вообще в любой области физики, такова селяви — то особо любопытным студентам и нужно это вот всё объяснять, во избежание брожений в головах :)

Gryphon88
25.02.2016 12:02Посоветуйте, плз, учебник по физике, где обсуждаются границы применимости формул и допустимый уровень абстракции. Очень часто не пишут даже для сферических коней какого диаметра описанное работает.

grekmipt
25.02.2016 12:19+1На мой взгляд тут всё зависит скорее от семинариста/лектора. Одни (редко) четко и осознанно акцентируют внимание на границах применимости, другие (большинство) это вообще не включают в фокус внимания студентов.
Пожалуй, Фейнман один из немногих кто действительно понимал важность этих разграничений (в головах), и всюду где это уместно акцентирует на этом внимание, и предельно честно пишет что как есть (например что само понятие энергии эм-поля до сих пор никак не доказано/не выведено, и скорее всего не может быть выведено/доказано, а сугубо постулируется, и возможно когда-то потребует пересмотра — такого рода нюансы даже многие преподаватели не осознают). Так что Фейнмановские лекции по физике в этом смысле особенно хороши, он в этом плане молодец (ну и не только в этом :) ).
Gryphon88
25.02.2016 12:39Ну и физика у меня непрофиль, давали её не шибко хорошо, а слушал я её не очень внимательно. К примеру, для меня стало некоторым откровением, что электрические и магнитные поля — это не самостоятельные сущности. Хотел бы почитать или послушать на coursera.

grekmipt
25.02.2016 12:54+1Я бы сказал, что если Фейнмана Вам мало, то это уже хороший уровень с которого можно далее разбираться самостоятельно ). Ну т.е. вот неких специальных учебников "для теоретиков", где специально максимально четко оговариваются границы применимости моделей и их взаимного перетекания друг в друга — мне не встречалось. Это уже сугубо личное развитие человека… Тут скорее нужно просто брать обычные учебники, и читая их — не упускать из виду этот вопрос (границ применимости), и периодически задавать его себе самому (ну или семинаристу). Тогда картинка начинает "складываться", но при этом приятная студенческая иллюзия что "в базовой физике всё давно понятно и искать там больше нечего" начинает стремительно таять… В контексте именно электродинамики — мне лично нравится Вайнштейн ("электромагнитные волны"), Стреттон ("Теория электромагнетизма"), и Фейнман разумеется. Но в целом, чем больше книг прочитать и с большим кол-вом трактовок/взглядов ознакомиться тем разумеется полнее будет понимание вопроса. Про coursera ничего сказать не могу — не в курсе что есть на этом ресурсе...

mkovalevich
25.02.2016 14:36Насчет полей grekmipt уже накидал тем — от них можно двигаться самостоятельно. Общий алгоритм для новой темы: сначала вики (которая лжет по самое немогу, поэтому чисто узнать темы), потом гугл — сперва более общие статьи, "популярные", причем разных и желательно противоречащих друг другу), потом уже по выбранным направлениям чисто академические, тоже желательно противоречивые. Потом ищете-смотрите, кто из них ошибается больше, и делаете выводы.
Более глубокого, пока не будет ясна скажем природа электрического заряда, не будет. Определять применимость можно самой/самому, узнавая, на каких основаниях строилась эта модель.
А по-быстрому, для любого источника, учитывая, что мы учим не физику, а то, что люди думают о физике, достоверной информации не может быть в принципе. Особенно в сегодняшней физике, стоящей на глиняных ногах.
Видео по-моему сразу в топку, ну разве что для развлечения. Хотя для начала это не повредит )
https://vk.com/video285931226_171528178?list=306f8c4abbf57554ee
Фейнман "для понимания" опасен по-моему. Его стоит знать, но эта модель будет заменена более фундаментальной, эта слишком "птолемеева". (хотя Фейнмана люблю)

FransuaMaryDelone
26.02.2016 14:14А! Так Вы говорите об одном и том же электромагнитном поле в разных системах отсчета, а не о том, что внешними воздействиями нельзя изменить это поле?
Или Вы говорите что-то другое? Не отрицаете же Вы, что если магнитное поле по какой-то внешней причине, где-то начнет меняться во времени, то в этом месте сразу вскочит ротор электрического поля? Я просто думаю про Ваше высказывание, где Вы говорили, что неправильно думать, будто поля порождают друг друга (или превращаются друг в друга) — но что тут неправильного?

grekmipt
26.02.2016 21:37+1Я говорю о том, что магнитное и электрическое поля не являются самостоятельными сущностями, а есть лишь две разные характеристики более общей сущности.
если магнитное поле по какой-то внешней причине, где-то начнет меняться во времени, то в этом месте сразу вскочит ротор электрического поля
Разумеется, это верно. Но есть нюанс. Если говорить предельно корректно, то изменение магнитного поля невозможно без того чтобы строго одновременно с этим в этой же точке имел место ротор электрического поля.
Когда говорят "магнитное поле вызывает электрическое" — такая формулировка задает причинно следственную связь. А причинно-следственная связь по определению имеет задержку во времени. Т.е. в такой формулировке по сути неявно имеется ввиду, что есть само по себе магнитное поле (как отдельный объект), и его изменение "вызывает к жизни" электрическое поле (и это "вызывание к жизни" по механизму причинно-следственной связи, вообще говоря, не может быть мгновенным, что противоречит уравнениям Максвелла). А реальность иная — отдельное создание переменного магнитного поля невозможно в принципе (потому что магнитное поле это лишь один из параметров общей сущности). Т.е. в реальности — изначально создается именно общая сущность, имеющая одним своим параметром — переменное магнитное поле, а другим параметром — переменное электрическое (и эти параметры связаны уравнениями Максвелла). Т.е. источник эм-поля задает изначальное одновременное существование (при возбуждении внешним источником) сразу двух характеристик общей сущности. Хотя с точки зрения "кручения формулами" эти тонкости понимания эм-поля разумеется обычно не критичны. Но по мне, всё-таки предпочтительнее понимать, что изначально прибором создается вовсе не магнитное поле, а сразу создается более сложный комплексный объект (электромагнитное поле), имеющий своими характеристикам сразу два поля (электрическое и магнитное), которые связаны формально в виде Максвелла. Т.е. строго говоря, создать можно лишь эм-поле, а создать только переменное магнитное поле в чистом виде (на самом деле даже для случая магнитостатики, но это длинный разговор) — невозможно.
В рамках моего пояснения про цилиндр (эм-поле) и его проекции (формальные электрическое и магнитное поля), это всё равно что создать одну из проекций цилиндра, не создавая остальные. Тут либо создаешь цилиндр сразу (и автоматически получаешь его проекции, связанные формулами), либо цилиндра просто нет (и тогда нет ни одной из его проекций).
ignat99
26.02.2016 22:04-3http://www.all-fizika.com/article/index.php?id_article=897
Похоже вы не дочитали лекции Фейнмана о которых говорили.
Нашёл вам первую попавшуюся ссылку с «магнитным полем в чистом виде».
Так же почитайте про Квантовую ёмкость.
https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D0%B0%D1%8F_%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C

grekmipt
26.02.2016 22:25Пардон, но обе Ваши ссылки вообще не по теме обсуждения.

ignat99
26.02.2016 23:56-1Есть известные опыты Герца в которых он впервые получил электромагнитные волны. Так же он освещал обкладки конденсатора ультрафиолетовым излучением. Заряженный конденсатор теряет свой заряд быстрее при освещении его пластин ультрафиолетовым излучением.
Если вы хотите выйти за рамки учебников, выпишите самостоятельно уравнение для заряда в вибраторе Герца на основе известных формул с учётом ёмкостей.
Если я не ошибаюсь, Материальные уравнения будут иметь несколько отличий от учебника.
Выпишите Уравнение переноса для материальных зарядов.
Получите Уравнение Умова — Пойнтинга.
Я бы мог углубиться тут в способы симуляции этой системы уравнений, но зачем…
grekmipt
27.02.2016 00:25При чем тут вообще ультрафиолетовое облучение конденсатора? Зачем это тут? )))
выпишите самостоятельно уравнение для заряда в вибраторе Герца на основе известных формул с учётом ёмкостей
Сделать то это разумеется можно. Получим небольшие поправки к "чистому" полю диполю, тем мЕньшие чем больше расстояние до диполя…
Но зачем этим заниматься? Результат и так примерно понятен, да и сделать это проще всего просто численным расчетом методом конечных элементов в том же скажем HFSS. Ибо учитывать конечную проводимость и конечную толщину провода антенны — это такой себе математический секос, а уж в случае электрически длинной антенны — так и вовсе врагу не пожелаешь такую математику крутить.
В общем, Вы что-то такое говорите, смысл чего от меня категорически ускользает.

FransuaMaryDelone
27.02.2016 15:48Когда говорят «магнитное поле вызывает электрическое» — такая формулировка задает причинно следственную связь. А причинно-следственная связь по определению имеет задержку во времени. Т.е. в такой формулировке по сути неявно имеется ввиду, что есть само по себе магнитное поле (как отдельный объект), и его изменение «вызывает к жизни» электрическое поле (и это «вызывание к жизни» по механизму причинно-следственной связи, вообще говоря, не может быть мгновенным, что противоречит уравнениям Максвелла)
Дело в том, что причинно-следственная связь имеет задержку по времени? Если мы вдруг будем считать, что это не так, что задержки по времени нет, то станет лучше? Уравнениям Максвелла не станет ничего противоречить? Или есть еще что-то?
grekmipt
28.02.2016 11:26Помимо того что причинно-следственная связь требует задержки по времени (отсутствующей в ур-ях Максвелла), есть еще и другая принципиальная причина с точки зрения логики. А именно, тот простой факт, что в определенной ситуации, в одной инерциальной системе отсчета сущность (скажем магнитное поле) существует, а в другой соответственно подобранной — нет. Объективно существующая (т.е. отдельная) физ-сущность разумеется не может так себя. Либо она существует (пусть и с разными параметрами/характеристиками её описывающими) во всех системах отсчета, либо нет. Это базовый филосовско-физический принцип. Такого, чтобы само существование сущности зависело от системы координат — этого быть, разумеется, не может. Именно поэтому физика и говорит, что деление общего эм-поля на электрическое и магнитное поля является условным, т.е. просто вопросом договоренности того — какие термины использовать для описания эм-поля.
Ну скажем, вот тут вчерась как раз под рукой оказалась статья из Вики про униполярную индукцию. И там совершенно верный вывод в конце статьи:
Таким образом, униполярная индукция — релятивистский эффект, в котором ясно проявляется относительный характер деления электромагнитного поля на электрическое и магнитное.

FransuaMaryDelone
28.02.2016 15:12Я не спорю с Вами. Мне интересно, как именно и где студенты находят "парадоксы", и чем им помочь — мне сложно представить преподавание электродинамики без преподавания электростатики и магнитостатики, однако судя по Вашим словам, есть какая-то проблема в таком подходе.

grekmipt
28.02.2016 15:43Разумеется, электростатика и магнитостатика это вполне корректные частные случаи, и разбирать электродинамику начиная со статики — вполне нормальный подход, это я никоим образом не оспариваю. Я говорю лишь, что преподавая статику — вполне уместно акцентировать внимание на том, что рассматривается, если угодно, "урезанное" (частичное) описание (часть) полного объекта.
Т.е. буквально, "для простоты — забудем пока про то, что суммарный объект сложнее, и рассмотрим его описания в тех ситуациях где он выглядит/описывается сильно попроще; вот вам один такой вариант (электростатика), вот другой (магнитостатика). Но постараемся не забывать что оба эти варианта являются проявлениями одной и той же общей и более сложной сущности". Т.е. вопрос сугубо в филосовских/концептуальных акцентах и нюансах, а разумеется не в основной структуре материала.
Но это, разумеется, моё личное убеждение. Иначе потом вот начинают буквально пытаться (и на формулах и на моделях) отделить магнитное поле от электрического (на всяких форумах альтернативщиков, строителей сверхединичных устройств и т.п. и т.д), изощряться со сдвигами фазы, и т.п., не понимания что это изначально противоречит самой сущности эм-поля, и попытки такие — это всё равно что пробовать отделять тень слона от самого слона :).

mkovalevich
24.02.2016 19:23-1Если бы успешно, вы бы меня не вычислили. Опять неладно с логикой. И не ходите за мной по пятам, оставьте в покое, просьба)

FransuaMaryDelone
24.02.2016 22:01Да как я Вас оставлю, когда Вы про электродинамику пишете?! У меня на уравнения Максвелла рефлекс же. Но я Вас услышал — попробую не комментировать.
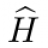
ivlis
24.02.2016 20:14+1Из теории линейных дифуравнений известно, что любая суперпозиция решений линейного уравнения — тоже решение линейного уравнения. Любую конфигурацию ЭМ поля можно составить из, вообще говоря бесконечного, набора плоских волн. Так что да, реализуется на практике повсеместно.

VaalKIA
27.02.2016 02:44>Физика построена на математическом аппарате, не зная аппарата невозможно оперировать физическими величинами.
А я всегда считал, что всё наоборот и физику придумали естествоиспытатели, а все открытия сделаны оттого, что постоянно математический аппарат не проходит проверку действительностью, то сверхпроводимость найдут, то сверхтекучесть, то твёрдо-жидкое тело, то какие-нибудь плоские кристалы типа графена… И вот нам начинают рассказывать, что такие прекрасные формулы не работают, потому что, то у них электроны сцепились в бусы, то вытесненны на переферию или какие-нибдуь плазмоны стоячие образовались, то ещё что-то…
ivlis
27.02.2016 02:45Это уже не так лет 200.

VaalKIA
27.02.2016 03:49Вы про то, что естествоиспытатели это теперь учёные занимающиеся ещё и эмпирической проверкой, или про то, что никаких необычных эффектов в хорошо изученных, и самое главное — описанных формулами, процессах уже лет 200 не находят?
ivlis
27.02.2016 03:53+2Я про то, что все перечисленные вами эффекты невозможно наблюдать невооруженным взглядом, а только с помощью приборов. А вот чтобы разобраться с приборами, нужны прекрасные формулы, иначе это только цифирки на вольтметре.
Естествоиспытатель, слово то какое :))))

saboteur_kiev
23.02.2016 11:49+1"Если эта схема вам прекрасно знакома и не вызывает рефлекса кое-что пояснить и дополнить, чтобы не ввела других в заблуждение, то прошу под кат. Если она вам прекрасно знакома, и вы поняли, что там требуется допояснять, то гуляйте дальше) Пост не для вас."
А тем, кому эта схема не очень знакома, и вызывает рефлекс уточнить ВСЕ?
Вот хочу почитать про электричество, электромагнитные поля "для самых маленьких", но без упрощений.
А то — или любое объяснение идет сразу с кучей формул, которые на самом деле нужны исключительно для расчетов, а не понимания сути. Или идет пояснение для детей, в которых многие вещи упрощаются вплоть до подтасовки фактов, в результате снова суть непонятна из-за взаимоисключающих параграфов.
Может есть что почитать или посмотреть, чтобы суть процессов пояснили понятным человеческим языком, но без сокрытия важных нюансов и деталей?

Throwable
23.02.2016 12:37-1По поводу «инь-ян»: не все так красиво, как хотелось бы. Вот электрический заряд существует, а магнитный почему-то нет. И уравнения ваши не симметричны…

Elrond16
23.02.2016 14:07+1Это не совсем так, это вопрос уговора и конвенции. На самом деле, уравнения Максвелла можно привести к симметричной форме преобразованием двойственности [см. Jackson. Classical Electrodynamics. 1999]. Теория, в которой у электрона нет электрического заряда, но есть магнитный, или есть и электрический, и магнитный в равных пропорциях, будет ничем не хуже описывать наблюдения. Однако пока все наблюдения показывают, что отношение электрического и магнитного зарядов для всех частиц одинаково, что и позволяет убирать в модели один из типов зарядов. Это сделано по историческим причинам и для удобства.

VIK52
23.02.2016 15:52Однако пока все наблюдения показывают, что отношение электрического и магнитного зарядов для всех частиц одинаково
— как это? нельзя ли в двух словах поподробнее, скажем, для протона и нейтрона?
Elrond16
23.02.2016 16:15+1В классическом варианте теории мы предполагаем отношение (магнитный заряд q_m)/(электрический заряд q_e) = 0, т.е. у всех известных частиц нет магнитного заряда. Ничто нам не мешает запостулировать в другом варианте теории, что у электрона электрический заряд -e/sqrt(2) и магнитный заряд -e/sqrt(2) (я буду писать в системе СГС, где заряды одной размерности). Тогда, если для всех остальных заряженных частиц отношение q_m/q_e мы тоже сделаем равным 1 (т.е. у протона заряды будут +e/sqrt(2) и +e/sqrt(2) соответственно и т.д.), то наша теория будет так же хорошо описывать все наблюдения, как и теория, где у электрона и протона есть только электрический заряд. Грубо говоря, мы можем выбирать бесконечно много вариантов теорий, где у электрона есть разные доли электрического и магнитного зарядов, но при этом отношение q_m/q_e мы должны сохранять одним и тем же для всех открытых частиц.
Однако, если бы в нашей текущей системе (где магнитных зарядов пока нет) мы бы нашли частицу, у которой есть магнитный заряд, это бы значило, что в системе, где у электрона q_m/q_e = 1, отношение q_m/q_e для этой новой частицы было бы другим.
У нейтрона вообще не может быть ни электрического, ни магнитного зарядов, он не является заряженной частицей, и для него это отношение (всегда 0/0) не имеет смысла, для него q_m/q_e = X выполняется для любого X.
VIK52
23.02.2016 16:21Как в варианте "только магнитный заряд, а электрического нет" будет описываться поле неподвижного электрона? У него же не должно быть магнитного поля в этом случае

Elrond16
23.02.2016 16:40+1У электрона в такой теории будет радиальное магнитное поле, и не будет электрического. И это ничему не противоречит, такая теория ничем не хуже той, в которой у электрона нет магнитного поля, но есть электрическое. Мы не можем измерять сами электрическое и магнитное поля, мы можем измерять только воздействие этих полей на другие заряженные частицы, т.е. силы. Силы при таком преобразовании не изменятся никак.

VIK52
23.02.2016 16:43То есть просто переобозначим/назовем электрическое поле магнитным, так получается

Elrond16
23.02.2016 16:48+1Да, если заменить заряд электрона на полностью магнитный, то это чисто переименование зарядов и полей. Но так можно делать и для любых других (кроме 1/0 и 0/1) пропорций между электрическим и магнитным зарядом.

FransuaMaryDelone
23.02.2016 13:09+1Вам-биологу тоже понадобился электромагнетизм с нелинейностями? Активны биологи стали в этой области в последнее время.

grekmipt
23.02.2016 13:15+11итоговый вывод — что мол
Однако в любом случае… сдвиг на пи/2 есть.
очень далек от реальности. Равно как и исходная мысль что изменение одного из полей порождает другое поле. Да, так пишут во всех учебниках — но это скорее стереотипная, устоявшаяся, и не вполне корректная формулировка. Но зато она создает некое ощущение понимания вопроса, чем и хороша.
Эм-поле это тензор. Иначе говоря, если бытовыми понятиями — это объект, имеющий сложные пространственные параметры. Эти параметры можно описать как в терминах векторов электрического и магнитного полей, так и в терминах скалярного и векторного потенциала. Суть объекта от этого не изменится. Но тут принципиальный момент — электрическое и магнитное поля это именно описание объекта под названием эм-поле (параметры комплексного объекта), а не сам объект.
Чтобы было понятнее о чем речь, возьмем в качестве объекта — скажем цилиндр. А в качестве параметров, описывающих объект — возьмем три проекции оного цилиндра. Понятно, что задав все 3 проекции цилиндра — мы тем самым полностью и однозначно определяем исходный объект (цилиндр). При этом, любой динамике цилиндра в пространстве (перемещению и/или вращение, равно как и масштабированию) можно сопоставить систему уравнений, связывающий между собой изменение проекций (т.е. параметров) цилиндра. Точно так же как существует связь параметров эм-поля при изменении самого поля. Но. Говорить о том, что скажем поворот одной проекции цилиндра вызывает (т.е. порождает по механизму причинно-следственной связи) некие изменения в других проекциях цилиндра — совершенно некорректно. Проекции — это лишь описание объекта. Корректно лишь говорить что такая-та динамика одного параметра объекта сопровождается такой-то динамикой другого параметра. Сопровождается (отсутствие причинно-следственной связи) и вызывает (наличие причинно-следственной связи, в т.ч. обязательная задержка во времени) это принципиальная разница. Изменение одного параметра объекта не может вызывать изменение других параметров. Речь может идти лишь о том, что изменения параметров объекта связаны формульно, но никак не причинно-следственно.
Строго то же самое применимо и к объекту под названием эм-поле. Изменение любого из его параметров (например магнитного поля) сопровождается изменением других параметров (например электрического поля). Но никоим образом не вызывает такое изменение. Не может изменение тени слона вызывать движение слона )))).
Далее, в части итогового вывода статьи что сдвиг на Пи/2 есть — вывод полностью не верный. Поток эм-энергии определяется вектором пойнтинга, т.е. векторным произведением электрического и магнитного полей. Если между полями есть сдвиг на Пи/2, то поток энергии в результате мотается туда-сюда с нулевым средним значением. Это то что называется реактивным полем — и именно такое поле присутствует около провода с переменным током, который автор статьи и рассматривает. Так что да, вблизи провода сдвиг фазы есть — и именно поэтому вблизи провода нет никакого излучения, т.е. нет эм-волны как таковой а есть просто локально колеблющиеся поля (которые никуда при этом "не убегают"). Если же говорить про большое (в длинах волн) расстояние от провода, т.е. про т.н. волновую зону — то там сдвиг фаз как раз принципиально отсутствует — и именно поэтому там появляется эм-волна, а поле становится уже не реактивным, а активным — т.е. уносящим энергию.
Таким образом, у автора статьи ИМХО нет четкого понимания того что такое эм-волна, и чем она отличается от просто колебания полей. Не всякое колебание полей есть эм-волна. Поля которые колеблются, но сдвинуты по фазе на Пи/2 — это не эм-волна, а просто реактивное локально-существующее поле. А эм-волна по определению требует отсутствия сдвига фаз — иначе поток энергии окажется в среднем нулевой (а значит и волны нет).
Соответственно и картинка с кружочками вызывающих друг друга полей — это стереотипное школьное заблуждение (но это полезное для школьного уровня заблуждение, позволяющее хоть как-то объяснить детям что такое эм-волна, без привлечения теорпола — вот эдакие вот колечки "цепляющиеся друг за друга" мол, вот так и волна бежит — детям понятно, ну и слава богу). В реальности электрическое и магнитное поля не вызывают друг друга (это в корне некорректная формулировка) — а сопровождают изменения друг у друга. Ибо электрическое и магнитное поля это лишь дополняющие друг друга части полного описания сложного объекта под названием эм-поле. Меняется сам объект — так что и описание этого объекта в виде его параметров (электрического и магнитного полей) тоже меняется, и это изменение разумеется одновременное (т.е. нет порождения одного поля другим, не может одна координата объекта порождать другую координату объекта, может быть лишь одновременное изменение координат объекта).
grekmipt
23.02.2016 14:43+2Изменение электрического поля порождает магнитное поле, которое, увеличиваясь (=изменяясь), порождает обратное электрическое поле, которое… и т.д. Это классическое (и верное) объяснение, известное наверное каждому.
Если совсем кратко резюмировать мой пост выше, то данная цитата автора это как раз классическое и не верное объяснение.

mkovalevich
23.02.2016 16:00изменения параметров объекта связаны формульно, но никак не причинно-следственно
Верно, но в электроприборах ведь используют причинно-следственные цепочки, переходя от электро к магнитному, от магнитного к электро в другом элементе? Как это объяснить?
Если между полями есть сдвиг на Пи/2, то поток энергии в результате мотается туда-сюда с нулевым средним значением.
Да.
и именно поэтому вблизи провода нет никакого излучения, т.е. нет эм-волны как таковой а есть просто локально колеблющиеся поля (которые никуда при этом «не убегают»).
В смысле, провод с переменным током не излучает эм волн? Это что-то новое для меня, по-моему вы неправы (но подкиньте обоснований, может и правда).
Не всякое колебание полей есть эм-волна. Поля которые колеблются, но сдвинуты по фазе на Пи/2 — это не эм-волна, а просто реактивное локально-существующее поле. А эм-волна по определению требует отсутствия сдвига фаз — иначе поток энергии окажется в среднем нулевой (а значит и волны нет).
Вот последнее "значит и волны нет" неверно, это покажет любой механический осциллятор.
Fullmoon
23.02.2016 16:13+3Верно, но в электроприборах ведь используют причинно-следственные цепочки, переходя от электро к магнитному, от магнитного к электро в другом элементе? Как это объяснить?
Как упрощённые модели, применимые в ограниченных случаях для облегчения расчётов. Путать инженерные модели и физическую теорию не следует.
В смысле, провод с переменным током не излучает эм волн?
Вблизи провода. Вблизи. В следующем же предложении говорится про излучение.
mkovalevich
23.02.2016 17:49-3То есть, на практике наблюдается причинность, но в теории мы ее не признаем? Может, стоит иногда согласиться с реальностью, вдруг она права?
Вблизи, т.е. near field, ок.
Fullmoon
23.02.2016 17:53+3На практике наблюдается теплород. На практике геометрическая оптика верна. На практике закон Ома линеен.
Какое из слов во фразе „упрощённая модель, применимая в ограниченных случаях“ вам не понятно?
mkovalevich
23.02.2016 18:03Неадекватные примеры. Я бросаю стакан, он разбивается. Причина в падении или это просто "формульная связь, а причинной зависимости нет"?

Fullmoon
23.02.2016 18:11+2Примеры совершенно адекватные. Отдельные электрическое и магнитное поля — это именно упрощение. Где упрощение в случае стакана?
И нет, ваш бросок к разбившемуся стакану прямого отношения как раз не имеет.
Стакан разбивается из-за внутренних напряжений, возникающих при столкновении с полом с некоторым импульсом, это физика деформаций. Что ему придало такой импульс — вопрос совершенно отдельный, им занимается динамика. В каком-то конкретном случае причинная связь (в смысле вашего броска) есть, в общем, для физической теории — нет (в смысле, такой же результат могло вызвать просто падение стакана со стола).

grekmipt
23.02.2016 20:14+3Верно, но в электроприборах ведь используют причинно-следственные цепочки, переходя от электро к магнитному, от магнитного к электро в другом элементе? Как это объяснить?
В электроприборах никто не использует причинно-следственной связи. Используют как раз формульную связь, т.е. тот факт что когда один параметр сущности (скажем электрическое поле) меняется, то это сопровождается изменением другого параметра сущности (магнитного поля), и прибор как раз и осуществляет использование одной (или нескольких) составляющих общей сущности в неких практических целях. Те. скажем при раскачке переменного тока в соленоиде — вокруг соленоида одновременно существуют и переменное магнитное поле, и переменное электрическое поле. Т.е. переменный ток в соленоиде создает общее эм-поле, характеризующееся меняющимися параметрами этого поля во времени (т.е. изменениями магнитного и электрического полей). Далее скажем один из параметров созданного эм-поля оказывается удобен для практического использования (например переменное электрическое поле), и получаем скажем трансформатор...
Ну т.е. совсем обобщенно говоря, любой электрический прибор принципиально создает именно общую сложную сущность, а использует, в зависимости от прибора, только некоторую часть такой сущности.
В смысле, провод с переменным током не излучает эм волн? Это что-то новое для меня, по-моему вы неправы (но подкиньте обоснований, может и правда).
Вообще, бесконечно длинный провод конечного сопротивления с переменным током действительно не излучает, но это слишком большой вопрос для короткого объяснения.
В Вашем же примере, если рассматривать короткий провод — то излучение разумеется есть. Однако, с точки зрения теории антенн, излучает фактически не сам провод, а "электромагнитная шуба" провода состоящая из как раз не излучающего реактивного поля. Т.е. буквально — около провода (то самое near field) поле почти полностью реактивное, но по мере удаления от провода — реактивная компонента поля падает (та которая имеет сдвиг фазы Пи/2), а активная растет (та у которой сдвига фазы нет). Если рассмотреть скажем теорию приема эм-энергии антеннами, то Вы узнаете массу интересного. Например, что именно реактивное ближнее поле антенны, накладываясь на активное поле падающей на антенну эм-волны, направляет потоки энергии в антенну. Так что эффективная площадь антенны (та площадь сквозь которую поступает заходящая в антенну энергия) равна именно площади реактивного поля антенны, а отнюдь не равна физической площади провода антенны. Выглядит это достаточно интересно — потоки энергии как-бы "сами собой" загибаются и со всех сторон устремляются к антенне (к проводу), но только в рамках той зоны где реактивное поле антенны велико.То же самое касается и обратного процесса — излучения (выгляди это так как если бы излучала "поверхность" реактивного поля антенны, а не сам провод). Так что излучение провода это достаточно глубокая тема, при желании в ней покопаться — можно нарыть массу интересного. Но на эту у студентов обычно времени нет ).
Вот последнее «значит и волны нет» неверно, это покажет любой механический осциллятор.
И снова не верно. Реактивное поле на то и реактивное что энергию не переносит, ибо усреднение вектора пойнтинга по времени даст нуль — что элементарно проверяется прямым расчетом. Но. Как только вы внесете в реактивное поле осцилятор, и оный начнет колебаться — это автоматически будет сопровождаться появлением аналогичного реактивного поля уже у осцилятора. А штука в том, что наложение двух реактивных полей в такой системе (просто в силу линейности полей) означает наличие уже ненулевой по амплитуде компоненты полей у которых сдвиг фазы отсутствует. Т.е. два реактивных поля, накладываясь, создают в пространстве между источником и приёмником (мы говорим про near field) уже активную, бегущую волну. Тем самым и происходит перенос энергии к осциллятору — но только потому, что эта самая активная волна появляется как следствие работы осциллятора (а без осциллятора — её нет, есть просто реактивное поле ничего не излучающее).
На этом принципе работает например волноводный аттеньюатор — когда источник поля создает в волноводе сугубо реактивное локальное поле, а приёмник энергии "цепляется" за это реактивное поле своим, встречно генерируемым реактивным полем, что и создает уже активную компоненту — переносящую энергию от источника к приёмнику.
grekmipt
23.02.2016 22:17+2если более четко расписать что происходит около провода (как и около любой другой излучающей системы), то картинка выглядит следующим образом. В близкой окрестности от источника излучения — есть одновременно и компонента активная (без сдвига фазы) и компонента реактивная (имеющая сдвиг фазы). Т.е. формально можно разложить полное поле на сумму из двух частей, часть которая соответствует реактивному полю без излучения, и на часть соответствующую полю излучения (уносящему энергию от источника). При этом реактивная компонента по модулю будет много больше активной компоненты. Однако закон убывания реактивной компоненты (от расстояния до источника поля) намного более крутой (быстрый) нежели для активной компоненты. Т.е. с ростом расстояния до источника поля — и реактивная, и активная компоненты убывают, однако активная компонента убывает намного медленнее чем реактивная, так что на каком-то расстоянии (порядка длины волны) подавляющая часть поля соответствует уже активной компоненте. Тем не менее и на расстоянии в сотни-тысячи-мильоны длин волн реактивная компонента по прежнему есть, однако соответственно на очень много порядков меньше активной компоненты, так что для простоты анализа наличием этой реактивной компоненты на таких дистанциях уже пренебрегают и оперируют сугубо активным полем излучения. И ровно точно так же на близком расстоянии от источника — пренебрегают компонентой активного поля (ибо оно хотя и велико в абсолютном выражении — но крайне мало в процентном выражении, относительно амплитуды реактивного поля). И штука в том, что само существование активного поля около источника — невозможно без одновременно сопровождающего его реактивного поля (запрещают ур-я Максвелла собственно), так что такое формальное рассмотрение является именно формализмом, физически отделить/отфильтровать малое по доле поле излучения от большого по доле реактивного поля около провода — невозможно. Так что в реальности около провода сложное поле, имеющее и реактивную и активную части, но подавляющим по амплитуде является именно реактивная, ничего не излучающая часть, имеющая сдвиг фазы Пи/2. А активная часть, не имеющая сдвига фазы, много меньше реактивной, хотя и велика по абсолютному значению (относительной её же величины на дистанции в несколько длин волн). Впрочем, не уверен что это поможет Вам понять тему излучения эм-волн, ибо тема достаточно обширная… Насколько я могу судить, Вам нужна просто хорошая лекция или работа с семинаристом по этой теме.

mkovalevich
24.02.2016 11:28Спасибо за подробный ответ. Надо будет изучить детально, что понаписали). Насчет магнитного и электрического, возможно действительно они — проявление одной "сущности". Вообще напоминают действие гироскопа — если раскрученный (тяжелый) гироскоп поднимаешь вверх на прямых руках, при этом "другая сила" пытается обернуть тебя вокруг оси тела.
Семинарист… а лучше два, чтобы друг с другом спорили, как оно на самом деле))

VIK52
23.02.2016 16:02+1Про тензор-цилиндр хорошо написано. Тут же вспомнилось такое же объяснение про корову-тензор, рассматриваемую с разных сторон с точки зрения количества ног (давно это было, но я помню)

Foolleren
24.02.2016 08:16-2вот вы упомянули про проэкции, и мне сразу вспомнилась эта
гифка

gleb_kudr
23.02.2016 14:07+5Нам, биологам, на первом курсе физику сходу стали преподавать так. "Запишем уравнение. Вот этот значок — дивергенция, вот этот — ротор. Дивергенция ротора. Непонятно? Ну да, вам же эту математику не преподают. Что ж, запоминайте просто так, на экзамене должны эту формулу воспроизвести."
Самое удивительное, что я эту безмозглую заумь потом прекрасно понял по англоязычным статьям. Где суть вещей прекрасно объясняется на пальцах, с постепенным погружением. А не как в той картинке с рисованием совы.

У вас, к сожалению, пока не получилось.

rusavden
23.02.2016 15:42У вас небольшая ошибка в последнем рисунке. У вас ток и первое электрическое поле имеют противоположные направления, находясь в одном магнитном поле.

realraven
24.02.2016 03:56Забавно, но при прочтении статьи я мысленно задал вращение и смещение синусоидам из КДПВ и у меня получилась…… модель ДНК.

Nubus
24.02.2016 07:10Специально посмотрел на картинку и залез в тех документацию дабы прояснить вопрос. Сдвига по фазе ЕМ (кажетса так на русский переводитса out of phase) нет для линейно поляризованной ЕМ волны, и есть для круглополяризованной волны.
For a linearly polarized wave, that leaves E and B in phase in the sense that they have nodes and peaks at the same places, but they're at 90° angles to each other, thanks to the type of spatial derivative involved (a curl). For a circularly polarized wave, both fields have uniform intensity. The circularly polarized wave can be expressed as two linearly polarized waves, shifted by 90° in phase and rotated by 90° in polarization. If you pick some direction to measure the fields along, the components of E and B along that direction have a 90° phase shift with respect to each other.
То есть картинка зависит строго от поляризации волны и оба варианта имеют место быть.

Nubus
24.02.2016 07:28Вообще, если вспомнить определение электромагнитной волны, то оно звучит так:
Электромагнитная волна это волна в которой электрическое и магнитное поле перпендикулярны друг другу а также перпендикулярны направлению движения волны.
Никаких намеков на то чтобы электрическое или магнитное поля должны быть в фазе или с каким-то спец сдвигом НЕТ.
mkovalevich
24.02.2016 11:20Вы удивитесь, но магнитное и электрическое поле могут быть не перпендикулярны друг другу.
("Free-space nonperpendicular electric–magnetic fields" 2015 Levy, Silberberg)

grekmipt
24.02.2016 11:49+1Электромагнитная волна это волна в которой электрическое и магнитное поле перпендикулярны друг другу а также перпендикулярны направлению движения волны.
Это явно Ваше личное определение. Причем заданное в неявном виде ), ибо по сути Вы пишете что "Электромагнитная волна это волна".
Волна это волна. Ну да, не поспоришь.
Вот мое (тоже личное) общее определение — бегущая волна это колебательный процесс, распространяющийся в пространстве, и переносящий энергию через пространство. Когда говорят про эм-волны то обычно (и неявно) подразумевают бегущую волну. А для бегущей эм-волны требование на наличие ненулевого потока энергии ею переносимого автоматически эквивалентно наличию такой компоненты полей, у которых сдвиг фаз отличается от Пи/2, и вектора полей не параллельны. Если сдвиг фаз точно равен Пи/2 и/или вектора полей параллельны, то как гласит вектор Пойнтинга, энергию такой колебательный процесс уже не переносит — а значит по определению не является бегущей (распространяющейся и переносящей энергию) волной.
Nubus
24.02.2016 16:27Да ладно? Возмем тогда определение от NASA, если вас что-то в классике не устраивает:
A changing magnetic field will induce a changing electric field and vice-versa—the two are linked. These changing fields form electromagnetic waves. Electromagnetic waves differ from mechanical waves in that they do not require a medium to propagate. This means that electromagnetic waves can travel not only through air and solid materials, but also through the vacuum of space.
Под картинкой:
Electromagnetic waves are formed by the vibrations of electric and magnetic fields. These fields are perpendicular to one another in the direction the wave is traveling. Once formed, this energy travels at the speed of light until further interaction with matter.
http://missionscience.nasa.gov/ems/02_anatomy.html
grekmipt
24.02.2016 16:43+2Как я подробно расписал выше, вот это утверждение, в контексте именно эм-волн, является классическим и строго не верным:
A changing magnetic field will induce a changing electric field and vice-versa—the two are linked
То что оно висит на сайте NASA говорит лишь о том что NASA, так же как и почти все учебники, предпочитает наглядное (и неверное) объяснение — сложному (но верному) объяснению. Что впрочем обычное дело при изучении физики. Аналогии на то и существуют.
И у NASA это не определение, а просто некий комментарий. Определением здесь, как говорится, и не пахнет. То же самое относится и к картинке с комментарием к ней. Комментарий верный, но никоим образом не является определением эм-волны.

Mogvay
24.02.2016 11:15Автор обладает определенным чувством юмора, если такую статью называет электромагнетизмом для самых маленьких :)

ignat99
24.02.2016 21:22-1Давайте начнём с самого начала, с треугольника Паскаля. Каждое число в треугольнике Паскаля равно количеству способов добраться до него из вершины.
Предположим что градиент плотности величины T можно представить одним квантом. Для удобства назовём его фотоном (это просто переменная в программе не имеет отношения к реальному фотону).
Так же давайте введём локальную метрику для этого псевдо пространства в каждой точке, скажем шестимерного. То есть для каждой точки у нас будет по 12 соседей.
Задача крайне простая найти значения для каждой точки нашего пространства, равные количеству способов добраться до этой точки из точки к которой у нас припаян фидер нашей простой системы.
Причём можно обойтись при такой постановки задачи без производных, интегралов, спиралей, колец и прочих индуцированных топологий.
То есть как раз задачка для самых маленьких.
ignat99
25.02.2016 00:48-1Далее предположим что в каждой точке нашего пространства биноминальных коэффициентов задан тензор a — элемент когомологии нашего пространства (Например: Куб, Плосткость, Прямая, Телесный угол, Тор, Спираль и т.д.).
А тензор b задаёт гомологию дополнительного пространства.
Для простоты будем считать a и b дуальными частями октониона (симметричными относительно умножения на i), а операцию перехода между ними (в физическом смысле) обозначим оператором Звезда ходжа (*). А общую сигнатуру пространства ограничим числом 7 (не более 7 операторов набла подряд).
Мы не рассматриваем геометрическое пространство размерности более 3, но используем операторы вплоть до L^2 — градиента плотности. Другими словами — не более 2 лаплассианов/даламберов подряд от телесного угла.
Впрочем, если мы имеем структуру с сигонией, то можем считать сигонию внутренней производной по трёхмерному пространству всего нашего объёма нашей системы решётки на выбранную ось симметрии.
ignat99
25.02.2016 03:10-1Для определённости будем считать поле тензора a — двухмерным.
А поле тензора b — трёхмерным.
Вектора этих полей будем получать через операцию «угол» c локальным базисом каждого тензора.
Операция «скобки ЛИ» (Скобки Пуассона) этих двух полей в точности дают пятимерное поле Вектора Пойнтинга.
Если мы будем пренебрегать (приравняем к единице) ток вакуума (Электрическую постоянную умножить на скорость света в 3 степени), то как раз получим релятивистское приближение.
Или другими словами проекцию Времястатического пятимерного поля на электромагнитное с компонентами (двухмерными и трёхмерными).
mkovalevich
25.02.2016 04:22+1Правильнее так: усаживаете самых маленьких и рассказываете им, что Земля круглая, а при этом показываете плоскую… и квадратную. И говорите: "Смотрите, какая она круглая!"
А если кто вдруг начнет подозревать подвох, терпеливо ему объясните, что если посмотреть вблизи, то она вполне плоская. А если запереться в комнате, то квадратная.
И все дела.

Nubus
25.02.2016 02:50-1Если хорошенько почитать литературу то вопросы отпадут сами собой:
Для Електромагнитной волны как излучения, линейная волна (свет, радио, X-ray), которая путешествует без проводника (воздух, вакум) поля E и B находятса в одной фазе!
Для электромагнитной волны которая возникает в случае прохождения тока по проводнику (круговая волна) поля E и B находятса в 90 градусном сдвиге относительно друг друга (запаздание магнитной волны).
На расстояние примерно с длину волны от источника (антенна и прочая) круговая волна переходит в линейную. Описано Герцем в труде Electric Waves, страница 152я.
Оригинал книги: https://books.google.com/books?id=jyRWAAAAMAAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
mkovalevich
25.02.2016 04:06-1Да, спасибо, про сдвиг вы писали раньше, это хороший пример естественной связи самого сдвига Е и В с "первичностью" круговых волн. Однофазность линейнополяризованной волны следует из суперпозиции круговых. "Неполяризованные" в данном контексте рассматривать нет смысла, только как сумму поляризованных.
А переход волны при удаленности от круговой к линейной — речь о дипольной антенне? Там как раз результат суперпозиции волн "с двух концов", т.е. с противоположным вращением.

grekmipt
25.02.2016 11:01+2Чем старее труды тем упрощённее (и дальше от современных представлений) понимание. Это очень любят альтернативщики — откопать какую-нибудь работу столетней давности, и апеллировать к ней как к чему-то более авторитетному нежели скажем какой-нибудь современный Фейнман или Ландавшиц.
Современная физика делит поля на активные (т.е. бегущую волну) энергию переносящие и реактивные (т.е. отсутствие бегущей волны — либо две одинаковые бегущие волны идущие встречно, либо вообще просто локальное "дышащее" поле) энергию не переносящие.
Активные волны — автоматически не имеют сдвига фазы, реактивные — имеют этот самый Пи/2. У Герца разумеется всё верно в смысле формул, но может не совпадать с современной трактовкой/терминологией, так что лучше не апеллировать к его текстовым выводам/определениям, а пользоваться только формулами.
С современных позиций — около проводника основное поле это стоячее реактивное поле, и далее эта стоячее реактивное поле плавно переходит в бегущую активную волну (по мере удаления от источника). Разумеется, возбуждение (равно как и приём) активной эм-волны невозможно без того чтобы где-то существовало реактивное стоячее поле.
Но понятие вектора Пойнтинга (уже после Герца) придумали не просто так, и локальность/реактивность/безизлучательность полей, имеющих сдвиг фазы Пи/2 — это общепринятое и общеизвестное понимание/трактовка, как раз и завязанное на понятие вектора Пойнтинга. Понятно что всегда можно накрутить свою терминологию (заменить "стоячее реактивное поле" на "волны с запаздыванием магнитной волны"), но это будет только вносить путаницу в головы, а никак не ясность. И термины и трактовки — не зря постепенно менялись и трансформировались сотню лет, то что есть сейчас это лучше чем то что было ранее. Ранее сам Максвелл искренне полагал что надо использовать полную производную по вектор-потенциалу, а не частную, но физики подумали, и решили что нет, всё-таки частную. Хотя аж сам Максвелл думал иначе. Ну и чо?...
Nubus
26.02.2016 00:28Вот вы сейчас с реактивным полем чушь пишете. Если бы Реактивное поле не переносило энергии, как по вашему бы трансформаторы работали? Они-то как раз работают с near (reactive) полем и потому имеют 180 градусный сдвиг относительно первичной обмотки.
Вот вам ссылка на описание данных полей: https://en.wikipedia.org/wiki/Near_and_far_field
grekmipt
26.02.2016 10:07+1Как работают трансформаторы я уже расписал где-то выше (на примере волноводных аттеньюаторов, физика у них по сути одинаковая).
А именно, работают они, разумеется, только на бегущей волне (созданной интерференцией двух реактивных полей — от двух обмоток). Каждое из этих двух реактивных полей имеет строго нулевой средний во времени поток энергии (т.е. мгновенные потоки энергии есть, но ходят туда-сюда, и при усреднении по времени дают нуль). Но наложение двух таких полей создает уже ненулевую бегущую компоненту (элементарно проверяется прямой подстановкой), которая то уже и имеет ненулевой (в среднем по времени) поток энергии. Так что чушь пишете как раз Вы. Само по себе реактивное поле энергию переносить не может. Уравнения Максвелла + вектор Пойнтинга это явным образом запрещают, и это есть общепринятое понимание в физике.
Энергия переносится только активной волной (которая при это таки да, может существовать локально как линейная комбинация двух реактивных полей, см например про волноводные аттеньюаторы в книге того же Вайнштейна "электромагнитные волны").
Ссылка мне Ваша не нужна, но если Вы сами дадите себе труда её прочитать, то подобной ерунды писать не будете. Потому что прямо на первой картинке сверху — написано применительно к ближней зоне "reactive, i.e. non radiative field". Не излучает ничего реактивное поле само по себе. Т.е. не переносит энергию.
Nubus
26.02.2016 11:04Начнем с малого, Radiative переводитса как ИЗЛУЧАЮЩЕЕ!
Следует вам почитать абзац относящийся именно к реактивному полю:
In the reactive near field (very close to the antenna), the relationship between the strengths of the E and H fields is often too complex to predict. Either field component (E or H) may dominate at one point, and the opposite relationship dominate at a point only a short distance away. This makes finding the true power density in this region problematic. This is because to calculate power, not only E and H both have to be measured but the phase relationship between E and H as well as the angle between the two vectors must also be known in every point of space.[4]
Энергия в этом поле есть, иначе откуда бы брались разработки для использования этого самого NEAR field для спертроскопии например?
https://en.wikipedia.org/wiki/Near-field_scanning_optical_microscope
Если бы энергия волны была-бы нулевой, мы бы просто не смогли реализовать всех методов ипользования данного региона.
grekmipt
26.02.2016 21:45+1Вы вообще читаете то на что отвечаете? )
- Я же Вам привел цитату. "reactive, i.e. non radiative field" = реактивное, не излучающее поле. non = не. Comprende?
Энергия в этом поле есть
Разумеется энергия в нем есть. Я Вам уже несколько раз написал что эта энергия есть и ходит туда-сюда (вместо того чтобы двигаться в одном направлении, как в случае активной волны т.е. в волновой зоне), поэтому в среднем по времени — поток энергии нуль. Могу совсем "разжевать". На первой половине периода энергия идет в одну сторону, на второй половине периода — ровно такое же кол-во энергии проходит обратно. В итоге за полный период — энергии и не ушло и не пришло. Это и есть определение реактивного поля, которое преимущественно и имеет место в том самом near field. Но. Если на такие ходящие туда-сюда потоки энергии наложить линейно такие же встречные потоки энергии (тоже ходящие туда-сюда, и с нужным сдвигом по фазе от первых потоков энергии), то окажется что такая комбинация полей уже содержит ненулевой итоговый поток энергии (т.е. активную волну).
Тот абзац который Вы привели — как раз и соответствует всему что я тут пытаюсь Вам объяснить. Впрочем, уже начинаю задумываться — может зря пытаюсь ))- Я же Вам привел цитату. "reactive, i.e. non radiative field" = реактивное, не излучающее поле. non = не. Comprende?

ignat99
25.02.2016 14:13https://ia601300.us.archive.org/19/items/b2172457x/b2172457x.pdf
Вот нашёл прямую ссылку на этот труд Герца. Так же считаю что лучше читать монографии по физике издательства Наука в переводе. (Например Ньютон, Максвелл, Франс Эпинус и т.д.) Или да же оригиналы. Так например в первом оригинальном издании Максвелла гораздо более современное изложение топологии электромагнитных волн, чем во втором томе. Возможно упрощения связанные со сферами были допущены как раз редактором второго издания. В первом издании всё чётко — топологические замкнутые области (воовсе не сферы).
Именно вектор Герца можно считать дополнительным пространством к пространству заряда. Вектор Герца даёт связь для диполей и моментов э/м полей. Топология вектора Герца очень интересная да же для обычной катушки, магнитную его составляющую можно зарегистрировать на специальных магнитных плёнках непосредственно. IMHO
Сдвиг фазы кажется связан с емкостью двойного провода (можно рассматривать его как длинный конденсатор).
mkovalevich
25.02.2016 14:53Спасибо, интересно. Кстати все не дойду ответить вам, чуть позже, ок.

ignat99
27.02.2016 23:11-1В этой книге Герц на страницах 22, 23 и 24 как раз говорит о трёх возможностях построения теории. Методами Ньютона, Гамильтона и Гельмгольца. Или, другими словами, системы уравнений записанные через силу, энергию или координату. Так же Герц говорит о световом эфире, который служит средой для передачи силы и имеет индуцированную поляризацию.
В работе Герца: «Принципы механики изложенные в новой связи» последний метод описан строго а достоинства/недостатки первых двух методов описаны подробно во введении. Герц указывает на достоинства этого методо в связи с изучением голономных систем. Похожий подход используется в современных методах конечных элементов (в частности в методе доменного анализа) для расчёта систем.
В современной физике полупроводников так же записываются уравнения для носителей заряда. Очень часто в работах классиков науки заложены возможности для дальнейшего развития теории. Часто приведены формулы, которые обычно не входят в учебники либо интересные гипотезы.
Видимо под световым эфиром Герц понимал вторичное квантование. Механизм косвенного взаимодействия фотонов планируют использовать как основу для работы Международного линейного коллайдера.

Gribs
26.02.2016 01:18Я конечно тут мимокрокодил, но просто в шоке от всего того что вы написали.
Для начала давайте определимся что у вас на кдпв. А там у вас график в трех измерениях с неподписанными осями. Что же это за оси? Очевидно что по вертикальной оси у нас электрическое поле, в системе СИ это вольты на метр. На другой оси магнитное поле (в СИ это теслы). А вот что на третьей оси непонятно. Это может быть временем, тогда на графике описано изменение электрического и магнитного поля в фиксированной точке пространства со временем. Но это может быть и координатой, когда мы видим значение для электрического и магнитного поля в различных точках пространства вдоль направления распространения в фиксированный момент времени. Обе интерпретации корректны для монохроматической волны в однородной анизотропной среде с граничными условиями на бесконечности.
Теперь давайте разберемся с уравнениями Максвела. Для этого нам бы как-нибудь упростить ротор. Вы говорите что есть большая разница между ротором и простой производной по пространсту, что несомненно верно. Однако мы можем эту сложность обойти для нашего специального случая плоской волны. В такой волне вектора E, B и k (направление распространения поля) являются правой тройкой векторов. А это значит что мы можем выбрать координатную систему, с осью х направленной вдоль Е, с осью у направленной вдоль В и осью z направленной вдоль k. В этом случае
Таким образом уравнения Максвелла перепишутся как
А теперь посмотрим на корень той, уж извините, ахинеи, которую вы написали. Просто сравните два уравнения: ваше «инь-ян» (которое обычно называется система охотник-жертва) и уравнения максвела для плоской волны. Эти уравнения принципиально различаются, и решения у них различные. Первое — система обыкновенных дифференциальных уравнений, а второе — система уравнений в частных производных. И очень глупо ждать от двух разных уравнений двух абсолютно одинаковых решений. Решение обоих уравнений известно. И в общем виде решения этих уравнений разные
А теперь, как вы любите, на пальцах. Вы ждете «круговой динамики» от решения уравнений максвела, и она есть. Только вот производная по времени электрического поля пропорциональна ротору магнитного поля. И она сдвинута относительно ротора магнитного поля на четверть периода. Да вот только ротор магнитного поля сдвинут относительно самого магнитного поля так же на четверть периода, но в другую сторону (мы говорим о монохроматической волне в однородной анизотропной среде с граничными условиями на бесконечности). Как результат — на графике электрическое и магнитное поле имеет максимумы и минимумы в одних и тех же точках. Да, изменение электрического поля пропорционально «закрученности» магнитного поля, однако эту закрученность можно увидеть и не кдпв, если внимательно посмотреть. Я сделал рисунок в предположении, что на оси c изображена координата.
Проекцию ротора на какое-либо направление можно вычислить как предел отношения интеграла по контуру поля к площади этого контура при площади контура стремащейся к нулю, при этом контур должен лежать в плоскости с нормалью параллельной к искомому направлению. Если на пальцах, то проекция ротора на ось это насколько сильно поле врящает кружок с этой осью. Я нарисовал два кружка — зеленое и желтое. Зеленый кружок очень сильно вращается полем против часовой стрелки, это значит что ротор там очень большой и направлен вверх. А значит и прирост электромагнитного поля в этой точке будет большой. Желтый же кружок полем не вращается, ротор там маленький, и электромагнитное поле со временем в нем не изменится. Надеюсь что это достаточно понятно.
tl;dr Для плоской волны в однородной изотропной среде сдвига в четверть периода между электрическим и магнитным полями нет.
Однако если вам так интересно поймать задержку в четверть периода, то вас возможно заинтересует что для полых волноводов (когда появляется металлические граничные условия) существует подобная задержка. Например, продольная компонента электрического поля для TEM волны отстает от поперечной компоненты магнитного поля на четверть периода. Но это уже совсем другая история.
mkovalevich
26.02.2016 01:47tl;dr Для плоской волны в однородной изотропной среде сдвига в четверть периода между электрическим и магнитным полями нет.
Понимаю много коментов, в общем об этом никто и не спорил. Речь о том, что из-за природы ротора это не "естественная" форма волны. Это вырожденная форма, через сумму противоположностей.
Есть разные способы искать ("решать") уравнения. Ну во-первых нужны крайние условия. Тут их немного, поэтому гуляй душа. Хочешь плоскую волну? Пожалуйста. Сходится, сходится. И давай во все учебники, так как плоско это понятно.
Можно отталкиваться от симуляции, т.е. принимаем некий источник излучения. Возьмите. Например, колеблющийся монополь (электрон). Получится совсем другая картина. И эта картина покажет больше природы ЭМ волн, потому что роторы там будут действовать "в естественных условиях", а не подогнанный синус.
А качественная разница между плоской и вращающейся волной… надеюсь понятно, насколько большая.
Эти уравнения принципиально различаются, и решения у них различные. Первое — система обыкновенных дифференциальных уравнений, а второе — система уравнений в частных производных. И очень глупо ждать от двух разных уравнений двух абсолютно одинаковых решений. Решение обоих уравнений известно. И в общем виде решения этих уравнений разные
Нет, если абстрагироваться от измерений, преобразований во времени, суть та же. И результаты естественной симуляции со сдвигом пи/2 это еще раз показывают.
Nubus
26.02.2016 03:03Нет, если абстрагироваться от измерений, преобразований во времени, суть та же. И результаты естественной симуляции со сдвигом пи/2 это еще раз показывают.
У вас одна ключевая проблема, все вышеприведенные уравнения типа:

Именно ДЛЯ полей БЕЗ источника энергии в вакуме.
Вы же в решениях выкидываете J для круговых волн которые возникают! ТАДАМ! В результате ВНЕШНЕГО ЭЛЕКТРИЧЕСКОГО ВОЗДЕЙСТВИЯ!
Но мы же забыли, чтона остальные параметры можно не обращать внимания, например «J» это внешнее электрическое воздействие, которое не будем рассматривать
и в итоге уравнением для элекромангитной волны в вакуме без электрического воздействия вы решаете вообще другой частный случай.
Прекращайте уже так издеватса над другими и собой.
mkovalevich
26.02.2016 04:04А оно ничего не меняет. Так же, как в дифф.ур. окружности можно начать с нуля и добавить "функцию старта", влияние которой убывает до нуля при некотором радиусе. Общая форма дифф.ур. обобщенного осциллятора включает разные вариации, но это именно вариации на тему, погоду не делающие.
Просто в "инь-ян дифф.ур." был взят самый простой вариант, чтобы выделить принцип. И тут то же. На расстоянии от заряда J уже не будет, а вращение все еще будет.
Nubus
26.02.2016 04:15Да, оно ничего не меняет кроме того что дает иммено сдвиг по фазе. А так ничего другого.

mkovalevich
26.02.2016 04:34Сдвиг по фазе есть всегда (как соотв. скалярный продукт = 0), также и в нулевом поле.

grekmipt
26.02.2016 10:48+2Например, колеблющийся монополь (электрон). Получится совсем другая картина.
Вы сильно удивитесь, но картина будет ровно та же самая. См. тему "дипольное излучение" (внезапно, колеблющийся электрон создает именно обычное дипольное излучение). А именно, вблизи источника действительно будут реактивные поля (со сдвигом фазы), но на расстоянии порядка длины волны — останется уже практически только поле излучения (сдвига фазы не имеющее), и на любых дальнейших дистанциях от диполя сдвиг фазы будет практически полностью отсутствовать (чем больше расстоянии тем ближе картинка будет к идеальному отсутствию сдвига фаз).
Все эти "круговые волны" — это, простите, отсебятина и альтернативщина. Как раз наоборот, волну с круговой поляризацией обычно представляют как сумму двух плоских волн (обратное разумеется тоже верно). При этом (снова внезапно) у волны с круговой поляризацией опять такие нет сдвига фаз. Двойка векторов полей, не имея никакого сдвига фазы, накручена на прямую линию по спирали. Поэтому совершенно вне зависимости от поляризации (плоской, круговой, эллиптической или любой другой вообще, без разницы совершенно) у бегущей эм-волны сдвига фазы между векторам — нет. Действительно, прекращайте слушать альтернативщиков и морочить голову себе и людям. Почитайте уже матчасть, всё расписано уж сотню лет как...
mkovalevich
26.02.2016 14:39Ну давайте, удивимся вместе...
Заголовок спойлера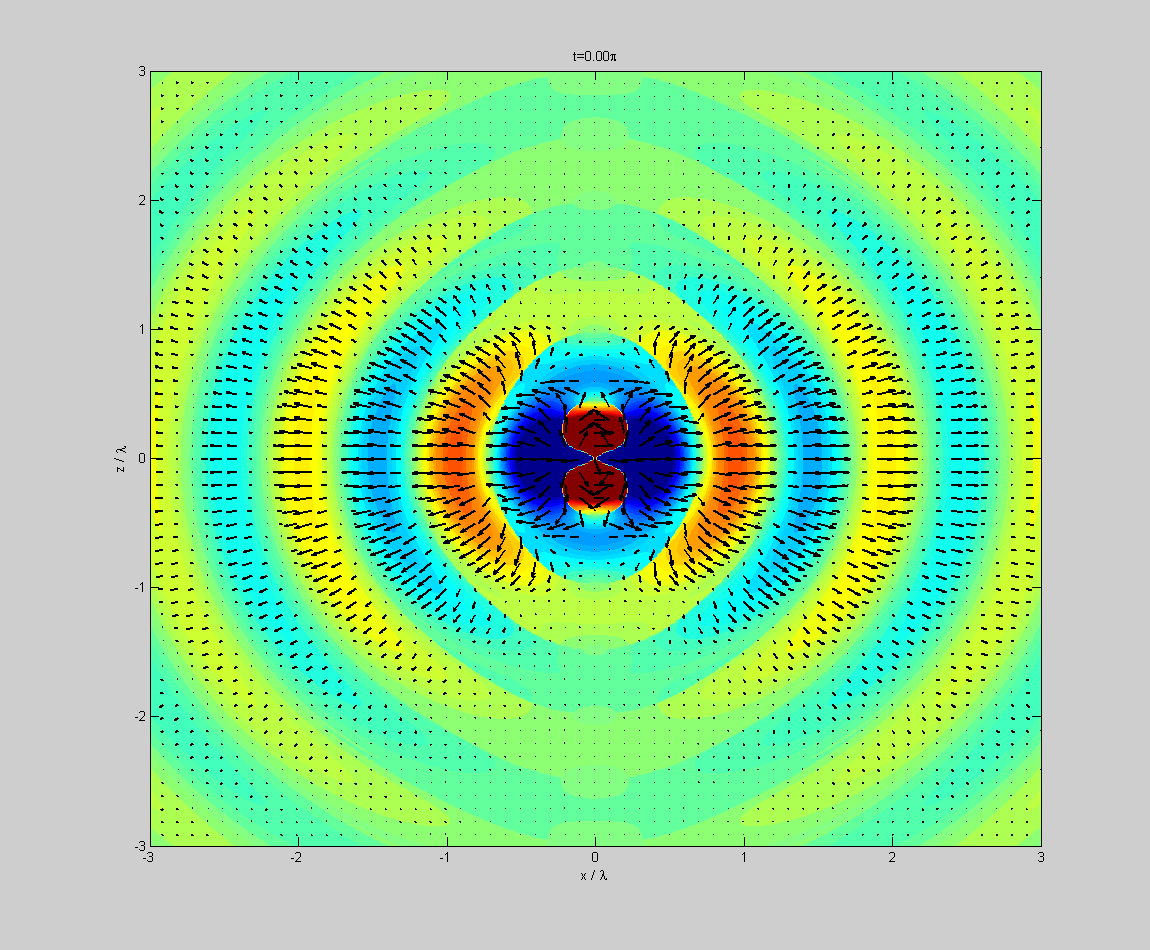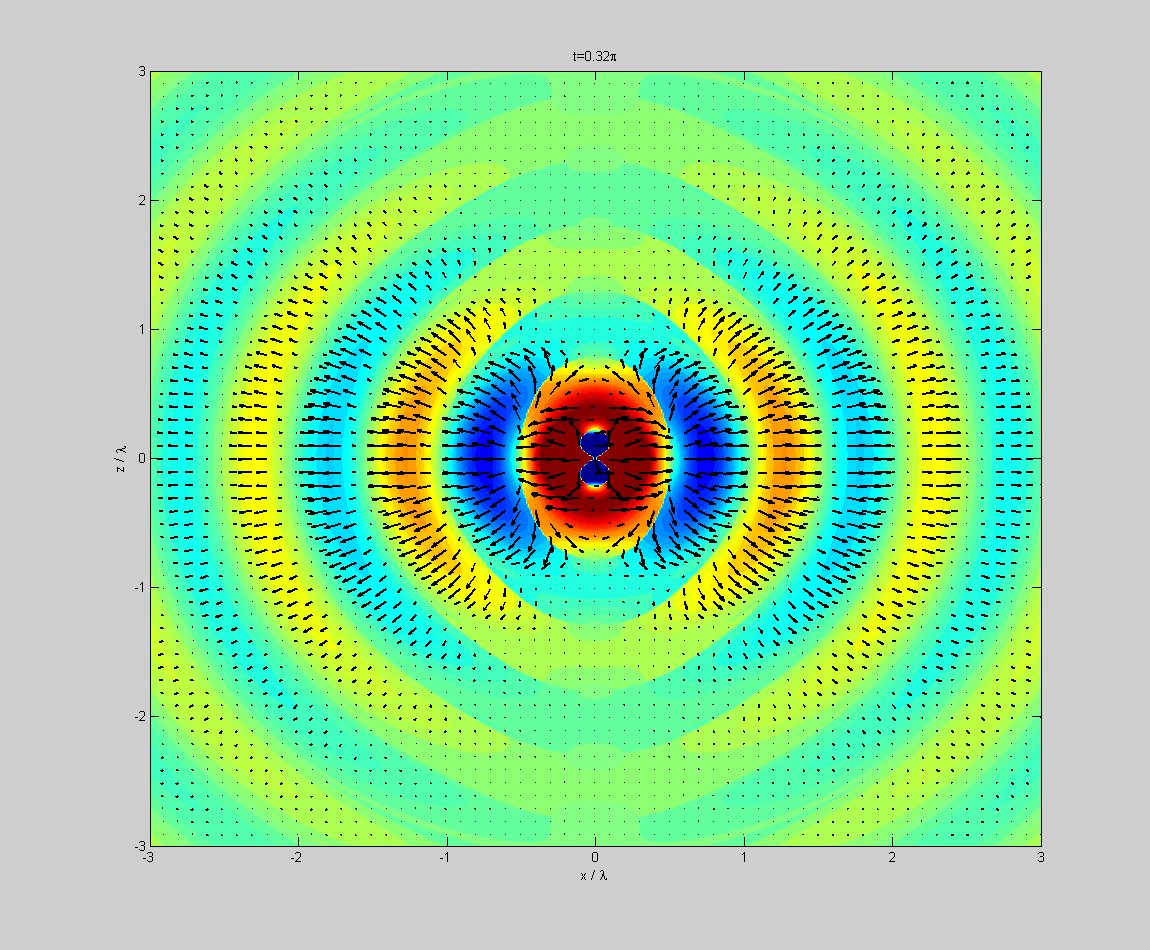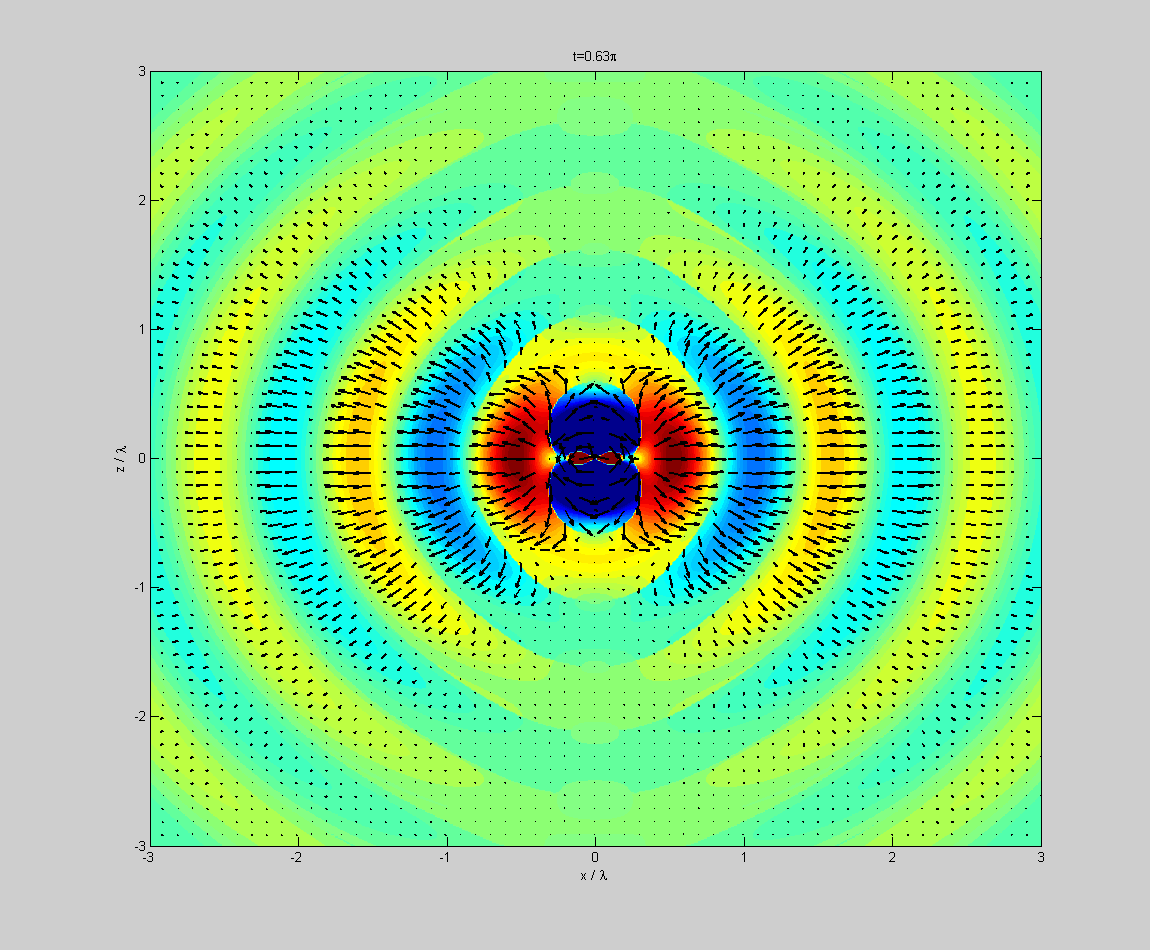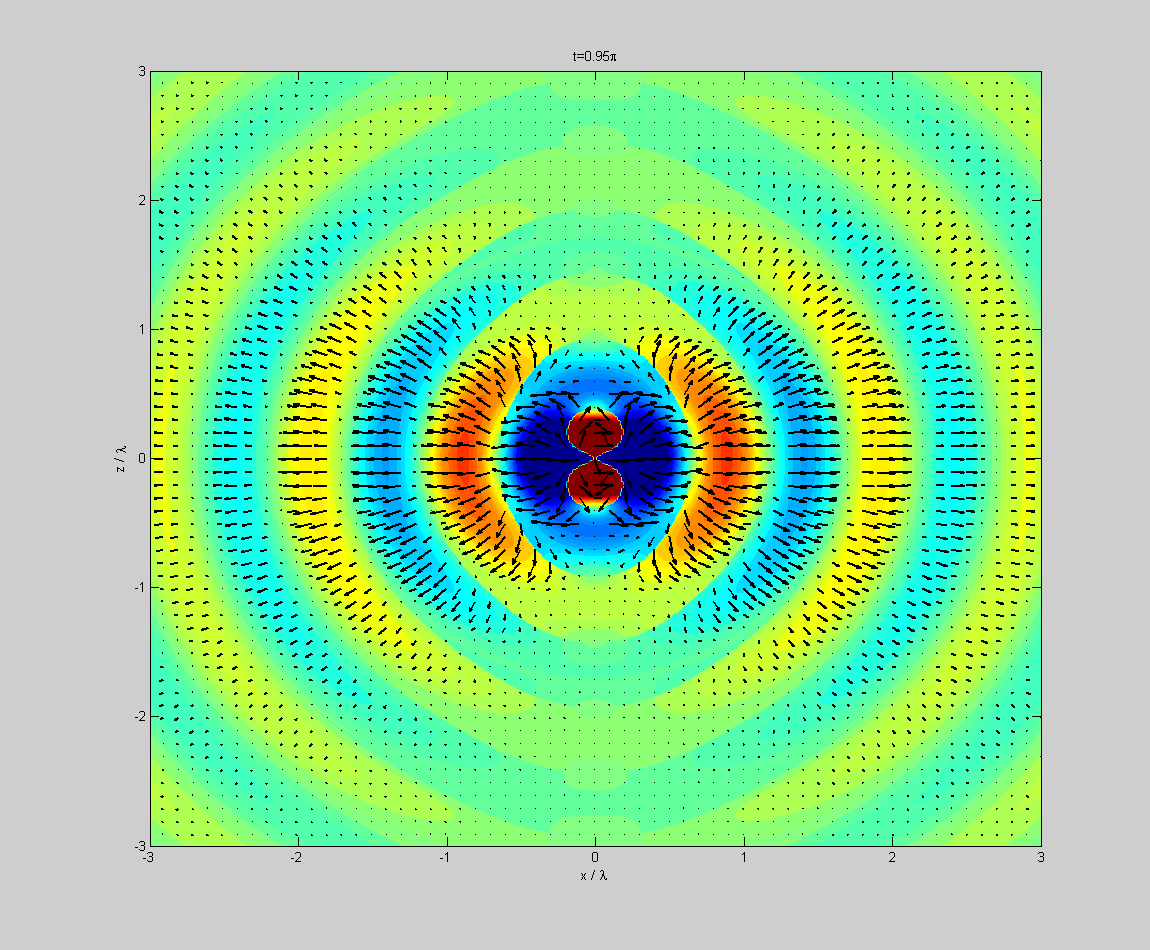

Elrond16
26.02.2016 15:27+1И нет такого расстояния, для которого не будет угла направления (уже очень близкого к вертикальному), на котором пойнтинг не будет вращаться. В общем случае он будет вращаться всегда!
Эм, как бы то, что диполь вообще не излучает вдоль направления собственных колебаний, общеизвестный факт. Соответственно, в некоторой окрестности оси oz на любом расстоянии от диполя доминировать будет его реактивное поле, и вектор Пойнтинга будет себя вести не так, как в случае излучения. Не понимаю вашего посыла. Может для вас это открытие, конечно...

Gribs
26.02.2016 18:20Откуда у вас первая гифка и что на ней изображено и как это было посчитано? Вы утверждаете что вектор Пойнтинга изображен стрелками, тогда что изображено цветом?
О какой суперпозиции вы говорите? Суперпозиции чего с чем?
Как вращение вектора пойнтинга связано со сдвигой по фазе между компонентами электрического поля? Вектор пойнтинга может вращаться если у вас источник имеет дипольный электрический и дипольный магнитный моменты, и что из этого?
Далее. Монополь не излучает. И к картинкам из статей принято давать цитаты.
Почему поле E вдоль какой-либо оси должно быть равно нулю если поле B по этой оси тоже равно нулю? То, что как вы говорите не надо доказывать, не просто надо доказывать. Для вашего утверждения есть простой контраргумент: плоская волна, в которой компанента поля Bx равна везде нулю, однако Ex ненулевая.
У вас с логикой какой-то большой и гремучий белый зверек.
ignat99
26.02.2016 19:09-1Мне кажется Gribs сам не в состоянии ответить на поставленные вопросы и тем более сделать симуляцию. Я да же не говорю про статьи. Всё что вы написали выше — бред до тех пор пока не изложите всё с формулами и чётко. Я бы хотел увидеть что вы в состоянии сделать 3D симуляцию на SymPy, PyDEC и VTK c учётом геометрии излучателя и вклада среды.
Про плоскую волну с «компАнентой поля» к месту в 6 классе детям рассказывать. У поля нет компонент реальная геометрия зависит многих факторов, в том числе от выбранного лично вами удобного базиса. Ещё лучше приведите скрипты, а не формулы что бы не кувыркаться тут с x, y и т.д.
Gribs
26.02.2016 20:38Естественно не в состоянии ответить на вопросы, поэтому и задаю. Мой последний пост с вопросами. Первый был с формулами и картинкой, да вот только они трутся гиктаймсом.
Симуляцию чего именно вы от меня хотите? Излучения дипольного источника? Пожалуйста (meep и матлаб для отрисовки. Что под рукой было): https://www.dropbox.com/s/5xbbnuadlukgtsm/sim.zip?dl=0. Если и эту ссылку потрут то могу вам на почту.
У векторного поля нету компонент? о_О Приплыли.

mkovalevich
27.02.2016 04:29Где вы были в ночь с 15 на 17е? Это не я, не виноватая я! Монополь не излучает. Покачиваем монополь. Монополь излучает. Конец связи.

Gribs
27.02.2016 13:18А что если я вам скажу, что покачивающийся электрон обладает дипольным моментом? Который меняется во времени. Дипольный момент будет -eAsin(wt), где e — заряд электрона, A — амплитуда его движения, w — чатота осциляций электрона. Можете проверить используя определение дипольного момента. И обычно в этом случае говорят что излучает диполь.
Вы кажется не понимаете что подразумевают под монопольным, дипольным, квадрупольным и т.д. излучением. По сути, если у вас есть какой-либо локализованный источник, излучаемая э/м волна от него может быть довольно сложной структуры. Для ее анализа результирующее поле раскладывается по сферическим функциям. Монопольное излучение предполагает независимость амплитуды излучения от направления наблюдения. Такое возможно только при изменении заряда локализованного источника, что невозможно из-за закона сохранения заряда.
mkovalevich
27.02.2016 17:25Вы уже проходили, что бывают более чем одно измерение? Когда пройдете, тогда поговорим, ок.

Gribs
27.02.2016 13:21+1Извините, но у вас жуткая каша в голове по этой теме. Попробуйте порешать задачи по электродинамике, это должно помочь.

grekmipt
26.02.2016 22:20+1Всё верно — чем ближе к оси диполя (прямой вдоль которой колеблется заряд) тем ближе поле к чисто реактивному (энергию не переносящему). Т.е. да, вектор пойнтинга крутится — что и означает нулевое кол-во энергии в среднем по времени (при интегрировании за период колебаний). Ииии… что Вас тут удивляет или где Вы находите тут что-либо несовпадающее с моими объяснениями?
Сдвиг фаз — да, есть, именно поэтому Пойнтинг и крутится, именно поэтому средний поток энергии в таких точках — нуль, и поле является реактивным. Стоит на месте и "дышит". Точно так же как оно стоит на месте и "дышит" прямо около самого диполя (на расстоянии много меньше длины волны), что даже можно как-то разглядеть на Вашей гифке. Чем ближе к ОХ тем больше поток энергии (и тем ближе поле к активному), чем ближе к OY тем меньше поток энергии (и тем ближе поле к стоячему реактивному).
Картинки про монополь — бррр… колеблющийся заряд (если Вы про колебание величины заряда при его полной неподвижности) явно запрещается уравнениями Максвелла (ибо уравнение непрерывности является прямым следствием из Максвелла, и это уравнение не позволяет существовать колебаниям плотности заряда самим по себе).
Посему конечно можно что-то там нарисовать на эту тему — но только причем тут Максвелл?
Тем не менее, я возможно понимаю, что именно Вас может подспудно смущать во всем этом. Когда-то давным давно я тоже сильно удивился этому вот чисто реактивному полю вдоль оси диполя. Но удивился по несколько другой, нежели Вы, причине. А именно, если в какой-то момент времени "включить" диполь, то фронт волны его излучения будет бежать разумеется со скоростью света С, причем во все стороны. Если для направления ОХ это вопросов не вызывает, то для направления ОУ — получаем логическую неувязку. С одной стороны, имеем факт распространения колебания эм-поля, причем со скоростью света (т.е. в точке в которой ранее колебаний не было — они появляются, а значит туда энергия эм-поля так или иначе как-то дошла). С другой стороны, переноса энергии вдоль оси ОУ в среднем нет (по Пойнтингу).
Т.е. если короче — есть прямая, вдоль которой со скоростью света распространяется фронт колебаний эм-волны, но переноса энергии вдоль этой прямой — нет. По мне это явное логическое противоречие. Которое формально (с точки зрения Пойнтинга) решается тем, что энергия в точки вдоль этой прямо таки приходит, но не вдоль прямой, а с боков (с точек около прямой), т.е. не от источника а из пространства окружающего эту прямую (что вообще обычное дело для электродинамики, см. например вектор Пойнтинга для плоского конденсатора с переменным напряжением — энергия так же "втекает" в конденсатор как-бы просто из внешнего пространства).
И скажу честно, как это логическое противоречие решать (фронт колебаний распространяется со скоростью света, а энергия — нет) так чтобы такого интуитивного вопроса не возникало — я не знаю.
Фактически аналогичный вопрос возникает и при просто прямолинейном смещении заряда. С точки зрения определения потока энергии через вектор Пойнтинга, если мы из кулоновского поля заряда выкинем ровно половину, т.е. обнулим вообще все компоненты электрического поля параллельные направлению движения заряда (оставляем "за кадром" возможно ли это в реальности :) ), то поток энергии эм-поля связанный с перемещением заряда — совершенно не изменится. Выкидываем по сути половину энергии/поля заряда, а поток энергии при его перемещении не меняется. Нууу… Мнда. Тем не менее, так нам говорит электродинамика.
Это всё привело меня к другому вопросу — а насколько корректно задается поток энергии в виде вектора Пойнтинга, возможно дело просто в том что это не универсальное понятие?
В итоге я нашел предельно честный ответ у самого Фейнмана в его лекциях, а именно "никто не знает какова правильная формула/определение для потока энергии эм-поля, вектор Пойнтинга это просто случайная и никак не обоснованная догадка, которая пока не противоречит экспериментам — так что физики дружно договорились использовать именно такое определение потока энергии эм-поля, и если нам всем повезет то оно окажется истинным, а если нет — то потребует пересмотра в будущем".
На этом и остановился. Ибо "изобретать" собственное определение потока энергии эм-поля — это надо быть кем-то из титанов, если даже Фейнман не решился то я точно не будут пробовать. Энергия это определяющее понятие во всей физике, и пересматривать определение энергии эм-поля это эквивалентно пересмотру всей электродинамики вообще. Безнадежное занятие для не-гения (а я себя гением точно не считаю, и Вам определенно не советую считать себя таковой :) ).
Gribs
26.02.2016 22:38К вектору Пойнтинга можно добавить ротор любока поля, и его физическая сущность не изменится =). Ну в смысле интеграл этого вектора по поверхности не изменится, что в конечном счете нам и нужно при наблюдении за переносом энергии.

grekmipt
26.02.2016 23:03Это понятно. Фейнман же говорит про другое — про то что не существует пока что в природе вывода формулы для энергии эм-поля. То что вектор Пойнтинга легко получается из Максвелла — это да. Но из Максвелла же можно "нагенерировать" любое произвольное кол-во выражений (в виде связок определения энергии поля и соответствующего выражения для потока такой энергии), которые подчиняются "закону сохранения". Т.е. фактически взяли самое простое выражение для энергии поля (по сути взятое из электро и магнито статики, и соответственно — хз насколько оно корректно для динамики) и для него — вывели из Максвелла понятие вектора Пойнтинга.
Иначе говоря, если взять (вообще произвольно, в принципе не важно как) любое выражение для энергии эм-поля, при условии что это выражении энергии эм-поля в случае статики сводится к известным квадратам амплитуд полей (определенным по сути эмпирически, из экспериментов) — то для любого такого определения энергии эм-поля можно из Максвелла вывести выражение для потока энергии, соответствующее такому определению энергии эм-поля. И это выражение разумеется уже будет не совпадать с Пойнтингом.
Сейчас в случае динамики, в качестве определения энергии эм-поля постулируются (это просто постулат, не более того — по сути никто его никак не обосновывал) квадраты амплитуд полей (с соответствующими коэффициентами разумеется), и для них автоматом из Максвелла получаем вектор Пойнтинга как выражение задающее поток так заданной (постулированной) энергии эм-поля. Возьмем любой другой постулат для энергии эм-поля (который обязан совпадать с известными из экспериментов выражениями для случая статики) — получим другое выражение для потока энергии.
О чем и пишет Фейнман в своих лекциях. Он в этом смысле молодец. Где есть вопрос — он его акцентировано озвучивает. А тут не вопрос, а прямо вопросищще ). Но ответа пока нет — видимо пока во всех экспериментах "прокатывает" общепринятое определение энергии и соответственно вектор Пойнтинга задающий поток (для так постулированной) энергии эм-поля.
Врочем, эти вот нюансы даже преподаватели зачастую не осознают ).
Gribs
26.02.2016 23:50Хммм, как я понимаю что все встает в вопрос "А что такое энергия электромагнитного поля?".
Смотрите, мы можем записать лагранжиан (и соответственно гамильтаниан) э/м поля через тензор F (а по сути через производные 4-потенциала A). Отсюда можно вывести и гамильтониан. А попутно и тензор энергии-импульса. 00 компонента этого тензора будет энергия поля, а 0i компоненты будут представлять импульс, ну или по-сути вектор пойнтинга. Об этом наверняка написано много где, но у меня под рукой сейчас есть только электродинамика джексона. В 3-ем издании английской версии это на страницах 606-607 (глава 12.10). И получаемые выражения для энергии и вектора Пойнтинга отличные. Однако проблема этого тензора в том, что он не симметричный. И при попытке сделать его симметричным получаются классические выражения для энергии поля и пойнтинга.
К чему я это. Если уравнения максвелла переписать через Лагранжиан (что возможно сделать множеством различных лагранжианов), то получается либо симметрично с энергией в классическом виде или несимметрично. Вопрос в том, должна ли быть симметрия в тензоре момента-импульса для э/м поля.
grekmipt
27.02.2016 00:14Да, можно и так переформулировать. Лагранжиан же эм-поля, насколько я (уже смутно) помню теорфиз, невозможно вывести из первых принципов, а можно только постулировать. Соответственно, вот про это и пишет Фейнман. Сейчас постулируется нечто одно. Насколько оно трушное — никто не знает, но пока вроде-бы нет экспериментов которые его опровергают.
Правда, справедливости ради, как пишет снова тот же Фейнман, никто таких экспериментов специально и не проводил вообще — т.е. целенаправленным поиском/проверкой никогда и не занимались.
Откуда и возникают вопросы того типа что я выше (например ситуация когда распространения фронта колебания эм-поля со скоростью света не сопровождается переносом энергии вдоль направления распространения фронта, что выглядит диковато), но такого рода вопросов в электродинамике можно задать множество (если озадачиться).
Некоторые из них сам же Фейнман рассматривает и приходит к выводу например что (это из его лекций в части импульса эм-поля) "да, полученный ответ не сходится, видимо мы в чем-то ошиблись, но не в формулах а в чем-то более важном, однако в чем — науке пока неизвестно, оставим это как парадокс электродинамики и пойдем дальше".
Поэтому, если вникать в эти нюансы электродинамики — то становится ясно, что это никак не "законченный продукт", и приятная студенческая иллюзия что это "давно выстроенная и полностью законченная теория" развеивается именно в вопросах энергии и импульса эм-поля. Теория то законченная, но непроясненные места в самом важном в ней таки есть. Однако, альтернативы пока нема, и не факт что она нужна, ибо с экспериментом пока всё бъется отлично. Будут эксперименты не укладывающиеся в принятое определение энергии поля — будут менять теорию, не будет таковых — ну на нет и суда нет.

mkovalevich
27.02.2016 04:23но на расстоянии порядка длины волны — останется уже практически только поле излучения (сдвига фазы не имеющее), и на любых дальнейших дистанциях от диполя сдвиг фазы будет практически полностью отсутствовать
Сдвиг фаз — да, есть
Ну и славно. А причину, похоже, так и не уловили, все "реактивное поле") А теперь начинаем монополь покачивать на бока… или просто вращать. Система "активное" "реактивное" "какое-то нечто среднее" все еще актуальна? Оно дышит? Будет жить?)
grekmipt
27.02.2016 10:40+1Вы упорно называете заряд — монополем. Называйте его уже просто зарядом, будет проще и вам и остальным (Вас понять).
Так вот, если Вы покачиваете заряд — то он создает дипольное излучение. Как покачивать (вдоль одной оси или вдоль другой) — роли не играет. Когда Вы колеблете заряд не строго вдоль прямой, а по кривой на окружности (ведь это Вы и имеете ввиду по сути?), то при условии малости амплитуды колебаний — снова получим чисто дипольное излучение (до тех пор пока кривизна траектории будет много меньше длины траектории, т.е. при малых колебаниях). А если амплитуда колебаний велика (так что кривизной траектории уже нельзя пренебречь), то получится более сложное эм-поле. Какое — с ходу не готов, тут надо формУлки пописать. Но в принципе, тема "излучение заряда при движении оного по круговой траектории" в физике хорошо известна и так же разжевана в учебниках. Хотя и без явных картинок поля (картинку для такой штуки, думаю, проще всего построить через запаздывающие потенциалы Лиенара-Вихерта, задав явным образом траекторию заряда и построив потенциалы в каком-нить маткаде).
Так что система активное/реактивное поле разумеется будет всё еще актуальной.

mkovalevich
27.02.2016 17:23Простите за резкость вчера… незаслуженно с учетом вашего вклада в тему.
Насчет словечек, просто "точечный заряд" менее информативно, т.к. подразумевает конкретную величину потенциала, например заряд электрона. Но в поле с этим же электростатическим потенциалом этот заряд будет пустышкой — не будет "монополем".
А "монополь" сразу указывает на источник разницы потенциала.
Но без разницы, пусть будет заряд)
Когда Вы колеблете заряд не строго вдоль прямой, а по кривой на окружности (ведь это Вы и имеете ввиду по сути?)
Да, например. Просто хочу показать, как быстро рушится картина с "реактивным непередавающим энергию полем", даже в случае дипольного излучения. Думаю, путаница в том, что вращение пойнтинга не означает отсутствие передачи энергии, ведь важен интеграл по циклу, и только если он нулевой, тогда да, энергия не передается. В случае дипольного излучения, когда пойнтинг вращался вблизи оси колебания на 1000км от источника, при этом менялась его мера, поэтому интеграл не нулевой.
А также, как быстро рушится картина с невращающимся пойнтингом. Добавляем колебания не только вдоль линии — и все. Шаг в лево, шаг в право… ) Идеальным был бы пример с монополем с колблющимся зарядом (потенциалом). В том примере с картинкой — взяли просто волновое уравнение такого вида (т.е. источника там по сути нет). Это мне не очень нравится, поэтому пример забираю.
Излучение заряда по круговой траектории можно сложить из перпендикулярных дипольных (со смещением). Хотя не знаю, что там с near field, но в простом случае особо влиять не должно. Т.е. в итоге трехмерное спиралевидное нечто. При этом, пойнтинг вращается везде.
grekmipt
28.02.2016 11:36вращение пойнтинга не означает отсутствие передачи энергии, ведь важен интеграл по циклу, и только если он нулевой, тогда да, энергия не передается. В случае дипольного излучения, когда пойнтинг вращался вблизи оси колебания на 1000км от источника, при этом менялась его мера, поэтому интеграл не нулевой.
Да, всё верно. Но ненулевая часть такого интеграла — только та, которая и соответствует активной компоненте поля (не имеющей сдвига фазы). А компонента поля реактивного характера — дает как раз нулевой интеграл "по циклу". Т.е. вы правы, но это никак не противоречит моим объяснениям.
Излучение заряда по круговой траектории можно сложить из перпендикулярных дипольных (со смещением).
Сильно подозреваю, что это не верно. Потому что поле дипольного излучения имеет ярко выраженную осевую симметрию. Складывая два поля с сильной осевой симметрией, сдвинутые по фазе и повернутые осями на 90 друг от друга — мы, навскидку, ну никак не получим системы имеющей одинаковое описание по всем направлениям (в плоскости таких двух осей). Т.е. по идее получим мы эдакий "крест", а это явно не будет полем заряда, движущегося по окружности...
Gribs
28.02.2016 13:49А вы тут не путаете интеграл по циклу (я это понимаю как интеграл по замкнутой кривой) и интеграл по замкнутой поверхности? Просто, как я говорил ранее, к вектору пойнтинга можно добавить ротор векторного поля и его физическая сущность не изменится. А вот интеграл по замкнутому пути ротора ненулевой (да это и не важно, так как интеграл по замкнутой поверхности ротора ноль).
Да и вообще пойнтинг имеет более-менее логичное значение только если вы его усредняете по времени (периода колебаний).
И диаграмма направленности вращающегося диполя — эллипс ~(1+cos^2 a), гда а — угол между осью ващения и направлением наблюдения. И он действительно получается сложением двух дипольных излучений. Могу предоставить свои записи по этому поводу, но подчерк у меня ужасный.
Ну а теперь о чем мы спорим? Возьмите электрическое и магнитное поле со сдвигом на пи пополам. Посчитайте пойнтинг. Пол периода он положительный, пол периода отрицательный, колеблется как sin(wt). Усредните по времени, получите отсутствие передачи энергии. Это же элементарная математика. grekmipt про это и говорит, в этом случае поле реактивное. Если сдвига фазы нет то поле чисто активное (S~cos^2(wt)) и передает энергию в одном направлениии. Ваш пойнтинг вращается? Усредните по периоду, неужели так сложно? Получите направление передачи энергии.

FransuaMaryDelone
28.02.2016 15:20Сильно подозреваю, что это не верно.
может и вызывает недоверие, но это верно: само движение по окружности одного заряда в проекциях на оси представляется как синус и косинус, что можно трактовать как скрещенное движение вдоль прямых двух отдельных зарядов с разными фазами. Точку ставит в рассуждениях суперпозиция.
grekmipt
28.02.2016 15:31Ммм… ну да, в случае двух точечных диполей (с поворотом осей и сдвигом фазы), и точечного же вращения вектора одного диполя поля отличаться не будут, т.к. и то и другое задает одинаковое изменение итогового суммарного вектора поляризации диполя… Отличия начнутся только если диполи уже нельзя считать точечным (т.е. если не выполняется что радиус орбиты много меньше длины волны), тогда уже пойдут добавки старших порядков по идее, т.е. потребуется полноценное мультипольное разложение которое ессно не совпадет с дипольным. Ага...

Geo_Evil
27.02.2016 01:11-1Интересно, если бы магнитное поле не существовало, могла бы распространяться электрическая волна самостоятельно? По типу гравитационных волн?

saboteur_kiev
28.02.2016 14:56Ребята, а именно Gribs, grekmipt,
Вашу бы энергию, да на новую статью, а то в каментах ругаетесь, а кто не в теме все равно ничего не понял...
grekmipt
28.02.2016 15:47Честно — статью делать лень. Одно дело просто текстом всё объяснить, накидав инфы для размышлений, а другое дело статью делать — т.е. картинки сооружать (а то и модельки самому обсчитывать), ссылками обвешивать, приводить массу аналогий и пояснений, т.е. фактически сделать хороший учебник по азам электродинамики (из серии "электродинамика для чайников").
Хотя такой учебник и будет, вероятно, актуален, но пока моральных сил на это нет, а в паре абзацев тему не объять никак. Вот и остается только разбирать ошибки в комментах ).
mkovalevich
28.02.2016 21:52Ой, вы еще сопротивляетесь? Казалось бы, пора и утихнуть… Реактивное поле, это которое часть "ближнего"? И по обещаниям, практически исчезает с расстоянием порядка больше длины волны? Натягивание флоры на фауну продолжается? Часть третья, "возвращение резиновых попугайчиков"...
Лень считать, ну ладно мне не лень… Ну то есть… лень)) Но зачем, все сделано до нас. Вращение магнитного диполя:
Электромагнитное поле вращающегося магнитного диполя и движение электрических зарядов в этом поле - 2009 Сарычев В.Т. Томск ГУ
Вращение с радиусом на порядки меньше длины порождаемой волны (для нашего рассуждения про вырожденность линейных волн это без разницы — но так проще расчитывать, да).
Полярные координаты, вращение диполя в плоскости (тета=0).
Ламбда — длина порождаемой волны. Омега — угловая скорость.

ignat99
29.02.2016 00:32IMHO: Просто пример ассоциаций.
Если смотреть на первую симуляцию, то можно представить, что из плоскости симуляции на нас постепенно надвигается тор, от которого в проекцию на окружающую мнимую сферу расходятся волны (условно 2 сферические гармоники). Которые можно представить как кольца дыма испускаемые вдоль оси X.
Из работы Гельмгольца, мы знаем, что подобное движение материи (если следовать определению Герца) может быть устойчивым, если тор будет двигаться вдоль оси X.
В реальном принимающем контуре Герца фазы на дипольных концах отличаются из за подвода сигнала в точке не равно удалённой от концов контура.
Движение в доль оси X можно создать поместив в эту ось вытянутый фидер, с пучностями волн которые которые синхронно с диполем движутся (например в положительном направлении оси X).
Казалось бы движение будет без потерь энергии. Однако это не так. В работе Гельмгольца используется модель несжимаемой жидкости. Силовые линии магнитного и электрического поля — сжимаемые. То есть действует объёмная сила. Её действие можно уподобить вязкости жидкости. Что должно привести помимо расходящихся колец, так же образование более мелких завихрений, которые в итоге приведут к исчезновению волн на удалении от диполя.
Однако, если предположить что диполь находиться на границе двух сред, при условии согласованной подпитки энергией от второй среды, можно добиться более длительного существования колебаний. Которые могут да же выглядеть, как самосогласованное движение солитона.
IMHO

Gribs
29.02.2016 01:25+1.<
Однако в Sr такой множитель… (омега/с)^3. Т.е. пока расстояние не сравняется со световыми масштабами (точнее r^2 порядка c^3 в числовом выражении), доминирует угловая координата, т.е. совсем не «уносящая»).
Если расскажете физикам, что near field исчезает на астронимических расстояниях, что они скажут?
w/c=2pi/l, где l — длина волны лямбда. Соответственно (w/c)^3 = 8 pi^3/l^3. Итого S_r ~ 1/r^2l^3, а S_ф ~ 1/r^3l^2. Какие атрономические расстояния? Вы и километровых волнах говорите?
А знаете что самое смешное? Это не важно! Потому что S_r и S_ф как бы активные. Ничего там не крутится (во времени) потому что нечем крутиться, временная зависимость была устранена и реактивная передача энергии туда-сюда занулилась.
А теперь посмотрите на формулы. При больших r (многим больше длины волны) у нас получается
E_th ~ 1/rsin Ф,
E_ф ~ 1/rcos th * cos Ф,
B_th ~ 1/r cos th cos Ф,
B_ф ~ 1/r sin ф,
B_r ~ 1/r^2 (пренебрегаем).
Знаете как такая картинка называется? Волна с круговой поляризацией. Когда у вас что-то крутиться вы это имеете в виду? Ну тогда да, я с вами согласен, вращающийся электрон дает волну круговой поляризации. То есть вы написали эту статью чтобы сказать что кроме линейной поляризации существует еще и круговая? То есть вам не хватало этой гифки: https://upload.wikimedia.org/wikipedia/commons/d/d1/Circular.Polarization.Circularly.Polarized.Light_Left.Hand.Animation.305x190.255Colors.gif
mkovalevich
29.02.2016 12:10Не годится эта гифка, линейные вы мои. Ф зависит также от r, поэтому вдоль прямой будет… ну совсем не это.
Про w/c верно, спасибо. Хотя теорию про реактивные поля это, как заметили, не спасает)0serg
29.02.2016 12:31При сколь-либо заметном удалении (большом r) как раз отличия от картинки будут пренебрежимо малы.

Gribs
29.02.2016 13:23Ф=wt-kr. Как и в любой другой волне. Просто для каждого направления ф появится еще своя фаза (большой роли не играет). Так что вдоль r будет именно это. И мне упорно кажется что вы не понимаете что мы назваем реактивным полем.
Пусть E=sin(Ф), B=sin(Ф-a), где Ф=wt-kr, а a — разница по фазе. Мы можем записать
B=sin(Ф)cos(a)+cos(Ф)sin(a). В этом случае вектор пойнтинга
S=sin^2(Ф)cos(a)+1/2 sin(2*Ф) sin(a).
Как можно заметить у пойнтинга есть две компоненты. При усреднении по периоду первая будет равно 1/2*cos(a), вторая будет равна нулю. Первую мы назыаем активной компонентой (она учавствует в передаче энергии), вторую реактивной (она не учавствует в передаче энергии). При расстоянии до источника много меньше длины волны наибольший вклад будут вносить компоненты, в которых B_th в противофазе с E_ф и B_ф в противофазе с E_th (посмотрите на формулы которые вы привели). Поле будет преимущественно реактивным. Когда расстояние примерно равно длине волны обе компоненты необходимо учитывать. Ну и при расстоянии много большем длине волны остается только активная компонента. Это все следует из приведенных выше формул. Вы согласны? Или вы по-другому их интерпретируете?
Почему мы сравниваем расстояние с длиной волны, а не с каким-то абстрактным астрономическим растоянием? Да потому что во всех формулах для B и E знаминатель имеет размерность растояния в кубе: r^i*l^j, i+j=3, i>0. Числитель же у всех одинаковый. Соответственно 1/r/l^2 > 1/r^2/l при r>l.
И самый главный вопрос. Кажется я перестал понимать что вы пытаетесь доказать. Вы можете сформулировать это?
mkovalevich
29.02.2016 14:08Не перестали, вы и не начинали) Но хорошо, что заинтересовались))
Началось примерно с
Все эти «круговые волны» — это, простите, отсебятина и альтернативщина.
И что сдвига нет.
Потом оказалось, что "да, круговые волны есть, да, сдвиг есть", но пошло в ход "это всё реактивная компонента".
Теперь когда оказалось, что это все-таки вполне себе "активная компонента", мы получаем в ответ, что "про круговые волны мы все прекрасно уже 500 лет знаем и без вас" ))
Картинка не годится, потому что она представляет как раз продукт линейного видения — сложение двух линейно поляризованных (как писал grekmipt или кто-то еще). Но в таком случае такая вращающаяся волна имеет однородную картину (везде одинаковую) — опять сплощенную! Опять пудрим мозги, что Земля плоская!
Тогда как в реальности (здесь например) — профиль волны меняется в окрестности. Т.е. если взять некий отрезок вдоль координаты "фи", увидим, что профиль вращается… Образно говоря, "вращение вращается"))
А если добавить колебания в третьей координате, то профиль меняется по обеим угловым координатам.
Это совсем другая картина...
Все, мне работать, пока.
Gribs
29.02.2016 15:28И мы возвращаемся к каше из непонятных определений. Что такое "профиль волны"? "Круговые волны" — это фолны с круговой поляризацией, или вы вкладываете в это определение что-то другое?
А теперь про сдвиг. Я утверждаю что на расстоянии от источника многим больше длины волны (а так же при условии что размер источника так же много меньше растояния до него) сдвиг между компонентами электрического и магнитного поля принебрежимо мал. Я считаю, что уравнения из Сарычева, которые вы привели выше, это подтверждают для вращающегося электрона. Причем, попрошу заметить, в соответствии с этими уравнениями, вдоль оси вращения волна имеет круговоую поляризацию, в плоскости вращения — линейную, а в пространстве между осью и плоскостью волна поляризована эллиптически.
Так же я считаю необходимым уточнить, что такое сдвиг фазы для электрического и магнитного поля, так как не совсем ясно как наблюдать сдвиг фаз для волны с круговой поляризацией, для которой амплитуда E и B не меняется во времени. Так вот, такую волну можно разложить как сумму двух линейно-поляризованных волн. И для каждой из них проналюдать сдвиг фаз между E и B (я утверждаю что он будет нулевой).
Вы понимаете мою формулировку? Согласны ли вы с ней?
ignat99
29.02.2016 16:25-1Посмотрим анализ диф. уравнений Максвелла для распространения электромагнитной волны с отличным по оси Z коэф. преломления. В целом задача аналогична передаче вращения на мельнице между двух конусов.
Прямо из системы можем записать матрицу передачи (Matlab):
M = [ 0, g * cos(t), –g * sin(t) * sin(k), o*m, 0, 0; –g*cos(t), 0, g*sin(t)cos(k), 0, o*m, 0;
g*sin(t)*sin(k), –g*sin(t)*cos(k), 0, 0, 0, o*mz;
o*e, 0, 0, 0, –g*cos(t), g*sin(t)*sin(k);
0, o*e, 0, g*cos(t), 0, –g*sin(t)*cos(k);
0, 0, o*ez, –g*sin(t)*sin(k), g*sin(t)*cos(k), 0]
где:
g — постоянная распространения волны по направлению,
o — круговая частота,
m,e,mz,ez — компоненты тензора параметров среды,
k,t — азимутальный и поляный углы.
detm = det(M)
detmsi = simple(detm)
detmsi =
o^2(e*g^2*sin(t)^2*sin(k)^2+e*g^2*sin(t)^2*cos(k)^2–e*m*ez*o^2+g^2*cos(t)^2*ez)(mz*m*o^2*e–g^2*sin(t)^2*m*cos(k)^2–g^2*sin(k)^2*m*sin(t)^2–g^2*cos(t)^2*mz)
или
detmsi =
o^2(e*g^2*sin(t)^2–e*m*ez*o^2+g^2*cos(t)^2*ez)*(mz*m*o^2*e–g^2*sin(t)^2–g^2*cos(t)^2*mz)
Приравняв это к 0 можно выразить g, это будет элипс зависящий от t и ez.
Аналогичный элипс для квази–магнитной волны.
Каждая из двух частей detmsi это набор гантелек или сечение тора.
(Если я не прав, скажите мне сразу об этом!!!!)
Произведение этих скобок даёт 4–х мерную сферу или произведение напряжённостей электромагнитного поля [E,H].
От функции g будет зависеть какое поле мы получим в итоге. Если частота o у нас будет меняться то надо будет учитывать дисперсию и пр.
ignat99
29.02.2016 21:52-1Вот картинка в более удобном виде:
http://homedevice.pro/wp-content/uploads/2016/02/g.png
На ней в частности в правом нижнем углу один из вариантов решения уравнения.
Gribs
01.03.2016 00:54+3Извините, но понять вас катастрофически, просто непреодолимо катастрофически сложно. И я вас уверяю, никто в этом типике не может вас понять. И для этого, по-моему, есть две причины.
Первая причина это то что вы изъясняетесь крайне запутанно и витиевато. Очень сложно понять о чем вообще вы говорите. Например, в этой ветке вы зачем-то выводите дисперсионные соотношения для волны в анизотропной среде. И понять это можно не сразу, поверьте мне, как человеку который на это смотрит. Я не утверждаю что мои сообщения просто образец кристально-чистых мыслей, но я хотя бы стараюсь объяснить о чем я говорю и что я имею в виду. Так вот, ваше сообщение я понял не до конца. Я искренне согласен с тем, что поверхности равных фаз в анизотропной среде это эллипсы. Но я не понимаю как эти эллипсы стали потом набором гантелек, потом (в следующей строке) гантельки превратились в четырехмерные сферы чтобы там же, в той же самой строке, стать произведением (векторным?) электрического и магнитного полей.
Вторая причина заключается в том, что выши комментарии в принципе не в тему дискуссии. Нам бы с изотропным пространством справиться. Нет, я понимаю что в анизотропном пространстве может произойти многих прикольных штук, и вектора E, B, и S перестанут быть взаимноперпендикулярными (что "поломает" саамую первую картинку в этой злополучной статье), но божежтымой, анизотропные среды это не что-то обычное.
Поэтому просто перестаньте заумничать и давайте по-сути, пожалуйста. И без обид.
ignat99
01.03.2016 01:29-3Видимо вам стоит изучить некоторые темы по подробнее, перед тем как писать. Топологию, Диф.формы, Фидеры, Замедлители. Я подробнее в личной почте вам ответил.
Анизотропные среды (с 1 коэффициентом отражения/преломления) это как раз самое обычное явление. Проще только (не намного) устройство деревенской мельницы (той в которую лошадь впрягали, упаси бог вас от ветряной мельницы — той с которой Донкихот ламанческий рубился — та вообще, по современным меркам, потянет на заявку в президиум АН по борьбе с нелинейными волнами).
IMHO


Shafikov
Я так и не понял, Вы в итоге доказали, что выражения вида
E = Emax cos(kx-wt)
B= Bmax cos(kx-wt)
не являются решением уравнений Максвелла, а
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt + pi/2)
же, наоборот, являются?