В прошлой части было рассказано как установить и настроить open-source электромагнитный симулятор openEMS . Теперь можно переходить к моделированию. Как производить моделирование ЭМВ при помощи openEMS и Octave будет рассказано в этой статье.

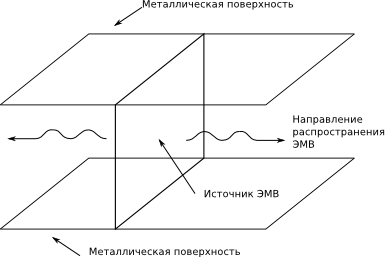
Мы будем моделировать процесс распространения электромагнитной волны (ЭМВ) между двумя параллельными металлическим пластинами.

Конфигурация объекта показана на рисунке. Предполагается прямоугольный источник ЭМВ, от которого ЭМВ распространяется в обе стороны.



Под катом приведён построчный разбор скрипта для моделирования такого объекта.

Как было сказано в предыдущей части, все симуляции в openEMS являются скриптами Octave/Matlab. Запускаем Octave/Matlab и вводим следующие команды. Сначала инициализируем пространство. Мы создаём специальный объект FDTD, который описывает пространство конечной разности во временной области:

FDTD = InitFDTD('NrTS',100,'EndCriteria',0,'OverSampling',50);

Параметры функции — это 100 точек расчёта по времени от нуля. Шаг расчёта по времени выбирается автоматически на основе частоты Найквиста и частоты источника ЭМВ. Попробуйте задать другое количество точек, например 1000.

Теперь устанавливаем источник ЭМВ частотой 10 МГц. Здесь параметры функции понятны из названия.

FDTD = SetSinusExcite(FDTD,10e6);

Для любого моделирования ЭМВ нужны граничные условия. Граничные условия описывают свойства материала, которым ограничено пространств в направлении каждой из трёх осей координат X,Y,Z. Порядок следования граничных условий в параметрах функции следующий X+, X-, Y+, Y-, Z+, Z- У нас пространство по оси Y в положительном направлении ограничено идеально проводящей поверхностью (PEC — Perfect Electric Conductor), в отрицательном направлении по Y — также проводящей поверхностью. PMC — это идеальный
магнитопроводник. MUR — это абсолютно поглощающий диэлектрик. Он приблизительно соответствует материалу стенок безэховой камеры.

FDTD = SetBoundaryCond(FDTD,{'PMC' 'PMC' 'PEC' 'PEC' 'MUR' 'MUR'});

Ещё доступен специальный многослойный материал (PML_x) для граничных условий. Он может иметь от 6 до 20 слоёв (например PML_8, PML_10). Этот материал тоже действует как поглощающий диэлектрик.

После того как заданы граничные условия инициализируем пространство CSX, в котором будет задана геометрия нашей системы.

CSX = InitCSX();

Теперь нужно создать сетку. Расчёт распространения ЭМВ будет выполняться внутри пространства, ограниченного сеткой. Сначала задаём размерность сетки по координатам (X*Y*Z=20х20*40 метров).

mesh.x = -10:10;
mesh.y = -10:10;
mesh.z = -10:30;

Теперь создаём собственно сетку в прямоугольных координатах при помощи функции
DefineRectGrid() и применяем её к геометрии (шаг сетки равен 1 метру):

CSX = DefineRectGrid(CSX,1,mesh);

Далее создаём источник ЭМВ. Задаём амплитуду ЭМВ и направление вектора ЭМВ. Для этого служит функция AddExcitation.

CSX = AddExcitation(CSX,'excitation',0,[0 1 0]);

Первый и второй параметры функции — это имя CSX-пространства и имя источника ЭМВ соответственно. Третий параметр функции — это тип поля. Доступны следующие типы:

• 0 — электрическое поле (Е), жёсткое возбуждение
• 1 — электрическое поле (Е), жёсткое возбуждение
• 2 — магнитное поле (Н), мягкое возбуждение
• 3 — магнитное поле (Р), жёсткое возбуждение
• 10 — плоская ЭМВ

Отличие жёсткого и мягкого возбуждения состоит в том, что при жёстком возбуждении амплитуда ЭМВ в данной точке пространства устанавливается принудительно заданному значению, а при мягком возбуждении рассчитывается суперпозиция полей, то есть ЭМВ накладывается на имеющиеся в данной точке пространства поля.

Четвёртый параметр — это вектор, компоненты которого задают амплитуду ЭМВ по трём направлениям X,Y,Z.

Таким образом мы задали возбуждение электрическим полем амплитудой 1 В/м в направлении оси Y.

Теперь создаём площадку (AddBox) с которой будем распространяться ЭМВ. Эта площадка и является собственно источником ЭМВ.

CSX = AddBox(CSX,'excitation',0,[-10 -10 0],[10 10 0]);

На этом описание геометрии завершено. После того как мы описали геометрию, нужно создать сечение, в котором мы будем наблюдать распространение ЭМВ. Это делается при помощи функций AddDump() и AddBox().

CSX = AddDump(CSX,'Et');
CSX = AddBox(CSX,'Et',0,[-10 0 -10],[10 0 30]);

Теперь подготавливаем временный каталог для хранения результатов расчётов и просматриваем геометрию при помощи CSXCAD.

mkdir('tmp');
WriteOpenEMS('/tmp/tmp.xml',FDTD,CSX);
CSXGeomPlot('/tmp/tmp.xml');
invoking AppCSXCAD, exit to continue script...
QCSXCAD - disabling editing

Всё, модель нашей структуры готова. Можно запускать симулятор. Если всё нормально, то мы увидим следующий отчёт:

RunOpenEMS('tmp','/tmp/tmp.xml','');
 ---------------------------------------------------------------------- 
 | openEMS 64bit -- version v0.0.32-14-g63adb58
 | (C) 2010-2013 Thorsten Liebig <thorsten.liebig@gmx.de>  GPL license
 ---------------------------------------------------------------------- 
        Used external libraries:
                CSXCAD -- Version: v0.5.2-15-gcb5b3cf
                hdf5   -- Version: 1.8.13
                          compiled against: HDF5 library version: 1.8.13
                tinyxml -- compiled against: 2.6.2
                fparser
                boost  -- compiled against: 1_54
                vtk -- Version: 5.10.1
                       compiled against: 5.10.1

Create FDTD operator (compressed SSE + multi-threading)
FDTD simulation size: 21x21x41 --> 18081 FDTD cells 
FDTD timestep is: 1.92583e-09 s; Nyquist rate: 25 timesteps @1.03851e+07 Hz
Excitation signal length is: 100 timesteps (1.92583e-07s)
Max. number of timesteps: 100 ( --> 1 * Excitation signal length)
Create FDTD engine (compressed SSE + multi-threading)
Running FDTD engine... this may take a while... grab a cup of coffee?!?
Time for 100 iterations with 18081 cells : 0.1624 sec
Speed: 11.1336 MCells/s

Симуляция завершена, и можно просмотреть результат. Запускаем Paraview. Затем выбираем File->Open и идём во временный каталог, где хранятся результаты симуляции. Там открываем файл Et_.vtr. Этот файл содержит информацию о результате расчёта процесса распространения ЭМВ во времени. Вот, что нужно открывать, путь к файлу у вас будет другой:



Теперь видим в окне Paraview плоскость, которая является сечением в котором мы смотрим амплитуду ЭМВ.



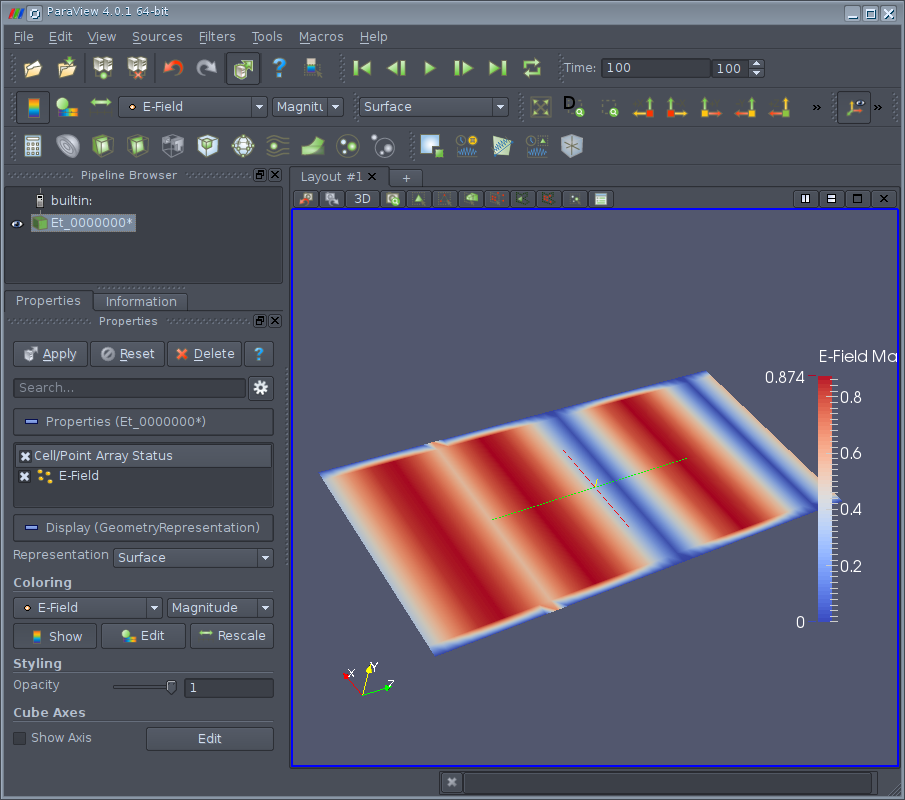
Чтобы визуализировать амплитуду ЭМВ, нужно в выпадающем списке Coloring выбрать E-field (по умолчанию там стоит SolidColor) и затем отобразить цветовую легенду (нажать Show). Теперь мы видим амплитуду ЭМВ в момент времени t=0. В начальный момент времени амплитуда ЭМВ тоже равна нулю во всём пространстве, поэтому вся плоскость будет закрашена в один цвет. Чтобы посмотреть распределение ЭМВ нужно установить время отличное от нуля и нажать кнопку Rescale. Теперь на плоскости отобразится распределение амплитуды ЭМВ.



Можно также запустить анимацию и просмотреть процесс распространения ЭМВ во времени. Как и следовало ожидать ЭМВ распространяется в обоих направлениях от плоскости-источника.

В результате мы смоделировали во временной области процесс распространения ЭМВ в некоторой области пространства. В заключении скрипт Octave/Matlab целиком:

FDTD = InitFDTD('NrTS',1000,'EndCriteria',0,'OverSampling',1);
FDTD = SetSinusExcite(FDTD,10e6);
FDTD = SetBoundaryCond(FDTD,{'PMC' 'PMC' 'PEC' 'PEC' 'MUR' 'MUR'});
CSX = InitCSX();
mesh.x = -10:10;
mesh.y = -10:10;
mesh.z = -10:30;
CSX = DefineRectGrid(CSX,1,mesh);
CSX = AddExcitation(CSX,'excitation',0,[0 1 0]);
CSX = AddBox(CSX,'excitation',0,[-10 -10 0],[10 10 0]);
CSX = AddDump(CSX,'Et');
CSX = AddBox(CSX,'Et',0,[-10 0 -10],[10 0 30]);
mkdir('tmp');
WriteOpenEMS('/tmp/tmp.xml',FDTD,CSX);
CSXGeomPlot('/tmp/tmp.xml');
RunOpenEMS('tmp','/tmp/tmp.xml','');

Ссылка на предыдущую статью по openEMS: habrahabr.ru/post/255317

Сайт проекта openEMS: openems.de