В данной публикации представлена инструкция по моделированию электрической цепи методом переменных состояния.
Эта публикация для того, чтобы был на русском языке хотя бы один how2 по моделированию электрических схем этим методом. В своё время я очень много гуглил и ни разу мне не попадалось нормального материала. Все методички и учебники содержали в себе только теорию. Вдобавок ни в одном, из найденных мной материалов, не было полного цикла решения:
схема ? уравнения ? численное решение ? графики.
Собственно, это и есть алгоритм действий.
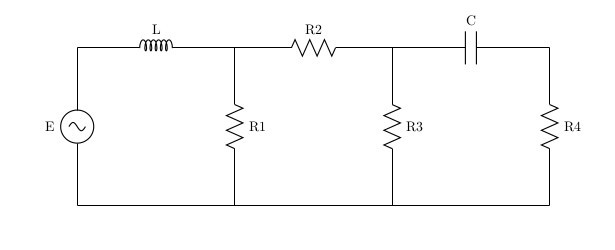
Схема есть, теперь нужно составить уравнения, используя законы Ома и Кирхгофа.
Компонентные уравнения:
Контурные уравнения:
Узловые уравнения:
Теперь нужно вывести дифференциальные уравнения. Отмечу, что в этом методе за переменные состояния принято брать заряды конденсаторов и потокосцепления индуктивностей. Зная эти величины, можно вывести любые напряжения и токи узлов и ветвей. Также:
- Уравнения должны быть независимыми;
- В уравнения должны входить только переменные состояния и источников; все остальные переменные должны быть выражены через переменные состояния;
- В левую часть каждого уравнения должна войти первая производная из переменных состояния; в правой части не должно быть производных.
Выведем первое дифференциальное уравнение:
Подставим ток конденсатора в уравнение напряжения катушки:
Преобразуя уравнение, получим первое дифференциальное уравнение:
Выведем второе дифференциальное уравнение:
Теперь у нас есть система дифференциальных уравнений, которые можно решить численно:
Воспользуемся методом Эйлера
import numpy as np
import matplotlib.pyplot as plt
#Input voltage amplitude
AMP = 21.0
#Active components
r1 = 2000.0; r2 = 10.0; r3 = 10.0; r4 =2000.0;
#Reactive components
c=0.0001; l=0.06;
#Time components
T=0.01; t0=0.0; step=T/1000;
tf=T*10
steps=int(tf/step);
#Input voltage
def E(t):
n=int(t/T)
if ((t >= n*T )and(t <= n*T + T/2)):
return AMP
else:
return 0.0
time = np.arange(t0, tf, step)
ul = []; il = []; uc = []; ic = []; y = [];
for i in range(0, steps, 1):
y.append(E(time[i]))
def dIl_dt(t):
return float((1.0/l)*(E(t) - (r1/((r1+r2)*(r3+r4)+r3*r4) * (il[int(t/step)]*(r2*(r3+r4)+r3) - uc[int(t/step)]*r3))))
def dUc_dt(t):
return float((1.0/c)* (r3/(r3+r4)) * (il[int(t/step)]-(E(t)-ul[int(t/step)])/r1 - uc[int(t/step)]/r3))
#Start condition
ul.append(E(0)); il.append(0.0); uc.append(0.0); ic.append(0.0);
#Euler method
for i in range(1, steps, 1):
il.append(il[i-1] + step*dIl_dt(time[i-1]))
uc.append(uc[i-1] + step*dUc_dt(time[i-1]))
ul.append(l*dIl_dt(time[i]))
ic.append(c*dUc_dt(time[i]))
plt.figure("charts")
e = plt.subplot(311)
e.plot(time, y)
e.set_xlabel('time (s)')
e.set_ylabel('E(t), (V)', color='b')
plt.grid(True)
UL = plt.subplot(312)
UL.plot(time, ul)
UL.set_xlabel('time (s)')
UL.set_ylabel('Ul(t), (V)', color = 'b')
IL = UL.twinx()
IL.plot(time, il, 'r')
IL.set_ylabel('Il(t), (A)', color = 'r')
plt.grid(True)
UC = plt.subplot(313)
UC.plot(time, uc)
UC.set_xlabel('time (s)')
UC.set_ylabel('Uc(t), (V)', color = 'b')
IC = UC.twinx()
IC.plot(time, ic, color = 'r')
IC.set_ylabel('Ic(t), (A)', color = 'r')
plt.grid(True)
plt.show()
Результаты моделирования:
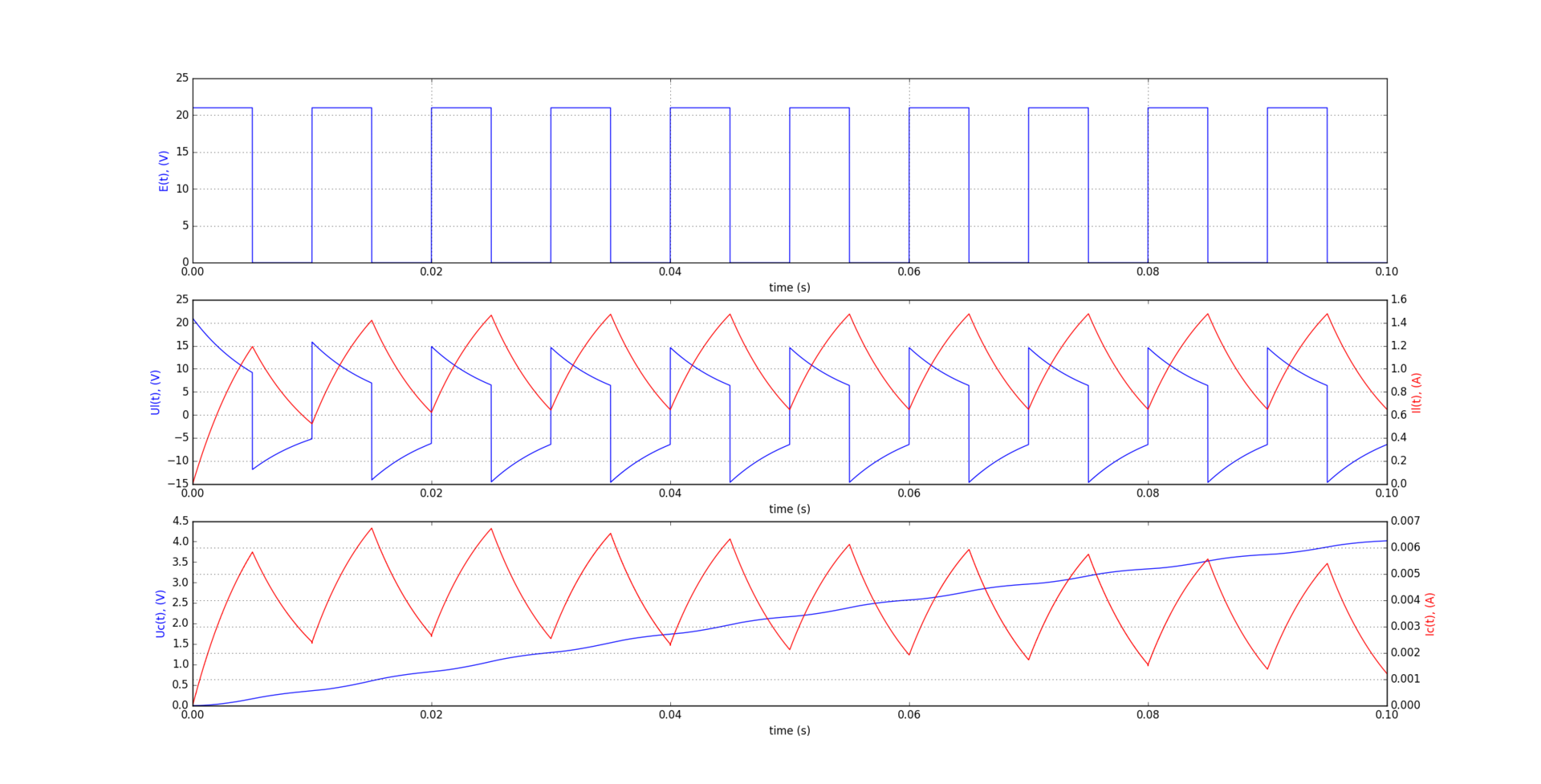
Использовать для реальных расчётов лучше другие методы решения дифур, а для получения графиков напряжений и токов элементов для самообучения достаточно и простейшего метода Эйлера. В электронике самый распространённый метод Ньютона-Рафсона- в большинстве САПР используется именно этот метод.
Из литературы советую книги Матханова П.Н. и Зевеке Г.В.
А методички всяких политехов (МГТУ, Питерский, Томский и т.п.) и подобный материал легче выкинуть, чем понять, что там написано. Здесь очень к месту крылатая фраза: «упрощять- сложно, усложнять- легко».
Комментарии (29)

maisvendoo
12.03.2017 14:42+1Эта публикация для того, чтобы был на русском языке хотя бы один how2 по моделированию электрических схем этим методом.
Не хочу придираться, но достаточно открыть любую русскую книгу по теории управления, чтобы увидеть там
— уравнение в пространстве состояний, которое получено у Вас и к которому сводятся все линейные системы. Собственно Ваш текст есть описание формализации к данной системе конкретной задачи из теории цепей, что в целом полезно, но новизны не несет
maisvendoo
12.03.2017 14:47+9Тем не менее плюсую, так как детально описан путь от постановки задачи до кода, а это большое подспорье для новичка, образовательная польза от статьи на лицо.
Да, и уберите в формулах символы вариаций (дельты) и замените на d. Вариация и дифференциал — разные вещи
htonych
12.03.2017 21:04+2Для новичка уж больно сложновато, на мой взгляд, для новичка, есть такой полезный ресурс как everycircuit.com

GreySS
12.03.2017 17:40Эта публикация для того, чтобы был на русском языке хотя бы один how2 по моделированию электрических схем этим методом.
А могли бы подсказать литературу how2 по моделированию на англ языке. Спасибо.

oklas
12.03.2017 22:12+2А методички всяких политехов (...) и подобный материал легче выкинуть, чем понять, что там написано. Здесь очень к месту крылатая фраза: «упрощять- сложно, усложнять- легко»
Вуз конечно вузу рознь и методичка методичке тем более рознь. Некоторые может и можно выбросить. А некоторые как раз наоборот упрощены и включают всё самое необходимое изложеное понятным образом. От автора или коллектива авторов зависит. Не без причины же говорят "методичка есть — идем сдавать". И не только сдавать но и для практической работы. Наши все достижения в том числе самые передовые в мире созданы людьми учившимися по методичкам и писавшими эти методички.

gazpar
13.03.2017 08:18Мне не попадались такие материалы.
Не без причины же говорят «методичка есть — идем сдавать».
Именно, что сдавать- а не понимать и использовать своё понимание.
Наши все достижения в том числе самые передовые в мире созданы людьми учившимися по методичкам и писавшими эти методички.
Не согласен с этим. Т.к. почти весь современный мир создан на базе трудов учёных, работавших с 30х по 80е годы прошлого века. А эти люди учились в школах по ~5 лет и в университетах ~3-4 года. И я более чем уверен, что учились они по книгам, а не по методичкам. Писать- писали, а сами учились по книгам.
Кстати, можете ради интереса поглядеть на царские учебники по математике и физике. А потом сравнить с теми, по которым Вы учились, а потом с современными. Уверен, Вы будете удивлены, быть может, даже шокированы.
leocat33
13.03.2017 09:14Раньше науки были зело суровы… Как пример:
Арифметика. Леонтий Филлипович Магницкий
Можете задачки посмотреть. И это первые 4 класса обучения!

potan
13.03.2017 15:19А чем плохи готовые, специально заточенные на моделирование, системы, типа универсальной Modelica или специализированной SPICE?

gazpar
13.03.2017 18:12Отсутствием абсолютного контроля над симуляцией(SPICE).
С Modelica не сталкивался.
nikolay_karelin
13.03.2017 21:58Насколько я читал, SPICE симуляторы могут тысячи элементов в цепи обрабатывать… В уже готовом софте.
А какие пределы у вашего подхода?

gazpar
13.03.2017 22:07Почитайте тогда ещё про степень детализации «элементов»(и линейных и нелинейных) и «моделей». А потом про сходимости и точности, с соответствующими алгоритмами.
К примеру, дипломная схема в пике (упрощенная до 9 дифур+ШИМ2) на 15 сек. симуляции моделировалась 1,2-1,5 часа(FX4300+8Gb+SSD+LT-Spice). В сумме в схеме 52 элемента. И это без учёта нагрева и т.п.

Itachi261092
14.03.2017 11:32Будь прокляты те дни, когда в институте мне убогий препод убого преподавал Электротехнику и требовал выполнения лабораторных в Electronic Workbench. Это были без преуменьшения худшие пары за всё время обучения. В этой статье больше понятной информации, чем за 1.5 года занятий у этого препода.

erwin_shrodinger
14.03.2017 18:15i2= U2/R2 = U1/(R1 + R3).
Из этого получаем, что i2 = i3. Это ниоткуда не следует
Ошибка?
gazpar
14.03.2017 18:16i2= U2/R2 = U1/(R1 + R3)
Неправильно, в статье так:
i2= U2/R2 = U1/(R2 + R3)
erwin_shrodinger
14.03.2017 18:24да, я тут опечатался.
i2= U2/R2 = U1/(R2 + R3) — это то, что я и имел в виду. это неверно
gazpar
14.03.2017 18:43нет- это верно.
i2=u2/r2;
u2=r2*u1/(r2+r3);
i2--->(r2*u1/(r2+r3))/r2=u1/(r2+r3)

erwin_shrodinger
15.03.2017 11:35u2=r2*u1/(r2+r3)
Да откуда ты это взял?
gazpar
15.03.2017 18:33не ты, а Вы
ключевые слова «делители напряжения» и «делители тока»
erwin_shrodinger
16.03.2017 17:53+1Это бы было так [ u2=r2*u1/(r2+r3) ], если бы не было C и R4 в цепи.
Они влияют на суммарное сопротивление правой части, а поэтому в знаменателе будет не (R2 + R3), а ещё и некоторым образом сопротивления C и R4. Это во-первых.
Во-вторых. Допустим, что ваш вариант правильный. Проверяем.
U2/R2 = U1/ (R2 + R3)
U1 = U2 * (R2 + R3) / R2
U1 = U2 + U2*R3/R2
U2 = i2 * R2 => (из уравнения выше) U1 = U2 + i2 * R3
По правилу Кирхгофа, которые вы написали чуть выше:
U1 — U2 — U3 = 0 => U1 = U2 + U3
Но мы уже получили, что U1 = U2 + i2*R3
Значит, из последних 2 уравнений следует, что U3 = i2 * R3, но U3 = i3 * R3 (это вы тоже писали)
Следовательно i2 * R3 = i3 * R3, а i2 = i3 (?)
В общем случае это неверно.
Можете это прокомментировать?


Uranix
Если вы используете Python, почему бы не взять любой интегратор из scipy.integrate? Избавились бы от жутких
А Ньютон-Рафсон — это вообще не метод решения ОДУ, это метод решения нелинейных алгебраических (систем) уравнений.