Года четыре назад, в универе услышал о таком методе оптимизации, как генетический алгоритм. О нем везде сообщалось ровно два факта: он клёвый и он не работает. Вернее, работает, но медленно, ненадежно, и нигде его не стоит использовать. Зато он красиво может продемонстрировать механизмы эволюции. В этой статье я покажу красивый способ вживую посмотреть на процессы эволюции на примере работы этого простого метода. Нужно лишь немного математики, программирования и все это приправить воображением.

Кратко об алгоритме

Итак, что же такое генетический алгоритм? Это, прежде всего, метод многомерной оптимизации, т.е. метод поиска минимума многомерной функции. Потенциально этот метод можно использовать для глобальной оптимизации, но с этим возникают сложности, опишу их позднее.

Сама суть метода заключается в том, что мы модулируем эволюционный процесс: у нас есть какая-то популяция (набор векторов), которая размножается, на которую воздействуют мутации и производится естественный отбор на основании минимизации целевой функции. Рассмотрим подробнее эти процессы.

Итак, прежде всего наша популяция должна размножаться. Основной принцип размножения — потомок похож на своих родителей. Т.е. мы должны задать какой-то механизм наследования. И лучше будет, если он будет включать элемент случайности. Но скорость развития таких систем очень низкая — разнообразие генетическое падает, популяция вырождается. Т.е. значение функции перестает минимизироваться.

Для решения этой проблемы был введен механизм мутации, который заключается в случайном изменении каких-то особей. Этот механизм позволяет привнести что-то новое в генетическое разнообразие.
Следующий важный механизм — селекция. Как было сказано, селекция — отбор особей (можно из только родившихся, а можно из всех — практика показывает, что это не играет решающую роль), которые лучше минимизируют функцию. Обычно отбирают столько особей, сколько было до размножения, чтобы из эпохи в эпоху у нас было постоянное количество особей в популяции. Также принято отбирать «счастливчиков» — какое-то число особей, которые, возможно, плохо минимизируют функцию, но зато внесут разнообразия в последующие поколения.

Этих трех механизмов чаще всего недостаточно, чтобы минимизировать функцию. Так популяция вырождается — рано или поздно локальный минимум забивает своим значением всю популяцию. Когда такое происходит, проводят процесс, называемый встряской (в природе аналогии — глобальные катаклизмы), когда уничтожается почти вся популяция, и добавляются новые (случайные) особи.

Вот описание классического генетического алгоритма, он прост в реализации и есть место для фантазии и исследований.

Постановка задачи

Итак, когда я уже решил, что хочу попробовать реализовать этот легендарный (пусть и неудачливый) алгоритм, речь зашла о том, что же я буду минизимировать? Обычно берут какую-нибудь страшную многомерную функцию с синусами, косинусами и т.д. Но это не очень интересно и вообще не наглядно. Пришла одна незатейливая идея — для отображения многомерного вектора отлично подходит изображение, где значение отвечает за яркость. Таким образом, мы можем ввести простую функцию — расстояние до нашего целевого изображения, измеряемое в разности яркости пикселей. Для простоты и скорости я взял изображения с яркостью 0, либо 255.

С точки зрения математики такая оптимизация — сущий пустяк. График такой функции представляет собой огромную многомерную «яму» (как трехмерный парабалоид на рисунке), в которую неизбежно скатишься, если идти по градиенту. Единственный локальный минимум является глобальным. .

Проблема только в том, что уже близко к минимуму количество путей, по которым можно спуститься вниз сильно сокращается, а всего у нас столько направлений, сколько измерений (т.е. количество пикселей). Очевидно, что решать эту задачу при помощи генетического алгоритма не стоит, но мы можем посмотреть на интересные процессы, протекающие в нашей популяции.

Реализация

Были реализованы все механизмы, описанные в первом параграфе. Размножение проводилось простым скрещиванием случайных пикселей от «мамы» и от «папы». Мутации производились путем изменения значения случайного пикселя у случайной особи на противоположное. А встряска производилась, если минимум не меняется на протяжении пяти шагов. Тогда производится «экстремальная мутация» — замена происходит более интенсивно, чем обычно.

В качестве исходных картинок я брал нонограмы («японские сканворды»), но, по правде говоря, можно брать просто черные квадраты — нет абсолютно никакой разницы. Ниже показаны результаты для нескольких изображений. Здесь для всех, кроме «домика», количество мутаций было 100 в среднем на каждую особь, особей в популяции было 100, при размножении популяция увеличивалась в 4 раза. Счастливчиков было 30% в каждой эпохе. Для домика значения были выбраны меньшие (30 особей в популяции, мутаций по 50 на особь).



Экспериментально я установил, что использование «счастливчиков» в селекции понижает скорость стремления популяции к минимуму, но зато помогает выбираться из стагнации — без «счастливчиков» стагнация будет постоянна. Что можно увидеть из графиков: левый график — развитие популяции «фараона» со счастливчиками, правый — без счастливчиков.



Таким образом, мы видим, что этот алгоритм позволяет решить поставленную задачу, пусть и за очень долгое время. Слишком большое количество встрясок, в случае больших изображений, может решить большее количество особей в популяции. Оптимальный подбор параметров для разных размерностей я оставляю за рамками данного поста.

Глобальная оптимизация

Как было сказано, локальная оптимизация — задача довольно тривиальная, даже для многомерных случаев. Гораздо интересней посмтреть, как будет алгоритм справляться с глобальной оптимизацией. Но для этого нужно сначала построить функцию со множеством локальных минимумов. А это в нашем случае не так сложно. Достаточно брать минимум из расстояний до нескольких изображений (домик, динозаврик, рыбка, кораблик). Тогда первоначальный алгоритм будет «скатываться» в какую-то случайную ямку. И можно просто запускать его несколько раз.

Но есть более интересное решение данной проблемы: можно понять, что мы скатились в локальный минимум, сделать сильную встряску (или вообще инициировать особи заново), и в дальнейшем добавлять штрафы при приближении к известному минимуму. Как видно, картинки чередуются. Замечу, что мы не имеем права трогать исходную функцию. Но мы можем запоминать локальные минимумы и самостоятельно добавлять штрафы.

На этой картинке изображен результат, когда при достижении локального минимума (сильная стагнация), популяция просто вымирает.



Здесь популяция вымирает, и добавляется небольшой штраф (в размере обычного расстояния до известного минимума). Это сильно снижает вероятность повторов.



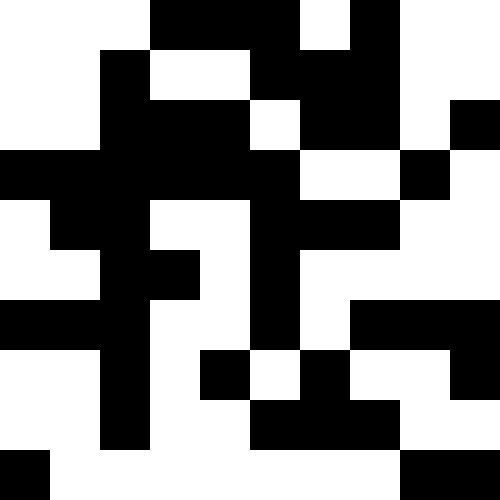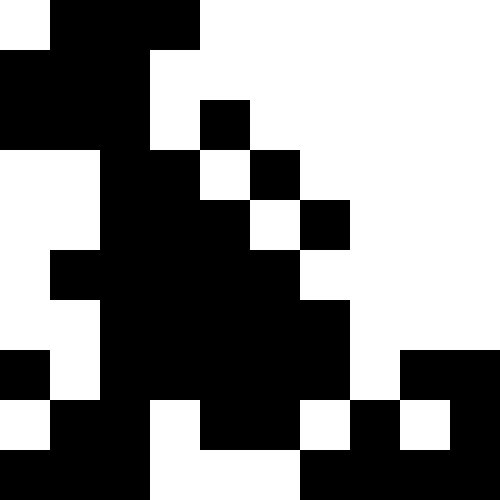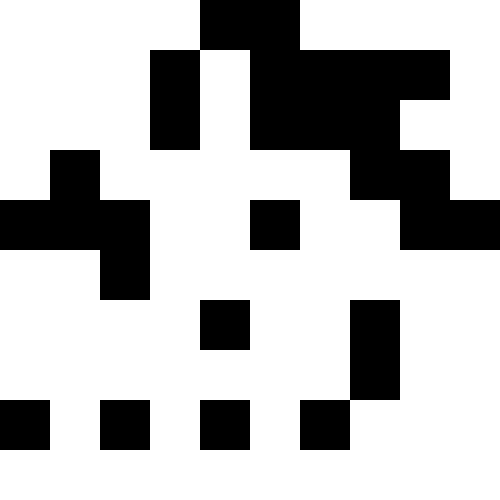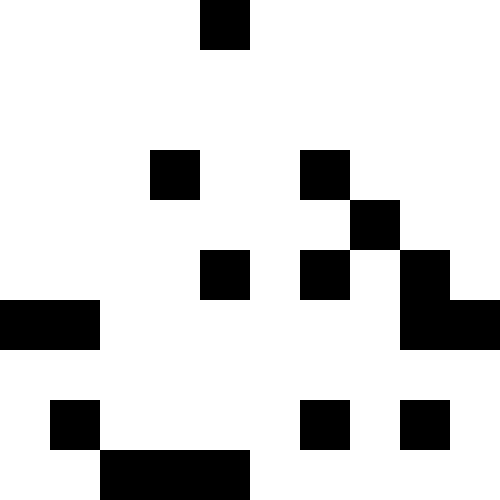
Более интересно, когда популяция не вымирает, а просто начинает подстрариваться под новые условия (след. рисунок). Это достигается при помощи штрафа в виде 0.000001 * sum ^ 4. В таком случае, новые образы становятся немного зашумлены:



Этот шум устраняется путем ограничения штрафа в max( 0.000001 * sum ^ 4, 20). Но мы видим, что четвертого локального минимума (динозавра) достичь не удается — скорее всего, потому, что он слишком близко расположен к какому-то другому.

Биологическая интерпретация

Какие же выводы мы можем сделать из, не побоюсь этого слова, моделирования? Прежде всего, мы видим, половое размножение — важнейший двигатель развития и приспосабливаемости. Но только его не достаточно. Роль случайных, маленьких изменений чрезвычайна важна. Именно они обеспечивают возникновение новых видов животных в процессе эволюции, а у нас обеспечивает разнообразие популяции.

Важнейшую роль в эволюции Земли играли природные катаклизмы и массовые вымирания (вымирания динозавров, насекомых и т.д. — крупных всего было около десяти — см. диаграмму ниже). Это было подтверждено и нашим моделированием. А отбор «счастливчиков» показал, что самые слабые организмы на сегодня способны в будущем стать основой для последующих поколений.

Как говорится, все как в жизни. Этот метод «сделай эволюцию сам» наглядно показывает интересные механизмы и их роль в развитии. Конечно, существует много более стоящих эволюционных моделей (основанных, конечно, на дифурах), учитывающих больше факторов, более приближенные к жизни. Конечно, существуют более эффективные методы оптимизации.

P.S.

Писал программу на Matlab (вернее, даже на Octave), потому что тут все — голимые матрицы, и есть инструменты для работы с картинками. Исходный код прилагается.