29.03.2017 19:19
LenaV 0 89 Источник

Не прошло и полгода, как мы завершаем цикл статей об адаптивном обучении на Stepik! А, нет, прошло… Но я рада наконец представить вашему вниманию заключительную статью о том, зачем вообще нужно адаптивное обучение, как оно реализовано на Stepik и причём тут шахматы.



Введение


Однажды мы решили рассказать на Хабре, как устроена система адаптивных рекомендаций на Stepik.org. Первые две статьи этого цикла были написаны ещё летом по горячим следам моего бакалаврского диплома на матмехе СПбГУ, первая была в целом про рекомендательные системы в онлайн-образовании, во второй мы немного заглянули под капот и рассказали об архитектуре нашей рекомендательной системы. Третья часть, в которой мы наконец дойдём собственно до адаптивных рекомендаций, писалась плохо, во многом потому, что эта часть платформы меняется очень быстро. Но теперь я готова опубликовать и её.


Зачем нужна адаптивность?


Когда говорят о преимуществах онлайн-обучения, часто в их числе упоминают массовость. Действительно, сложно сравнивать пропускную способность очного курса в университете, пусть даже потокового, и массового онлайн-курса, практически не имеющего ограничений для масштабирования — разница в размере аудитории составит порядки.


Но эта черта является также и недостатком онлайн-образования: в случае занятий в аудитории преподаватель может подстраивать свои лекции под студентов: провести опрос в начале семестра, следить на занятиях, все ли понимают материал, даже общаться с отдельными студентами лично, если они что-то не усвоили или, наоборот, хотят больше углубиться в какие-то темы. Разумеется, в случае массового онлайн-курса ресурсов преподавателя на подобное взаимодействие не хватает, а студенты оказываются в строгих рамках линейно составленного курса без возможности подробнее разобрать сложные задания или пропустить простые.


Тем не менее, существуют способы реализовать что-то подобное и в автоматическом (массовом) режиме. Эти способы можно разделить на три основные группы:


  1. Дифференцированное обучение. Самый простой способ подстроить материал под уровень знаний учащегося: преподавателем заранее создаётся несколько фиксированных учебных траекторий разной сложности, а студент выбирает для себя подходящую и далее учится по ней в обычном, линейном режиме. Например, серия учебников для разного уровня знания языка.
  2. Персонализированное обучение. В этом случае траектория строится в процессе обучения в зависимости от результатов учащегося в промежуточных тестированиях. Правила о том, в какой момент проводить тестирование и что советовать изучать дальше при разных результатах, заранее задаёт преподаватель. Получается что-то похожее на дерево решений, по которому студенты будут идти по-разному в зависимости от своих успехов, но само дерево должно быть продумано и создано преподавателем.
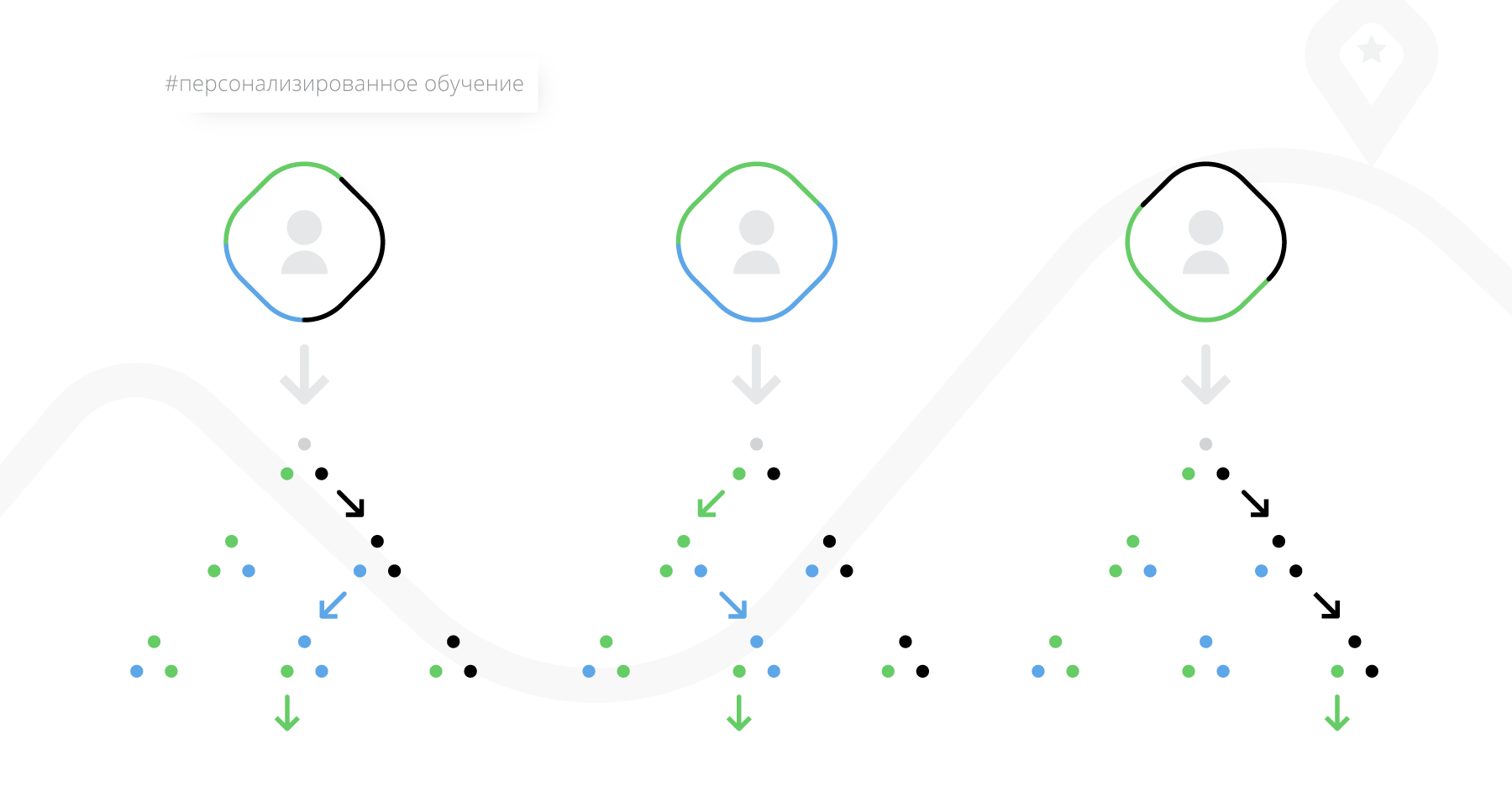
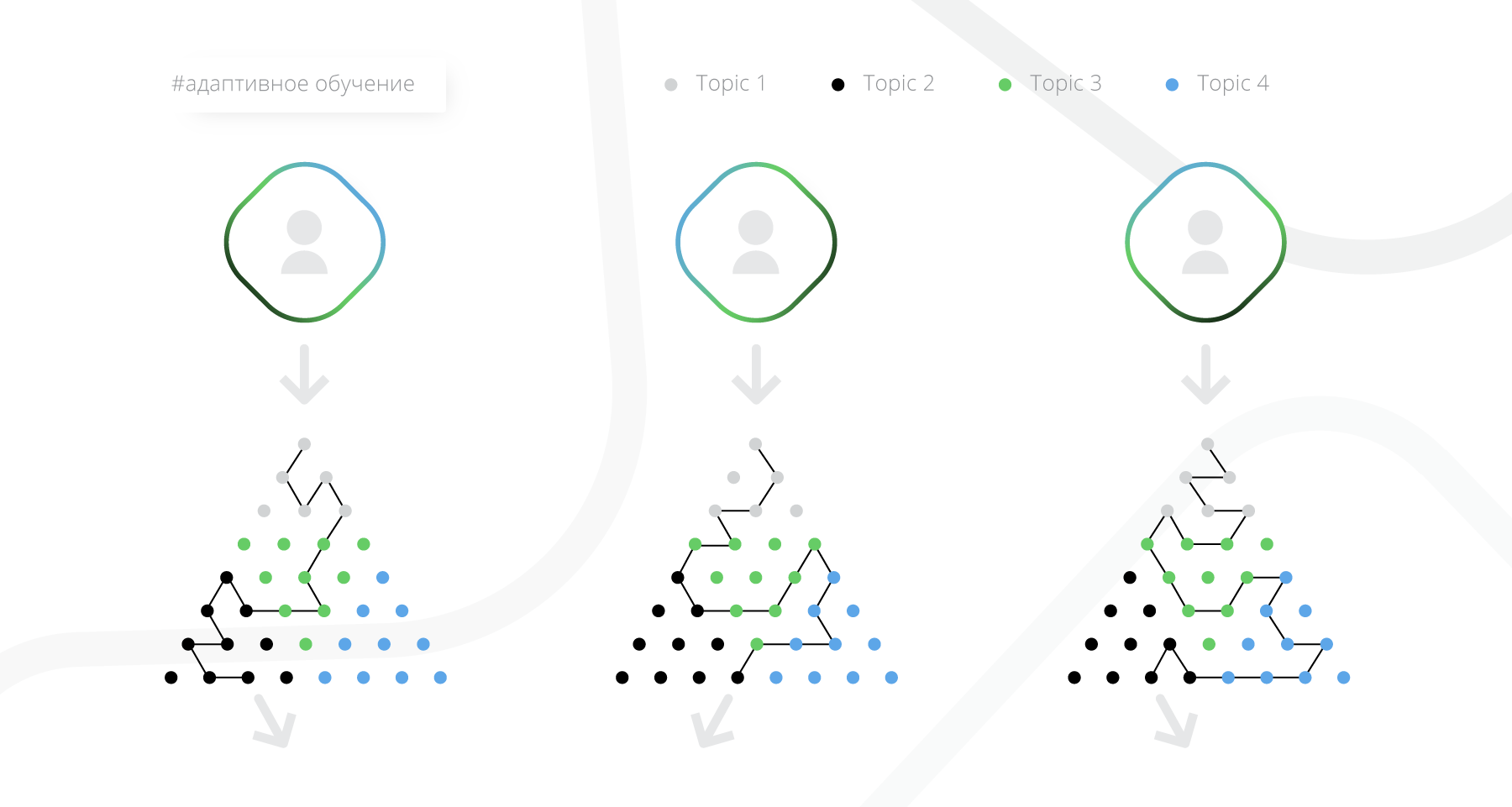
  3. Адаптивное обучение. Самая интересная с точки зрения алгоритмов группа. Траектория также строится в процессе обучения, но не требует начальной разметки от преподавателя, а использует максимум информации о том, как студент изучает материал и как этот материал изучали до него. Далее в статье об этом будет рассказано подробнее.

Механизмы адаптивного обучения


Адаптивное обучение на Stepik сделано в виде рекомендательной системы, которая советует пользователю, какой урок ему стоит изучить следующим, в зависимости от его предыдущих действий. Пока рекомендации даются в рамках материалов выбранного курса (например, тренажер по Python), но в скором будущем станут доступны также рекомендации в рамках произвольной темы (например, C++ или интегралы). В перспективе любую тему можно будет изучить в адаптивном режиме.


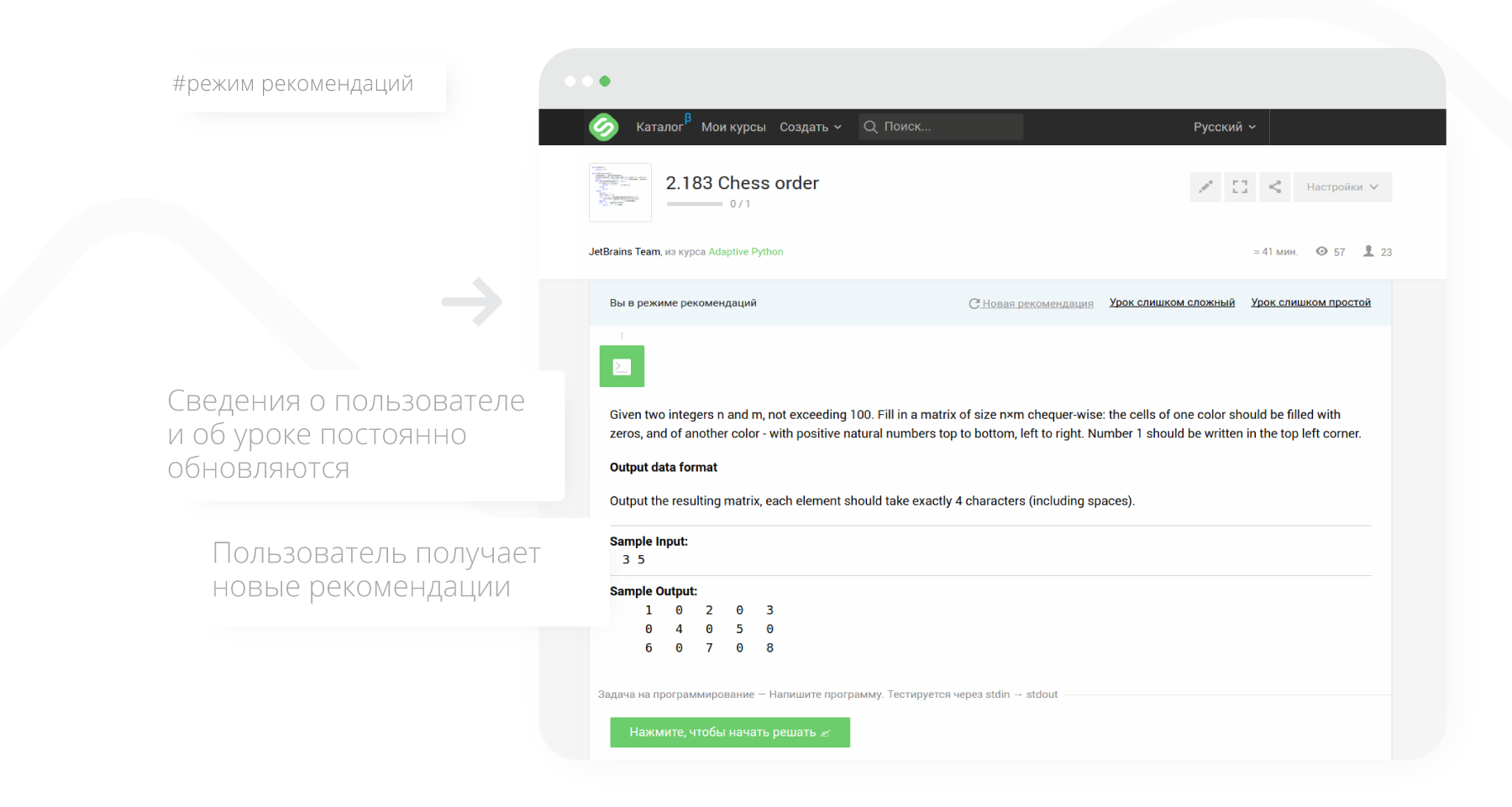
Зарегистрированному пользователю для начала обучения в адаптивном режиме достаточно нажать кнопку “Учиться” в адаптивном курсе (она станет доступна после записи на курс).


Получив рекомендованный к обучению материал (урок), пользователь может отреагировать на него одним из трех способов:


  1. пройти урок (решить задачи в нём),
  2. пометить урок как слишком простой,
  3. пометить урок как слишком сложный.

После получения реакции сведения о знаниях пользователя и о сложности урока обновляются, и пользователь получает новую рекомендацию.



Для адаптивных рекомендаций используется два метода (“хендлера”): на основе сложности и на основе зависимостей между темами (подробнее о хендлерах можно почитать во второй статье цикла).


Под капотом рекомендаций на основе сложности лежит две идеи:


  1. Item Response Theory. Эта психометрическая парадигма с непереводимым на русский язык названием может быть сформулирована очень просто: вероятность, что учащийся решит задачу, выражается как некоторая функция от параметров учащегося и задачи. В качестве параметров можно использовать, например, как-то вычисленные уровень знаний пользователя и сложность задачи, а также то, насколько мы уверены в этих значениях.
  2. Шахматный рейтинг Эло. Модель для оценки рейтинга шахматистов, разработанная Арпадом Эло в 1960-х годах, работает следующим образом: каждому новому игроку назначается рейтинг по умолчанию (например, ноль), а затем после каждой игры рейтинги обоих игроков обновляются. Для этого сначала вычисляется матожидание результата игры для каждого из игроков ($inline$\mathbb{E}_A= 0$inline$ в случае проигрыша игрока A, $inline$1$inline$ — в случае победы, $inline$0.5$inline$ — ничьи), а затем рейтинги обновляются в зависимости от разницы между предсказанным результатом игры и фактическим.
    Формула для предсказания результата $inline$\mathbb{E}_A = 1 / ({1 + 10^{\frac{R_B - R_A}{400}}})$inline$,
    для обновления рейтинга $inline$R_A^\prime = R_A + K \cdot (S_A - \mathbb{E}_A)$inline$,
    где $inline$R_A$inline$, $inline$R_B$inline$ — рейтинги игроков A и B, $inline$R_A^\prime$inline$ — обновленный рейтинг игрока A, $inline$S_A$inline$ — фактический результат игры для игрока A. Коэффициент $inline$K$inline$ характеризует нашу уверенность в оценке рейтинга: если мы еще мало знаем об игроке, его рейтинг должен меняться быстро, но когда речь идет об опытном мастере, одна игра, далекая от предсказания, не должна сильно изменить рейтинг.

В результате слияния этих двух идей получаем следующую модель работы системы. Пользователей и уроки мы рассматриваем как “игроков”, реакцию пользователя на рекомендацию урока — как результат “игры”, а предсказываем мы этот результат на основе некоторых параметров учащегося и урока. Основные черты этой модели мы взяли из научной статьи о Maths Garden, сервисе для изучения арифметики для детей. Для рекомендаций мы подбираем такие уроки, вероятность решить которые для пользователя близка к оптимальной.


Помимо сложности уроков мы хотим учитывать также разметку контента темами. Мы используем граф знаний из Wikidata, и даём возможность авторам уроков тегировать их темами двух типов:


  1. темы, к которым этот урок относится (которые в нём разъясняются),
  2. темы, знание которых необходимо для понимания этого урока.

Например, в случае, если пользователь пометил урок как слишком сложный, мы можем посоветовать ему изучить темы, которые необходимы для данного урока.


Метрики


Основные метрики для оценки качества адаптивных рекомендаций — это, во-первых, доля решённых уроков от числа рекомендованных (по сути retention), и во-вторых, разница между предсказанным результатом решения и реальным (из модели на основе шахматного рейтинга).


Доля решённых уроков больше говорит о том, насколько полезными и подходящими по сложности пользователи считают рекомендации. Эту метрику мы вычисляем регулярно по итогам последних 7 дней, и она с конца прошлого года выросла с 60 до 80 процентов.


Вторая же метрика, ошибка предсказания, скорее характеризует точность внутренней машинерии адаптивной системы. При этом её сложнее интерпретировать, ведь изменяя модели для предсказания реакции пользователя и для оценки фактического поведения пользователей, мы можем получить значительные изменения в этой метрике, которые едва ли будут показывать, лучше стала модель или хуже по сравнению с предыдущей версией. Потому что оцениваем ошибку мы теперь тоже по-другому.


Например, если раньше значения predicted_score и real_score лежали в интервале $inline$[-1, 1]$inline$, а в новой версии — в $inline$[-100, 100]$inline$, абсолютные значения ошибки драматично вырастут, но это не будет значить, что нужно срочно откатываться. Разумеется, пример утрированный, но подобные причины изменения ошибки нужно учитывать при анализе метрик.


Как я писала, эти две метрики являются основными, но не исчерпывающими. Также мы отслеживаем состояние системы по количеству запросов рекомендаций (порядка нескольких тысяч в неделю), по скользящему среднему ошибки предсказания по нескольким дням (помогает выявить тенденцию к улучшению или ухудшению, сгладив пики), по времени обработки запроса новой рекомендации (ну по этому параметру всегда есть к чему стремиться :) ).


Также мы проводим A/B-тестирование для сравнения работы разных моделей. Тогда, помимо вышеперечисленных метрик для ежедневного мониторинга, дашборд может расширяться специфичными метриками для конкретного эксперимента. Тем не менее, решение о том, какую модель оставлять, обычно принимается исходя из основных метрик.


История адаптивного проекта


  • 1 марта 2016 — появился первый прототип адаптивных рекомендаций в Stepik (который в те времена ещё назывался Stepic)
  • 21 марта 2016 — начало бета-тестирования (русскоязычный задачник по Python)
  • 11 августа 2016 — интеграция адаптивной системы в PyCharm Edu 3, инструмент для обучения языку Python от JetBrains
  • Сентябрь 2016 — пик активности пользователей в связи с тем, что за достижение определённого уровня “адаптивных” знаний по Python давалась скидка на обучение программированию по онлайн-программе Computer Science Center и Академического университета. Исправили несколько смешных багов.
  • Декабрь 2016 – март 2016 — конкурс на создание адаптивного контента, о котором мы уже подробно писали на Хабре.

Заключение


В этой статье я рассказала об общих чертах системы адаптивных рекомендаций на платформе Stepik. За кадром осталось многое: как мы предсказываем результат решения студентом материала, как мы оцениваем реальное поведение, а также каким образом обновляем оценки знаний пользователя и сложности урока. Возможно однажды на хабрахабре появятся статьи и об этом, но сейчас эти части системы меняются быстрее, чем их можно успеть описать.


Тем не менее, надеюсь, вам было интересно читать эту статью. Буду рада ответить на ваши вопросы в личных сообщениях или комментариях.

Поделиться с друзьями
-->

Комментарии (0)