04.08.2017 09:13
PatientZero 11 8900 Источник
image

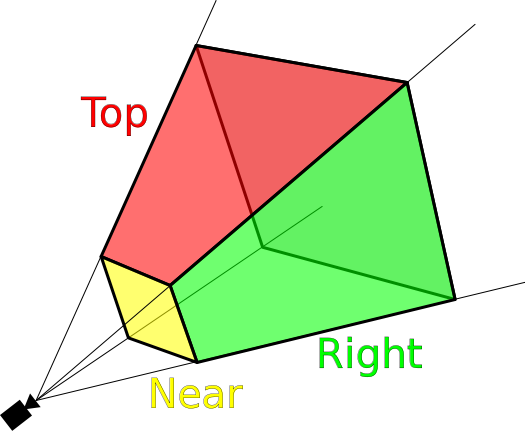
Часть 1: точки, векторы и базовые принципы


Современные трёхмерные игровые движки, используемые в крупнейших проектах — это тонкая смесь математики и программирования. Многие программисты игр признают, что всецело понять их очень непросто. Если вам не хватает опыта (или профессионального образования, как мне), эта задача становится ещё более сложной. Я хочу познакомить вас с основами графических систем 3D-движков.

В этой части мы рассмотрим точки и векторы, а также всё интересное, что с ними связано. Если вы владеете основами алгебры (переменные и математика переменных) и информатики (основы любого объектно-ориентированного языка), то сможете разобраться в этой статье. Но учтите, некоторые из тем будут довольно сложными.

Основные систем координат


Начнём с азов. Для трёхмерной графики требуется концепция трёхмерного пространства. Наиболее часто из всех видов пространств используется декартово пространство, которое позволяет нам применять декартовы координаты (стандартная запись $(x,y)$ и двухмерные графики, которые изучают в большинстве школ).


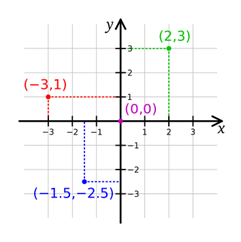
Проклятье, отравляющее жизнь многим школьникам

Трёхмерное декартово пространство даёт нам оси x, y и z (описывающие положение по горизонтали, вертикали и в глубину). Координаты любой точки в этом пространстве обозначаются как несколько чисел (в нашем случае три числа, потому что у нас три оси). На двухмерной плоскости запись обозначается как $(x,y)$, а в трёхмерном пространстве — как $(x,y,z)$. Эта запись (кортеж) показывает положение точки относительно исходной точки пространства (которая обычно обозначается как $(0,0,0)$.

Подсказка: кортеж — это упорядоченный список (или последовательность) элементов в информатике или математике. То есть запись $(K,y,l,e)$ будет кортежем из четырёх элементов, показывающим последовательность символов, составляющих моё имя.



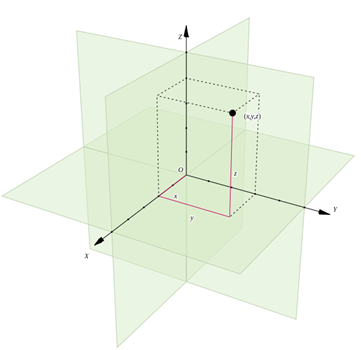
В этом пространстве мы будем определять точку как кортеж из трёх элементов. Это можно обозначить так:

$P = (x,y,z)$



Кроме задания точки нам нужно определить её части.

Каждый из элементов кортежа является скалярным числом, определяющим положение вдоль базисного вектора. Каждый базисный вектор должен иметь единичную длину (его длина равна 1), то есть такие кортежи как $(1,1,1)$ и $(2,2,2)$ не могут быть базисными векторами, потому что они слишком длинные.

Мы определим три базисных вектора в нашем пространстве:

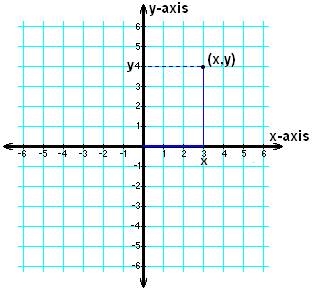
$\begin{aligned} X & = (1,0,0)\\ Y & = (0,1,0)\\ Z & = (0,0,1) \end{aligned}$




Источник: http://www.thefullwiki.org/Arithmetics/Cartesian_Coordinate.


Система координат


Теперь поговорим о математическом определении нашей системы координат, о том, как она влияет на графическую систему и о вычислениях, которые мы можем произвести.

Обозначение точек


Точку начала координат системы координат можно обозначить точкой $O$, которая описывается кортежем из трёх элементов (0,0,0). Это значит, что математическое представление системы координат можно изобразить так:

$\{O;X,Y,Z\}$


Этой записью мы можем сказать, что $(x,y,z)$ представляют собой положение точки относительно начала координат. Такое определение означает, что любую точку $P$, $(a, b, c)$ можно представить как:

$P = O + aX + bY + cZ$


С этого момента мы будем обозначать скалярные значения строчными буквами, а векторы — прописными, то есть $a$, $b$ и $c$ — это скаляры, а $X$, $Y$ и $Z$ — векторы. (На самом деле это базисные векторы, определение которым мы дали выше.)

Это значит, что точка, записываемая кортежем (2,3,4), может быть представлена так:

$\begin{aligned} (2,3,4) & = (2,0,0) + (0,3,0) + (0,0,4)\& = (0,0,0) + (2,0,0) + (0,3,0) + (0,0,4)\& = (0,0,0) + 2(1,0,0) + 3(0,1,0) + 4(0,0,1)\& = O + 2X + 3Y + 4Z\\end{aligned}$


Итак, мы взяли абстрактное понятие «точки в трёхмерном пространстве» и определили его как сумму четырёх объектов. Такое определение будет очень важным, когда дело дойдёт до реализации понятия в коде.

Взаимная перпендикулярность


Система координат, которую мы будем использовать, обладает очень ценным свойством: взаимной перпендикулярностью. Это значит, что в пересечении каждой из осей на своей соответствующей плоскости угол между ними равен 90 градусам.



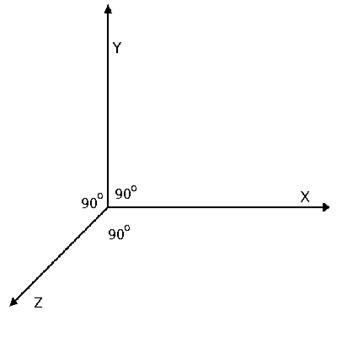
Нашу систему координат можно также назвать «правой»:


Источник: http://viz.aset.psu.edu/gho/sem_notes/3d_fundamentals/html/3d_coordinates.html.

На языке математики это значит, что:

$X = Y \times Z$


где $\times$ обозначает оператор векторного произведения.

Векторное произведение можно определить следующим уравнением (при условии, что у нас есть два кортежа из трёх элементов):

$(a,b,c) \times (d,e,f) = (bf - ce, cd - af, ae - bd)$


Эти выражения могут показаться скучными, но позже они позволят нам проще выполнять множество различных вычислений и преобразований. К счастью, при создании игрового движка нам необязательно запоминать все эти уравнения — можно начать с этих выражений, а затем надстраивать поверх них менее сложные системы. По крайней мере, пока вы не захотите изменить в движке нечто фундаментальное!


Точки и векторы


Определившись с основами системы координат, мы можем поговорить о точках и векторах, и, что более важно — о том, как они взаимодействуют друг с другом. По-первых, стоит заметить, что точки и векторы — это совершенно разные объекты: точка — это физическое место в пространстве, вектор — пространство между двумя точками.



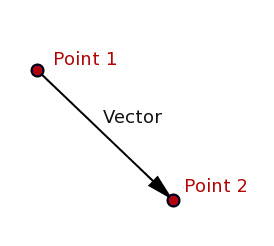
Чтобы не перепутать эти два типа объектов, я буду записывать точки курсивными прописными буквами, например, $P$, а векторы — полужирными прописными, например, $\mathbf{V}$.

При работе с точками и векторами мы будем использовать две основные аксиомы. Вот они:

  • Аксиома 1: разность между двумя точками — это вектор, то есть $\mathbf{V} = P - Q$
  • Аксиома 2: сумма точки и вектора — это точка, то есть $Q = P + \mathbf{V}$

Подсказка: аксиома — это логическое утверждение, считаемое достаточно очевидным для принятия без доказательств.


Создание движка


Благодаря этим двум аксиомам у нас есть достаточно информации для создания классов-«кирпичиков», которые являются сердцем любого трёхмерного игрового движка: класса Point и класса Vector. Если бы мы собирались создавать свой движок на основе этой информации, то нам бы нужно было сделать и другие важные шаги при создании этих классов (в основном связанных с оптимизацией и работой с существующими API), но мы опустим это ради упрощения.

Все примеры классов будут написаны псевдокодом, чтобы вы могли реализовать их на своём любимом языке. Вот наброски наших двух классов:

Point Class
{
	Variables:
		num tuple[3]; //(x,y,z)

	Operators:
		Point AddVectorToPoint(Vector);
		Point SubtractVectorFromPoint(Vector);
		Vector SubtractPointFromPoint(Point);

	Function:
		//позже здесь будет вызываться функция графического API, но пока
		//она выводит на экран координаты точек
		drawPoint; 
}

Vector Class
{
	Variables:
		num tuple[3]; //(x,y,z)

	Operators:
		Vector AddVectorToVector(Vector);
		Vector SubtractVectorFromVector(Vector);
}

В качестве упражнения попробуйте заполнить каждую из функций этих классов работающим кодом (на основании того, что мы разобрали выше). Закончив с этим, протестируйте работу, выполнив эту простую программу:

main
{
    var point1 = new Point(1,2,1);
    var point2 = new Point(0,4,4);
    var vector1 = new Vector(2,0,0);
    var vector2;

    point1.drawPoint(); //должна вывести (1,2,1)
    point2.drawPoint(); //должна вывести (0,4,4)

    vector2 = point1.subtractPointFromPoint(point2);

    vector1 = vector1.addVectorToVector(vector2);

    point1.addVectorToPoint(vector1);
    point1.drawPoint(); //должна вывести (4,0,-2)

    point2.subtractVectorFromPoint(vector2);
    point2.drawPoint(); //должна вывести (-1,6,7)
}


Заключение


Мы добрались до конца первой части! Кажется, что тут использована куча математики просто для написания двух классов, и это на самом деле так. В большинстве случаев вам никогда не придётся работать с игрой на таком уровне, но знание подробностей внутренней работы игрового движка всё равно будет полезным (хотя бы для собственного удовольствия).

Часть 2: линейные преобразования


Теперь мы поговорим о линейных преобразованиях, которые позволят нам изменять такие свойства векторов, как поворот и масштаб. Мы узнаем, как применить их в уже созданных нами классах.

Для обсуждения линейных преобразований нам нужно внести небольшое изменение в класс Point: вместо вывода данных в консоль воспользуйтесь любым удобным вам графическим API, чтобы функция отрисовывала текущую точку на экране.


Основы линейных преобразований


Просто предупреждение: уравнения линейных преобразований всегда выглядят намного сложнее, чем есть на самом деле. Мы применим тригонометрию, но вам на самом деле не обязательно знать как выполняются тригонометрические операции: я объясню, что нужно будет передавать каждой функции и что мы будем от неё получать, а для всех промежуточных действий можно использовать любой калькулятор или математическую библиотеку.

Подсказка: если вы хотите глубже разобраться во внутренней работе этих уравнений, то стоит посмотреть это видео и прочитать этот PDF.

Все линейные преобразования имеют следующую форму:

$B = F(A)$


Из этого понятно, что у нас есть функция преобразования $F()$, в качестве входных данных используется вектор $A$, а на выходе мы получим вектор $B$.

Каждую из этих частей — два вектора и функцию — можно представить в виде матрицы: вектор $B$ — как матрицу 1x3, вектор $A$ — как ещё одну матрицу 1x3, а линейное преобразование $F()$ — как матрицу 3x3 (матрицу преобразований).

Это значит, что развернув уравнение, мы получим следующее:

$ \begin{bmatrix} b_{0} \b_{1} \b_{2} \end{bmatrix} = \begin{bmatrix} f_{00} & f_{01} & f_{02}\f_{10} & f_{11} & f_{12}\f_{20} & f_{21} & f_{22} \end{bmatrix} \begin{bmatrix} a_{0}\a_{1}\a_{2} \end{bmatrix} $


Если вы проходили тригонометрию или линейную алгебру, то, возможно, уже припоминаете кошмар математики матриц. К счастью, есть более простой способ записи этого выражения, позволяющий избавиться от большинства проблем. Он выглядит вот так:

$\begin{bmatrix} b_{0}\b_{1}\b_{2} \end{bmatrix} = \begin{bmatrix} f_{00}a_{0} + f_{01}a_{1} + f_{02}a_{2}\f_{10}a_{0} + f_{11}a_{1} + f_{12}a_{2}\f_{20}a_{0} + f_{21}a_{1} + f_{22}a_{2}\\end{bmatrix} $


Однако эти уравнения могут меняться при наличии второго источника входных данных, как в случае с поворотами, когда должны задаваться вектор и количество его вращения. Давайте посмотрим, как работают повороты.


Повороты


Поворот, по самому определению — это круговое движение объекта вокруг точки поворота. Точка поворота в нашем пространстве может принадлежать плоскости XY, плоскости XZ или плоскости YZ (где каждая плоскость составлена из двух базисных векторов, которые мы обсуждали в первой части).



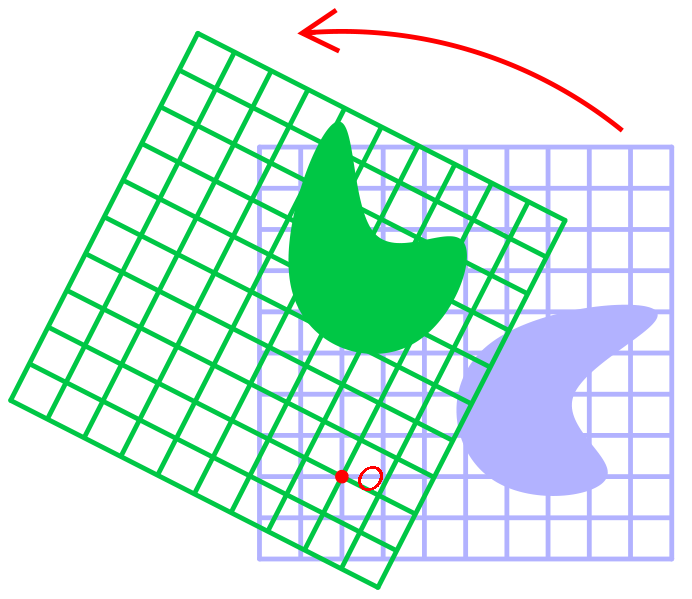
Три точки поворота означают, что у нас есть три отдельных матрицы вращения:

Матрица поворота по XY:

$\begin{bmatrix} cos \theta & -sin \theta & 0\sin \theta & cos \theta & 0\0 & 0 & 1\\end{bmatrix} $


Матрица поворота по XZ:

$\begin{bmatrix} cos \theta & 0 & sin \theta\0 & 1 & 0\-sin \theta & 0 & cos \theta \end{bmatrix} $


Матрица поворота по YZ:

$\begin{bmatrix} 1 & 0 & 0\0 & cos \theta & -sin \theta\0 & sin \theta & cos \theta \end{bmatrix} $


То есть для поворота точки $A$ вокруг плоскости XY на 90 градусов ($\pi/2$ радиан — в большинстве математических библиотек есть функция преобразования градусов в радианы), нужно выполнить следующие действия:

$\begin{aligned} \begin{bmatrix} b_{0}\b_{1}\b_{2} \end{bmatrix} & = \begin{bmatrix} cos \frac{\pi}{2} & -sin \frac{\pi}{2} & 0\sin \frac{\pi}{2} & cos \frac{\pi}{2} & 0\0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_{0}\a_{1}\a_{2} \end{bmatrix}\& = \begin{bmatrix} cos \frac{\pi}{2}a_{0} + -sin \frac{\pi}{2}a_{1} + 0a_{2}\sin \frac{\pi}{2}a_{0} + cos \frac{\pi}{2}a_{1} + 0a_{2}\0a_{0} + 0a_{1} + 1a_{2} \end{bmatrix}\& = \begin{bmatrix} 0a_{0} + -1a_{1} + 0a_{2}\1a_{0} + 0a_{1} + 0a_{2}\0a_{0} + 0a_{1} + 1a_{2} \end{bmatrix}\& = \begin{bmatrix} -a_{1}\a_{0}\a_{2} \end{bmatrix} \end{aligned} $


То есть если начальная точка $A$ имела координаты $(3,4,5)$, то выходная точка $B$ будет иметь координаты $(-4,3,5)$.

Упражнение: функции поворота


В качестве упражнения попробуйте создать три новые функции для класса Vector. Одна должна поворачивать вектор вокруг плоскости XY, другая — вокруг YZ, а третья — вокруг XZ. На входе функции должны получать нужное число градусов поворота, а на выходе возвращать вектор.

В целом функции должны работать следующим образом:

  1. Создание выходного вектора.
  2. Преобразование входа в градусах в радианы.
  3. Решение каждого из элементов кортежа выходного вектора с помощью приведённых выше уравнений.
  4. Возврат выходного вектора.


Масштабирование


Масштабирование — это преобразование, увеличивающее или уменьшающее объект в соответствии с заданным масштабом.

Это преобразование выполнить довольно просто (по крайней мере, по сравнению с поворотами). Преобразование масштабирования требует двух типов входных данных: входного вектора и кортежа масштабирования из трёх элементов, который определяет масштаб входного вектора по каждой из осей пространства.

Например, в кортеже масштабирования $(s_{0},s_{1},s_{2})$ величина $s_{0}$ представляет собой масштаб по оси X, $s_{1}$ — по оси Y, а $s_{2}$ — по оси Z.

Матрица масштабного преобразования имеет следующий вид (где $s_{0}$, $s_{1}$ и $s_{2}$ — это элементы кортежа масштабирования):

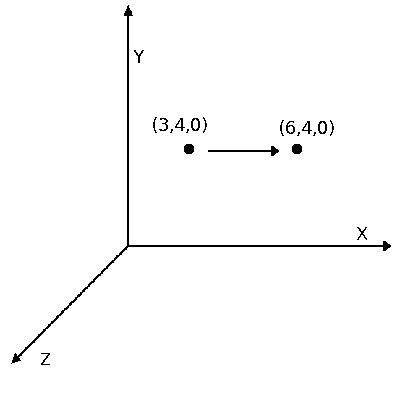
$\begin{bmatrix} s0 & 0 & 0\0 & s1 & 0\0 & 0 & s2 \end{bmatrix} $


Чтобы сделать входной вектор A $(a_{0}, a_{1}, a_{2})$ вдвое больше по оси X (то есть использовать кортеж $S = (2, 1, 1)$), вычисления должны иметь следующий вид:

$\begin{aligned} \begin{bmatrix} b_{0}\b_{1}\b_{2} \end{bmatrix} & = \begin{bmatrix} s0 & 0 & 0\0 & s1 & 0\0 & 0 & s2 \end{bmatrix} \begin{bmatrix} a_{0}\a_{1}\a_{2} \end{bmatrix}\& = \begin{bmatrix} 2 & 0 & 0\0 & 1 & 0\0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_{0}\a_{1}\a_{2} \end{bmatrix}\& = \begin{bmatrix} 2a_{0} + 0a_{1} + 0a_{2}\0a_{0} + 1a_{1} + 0a_{2}\0a_{0} + 0a_{1} + 1a_{2} \end{bmatrix}\& = \begin{bmatrix} 2a_{0}\a_{1}\a_{2} \end{bmatrix} \end{aligned} $


То есть при входном векторе $A = (3,4,0)$ выходной вектор $B$ будет равен $(6,4,0)$.



Упражнение: функции масштабирования


В качестве ещё одного упражнения добавьте новую функцию в класс Vector. Эта новая функция должна получать кортеж масштабирования и возвращать выходной вектор.

В целом функция должна работать следующим образом:

  1. Создание выходного вектора.
  2. Решение каждого элемента кортежа выходного вектора с помощью приведённого выше уравнения (которое можно упростить до y0 = x0 * s0; y1 = x1*s1; y2 = x2*s2).
  3. Возврат выходного вектора.


Давайте что-нибудь создадим!


Теперь, когда у нас есть в распоряжении линейные преобразования, давайте создадим небольшую программу, чтобы продемонстрировать новые возможности. Мы создадим программу, отрисовывающую на экране группу точек и позволяющую изменять их как целое, выполняя над ними линейные преобразования.

Прежде чем начать, нам нужно добавить ещё одну функцию в класс Point. Мы назовём её setPointToPoint(), она будет просто задавать положение текущей точки в точке, которая ей передаётся. На входе она будет получать точку и ничего не возвращать.

Вот краткие характеристики программы:

  • Программа будет хранить в массиве 100 точек.
  • При нажатии клавиши D программа будет очищать текущий экран и перерисовывать точки.
  • При нажатии клавиши A программа будет масштабировать положения всех точек на 0,5.
  • При нажатии клавиши S программа будет масштабировать положения всех точек на 2,0.
  • При нажатии клавиши R будет поворачивать положение всех точек на 15 градусов на плоскости XY.
  • При нажатии клавиши Escape программа закрывается (если вы не пишете её на JavaScript или другом веб-ориентированном языке).

Имеющиеся у нас классы:

Point Class
{
	Variables:
		num tuple[3]; //(x,y,z)

	Operators:
		Point AddVectorToPoint(Vector);
		Point SubtractVectorFromPoint(Vector);
		Vector SubtractPointFromPoint(Point);
		//использует входную точку для задания положения текущей точки
		Null SetPointToPoint(Point);
	Functions:
		//отрисовывает точку в кортеже положения с помощью выбранного вами графического API
		drawPoint;
}

Vector Class
{
	Variables:
		num tuple[3]; //(x,y,z)

	Operators:
		Vector AddVectorToVector(Vector);
		Vector SubtractVectorFromVector(Vector);
		Vector RotateXY(degrees);
		Vector RotateYZ(degrees);
		Vector RotateXZ(degrees);
		Vector Scale(s0,s1,s2);
}

Давайте посмотрим, как может выглядеть код с учётом приведённых требований:

main{
    //настройка выбранного графического API
    //настройка клавиатурного ввода (может и не потребоваться)
    
	//создание массива из 100 точек
	Point Array  pointArray[100];
	
    for (int x = 0; x < pointArray.length; x++) 
    {
        //Задание точке случайного положения на экране
        pointArray[x].tuple = [random(0,screenWidth), random(0,screenHeight), random(0,desiredDepth));
    }

	//эта функция очищает экран и отрисовывает все точки заново
    function redrawScreen()
    {
	    //используйте функцию очистки экрана выбранного графического API
        ClearTheScreen();  
		
        for (int x = 0; x < pointArray.length; x++)
        {
		    //отрисовка текущей точки на экране
            pointArray[x].drawPoint();
        }
    }

	// пока не нажата клавиша escape, выполнять основной цикл
    while (esc != pressed)
    {
	    // выполнение различных действий на основании нажатых клавиш
        if (key('d') == pressed)
        {
            redrawScreen();
        }
        if (key('a') == pressed)
        {
		    //создание начала координат пространства как точки
            Point origin = new Point(0,0,0);
            
			Vector tempVector;
            for (int x = 0; x < pointArray.length; x++)
            {
                //сохранение адреса текущего вектора для точки и задание точки
                tempVector = pointArray[x].subtractPointFromPoint(origin);
                //сброс точки, чтобы можно было добавить отмасштабированный вектор
                pointArray[x].setPointToPoint(origin);
                //масштабирование вектора и задание точки в её новой отмасштабированной координате
                pointArray[x].addVectorToPoint(tempVector.scale(0.5,0.5,0.5));
            }
            redrawScreen();
        }
		
        if(key('s') == pressed)
        {
		    //создание начала координат пространства как точки
            Point origin = new Point(0,0,0);
			
            Vector tempVector;
            for (int x = 0; x < pointArray.length; x++)
            {
                //сохранение адреса текущего вектора для точки и задание точки
                tempVector = pointArray[x].subtractPointFromPoint(origin);
                //сброс точки, чтобы можно было добавить отмасштабированный вектор
                pointArray[x].setPointToPoint(origin);
                //масштабирование вектора и задание точки в её новой отмасштабированной координате
                pointArray[x].addVectorToPoint(tempVector.scale(2.0,2.0,2.0));
            }
            redrawScreen();
        }
		
        if(key('r') == pressed)
        {
		    //создание начала координат пространства как точки
            Point origin = new Point(0,0,0);
            Vector tempVector;
            for (int x = 0; x < pointArray.length; x++)
            {
                //сохранение адреса текущего вектора для точки и задание точки
                tempVector = pointArray[x].subtractPointFromPoint(origin);
                //сброс точки, чтобы можно было добавить отмасштабированный вектор
                pointArray[x].setPointToPoint(origin);
                //масштабирование вектора и задание точки в её новой отмасштабированной координате
                pointArray[x].addVectorToPoint(tempVector.rotateXY(15));
            }
            redrawScreen();
        }
    }
}

Итак, у нас получилась короткая хорошая программа, демонстрирующая все наши новые возможности!


Заключение


Хоть мы и не рассмотрели все возможные линейные трансформации, наш микродвижок начинает обретать свою форму.

Как обычно, для упрощения я убрал из движка некоторые вещи (а именно перемещение и отражения). Если вы хотите больше узнать об этих двух типах линейных преобразований, то можете почитать в статье Википедии и по ссылкам в статье.

В следующей части мы рассмотрим различные пространства обзора и отсечение объектов, находящихся за пределами области видимости.

Часть 3: пространства и отсечение


Видно, что пока использование двух созданных нами классов самих по себе — довольно запутанный процесс, к тому же отрисовка каждой возможной точки может довольно быстро истощить память системы. Для решения этих проблем мы добавим в игровой движок новый класс: камеру.

Рендеринг будет происходить только в пределах камеры, она отсекает все объекты до размеров экрана, а также управляет всеми нашими точками.

Но прежде чем мы приступим ко всему этому, надо для начала поговорить об отсечении.


Отсечение


По своему определению отсечение — это выборка объектов из большей группы объектов. В нашем игровом движке меньшей группой будут точки, которые нужно отрисовать на экране. Большей группой объектов будет множество всех существующих точек.

Благодаря отсечению движок значительно снизит потребление памяти системы. Он будет отрисовывать только то, что игрок может увидеть, а не весь мир точек. В нашем движке мы реализуем это заданием параметров пространства обзора.

Пространство обзора будет задаваться по всем трём нашим традиционным осям: x, y и z. Её границы по x состоят из всего между левой и правой границами окна, границы по y — из всего между верхней и нижней границами окна, а границы по z находятся в пределах от 0 (куда установлена камера) до расстояния видимости игрока (в нашем демо мы будем использовать произвольно выбранное значение 100).

Перед отрисовкой точки класс камеры будет проверять, находится ли точка в пространстве обзора. Если находится, то точка отрисовывается, в противном случае — не отрисовывается.


Может, пора добавить камеру?


Поняв основы отсечения, мы можем создать класс камеры:

Camera Class
{
Vars:
    int minX, maxX; //минимальная и максимальная границы X
    int minY, maxY; //мин. и макс. границы Y
    int minZ, maxZ; //мин. и макс. границы Z
}

Также мы возложим на камеру весь процесс рендеринга в движке. Часто в движках рендереры отделены от систем камер. Обычно это делается для удобства инкапсуляции систем, потому что в некоторых движках при их совместном хранении возникает путаница. Однако для нашего туториала будет проще обращаться с ними как с единой системой.

Для начала нам потребуется функция, которую можно будет вызывать извне из класса для отрисовки сцены. Эта функция будет циклически перебирать все существующие точки, сравнивать их с параметрами отсечения камеры и отрисовывать их при соблюдении условий.


Источник: http://en.wikipedia.org/wiki/File:ViewFrustum.svg

Подсказка: если вы хотите отделить систему камер от рендерера, то можно просто создать класс Renderer, отсечь системой камер точки, сохранить в массиве те из них, которые нужно отрисовывать, а затем отправить массив в функцию draw() рендерера.


Управление точками


Последней частью класса камеры будет система управления точками. В зависимости от используемого языка программирования это может быть просто массив всех объектов для отрисовки (позже мы будем обрабатывать не только точки), или же может потребоваться использование родительского класса объектов по умолчанию. Если вам очень не повезло с выбором, то придётся реализовать собственный родительский класс объектов и сделать так, чтобы все отрисовываемые классы (пока это только точки) наследовали от этого класса.

После добавления системы управления в класс наша камера будет выглядеть примерно так:

Camera Class
{
    Vars:
        int minX, maxX; //минимальная и максимальная границы X
        int minY, maxY; //минимальная и максимальная границы Y
        int minZ, maxZ; //минимальная и максимальная границы Z
        array objectsInWorld; //массив всех существующих объектов
    Functions:
        null drawScene(); //отрисовывает все необходимые объекты на экран, не возвращает ничего
}

Внеся все эти дополнения, давайте немного улучшим программу, написанную в прошлой части.


Больше и лучше


Мы собираемся создать простую программу отрисовки точек на основе примера программы, созданной в прошлой части.

В этой итерации программы мы добавим использование нового класса камеры. При нажатии клавиши D программа будет перерисовывать экран без отсечения, показывая количество отрендеренных объектов в верхнем правом углу экрана. При нажатии клавиши C программа будет перерисовывать экран с отсечением, также показывая количество отрендеренных объектов.

Давайте взглянем на код:

main{
	//настройка выбранного графического API
	//настройка клавиатурного ввода (может и не потребоваться)

var camera = new Camera(); //создаём экземпляр класса камеры
camera.objectsInWorld[100]; //создаём пространство под 100 объектов в массиве камеры

//задаём пространство обзора камеры
camera.minX = 0;
camera.maxX = screenWidth;
camera.minY = 0;
camera.maxY = screenHeight;
camera.minZ = 0;
camera.maxZ = 100;

	for(int x = 0; x < camera.objectsInWorld.length; x++)
	{
		//Задание точке случайного положения на экране
		camera.objectsInWorld[x].tuple = [random(-200,1000), random(-200,1000), random(-100,200));
	}

	function redrawScreenWithoutCulling() //эта функция очищает экран и отрисовывает все точки заново
	{
		ClearTheScreen();  //используйте функцию очистки экрана выбранного графического API
		for(int x = 0; x < camera.objectsInWorld.length; x++)
		{
			camera.objectsInWorld[x].drawPoint();   //отрисовка текущей точки на экране
		}
	}

	while(esc != pressed)  // основной цикл
	{
		if(key('d') == pressed)
		{
			redrawScreenWithoutCulling();
		}
		if(key('c') == pressed)
		{
			camera.drawScene();
		}
		if(key('a') == pressed)
		{
			Point origin = new Point(0,0,0);
			Vector tempVector;
			for(int x = 0; x < camera.objectsInWorld.length; x++)
			{
				//сохранение адреса текущего вектора для точки и задание точки
				tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin);
				//сброс точки, чтобы можно было добавить отмасштабированный вектор
				camera.objectsInWorld[x].setPointToPoint(origin);
				//масштабирование вектора и задание точки в её новой отмасштабированной координате
				camera.objectsInWorld[x].addVectorToPoint(tempVector.scale(0.5,0.5,0.5));
			}
		}
		if(key('s') == pressed)
		{
			Point origin = new Point(0,0,0);  //create the space's origin as a point
			Vector tempVector;
			for(int x = 0; x < camera.objectsInWorld.length; x++)
			{
				//сохранение адреса текущего вектора для точки и задание точки
				tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin);
				//сброс точки, чтобы можно было добавить отмасштабированный вектор
				camera.objectsInWorld[x].setPointToPoint(origin);
				//масштабирование вектора и задание точки в её новой отмасштабированной координате
				camera.objectsInWorld[x].addVectorToPoint(tempVector.scale(2.0,2.0,2.0));
			}
		}
		if(key('r') == pressed)
		{
			Point origin = new Point(0,0,0);  //create the space's origin as a point
			Vector tempVector;
			for(int x = 0; x < camera.objectsInWorld.length; x++)
			{
				//сохранение адреса текущего вектора для точки и задание точки
				tempVector = camera.objectsInWorld[x].subtractPointFromPoint(origin);
				//сброс точки, чтобы можно было добавить отмасштабированный вектор
				camera.objectsInWorld[x].setPointToPoint(origin);
				//масштабирование вектора и задание точки в её новой отмасштабированной координате
				camera.objectsInWorld[x].addVectorToPoint(tempVector.rotateXY(15));
			}
		}
	}
}

Теперь вы своими глазами можете увидеть всю мощь отсечения! Заметьте, что в коде примера, некоторые вещи реализуются немного иначе, чтобы сделать демо более веб-совместимым.


Заключение


Создав систему камер и рендеринга, технически можно сказать, что у нас есть готовый трёхмерный игровой движок! Пока он не слишком впечатляет, но всему своё время.

В следующей части мы узнаем, как добавить в движок геометрические формы (а именно отрезки прямых и окружности), а также поговорим об алгоритмах, которые можно использовать для приведения их уравнений к экранным пикселям.

Часть 4: растеризация отрезков прямых и окружностей


Растеризация


Растеризация — это процесс преобразования формы, описанной в векторном графическом формате (или в нашем случае математически) в растровое изображение (в котором форма вписывается в пиксельную структуру).

Поскольку математика не всегда так точна, как нам нужно для компьютерной графики, нам нужно использовать алгоритмы для адаптации описанной ею форм в наш целочисленнй экран. Например, в математике точка может находиться в координате $(3.2, 4.6)$, но при рендеринге необходимо сместить её в $(3, 5)$, чтобы она вписывалась в пиксельную структуру экрана.

Для каждого типа форм будет собственный алгоритм растеризации. Давайте начнём с наиболее простых для растеризации форм: отрезка прямой.


Отрезки прямых



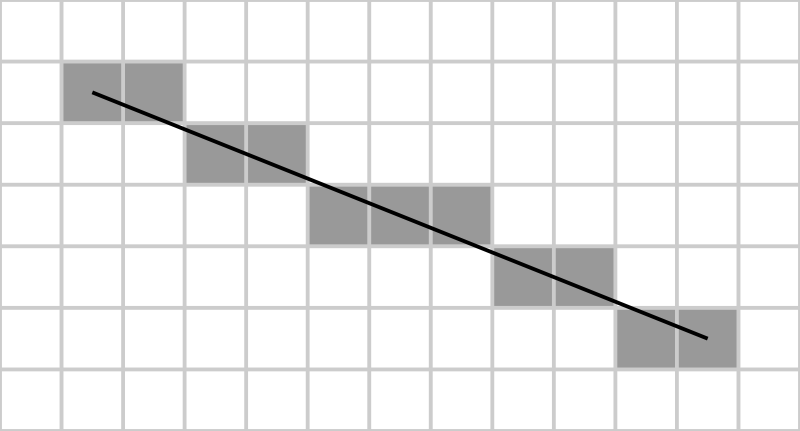
Источник: http://en.wikipedia.org/wiki/File:Bresenham.svg

Отрезки прямых — это одни из простейших изображаемых форм, поэтому часто это одно из первых понятий, изучаемых на геометрии. Они описываются двумя отдельными точками (начальной и конечной) и соединяющей их прямой. Наиболее часто используемый алгоритм растеризации отрезка прямой называется алгоритмом Брезенхэма.

Поэтапно алгоритм Брезенхэма выглядит так:

  1. Получение на входе начальной и конечной точек отрезка прямой.
  2. Определение направления отрезка прямой вычислением его свойств $dx$ и $dy$ ($dx = x_{1} - x_{0}$, $dy = y_{1} - y_{0}$).
  3. Определение свойств sx, sy и обнаружения ошибки (математическое определение приведено ниже).
  4. Округление каждой точки в отрезке до пикселя выше/ниже.

Перед реализацией алгоритма Брезенхэма давайте создадим базовый класс отрезка, который можно будет использовать в движке:

LineSegment Class
{
	Variables:
		int startX, startY; //начальная точка отрезка
		int endX, endY; //конечная точка отрезка
	Function:
		array returnPointsInSegment; //все точки, находящиеся на этом отрезке
}

Если нужно выполнить преобразование с новым классом LineSegment, то для этого достаточно применить соответствующее преобразование к начальной и конечной точкам LineSegment, а затем передать их обратно в класс. Все точки между нии будут обработаны при отрисовке самого LineSegment, потому что для поиска всех последующих точек алгоритму Брезенхэма требуются только начальная и конечная точки.

Чтобы встроить класс LineSegment в уже существующий движок, нам нужно добавить в класс функцию draw(), поэтому я отказался от использования функции returnPointsInSegment. Эта функция будет возвращать массив всех точек, находящихся в отрезке прямой, что позволит нам удобно отрисовывать и отсекать отрезок.

Функция returnPointsInSegment() будет выглядеть примерно так (в JavaScript):

function returnPointsInSegment()
{
	//создаём список для хранения всех точек отрезка прямой
	var pointArray = new Array();
	//задаём переменные функции на основании начальной и конечной точек класса
	var x0 = this.startX;
	var y0 = this.startY;
	var x1 = this.endX;
	var y1 = this.endY;
	//вычисляем разность векторов и другие переменные, необходимые для алгоритма Брезенхэма
	var dx = Math.abs(x1-x0);
	var dy = Math.abs(y1-y0);
	var sx = (x0 & x1) ? 1 : -1; //шаг по x
	var sy = (y0 & y1) ? 1 : -1; //шаг по y
	var err = dx-dy; //получаем начальное значение ошибки
	//задаём первую точку в массиве
	pointArray.push(new Point(x0,y0));

	//Основной цикл обработки
	while(!((x0 == x1) && (y0 == y1)))
	{
		var e2 = err * 2; //содержит значение ошибки
		//используем значение ошибки определения того, в какую сторону нужно округлять точку (вверх или вниз)
 		if(e2 => -dy)
		{
			err -= dy;
			x0 += sx;
		}
		if(e2 < dx)
		{
			err += dx;
			y0 += sy;
		}
		//добавляем новую точку в массив
		pointArray.push(new Point(x0, y0));
	}
	return pointArray;
}

Простейший способ добавить рендеринг отрезков прямых в класс камеры — добавление простой структуры if, например, вот такой:

	//обходим в цикле массив объектов
	if (class type == Point)
	{
		//выполняем имеющийся код рендеринга
	}
	else if (class type == LineSegment)
	{
		var segmentArray = LineSegment.returnPointsInSegment();
		//обходим в цикле точки в массиве, отрисовывая и отсекая их, как мы делали ранее
	}

И это всё, что понадобится для работы нашего первого класса формы! Если вы хотите подробнее узнать технические аспекты алгоритма Брезенхэма (в особенности об ошибках), то можно прочитать о них в статье в Википедии.


Окружности



Источник: http://en.wikipedia.org/wiki/File:Bresenham_circle.svg

Растеризация окружности немного сложнее, чем растеризация отрезка прямой. Для большей части работы мы будем использовать алгоритм центральной точки окружности, который является развитием алгоритма Брезенхэма. То есть он состоит из похожих этапов, с некоторыми отличиями.

Новый алгоритм будет работать так:

  1. Получение центральной точки и радиуса окружности.
  2. Принудительное задание точек в каждом основном направлении
  3. Циклический обход каждого из квадрантов, отрисовка их дуг

Класс окружности очень похож на класс отрезка прямой и будет выглядеть примерно так:

Circle Class
{
	Variables:
		int centerX, centerY; //центральная точка окружности
		int radius; //радиус окружности
	Function:
		array returnPointsInCircle; //все точки, принадлежащие этой окружности Circle
}

Функция returnPointsInCircle() будет вести себя так же, как функция класса LineSegment, возвращая массив точек, чтобы камера могла отрендерить и отсечь их. Это позволяет движку обрабатывать множество разных форм, в каждую из которых нужно вносить только незначительные изменения.

Вот как будет выглядеть функция returnPointsInCircle() (в JavaScript):

function returnPointsInCircle()
{
	//сохраняем все точки окружности в массив
	var pointArray = new Array();
	//задаём значения, необходимые для алгоритма
	var f = 1 - radius; //используется для отслеживания процесса отрисованной окружности (потому что функция полурекурсивная)
	var ddFx = 1; //шаг по x
	var ddFy = -2 * this.radius; //шаг по y
	var x = 0;
	var y = this.radius;

	//этот алгоритм не учитывает самые дальние точки, 
	//так что нам нужно задать их вручную
	pointArray.push(new Point(this.centerX, this.centerY + this.radius));
	pointArray.push(new Point(this.centerX, this.centerY - this.radius));
	pointArray.push(new Point(this.centerX + this.radius, this.centerY));
	pointArray.push(new Point(this.centerX - this.radius, this.centerY));

	while(x < y) {
	 	if(f >= 0) {
			y--;
			ddFy += 2;
			f += ddFy;
		}
		x++;
		ddFx += 2;
		f += ddFx;

		//построение текущей дуги
		pointArray.push(new Point(x0 + x, y0 + y));
		pointArray.push(new Point(x0 - x, y0 + y));
		pointArray.push(new Point(x0 + x, y0 - y));
		pointArray.push(new Point(x0 - x, y0 - y));
		pointArray.push(new Point(x0 + y, y0 + x));
		pointArray.push(new Point(x0 - y, y0 + x));
		pointArray.push(new Point(x0 + y, y0 - x));
		pointArray.push(new Point(x0 - y, y0 - x));
	}

	return pointArray;
}

Теперь мы просто добавим ещё одну конструкцию if в основной цикл отрисовки, и эти окружности будут полностью интегрированы в код!

Вот как может выглядеть обновлённый цикл отрисовки:

	//обходим в цикле массив объектов
	if(class type == point)
	{
		//выполняем текущий код рендеринга
	}
	else if(class type == LineSegment)
	{
		var segmentArray = LineSegment.returnPointsInSegment();
		//loop through points in the array, drawing and culling them as we have previously
	}
	else if(class type == Circle)
	{
		var circleArray = Circle.returnPointsInCircle();
		//обходим в цикле точки в массиве, отрисовывая и отсекая их, как мы делали ранее
	}

Теперь, когда у нас есть два новых класса, давайте сделаем что-нибудь!


Мастер растеризации


На этот раз наша программа будет простой. Когда пользователь нажимает кнопку мыши, мы будем отрисовывать окружность с центром в точке нажатия и со случайным радиусом.

Давайте посмотрим на код:

main{
	//настройка выбранного графического API
	//настройка клавиатурного ввода (может и не потребоваться)

	var camera = new Camera(); //создаём экземпляр класса камеры
	camera.objectsInWorld[]; //создаём пространство под 100 объектов в массиве камеры

	//задаём пространство обзора камеры
	camera.minX = 0;
	camera.maxX = screenWidth;
	camera.minY = 0;
	camera.maxY = screenHeight;
	camera.minZ = 0;
	camera.maxZ = 100;

	while(key != esc) {
		if(mouseClick) {
			//создаём новую окружность
			camera.objectsInWorld.push(new Circle(mouse.x,mouse.y,random(3,10));
			//рендерим всё в сцене
			camera.drawScene();
		}
	}
}

Если всё получится успешно, то вы сможете отрисовывать с помощью движка отличные окружности.


Заключение


Добавив к движку базовые возможности растеризации, мы наконец начинаем отрисовку на экране полезных объектов! Пока не было ничего сложного, но если хотите, можете попробовать рисовать людей из отрезков и окружностей, или что-то в таком духе.

В следующей части мы ещё раз взглянем на растеризацию. Только на этот раз мы добавим в движок ещё два класса: треугольники и четырёхугольники.

Часть 5: растеризация треугольников и четырёхугольников


Для создания классов Triangle и Quad мы будем активно использовать класс LineSegment.


Растеризация треугольников




Реализация класса Triangle в движке довольно проста, особенно благодаря использованию класса LineSegment, в которой и будет происходить вся растеризация. Этот класс позволит назначить три точки и отрисовать между ними отрезки прямых, чтобы создать замкнутый треугольник.

Набросок класса будет выглядеть так:

Triangle Class
{
	Variables:
		//координаты трёх точек треугольника
		int Point1X, Point1Y; 
		int Point2X, Point2Y;
		int Point3X, Point3Y;
	Function:
		array returnPointsInTriangle; //все точки периметра треугольника
}

Ради стандартизации мы предположим, что три точки объявляются в треугольнике по часовой стрелке.

Тогда с помощью класса LineSegment можно написать следующую функцию returnPointsInTriangle():

function returnPointsInTriangle()
{
	array PointsToReturn; //создаём временный массив для хранения точек треугольника

	//создаём три отрезка прямых и сохраняем их точки в массиве
	PointsToReturn.push(new LineSegment(this.Point1X, this.Point1Y, this.Point2X, this.Point2Y));
	PointsToReturn.push(new LineSegment(this.Point2X, this.Point2Y, this.Point3X, this.Point3Y));
	PointsToReturn.push(new LineSegment(this.Point3X, this.Point3Y, this.Point1X, this.Point1Y));

	return(PointsToReturn);
}

Неплохо, правда? Мы уже проделали большую работу в классе LineSegment, поэтому нам просто последовательно соединить отрезки вместе для создания более сложных форм. Это позволяет нам с лёгкостью создавать на экране гораздо более сложные многоугольники (полигоны) простым добавлением новых LineSegment (и хранением большего количества точек в самом классе).

Теперь давайте посмотрим, как добавить в эту систему ещё точек, создав класс квадрата.


Работаем с квадратами




Для реализации класса управления четырёхугольниками нужно всего лишь добавить несколько дополнений в класс Triangle. С другим множеством точек класс четырёхугольника будет выглядеть так:

Quad Class
{
	Variables:
		int Point1X, Point1Y; //координаты четырёх точек четырёхугольника
		int Point2X, Point2Y;
		int Point3X, Point3Y;
		int Point4X, Point4Y;

 	Function:
		 array returnPointsInQuad; //возврат всех точек четырёхугольника
}

Теперь нам нужно просто добавить ещё один отрезок прямой в функцию returnPointsInQuad, вот так:

function returnPointsInQuad()
{
	array PointsToReturn; //создаём временный массив для хранения точек четырёхугольника

	//Создаём отрезки прямых и сохраняем их точки в массив
	PointsToReturn.push(new LineSegment(this.Point1X, this.Point1Y, this.Point2X, this.Point2Y));
	PointsToReturn.push(new LineSegment(this.Point2X, this.Point2Y, this.Point3X, this.Point3Y));
	PointsToReturn.push(new LineSegment(this.Point3X, this.Point3Y, this.Point4X, this.Point4Y));
	PointsToReturn.push(new LineSegment(this.Point4X, this.Point4Y, this.Point1X, this.Point1Y));

	return(PointsToReturn);
}

Хотя такой способ создания классов довольно прост, есть гораздо более лёгкий способ инкапсуляции всех полигонов в один класс. С помощью магии циклов и массивов мы можем реализовать класс полигонов, который сможет вмещать в себя формы почти любой сложности!


Работаем с полигонами


Для создания постоянно расширяющегося класса полигона нам нужны два серьёзных шага. Первый — поместить все точки в массив, который даст нам набросок класса, похожего на такой:

Polygon Class
{
	Variables:
		array Points; //содержит все точки полигона в массиве

	Function:
		array returnPointsInPolygon; //массив, содержащий все точки полигона
}

Второй — использование цикла для обхода всего неопределённого количества отрезков прямых в функции returnPointsInPolygon(), которая может выглядеть примерно так:

function returnPointsInPolygon
{
	array PointsToReturn; //временный массив для хранения точек полигона

	//циклический обход всех точек в полигоне с перемещением по одной паре координат за раз (с шагом два)
	for(int x = 0; x < this.Points.length; x+=2)
	{
		if(это не последняя точка)
		{
			//создаём отрезок прямой между этой точкой и следующей в массиве
			PointsToReturn.push(new LineSegment(this.Points[x], this.Points[x+1], this.Points[x+2], this.Points[x+3]));
		}
		else if(это последняя точка)
		{
			//создаём отрезок прямой между этой точкой и первой точкой массива
			PointsToReturn.push(new LineSegment(this.Points[x-2], this.Points[x-1], this.Points[0], this.Points[1]));
		}
	}

	//возврат массива точек
	return PointsToReturn;
}

Добавив в движок этот класс, мы можем одной строкой кода создавать что угодно — от треугольника до 39-стороннего чудовища.


Создатель полигонов


Чтобы поэкспериментировать с новым классом полигона, давайте создадим программу, демонстрирующую все его возможности. Наша программа позволит пользователю добавлять или удалять стороны отображаемого полигона с помощью клавиш. Разумеется, нужно сделать ограничение на количество сторон полигона, потому что при меньше чем трёх сторонах он перестаёт быть полигоном. Нас не очень волнует верхний предел сторон полигона, потому что он будет хорошо масштабироваться. Однако мы ограничим количество сторон десятью, потому что будем задавать новые точки в коде.

Спецификации программы можно разбить на следующие части:

  • Первоначальная отрисовка полигона на экране.
  • При нажатии клавиши A снижать количество сторон полигона на 1.
  • При нажатии клавиши S увеличивать количество сторон полигона на 1.
  • Количество сторон полигона не должно быть меньше 3.
  • Количество сторон полигона не должно быть больше 10.

Давайте посмотрим, как должен выглядеть наш код:

main{
	//настройка выбранного графического API
	//настройка клавиатурного ввода (может и не потребоваться)

	var camera = new Camera(); //создаём экземпляр класса камеры
	camera.objectsInWorld[]; //инициализируем массив объектов камеры

	//задаём пространство обзора камеры
	camera.minX = 0;
	camera.maxX = screenWidth;
	camera.minY = 0;
	camera.maxY = screenHeight;
	camera.minZ = 0;
	camera.maxZ = 100;

	//cоздаём массив точек для каждого размера полигонов
	var threeSides = new Array(100,100,100,50,50,50);
	var fourSides = new Array(points in here);
	var fiveSides = new Array(points in here);
	var sixSides = new Array(points in here);
	var sevenSides = new Array(points in here);
	var eightSides = new Array(points in here);
	var nineSides = new Array(points in here);
	var tenSides = new Array(points in here);

	//для удобства доступа сохраняем все массивы в другом массиве
	var sidesArray = new Array(threeSides, fourSides, fiveSides, sixSides, sevenSides, eightSides, nineSides, tenSides);

	//отслеживаем текущее количество сторон полигона
	var polygonPoints = 3;

	//создаём изначальный отображаемый полигон
	var polygon = new Polygon(sidesArray[0][0], sidesArray[0][1], sidesArray[0][2], sidesArray[0][3], sidesArray[0][4], sidesArray[0][5],);
	//отрисовываем изначальный полигон на экране
	camera.drawScene();

	//пока пользователь не нажал клавишу escape
	while(key != esc) {
		if(key pressed == 'a')
		{
			//если количество сторон полигона не может стать меньше 3
			if(polygonPoints != 3)
			{
				//уменьшить количество точек
				polygonPoints--;
				//изменяем полигон, чтобы он имел нужное количество точек
			}
			//перерисовка сцены
			camera.drawScene();
		}
		else if(key pressed == 's')
		{
			//если количество сторон полигона не может стать больше 10
			if(polygonPoints != 10)
			{
				//увеличиваем количество точек
				polygonPoints++;
				//изменяем полигон, чтобы он имел нужное количество точек
			}
			//перерисовка сцены
			camera.drawScene();
		}
	}
}

Наша маленькая программа теперь позволит вам менять полигон на экране! Если вы хотите сделать программу немного мощнее, то можете добавить в часть с изменением полигона какой-нибудь алгоритм для упрощения масштабирования. Не знаю, существует ли он, но если да, то вы с лёгкостью можете получить бесконечно масштабируемый полигон!


Заключение


Теперь в нашем движке довольно много операций растеризации, что позволяет нам создать почти любую необходимую форму (однако некоторые из них потребуют комбинирования). В следующей части мы отойдём от рисования форм и поговорим о других свойствах. Если вам интересно добавить на экран немного цвета, то читайте следующую часть!

Часть 5: цвета


Наш теоретический движок уже содержит почти всё необходимое, а именно:

  • Классы Point и Vector (строительные кирпичики движка).
  • Функции преобразований точек.
  • Класс Camera (задаёт область видимости и отсекает точки за пределами экрана).
  • Три класса для растеризации (отрезков прямых, окружностей и полигонов).

Теперь давайте добавим цвета!


Цвет для всех!


Наш движок будет обрабатывать цвета, храня их значения в классе Point. Это позволит каждой точке иметь собственный цвет, что намного упростит расчёты освещения и затенения (по крайней мере, для человека — иногда такой код движка менее эффективен). При вычислении освещения и затенения сцены мы можем создать функцию со списком точек и обработать все их с учётом расстояния до источника света, чтобы соответствующим образом изменить их цвет.

Один из самых стандартных способов хранения цвета в программировании — использование красного, зелёного и синего значений (обычно это называется аддитивным смешением цветов). Сохраняя значение от 0 до 255 каждого из компонентов цвета, можно создать большую палитру цветов. (Таким образом определяют цвет большинство API, поэтому для совместимости логично использовать этот способ).

В зависимости от используемого графического API эти значения можно передавать или в десятеричном (255,0,0), или в шестнадцатеричном виде (0xFF0000 или #FF0000). Мы будем использовать десятеричный формат, потому что с ним гораздо проще работать. Кроме того, если ваш графический API использует шестнадцатеричные значения, то в нём скорее всего есть функция для преобразования десятеричных значений в шестнадцатеричные, то есть это не будет проблемой.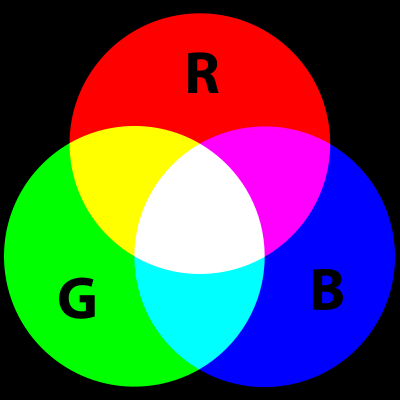



Чтобы начать реализацию цветовой модели, мы добавим три новых переменных в класс Point: red, blue и green. Пока не происходит ничего непонятного, но вот как должен теперь выглядеть набросок нашего класса Point:

Point Class
{
	Variables:
		num tuple[3]; //(x,y,z)
		num red, green, blue; //при желании можно сократить до r, g, b
	Operators:
		Point AddVectorToPoint(Vector);
		Point SubtractVectorFromPoint(Vector);
		Vector SubtractPointFromPoint(Point);
		Null SetPointToPoint(Point);
	Functions:
		drawPoint; //отрисовка точки в её кортеже положения
}

Вот и всё, что нам нужно для хранения цвета точки. Теперь нам просто нужно изменить функцию отрисовки камеры, чтобы она использовала указанный цвет.

Вид функции очень сильно зависит от используемого графического API, но во всех интерфейсах обычно есть похожая функция:

object.setColor(red, green, blue)

Если в вашем графическом API используются шестнадцатеричные, а не десятеричные значения цвета, то функция будет выглядеть примерно так:

object.setColor(toHex(red,green,blue))

В этой строке используется функция toHex() (повторюсь, в разных API названия функций будут разными), преобразующая значение RGB в шестнадцатеричное значение, чтобы не пришлось этого делать вручную.

Внеся эти изменения, вы сможете получить в сцене цветные точки. На следующем этапе мы дополним классы растеризации, чтобы можно было раскрашивать формы целиком.

Чтобы добавить в классы такую возможность, мы просто должны добавить к функциям конструкторов управление цветом. Это может выглядеть так:

lineSegment::constructor(startX, startY, endX, endY, red, green, blue)
{
    this.startX = startX;
    this.startY = startY;
    this.endX = endX;
    this.endY = endY;
    this.red = red;
    this.green = green;
    this.blue = blue;
}

Теперь нам просто нужно изменить функцию возвращаемых им точек, чтобы каждая точка в массиве имела указанный цвет. Новая функция будет выглядеть так:

function returnPointsInSegment()
{
    //создаём список для хранения всех точек отрезка прямой
    var pointArray = new Array();
    //задаём переменные функции на основании начальной и конечной точек класса
    var x0 = this.startX;
    var y0 = this.startY;
    var x1 = this.endX;
    var y1 = this.endY;
    //вычисляем разность векторов и другие переменные, необходимые для алгоритма Брезенхэма
    var dx = Math.abs(x1-x0);
    var dy = Math.abs(y1-y0);
    var sx = (x0 & x1) ? 1 : -1; //шаг по x
    var sy = (y0 & y1) ? 1 : -1; //шаг по y
    var err = dx-dy; //получаем начальное значение ошибки
    //задаём первую точку в массиве
    pointArray.push(new Point(x0,y0,this.red,this.green,this.blue));

    //Основной цикл обработки
    while(!((x0 == x1) && (y0 == y1)))
    {
        var e2 = err * 2; //содержит значение ошибки
        //используем значение ошибки определения того, в какую сторону нужно округлять точку (вверх или вниз)
        if(e2 => -dy)
        {
            err -= dy;
            x0 += sx;
        }
        if(e2 < dx)
        {
            err += dx;
            y0 += sy;
        }
        //добавляем новую точку в массив
        pointArray.push(new Point(x0, y0,this.red,this.green,this.blue));
    }
    return pointArray;
}

Теперь каждая точка на отрезке прямой имеет одинаковый цвет, переданный в отрезок прямой. Можно использовать этот способ для задания цветов и других классов растеризации, и тогда ваша сцена будет раскрашена разными цветами!

Давайте используем наши новые возможности, написав программу.


Экспериментируем с 16,7 миллиона цветов


С помощью аддитивного смешения цветов мы с лёгкостью можем создать больше 16,7 миллиона цветов, используя простую запись (r,g,b). Мы создадим программу, которая пользуется всем этим огромным количеством цветов.

Мы позволим пользователю с помощью нажатий клавиш отдельно управлять красным, зелёным и синим компонентами цвета и он сможет выбрать любой понравившийся цвет.

Программа будет иметь следующие спецификации:

  • Отрисовка объекта на экране.
  • При нажатии клавиши A значение красного компонента снижается, при нажатии Q — увеличивается.
  • При нажатии клавиши S значение зелёного компонента снижается, при нажатии W — увеличивается.
  • При нажатии клавиши D значение синего компонента снижается, при нажатии E — увеличивается.
  • Перерисовка объекта после обновления цвета.
  • Необходимо ограничивать значения компонентов и не давать им уходить за пределы от 0 до 255.

С учётом всего этого давайте посмотрим на то, как может выглядеть набросок нашей программы:

main{

    //настройка выбранного графического API
    //настройка клавиатурного ввода (может и не потребоваться)

    var camera = new Camera(); //создаём экземпляр класса камеры

    //задаём пространство обзора камеры
    camera.minX = 0;
    camera.maxX = screenWidth;
    camera.minY = 0;
    camera.maxY = screenHeight;
    camera.minZ = 0;
    camera.maxZ = 100;

    //храним цвет, чтобы им можно было управлять
    var red, green, blue;

    //отрисовка изначального объекта и присваивание его переменной

    while(key != esc) {
        if(key press = 'a')
        {
            if(red > 0)
            {
                red --;
                object.red = red;
                //перерисовка объекта
            }
        }
        if(key press = 'q')
        {
            if(red < 255)
            {
                red ++;
                object.red = red;
                //перерисовка объекта
            }
        }
        if(key press = 's')
        {
            if(green > 0)
            {
                green --;
                object.green = green;
                //перерисовка объекта
            }
        }
        if(key press = 'w')
        {
            if(green < 255)
            {
                green ++;
                object.green = green;
                //перерисовка объекта
            }
        }
        if(key press = 'd')
        {
            if(blue > 0)
            {
                blue --;
                object.blue = blue;
                //перерисовка объекта
            }
        }
        if(key press = 'e')
        {
            if(blue < 255)
            {
                blue ++;
                object.blue = blue;
                //перерисовка объекта
            }
        }
    }
}

Теперь мы можем поэкспериментировать с объектом и придать ему любой цвет!



Заключение


Мы добавили в движок цвет и теперь у нас есть всё необходимое для работы с освещением. В следующей части мы рассмотрим процесс создания источником освещения и напишем функции, позволяющие этим источникам влиять на цвета точек.

Часть 7: динамическое освещение


В этой части мы рассмотрим только самые основы динамического освещения, так что не слишком пугайтесь (вся эта тема очень обширна и о ней пишут целые книги).

Если конкретнее, то мы будем создавать одноточечную одноцветную систему динамического освещения с постоянным радиусом. Но прежде чем начать, давайте рассмотрим некоторые из ранее созданных классов, которые нам пригодятся.


Повторение


Наше динамическое освещение будет обрабатываться для каждой точки в процессе их вывода на экран. Это значит, что мы будем активно использовать два наших предыдущих класса: класс Point и класс Camera. Вот как они выглядят:

Point Class
{
	Variables:
		num tuple[3]; //(x,y,z)
	Operators:
		Point AddVectorToPoint(Vector);
		Point SubtractVectorFromPoint(Vector);
		Vector SubtractPointFromPoint(Point);
		Null SetPointToPoint(Point);
	Functions:
		drawPoint; //отрисовывает точку в кортеже её положения
}

Camera Class
{
    Vars:
        int minX, maxX;
        int minY, maxY;
        int minZ, maxZ;
        array objectsInWorld; //массив всех существующих объектов
    Functions:
        null drawScene(); //отрисовывает все нужные объекты на экран
}

Давайте создадим на основе этой информации простой класс освещения.


Класс освещения



Пример динамического освещения. Источник: http://redeyeware.zxq.net

Для работы класс освещения потребуется некоторая информация, а именно положение, цвет, тип и интенсивность (или радиус освещения).

Как я говорил ранее, освещение будет рассчитываться для каждой точки перед её отрисовкой. Преимущества такого подхода в том, что это проще для структуры движка и переносит большую часть нагрузки программы на центральный процессор. Если вы будете вычислять освещение предварительно, то нагрузка переместится на жёсткий диск компьютера и в зависимости от конструкции движка это будет реализовать легче или сложнее.

С учётом всего этого класс будет выглядеть примерно так:

Lighting Class
{
	Variables:
		num position[3]; //(x,y,z)
		num red = 255; //значение, прибавляемое к значению r точки при полной интенсивности
		num green = 255; //значение, прибавляемое к значению g точки при полной интенсивности
		num blue = 255; //значение, прибавляемое к значению b точки при полной интенсивности
		string lightType = "point"; //тип освещения
		num radius = 50; //радиус источника света в пикселях
}

Пока мы для простоты оставим все эти значения жёстко заданными, но если вы захотите расширить возможности классов освещения, то легко сможете изменять эти значения через другие функции, конструктор и т.д.

Однако все важные вычисления для динамического освещения будут выполняться в классе камеры, поэтому давайте рассмотрим его.


Свет? Камера? Мотор.



Ещё один пример динамического освещения. Источник: http://blog.illuminatelabs.com/2010/04/hdr-and-baked-lighting.html

Теперь мы добавим в класс камеры новую переменную, которую используем для хранения источника света. Пока эта переменная будет содержать только один экземпляр источника, но её можно легко расширить, чтобы можно было хранить несколько точечных источников.

Непосредственно перед отрисовкой точки мы будем проверять, находится ли она в радиусе источника света. Если находится, то нам нужно найти расстояние между точкой и положением источника, а затем изменить цвет точки в соответствии с расстоянием.

С учётом всего этого мы можем добавить код, похожий на код из функции камеры drawScene():

if(currentPoint.x >= (light.x - light.radius)){ //если точка находится в пределах левой границы источника
	if(currentPoint.x <= (light.x + light.radius)){ //если точка находится в пределах правой границы источника
		if(currentPoint.y >= (light.y - light.radius)){ //если точка находится в пределах верхней границы источника
			if(currentPoint.y <= (light.y + light.radius)){ //если точка находится в пределах нижней границы источника
				//вычисление расстояния между точкой и источником (distance)
				//вычисление процента применяемого освещения (percentage = distance / radius)
				point.red += (light.red * percentage); //прибавляем красный компонент освещения, уменьшенный в соответствии с расстоянием
				point.green += (light.green * percentage); //прибавляем зелёный компонент освещения, уменьшенный в соответствии с расстоянием
				point.blue += (light.blue * percentage); //прибавляем синий компонент освещения, уменьшенный в соответствии с расстоянием
			}
		}
	}
}

Как вы видите, наш способ изменения цвета точки пока не слишком сложен (однако существуют и многие другие, которые можно при желании использовать). Мы меняем цвет точки на процент, зависящий от расстояния до центра источника освещения. Наш способ освещения совершенно не учитывает затенения, поэтому далёкие от источника света точки не становятся темнее, а объекты не перекрывают свет от других объектов, которые могут находиться за ними.


Следуй за светом


На этот раз в программе мы будем использовать несколько постоянных форм на экране. Вы можете выбрать любые формы, но в нашем примере я использую несколько простых точек. Когда пользователь нажимает мышью на экране, мы создаём в этой точке источник света. При следующем нажатии мы перемещаем точку в новое положение, и так далее. Это позволит нам понаблюдать за динамическим освещением в действии.

Вот как может выглядеть программа:

main{

    //настройка выбранного графического API
    //настройка клавиатурного ввода (может и не потребоваться)

    var camera = new Camera(); //создаём экземпляр класса камеры

    //задаём пространство обзора камеры
    camera.minX = 0;
    camera.maxX = screenWidth;
    camera.minY = 0;
    camera.maxY = screenHeight;
    camera.minZ = 0;
    camera.maxZ = 100;

    //отрисовка изначальных объектов и расположение их в пространстве камеры

    while(key != esc) {
        if(mouseClick) {
                if(firstClick) {
                        //создание изначального объекта источника света в точке курсора мыши
                }
                else {
                        //изменение положения объекта источника освещения
                }
                camera.drawScene();
        }
    }

Теперь вы сможете оценить динамическое освещение в действии и увидеть, какую глубину оно добавляет игровому движку.


Заключение


Хотя наше динамическое освещение и простое, его можно при желании запросто расширить. Некоторые довольно простые, но интересные дополнения:

  • изменяемый радиус освещения
  • изменяемый цвет освещения (вместо однообразного изменения цвета можно изменять его на часть заданного цвета)
  • блокировка света сплошными объектами
  • обработка нескольких источников света
  • добавление тени всем точкам за пределами радиуса источника света
  • эксперименты с другими типами источников (направленный, конический и т.д.)

Комментарии (11)


  1. da-nie
    04.08.2017 14:26
    #10343728
    +1

    Это давным-давно описано хотя бы тем же Боресковым в «Компьютерная графика. Полигональные модели» для широких масс (году так в 2000). И в статье описан вовсе не движок, а только основы 3D преобразований — это библиотека растеризации и преобразований координат. С потерявшимся по дороге текстурированием (которое на ваших картинках-таки есть). К сожалению, всё это будет тормозить даже на самых современных системах без системы эффективного удаления невидимых граней (запустите Duke Nukem 3d for Windows на 1024x768 (или выше) и посмотрите, как уменьшается FPS по сравнению с 320x200 и 640x480 — так тут ещё портал грани отсекает с высокой эффективностью, а представляете, как работать без отсечения будет?).


    1. BogdanF
      04.08.2017 14:38
      #10343756

      Да я думаю, тут с реализацией довольно длинно будет, как то не тот формат. На эту тему книги, всё таки, есть.


    1. brzsmg
      04.08.2017 15:13
      #10343814
      +2

      Согласен, невозможно создать полноценную статью «Создаём собственный программный 3D-движок», потому что это слишком огромное количество информации:
      1. Математические объекты и операции с ними (точки, векторы, матрицы, кватернионы).
      2. Организация объектов их атрибутов, и операции с ними (движение, вращение, масштабирование).
      3. Рендеринг (flustrum, текстуры, материалы, шейдеры).
      4. Ввод (Клавиатура, Мышь, Джойстик, VR).
      5. Жизненный цикл (сцена, время, Коллизии, ИИ).

      Только эти 5 пунктов, тянут на несколько томов статей. Но даже описав их все равно для полноценного движка не будет хватать всяких:
      Звука, Освещения, Туманов, Теней, Скриптов, UI, BSP, Порталов, Физики, Карт высот, Поисков путей, Зеркал, Триангуляций, Сети, Видеороликов, и тд.


      1. BogdanF
        04.08.2017 15:44
        #10343894

        Ну то уже отдельные вещи, имеется ввиду ведь только отображение 3D пространства на мониторе, так что некоторую часть из приведенного вами списка можно убрать и отдать на аутсорсинг, ну, то есть, ввод и звук — это отдельные заботы :) Но так то, по меньшей мере, нужен OpenGL или D3D. Но начинать то с чего то надо? Вот как раз не хватает часто, для изучения чего то нового, некой «эссенции», основных положений. Те же языки проще изучать, когда берешь основу, главные конструкции, а вдаёшься в мелкие подробности уже по мере надобности.


  1. BogdanF
    04.08.2017 14:36
    #10343746

    Спасибо за перевод! Доступное изложение материала по теме основных концепций, без лишних подробностей, что и необходимо новичку. Хорошая статья.


  1. merl1n
    04.08.2017 16:52
    #10344100

    Почти все начинают со своего 3d движка :)


    1. da-nie
      04.08.2017 17:04
      #10344130
      +1

      Только почему-то почти никто их не показывает. :)


    1. BogdanF
      05.08.2017 04:59
      #10344924

      Смотря что начинать. Лично мне просто любопытно сделать какую нибудь простенькую вещь на GLEW/GLFW, чтобы она перемещалась, вращалась, свистела и п…


  1. temnayanoch
    05.08.2017 00:56
    #10344818

    > аксиома — это логическое утверждение, считаемое достаточно очевидным для принятия без доказательств. 
    Аксиома это скорее правило, по которому строится та или иная теория. Поэтому аксиома считается истиной, так как если это не так, то это будет уже другая теория.


  1. alex_zzzz
    06.08.2017 02:31
    #10345644

    Вряд ли имеет смысл выделять точки и вектора в отдельные типы. Во-первых, иногда точку удобнее воспринимать как её смещение относительно начала координат, и тогда это уже не очень точка. Во-вторых, геометрических смыслов у векторов даже не два, а три: точка, смещение и направление. И если уж использовать отдельные типы, то их надо тоже три, плюс четвёртый ? абстрактный вектор, где в одном месте будут собраны все полезные для работы с векторами математические операции.


    Проще работать с абстрактными векторами, не забывая конечно про геометрический смысл каждого конкретного вектора:


    1. Точка. Вектор задаёт её координаты относительно начала координат.


    2. Смещение. Вектор задаёт его направление и дальность. Смещение относительно, к началу координат не привязано.


    3. Направление. Например, нормаль треугольника, нормаль к поверхности в какой-то точке, направление взгляда персонажа, ось вращения. У такого вектора главное ? направление. Длина не принципиальна, но очень удобно, чтобы она всегда была единичной.

    Имеется три основных типа преобразований при переводе вектора из одной системы координат в другую: поворот, масштабирование и перенос. Геометрический смысл вектора определяет, какие преобразования к нему нужно применять, а какие не нужно:


    1. К точке надо примерять все три: поворот, масштабирование и перенос.


    2. К смещению только два: поворот и масштабирование. Перенос изменяет длину вектора смещения, а она при переносе меняться не должна.


    3. Для вектора направления важен только поворот. Применение переноса нарушает и направление вектора и его длину. Равномерное по всем осям масштабирование сохранит направление, но нарушит единичную длину; неравномерное масштабирование нарушит всё.


  1. alex_zzzz
    06.08.2017 02:53
    #10345666

    Система координат, которую мы будем использовать, обладает очень ценным свойством: взаимной перпендикулярностью. Это значит, что в пересечении каждой из осей на своей соответствующей плоскости угол между ними равен 90 градусам.

    Нашу систему координат можно также назвать «правой»:
    [картинка]
    Источник: http://viz.aset.psu.edu/gho/sem_notes/3d_fundamentals/html/3d_coordinates.html.

    На языке математики это значит, что: X=Y?Z
    где ? обозначает оператор векторного произведения.

    Текст читается так, словно равенство X=Y?Z выполняется только для правосторонней системы координат. Хотя на самом деле в левосторонней оно верно тоже.