
Что такое октодеревья? Если вам совершенно неизвестно это понятие, то рекомендую прочитать статью в Википедии (это займёт около пяти минут). Она даёт достаточное представление, но едва ли её будет достаточно, чтобы понять, для чего они используются и как их реализовать.
В этой статье я постараюсь рассказать обо всех этапах, необходимых для создания структуры данных октодеревьев, на примере объяснения концепций, иллюстраций и кода. Также я опишу свои решения, которые принимал на каждом из этапов. Не думайте, что эта статья будет единственно верным руководством к реализации октодеревьев, но она должна дать вам хороший фундамент и её можно использовать для справки.
Необходимые знания
При написании этой статьи я предполагал, что читатель:
- Хорошо разбирается в программировании на языке с синтаксисом в стиле C (я буду использовать C# с XNA).
- Уже программировал какую-нибудь древообразную структуру данных, например, двоичное дерево поиска, знаком с рекурсией, её сильными и слабыми сторонами.
- Знает, как реализуется распознавание коллизий с граничными прямоугольниками, сферами и усечёнными пирамидами.
- Разбирается в стандартных структурах данных (массивах, списках и т.д), понимает, что такое большое «O» (про большое «O» можно также прочитать в этой статье GDnet).
- Работает над проектом, в котором есть пространственные объекты, нуждающиеся в проверке коллизий.
Подготовка сцены
Предположим, что мы создаём очень масштабную игру, в которой могут содержаться тысячи физических объектов разных типов, форм и размеров, и некоторые из них должны сталкиваться друг с другом. В каждом кадре нам придётся определять, какие объекты пересекаются друг с другом и каким-то образом обрабатывать эти пересечения. Как это сделать, чтобы скорость игры не падала?

Распознавание коллизий простым перебором
Простейший способ решения — сравнивать каждый объект со всеми объектами в мире. Обычно это можно сделать в двух циклах for. Код будет выглядеть примерно так:
foreach(gameObject myObject in ObjList)
{
foreach(gameObject otherObject in ObjList)
{
if(myObject == otherObject) continue; //не проверяем коллизию объекта с ним самим
if(myObject.CollidesWith(otherObject))
{
//код обработки коллизии
}
}
}Графически это можно представить так:
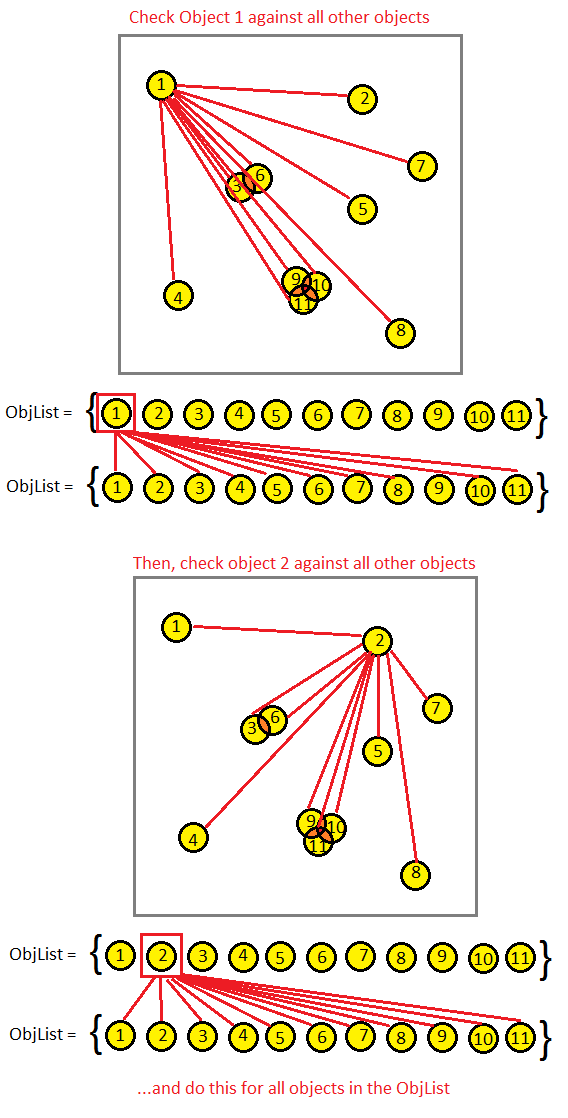
Каждая красная линия — это затратная проверка пересечений в ЦП.
Естественно, такой код должен привести вас в ужас, потому что он будет выполняться O(N2) раз. Если у нас будет 10 000 объектов, то придётся выполнять 100 000 000 проверок коллизий (сто миллионов). Неважно, насколько быстрый у вас процессор и насколько вы усовершенствовали математический код — такая программа будет тормозить в компьютере. Если игра работает с 60 кадрами в секунду, то в секунду будет выполняться 60 * 100 миллионов вычислений! Это совершенное безумие.
Если можно этого избежать, давайте не будем так делать, по крайней мере, для больших множеств объектов. Это будет приемлемо только если, допустим, проверка выполняется всего для 10 объектов (100 проверок). Если вы заранее знаете, что в игре будет мало объектов (например, астероидов), то, возможно, вам вполне подойдёт простой перебор и от октодеревьев можно полностью отказаться. Если вы начали замечать проблемы с производительностью из-за слишком большого количества проверок коллизий за кадр, можно использовать очень простые оптимизации:
1. Сколько вычислений требуется для вашей процедуры расчёта коллизий? Может быть, в ней где-то скрыто вычисление квадратного корня (например, в проверке расстояний)? Выполняете ли вы детализированную проверку коллизий (пересечения пикселей, треугольников и т.д.)? Есть стандартная техника: сначала выполняйте грубую проверку коллизий, а потом переходите к более детальной. Можно добавить объектам описывающую их прямоугольную или сферическую границу и проверять пересечение между границами, а потом уже выполнять детализированную проверку, требующую больше математических вычислений и ресурсов.
Для сравнения расстояний между объектами используйте проверку квадрата расстояния между объектами, чтобы избежать вычисления квадратного корня. Для вычисления квадратного корня обычно используется аппроксимация методом Ньютона и оно может быть очень затратным.
2. Можно ли обойтись вычислением меньшего количества проверок коллизий? Если игра работает с частотой 60 кадров в секунду, можно ли пропустить несколько кадров? Если поведение некоторых объектов детерминировано, то их коллизии можно вычислить заранее (например, между бильярдным шаром и бортом стола). Можно ли уменьшить количество объектов, для которых выполняется проверка? Попробуйте разделить объекты в разные списки. В одном списке могут быть «стационарные» объекты. Их коллизии между друг другом можно никогда не проверять. В другом списке могут находиться «подвижные» объекты, для которых нужно проверять коллизии со всеми другими подвижными и всеми стационарными объектами. Это может снизить количество необходимых проверок коллизий до приемлемого с точки зрения производительности уровня.
3. Можно ли отказаться от проверки коллизий некоторых объектов, когда возникают проблемы с производительностью? Например, частица дыма может взаимодействовать с объектом поверхности и следовать за его контурами для создания красивого эффекта, но это не должно мешать геймплею. Если количество проверок превышает определённый предел, то можно прекратить вычисление коллизий для частиц дыма. Однако игнорирование движения важных игровых объектов тоже разрушит игровой процесс (например, пули игрока перестанут взаимодействовать с монстрами). То есть полезно будет хранить список приоритетов проверок коллизий. Сначала обрабатываются коллизии с высоким приоритетом, и если предел не превышен, то можно обработать коллизии с низким приоритетом. При достижении предела игра должна отбрасывать все оставшиеся элементы в списке приоритетов или откладывать их проверку на будущее.
4. Можно ли использовать более быстрый, но всё равно простой способ распознавания коллизий, чтобы избавиться от O(N2) во время выполнения? Если устранить объекты, для которых уже проверены коллизии, то вы снизите время выполнения до O(N(N+1)/2), что гораздо быстрее, но всё равно довольно просто реализовать (технически, это по-прежнему O(N2)). С точки зрения разработки ПО, вы можете потратить в результате больше времени, чем стоит, для выжимания капель производительности из улучшения плохого алгоритма и неверно выбранной структуры данных. Соотношение затрат и преимуществ становится всё невыгоднее и наступает время выбрать для обработки распознавания коллизий более подходящую структуру данных.
Как решение проблемы распознавания коллизий во время выполнения активно используются алгоритмы разбиения пространства. Они заранее отбирают небольшую часть скорости, зато логарифмически снижают количество проверок коллизий. Предварительные затраты времени разработки и ЦП легко перевешиваются преимуществами масштабируемости и увеличения скорости.
Концепция разбиения пространства
Давайте сделаем шаг назад и прежде чем переходить к октодеревьям, рассмотрим идею разбиения пространства и деревьев в целом. Если вы не поймёте эту концепцию, то никак не сможете реализовать её в коде.
В реализации простого перебора выше мы брали каждый объект в игре и сравнивали его положение с положениями всех других объектов, чтобы проверить, касаются ли они. Все эти объекты пространственно расположены в мире игры. Если мы создадим фигуру, ограничивающую игровой мир и выясним, какие из объектов содержатся в этой фигуре, то у нас будет область пространства со списком содержащихся в нём объектов. В нашем случае он будет содержать все объекты игры.
Мы можем заметить, что один объект находится в одном конце мира, а другой — в противоположном, поэтому нам не нужно вычислять проверки коллизий между ними в каждом кадре. Это будет пустой тратой драгоценного времени процессора. Давайте попробуем сделать что-нибудь интересное! Если мы разделим мир ровно пополам, то можем создать три отдельных списка объектов.
В первом списке, List A, будут содержаться все объекты в левой части мира.
Во втором списке, List B, содержатся объекты правой части мира.
Некоторые объекты могут касаться разделительной линии между частями, то есть находиться по обе её стороны. Для таких объектов мы создадим третий список, List C.

Можно заметить, что при каждом разделении мы пространственно уменьшаем мир вдвое и собираем список объектов, оказавшихся в полученной половине. Для хранения этих списков мы можем создать двоичное дерево поиска. Концепция такого дерева будет выглядеть примерно так:
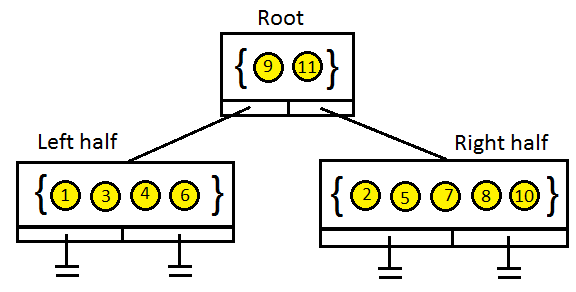
Структура данных дерева в псевдокоде выглядит примерно так:
public class BinaryTree
{
//Это список всех объектов, содержащихся в этом узле дерева
private List m_objectList;
//Это указатели на левый и правый дочерние узлы дерева
private BinaryTree m_left, m_right;
//Это указатель на родительский объект (для обхода дерева вверх).
private BinaryTree m_parent;
}Мы знаем, что все объекты в List A никогда не будут пересекаться с объектами в List B, поэтому можно отказаться почти от половины проверок коллизий. У нас по-прежнему есть объекты в List C, которые могут касаться объектов в списках A и B, поэтому нужно будет проверять все объекты List C на коллизии со всеми объектами в списках A, B и C.
Если мы продолжим разделять мир на всё меньшие и меньшие части, то и дальше будем уменьшать количество проверок, каждый раз наполовину. Вот в этом заключается основная идея разбиения пространства. Существует множество способов разбиения мира в древоподобную структуру данных (двоичное разбиение пространства (BSP), деревья квадрантов, K-мерные деревья, октодеревья, и т.д.).
Теперь мы просто будем по умолчанию предполагать, что наилучшим разбиением будет деление пополам, ровно посередине, потому что мы считаем, что все объекты распределены по миру приблизительно равномерно. Это неплохое предположение, но в некоторых алгоритмах разбиения пространства выполняют разбиение таким образом, чтобы в каждой из половин было равное количество объектов (взвешенное разделение), чтобы получившееся дерево было бы более сбалансированным. Однако что случится, если все эти объекты начнут двигаться? Чтобы поддерживать примерно равное разбиение, придётся или перемещать секущую плоскость, или полностью перестраивать дерево в каждом кадре. Это довольно запутанно и сложно.
Поэтому для своей реализации дерева разбиения пространства я решил каждый раз делить его пополам. В результате некоторые деревья окажутся более разреженными, но это нормально и не приведёт к большим затратам.
Делить иль не делить? Вот в чём вопрос.
Предположим, у нас есть довольно разреженная область всего с несколькими объектами. Мы можем продолжить выполнять разбиение, пока не обнаружим минимально возможное ограничивающее пространство для последнего объекта. Но необходимо ли это? Вспомним, что причиной создания дерева стало снижение количества проверок коллизий, выполняемых в каждом кадре, а не создание идеально ограничивающей каждый объект области пространства. Вот какие правила я выбрал для принятия решения о том, нужно разбиение или нет:
- Если мы создаём разделение, в котором будет только один объект, то мы прекращаем разбиение, несмотря на то, что можем разбивать пространство и дальше. Это правило будет важной частью критериев, определяющих «узел листа» в октодереве.
- Ещё один важный критерий — задание минимального размера области. Если у вас есть очень мелкий объект размером в несколько нанометров (или в коде есть баг и вы забыли инициализировать размер объекта!), то разделение продолжится и потенциально вы можете переполнить стек вызовов. Для своей реализации я выбрал минимальную область — куб размером 1x1x1. Для всех объектов в этом кубе нужно будет выполнять проверку коллизий простым перебором (O(N2)) (Я не рассчитываю на большее количество объектов!).
- Если область не содержит объектов, я не буду добавлять её в дерево.
Можно сделать ешё один шаг в разбиении пополам и делить двухмерное пространство мира на квадранты. Логика, в сущности, та же самая, но теперь мы проверяем коллизии между четырьмя квадратами, а не двумя прямоугольниками. Мы можем продолжать разбиение, пока не будут удовлетворены условия завершения. Пространство мира и соответствующая структура данных для дерева квадрантов будут выглядеть примерно так:
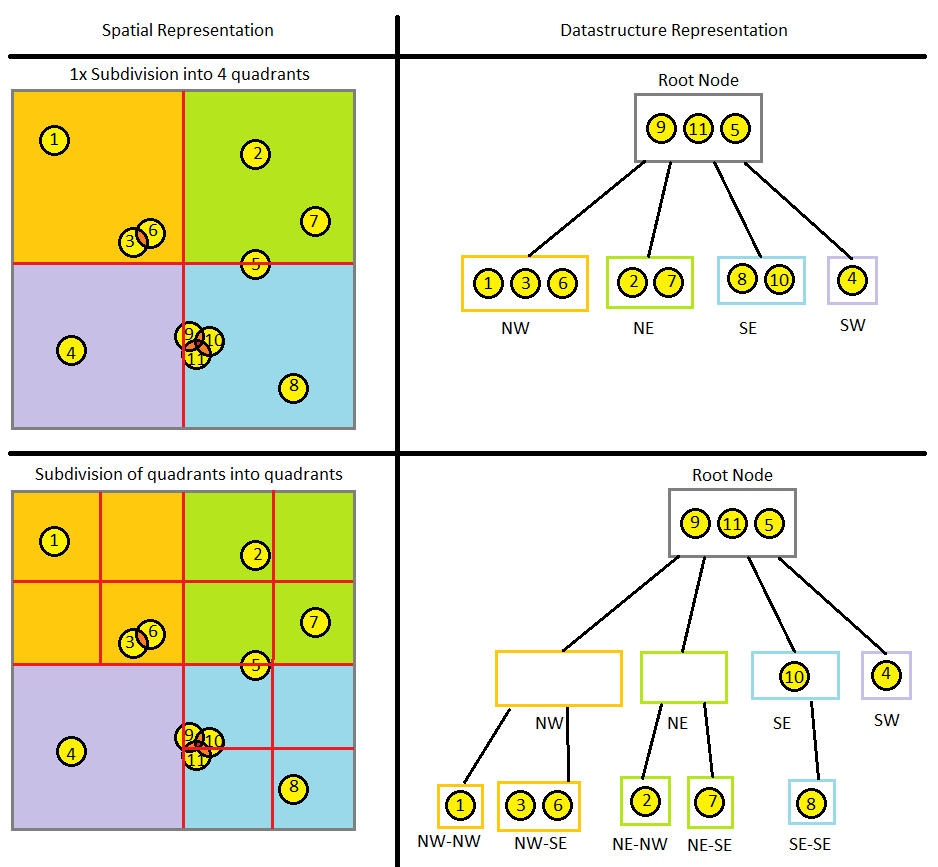
Если разбиение на дерево квадрантов и структура данных выглядят для вас логично, то и октодерево тоже будет понятным. Мы просто добавляем третье измерение и используем ограничивающие кубы, а не квадраты, то есть у нас будет восемь, а не четыре возможных дочерних узлов. Можно задаться вопросом — что будет, если игровой мир имеет некубические размеры, например, 200x300x400. Всё равно можно использовать октодерево с кубическими размерами — некоторые дочерние узлы просто окажутся пустыми, если в них в пространстве мира ничего нет. Очевидно, нужно, чтобы размеры октодерева были как минимум равны большей из размерностей игрового мира.
Создание октодеревьев
Итак, как вы уже прочитали, октодерево — это особый тип дерева разбиения, обычно используемый для объектов в трёхмерном пространстве (или чего угодно с тремя размерностями). Ограничивающей областью будет трёхмерный прямоугольник (параллелепипед) (обычно это куб). Затем мы применяем описанную выше логику и разрезаем ограничивающую область на восемь меньших параллелепипедов. Если игровой объект целиком помещается в одну из этих подразделённых областей, мы спускаем его вниз по дереву в узел содержащей его области. Затем мы продолжаем рекурсивно разделять каждую получившуюся область, пока не выполнится одно из условий завершения. В результате у нас должна получиться красивая древообразная структура данных.
В моей реализации октодерева будут содержаться объекты, имеющие ограничивающую сферу и/или ограничивающий параллелепипед. Вы увидите, что я применяю большой объём кода для определения того, какая ограничивающая фигура используется.
Для структуры данных класса Octree я выбрал для каждого дерева следующие правила:
- Каждый узел имеет ограничивающую область, определяющую включающую его область
- Каждый узел имеет ссылку на родительский узел
- Содержит массив восьми дочерних узлов (массивы используются для простоты кода и скорости кеша)
- Содержит список объектов, находящихся в текущей области
- Я использовал битовую маску размером в байт для определения того, какие дочерние узлы активно используются (преимущества оптимизации ценой дополнительной сложности — довольно спорный вопрос)
- Для указания состояния дерева я использовал несколько статичных переменных
Вот код наброска моего класса Octree:
public class OctTree
{
BoundingBox m_region;
List m_objects;
///
/// Это объекты, которые мы будем вставлять в структуру данных.
/// Здесь мы хотим накопить как можно больше объектов, прежде чем вставлять их в дерево. Это будет более удобно для кеширования.
///
static Queue m_pendingInsertion = new Queue();
///
/// Это все возможные дочерние октанты этого узла дерева.
///
OctTree[] m_childNode = new OctTree[8];
///
/// Это битовая маска, показывающая, какие дочерние узлы активно используются.
/// Она немного добавляет сложности, но улучшает производительность, потому что используется всего одно сравнение вместо восьми.
///
byte m_activeNodes = 0;
///
/// Минимальный размер ограничивающей области - куб 1x1x1.
///
const int MIN_SIZE = 1;
///
/// количество кадров, после которого мы удаляем пустую ветвь дерева. заметьте, что это не константа. Максимальный срок жизни удваивается
/// при каждом повторном использовании узла, пока не "упрётся" в жёстко заданную константу (64)
///
int m_maxLifespan = 8; //
int m_curLife = -1; // это время обратного отсчёта, показывающий оставшийся срок жизни
///
/// Ссылка на родительский узел. Удобно использовать её при обновлении дерева.
///
OctTree _parent;
static bool m_treeReady = false; // у дерева есть несколько объектов, которые нужно вставить, прежде чем оно станет завершённым
static bool m_treeBuilt = false; // готового дерева ещё не существует
}Инициализация ограничивающей области
Первый шаг в создании октодерева — задание ограничивающей области всего дерева. Это будет ограничивающий параллелепипед для корневого узла дерева, который изначально содержит все объекты игрового мира. Прежде чем инициализировать ограничивающий объём, нам нужно принять решения относительно дизайна:
1. Что должно происходить, когда объект перемещается за пределы ограничивающего объёма корневого узла? Будем ли мы изменять размер всего дерева, чтобы были ограничены все объекты? Если да, то нам придётся полностью перестраивать октодерево с нуля. Если нет, то нужно найти какой-то способ обработки объектов за пределами границ, или сделать так, чтобы объекты никогда не выходили за границы.
2. Как мы будем создавать ограничивающую область для октодерева? Будем ли мы использовать заранее заданные размеры, например, параллелепипед 200x400x200 (X,Y,Z)? Или мы будем использовать кубические размеры. являющиеся степенью двойки? Что произойдёт, если минимальную допустимую ограничивающую область нельзя будет разделить? Я решил, что буду использовать кубическую ограничивающую область с размерами, равными степени двойки, достаточно большую для полного ограничения всего мира. Минимальной допустимой областью будет куб размером 1x1x1 единиц. Благодаря этому я буду чётко делить мир и получать целые числа (даже несмотря на то, что Vector3 имеет формат с плавающей запятой). Также я решил, что моя ограничивающая область будет ограничивать весь мир, так что если объект покидает эту область, он будет уничтожаться. Для минимального октанта я буду выполнять проверку коллизий простым перебором. Но я ожидаю, что такую маленькую область будут занимать одновременно не более трёх объектов, так что затраты производительности O(N2) абсолютно приемлемы. Я стандартно инициализирую октодерево с помощью конструктора, получающего размер области и список объектов, вставляемых в дерево. Мне показалось, что не стоит показывать эту часть кода, потому что она элементарна, но добавил её для полноты.
Вот мои конструкторы:
/*Примечание: мы как можно дольше стараемся избежать выделения памяти, потому что у нас может быть множество узлов.*/
///
/// Создаём октодерево, которое ограничивает заданную область и содержит все переданные объекты.
///
/// Ограничивающая область октодерева.
/// Список объектов, содержащихся внутри ограничивающей области
private OctTree(BoundingBox region, List objList)
{
m_region = region;
m_objects = objList;
m_curLife = -1;
}
public OctTree()
{
m_objects = new List();
m_region = new BoundingBox(Vector3.Zero, Vector3.Zero);
m_curLife = -1;
}
///
/// Создание октодерева с предположением, что ограничивающая область содержит объекты.
///
/// Предполагаемые размеры ограничивающей области.
/// Примечание: если объекты находятся за пределами этой области, размер области будет автоматически изменён.
public OctTree(BoundingBox region)
{
m_region = region;
m_objects = new List();
m_curLife = -1;
}Создание первоначального октодерева
Я большой поклонинк отложенной инициализации. Я стараюсь избежать выделения памяти и совершения работы до того момента, когда это абсолютно необходимо. В случае октодерева я как можно дольше избегаю создания структуры данных. Мы получаем запрос пользователя на вставку объекта в структуру данных, но на самом деле мы не обязаны создавать дерево, пока кто-нибудь не запустит для него очередь.
Что это нам даёт? Ну, предположим, что процесс создания и обхода дерева будет довольно ресурсозатратен. Если пользователь хочет передать нам для вставки в дерево 1000 объектов, имеет ли смысл пересчитывать каждую последующую ограничивающую область тысячу раз? Или мы можем сэкономить часть времени и обработать их скопом?
Я создал «ожидающую» очередь элементов и несколько флагов, указывающих на состояние построения дерева. Все вставленные элементы поступают в ожидающую очередь и после завешения подготовки очереди все эти ожидающие запросы передаются и вставляются в дерево. Это особенно удобно при загрузке игры, потому что вы скорее всего одновременно будете вставлять тысячи объектов. После загрузки игрового мира количество объектов, вставляемых в дерево, оказывается на порядки меньше. Моя процедура отложенной инициализации содержится внутри метода UpdateTree(). Она проверяет, построено ли дерево, строит структуру данных, если она не существует и имеет отложенные объекты.
///
/// Обработка всех отложенных вставок их вставкой в дерево.
///
/// Нужно ли отказаться от этого?
private void UpdateTree() // завершено и протестировано
{
if (!m_treeBuilt)
{
while (m_pendingInsertion.Count != 0)
m_objects.Add(m_pendingInsertion.Dequeue());
BuildTree();
}
else
{
while (m_pendingInsertion.Count != 0)
Insert(m_pendingInsertion.Dequeue());
}
m_treeReady = true;
}Для построения самого дерева можно использовать её рекурсивно.
То есть для каждой рекурсивной итерации я начинаю со списка объектов, содержащихся в ограничивающей области. Я проверяю, соблюдены ли условия завершения, и если нет, то мы создаём восемь разделённых ограничивающих пространств, которые идеально вписываются в нашу ограничивающую область. Затем я обхожу каждый из объектов в заданном списке и проверяю, вписывается ли он полностью в один из октантов. Если вписывается, то я вставляю его в соответствующий список этого октанта. В самом конце я проверяю количества в соответствующих списках октантов, создаю новые октодеревья, присоединяю их к текущему узлу и помечаю в битовой маске те дочерние октанты, которые активно используются.
Все оставшиеся объекты передаются вниз от родительского узла, но их нельзя просто опустить вниз в любой из дочерних узлов. Поэтому логично, что это должен быть самый маленький октант, который может содержать этот объект.
///
/// Наивное построение октодерева с нуля.
///
private void BuildTree() //завершено и протестировано
{
//завершаем рекурсию, если мы находимся в узле листа
if (m_objects.Count <= 1)
return;
Vector3 dimensions = m_region.Max - m_region.Min;
if (dimensions == Vector3.Zero)
{
FindEnclosingCube();
dimensions = m_region.Max - m_region.Min;
}
//Проверяем, больше ли размеры параллелепипеда минимальных размеров
if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE)
{
return;
}
Vector3 half = dimensions / 2.0f;
Vector3 center = m_region.Min + half;
//Создаём подразделённые области для каждого октанта
BoundingBox[] octant = new BoundingBox[8];
octant[0] = new BoundingBox(m_region.Min, center);
octant[1] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z));
octant[2] = new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z));
octant[3] = new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z));
octant[4] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z));
octant[5] = new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z));
octant[6] = new BoundingBox(center, m_region.Max);
octant[7] = new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z));
//Здесь будут содержаться все наши объекты, которые входят в каждый из соответствующих октантов.
List[] octList = new List[8];
for (int i = 0; i < 8; i++) octList = new List();
//В этом списке содержатся все объекты, перемещённые вниз по дереву. Их можно удалить из списка этого объекта.
List delist = new List();
foreach (Physical obj in m_objects)
{
if (obj.BoundingBox.Min != obj.BoundingBox.Max)
{
for (int a = 0; a < 8; a++)
{
if (octant[a].Contains(obj.BoundingBox) == ContainmentType.Contains)
{
octList[a].Add(obj);
delist.Add(obj);
break;
}
}
}
else if (obj.BoundingSphere.Radius != 0)
{
for (int a = 0; a < 8; a++)
{
if (octant[a].Contains(obj.BoundingSphere) == ContainmentType.Contains)
{
octList[a].Add(obj);
delist.Add(obj);
break;
}
}
}
}
//Убираем из списка каждый перемещённый из этого узла объект.
foreach (Physical obj in delist)
m_objects.Remove(obj);
//Создаём дочерние узлы, в которых находятся элементы, содержащиеся в ограничивающей области
for (int a = 0; a < 8; a++)
{
if (octList[a].Count != 0)
{
m_childNode[a] = CreateNode(octant[a], octList[a]);
m_activeNodes |= (byte)(1 << a);
m_childNode[a].BuildTree();
}
}
m_treeBuilt = true;
m_treeReady = true;
}
private OctTree CreateNode(BoundingBox region, List objList) //завершено и протестировано
{
if (objList.Count == 0)
return null;
OctTree ret = new OctTree(region, objList);
ret._parent = this;
return ret;
}
private OctTree CreateNode(BoundingBox region, Physical Item)
{
List objList = new List(1); //жертвуем потенциальным процессорным временем ради меньшего объёма занимаемой памяти
objList.Add(Item);
OctTree ret = new OctTree(region, objList);
ret._parent = this;
return ret;
}Обновление дерева
Представим, что в нашем дереве есть множество движущихся объектов. Если какой-то объект переместился, есть высокая вероятность того, что он вышел за пределы ограничивающего его октанта. Как обрабатывать изменения положений объектов, сохраняя целостность структуры дерева?
Техника 1: делаем очень просто, удаляем и перестраиваем всё заново.
В некоторых реализациях октодеревьев в каждом кадре создаётся новое дерево и удаляется старое. Это очень просто, такая техника работает и если она вам подходит, то стоит выбрать её. Обычно считается, что предварительные затраты времени процессора на перестроение дерева в каждом кадре намного дешевле, чем выполнение проверок коллизий простым перебором, а время программистов слишком ценно, чтобы тратить его на необязательные оптимизации. У тех из нас, кто любит трудности и переусложнения, техника «удалить и перестроить» вызовет небольшие проблемы:
- Каждый раз при перестроении дерева вы постоянно выделяете и освобождаете память. На выделение новой памяти тратится немного ресурсов. По возможности вы стремитесь минимизировать количество выделяемой и освобождаемой памяти, повторно используя уже имеющуюся память.
- Бо?льшая часть дерева не изменяется, поэтому постоянная перестройка одних и тех же ветвей — это пустая трата процессорного времени.
Техника 2: сохраняем существующее дерево, обновляем изменённые ветви.
Я заметил, что большинство ветвей дерева не требует обновлений. Они просто содержит стационарные объекты.
Разве не будет замечательно, если вместо перестройки всего дерева в каждом кадре мы просто будем обновлять части дерева, требующие обновления? Эта техника сохраняет существующее дерево и обновляет только те ветви, в которых содержится переместившийся объект. Её реализовать немного сложнее, но и интереснее, так что давайте этим займёмся!
В своём первом эксперименте я ошибочно считал, что объект в дочернем узле может подняться или спуститься только на один переход дерева. Это неверно. Если объект в дочернем узле достигает края узла, и этот край тоже является краем ограничивающего родительского узла, то объект нужно будет вставить выше его родителя, а возможно, и ещё выше. То есть в результате мы не знаем, как высоко может подняться объект в дереве. Кроме того, объект может или удобно разместиться в дочернем узле, или в дочернем узле дочернего узла. Мы не знаем и как далеко вниз он может спуститься по дереву.
К счастью, поскольку мы храним ссылку на родителя каждого узла, мы можем просто решить эту проблему рекурсией, задействовав минимальные вычисления!
Основная идея алгоритма обновления заключается в том, чтобы дать всем объектам в дереве сначала обновиться самим. Некоторые из них перемещаются или меняют размер. Мы хотим получить список всех переместившихся объектов, чтобы метод обновления объектов возвращал нам булево значение, определяющее, сменилось ли ограничивающее его пространство.
Получив список всех переместившихся объектов, мы начнём с текущего узла и попробуем обходить дерево вверх, пока не найдём узел, полностью вмещающий в себя переместившийся объект (в большинстве случаев объект будет по-прежнему находиться в текущем узле). Если объект не полностью находится в текущем узле, мы продолжаем двигаться вверх до следующего родительского узла. В наихудшем случае объект будет гарантированно находиться в корневом узле.
После того, как мы переместили объекты как можно выше по дереву, мы попробуем спустить их как можно ниже по дереву. Чаще всего, если нам удалось переместить объект вверх, то опустить вниз его уже не удастся. Но если объект переместился так, что его может содержать дочерний узел текущего узла, то мы имеем возможность спустить его вниз по дереву. Важно иметь возможность двигать объекты и вниз по дереву, или все подвижные объекты постепенно переместятся вверх, и у нас возникнут проблемы со скоростью в процедурах распознавания коллизий.
Удаление ветвей
В некоторых случаях объект может переместиться из узла и этот узел больше не будет содержать объекты, как и все его потомки. В таком случае у нас образуется пустая ветвь. Тогда нам нужно пометить её и отсечь эту мёртвую ветвь от дерева.
Здесь возникает интересный вопрос: когда нужно отрезать мёртвые ветви от дерева? На выделение новой памяти тратится время, так что если мы будем повторно использовать ту же область в течение нескольких циклов, то зачем удалять её сразу? Как долго можно хранить её, пока не станет затратнее сохранять мёртвую ветвь?
Я решил дать каждому из узлов таймер обратного отсчёта, активирующийся, когда ветвь становится мёртвой. Если объект перемещается в октант этого узла, когда активен таймер смерти, я удваиваю срок жизни и сбрасываю таймер. Это гарантирует, что часто используемые октанты останутся активными и не будут удаляться, а нечасто используемые узлы будут удаляться до того, как их хранение станет слишком затратным.
Полезность этой техники очевидна из практического примера с пулемётом, выпускающим поток пуль. Эти пули летят очень близко друг к другу, поэтому было бы неудобно удалять узел сразу после того, как из него вылетит первая пуля, чтобы потом восстановить его через доли секунды при попадании в него второй пули. Пуль много, поэтому лучше сохранять эти октанты на какое-то время. Если дочерняя ветвь пуста и долго не использовалась, то можно без проблем отрезать её от дерева.
Давайте теперь посмотрим на код, выполняющий всю эту магию.
Для начала, у нас есть метод Update(). В нём рекурсивно вызываются все дочерние деревья. Он перемещает все объекты, наводит порядок в структуре данных, а затем перемещает каждый сдвинувшийся объект в соответствующий узел (родительский или дочерний).
public void Update(GameTime gameTime)
{
if (m_treeBuilt == true)
{
//Начинаем обратный отсчёт таймера смерти для каждого узла листа, у которого нет объектов или потомков.
//Когда таймер достигает нуля, мы удаляем лист. Если узел повторно использован до его смерти, то удваиваем срок жизни.
//Это даёт нам характеристику частотности использования и позволяет нам избежать необязательного выделения и освобождения памяти
if (m_objects.Count == 0)
{
if (HasChildren == false)
{
if (m_curLife == -1)
m_curLife = m_maxLifespan;
else if (m_curLife > 0)
{
m_curLife--;
}
}
}
else
{
if (m_curLife != -1)
{
if(m_maxLifespan <= 64)
m_maxLifespan *= 2;
m_curLife = -1;
}
}
List movedObjects = new List(m_objects.Count);
//Обходим и обновляем каждый объект в текущем узле дерева
foreach (Physical gameObj in m_objects)
{
//мы должны выяснить, переместился ли объект, то есть нужно ли обновлять этот узел дерева.
if (gameObj.Update(gameTime))
{
movedObjects.Add(gameObj);
}
}
//отсекаем все мёртвые объекты от дерева.
int listSize = m_objects.Count;
for (int a = 0; a < listSize; a++)
{
if (!m_objects[a].Alive)
{
if (movedObjects.Contains(m_objects[a]))
movedObjects.Remove(m_objects[a]);
m_objects.RemoveAt(a--);
listSize--;
}
}
//рекурсивно обновляем все дочерние узлы.
for( int flags = m_activeNodes, index = 0; flags > 0; flags >>=1, index++)
if ((flags & 1) == 1) m_childNode[index].Update(gameTime);
//Если объект переместился, мы можем вставить его в родительский узел, таким образом он вставится в правильный узел дерева.
//учтите, что это нужно делать в последнюю очередь, чтобы случайно не обновить один объект несколько раз за кадр.
foreach (Physical movedObj in movedObjects)
{
OctTree current = this;
//выясняем, насколько высоко по дереву нам нужно подняться, чтобы вставить перемещённый объект
//мы используем ограничивающий параллелепипед или сферу
//пробуем переместить объект в ограничивающий родительский узел, пока он не поместится полностью
if (movedObj.BoundingBox.Max != movedObj.BoundingBox.Min)
{
while (current.m_region.Contains(movedObj.BoundingBox) != ContainmentType.Contains)
if (current._parent != null) current = current._parent;
else break; //предотвращаем бесконечные циклы, когда выходим за границы области корневого узла
}
else
{
while (current.m_region.Contains(movedObj.BoundingSphere) != ContainmentType.Contains)//получается, что мы используем ограничивающую сферу, так что проверяем её содержимое.
if (current._parent != null) current = current._parent;
else break;
}
//теперь удаляем объект из текущего узла и вставляем в содержащий его узел.
m_objects.Remove(movedObj);
current.Insert(movedObj); //здесь мы пытаемся вставить объект настолько глубоко в дерево, насколько можем.
}
//отсекаем все мёртвые ветви дерева
for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++)
if ((flags & 1) == 1 && m_childNode[index].m_curLife == 0)
{
m_childNode[index] = null;
m_activeNodes ^= (byte)(1 << index); //удаляем узел из списка флагов активных узлов
}
//теперь, когда все объекты перемещены и вставлены в правильные узлы октодерева, можно проверить коллизии.
if (IsRoot == true)
{
//Рекурсивно собираем все коллизии и составляем их список.
//это простое сравнение всех объектов в текущем корневом узле со всеми объектами во всех дочерних узлах.
//примечание: можно предположить, что коллизии могут происходить только между переместившимися объектами.
//примечание 2: взрыв может центрироваться в точке, но со временем увеличиваться. В этом случае следует заменить метод обновления для взрыва.
List irList = GetIntersection(new List());
foreach (IntersectionRecord ir in irList)
{
if (ir.PhysicalObject != null)
ir.PhysicalObject.HandleIntersection(ir);
if (ir.OtherPhysicalObject != null)
ir.OtherPhysicalObject.HandleIntersection(ir);
}
}
}
else
{
}
}Заметьте, что для перемещённых объектов мы вызываем метод Insert(). Вставка объектов в дерево очень похожа на метод, использованный для создания первоначального дерева. Insert() пытается как можно ниже спустить объекты вниз по дереву. Также я стремлюсь избегать создания новых ограничивающих пространств, если можно использовать уже имеющиеся в дочернем узле.
///
/// Дерево уже создано, поэтому мы попробуем вставить элемент в дерево, не перестраивая его полностью
///
/// Физический объект
/// Физический объект для вставки в дерево
private void Insert(T Item) where T : Physical
{
/*проверяем, что не вставляем объект глубже, чем нужно
- если текущий узел является пустым узлом листа, то просто вставляем.*/
if (m_objects.Count <= 1 && m_activeNodes == 0)
{
m_objects.Add(Item);
return;
}
Vector3 dimensions = m_region.Max - m_region.Min;
//Проверяем, больше ли размеры параллелепипеда минимальных размеров
if (dimensions.X <= MIN_SIZE && dimensions.Y <= MIN_SIZE && dimensions.Z <= MIN_SIZE)
{
m_objects.Add(Item);
return;
}
Vector3 half = dimensions / 2.0f;
Vector3 center = m_region.Min + half;
//Находим или создаём подразделённые области для каждого октанта в текущей области
BoundingBox[] childOctant = new BoundingBox[8];
childOctant[0] = (m_childNode[0] != null) ? m_childNode[0].m_region : new BoundingBox(m_region.Min, center);
childOctant[1] = (m_childNode[1] != null) ? m_childNode[1].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, m_region.Min.Z), new Vector3(m_region.Max.X, center.Y, center.Z));
childOctant[2] = (m_childNode[2] != null) ? m_childNode[2].m_region : new BoundingBox(new Vector3(center.X, m_region.Min.Y, center.Z), new Vector3(m_region.Max.X, center.Y, m_region.Max.Z));
childOctant[3] = (m_childNode[3] != null) ? m_childNode[3].m_region : new BoundingBox(new Vector3(m_region.Min.X, m_region.Min.Y, center.Z), new Vector3(center.X, center.Y, m_region.Max.Z));
childOctant[4] = (m_childNode[4] != null) ? m_childNode[4].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, m_region.Min.Z), new Vector3(center.X, m_region.Max.Y, center.Z));
childOctant[5] = (m_childNode[5] != null) ? m_childNode[5].m_region : new BoundingBox(new Vector3(center.X, center.Y, m_region.Min.Z), new Vector3(m_region.Max.X, m_region.Max.Y, center.Z));
childOctant[6] = (m_childNode[6] != null) ? m_childNode[6].m_region : new BoundingBox(center, m_region.Max);
childOctant[7] = (m_childNode[7] != null) ? m_childNode[7].m_region : new BoundingBox(new Vector3(m_region.Min.X, center.Y, center.Z), new Vector3(center.X, m_region.Max.Y, m_region.Max.Z));
//Во-первых, полностью ли помещается элемент в корневой ограничивающий параллелепипед?
//примечание 2: на самом деле это не стоит компенсировать. Если объект находится за пределами заданных границ, то у нас возникла проблема/ошибка.
// Неверно. Наш первоначальный ограничивающий параллелепипед рельефа ограничивает её высоту самым большим пиком. Летающие объекты будут выше него.
// Исправление: я изменил размеры ограничивающего параллелепипеда до 256x256x256. Этого должно быть достаточно.
if (Item.BoundingBox.Max != Item.BoundingBox.Min && m_region.Contains(Item.BoundingBox) == ContainmentType.Contains)
{
bool found = false;
//пробуем поместить объект в дочерний узел. Если он не помещается в дочерний узел, то вставляем его в список объектов текущего узла.
for(int a=0;a<8;a++)
{
//полностью ли объект помещается в квадрант?
if (childOctant[a].Contains(Item.BoundingBox) == ContainmentType.Contains)
{
if (m_childNode[a] != null)
m_childNode[a].Insert(Item); //Добавляем элемент в это дерево и пусть дочернее дерево само разбирается, что с ним делать
else
{
m_childNode[a] = CreateNode(childOctant[a], Item); //создаём новый узел дерева с элементом
m_activeNodes |= (byte)(1 << a);
}
found = true;
}
}
if(!found) m_objects.Add(Item);
}
else if (Item.BoundingSphere.Radius != 0 && m_region.Contains(Item.BoundingSphere) == ContainmentType.Contains)
{
bool found = false;
//пробуем поместить объект в дочерний узел. Если он не помещается в дочерний узел, то вставляем его в список объектов текущего узла.
for (int a = 0; a < 8; a++)
{
//помещается ли объект в дочерний квадрант?
if (childOctant[a].Contains(Item.BoundingSphere) == ContainmentType.Contains)
{
if (m_childNode[a] != null)
m_childNode[a].Insert(Item); //AДобавляем элемент в это дерево и пусть дочернее дерево само разбирается, что с ним делать
else
{
m_childNode[a] = CreateNode(childOctant[a], Item); //создаём новый узел дерева с элементом
m_activeNodes |= (byte)(1 << a);
}
found = true;
}
}
if (!found) m_objects.Add(Item);
}
else
{
//Элемент или находится за пределами ограничивающего параллелепипеда, или пересекает его. Как бы то ни было, нам нужно перестроить
//всё дерево, увеличив содержащий её ограничивающий параллелепипед
//BoundingBox enclosingArea = FindBox();
BuildTree();
}
}Распознавание коллизий
Наконец, мы построили октодерево и все объекты находятся там, где нужно. Как выполнить распознавание коллизий? Для начала давайте перечислим различные способы, которыми мы хотим распознавать коллизии:
- Пересечения с усечёнными пирамидами. У нас может быть усечённая пирамида, пересекающаяся с областью мира. Нам нужны только объекты, пересекающиеся с этой усечённой пирамидой. Это особенно удобно для отсечения областей за пределами области видимости камеры и для определения того, какие объекты находятся в области выбора мыши.
- Пересечения с лучами. Нам может понадобиться испустить направленный луч из заданной точки и узнать, с каким первым объектом он пересечётся, или получить список всех объектов, которые пересекаются с лучом (например, для рейлгана). Это очень удобно для выделения мышью. Если пользователь щёлкает на экране, мы должны отрисовать луч и узнать, на что он нажал.
- Пересечения с ограничивающими параллелепипедами. Нам нужно знать, какие объекты мира пересекаются с заданным параллелепипедом. Это наиболее полезно для игровых объектов в форме «коробки» (домов, машин и т.д.).
- Пересечения с ограничивающими сферами. Мы хотим знать, какие объекты пересекаются с заданной ограничивающей сферой. У большинства объектов скорее всего будет использоваться для грубого распознавания коллизий ограничивающие сферы, потому что математика их расчётов наименее затратна и довольно проста.
Основная идея рекурсивной обработки распознавания коллизий для октодерева заключается в том, что мы начинаем с корневого/текущего узла и проверяем пересечения всех объектов в этом узле с пересекающей фигурой.
Затем выполняется проверка пересечения с ограничивающим параллелепипедом для всех активных дочерних узлов с пересекающей фигурой. Если проверка пересечения для дочернего узла оканчивается неудачей, мы полностью игнорируем остальную часть дерева этого дочернего узла. Если дочерний узел проходит проверку на пересечение, то мы рекурсивно обходим вниз дерево и повторяем процесс. Каждый узел должен передать вызывающей его процедуре список записей пересечений. Эти пересечения процедура присоединяет к собственному списку пересечений. После завершения рекурсии исходная вызывающая процедура будет иметь список всех пересечений для заданной пересекающей фигуры.
Красота такого подхода в том, что для его реализации нужно очень мало кода, а его производительность очень высока. Во множестве таких коллизий вы, скорее всего, будете получать множество результатов. Нам также нужен какой-то способ отклика на каждую коллизию в зависимости от того, какие объекты в неё вступили. Например, персонаж игрока должен подбирать висящий в воздухе бонус (quad damage!), но ракета не может взрываться, сталкиваясь с этим бонусом.
Я создал новый класс, в котором будет храниться информация о каждом пересечении. Этот класс содержит ссылки на пересекающиеся объекты, точку пересечения, нормаль в точках пересечения и т.д. Такие записи пересечений становятся очень полезными, когда мы будем передавать их объекту, чтобы он их обработал.
Для полноты и ясности я представил ниже мой код записи пересечений:
public class IntersectionRecord
{
Vector3 m_position;
///
/// Конкретная точка в 3D-пространстве, в которой произошло пересечение.
///
public Vector3 Position
{
get
{
return m_position;
}
}
Vector3 m_normal;
///
/// Это нормаль поверхности в точке пересечения
///
public Vector3 Normal
{
get
{
return m_normal;
}
}
Ray m_ray;
///
/// Это луч, который создаёт пересечение
///
public Ray Ray
{
get
{
return m_ray;
}
}
Physical m_intersectedObject1;
///
/// Это объект, который был пересечён
///
public Physical PhysicalObject
{
get
{
return m_intersectedObject1;
}
set
{
m_intersectedObject1 = value;
}
} Physical m_intersectedObject2;
///
/// Это другой пересечённый объект (может быть равным null, например, в случае пересечения луч-объект)
///
public Physical OtherPhysicalObject
{
get
{
return m_intersectedObject2;
}
set
{
m_intersectedObject2 = value;
}
}
///
/// Это ссылка на текущий узел в октодереве, в котором возникла коллизия. В некоторых случаях обработчику коллизий
/// может потребоваться возможность создания новых объектов и их вставки в дерево. Этот узел - хорошая начальная точка для вставки таких объектов,
/// потому что это очень близкое приближение к тому, где они должны находиться в дереве.
///
OctTree m_treeNode;
///
/// Сверяем идентификаторы объектов между двумя записями пересечений. Если они совпадают в любом порядке, то у нас есть дубликат.
///
///другой объект, с которым мы сравниваем
/// истинно, если записи - это пересечение для одной пары объектов, в противном случае ложно.
public override bool Equals(object otherRecord)
{
IntersectionRecord o = (IntersectionRecord)otherRecord;
// //возврат
(m_intersectedObject1 != null && m_intersectedObject2 != null && m_intersectedObject1.ID == m_intersectedObject2.ID);
if (otherRecord == null) return false;
if (o.m_intersectedObject1.ID == m_intersectedObject1.ID && o.m_intersectedObject2.ID == m_intersectedObject2.ID) return true;
if (o.m_intersectedObject1.ID == m_intersectedObject2.ID && o.m_intersectedObject2.ID == m_intersectedObject1.ID) return true;
return false;
}
double m_distance;
///
/// Это расстояние от луча до точки пересечения.
/// Если вы получаете несколько пересечений, обычно нужно использовать ближайшую точку коллизии.
///
public double Distance
{
get
{
return m_distance;
}
}
private bool m_hasHit = false;
public bool HasHit
{
get
{
return m_hasHit;
}
}
public IntersectionRecord()
{
m_position = Vector3.Zero;
m_normal = Vector3.Zero;
m_ray = new Ray();
m_distance = float.MaxValue;
m_intersectedObject1 = null;
}
public IntersectionRecord(Vector3 hitPos, Vector3 hitNormal, Ray ray, double distance)
{
m_position = hitPos;
m_normal = hitNormal;
m_ray = ray;
m_distance = distance;
//
m_hitObject = hitGeom; m_hasHit = true;
}
///
/// Создаёт новую запись пересечений, сообщающую о том, было ли пересечение, и с каким объектом оно произошло.
///
///Не обязательно: объект, с которым произошло пересечение. По умолчанию null.
public IntersectionRecord(Physical hitObject = null)
{
m_hasHit = hitObject != null;
m_intersectedObject1 = hitObject;
m_position = Vector3.Zero;
m_normal = Vector3.Zero;
m_ray = new Ray();
m_distance = 0.0f;
}
}Пересечение с ограничивающей усечённой пирамидой
///
/// Даёт список всех записей пересечений, которые пересекают или содержатся в области заданной усечённой пирамиды
///
/// Ограничивающая усечённая пирамида для проверки пересечения/нахождения внутри
/// Список записей пересечений с коллизиями
private List GetIntersection(BoundingFrustum frustum, Physical.PhysicalType type = Physical.PhysicalType.ALL)
{
if (m_objects.Count == 0 && HasChildren == false)
//завершение всех рекурсий
return null;
List ret = new List();
//проверка каждого объекта в списке на пересечение
foreach (Physical obj in m_objects)
{
//пропуск всех объектов, не удовлетворяющих заданным критериям
if ((int)((int)type & (int)obj.Type) == 0) continue;
//проверка на пересечение
IntersectionRecord ir = obj.Intersects(frustum);
if (ir != null) ret.Add(ir);
}
//проверка каждого объекта в списке на пересечение
for (int a = 0; a < 8; a++)
{
if (m_childNode[a] != null && (frustum.Contains(m_childNode[a].m_region) == ContainmentType.Intersects || frustum.Contains(m_childNode[a].m_region) == ContainmentType.Contains))
{
List hitList = m_childNode[a].GetIntersection(frustum);
if (hitList != null)
{
foreach (IntersectionRecord ir in hitList) ret.Add(ir);
}
}
}
return ret;
}Список пересечений ограничивающей усечённой пирамиды можно использовать для рендеринга тех объектов, которые будут видимы в текущей области видимости камеры. Я использую базу данных сцены, чтобы выяснить, как рендерить все объекты в игровом мире. Вот фрагмент кода из моей функции рендеринга, использующей ограничивающую усечённую пирамиду активной камеры:
///
/// Рендерит каждый активный объект в базе данных сцены
///
///
public int Render()
{
int triangles = 0;
// Рендерит все видимые объекты, рекурсивно обходя октодерево и проверяя пересечения
//с текущей усечённой пирамидой области видимости камеры
foreach (IntersectionRecord ir in m_octTree.AllIntersections(m_cameras[m_activeCamera].Frustum))
{
ir.PhysicalObject.SetDirectionalLight(m_globalLight[0].Direction, m_globalLight[0].Color);
ir.PhysicalObject.View = m_cameras[m_activeCamera].View;
ir.PhysicalObject.Projection = m_cameras[m_activeCamera].Projection;
ir.PhysicalObject.UpdateLOD(m_cameras[m_activeCamera]);
triangles += ir.PhysicalObject.Render(m_cameras[m_activeCamera]);
}
return triangles;
}Пересечение с лучом
///
/// Передаёт список записей пересечений для всех объектов, пересекающихся с заданным лучом
///
/// Луч, с которым пересекаются объекты
/// Список всех пересечений
private List GetIntersection(Ray intersectRay, Physical.PhysicalType type = Physical.PhysicalType.ALL)
{
if (m_objects.Count == 0 && HasChildren == false)
//завершение всех рекурсий
return null;
List ret = new List();
// луч пересекает эту область, поэтому нам нужно проверить пересечения со всеми содержащимися в ней объектами и дочерними областями.
// проверяем на пересечения каждый объект в списке
foreach (Physical obj in m_objects)
{
// пропуск всех объектов, не удовлетворяющих заданным критериям
if ((int)((int)type & (int)obj.Type) == 0) continue;
if (obj.BoundingBox.Intersects(intersectRay) != null)
{
IntersectionRecord ir = obj.Intersects(intersectRay);
if (ir.HasHit) ret.Add(ir);
}
}
// проверка на пересечение каждого дочернего октанта
for (int a = 0; a < 8; a++)
{
if (m_childNode[a] != null && m_childNode[a].m_region.Intersects(intersectRay) != null)
{ List hits = m_childNode[a].GetIntersection(intersectRay, type);
if (hits != null)
{
foreach (IntersectionRecord ir in hits) ret.Add(ir);
}
}
}
return ret;
}Пересечение со списком объектов
Это особенно полезный рекурсивный способ определения пересечения списка объектов в текущем узле с объектами во всех дочерних узлах (применение см. в методе Update()). Этот метод будет вызываться наиболее часто, поэтому неплохо бы сделать его правильным и эффективным.
Начнём с корневого узла дерева. Сравниваем на предмет коллизий все объекты в текущем узле со всеми остальными объектами текущего узла. Фиксируем все коллизии как записи пересечений и вставляем их в список. Затем передаём список проверенных объектов вниз, к дочерним узлам. Дочерние узлы проверяют пересечение своих объектов с ними же, а потом с объектами, которые мы передали вниз. Дочерние узлы сохраняют все коллизии в список и передают этот список родителю. Затем родитель берёт список коллизий, полученный из дочерних узлов, добавляет его к собственному списку коллизий, и передаёт его вызывающей процедуре.
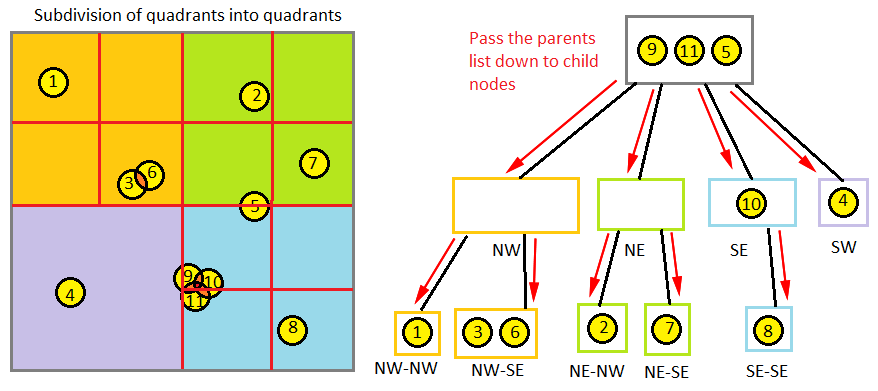
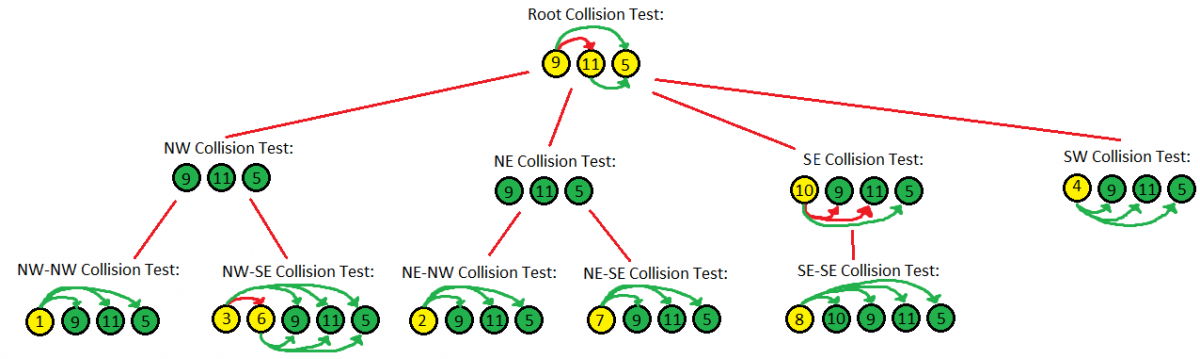
Если посчитать количество проверок коллизий на иллюстрациях, то можно увидеть, что проверено 29 возможных коллизий и обнаружено 4. Это намного лучше, чем [11*11 = 121] проверка коллизий.
private List GetIntersection(List parentObjs, Physical.PhysicalType type = Physical.PhysicalType.ALL)
{
List intersections = new List();
// считаем, что для всех родительских объектов уже были выполнены проверки коллизий.
// проверяем коллизии всех родительских объектов со всеми объектами в локальном узле
foreach (Physical pObj in parentObjs)
{
foreach (Physical lObj in m_objects)
{
// Проверяем коллизию двух объектов. Они сами решают, выполнять ли грубые или детальные проверки.
// Нам важно только, произошла ли коллизия.
IntersectionRecord ir = pObj.Intersects(lObj);
if (ir != null)
{
intersections.Add(ir);
}
}
}
// Теперь проверяем коллизии всех локальных объектов между собой
if (m_objects.Count > 1)
{ #region self-congratulation
/* * Это довольно примечательная часть кода. Обычно используется просто два цикла foreach, примерно так:
* foreach(Physical lObj1 in m_objects)
* {
* foreach(Physical lObj2 in m_objects)
* {
* // код проверки пересечения
* }
* }
*
* Проблема в том, что они выполняются O(N*N) раз и в том, что проверяются коллизии уже проверенных объектов.
* Представьте, что у нас есть множество из четырёх элементов: {1,2,3,4}
* Сначала мы проверяем {1} с {1,2,3,4}
* Затем проверяем {2} с {1,2,3,4},
* но мы уже проверяли {1} с {2}, так что проверка {2} с {1} будет пустой тратой времени. Можно ли пропустить эту проверку, устранив {1}?
* Тогда всего мы получим 4+3+2+1 проверок коллизий, что равно времени O(N(N+1)/2). Если N = 10, мы уже делаем вдвое меньшее количество проверок.
* Мы не можем просто удалять элемент в конце второго цикла for, потому что прервём итератор первого цикла foreach, поэтому придётся использовать
* обычное
for(int i=0;i tmp = new List(m_objects.Count);
tmp.AddRange(m_objects);
while (tmp.Count > 0)
{
foreach (Physical lObj2 in tmp)
{
if (tmp[tmp.Count - 1] == lObj2 || (tmp[tmp.Count - 1].IsStatic && lObj2.IsStatic)) continue;
IntersectionRecord ir = tmp[tmp.Count - 1].Intersects(lObj2);
if (ir != null) intersections.Add(ir);
}
// Удаляем этот объект из временного списка, чтобы выполнять процедуру O(N(N+1)/2) раз вместо O(N*N)
tmp.RemoveAt(tmp.Count-1);
}
}
// Теперь объединяем список локальных объектов со списком родительских объектов, а затем передаём его вниз всем дочерним узлам.
foreach (Physical lObj in m_objects) if (lObj.IsStatic == false) parentObjs.Add(lObj);
//parentObjs.AddRange(m_objects);
//каждый дочерний узел даст нам список записей пересечений, который мы затем объединим с собственными записями пересечений.
for (int flags = m_activeNodes, index = 0; flags > 0; flags >>= 1, index++)
if ((flags & 1) == 1) intersections.AddRange(m_childNode[index].GetIntersection(parentObjs, type));
return intersections;
} ;i++)>Скриншоты демо
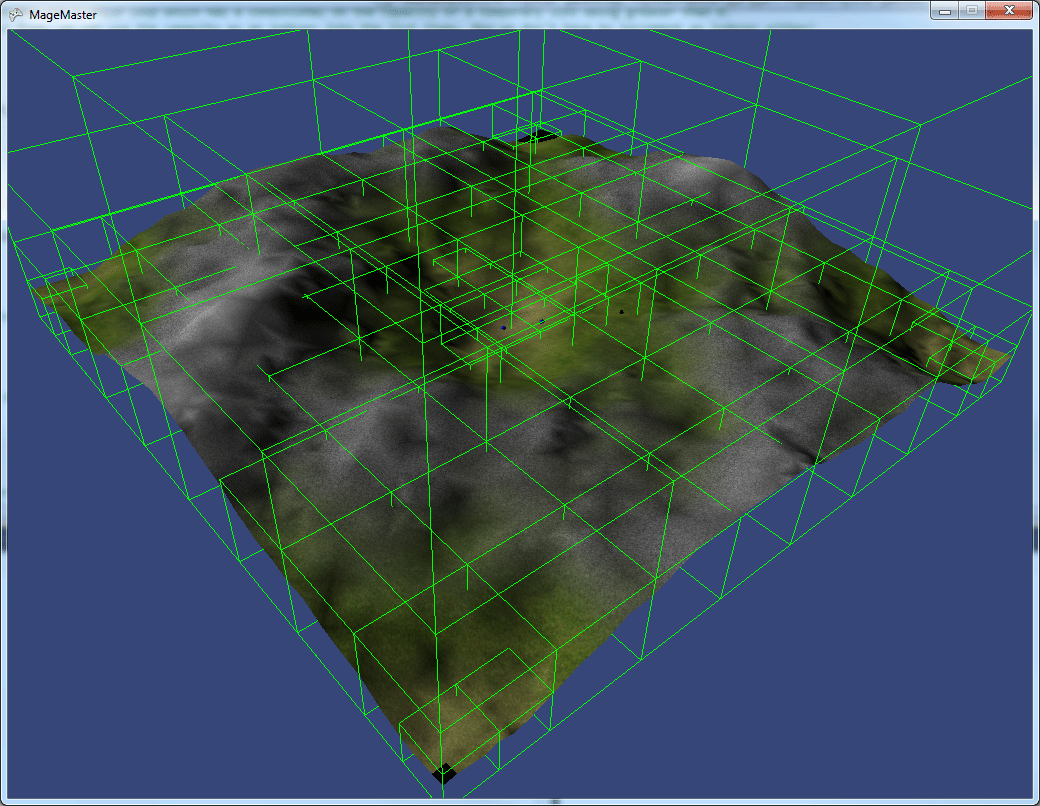
Это вид игрового мира с расстояния, показывающий контуры всех ограничивающих объёмов октодерева.
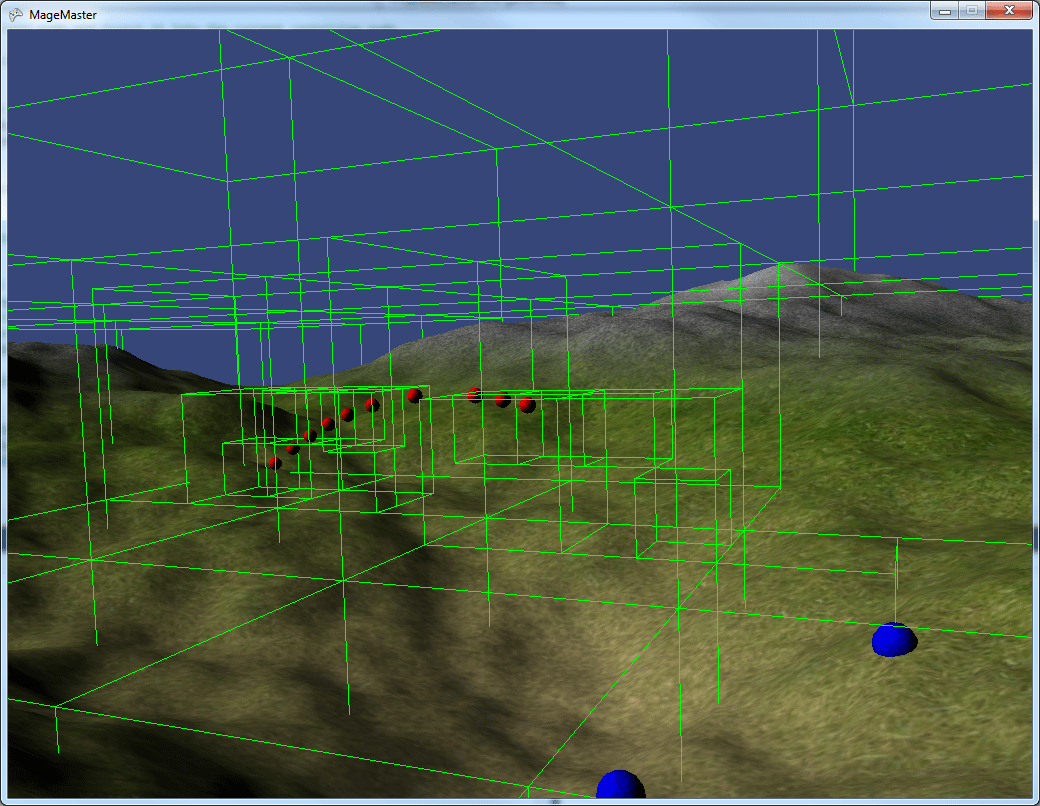
Здесь показана очередь из снарядов, летящих через игровой мир. Часто используемые узлы сохраняются, а не удаляются.
Комментарии (16)

Ckpyt
09.08.2017 15:25Я в свое время использовал разреженный массив: пространство бьется на кубы по 2*largeObjectSize, потом каждый объект попадает в тот или иной куб. Потом просто прохожусь по всем объектам, смотрю кто в каком кубе и есть ли в этом кубе еще кто-нибудь. Итоговая сложность получается O(N).
Это ОЧЕНЬ полезно при поиске коллизий в гигантском объеме(писал космосим. Расстояния — соответствующие).
Ogoun
09.08.2017 16:09Делал похоже, только разбивал пространство на кубы со стороной 2^N, чтобы преобразование координат для проверки вхождения в куб можно было считать через битовые сдвиги (x>>N; y>>N; z>>N).

Ckpyt
09.08.2017 16:32-1Вроде бы как, сейчас процессор одинаково обрабатывает деление и битовый сдвиг — за один такт(если конвейер не сброшен). Больше времени занимает пересылка данных. Но тут уже надо мучаться с ассемблерными вставками.

AxisPod
09.08.2017 19:13Зачем они? Компиляторы и сами не плохо справляются, хотя конечно понимать придется, как и что компилятор может соптимизировать. Опять же для simd уже есть готовые библиотеки.
khim
10.08.2017 03:29+2Вроде бы как, сейчас процессор одинаково обрабатывает деление и битовый сдвиг — за один такт(если конвейер не сброшен).
Деление? За один такт? Это кто ж продаёт такие грибы и сколько они стоят?
Skylake — 23 для восьмибитовых регистров, от 42 — для 64-битовых, на старых процессорах ещё медленнее, на многих ARM'ах вообще реализация через подпрограмму в ядре. Для разных видов x86 тайминги есть тут.
Больше времени занимает пересылка данных.
Только если уж совсем в оперативную память «мимо» всех кешей. Деление — это вообще самое медленное, что процессор умеет делать с целыми числами. С огроооомным отрывом от умножения (не зря компиляторы заменяют деление на константу умножением, ох не зря).

MaximSuvorov
10.08.2017 14:19Точно такой же способ был в Казаки-1, там через битовые сдвиги тоже считалось в какой зоне юнит.

Psychopompe
10.08.2017 18:32Так это же стандартные алгоритмы: Barnes–Hut simulation и Сell linked-lists
Idot
10.08.2017 12:54А через вертексные шейдеры обработать это дерево можно ведь?

MaximSuvorov
10.08.2017 14:17плохая идея, дерево гарантировано не влезет в кеш юни-шейдера, что приведёт к постоянному чтению/записи памяти и кеша.

PlatinumThinker
10.08.2017 16:14В своё время баловался с генерацией из obj формата (текстовый формат описывающий полигоны модели) в октодерево

В итоге если заморачиваться с рендером всего этого на видеокарте оптимальнее всего хранить не разряженное дерево, а на cpu (писал на java) рейтрейсинг у меня жутко тормозил (5cps на томографных снимках крокодильей головы), хотя не исключаю криворукости


Sklott
«Получив список всех переместившихся объектов, мы начнём с текущего узла и попробуем обходить дерево вверх, пока не найдём узел, полностью вмещающий в себя переместившийся объект»
Зачем такие сложности? При глубине в 9-10 шагов (да даже если и несколько больше, не страшно) проще просто удалять объект из дерева и вставлять заново «сверху». Иначе у тебя появляется неявное дублирование кода которое может привести к проблемам.