По сути этот пост – продолжение статьи о методах кластеризации ключевых фраз в оптимизаторах: зачем нужны оптимизаторы конверсии в контекстной рекламе и почему качество их работы снижается, если они имеют дело с ключевыми фразами, по которым собрано недостаточно статистики (об этом в первых двух частях статьи). Как вариант решения проблемы отсутствия или недостатка данных для прогнозирования конверсии мы рассматривали классический и альтернативные методы пулинга — наращивания статистики по фразе за счет заимствования статистики по другим фразам.
В этом посте старший продакт менеджер Calltouch Федор Иванов расскажет о важности другого подхода к прогнозированию конверсии по ключевым фразам — анализе микроконверсий как ключевых метрик, влияющих на итоговую конверсию на сайте (которую мы будем называть макроконверсией).
В повседневной практике мы часто сталкиваемся с понятием «конверсия». Под этим термином мы понимаем некоторое целевое действие, совершенное пользователем на сайте. Примерами таких целевых действий могут быть транзакция, телефонный звонок, отправка заявки, регистрация на сайте и т. д. Какое действие считать конверсионным – это в первую очередь выбор рекламодателя, который он делает исходя из специфики бизнеса, функционала сайта и т. д.
Интуитивно понятно, что конверсия обладает некоторой ценностью, а потому чем больше конверсий происходит на сайте в единицу времени – тем больше выгоды (прямой или косвенной) получает рекламодатель. В этой связи коэффициент конверсии можно рассматривать как долю тех посетителей сайта, которые в конечном счете совершили конверсию, а CPA – как среднюю цену привлечения одного «конверсионного» посетителя.

Итак, данная модель представляет из себя простейшую воронку продаж: на вход в нее попадает вся аудитория сайта, а на выходе – та ее часть, которая совершила конверсию (макро).
Однако в процессе своей «жизни» на сайте посетители могут совершать те или иные действия, которые так или иначе позволяют оценить их лояльность и готовность совершить целевое действие на сайте. Примерами таких действий могут быть:
Такие действия называются «микроконверсиями». Если подытожить, то микроконверсии – это промежуточные действия пользователя на сайте, которые в определенной степени отражают его меру вовлеченности и заинтересованности в предлагаемых товарах и услугах. Если система аналитики, настроена таким образом, что указанные действия отслеживаются, то мы можем значительно обогатить нашу исходную воронку продаж:

При этом очевидно, что статистика по микроконверсиям может копиться в несколько раз быстрее, чем статистика по основным макроконверсиям. Например, пользователей, которые просматривают 5 страниц сайта, значительно больше чем тех, кто приобретает товар. Этот факт позволит существенно ускорить сбор статистики, необходимой для запуска оптимизатора.
С другой стороны анализ микроконверсий позволит отследить слабые места в воронке продаж, что упростит аналитику сайта. Например, если из 1000 посетителей сайта 200 перешли в раздел «корзина», а из «корзины» только 10 оформили заказ, то разумно будет предположить, что форма, где пользователю предлагается оформить заказ, нуждается в переработке и улучшении.
Тем не менее, когда мы приводили определение микроконверсии, мы не зря упомянули, что показатель той или иной микроконверсии «в определенной степени» отражает лояльность пользователя и его готовность совершить макроконверсию. Например, если в качестве микроконверсии выбрана цель «длина пользовательской сессии не менее 10 минут», то высокий коэффициент конверсии в эту цель не обязательно означает высокую конверсионность сайта в целом.
Поэтому важным является вопрос анализа влияния той или иной микроконверсии на макроконверсию. В следующем разделе мы подробно обсудим существующие подходы к такому анализу.
Самым простым методом оценки влияния одной величины на другую (в нашем случае – микроконверсии по заданной цели на макроконверсию) является корреляционный анализ. Данный подход разработан в одном из разделов математической статистики, науки, которая оперирует со случайными величинами.
Случайной величиной называется событие, которое происходит с определенной вероятностью, которая подчиняется некоторому закону распределения. Поэтому мы абстрагируемся от понятия конверсии и микроконверсии, а будем говорить о случайных величинах – количества макроконверсий и — количества микроконверсий по некоторой цели . Значения данных показателей, которые мы наблюдает в любых разрезах (по сайту, по отдельной рекламной кампании и даже по отдельному кейворду) называются реализациями (значениями) данной случайной величины.
Коэффициент корреляции (линейной корреляции Пирсона) позволяет оценить взаимосвязь случайных величин и по их наблюдаемым N значениям (конкретным реализациям). Данная величина принимает значение от -1 до 1. Чем ближе значение к единице (или к -1), тем более «связаны» (напрямую или в обратной зависимости) случайные величины. Иначе говоря, тем более точно мы можем «угадывать» значение , имея информацию о . В первом случае зависимость прямая:, а во втором – обратная:.
В нашей интерпретации это означает, что если , то чем больше произошло микроконверсий , тем больше следует ожидать макроконверсий . Если же , то чем больше произошло микроконверсий , тем меньше следует ожидать макроконверсий .
Примером коррелирующих напрямую случайных величин являются количество пользователей, совершивших покупку и количество пользователей, положивших товар в корзину. Примером обратно коррелирующих случайных величин является количество транзакций и количество отказов.
Коэффициент корреляции позволяет достаточно точно спрогнозировать поведение одной случайной величины относительно другой, однако существует ряд ограничений. Во-первых, объемы выборок (наблюдаемых значений) должны быть достаточно велики (несколько десятков наблюдений), что автоматически не позволит выявить влияние одной величины на другую на микроуровне (например, на уровне ключевой фразы). Кроме того, формулы вычисления корреляции точны только тогда, когда распределения для и являются гауссовыми (нормальными). Помимо этого, при расчете коэффициента используются только наблюдаемые значения, при сглаживании которых (например, пулингом) нарастает систематическая ошибка.
Кроме того, интересен факт, что отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет. То есть широко распространенное мнение, что нулевая корреляция означает независимость событий, является неправильным. Наглядной демонстрацией вышесказанного является следующая картинка:

Над рисунком указан коэффициент корреляции двух случайных величин, а на самом рисунке нанесены значения данных величин. Легко заметить, что корреляция хорошо «предсказывает» только линейную зависимость, не детектируя при этом никакие другие.
Нами был предложен альтернативный подход к анализу микроконверсий, основанный на принципах и фундаментальных понятиях теории информации, который позволяет существенно упростить поиск взаимосвязей между конверсиями разных уровней даже в том случае, если эта зависимость имеет сложный, нелинейный характер.
Взаимная информация – одно из базовых понятий общей теории информации. Определяется она следующим образом: Взаимная информация — статистическая функция двух случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой.
Таким образом, зная распределения двух случайных величин, мы можем вычислить насколько они взаимосвязаны между собой (при любой форме зависимости) с точки зрения того, сколько информации об одном событии (например, макроконверсии) говорит наступление (или не наступление) другого события (например, микроконверсии по некоторой цели).
Общая формула для расчета взаимной информации между случайными величинами и следующая:, где – энтропии величин и, а – условная энтропия события при наступлении события . Чуть позже мы рассмотрим способы вычисления каждой из величин, входящих в формулу, но прежде обсудим основные свойства взаимной информации.
• Она симметрична:
• Она ограничена:
• Она равна энтропии, если события связаны любой функциональной зависимостью
Наличие всех указанных выше свойств позволяет считать взаимную информацию хорошим аналогом корреляции при расчете взаимосвязи между событиями. В частности, последнее свойство позволит обнаружить зависимость произвольной природы, но к сожалению установление ее формы является отдельной и достаточно нетривиальной задачей.
Все свойства, которые мы рассмотрели выше, указывают на то, что взаимная информация может быть рассмотрена в качестве метрики между событиями (конверсиями и микроконверсиями). Однако на практике удобно пользоваться нормализованной взаимной информацией:В этом случае . Причем чем меньше взаимосвязаны величины, тем ближе значение метрики к 1, и наоборот – чем больше наступление одного события говорит о другом, тем ближе метрика к 0. Формулы такого вида часто используются в задачах машинного обучения для отбора значимых признаков (что способствует снижению размерности задачи). Кроме того, подобный подход активно используется в задачах классификации и кластеризации. Мы же предлагаем использовать его для оценки влияния микроконверсии на формирование итоговой конверсии (макро).
Так как взаимная информация может быть рассчитана только для случайных величин с заданными функциями распределений, прежде всего необходимо выбрать распределения для и . В связи с тем, что конверсии (и микроконверсии) происходят независимо друг от друга с некоторыми вероятностями (вероятностями конверсии и микроконверсии) и , то лучше всего поведение таких величин описывается при помощи биномиального закона распределения, а именно:
где под и мы понимаем вероятность того, что конверсия (микроконверсия) произошла и вероятность противоположного события соответственно. Такая модель помимо своей простоты удобна тем, что при недостаточном объеме статистических данных, необходимых для расчета и , данные величины могут быть рассчитаны при помощи метода пулинга (см. ppcworld). Помимо этого, для биномиально распределенной случайной величины достаточно просто рассчитывается :А значит:
Наибольшую сложность в расчете взаимной информации между конверсией и микроконверсией вызывает расчет условной энтропии, данной проблеме мы посвятим следующий раздел данной статьи.
Условная энтропия между случайными величинами и может быть рассчитана по формуле:
где:
Исходя из определения условной вероятности, мы можем рассчитать:Таким образом, необходимо вычислить только .
По определению:
Расчет данных четырех вероятностей требует накопления следующей статистики: для каждого клика, который мы пронумеруем некоторым clickID, требуется составить вектор-индикатор того, привела ли пользовательская сессия, инициированная этим кликом к микроконверсии по цели и к макроконверсии на сайте:где если конверсии по цели i не было, если была конверсия по цели i.
Если дополнительно мы добавим в статистику keywordID, bannerID, campaignID, мы сможем рассчитать влияние микроконверсий на конверсию для каждого кейворда, баннера, кампании. Если окажется, что собственной статистики для расчета недостаточно, то она всегда может быть «унаследована» с более высокого уровня при помощи метода пулинга. Таким образом, окончательно имеем:
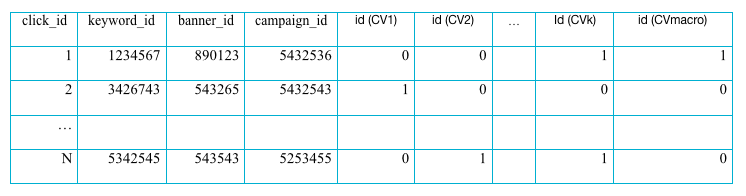
Агрегированная таким образом статистика позволит рассчитать как числители, так и знаменатели в , что в конечном счете сделает возможным вычисление условной энтропии между конверсией и каждой микроконверсией, а значит задача по расчету влияния микроконверсий на итоговую конверсию на сайте полностью решена.
Кроме того, суммируя данные на уровнях кейворда, баннера, кампании, мы сможем рассчитать зависимости между конверсиями и микроконверсиями не только на уровне сайта в целом, но и на более низких уровнях, что значительно повысит эффект от оптимизации.
В следующей главе мы рассмотрим вопрос того, как на основании полученных данных оценить вес микроконверсии, и как использовать данную информацию для оптимизации.
Для оценки влияния микроконверсии по некоторой цели на общую конверсию на сайте удобно пользоваться нормированной формулой весов: В данном случае суммарное влияние микроконверсий по всем выбранным целям на итоговую конверсию на сайте равно 1.
Если мы вычислили коэффициент влияния (вес) по всем переходам на сайт, то выбрав цели с наибольшим влиянием, мы можем оптимизировать (например, методами A/Б тестирования) те участки сайта, где происходит сбор данных микроконверсий для повышения общей конверсии.
Если же перед нами стоит цель оптимизации ставок для контекстной рекламы, то необходимо рассчитать на уровне каждого кейворда (именно для них оптимизатор конверсий рассчитывает и отправляет оптимальные ставки):Очевидно, что ставка по ключевой фразе (кейворду X) – это некоторая функция , которая зависит от статистики (в первую очередь от коэффициента макроконверсии ) и от KPI, которые установлены в качестве целевых:Тогда для оптимизации с учетом микроконверсий мы можем воспользоваться обобщением последней формулы:где параметр является некоторой монотонно убывающей функцией от количества кликов и макроконверсий по кейворду: чем больше кликов и макроконверсий, тем меньше величина (тем меньше нам требуется знаний о поведении микроконверсий для расчета ставок).
Таким образом, информация о микроконверсиях является особенно ценной в случае малого объема статистики по кейворду.
Описанные в данной работы алгоритмы являются неотъемлемой частью оптимизатора конверсий Calltouch. Оптимизация с учетом микроконверсий оказывается особенно эффективной в том случае, если количество конверсий, которое оптимизатор старается максимизировать в рамках установленных KPI, невелико. Это имеет место быть либо для небольших рекламных аккаунтов, либо в случае выбора специфического типа конверсии. Если рассматривать оптимизацию по звонкам (именно на таком типе оптимизации специализируется сервис Calltouch), то специфическим типом конверсии является тегированный звонок. Система позволяет тегировать звонки как вручную, так и с использованием инструмента автоматического тегирования Calltouch Predict.
В данном разделе мы приведем результаты совместного с агентством «Ашманов и Партнеры» кейса по оптимизации контекста для компании BIIKS (Бурение скважин). Целью тестирования являлось увеличение числа прослушанных целевых звонков в рамках текущего CPA.
Стоимость конверсии: подключая рекламные кампании к Оптимизатору Calltouch, клиент рассчитывал сохранить текущую стоимость конверсии, при этом получить максимум звонков. За первые 4 недели теста были достигнуты следующие результаты:
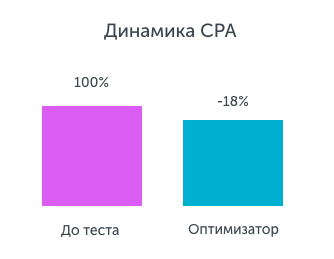
Коэффициент конверсии: на рекламных кампаниях, подключенных к Оптимизатору Calltouch, коэффициент конверсии за период теста вырос на 55 %.

Количество конверсий: количество конверсий в период теста значительно выросло: прирост при использовании Оптимизатора составил 91%

В работе рассмотрен новый подход к анализу микроконверсий и их влиянию на основную конверсию на сайте. Данный подход базируется на принципах теории информации. Для его реализации достаточно выбрать определенные цели, которые будут отслеживаться системой аналитики, и выбрать среди них основную (конверсию) и накопить статистику по переходам на сайт хотя бы за 30 дней. Предложенная в статье методика может быть использована как для выявления «слабых» мест на сайте, так и для оптимизации ставок в контекстной рекламе.
В этом посте старший продакт менеджер Calltouch Федор Иванов расскажет о важности другого подхода к прогнозированию конверсии по ключевым фразам — анализе микроконверсий как ключевых метрик, влияющих на итоговую конверсию на сайте (которую мы будем называть макроконверсией).
Что нам могут дать микроконверсии?
В повседневной практике мы часто сталкиваемся с понятием «конверсия». Под этим термином мы понимаем некоторое целевое действие, совершенное пользователем на сайте. Примерами таких целевых действий могут быть транзакция, телефонный звонок, отправка заявки, регистрация на сайте и т. д. Какое действие считать конверсионным – это в первую очередь выбор рекламодателя, который он делает исходя из специфики бизнеса, функционала сайта и т. д.
Интуитивно понятно, что конверсия обладает некоторой ценностью, а потому чем больше конверсий происходит на сайте в единицу времени – тем больше выгоды (прямой или косвенной) получает рекламодатель. В этой связи коэффициент конверсии можно рассматривать как долю тех посетителей сайта, которые в конечном счете совершили конверсию, а CPA – как среднюю цену привлечения одного «конверсионного» посетителя.

Итак, данная модель представляет из себя простейшую воронку продаж: на вход в нее попадает вся аудитория сайта, а на выходе – та ее часть, которая совершила конверсию (макро).
Однако в процессе своей «жизни» на сайте посетители могут совершать те или иные действия, которые так или иначе позволяют оценить их лояльность и готовность совершить целевое действие на сайте. Примерами таких действий могут быть:
- Просмотр не менее 5 страниц сайта
- Переход в раздел «корзина»
- Просмотр контактной информации
- Подписка на рассылку
Такие действия называются «микроконверсиями». Если подытожить, то микроконверсии – это промежуточные действия пользователя на сайте, которые в определенной степени отражают его меру вовлеченности и заинтересованности в предлагаемых товарах и услугах. Если система аналитики, настроена таким образом, что указанные действия отслеживаются, то мы можем значительно обогатить нашу исходную воронку продаж:

При этом очевидно, что статистика по микроконверсиям может копиться в несколько раз быстрее, чем статистика по основным макроконверсиям. Например, пользователей, которые просматривают 5 страниц сайта, значительно больше чем тех, кто приобретает товар. Этот факт позволит существенно ускорить сбор статистики, необходимой для запуска оптимизатора.
С другой стороны анализ микроконверсий позволит отследить слабые места в воронке продаж, что упростит аналитику сайта. Например, если из 1000 посетителей сайта 200 перешли в раздел «корзина», а из «корзины» только 10 оформили заказ, то разумно будет предположить, что форма, где пользователю предлагается оформить заказ, нуждается в переработке и улучшении.
Тем не менее, когда мы приводили определение микроконверсии, мы не зря упомянули, что показатель той или иной микроконверсии «в определенной степени» отражает лояльность пользователя и его готовность совершить макроконверсию. Например, если в качестве микроконверсии выбрана цель «длина пользовательской сессии не менее 10 минут», то высокий коэффициент конверсии в эту цель не обязательно означает высокую конверсионность сайта в целом.
Поэтому важным является вопрос анализа влияния той или иной микроконверсии на макроконверсию. В следующем разделе мы подробно обсудим существующие подходы к такому анализу.
Методы оценки влияния микроконверсий
Самым простым методом оценки влияния одной величины на другую (в нашем случае – микроконверсии по заданной цели на макроконверсию) является корреляционный анализ. Данный подход разработан в одном из разделов математической статистики, науки, которая оперирует со случайными величинами.
Случайной величиной называется событие, которое происходит с определенной вероятностью, которая подчиняется некоторому закону распределения. Поэтому мы абстрагируемся от понятия конверсии и микроконверсии, а будем говорить о случайных величинах – количества макроконверсий и — количества микроконверсий по некоторой цели . Значения данных показателей, которые мы наблюдает в любых разрезах (по сайту, по отдельной рекламной кампании и даже по отдельному кейворду) называются реализациями (значениями) данной случайной величины.
Коэффициент корреляции (линейной корреляции Пирсона) позволяет оценить взаимосвязь случайных величин и по их наблюдаемым N значениям (конкретным реализациям). Данная величина принимает значение от -1 до 1. Чем ближе значение к единице (или к -1), тем более «связаны» (напрямую или в обратной зависимости) случайные величины. Иначе говоря, тем более точно мы можем «угадывать» значение , имея информацию о . В первом случае зависимость прямая:, а во втором – обратная:.
В нашей интерпретации это означает, что если , то чем больше произошло микроконверсий , тем больше следует ожидать макроконверсий . Если же , то чем больше произошло микроконверсий , тем меньше следует ожидать макроконверсий .
Примером коррелирующих напрямую случайных величин являются количество пользователей, совершивших покупку и количество пользователей, положивших товар в корзину. Примером обратно коррелирующих случайных величин является количество транзакций и количество отказов.
Коэффициент корреляции позволяет достаточно точно спрогнозировать поведение одной случайной величины относительно другой, однако существует ряд ограничений. Во-первых, объемы выборок (наблюдаемых значений) должны быть достаточно велики (несколько десятков наблюдений), что автоматически не позволит выявить влияние одной величины на другую на микроуровне (например, на уровне ключевой фразы). Кроме того, формулы вычисления корреляции точны только тогда, когда распределения для и являются гауссовыми (нормальными). Помимо этого, при расчете коэффициента используются только наблюдаемые значения, при сглаживании которых (например, пулингом) нарастает систематическая ошибка.
Кроме того, интересен факт, что отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет. То есть широко распространенное мнение, что нулевая корреляция означает независимость событий, является неправильным. Наглядной демонстрацией вышесказанного является следующая картинка:

Над рисунком указан коэффициент корреляции двух случайных величин, а на самом рисунке нанесены значения данных величин. Легко заметить, что корреляция хорошо «предсказывает» только линейную зависимость, не детектируя при этом никакие другие.
Нами был предложен альтернативный подход к анализу микроконверсий, основанный на принципах и фундаментальных понятиях теории информации, который позволяет существенно упростить поиск взаимосвязей между конверсиями разных уровней даже в том случае, если эта зависимость имеет сложный, нелинейный характер.
Что такое взаимная информация?
Взаимная информация – одно из базовых понятий общей теории информации. Определяется она следующим образом: Взаимная информация — статистическая функция двух случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой.
Таким образом, зная распределения двух случайных величин, мы можем вычислить насколько они взаимосвязаны между собой (при любой форме зависимости) с точки зрения того, сколько информации об одном событии (например, макроконверсии) говорит наступление (или не наступление) другого события (например, микроконверсии по некоторой цели).
Общая формула для расчета взаимной информации между случайными величинами и следующая:, где – энтропии величин и, а – условная энтропия события при наступлении события . Чуть позже мы рассмотрим способы вычисления каждой из величин, входящих в формулу, но прежде обсудим основные свойства взаимной информации.
• Она симметрична:
• Она ограничена:
• Она равна энтропии, если события связаны любой функциональной зависимостью
Наличие всех указанных выше свойств позволяет считать взаимную информацию хорошим аналогом корреляции при расчете взаимосвязи между событиями. В частности, последнее свойство позволит обнаружить зависимость произвольной природы, но к сожалению установление ее формы является отдельной и достаточно нетривиальной задачей.
Взаимная информация как метрика зависимости событий
Все свойства, которые мы рассмотрели выше, указывают на то, что взаимная информация может быть рассмотрена в качестве метрики между событиями (конверсиями и микроконверсиями). Однако на практике удобно пользоваться нормализованной взаимной информацией:В этом случае . Причем чем меньше взаимосвязаны величины, тем ближе значение метрики к 1, и наоборот – чем больше наступление одного события говорит о другом, тем ближе метрика к 0. Формулы такого вида часто используются в задачах машинного обучения для отбора значимых признаков (что способствует снижению размерности задачи). Кроме того, подобный подход активно используется в задачах классификации и кластеризации. Мы же предлагаем использовать его для оценки влияния микроконверсии на формирование итоговой конверсии (макро).
Моделирование случайных величин
Так как взаимная информация может быть рассчитана только для случайных величин с заданными функциями распределений, прежде всего необходимо выбрать распределения для и . В связи с тем, что конверсии (и микроконверсии) происходят независимо друг от друга с некоторыми вероятностями (вероятностями конверсии и микроконверсии) и , то лучше всего поведение таких величин описывается при помощи биномиального закона распределения, а именно:
где под и мы понимаем вероятность того, что конверсия (микроконверсия) произошла и вероятность противоположного события соответственно. Такая модель помимо своей простоты удобна тем, что при недостаточном объеме статистических данных, необходимых для расчета и , данные величины могут быть рассчитаны при помощи метода пулинга (см. ppcworld). Помимо этого, для биномиально распределенной случайной величины достаточно просто рассчитывается :А значит:
Наибольшую сложность в расчете взаимной информации между конверсией и микроконверсией вызывает расчет условной энтропии, данной проблеме мы посвятим следующий раздел данной статьи.
Расчет условной энтропии
Условная энтропия между случайными величинами и может быть рассчитана по формуле:
где:
- – вероятность того, что клик не привел ни к микро, ни к макроконверсии
- — вероятность того, что клик привел к макроконверсии, но при этом не было микроконверсии
- — вероятность того, что клик привел к микроконверсии, но при этом не было макроконверсии
- — вероятность того, что клик приведет как к микро, так к макроконверсии
- – вероятность отсутствия микроконверсии, при условии что макроконверсии не было
- – вероятность отсутствия микроконверсии, при условии что произошла макроконверсия
- – вероятность микроконверсии, если макроконверсии не было
- – вероятность микроконверсии, при условии того, что произошла макроконверсия
Исходя из определения условной вероятности, мы можем рассчитать:Таким образом, необходимо вычислить только .
По определению:
Расчет данных четырех вероятностей требует накопления следующей статистики: для каждого клика, который мы пронумеруем некоторым clickID, требуется составить вектор-индикатор того, привела ли пользовательская сессия, инициированная этим кликом к микроконверсии по цели и к макроконверсии на сайте:где если конверсии по цели i не было, если была конверсия по цели i.
Если дополнительно мы добавим в статистику keywordID, bannerID, campaignID, мы сможем рассчитать влияние микроконверсий на конверсию для каждого кейворда, баннера, кампании. Если окажется, что собственной статистики для расчета недостаточно, то она всегда может быть «унаследована» с более высокого уровня при помощи метода пулинга. Таким образом, окончательно имеем:

Агрегированная таким образом статистика позволит рассчитать как числители, так и знаменатели в , что в конечном счете сделает возможным вычисление условной энтропии между конверсией и каждой микроконверсией, а значит задача по расчету влияния микроконверсий на итоговую конверсию на сайте полностью решена.
Кроме того, суммируя данные на уровнях кейворда, баннера, кампании, мы сможем рассчитать зависимости между конверсиями и микроконверсиями не только на уровне сайта в целом, но и на более низких уровнях, что значительно повысит эффект от оптимизации.
В следующей главе мы рассмотрим вопрос того, как на основании полученных данных оценить вес микроконверсии, и как использовать данную информацию для оптимизации.
Оценка весов микроконверсий и оптимизация ставок
Для оценки влияния микроконверсии по некоторой цели на общую конверсию на сайте удобно пользоваться нормированной формулой весов: В данном случае суммарное влияние микроконверсий по всем выбранным целям на итоговую конверсию на сайте равно 1.
Если мы вычислили коэффициент влияния (вес) по всем переходам на сайт, то выбрав цели с наибольшим влиянием, мы можем оптимизировать (например, методами A/Б тестирования) те участки сайта, где происходит сбор данных микроконверсий для повышения общей конверсии.
Если же перед нами стоит цель оптимизации ставок для контекстной рекламы, то необходимо рассчитать на уровне каждого кейворда (именно для них оптимизатор конверсий рассчитывает и отправляет оптимальные ставки):Очевидно, что ставка по ключевой фразе (кейворду X) – это некоторая функция , которая зависит от статистики (в первую очередь от коэффициента макроконверсии ) и от KPI, которые установлены в качестве целевых:Тогда для оптимизации с учетом микроконверсий мы можем воспользоваться обобщением последней формулы:где параметр является некоторой монотонно убывающей функцией от количества кликов и макроконверсий по кейворду: чем больше кликов и макроконверсий, тем меньше величина (тем меньше нам требуется знаний о поведении микроконверсий для расчета ставок).
Таким образом, информация о микроконверсиях является особенно ценной в случае малого объема статистики по кейворду.
Кейс по оптимизации
Описанные в данной работы алгоритмы являются неотъемлемой частью оптимизатора конверсий Calltouch. Оптимизация с учетом микроконверсий оказывается особенно эффективной в том случае, если количество конверсий, которое оптимизатор старается максимизировать в рамках установленных KPI, невелико. Это имеет место быть либо для небольших рекламных аккаунтов, либо в случае выбора специфического типа конверсии. Если рассматривать оптимизацию по звонкам (именно на таком типе оптимизации специализируется сервис Calltouch), то специфическим типом конверсии является тегированный звонок. Система позволяет тегировать звонки как вручную, так и с использованием инструмента автоматического тегирования Calltouch Predict.
В данном разделе мы приведем результаты совместного с агентством «Ашманов и Партнеры» кейса по оптимизации контекста для компании BIIKS (Бурение скважин). Целью тестирования являлось увеличение числа прослушанных целевых звонков в рамках текущего CPA.
Результаты тестирования:
Стоимость конверсии: подключая рекламные кампании к Оптимизатору Calltouch, клиент рассчитывал сохранить текущую стоимость конверсии, при этом получить максимум звонков. За первые 4 недели теста были достигнуты следующие результаты:

Коэффициент конверсии: на рекламных кампаниях, подключенных к Оптимизатору Calltouch, коэффициент конверсии за период теста вырос на 55 %.

Количество конверсий: количество конверсий в период теста значительно выросло: прирост при использовании Оптимизатора составил 91%

Заключение
В работе рассмотрен новый подход к анализу микроконверсий и их влиянию на основную конверсию на сайте. Данный подход базируется на принципах теории информации. Для его реализации достаточно выбрать определенные цели, которые будут отслеживаться системой аналитики, и выбрать среди них основную (конверсию) и накопить статистику по переходам на сайт хотя бы за 30 дней. Предложенная в статье методика может быть использована как для выявления «слабых» мест на сайте, так и для оптимизации ставок в контекстной рекламе.

