Технологии определяют результат. Компания Calltouch давно приняла для себя эту истину.
Наш старший продакт-менеджер Федор Иванов mthmtcn написал материал об использовании различных метрик для кластеризации ключевых запросов.
На сегодняшний день инструменты по оптимизации конверсий в контекстной рекламе широко используются как прямыми рекламодателями, так и агентствами. Мы в компании Calltouch уже больше года ведем разработку своего инструмента по оптимизации ставок в контекстной рекламе. Основная цель оптимизаторов – расчет таких ставок для ключевых слов, выставление которых позволило бы достичь тех желаемых ключевых показателей (KPI), которые установлены в качестве цели оптимизации. Классическим примером такой постановки задачи является оптимизация по CPA (Cost Per Action). В данном случае основная цель оптимизатора – получение как можно большего числа конверсий (целевых действий) так, чтобы средняя стоимость этого действия не превосходила установленного целевого ограничения CPA. Также существуют такие стратегии оптимизации, как максимизация ROI (Return of Investment), привлечение максимума конверсий при заданном бюджете рекламных кампаний и т. д.
Сегодня на рынке представлено значительное число систем, которые занимаются управлением ставками. Каждый инструмент имеет свои особенности по первичной настройке, функционалу, дополнительным опциям и т. д. В частности, оптимизатор Calltouch специализируется на оптимизации контекстной рекламы в звонящих тематиках (хотя его возможности не ограничены оптимизацией только по звонкам). Системы по оптимизации контекста в целом успешно справляются с теми задачами, которые ставят перед ними рекламодатели. Однако значительного эффекта от оптимизации добиваются в основном те клиенты, которые располагают крупными рекламными бюджетами. Понять эту зависимость достаточно просто. Все оптимизаторы конверсий так или иначе отталкиваются от собранных за некоторый опорный период данных. Чем крупнее бюджет рекламного аккаунта, тем больше статистики, необходимой для расчета оптимальных ставок, удается собрать. Кроме того, размер бюджета на контекст напрямую влияет и на скорость сбора данных, а значит и на скорость, с которой «разгоняются» оптимизаторы. Вышесказанное ярко иллюстрируется справкой Яндекс Директа по автоматической стратегии управления ставками в кампании:
Очевидно, что лишь очень небольшое число рекламных кампаний подходит под рассмотренный выше «фильтр». Для рекламодателей с небольшими бюджетами, а также для только что созданных рекламных кампаний запуск такого рода оптимизатора невозможен. Конечно, «сторонние» оптимизаторы не так требовательны к объему трафика (мы в частности установили минимальный порог в 1 целевой визит и 10 кликов среднесуточно на «папку» – пакет оптимизируемых кампаний с едиными KPI и стратегией оптимизации), но и они так или иначе вынуждены существовать в условиях существенного дефицита накопленной статистики. Рассмотрим проблему недостатка данных более подробно.
Широко известен принцип Парето, который можно сформулировать как: «20% усилий дают 80% результата»:
Исходя из наших наблюдений, в контекстной рекламе также имеет место этот принцип, но пропорция немного иная: «На 5% ключевых фраз приходится 95% трафика (статистики)»:

Поскольку оптимизаторы конверсий принимают решение об оптимальной ставке для каждой ключевой фразы отдельно, то обоснованное решение может быть принято только по примерно 5% фраз. Если рассмотреть эту картину более детально, то все ключевые фразы можно разделить на 3 группы по объему статистики (за некоторый период ее сбора, который иначе называется опорным):

Конечно, вопрос достаточности статистики должен быть согласован с некоторым критерием оценки объема данных. Расчет этого критерия основан на методах теории вероятностей и математической статистики, связанных с оценкой достаточности объема выборки значений некоторого распределения.
Таким образом, все ключевые фразы фразы можно разделить на 3 основные группы:
Прежде чем приступить к обсуждению различных подходов по вычислению ставок при условиях недостаточного объема данных, необходимо понять, каким образом эти данные преобразуются в оптимальную ставку. Это преобразование можно разделить на 2 основных блока:
Вначале рассмотрим второй блок. Будем считать, что мы спрогнозировали коэффициент конверсии по фразе. Если клиент установил целевые и по фразе была накоплена некоторая статистика по требуемым ключевым метрикам, то оптимальная ставка рассчитывается как некоторая функция от рассмотренных выше параметров:.Очевидно, что сам коэффициент конверсии также зависит от накопленной статистики, но не зависит от :Поэтому окончательная формула для расчета оптимальной ставки имеет вид:Конкретный вид функции зависит как от используемых метрик, которые содержатся в , так и от стратегии оптимизации и . Например, для стратегии оптимизации по простейшая формула для расчета ставки имеет вид: Для других стратегий используются более сложные формулы для расчета ставок.
Ключевым моментом в вычислении ставки является как можно более точное прогнозирование коэффициента конверсии, которое производится до момента расчета ставки. По определению коэффициент конверсии ключевой фразы – это вероятность того, что клик по этой фразе приведет к конверсии. При достаточном объеме кликов и конверсий , этот коэффициент может быть вычислен как: Однако применение этой формулы «в лоб» при малом объеме статистики может привести к заведомо неточному прогнозу коэффициента конверсии.
Например, предположим, что по фразе за некоторый период было 2 клика и 1 конверсия. В этом случае формула даст значение . Пусть стратегия оптимизации – «максимум конверсий при руб.», тогда руб. Осталось надеяться, что фраза относится не к РСЯ-кампании…
Противоположный случай. Пусть по фразе было 2 клика и 0 конверсий. В этом случае формула даст значение . Пусть стратегия оптимизации – «максимум конверсий при руб», тогда руб. В этом случае будет отправлена минимально возможная для валюты данного аккаунта ставка. Показы по фразе практически прекратятся, и она уже никогда в будущем не принесет конверсии.
Если же по фразе было 0 кликов и 0 конверсий, то вычисление «напрямую» в принципе невозможно ввиду неопределенности выражения «0/0».
Таким образом, «простая» формула вычисления может быть использована только для ключевых фраз с достаточным объемом статистики (как мы помним, таких фраз около 5%), и мы не можем принять «взвешенного» решения по оставшимся 95% фраз.
Для того, чтобы выйти из данного положения, могут быть использованы различные методики, например:
Методики 2 и 5 активно используются в нашем инструменте, в ближайшем будущем мы также планируем добавить возможность гибкой настройки опорного периода. О том как это сделать, мы напишем отдельную статью. А в данной работе мы рассмотрим метод «пулинга», который показал наибольшую эффективность и широко используется в системах по оптимизации контекстной рекламы.
Методы пулинга
Пулинг (англ. Pooling) по сути представляет собой «разумное» наращивание статистики по ключевой фразе за счет заимствования статистики по другим фразам. Для того, чтобы понять принцип классического пулинга, обратимся к структуре рекламного аккаунта (например, Яндекс Директа):
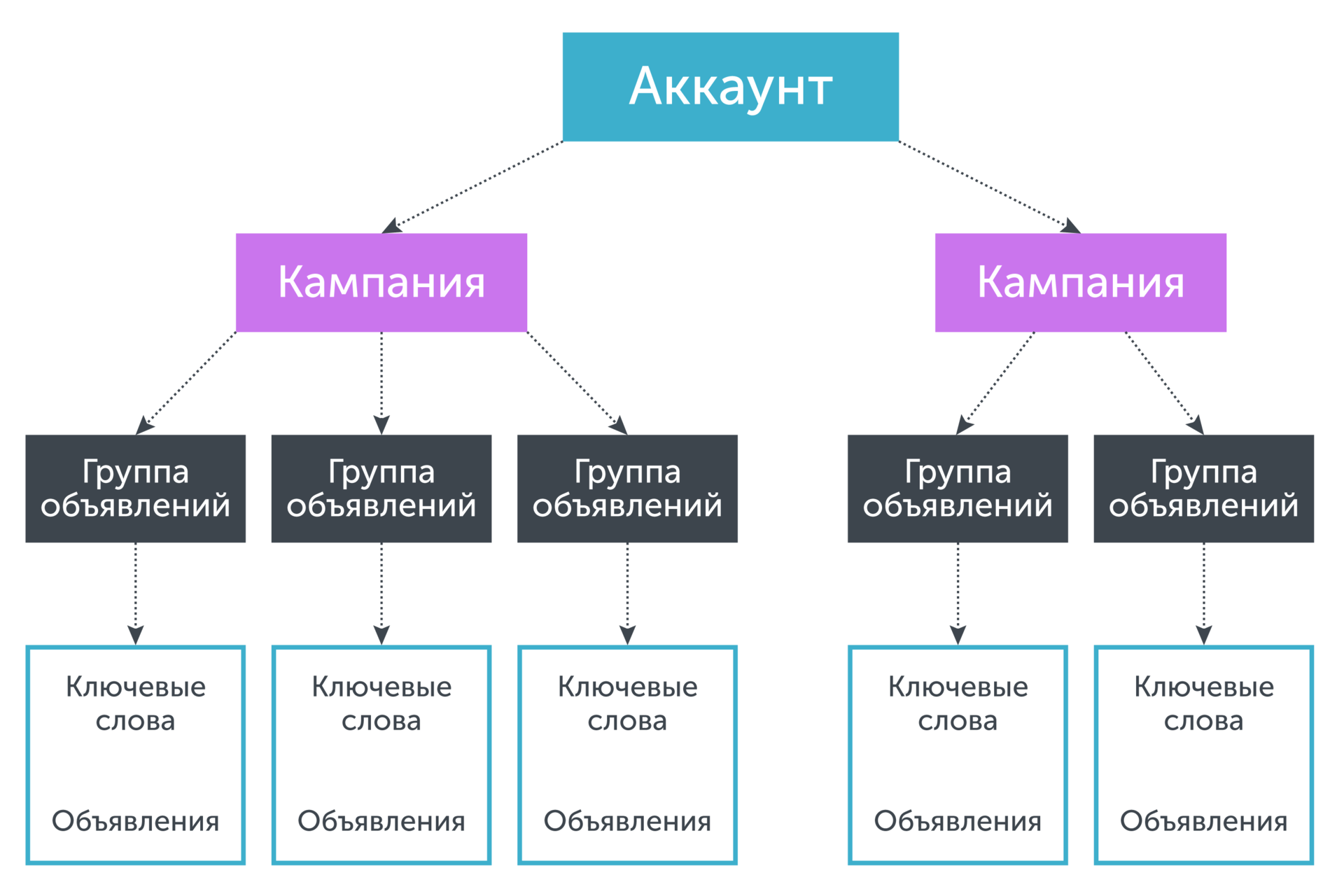
Аккаунт имеет древовидную структуру, где «корнем» являются сам аккаунт, а «листьями» — ключевые фразы. Ключевые фразы определенным образом связаны с объявлениями, показ которых они инициируют. Объявления в свою очередь собираются в группы объявлений, которые в свою очередь объединяются в рамках рекламной кампании. Если нам необходимо спрогнозировать коэффициент конверсии по ключевой фразе, собственной статистики по которой недостаточно, то мы объединяем статистику по ключевой фразе и объявлениям, группе объявлений, которой данная фраза принадлежит, кампании, которой принадлежит данная группа объявлений и так далее до тех пор, пока набранной таким образом статистики не окажется достаточно для принятия решения о значении прогнозируемого параметра. Графически это эквивалентно «движению вниз» по дереву от «листьев» до «корня»:
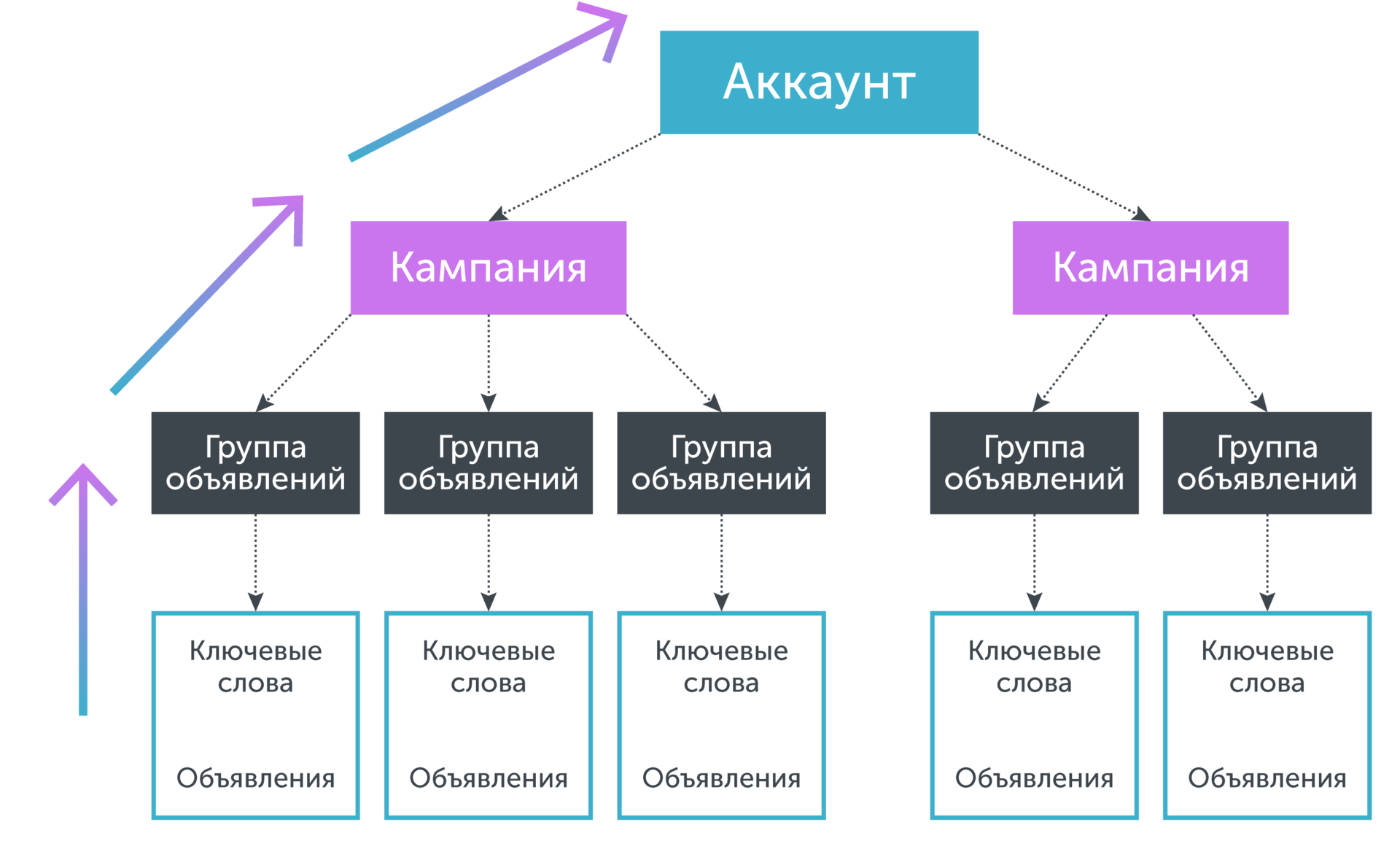
Простейшая формула пулинга имеет вид:где – прогнозируемый ключевой фразы, – количество конверсий по ключевой фразе, – количество кликов по ключевой фразе, – значение коэффициента конверсии для следующего уровня пулинга (например, значение коэффициента конверсии кампании). Таким образом, данная модель прогнозирует, сколько фразе потребуется дополнительных кликов, чтобы получить еще одну конверсию, предполагая, что в среднем все фразы имеют близкий к. В свою очередь может быть рассчитан напрямую, при условии, что на данном уровне достаточно статистических данных, в противном случае он может быть вычислен с использованием пулинга более высокого уровня. В этом случае получается сложная вложенная модель.
Приведем пример. Пусть по фразе было 5 кликов и 1 конверсия, а по группе объявлений, в которой находится , набралось 100 кликов и 5 конверсий. Если предположить, что ста кликов достаточно для принятия решения об оптимальной ставке, получим: Метод пулинга и различные его обобщения получили широкое распространение в системах по автоматизации контекстной рекламы. Например, самая популярная в мире платформа по управлению рекламой в Интернете Marin Software запатентовала свою модель (патент US PTO 60948670):
где – среднее значение вероятности конверсии для следующего уровня пулинга, – дисперсия (мера разброса) значений вероятности конверсии следующего уровня пулинга.
Очевидно, что чем больше величина дисперсии, тем меньше , а значит тем меньше влияния оказывает следующий уровень пулинга в прогнозировании коэффициента конверсии. Величина определяется тем, насколько близки друг к другу коэффициенты конверсии. При классической модели пулинга будет напрямую зависеть от того, насколько качественно проработан рекламный аккаунт, а значит качество прогнозирования напрямую зависит от человеческого фактора.
Кроме того, иерархический пулинг учитывает только статистику по фразам, оставляя в стороне ее структуру.
В связи со всем вышесказанным, командой Calltouch был разработан другой подход к прогнозированию коэффициента конверсии.
Основной идеей нашего подхода является отказ от иерархической структуры при пулинге. Вместо этого вводится специальная метрика (мера расстояния), позволяющая оценивать схожесть текстов ключевых фраз между собой.
Для заданной ключевой фразы мы будем подбирать такие элементы из множества фраз с достаточным объемом статистики (которое мы назовем ядром кластеризации), чтобы расстояние между текстом и выбранными элементами не превосходило некоторого наперед заданного числа : Если для заданного кластер не содержит достаточного объема статистики, то увеличивается на определенный шаг : до тех пор, пока в не наберется достаточного объема статистики для прогнозирования коэффициента конверсии фразы . Как только кластер составлен, среднее значение коэффициента конверсии фраз внутри кластера выбирается в качестве значения . Графически этот процесс можно представить в следующем виде:

Теперь рассмотрим структуру кластеров более детально:
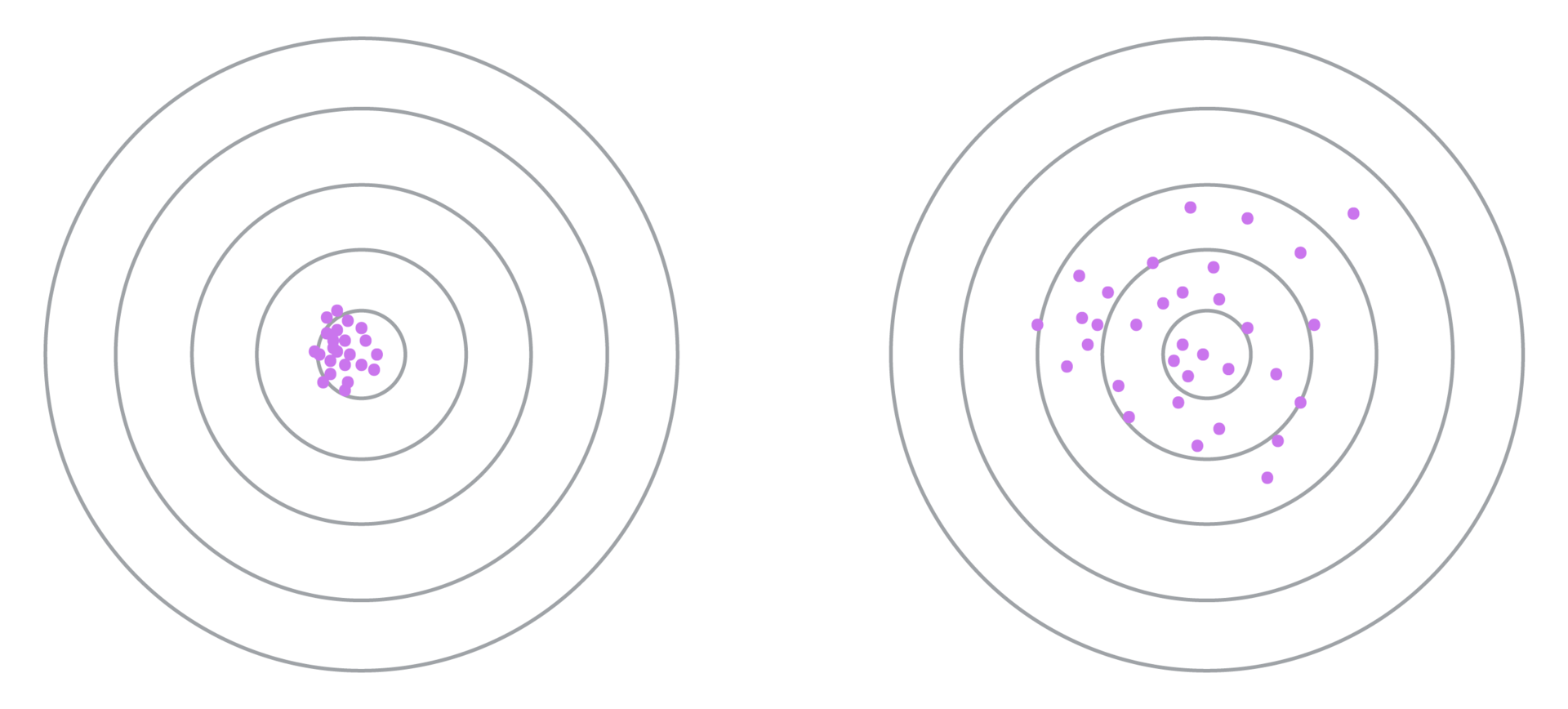
На левом рисунке выбраны ключевые фразы с малой дисперсией коэффициента конверсии, в то время как на правом – с большой. Видно, что в случае большой дисперсии алгоритм сходится медленнее (требуется несколько раз увеличивать порог , а сам прогноз является менее точным. Поэтому требуется заранее выбрать такую метрику схожести фраз, которая бы минимизировала дисперсию.
Существует множество различных метрик, позволяющих вычислить сходство двух текстов (ключевых фраз в нашем случае). Каждая из этих метрик обладает как своими достоинствами, так и недостатками, которые сужают область их возможного применения. В исследовании, проведенном нашей командой, были рассмотрены следующие виды расстояний:
Рассмотрим каждую из метрик более детально.
Расстояние Левенштейна определяется как минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой, необходимых для превращения одной строки в другую. Обозначим это расстояние между строками и как . Ясно, что чем больше, тем меньше строки и похожи друг на друга.
Приведем несколько примеров.
Пусть и , тогда чтобы превратить в , требуется заменить «т» на «о», «р» на «б» и «о» на «а», а значит .
Если 'это одна фраза' и 'а это совсем другая фраза', то .
Основными преимуществами расстояния Левенштейна являются его слабая зависимость от форм слова в тексте а также простота реализации, а к основному недостатку следует отнести зависимость от порядка слов.
Основная идея, лежащая в основе вычисления N-граммного расстояния – это разбиение строк на подстроки длины N и подсчет количества совпадающих подстрок.
Например, если N=2 (разбиение на биграммы) и 'раз кейворд,' а 'два кейворд', то соответствует следующий набор биграмм: ‘ра’, ‘aз’, ‘ке’, ‘ей’, …, ‘рд’, а строке : ‘дв’, ‘ва’, ‘ке’,‘ей’, …, ‘рд’.
Если N=3 (разбиение на триграммы), то для тех же и получим:
: ‘раз’, ‘aзк ’, ‘зке’, ‘кей’, ‘ейр’, …, ‘орд’
: ‘два’, ‘вак ’, ‘аке’, ‘ кей’, ‘ейр’, …, ‘орд’
Само N-граммное расстояние вычисляется по следующей формуле: где — количество N-грамм в, — количество N-грамм в и — количество общих N-грамм у и .
В нашем случае: и .
Основным преимуществом такого подхода к вычислению схожести ключевых фраз является то, что он слабо зависит от форм слов в тексте. Главным недостатком является зависимость от свободного параметра N, выбор которого может оказать сильное влияние на дисперсию внутри кластера.
Основная идея, на которой базируется расчет косинусного расстояния, заключается в том, что строку из символов можно преобразовать в числовой вектор. Если проделать эту процедуру с двумя сравниваемыми строками, то меру их сходства можно оценить через косинус между двумя числовыми векторами. Из курса школьной математики известно, что если угол между векторами равен 0 ( то есть векторы полностью совпадают), то косинус равен 1. И наоборот: если угол между векторами равен 90 градусов ( векторы ортогональны – то есть полностью не совпадают), то косинус между ними равен 0.
Прежде чем вводить формальное определение косинусного расстояния требуется определить способ отображения строки в числовой вектор. В качестве такого отображения мы использовали преобразование текстовой строки в вектор индикаторов.
Рассмотрим пример. Пусть
'купить пластиковые окна со скидкой',
'купить недорого пластиковые окна с бесплатной доставкой по Москве'
Составим таблицу:

В первой строке таблицы указаны все различные слова, которые встречаются в текстах и , вторая и третья строки – это индикаторы того, что данное слово встречается в строке или соответственно. Таким образом, если мы заменим каждую из строк и на векторы из индикаторов (назовем их соответственно и ), то мы можем вычислить косинус между строками по формуле:Для нашего примера:Расстояние между и будем считать по формуле:Тогда в нашем случае:Основным преимуществом косинусного расстояния является то, что данная метрика хорошо работает на разреженных данных (реальные тексты ключевых фраз могут быть очень длинными, содержать значительные объемы служебной информации, такой как минус-слова, стоп-слова и т. д.) Ключевым недостатком косинусного расстояния является его очень сильная зависимость от форм слова.
Проиллюстрируем это показательным примером. Пусть,
'купить пластиковые окна'
'куплю окно из пластика'
Легко заметить, что все слова в двух на первый взгляд очень похожих текстах употребляются в разной форме. Если вычислить косинусное расстояние между такими строками, то получим . Это значит, что между и нет вообще ничего общего, что никак не согласуется со здравым смыслом.
Исправить ситуацию позволяет предварительная предобработка текста (лемматизация).
Приведем краткую справку из Википедии.
В нашем случае из «купить пластиковые окна» получим “купить пластиковый окно”, а из “куплю окно из пластика” - “купить окно пластик”. Тогда для нормализованных текстов имеем:Таким образом, косинусное расстояние следует вычислять после предварительной обработки текста.
Мы с командой по разработке оптимизатора провели тестирование рассмотренных выше метрик на статистике, собранной в рекламных аккаунтах наших клиентов. Рассматривались различные тематики, такие как: недвижимость, автомобили, медицина и т. д. Поскольку база сервиса Calltouch содержит данные о более чем 10000 клиентов, мы располагали более чем достаточным объемом данных для проведения достоверных тестов с метриками. В таблице приведены усредненные показатели дисперсии, вычисленной при кластеризации ключевых фраз с использованием различных метрик.
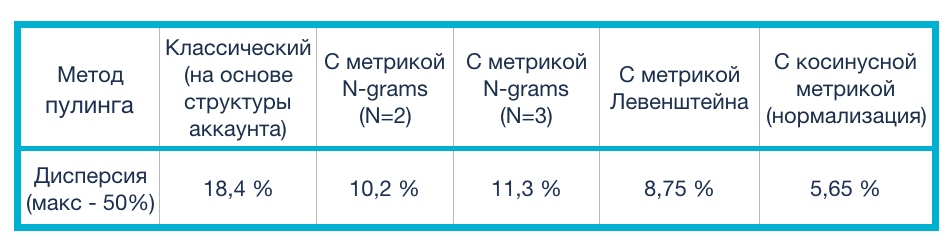
В качестве ядра кластеризации выбирались такие ключевые фразы, по которым за последние 28 дней была хотя бы одна конверсия и количество кликов по которым удовлетворяло соотношению:где - коэффициент конверсии кампании, которой принадлежит ключевая фраза.
Из приведенной таблицы видно, что классический метод пулинга обладает наибольшей дисперсией (а значит его использование приводит к наименее точному прогнозу ), в то время как использование любой из приведенных метрик схожести фраз между собой существенно понижает этот показатель. Наилучшей метрикой для кластеризации оказалось косинусное расстояние.
В данной статье рассмотрен новый подход к кластеризации ключевых фраз, основанный на текстовом сходстве. Показано, что данный метод существенно уменьшает внутрикластерную дисперсию коэффициента конверсии, что значительно улучшает точность прогнозирования конверсии по ключевой фразе. Описанные в статье методы могут быть использованы для оптимизации даже тех фраз, собственной статистики по которым недостаточно для принятия решения об оптимальной ставке. Приведенные методы расчета коэффициента конверсии являются элементами оптимизатора конверсий Calltouch, который на практике показывает высокую эффективность как на крупных проектах, так и на аккаунтах со сравнительно небольшим рекламным бюджетом.
Наш старший продакт-менеджер Федор Иванов mthmtcn написал материал об использовании различных метрик для кластеризации ключевых запросов.
Введение
На сегодняшний день инструменты по оптимизации конверсий в контекстной рекламе широко используются как прямыми рекламодателями, так и агентствами. Мы в компании Calltouch уже больше года ведем разработку своего инструмента по оптимизации ставок в контекстной рекламе. Основная цель оптимизаторов – расчет таких ставок для ключевых слов, выставление которых позволило бы достичь тех желаемых ключевых показателей (KPI), которые установлены в качестве цели оптимизации. Классическим примером такой постановки задачи является оптимизация по CPA (Cost Per Action). В данном случае основная цель оптимизатора – получение как можно большего числа конверсий (целевых действий) так, чтобы средняя стоимость этого действия не превосходила установленного целевого ограничения CPA. Также существуют такие стратегии оптимизации, как максимизация ROI (Return of Investment), привлечение максимума конверсий при заданном бюджете рекламных кампаний и т. д.
Сегодня на рынке представлено значительное число систем, которые занимаются управлением ставками. Каждый инструмент имеет свои особенности по первичной настройке, функционалу, дополнительным опциям и т. д. В частности, оптимизатор Calltouch специализируется на оптимизации контекстной рекламы в звонящих тематиках (хотя его возможности не ограничены оптимизацией только по звонкам). Системы по оптимизации контекста в целом успешно справляются с теми задачами, которые ставят перед ними рекламодатели. Однако значительного эффекта от оптимизации добиваются в основном те клиенты, которые располагают крупными рекламными бюджетами. Понять эту зависимость достаточно просто. Все оптимизаторы конверсий так или иначе отталкиваются от собранных за некоторый опорный период данных. Чем крупнее бюджет рекламного аккаунта, тем больше статистики, необходимой для расчета оптимальных ставок, удается собрать. Кроме того, размер бюджета на контекст напрямую влияет и на скорость сбора данных, а значит и на скорость, с которой «разгоняются» оптимизаторы. Вышесказанное ярко иллюстрируется справкой Яндекс Директа по автоматической стратегии управления ставками в кампании:
Целевые визиты за 28 дней+0,01 х клики за 28 дней ? 40– это порог оптимизации для автоматической стратегии по CPA (для 1 кампании).
Стратегия эффективна для кампаний с количеством кликов за неделю более 200 и количеством целевых визитов за неделю более 10.– а это критерий, гарантирующий эффективность оптимизации.
Очевидно, что лишь очень небольшое число рекламных кампаний подходит под рассмотренный выше «фильтр». Для рекламодателей с небольшими бюджетами, а также для только что созданных рекламных кампаний запуск такого рода оптимизатора невозможен. Конечно, «сторонние» оптимизаторы не так требовательны к объему трафика (мы в частности установили минимальный порог в 1 целевой визит и 10 кликов среднесуточно на «папку» – пакет оптимизируемых кампаний с едиными KPI и стратегией оптимизации), но и они так или иначе вынуждены существовать в условиях существенного дефицита накопленной статистики. Рассмотрим проблему недостатка данных более подробно.
Статистика по ключевым словам
Широко известен принцип Парето, который можно сформулировать как: «20% усилий дают 80% результата»:

Исходя из наших наблюдений, в контекстной рекламе также имеет место этот принцип, но пропорция немного иная: «На 5% ключевых фраз приходится 95% трафика (статистики)»:

Поскольку оптимизаторы конверсий принимают решение об оптимальной ставке для каждой ключевой фразы отдельно, то обоснованное решение может быть принято только по примерно 5% фраз. Если рассмотреть эту картину более детально, то все ключевые фразы можно разделить на 3 группы по объему статистики (за некоторый период ее сбора, который иначе называется опорным):

Конечно, вопрос достаточности статистики должен быть согласован с некоторым критерием оценки объема данных. Расчет этого критерия основан на методах теории вероятностей и математической статистики, связанных с оценкой достаточности объема выборки значений некоторого распределения.
Таким образом, все ключевые фразы фразы можно разделить на 3 основные группы:
- Фразы с достаточным объемом статистики за опорный период
- Фразы со статистикой, которой недостаточно для принятия решения
- Фразы без статистики за опорный период
Прежде чем приступить к обсуждению различных подходов по вычислению ставок при условиях недостаточного объема данных, необходимо понять, каким образом эти данные преобразуются в оптимальную ставку. Это преобразование можно разделить на 2 основных блока:
- Вычисление прогнозируемого коэффициента конверсии ключевого слова
- Вычисление оптимальной ставки по вычисленному и установленных
Вначале рассмотрим второй блок. Будем считать, что мы спрогнозировали коэффициент конверсии по фразе. Если клиент установил целевые и по фразе была накоплена некоторая статистика по требуемым ключевым метрикам, то оптимальная ставка рассчитывается как некоторая функция от рассмотренных выше параметров:.Очевидно, что сам коэффициент конверсии также зависит от накопленной статистики, но не зависит от :Поэтому окончательная формула для расчета оптимальной ставки имеет вид:Конкретный вид функции зависит как от используемых метрик, которые содержатся в , так и от стратегии оптимизации и . Например, для стратегии оптимизации по простейшая формула для расчета ставки имеет вид: Для других стратегий используются более сложные формулы для расчета ставок.
Ключевым моментом в вычислении ставки является как можно более точное прогнозирование коэффициента конверсии, которое производится до момента расчета ставки. По определению коэффициент конверсии ключевой фразы – это вероятность того, что клик по этой фразе приведет к конверсии. При достаточном объеме кликов и конверсий , этот коэффициент может быть вычислен как: Однако применение этой формулы «в лоб» при малом объеме статистики может привести к заведомо неточному прогнозу коэффициента конверсии.
Например, предположим, что по фразе за некоторый период было 2 клика и 1 конверсия. В этом случае формула даст значение . Пусть стратегия оптимизации – «максимум конверсий при руб.», тогда руб. Осталось надеяться, что фраза относится не к РСЯ-кампании…
Противоположный случай. Пусть по фразе было 2 клика и 0 конверсий. В этом случае формула даст значение . Пусть стратегия оптимизации – «максимум конверсий при руб», тогда руб. В этом случае будет отправлена минимально возможная для валюты данного аккаунта ставка. Показы по фразе практически прекратятся, и она уже никогда в будущем не принесет конверсии.
Если же по фразе было 0 кликов и 0 конверсий, то вычисление «напрямую» в принципе невозможно ввиду неопределенности выражения «0/0».
Таким образом, «простая» формула вычисления может быть использована только для ключевых фраз с достаточным объемом статистики (как мы помним, таких фраз около 5%), и мы не можем принять «взвешенного» решения по оставшимся 95% фраз.
Для того, чтобы выйти из данного положения, могут быть использованы различные методики, например:
- Выставление единых ставок на уровне рекламной кампании
- Анализ метрик, коррелирующих с (например, показатель отказов)
- Повышение ставок до тех пор, пока фразы не начнут набирать статистику
- Расширение опорного периода
- Применение «пулинга» (умное наследование и усреднение статистики)
Методики 2 и 5 активно используются в нашем инструменте, в ближайшем будущем мы также планируем добавить возможность гибкой настройки опорного периода. О том как это сделать, мы напишем отдельную статью. А в данной работе мы рассмотрим метод «пулинга», который показал наибольшую эффективность и широко используется в системах по оптимизации контекстной рекламы.
Методы пулинга
Пулинг (англ. Pooling) по сути представляет собой «разумное» наращивание статистики по ключевой фразе за счет заимствования статистики по другим фразам. Для того, чтобы понять принцип классического пулинга, обратимся к структуре рекламного аккаунта (например, Яндекс Директа):

Аккаунт имеет древовидную структуру, где «корнем» являются сам аккаунт, а «листьями» — ключевые фразы. Ключевые фразы определенным образом связаны с объявлениями, показ которых они инициируют. Объявления в свою очередь собираются в группы объявлений, которые в свою очередь объединяются в рамках рекламной кампании. Если нам необходимо спрогнозировать коэффициент конверсии по ключевой фразе, собственной статистики по которой недостаточно, то мы объединяем статистику по ключевой фразе и объявлениям, группе объявлений, которой данная фраза принадлежит, кампании, которой принадлежит данная группа объявлений и так далее до тех пор, пока набранной таким образом статистики не окажется достаточно для принятия решения о значении прогнозируемого параметра. Графически это эквивалентно «движению вниз» по дереву от «листьев» до «корня»:

Простейшая формула пулинга имеет вид:где – прогнозируемый ключевой фразы, – количество конверсий по ключевой фразе, – количество кликов по ключевой фразе, – значение коэффициента конверсии для следующего уровня пулинга (например, значение коэффициента конверсии кампании). Таким образом, данная модель прогнозирует, сколько фразе потребуется дополнительных кликов, чтобы получить еще одну конверсию, предполагая, что в среднем все фразы имеют близкий к. В свою очередь может быть рассчитан напрямую, при условии, что на данном уровне достаточно статистических данных, в противном случае он может быть вычислен с использованием пулинга более высокого уровня. В этом случае получается сложная вложенная модель.
Приведем пример. Пусть по фразе было 5 кликов и 1 конверсия, а по группе объявлений, в которой находится , набралось 100 кликов и 5 конверсий. Если предположить, что ста кликов достаточно для принятия решения об оптимальной ставке, получим: Метод пулинга и различные его обобщения получили широкое распространение в системах по автоматизации контекстной рекламы. Например, самая популярная в мире платформа по управлению рекламой в Интернете Marin Software запатентовала свою модель (патент US PTO 60948670):
где – среднее значение вероятности конверсии для следующего уровня пулинга, – дисперсия (мера разброса) значений вероятности конверсии следующего уровня пулинга.
Очевидно, что чем больше величина дисперсии, тем меньше , а значит тем меньше влияния оказывает следующий уровень пулинга в прогнозировании коэффициента конверсии. Величина определяется тем, насколько близки друг к другу коэффициенты конверсии. При классической модели пулинга будет напрямую зависеть от того, насколько качественно проработан рекламный аккаунт, а значит качество прогнозирования напрямую зависит от человеческого фактора.
Кроме того, иерархический пулинг учитывает только статистику по фразам, оставляя в стороне ее структуру.
В связи со всем вышесказанным, командой Calltouch был разработан другой подход к прогнозированию коэффициента конверсии.
Основные идеи нашего подхода
Основной идеей нашего подхода является отказ от иерархической структуры при пулинге. Вместо этого вводится специальная метрика (мера расстояния), позволяющая оценивать схожесть текстов ключевых фраз между собой.
Для заданной ключевой фразы мы будем подбирать такие элементы из множества фраз с достаточным объемом статистики (которое мы назовем ядром кластеризации), чтобы расстояние между текстом и выбранными элементами не превосходило некоторого наперед заданного числа : Если для заданного кластер не содержит достаточного объема статистики, то увеличивается на определенный шаг : до тех пор, пока в не наберется достаточного объема статистики для прогнозирования коэффициента конверсии фразы . Как только кластер составлен, среднее значение коэффициента конверсии фраз внутри кластера выбирается в качестве значения . Графически этот процесс можно представить в следующем виде:

Теперь рассмотрим структуру кластеров более детально:

На левом рисунке выбраны ключевые фразы с малой дисперсией коэффициента конверсии, в то время как на правом – с большой. Видно, что в случае большой дисперсии алгоритм сходится медленнее (требуется несколько раз увеличивать порог , а сам прогноз является менее точным. Поэтому требуется заранее выбрать такую метрику схожести фраз, которая бы минимизировала дисперсию.
Метрики схожести
Существует множество различных метрик, позволяющих вычислить сходство двух текстов (ключевых фраз в нашем случае). Каждая из этих метрик обладает как своими достоинствами, так и недостатками, которые сужают область их возможного применения. В исследовании, проведенном нашей командой, были рассмотрены следующие виды расстояний:
- Расстояние Левенштейна
- N-граммное расстояние
- Косинусное расстояние
Рассмотрим каждую из метрик более детально.
Расстояние Левенштейна
Расстояние Левенштейна определяется как минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой, необходимых для превращения одной строки в другую. Обозначим это расстояние между строками и как . Ясно, что чем больше, тем меньше строки и похожи друг на друга.
Приведем несколько примеров.
Пусть и , тогда чтобы превратить в , требуется заменить «т» на «о», «р» на «б» и «о» на «а», а значит .
Если 'это одна фраза' и 'а это совсем другая фраза', то .
Основными преимуществами расстояния Левенштейна являются его слабая зависимость от форм слова в тексте а также простота реализации, а к основному недостатку следует отнести зависимость от порядка слов.
N-граммное расстояние
Основная идея, лежащая в основе вычисления N-граммного расстояния – это разбиение строк на подстроки длины N и подсчет количества совпадающих подстрок.
Например, если N=2 (разбиение на биграммы) и 'раз кейворд,' а 'два кейворд', то соответствует следующий набор биграмм: ‘ра’, ‘aз’, ‘ке’, ‘ей’, …, ‘рд’, а строке : ‘дв’, ‘ва’, ‘ке’,‘ей’, …, ‘рд’.
Если N=3 (разбиение на триграммы), то для тех же и получим:
: ‘раз’, ‘aзк ’, ‘зке’, ‘кей’, ‘ейр’, …, ‘орд’
: ‘два’, ‘вак ’, ‘аке’, ‘ кей’, ‘ейр’, …, ‘орд’
Само N-граммное расстояние вычисляется по следующей формуле: где — количество N-грамм в, — количество N-грамм в и — количество общих N-грамм у и .
В нашем случае: и .
Основным преимуществом такого подхода к вычислению схожести ключевых фраз является то, что он слабо зависит от форм слов в тексте. Главным недостатком является зависимость от свободного параметра N, выбор которого может оказать сильное влияние на дисперсию внутри кластера.
Косинусное расстояние
Основная идея, на которой базируется расчет косинусного расстояния, заключается в том, что строку из символов можно преобразовать в числовой вектор. Если проделать эту процедуру с двумя сравниваемыми строками, то меру их сходства можно оценить через косинус между двумя числовыми векторами. Из курса школьной математики известно, что если угол между векторами равен 0 ( то есть векторы полностью совпадают), то косинус равен 1. И наоборот: если угол между векторами равен 90 градусов ( векторы ортогональны – то есть полностью не совпадают), то косинус между ними равен 0.
Прежде чем вводить формальное определение косинусного расстояния требуется определить способ отображения строки в числовой вектор. В качестве такого отображения мы использовали преобразование текстовой строки в вектор индикаторов.
Рассмотрим пример. Пусть
'купить пластиковые окна со скидкой',
'купить недорого пластиковые окна с бесплатной доставкой по Москве'
Составим таблицу:

В первой строке таблицы указаны все различные слова, которые встречаются в текстах и , вторая и третья строки – это индикаторы того, что данное слово встречается в строке или соответственно. Таким образом, если мы заменим каждую из строк и на векторы из индикаторов (назовем их соответственно и ), то мы можем вычислить косинус между строками по формуле:Для нашего примера:Расстояние между и будем считать по формуле:Тогда в нашем случае:Основным преимуществом косинусного расстояния является то, что данная метрика хорошо работает на разреженных данных (реальные тексты ключевых фраз могут быть очень длинными, содержать значительные объемы служебной информации, такой как минус-слова, стоп-слова и т. д.) Ключевым недостатком косинусного расстояния является его очень сильная зависимость от форм слова.
Проиллюстрируем это показательным примером. Пусть,
'купить пластиковые окна'
'куплю окно из пластика'
Легко заметить, что все слова в двух на первый взгляд очень похожих текстах употребляются в разной форме. Если вычислить косинусное расстояние между такими строками, то получим . Это значит, что между и нет вообще ничего общего, что никак не согласуется со здравым смыслом.
Исправить ситуацию позволяет предварительная предобработка текста (лемматизация).
Приведем краткую справку из Википедии.
Лемматизация (нормализация) – это процесс приведения словоформы к лемме — её нормальной (словарной) форме.
В русском языке нормальными считаются следующие морфологические формы:
- для существительных — именительный падеж, единственное число;
- для прилагательных — именительный падеж, единственное число, мужской род;
- для глаголов, причастий, деепричастий — глагол в инфинитиве.
Кроме того, лемматизация удаляет из текста все служебные слова – предлоги, союзы, частицы и т. д.
В нашем случае из «купить пластиковые окна» получим “купить пластиковый окно”, а из “куплю окно из пластика” - “купить окно пластик”. Тогда для нормализованных текстов имеем:Таким образом, косинусное расстояние следует вычислять после предварительной обработки текста.
Результаты
Мы с командой по разработке оптимизатора провели тестирование рассмотренных выше метрик на статистике, собранной в рекламных аккаунтах наших клиентов. Рассматривались различные тематики, такие как: недвижимость, автомобили, медицина и т. д. Поскольку база сервиса Calltouch содержит данные о более чем 10000 клиентов, мы располагали более чем достаточным объемом данных для проведения достоверных тестов с метриками. В таблице приведены усредненные показатели дисперсии, вычисленной при кластеризации ключевых фраз с использованием различных метрик.

В качестве ядра кластеризации выбирались такие ключевые фразы, по которым за последние 28 дней была хотя бы одна конверсия и количество кликов по которым удовлетворяло соотношению:где - коэффициент конверсии кампании, которой принадлежит ключевая фраза.
Из приведенной таблицы видно, что классический метод пулинга обладает наибольшей дисперсией (а значит его использование приводит к наименее точному прогнозу ), в то время как использование любой из приведенных метрик схожести фраз между собой существенно понижает этот показатель. Наилучшей метрикой для кластеризации оказалось косинусное расстояние.
Заключение
В данной статье рассмотрен новый подход к кластеризации ключевых фраз, основанный на текстовом сходстве. Показано, что данный метод существенно уменьшает внутрикластерную дисперсию коэффициента конверсии, что значительно улучшает точность прогнозирования конверсии по ключевой фразе. Описанные в статье методы могут быть использованы для оптимизации даже тех фраз, собственной статистики по которым недостаточно для принятия решения об оптимальной ставке. Приведенные методы расчета коэффициента конверсии являются элементами оптимизатора конверсий Calltouch, который на практике показывает высокую эффективность как на крупных проектах, так и на аккаунтах со сравнительно небольшим рекламным бюджетом.


vassabi
странно, что самая «нечеловеческая» метрика оказалось самой лучшей. Хотя, судя по описанию, векторы «новая прокладка» \ «новая рубашка» или «свежая коллекция» \ «свежая зелень» перекидываются в очень близкие точки по хеммингу, так что может быть дело в этом… вы же сортируете слова в фразе по алфавиту или там минимизация расстояния Левенштейна для слов?
Есть ли у вас априорная оценка? Т.е. когда таких фраз\слов вообще не было использовано, посмотреть в статистику гугла\яндекса — насколько популярна эта фраза в соцсетях? (а то будет «100% потерянных вещей, которые мы нашли — оказались под фонарём»)
CalltouchForever Автор
Мы пробовали сортировать слова по алфавиту, но выигрыша от этого в дисперсии не наблюдали. Поэтому решили оставить «как есть», но легко заметить, что косинусная метрика не зависит от порядка слов, так что сортировка там ничего не даст.
Априорную оценку мы не строили, так как мы привязаны к конкретному типу обращения, и я не представляю, как собрать нужную мне статистику не в рамках наших текущих аккаунтов. Наша методика типична для задач машинного обучения: мы собирали ядро фраз с достаточным числом конверсий и кликов, часть фраз использовалась для предсказания как ядро, а на остальной части данных мы пытались предсказать, а потом сравнивали результаты с истинными.
tiendi3
В контекстной рекламе никто не будет мешать несмешиваемое, поэтому тут подход имеет место быть. Например, свежую зелень будут продавать вместе со свежими овощами