В анкетных маркетинговых исследованиях довольно часто встречаются вопросы, в которых респонденты могут выбрать несколько подходящих вариантов из списка возможных ответов (check all that apply questions). Ответы респондентов на такие вопросы задают переменные с множественным откликом (multiple-response variables). Подходящие статистического методы для работы с multiple-response переменными не являются широко известными. В этой статье мы рассмотрим анализ таких переменных на примере данных об автомобильных рейтингах.
Данные
Это типичный пример вопроса анкеты, допускающего несколько вариантов ответа
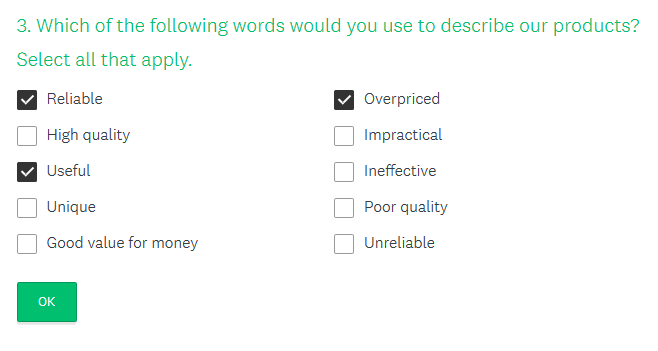
Customer Satisfaction Survey Template. Источник: Survey Monkey
Мы будем использовать в этой статье данные об автомобильных рейтингах (Van Gysel 2011). Они являются свободно распространяемыми и включены в R-пакет plfm. Эти данные стоит воспринимать только как объект для демонстрации математических методов и средств визуализации. Не стоит полагать, что результаты получены на основе полноценного репрезентативного опроса какой-либо группы.
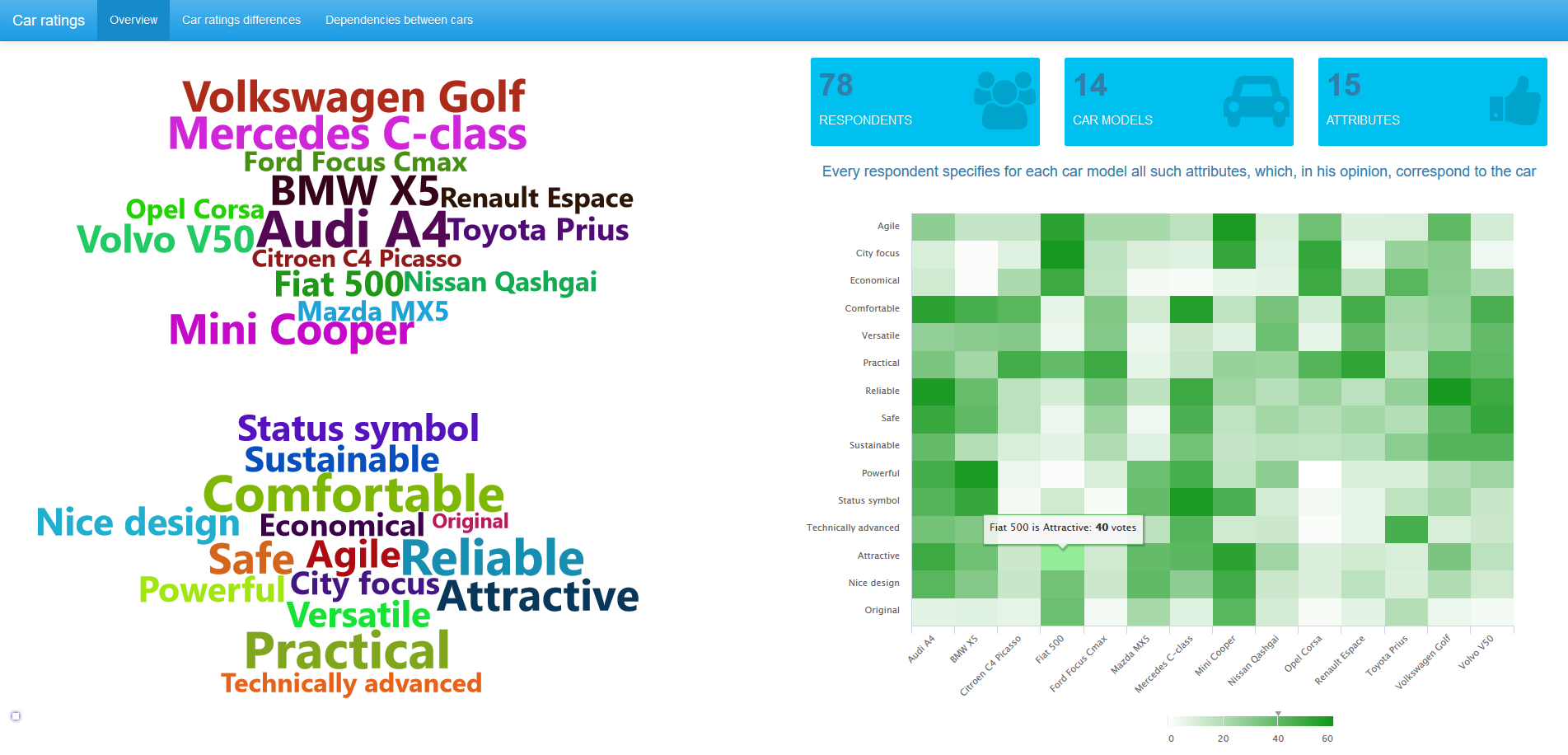
В заглавной картинке приведен обзор данных, все снимки по клику открываются в полном размере. Мы видим, что в опросе приняло участие 78 респондентов. Анкета исследования выясняла мнения о 14 автомобильных марках. Для каждого из них респонденты отмечали те характеристики (из предложенного списка с 15 наименованиями), которым автомобиль соответствует. На снимке выше показано, что 40 респондентов полагают, что Fiat 500 является привлекательным автомобилем.
Сравнение рейтингов
Для сравнения рейтингов по характеристикам между двумя автомобилями используется хорошо известный тест МакНемара, точнее его вариация McNemar mid-p test. Этот тест анализирует парные наблюдения. Поправка mid-p позволяет работать с выборками малого размера и является менее консервативной чем точный биномиальный тест. Подробности можно найти, например, в этой статье (Fagerland, Lydersen, and Laake 2013).
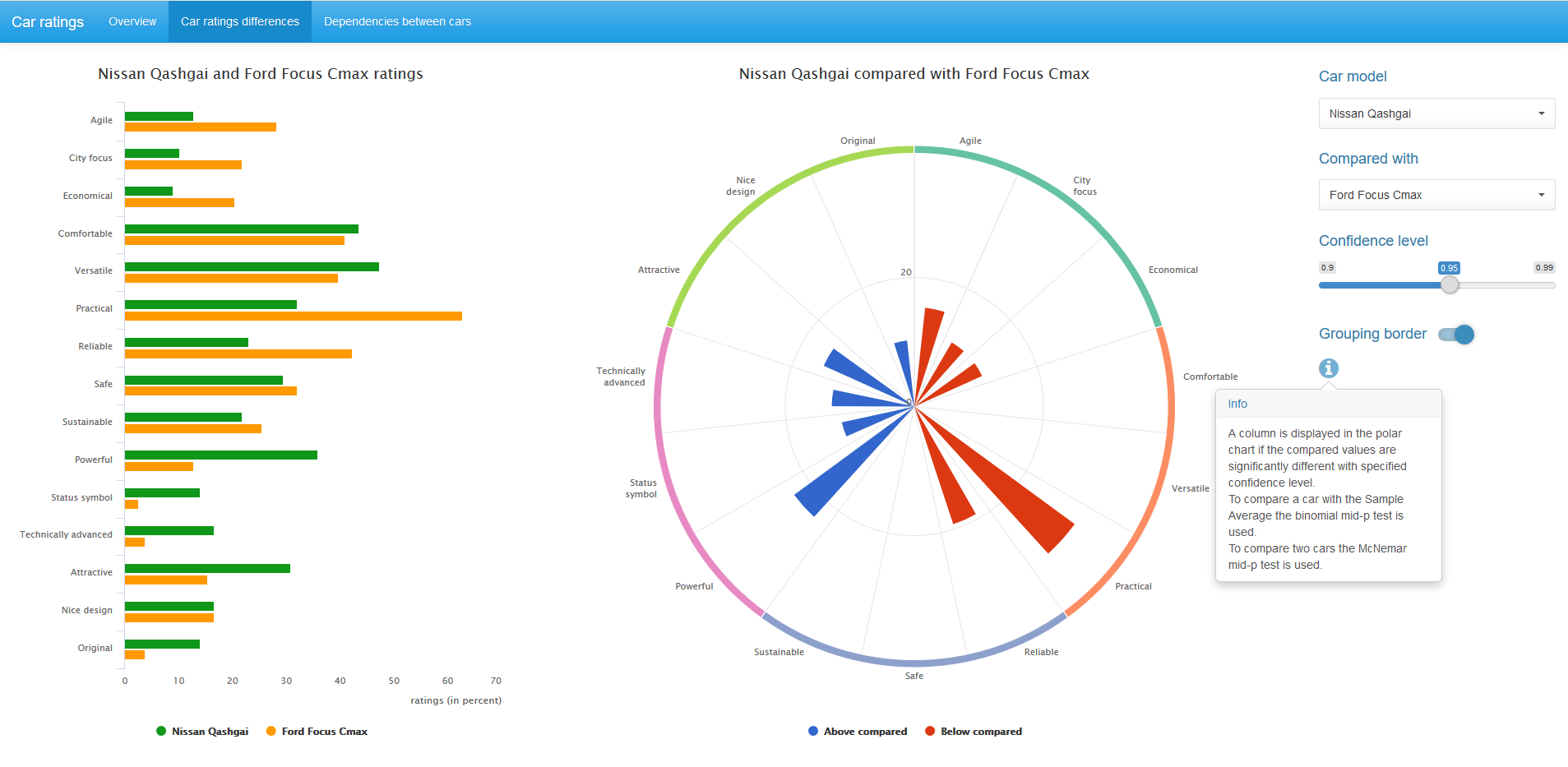
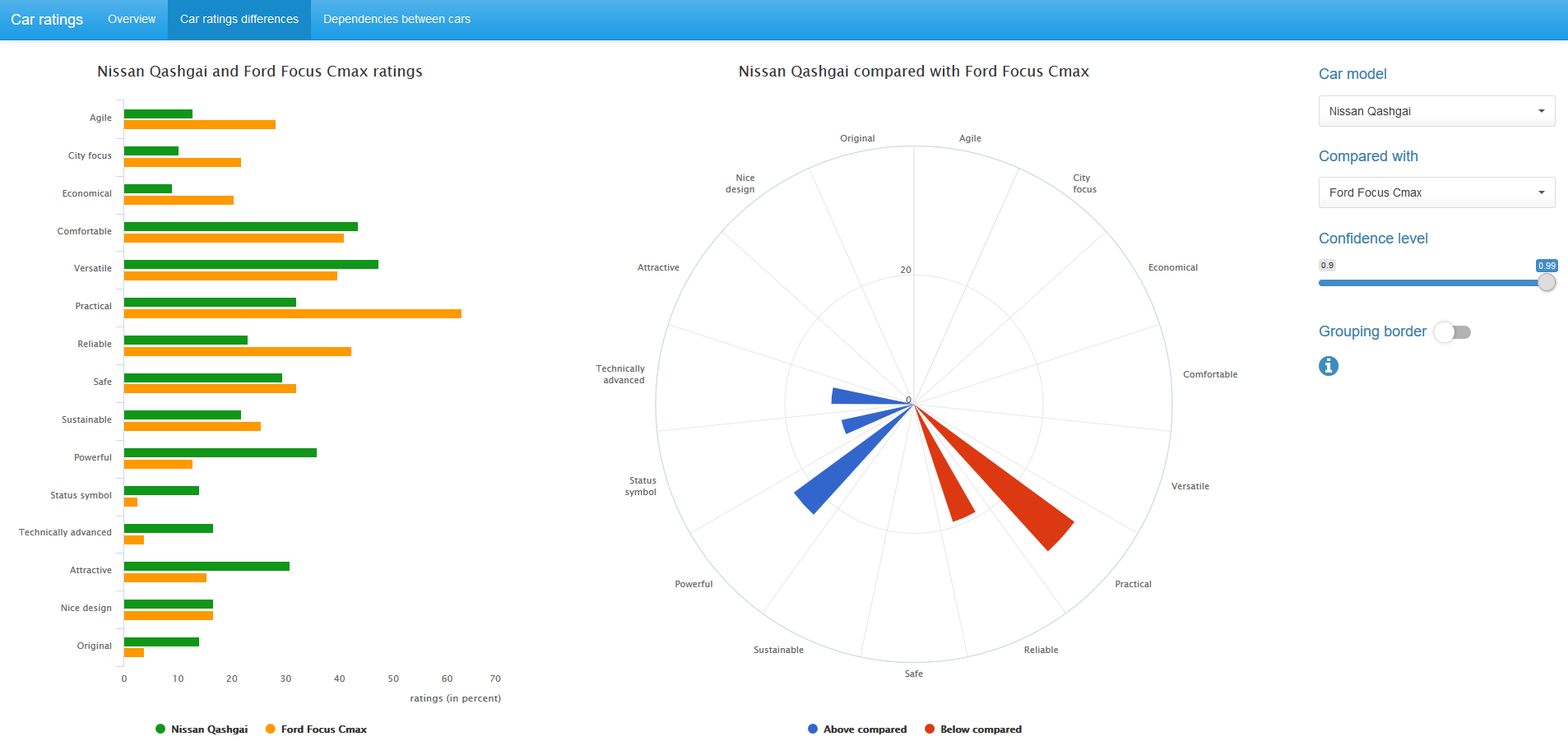
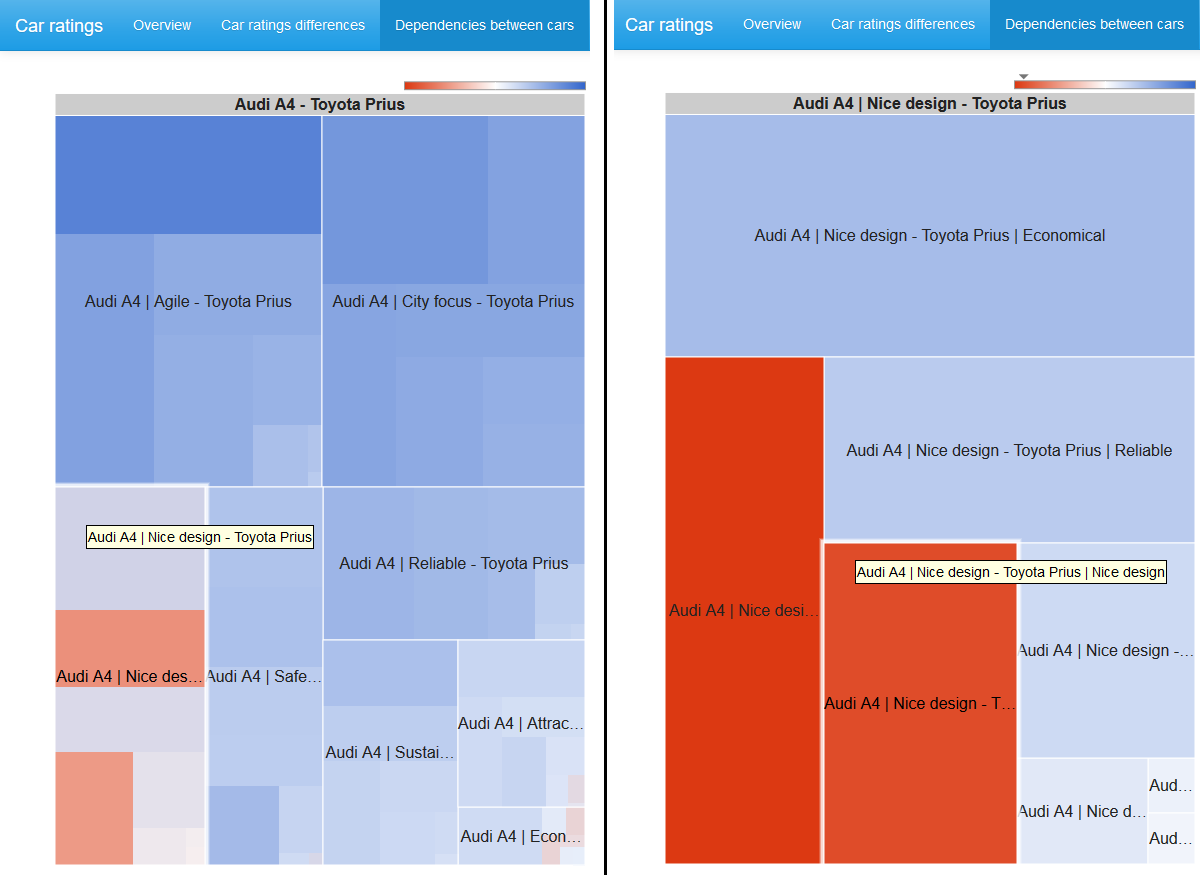
На диаграмме в центе отображаются только статистически значимые, при заданном confidence level, различия в рейтингах между парой сравниваемых автомобилей. Синий цвет соответствует более высокому значению рейтинга для первого автомобиля, красный — для второго.
Мы можем поменять confidence level значение и, при желании, убрать группирующую каёмку на диаграмме.
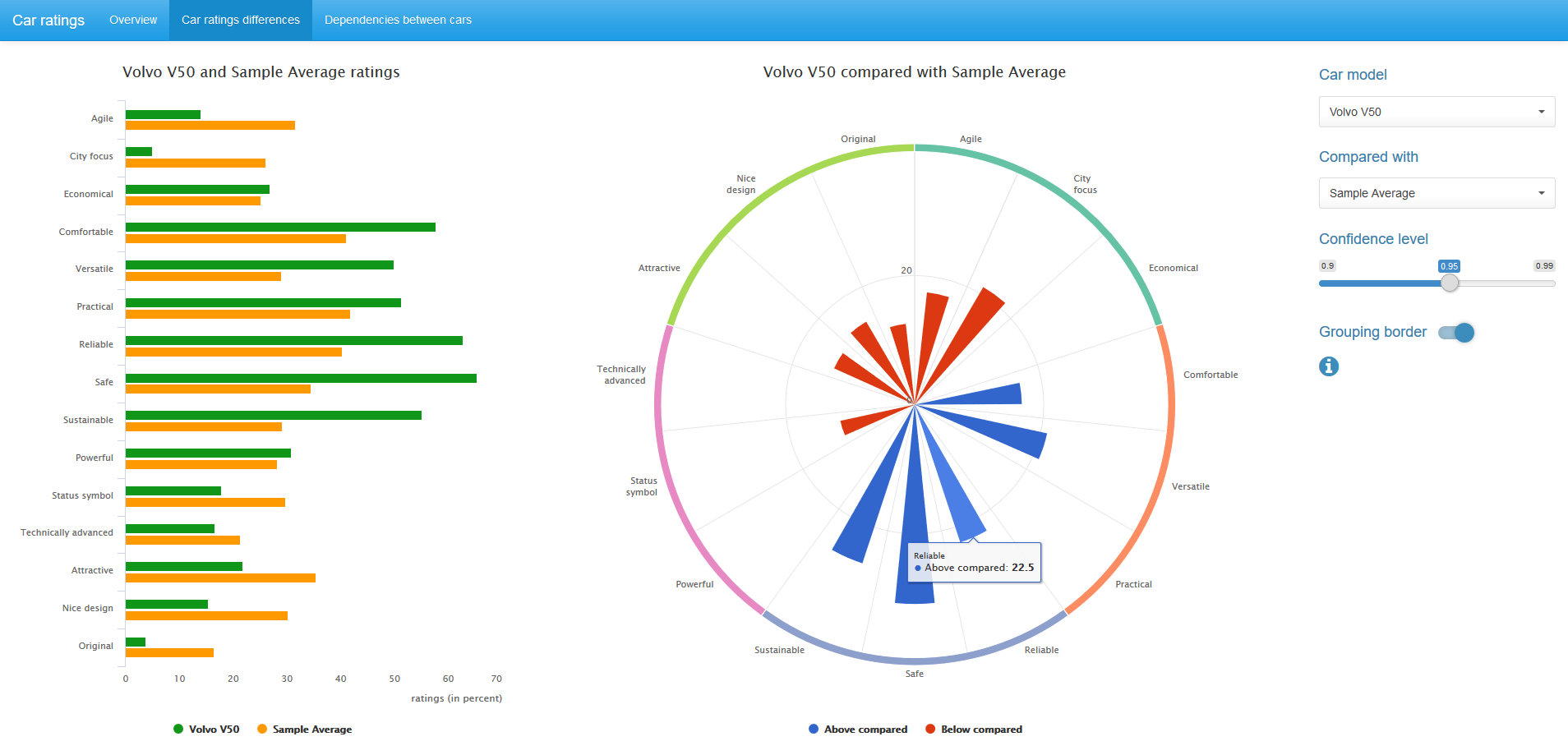
Также можно сравнить значения рейтингов автомобиля со средне-выборочными рейтингами по всем 14 автомобилям. В этом случае используется binomial mid-p тест.
И McNemar mid-p тест, и binomial mid-p тест доступны в R-пакете exact2x2, но могут быть легко реализованы базовыми средствами R.
Зависимость между двумя multiple-response переменными
Задача стоит так: мы выбрали какой-либо набор характеристик и произвольную пару моделей автомобилей. Можно ли утверждать, что распределения ответов респондентов для этих автомобилей независимо? Иными словами, у нас нет оснований полагать, что существует какая-то статистическая взаимосвязь в выставлении оценок для этих двух марок в заданном множестве характеристик.
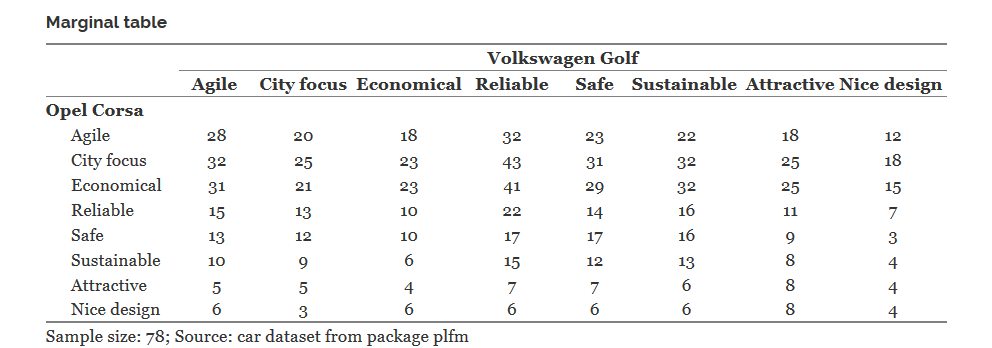
Рассмотрим для примера такую таблицу 8x8:
В ней значение клетки, скажем Opel Corsa | Economical — Volkswagen Golf | Relible, равное 41, означает, что ровно 41 респондент указал, что Opel Corsa экономичный автомобиль и Volkswagen Golf — надежный.
Если и Opel Corsa, и Volkswagen Golf были бы single-response переменными, то эта таблица задавала бы совместное распределение этих переменных. Тогда мы могли бы применить к этой таблице критерий хи-квадрат для проверки независимости этой пары переменных. Но у нас совсем другой случай и по данным этой таблицы, например, даже неясно какое число респондентов полагает, что Opel Corsa — это экономичный автомобиль.
За каждой клеткой этой маргинальной таблицы сидит таблица 2x2, которая определяет распределение в отдельной паре выбранных характеристик. Эти 8 таблиц для диагональных клеток маргинальной таблицы как раз использовались в тестах МакНемара для этой пары автомобилей.
Но и этого набора из всех 64 таблиц недостаточно, чтобы задать совместное распределение двух multiple-response переменных с 8 категориями каждая. В общем случае, для этого понадобится таблица размером . Так, сумма 64 хи-квадрат статистик, найденных для таблиц 2x2, из-за зависимости наблюдений (не переменных) во входных данных, не является значением распределения. Сведения из таблицы позволяют найти поправку Рао-Скотта 2-ого порядка и применить ее к сумме этих 64 хи-квадрат значений. Подробности и формулировка критерия о независимости могут быть найдены в статье (Bilder and Loughin 2004).
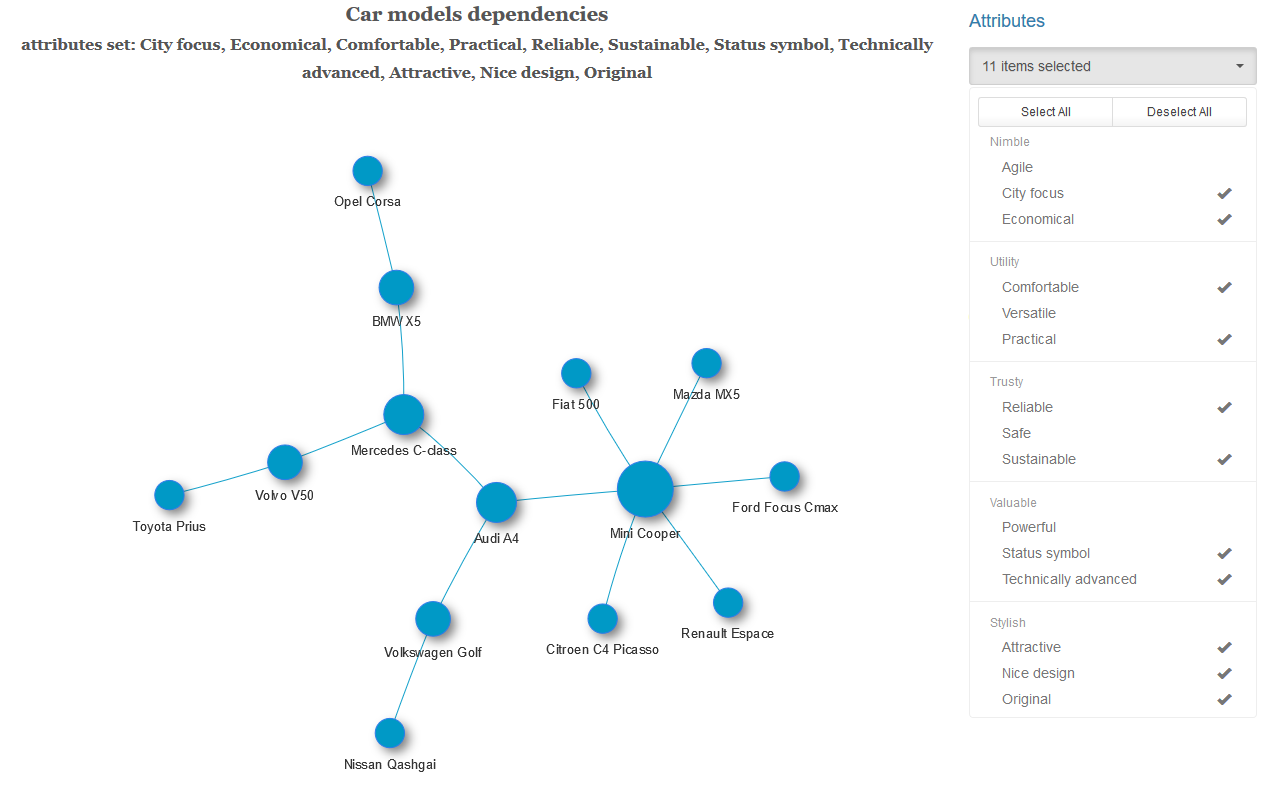
Для каждой пары автомобилей с заданным набором характеристик и при выбранном уровне значимости проверяем гипотезу о независимости этих переменных. Если гипотеза о независимости отвергается, эту пару автомобилей соединяем ребром с весом равным p-значению полученной статистики Рао-Скотта. Получаем взвешенный граф, к которому опционально применяем алгоритм нахождения минимального остовного дерева (для каждой связной компоненты графа). То есть, оставляем минимально возможное число наиболее сильных связей.
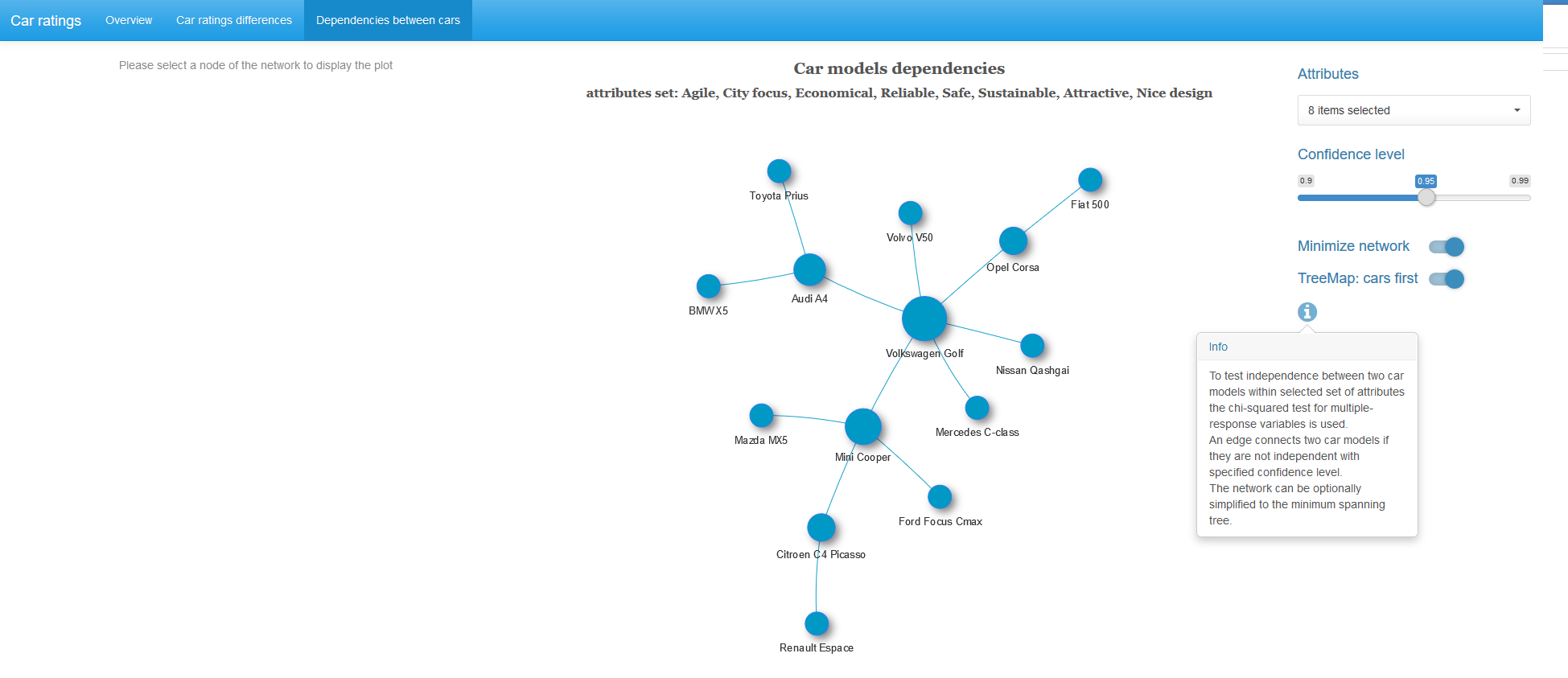
При клике на картинку она откроется в полном размере.
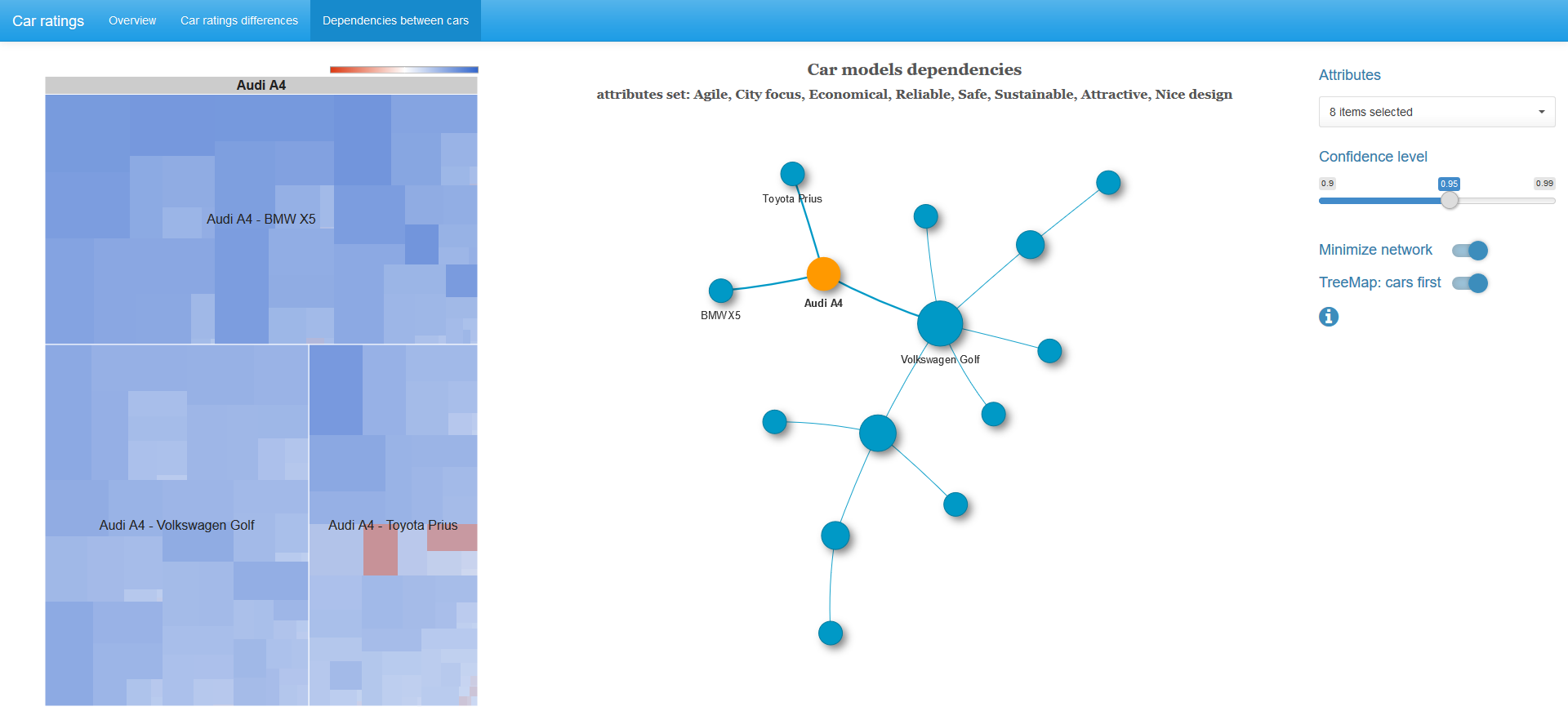
Почти у половины автомобилей в полученном графе наиболее сильная зависимость наблюдается с Volkswagen Golf.
Если выбрана вершина графа, то в дополнение отображается treemap диаграмма хи-квадрат статистик 2x2 таблиц с парами характеристик для смежных вершин.
Размер клетки пропорционален значению хи-квадрат статистики, цвет определяется логарифмом отношения шансов: синий спектр — положительные величины, белый цвет — ноль, красный спектр — отрицательные величины. Цветовая шкала не симметрична, то есть левая граница по абсолютной величине не обязательно совпадает с правой границей шкалы.
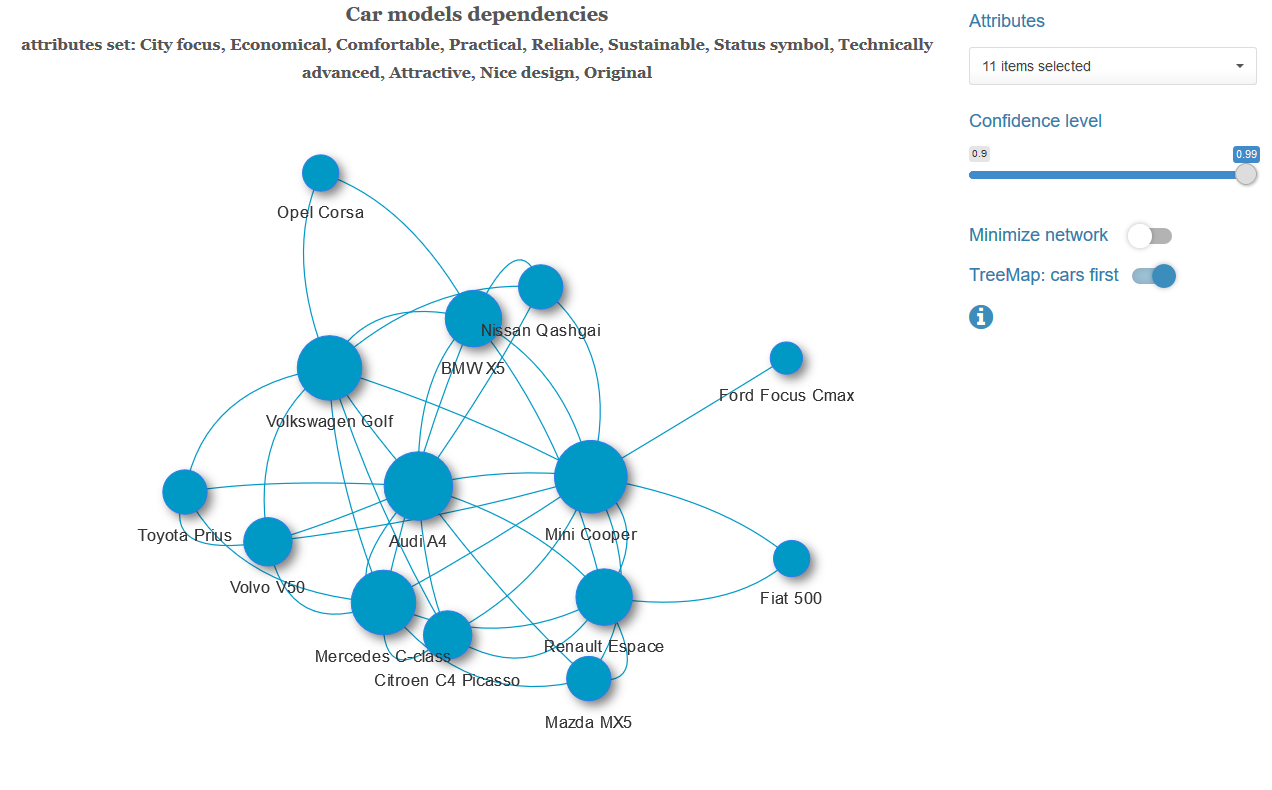
Ниже показаны примеры минимального остовного дерева с другим набором характеристик и графа с полным набором связей.
Вычисления и запуск приложения
Подход предложенный в работе (Bilder and Loughin 2004) реализован в R-пакете MRCV. Однако для рассмотренной выше маргинальной таблицы 8x8 функция проверки независимости для этих переменных из этой библиотеки возвращает ошибку: cannot allocate vector of size 32.0 Gb. Причина в том, что в процессе вычислений возникают матрицы порядка .
Был предложен подход, в котором реализация этого теста в R не требует столь большого объема памяти и является значительно более производительным. Для сравнения, вычисление полного графа с 14 вершинами и 7 характеристиками в пакете MRCV потребует более 30 минут. В улучшенной реализации это вычисление выполняется около 1 секунды. В этом pdf можно найти подробности этого метода вычислений. Исходный код и тесты производительности доступны на github.
Вы можете самостоятельно запустить это shiny приложение выполнив в R команды
library(shiny)
runGitHub("BrandsAnalysis", "e-chankov")Предварительно убедитесь, что у вас установлены
#### shiny libraries
library(shiny) # version 1.0.5
library(shinythemes) # version 1.1.1
library(shinydashboard) # version 0.6.1
library(shinyBS) # version 0.61
library(shinyWidgets) # version 0.3.6
#### libraries for visualization
library(wordcloud2) # version 0.2.0
library(highcharter) # version 0.5.0
library(googleVis) # version 0.6.2
library(visNetwork) # version 2.0.1
library(RColorBrewer) # version 1.1-2
#### data munging libraries
library(data.table) # version 1.10.4
library(checkmate) # version 1.8.4
library(Matrix) # version 1.2-11
library(igraph) # version 1.1.2
library(stringi) # version 1.1.5Входные данные читаются из текстового файла. Приложение можно применить для анализа данных опросов о любых брендах со своим набором характеристик. Требования ко входным данным можно прочитать в описании приложения.
Литература
Bilder, C., and T. Loughin. 2004. “Testing for Marginal Independence Between Two Categorical Variables with Multiple Responses.” Biometrics 60 (1): 241–48. http://dx.doi.org/10.1111/j.0006-341X.2004.00147.x.
Fagerland, Morten W., Stian Lydersen, and Petter Laake. 2013. “The Mcnemar Test for Binary Matched-Pairs Data: Mid-P and Asymptotic Are Better Than Exact Conditional.” BMC Medical Research Methodology 13 (1): 91. https://doi.org/10.1186/1471-2288-13-91.
Van Gysel, E. 2011. “Perceptuele Analyse van Automodellen Met Probabilistische Feature Modellen.”
Master’s thesis, Hogeschool-Universiteit Brussel.


OlegUV
Маленькая идея для визуализации — облако слов может выглядеть нагляднее, если добавить цветовую шкалу. Например, монохром, чем больше вес слова (и размер, соответственно) тем цвет темнее.
PS статья очень интересная, спасибо!
jzha Автор
Спасибо за отклик!
Сравнил цветное облако слов и в однотонной палитре. Согласен с вами.