Введение

Давным-давно американский психолог Дж. Стоунер провел интересный эксперимент (в те времена, когда над людьми можно было так безнаказанно издеваться). Он взял группу студентов и каждому вручил опросник с (условно) дихотомическими вопросами. После того, как они ответили, Стоунер предложил им обсудить эти вопросы всем вместе. А после обсуждения еще раз ответить на те же вопросы. К его большой научной удаче, результат получился крайне интересный.

После группового обсуждения ответы стали носить более «рискованный» характер. Слово «рискованный» это, естественно, такой как бы эвфемизм, за которым скрывается то, что люди столкнувшись в группе единомышленников с группой идейных противников немножко озверели и стали более агрессивно отстаивать свои первоначальные взгляды. Этот феномен назвали «групповая поляризация».



По наивности, ученые тогда (а многие и сейчас) думают, что обсуждение помогает достичь консенсуса. Нет. Обсуждение дихотомии не помогает достичь консенсуса, если его и не намечалось. Обсуждение помогает обществу разделиться на два лагеря, которые друг друга терпеть не могут. А с приходом интернета и бесконечных интернет-споров по любому поводу этот процесс принял еще более масштабный характер.

Но, сколь бы ни было это печально, социальные последствия такого процесса и бесконечные поляризующие выкрики различных борцов за идею меня волнуют мало. А вот возможность промоделировать это с помощью математики меня интересует.

Основная идея

Генерируется общество, где каждый член имеет свое дихотомичное мнение по особо животрепещущему вопросу в виде чисел от -1 до 1. Например, носить красные штаны или синие. Например, человек, которому соответствует цифра -0.9 — очень любит красные штаны, а 0.9 — синие. Человек с нулем к штанам безразличен и носит юбки.

Кроме этого, у каждого человека есть уровень защитных реакций, который мешает ему принять новые взгляды и желание по любому поводу перейти на личности.

Раз в итерацию происходит какой-то социальный акт. Условно — «Люди в красных штанах пошли на митинг». Не все, но особо идейные. На митинге каждый из них взаимодействует со случайными людьми. Он может с ними договориться или не договориться, в зависимости от того, насколько собеседник с ним единодушен и не склонен переходить на личности.
Вот собственно и все.

После нескольких итераций смотрится, как изменилось распределение любви к разному цвету штанов по населению.

Описание модели

Моделируется «общество» из $$ индивидов. Каждый индивид имеет несколько характеристик:

$$ — культурная принадлежность. Число от -1 до 1.
$$ — уровень защитных реакций, «коррелированный» с $$. Чем больше ты вписан в культуру, тем сильнее защитная реакция. $$ — случайная величина, распределенная нормально относительно 0 с СКО 0.4.
$$ — Ad hominem rate. Желание по любому поводу перейти на личности. Естественно, чем оно больше, тем меньше понимания с человеком, с которым у тебя разные взгляды. $$ — равномерное распределение от 0 до 1.

Константы:
$$ — базовый шаг изменения культурного контекста (любви к цвету штанов).
$$ — базовый шаг изменения уровня защиты.

Итерация (публичный социальный акт):
Для случайных людей с идеалами, у которых $$, проверяется насколько идеалы большие, путем сравнения со случайным числом:
Если $$, то человек взаимодействует с [1:6] случайными людьми из всей выборки. И так для всех, у кого выполняется неравенство.
Могут возникнуть вопросы — почему $$, а не $$. Может оказаться так, что в распределении слишком мало людей с достаточно большой идейностью, поэтому $$ умножается на 2. Но вообще это все может от $$ и не зависеть.

Собственно взаимодействие людей:
Если люди одних взглядов
Естественно, они не могут по вопросу поругаться, поэтому для них успешность и неуспешность не проверяется. Но они могут самоутверждаться за счет согласия друг с другом. Поэтому вначале находим насколько они близки в своем единодушии $$, а потом:

Если $$ то у каждого из них:

$$

$$

Т.е. они больше верят в свою теорию и их защиты относительно своей теории укрепляются.

Если люди разных взглядов
То у них $$, 0.5, чтобы за единицу не залезало. И вероятность согласия считается так:

$$

Тут $$ — желание переходить на личности участника взаимодействия в своем тексте, $$ — защитная реакция прочитавшего. Естественно, полный переход на личности гарантирует 0 понимания, как и слишком сильные защитные реакции.

Если коммуникация успешная и $$ больше случайного $$, то:

$$

$$

$$

Воспринявший сдвигается взглядами в сторону участника. У обоих защиты падают.

Если коммуникация НЕуспешная и $$ меньше случайного $$, то:

$$

$$

Прочитавший отодвигается взглядами от участника и у обоих защиты поднимаются.
Значения $$ и $$ — ограничены максимальными значениями, которые вычисляются по изначальной выборке.

Опять-таки, могут возникнуть вопросы по такому расчету вероятности договориться, при условии отсутствия защитных реакций и перехода на личности: $$. Но тут все просто $$ — член который не может превышать 1. «5» это коэффициент, который хорошо бы подбирать эмпирически, но в данном случае он просто волюнтаристски назначен, чтобы процесс сходился за приемлемое число итераций.

Некоторые сценарии при моделировании

Нейтральное общество

1000 человек, $$. 150 итераций.


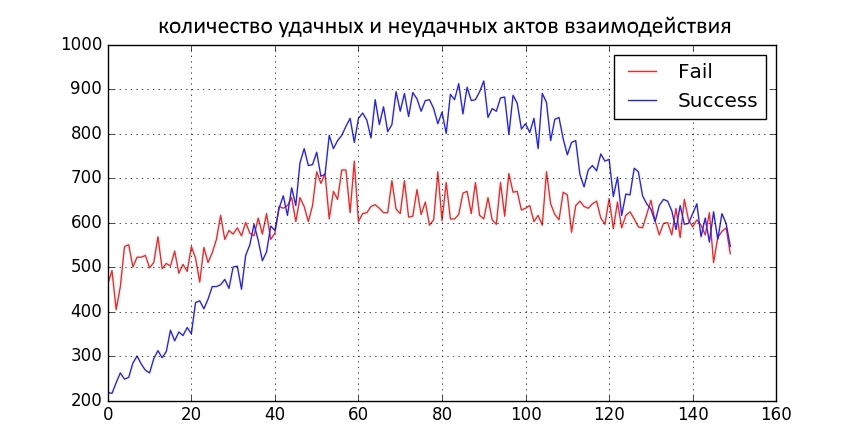
Верхние два графика показывают, как менялся вид распределения взглядов за 150 итераций. По оси x — выраженность взглядов. По оси y — количество носителей взглядов (нормированное). Нижний график показывает количество успешных и неуспешных актов взаимодействия с людьми противоположных взглядов за итерацию.

Что можно увидеть на графиках?

1. Общество дихотомизировалось.
2. Красная часть распределения «прижалась» к 0, но осталась красной. Т.е. Стало очень много умеренных любителей красных шапок.
3. «Синяя» часть или ушла в умеренный минус (к красным), или уползла в «синий» радикализм.
4. Количество хороших взаимодействий за период возросло, потом уменьшилось. Это предсказуемо, потому что синие радикализировались, а красные остались красными.
5. Из-за радикализации больше людей стало участвовать в акциях. Потом синяя часть распределения начала размазываться и участвовать стало меньше.

Общество красных шапок

1000 человек, $$, 150 итераций.

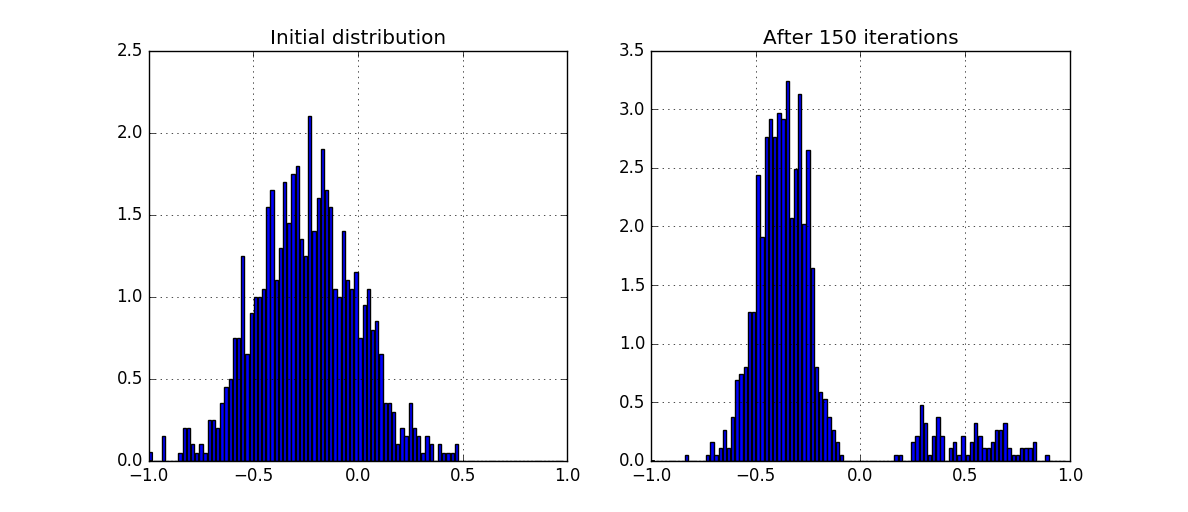
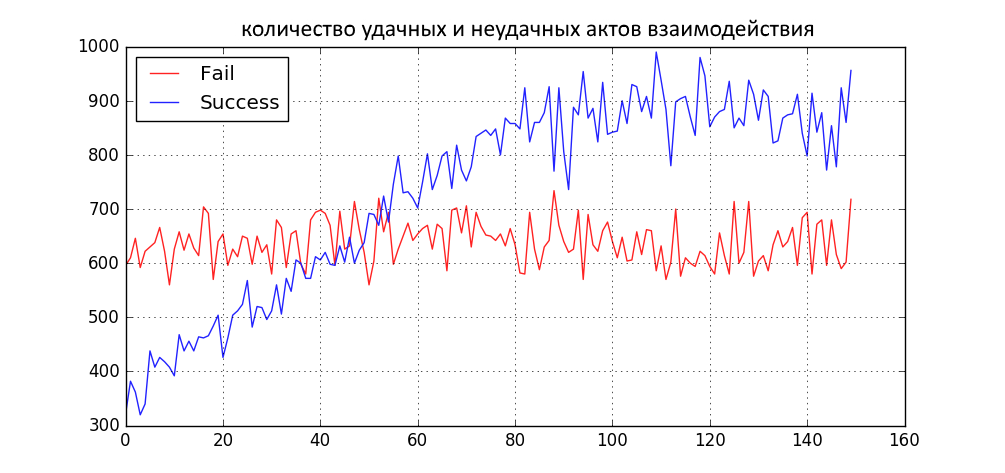
1. Общество дихотомизировалось.
2. «Красная часть» НЕ «схлопнулась» к 0, хотя имеет такую не сильную тенденцию.
3. Синяя часть размазалась в примерно «равномерное» распределение.
4. Количество как успешных, так и не очень коммуникаций увеличилось.

Двойственное общество

500 человек с $$, 500 человек с $$, 150 флэшмобов.




Ситуация близка к первой, но сразу большой уровень провалов коммуникаций в силу большой радикальности обеих групп.

Нейтральное однородное общество

1000 человек с c=N(0,1). 150 итераций. Однородность заключается в том, что распределение гораздо более узкое, чем в первом варианте. Т.е. все люди очень близки в своем изначальном пофигизме к цвету штанов. Только чуть-чуть не пофиг. Совсем чуть-чуть.

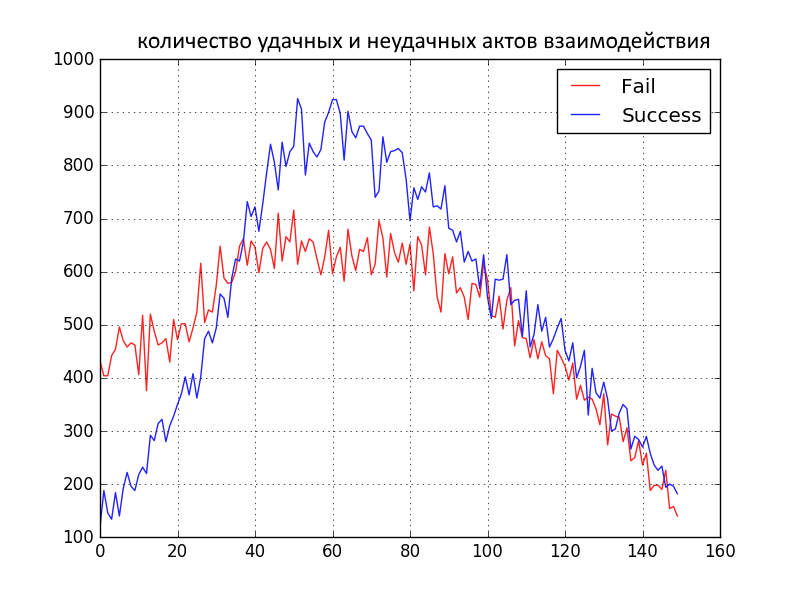
1. Это единственный вариант, когда синие штаны «побеждают», а красные остаются в меньшинстве. Во многом это происходит за счет более узкого начального распределения, вследствие наличия которого люди предположительно меньше ругаются, потому что меньше радикализма во взглядах и защитных реакций. Плавно безразличное к цвету штанов население смещается в сторону общего принятия синих штанов.
2. Положительные и отрицательные взаимодействия уходят в 0, потому что для взаимодействий людей одних взглядов эти параметры не считаются.

Соображения по ограничениям модели

• Тут не учитывается, что люди крутятся в близких им кругах, поэтому по большей части взаимодействуют со своими. НО. Это только хуже сказывается на способности слушать противоположную точку зрения, поэтому мы можем считать, что в этой модели достаточно позитивный вариант взаимодействия.
• Не учитывается, что есть всякие лидеры мнений, которые могут обращаться сразу к большой части выборки.
• Активную позицию занимает только сторона синих штанов. Только она проводит «акции». Но это как бы фича by design, а не бага.
• Коэффициенты несколько с потолка, ну а откуда их взять? Можно настроить по данным оригинального эксперимента или результатов голосования в каком-нибудь ток-шоу. Посмотрим.

Мини-вывод

В рамках этой модели у людей все-таки получается договариваться по дихотомическим вопросам. Но только в том случае, если им изначально на вопрос достаточно наплевать. Это неплохо вписывается в качественное описание феномена, где «групповая поляризация» не возникает в случае, когда людям вопрос не интересен или незнаком. Более того, из модели следует, что если людям изначально наплевать на что-то, им гораздо проще это что-то принять как свои собственные взгляды. Вещь сколь банальная, столь и никогда не применяемая на практике глубоко-идейными лидерами мнений. Вечно им надо сразу начинать что-нибудь громко орать, чтобы люди сразу разделились на две команды.

Автор статьи: Александр Беспалов, Специалист по анализу данных, Maxilect