30.12.2017 12:14
magisterbes 0 5900 Источник

Бизнес задача


Один из наших клиентов активно использовал маркетинговые каналы трафика для продвижения своих услуг и товаров. Через какое-то время данные по всем маркетинговым каналам выгрузили в хранилище BigQuery, и решили, что пришло время сделать с ними что-нибудь интересное. Например, расширять и модифицировать свои аналитические модули для оптимизации маркетинговых расходов. В частности, реализовать возможность использовать более сложную атрибуцию каналов с помощью цепочек Маркова, которой не было Google Analytics на тот момент, а возможно и сейчас нет.


Мы рассказывали в своем блоге о некоторых общих проблемах атрибуции рекламных каналов. Здесь же речь пойдет исключительно об использовании цепочек Маркова.



Цепи Маркова


Цепи Маркова ? один из крайне простых, но изящных инструментов исследования динамики в стохастических системах, который используется, в том числе, при атрибуции товаров. Об этом написано довольно много, и примеры описания такой атрибуции в интернете находятся довольно легко. Наше дело ? представить свой метод атрибуции с использованием этого инструмента. Но для начала надо рассказать немного о том, что это такое для тех, кто не знает. А кто знает, может смело эту часть пропускать.


Пусть у нас система может находиться только в нескольких фиксированных состояниях. И в каждом состоянии строго и однозначно определена вероятность перехода в любое другое возможное состояние этой системы.


Чтобы понять, как это бывает, можно рассмотреть пример системы, которую исследовал сам Андрей Андреевич Марков (старший). В качестве системы он рассматривал случайный процесс появления буквы в тексте. За основу для формирования модели он использовал текст “Евгения Онегина”. Интуитивно очевидно, что вероятность следующей буквы во многом определяется предыдущей. Например, буква «з» редко приходит после «ч», а буква «а» часто, а сочетание «пробел»-«ы» вообще в литературном языке невозможно. В общем, бедному Андрею Андреевичу пришлось пересчитать все буквы этого прекрасного произведения Пушкина, чтобы понять, какие буквы часто следуют за какими, потому что компьютеров тогда не было.


Единственное, что осталось, это описать происходящее на языке математики.


Пусть есть система с дискретными состояниями $ S=\lbrace s_1, s_2,...,s_N \rbrace $. Время задается таким образом, что на каждом дискретном шаге времени происходит переход в одно из существующих состояний. Таким образом, по сути, время мы из рассмотрения исключаем и рассматриваем только те итерации, в которых происходят скачки состояний. Каждое состояние описывается множеством условных вероятностей перехода в любое состояние системы:

$ s_1 = \lbrace p(s_1|s_1),p(s_2|s_1),... \rbrace $

Для большей наглядности и полезности люди имеют тенденцию выписывать это в виде матрицы вероятностей переходов:

$M=\begin{bmatrix} p(s_1|s_1)& p(s_1|s_2) & ...\\ p(s_2|s_1)& p(s_2|s_2) & ...\\ \vdots & \vdots& \ddots \end{bmatrix}$

Или в виде графа переходов, как в примере из Википедии:



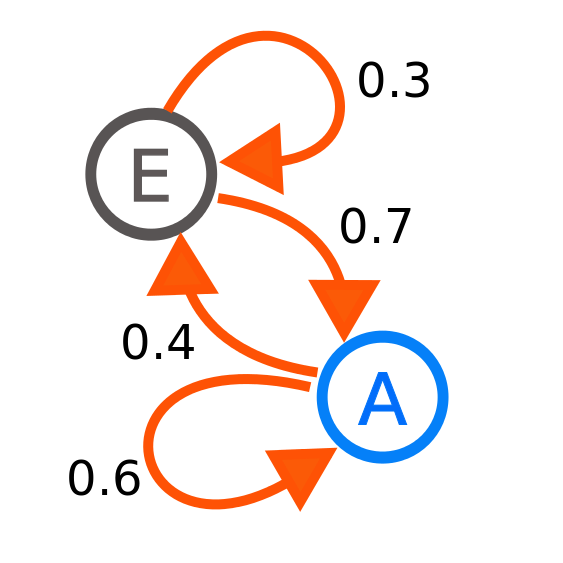
Автор: Joxemai4 — собственная работа, CC BY-SA 3.0, commons.wikimedia.org/w/index.php?curid=10284158

На картинке показана система с двумя состояниями E и A. Вероятность перехода из A в A равна 0.6, а из А в E ? 0.4. Очевидно, что суммы условных вероятностей перехода из одного состояния должны равняться единице. И суммы каждой из строчек матрицы M тоже должны быть равны 1.


Но условные вероятности нам не сильно нужны. Нам нужны абсолютные вероятности того, в каком состоянии будет система. И у нас есть возможность узнавать это, при условии, что мы знаем с какого состояния s0 мы начали, т.е. имеем вектор из нулей с единицей в том состоянии, в котором мы находимся. Для этого мы для первого шага системы пользуемся формулой полной вероятности:

$s^1 = s^0 \times M$

Из этого выражения очевидна рекуррентная формула, по которой можно найти абсолютную вероятность на любом шаге системы, имея распределение с предыдущего шага. Иногда эти распределения сходятся, иногда нет. Например, для вышеуказанного примера с картинки, абсолютная вероятность нахождения в E стремится к 0.3636(36), а для A к 0.6363(63).


Но в нашей задаче это не тот случай, поэтому на этом стоит остановиться и перейти собственно к атрибуции каналов.


Атрибуция с использованием цепи Маркова


Для начала стоит немного рассказать о том, как составляется матрица вероятностей переходов.


Как каждая строка “Евгения Онегина” внимательно рассматривалась А. Марковым, нами рассматриваются цепочки каналов и в матрице фиксируются переходы между каналами. Например, если мы попали в цепочке из канала с индексом 1 в канал с индексом 2, то к элементу матрицы в первой строке и втором столбце прибавляется единица.


Когда мы прошлись таким образом по всей статистике цепочек, мы делим каждую строку получившейся матрицы на сумму элементов этой строки и получаем те самые условные вероятности. И дальше собственно начинается метод атрибуции.


Пусть есть $N $ каналов атрибуции и рассчитанная матрица вероятностей переходов $M $ размерности $(N+1)?(N+1) $. $(N+1) $ потому что, кроме всех каналов, есть еще переход в состояние «конверсия». Это терминальное состояние, поэтому последняя строка матрицы $M $ состоит из нулей и последний элемент равен 1. Кроме этого, мы имеем вектор $L $ ? распределение длин конвертированных цепочек атрибуции за весь период. Т.е. если $L_5=100,$ это значит, что в базе лежит 100 цепочек, содержащих 5 каналов атрибуции, которые заканчиваются конверсией. В дальнейшем мы используем:

$$display$$\begin{equation} L’(K)=\lbrack L_1,L_2,....,L_K \rbrack/\sum\limits_{k=1}^{K},L_k \tag{1}\end{equation}$$display$$

нормированное до определенного члена $K \le |L|$ распределение.


Для каждого канала $i \in 1,2,...,N$ считается некоторый показатель вероятности прийти к конверсии при условии, что цепочка начинается с этого канала. Естественно, слово вероятность тут уже используется достаточно условно, потому что это просто некоторый показатель, который можно сравнивать с показателями для других каналов. Этот показатель считается следующим образом:


Пусть есть начальная точка марковской цепи, которая указывает на тот канал, с которого мы начинаем рассматривать вероятности. Это вектор $V_0, |V_0|=N+1$. Вектор состоит из нулей и только $V_i^0=1$. Mы рассматриваем цепочки длин от 1 до $K \le |L|$. Для каждой цепочки рассчитывается распределение абсолютных вероятностей, при условии начала из $V_0$.:

$D_k = D_{k-1}\times M, \tag{2}$

где $D_k-1$ распределение абсолютных вероятностей на $k-1$ шаге цепочки, а (?) ? матричное умножение. Очевидно, что $D_0=V_0$. На последнем шаге, мы выбираем вероятность перехода в терминальное $p_{N+1,k}$ состояние как «меру» эффективности начального канала. Далее мы считаем показатель эффективности канала по такой формуле:

$E_i=\sum\limits_{k=1}^{K}p_{N+1,k}*\tilde{L}_k, \tag{3}$

где (*) ? поэлементное умножение, а $\tilde{L}=L’(K)$.


Считая таким образом значения показателей для каждого из каналов, мы получаем сравнимые оценки эффективности в массиве $E$, которые можно использовать при атрибуции. При атрибуции каждому каналу в цепочке присваивается вес из $E$ и дальше веса нормируются. Пусть есть цепочка индексов каналов $C$, в которой нет одинаковых смежных каналов и которая заканчивается конверсией. Тогда можно посчитать атрибуцию каналов следующим образом. Зададим вектор нулей $W$ размерности $N$ и будем заполнять его следующим образом:

$ W_i = \sum\limits_{j=1}^{|C|} \left\{\begin{array}{ll}C_i=1, if&i=j\\C_i=0,if&i \ne j\end{array}\right.\tag{4}$

Тогда нормированный вектор атрибуции каналов будет считаться так:

$A=(E*W)/\sum(E*W)\tag{5}$

.

Нормировка в данной ситуации требуется для того, чтобы атрибутировать ровно одну конверсию. Или, если мы рассматриваем конверсию через доход, который она принесла, доход распределенный по каналам в сумме должен сходиться, соответственно у формулы (5) просто появляется множитель дохода с конверсии.


Пример


Пусть есть два канала атрибуции с определенными вероятностями перехода, которые заданы матрицей переходный вероятностей:

$M = \begin{bmatrix} 0.7& 0.1 & 0.2\\0.5& 0.2 & 0.3\\0 & 0& 1 \end{bmatrix}, L=\lbrack 100, 50, 30, 10, 5, 0,... \rbrack $

Будем рассматривать K=2, тогда, по формуле (1) $L’(2)=\lbrack 0.67, 0.33 \rbrack$. Рассчитываем абсолютные вероятности для цепочек длины 1 и 2 для первого канала по формуле (2):

$D_{1,1} = \begin{bmatrix} 1&0&0 \end{bmatrix} \times \begin{bmatrix} 0.7& 0.1 & 0.2\\0.5& 0.2 & 0.3\\0 & 0& 1 \end{bmatrix} = \begin{bmatrix} 0.7&0.1&0.2 \end{bmatrix} $

$D_{1,2} = \begin{bmatrix} 0.7&0.1&0.2 \end{bmatrix} \times \begin{bmatrix} 0.7& 0.1 & 0.2\\0.5& 0.2 & 0.3\\0 & 0& 1 \end{bmatrix} = \begin{bmatrix} 0.54&0.09&0.37 \end{bmatrix} $

Тогда показатель эффективности канала рассчитывается следующим образом по формуле (3):


$ E_1=0.2*0.67+0.37*0.33=0.256$

Рассчитываем абсолютные вероятности для цепочек длины 1 и 2 для второго канала:

$ D_{2,1} = \begin{bmatrix} 0&1&0 \end{bmatrix} \times \begin{bmatrix} 0.7& 0.1 & 0.2\\0.5& 0.2 & 0.3\\0 & 0& 1 \end{bmatrix} = \begin{bmatrix} 0.5& 0.2 & 0.3 \end{bmatrix}$

$ D_{2,2} = \begin{bmatrix} 0.5& 0.2 & 0.3 \end{bmatrix} \times \begin{bmatrix} 0.7& 0.1 & 0.2\\0.5& 0.2 & 0.3\\0 & 0& 1 \end{bmatrix} = \begin{bmatrix} 0.45& 0.09 & 0.46 \end{bmatrix}$

Тогда показатель эффективности канала рассчитывается следующим образом:

$ E2=0.3*0.67+0.46*0.33=0.353$

Таким образом, полный вектор показателей эффективности каналов $E = [0.256, 0.353]^T$.

Пусть у нас есть цепочка каналов $C=[1,2,1]$, которая заканчивается конверсией. Тогда по формуле (4):


$W1=1+0+1=2,W2=0+1+0=1.$

И по формуле (5) можно рассчитать атрибуцию этой конверсии:

$A=([0.256, 0.353]T*[2,1])/(0.256*2+0.353*1)=[0.59, 0.41].$


Дополнение


В принципе, во время атрибуции можно использовать для каждого канала вес, который соответствует вероятности перехода для длины цепочки равной «расстоянию» в цепочке от данного канала до конверсии. Тогда, например, в вышеуказанном примере атрибуция считалась бы так:

$A = \frac{[(D_{1,1}+D_{1,3}),D_{2,2}]}{D_{1,1}+D_{1,3}+D_{2,2}}=\frac{[(0.2+0.51),0.46]}{0.2+0.51+0.46}=[0.61,0.39]$

Тоже самое можно сделать с учетом весов $L’$, которые для цепочки длиной 3 рассчитаются так $L’(3) = [0.55, 0.28, 0.17]$. Тогда атрибуция будет такая:

$A = \frac{[(D_{1,1}\tilde{L}_1+D_{1,3}\tilde{L}_3),D_{2,2}\tilde{L}_2]}{D_{1,1}\tilde{L}_1+D_{1,3}\tilde{L}_3+D_{2,2}\tilde{L}_2}=\frac{[(0.2\cdot 0.55+0.51\cdot 0.17),0.46\cdot 0.28]}{0.2\cdot 0.55+0.51\cdot 0.17+0.46\cdot 0.28}=[0.6,0.4] $

Таким образом, подобная атрибуция может стать крайне полезным инструментом анализа трафика, который позволит взглянуть на него с различных сторон, даже в рамках одного подхода. Такого рода методы легко адаптируются под поставленные цели и дополняются с учетом известных данных. Например, естественным следующим шагом “развития” этого подхода может быть добавление в анализ времени и учет количества времени между транзакциями (еще одно промежуточное положение в матрице условных вероятностей, когда за некоторый период никаких переходов не было). Все для людей, как говорится.


Этот проект был выполнен в рамках работ, выполняемых компанией Maxilect, другие проекты этой категории можно посмотреть здесь.

Комментарии (0)