Первые сканеры сетчатки появились ещё в 80-х годах прошлого столетия. Они получили широкое распространение в системах контроля доступа на особо секретные объекты, так как у них один из самых низких процентов отказа в доступе зарегистрированных пользователей и практически не бывает ошибочного разрешения доступа, но, несмотря на это, сканеры сетчатки не получили широкого распространения в массы из-за дороговизны и сложности оптической системы сканирования. И до недавнего времени всё так и оставалось, хотя алгоритмы продолжали развиваться.
На сегодняшний день технология 3d печати позволила сильно удешевить сканеры сетчатки глаза. Эндрю Баставрус вместе со своей командой напечатали на 3d принтере насадку для смартфона, которая позволяет наблюдать сетчатку через камеру телефона.
Данная статья посвящена описанию алгоритмов сопоставления признаков сетчатки глаза и является продолжением статьи о сегментации кровеносных сосудов.
Обзор методов биометрической идентификации/аутентификации приведён здесь.
Одной из наиболее важных проблем при использовании сетчатки глаза для распознавания личности является движение головы или глаза во время сканирования. Из-за этих движений может возникнуть смещение, вращение и масштабирование относительно образца из базы данных (рис. 1).
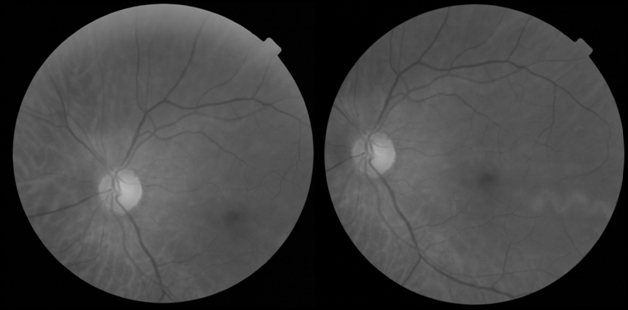
Рис. 1. Результат движения головы и глаза при сканировании сетчатки.
Влияние изменения масштаба на сравнение сетчаток не так критично, как влияние других параметров, поскольку положение головы и глаза более или менее зафиксировано по оси, соответствующей масштабу. В случае, когда масштабирование всё же есть, оно столь мало, что не оказывает практически никакого влияния на сравнение сетчаток. Таким образом, основным требованием к алгоритму является устойчивость к вращению и смещению сетчатки.
Алгоритмы аутентификации по сетчатке глаза можно разделить на два типа: те, которые для извлечения признаков используют алгоритмы сегментации (алгоритм, основанный на методе фазовой корреляции; алгоритм, основанный на поиске точек разветвления) и те, которые извлекают признаки непосредственно с изображения сетчатки (алгоритм, использующий углы Харриса).
Суть алгоритма заключается в том, что при помощи метода фазовой корреляции оцениваются смещение и вращение одного изображения относительно другого. После чего изображения выравниваются и вычисляется показатель их схожести.
В реализации метод фазовой корреляции работает с бинарными изображениями, однако может применяться и для изображений в 8-битном цветовом пространстве.
Пусть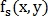 и
и 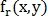 – изображения, одно из которых сдвинуто на
– изображения, одно из которых сдвинуто на 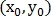 относительно другого, а
относительно другого, а 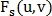 и
и 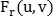 – их преобразования Фурье, тогда:
– их преобразования Фурье, тогда:
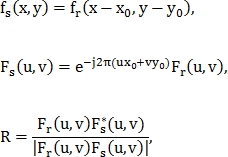
где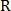 – кросс-спектр;
– кросс-спектр;
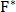 – комплексно сопряженное
– комплексно сопряженное 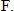
Вычисляя обратное преобразование Фурье кросс-спектра, получим импульс-функцию:
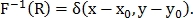
Найдя максимум этой функции, найдём искомое смещение.
Теперь найдём угол вращения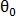 при наличии смещения
при наличии смещения 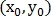 , используя полярные координаты:
, используя полярные координаты:
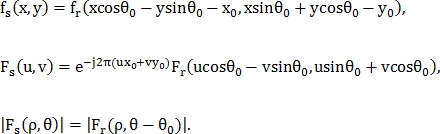
Далее применяется метод фазовой корреляции, как в предыдущем случае. Можно отметить, что такая модификация фазовой корреляции позволяет найти и масштаб по параметру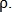
Данная техника не всегда показывает хорошие результаты на практике из-за наличия небольших шумов и того, что часть сосудов может присутствовать на одном изображении и отсутствовать на другом. Чтобы это устранить применяется несколько итераций данного алгоритма, в том числе меняется порядок подачи изображений в функцию и порядок устранения смещения и вращения. На каждой итерации изображения выравниваются, после чего вычисляется их показатель схожести, затем находится максимальный показатель схожести, который и будет конечным результатом сравнения.
Показатель схожести вычисляется следующим образом:

Данный алгоритм, в отличие от предыдущего, не требует сегментации сосудов, поскольку может определять признаки не только на бинарном изображении.
В начале изображения выравниваются при помощи метода фазовой корреляции, описанного в предыдущем разделе. Затем на изображениях ищутся углы Харриса (рис. 2).
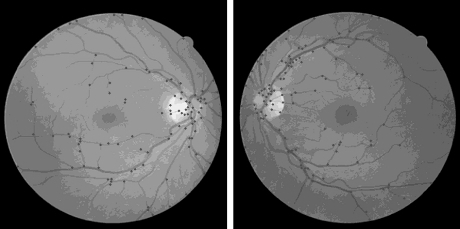
Рис. 2. Результат поиска углов Харриса на изображениях сетчатки.
Пусть найдена M+1 точка, тогда для каждой j-й точки её декартовы координаты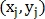 преобразуются в полярные
преобразуются в полярные 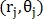 и определяется вектор признаков
и определяется вектор признаков 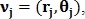 где
где
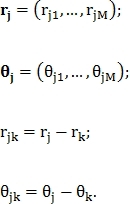
Модель подобия между неизвестным вектором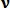 и вектором признаков
и вектором признаков 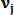 размера N в точке j определяется следующим образом:
размера N в точке j определяется следующим образом:
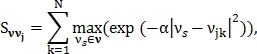
где – константа, которая определяется ещё до поиска углов Харриса.
– константа, которая определяется ещё до поиска углов Харриса.
Функция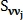 описывает близость и похожесть вектора
описывает близость и похожесть вектора 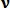 ко всем признакам точки j.
ко всем признакам точки j.
Пусть вектор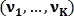 – вектор признаков первого изображения, где
– вектор признаков первого изображения, где 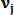 размера K–1, а вектор
размера K–1, а вектор 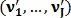 – вектор признаков второго изображения, где
– вектор признаков второго изображения, где 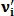 размера J–1, тогда показатель схожести этих изображений вычисляется следующим образом:
размера J–1, тогда показатель схожести этих изображений вычисляется следующим образом:
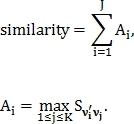
Нормировочный коэффициент для similarity равняется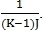
Коэффициент в оригинальной статье предлагается определять по следующему критерию: если разница между гистограммами изображений меньше заранее заданного значения, то
в оригинальной статье предлагается определять по следующему критерию: если разница между гистограммами изображений меньше заранее заданного значения, то  = 0.25, в противном случае
= 0.25, в противном случае  = 1.
= 1.
Данный алгоритм, как и предыдущий, ищет точки разветвления у системы кровеносных сосудов. При этом он более специализирован на поиске точек бифуркации и пересечения (рис. 3) и намного более устойчив к шумам, однако может работать только на бинарных изображениях.
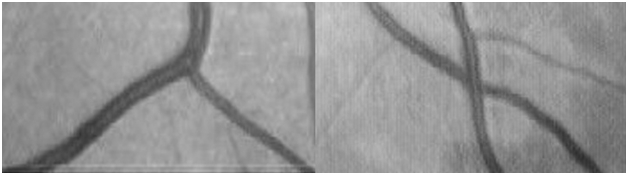
Рис. 3. Типы признаков (слева – точка бифуркации, справа – точка пересечения).
Для поиска точек, как на рис. 3, сегментированные сосуды сжимаются до толщины одного пикселя. Таким образом, можно классифицировать каждую точку сосудов по количеству соседей S:
Вначале выполняется поиск пикселя, являющегося частью сосуда, сверху вниз слева направо. Предполагается, что каждый пиксель сосуда может иметь не более двух соседних пикселей сосудов (предыдущий и следующий), во избежание двусмысленности в последующих вычислениях.
Далее анализируются 4 соседних пикселя найденной точки, которые ещё не были рассмотрены. Это приводит к 16 возможным конфигурациям (рис. 4). Если пиксель в середине окна не имеет соседей серого цвета, как показано на рис. 4 (a), то он отбрасывается и ищется другой пиксель кровеносных сосудов. В других случаях это либо конечная точка, либо внутренняя (не включая точки бифуркации и пересечения).
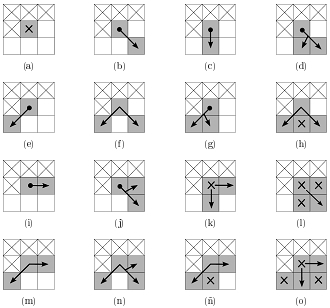
Рис. 4. 16 возможных конфигураций четырёх соседних пикселей (белые точки – фон, серые – сосуды). 3 верхних пикселя и один слева уже были проанализированы, поэтому игнорируются. Серые пиксели с крестиком внутри также игнорируются. Точки со стрелочкой внутри – точки, которые могут стать следующим центральным пикселем. Пиксели с чёрной точкой внутри – это конечные точки.
На каждом шаге сосед серого цвета последнего пикселя помечается как пройденный и выбирается следующим центральным пикселем в окошке 3 x 3. Выбор такого соседа определяется следующим критерием: наилучший сосед тот, у которого наибольшее количество непомеченных серых соседей. Такая эвристика обусловлена идеей поддержания однопиксельной толщины в середине сосуда, где большее число соседей серого цвета.
Из вышеизложенного алгоритма следует, что он приводит к разъединению сосудов. Также сосуды могут разъединиться ещё на этапе сегментации. Поэтому необходимо соединить их обратно.
Для восстановления связи между двумя близлежащими конечными точками определяются углы и
и 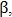 как на рис. 5, и если они меньше заранее заданного угла
как на рис. 5, и если они меньше заранее заданного угла 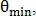 то конечные точки объединяются.
то конечные точки объединяются.
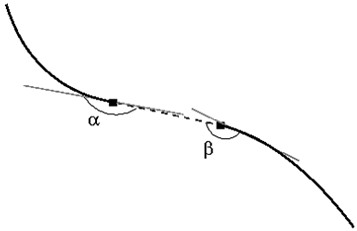
Рис. 5. Объединение конечных точек после сжатия.
Чтобы восстановить точки бифуркации и пересечения (рис. 6) для каждой конечной точки вычисляется её направление, после чего производится расширение сегмента фиксированной длины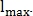 Если это расширение пересекается с другим сегментом, то найдена точка бифуркации либо пересечения.
Если это расширение пересекается с другим сегментом, то найдена точка бифуркации либо пересечения.
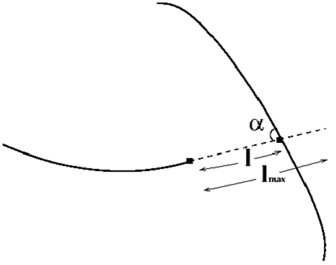
Рис. 6. Восстановление точки бифуркации.
Точка пересечения представляет собой две точки бифуркации, поэтому для упрощения задачи можно искать только точки бифуркации. Чтобы удалить ложные выбросы, вызванные точками пересечения, можно отбрасывать точки, которые находится слишком близко к другой найденной точке.
Для нахождения точек пересечения необходим дополнительный анализ (рис. 7).
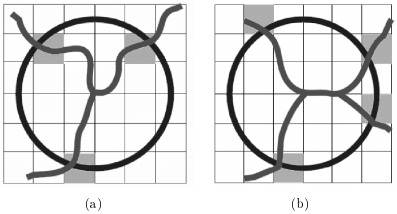
Рис. 7. Классификация точек разветвления по количеству пересечений сосудов с окружностью. (a) Точка бифуркации. (b) Точка пересечения.
Как видно на рис. 7 (b), в зависимости от длины радиуса окружность с центром в точке разветвления может пересекаться с кровеносными сосудами либо в трех, либо в четырёх точках. Поэтому точка разветвления может быть не правильно классифицирована. Чтобы избавиться от этой проблемы используется система голосования, изображённая на рис. 8.
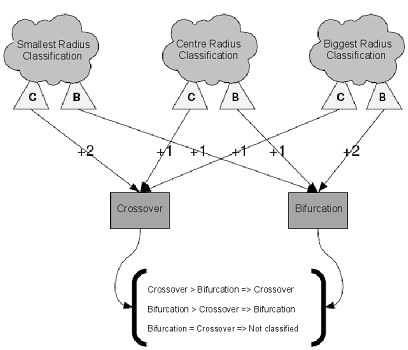
Рис. 8. Схема классификации точек бифуркации и пересечения.
В этой системе голосования точка разветвления классифицируется для трёх различных радиусов
классифицируется для трёх различных радиусов 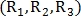 по количеству пересечений окружности с кровеносными сосудами. Радиусы определяются как:
по количеству пересечений окружности с кровеносными сосудами. Радиусы определяются как: 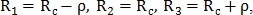 где
где 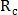 и
и  принимают фиксированные значения. При этом вычисляются два значения
принимают фиксированные значения. При этом вычисляются два значения 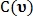 и
и 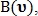 означающие количество голосов за то, чтобы точка
означающие количество голосов за то, чтобы точка  была классифицирована как точка пересечения и как точка бифуркации соответственно:
была классифицирована как точка пересечения и как точка бифуркации соответственно:
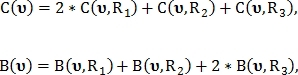
где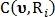 и
и 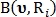 – бинарные значения, указывающие идентифицирована ли точка
– бинарные значения, указывающие идентифицирована ли точка  с использованием радиуса
с использованием радиуса 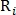 как точка пересечения либо как точка бифуркации соответственно.
как точка пересечения либо как точка бифуркации соответственно.
В случае если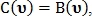 то тип точки
то тип точки  не определён. Если же значение отличаются друг от друга, то при
не определён. Если же значение отличаются друг от друга, то при 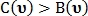 точка
точка  классифицируется как точка пересечения, в противном случае как точка бифуркации.
классифицируется как точка пересечения, в противном случае как точка бифуркации.
После того, как точки найдены, необходимо найти преобразование подобия. Это преобразование описывается 4 параметрами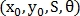 – смещение по оси
– смещение по оси  и
и  , масштаб и вращение соответственно.
, масштаб и вращение соответственно.
Само преобразование определяется как:
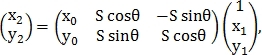
где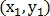 – координаты точки на первом изображении
– координаты точки на первом изображении 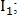
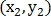 – на втором изображении
– на втором изображении 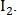
Для нахождения преобразования подобия используются пары контрольных точек. Например, точки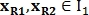 определяют вектор
определяют вектор 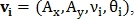 где
где 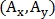 – координаты начала вектора,
– координаты начала вектора, 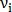 – длина вектора и
– длина вектора и 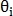 – направление вектора. Таким же образом определяется вектор
– направление вектора. Таким же образом определяется вектор 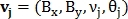 для точек
для точек 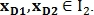 Пример представлен на рис. 9.
Пример представлен на рис. 9.
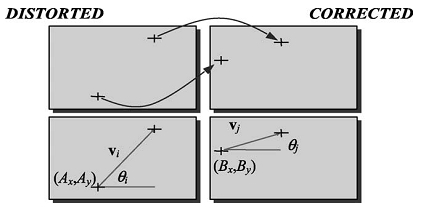
Рис. 9. Пример двух пар контрольных точек.
Параметры преобразования подобия находятся из следующих равенств:
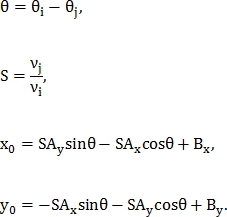
Пусть количество найденных точек на первом изображения равняется M, а на втором N, тогда количество пар контрольных точек на первом изображении равно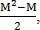 а на втором
а на втором  Таким образом, получаем
Таким образом, получаем 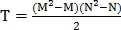 возможных преобразований, среди которых верным выбирается то, при котором количество совпавших точек наибольшее.
возможных преобразований, среди которых верным выбирается то, при котором количество совпавших точек наибольшее.
Поскольку значение параметра S близко к единице, то T можно уменьшить, отбрасывая пары точек, неудовлетворяющие следующему неравенству:
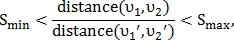
где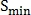 – это минимальный порог для параметра
– это минимальный порог для параметра 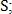
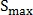 – это максимальный порог для параметра
– это максимальный порог для параметра 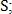
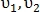 – пара контрольных точек из
– пара контрольных точек из 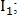
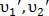 – пара контрольных точек из
– пара контрольных точек из 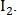
После применения одного из возможных вариантов выравнивания для точек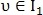 и
и 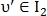 вычисляется показатель схожести:
вычисляется показатель схожести:
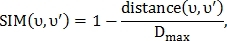
где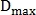 – пороговая максимальная дистанция между точками.
– пороговая максимальная дистанция между точками.
В случае если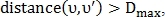 то
то 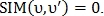
В некоторых случаях обе точки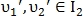 могут иметь хорошее значение похожести с точкой
могут иметь хорошее значение похожести с точкой 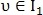 . Это случается, когда
. Это случается, когда 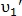 и
и 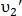 находятся близко друг к другу. Для определения наиболее подходящей пары вычисляется вероятность схожести:
находятся близко друг к другу. Для определения наиболее подходящей пары вычисляется вероятность схожести:
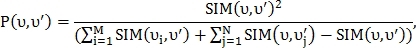
где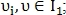
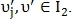
Если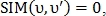 то
то 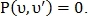
Чтобы найти количество совпавших точек строится матрица Q размера M x N так, что в i-й строке и j-м столбце содержится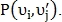
Затем в матрице Q ищется максимальный ненулевой элемент. Пусть этот элемент содержится в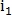 -й строке и
-й строке и 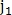 -м столбце, тогда точки
-м столбце, тогда точки 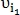 и
и 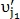 определяются как совпавшие, а
определяются как совпавшие, а 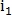 -я строка и
-я строка и 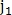 -й столбец обнуляются. После чего опять ищется максимальный элемент. Поиск таких максимумов повторяется до тех пор, пока все элементы матрицы Q не обнулятся. На выходе алгоритма получаем количество совпавших точек C.
-й столбец обнуляются. После чего опять ищется максимальный элемент. Поиск таких максимумов повторяется до тех пор, пока все элементы матрицы Q не обнулятся. На выходе алгоритма получаем количество совпавших точек C.
Метрику схожести двух сетчаток можно определить несколькими способами:
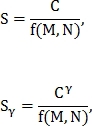
где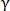 – параметр, который вводится для настройки влияния количества совпавших точек;
– параметр, который вводится для настройки влияния количества совпавших точек;
f выбирается одним из следующих вариантов:
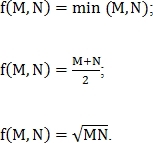
Метрика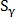 нормализуется одним из двух способов:
нормализуется одним из двух способов:
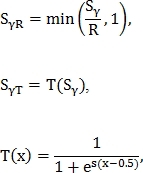
где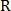 и
и  – некоторые константы.
– некоторые константы.
Метод, основанный на поиске точек разветвления, можно усложнить, добавляя дополнительные признаки, например углы, как на рис. 10.

Рис. 10. Углы, образованные точками разветвления, в качестве дополнительных признаков.
Также можно применять шифр гаммирования. Как известно, сложение по модулю 2 является абсолютно стойким шифром, когда длина ключа равна длине текста, а поскольку количество точек бифуркации и пересечения не превышает порядка 100, но всё же больше длины обычных паролей, то в качестве ключа можно использовать комбинацию хешей пароля. Это избавляет от необходимости хранить в базе данных сетчатки глаза и хеши паролей. Нужно хранить только координаты, зашифрованные абсолютно стойким шифром.
Аутентификация по сетчатке действительно показывает точные результаты. Алгоритм, основанный на методе фазовой корреляции, не допустил ни одной ошибки при тестировании на базе данных VARIA. Также алгоритм был протестирован на неразмеченной базе MESSIDOR с целью проверки алгоритма на ложные срабатывания. Все найденные алгоритмом пары похожих сетчаток были проверены вручную. Они действительно являются одинаковыми. На сравнение кровеносных сосудов двух сетчаток глаз из базы VARIA уходит в среднем 1.2 секунды на двух ядрах процессора Pentium ® Dual-CoreT4500 с частотой 2.30 GHz. Время исполнения алгоритма получилось довольно большое для идентификации, но оно приемлемо для аутентификации.
Также была предпринята попытка реализации алгоритма, использующего углы Харриса, но получить удовлетворительных результатов не удалось. Как и в предыдущем алгоритме, возникла проблема в устранении вращения и смещения при помощи метода фазовой корреляции. Вторая проблема связана с недостатками алгоритма поиска углов Харриса. При одном и том же пороговом значении для отсева точек, количество найденных точек может оказаться либо слишком большим либо слишком малым.
В дальнейших планах стоит разработка алгоритма, основанного на поиске точек разветвления. Он требует гораздо меньше вычислительных ресурсов по сравнению с алгоритмом, основанном на методе фазовой корреляции. Кроме того, существуют возможности для его усложнения в целях сведения к минимуму вероятности взлома системы.
Другим интересным направлением в дальнейших исследованиях является разработка автоматических систем для ранней диагностики заболеваний, таких как глаукома, сахарный диабет, атеросклероз и многие другие.
p.s. по немногочисленным просьбам выкладываю ссылку на проект на гитхабе.
На сегодняшний день технология 3d печати позволила сильно удешевить сканеры сетчатки глаза. Эндрю Баставрус вместе со своей командой напечатали на 3d принтере насадку для смартфона, которая позволяет наблюдать сетчатку через камеру телефона.
Данная статья посвящена описанию алгоритмов сопоставления признаков сетчатки глаза и является продолжением статьи о сегментации кровеносных сосудов.
Обзор методов биометрической идентификации/аутентификации приведён здесь.
Способы сопоставления признаков сетчатки глаза
Одной из наиболее важных проблем при использовании сетчатки глаза для распознавания личности является движение головы или глаза во время сканирования. Из-за этих движений может возникнуть смещение, вращение и масштабирование относительно образца из базы данных (рис. 1).

Рис. 1. Результат движения головы и глаза при сканировании сетчатки.
Влияние изменения масштаба на сравнение сетчаток не так критично, как влияние других параметров, поскольку положение головы и глаза более или менее зафиксировано по оси, соответствующей масштабу. В случае, когда масштабирование всё же есть, оно столь мало, что не оказывает практически никакого влияния на сравнение сетчаток. Таким образом, основным требованием к алгоритму является устойчивость к вращению и смещению сетчатки.
Алгоритмы аутентификации по сетчатке глаза можно разделить на два типа: те, которые для извлечения признаков используют алгоритмы сегментации (алгоритм, основанный на методе фазовой корреляции; алгоритм, основанный на поиске точек разветвления) и те, которые извлекают признаки непосредственно с изображения сетчатки (алгоритм, использующий углы Харриса).
1. Алгоритм, основанный на методе фазовой корреляции
Суть алгоритма заключается в том, что при помощи метода фазовой корреляции оцениваются смещение и вращение одного изображения относительно другого. После чего изображения выравниваются и вычисляется показатель их схожести.
В реализации метод фазовой корреляции работает с бинарными изображениями, однако может применяться и для изображений в 8-битном цветовом пространстве.
Пусть
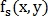 и
и 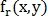 – изображения, одно из которых сдвинуто на
– изображения, одно из которых сдвинуто на 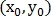 относительно другого, а
относительно другого, а 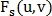 и
и 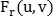 – их преобразования Фурье, тогда:
– их преобразования Фурье, тогда: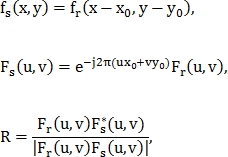
где
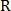 – кросс-спектр;
– кросс-спектр;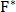 – комплексно сопряженное
– комплексно сопряженное 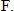
Вычисляя обратное преобразование Фурье кросс-спектра, получим импульс-функцию:
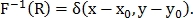
Найдя максимум этой функции, найдём искомое смещение.
Теперь найдём угол вращения
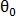 при наличии смещения
при наличии смещения 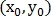 , используя полярные координаты:
, используя полярные координаты: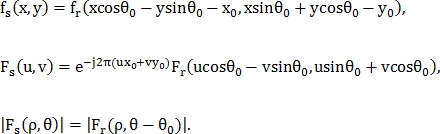
Далее применяется метод фазовой корреляции, как в предыдущем случае. Можно отметить, что такая модификация фазовой корреляции позволяет найти и масштаб по параметру
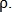
Данная техника не всегда показывает хорошие результаты на практике из-за наличия небольших шумов и того, что часть сосудов может присутствовать на одном изображении и отсутствовать на другом. Чтобы это устранить применяется несколько итераций данного алгоритма, в том числе меняется порядок подачи изображений в функцию и порядок устранения смещения и вращения. На каждой итерации изображения выравниваются, после чего вычисляется их показатель схожести, затем находится максимальный показатель схожести, который и будет конечным результатом сравнения.
Показатель схожести вычисляется следующим образом:

2. Алгоритм, использующий углы Харриса
Данный алгоритм, в отличие от предыдущего, не требует сегментации сосудов, поскольку может определять признаки не только на бинарном изображении.
В начале изображения выравниваются при помощи метода фазовой корреляции, описанного в предыдущем разделе. Затем на изображениях ищутся углы Харриса (рис. 2).

Рис. 2. Результат поиска углов Харриса на изображениях сетчатки.
Пусть найдена M+1 точка, тогда для каждой j-й точки её декартовы координаты
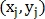 преобразуются в полярные
преобразуются в полярные 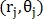 и определяется вектор признаков
и определяется вектор признаков 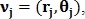 где
где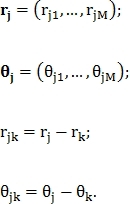
Модель подобия между неизвестным вектором
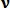 и вектором признаков
и вектором признаков 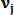 размера N в точке j определяется следующим образом:
размера N в точке j определяется следующим образом: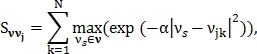
где
 – константа, которая определяется ещё до поиска углов Харриса.
– константа, которая определяется ещё до поиска углов Харриса.Функция
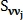 описывает близость и похожесть вектора
описывает близость и похожесть вектора 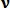 ко всем признакам точки j.
ко всем признакам точки j.Пусть вектор
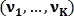 – вектор признаков первого изображения, где
– вектор признаков первого изображения, где 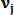 размера K–1, а вектор
размера K–1, а вектор 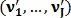 – вектор признаков второго изображения, где
– вектор признаков второго изображения, где 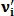 размера J–1, тогда показатель схожести этих изображений вычисляется следующим образом:
размера J–1, тогда показатель схожести этих изображений вычисляется следующим образом: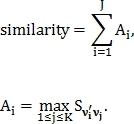
Нормировочный коэффициент для similarity равняется
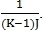
Коэффициент
 в оригинальной статье предлагается определять по следующему критерию: если разница между гистограммами изображений меньше заранее заданного значения, то
в оригинальной статье предлагается определять по следующему критерию: если разница между гистограммами изображений меньше заранее заданного значения, то  = 0.25, в противном случае
= 0.25, в противном случае  = 1.
= 1.3. Алгоритм, основанный на поиске точек разветвления
Данный алгоритм, как и предыдущий, ищет точки разветвления у системы кровеносных сосудов. При этом он более специализирован на поиске точек бифуркации и пересечения (рис. 3) и намного более устойчив к шумам, однако может работать только на бинарных изображениях.

Рис. 3. Типы признаков (слева – точка бифуркации, справа – точка пересечения).
Для поиска точек, как на рис. 3, сегментированные сосуды сжимаются до толщины одного пикселя. Таким образом, можно классифицировать каждую точку сосудов по количеству соседей S:
- если S = 1, то это конечная точка;
- если S = 2, то это внутренняя точка;
- если S = 3, то это точка бифуркации;
- если S = 4, то это точка пересечения.
3.1. Алгоритм сжатия сосудов до толщины одного пикселя и классификация точек разветвления
Вначале выполняется поиск пикселя, являющегося частью сосуда, сверху вниз слева направо. Предполагается, что каждый пиксель сосуда может иметь не более двух соседних пикселей сосудов (предыдущий и следующий), во избежание двусмысленности в последующих вычислениях.
Далее анализируются 4 соседних пикселя найденной точки, которые ещё не были рассмотрены. Это приводит к 16 возможным конфигурациям (рис. 4). Если пиксель в середине окна не имеет соседей серого цвета, как показано на рис. 4 (a), то он отбрасывается и ищется другой пиксель кровеносных сосудов. В других случаях это либо конечная точка, либо внутренняя (не включая точки бифуркации и пересечения).

Рис. 4. 16 возможных конфигураций четырёх соседних пикселей (белые точки – фон, серые – сосуды). 3 верхних пикселя и один слева уже были проанализированы, поэтому игнорируются. Серые пиксели с крестиком внутри также игнорируются. Точки со стрелочкой внутри – точки, которые могут стать следующим центральным пикселем. Пиксели с чёрной точкой внутри – это конечные точки.
На каждом шаге сосед серого цвета последнего пикселя помечается как пройденный и выбирается следующим центральным пикселем в окошке 3 x 3. Выбор такого соседа определяется следующим критерием: наилучший сосед тот, у которого наибольшее количество непомеченных серых соседей. Такая эвристика обусловлена идеей поддержания однопиксельной толщины в середине сосуда, где большее число соседей серого цвета.
Из вышеизложенного алгоритма следует, что он приводит к разъединению сосудов. Также сосуды могут разъединиться ещё на этапе сегментации. Поэтому необходимо соединить их обратно.
Для восстановления связи между двумя близлежащими конечными точками определяются углы
 и
и 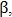 как на рис. 5, и если они меньше заранее заданного угла
как на рис. 5, и если они меньше заранее заданного угла 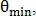 то конечные точки объединяются.
то конечные точки объединяются.
Рис. 5. Объединение конечных точек после сжатия.
Чтобы восстановить точки бифуркации и пересечения (рис. 6) для каждой конечной точки вычисляется её направление, после чего производится расширение сегмента фиксированной длины
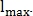 Если это расширение пересекается с другим сегментом, то найдена точка бифуркации либо пересечения.
Если это расширение пересекается с другим сегментом, то найдена точка бифуркации либо пересечения.
Рис. 6. Восстановление точки бифуркации.
Точка пересечения представляет собой две точки бифуркации, поэтому для упрощения задачи можно искать только точки бифуркации. Чтобы удалить ложные выбросы, вызванные точками пересечения, можно отбрасывать точки, которые находится слишком близко к другой найденной точке.
Для нахождения точек пересечения необходим дополнительный анализ (рис. 7).

Рис. 7. Классификация точек разветвления по количеству пересечений сосудов с окружностью. (a) Точка бифуркации. (b) Точка пересечения.
Как видно на рис. 7 (b), в зависимости от длины радиуса окружность с центром в точке разветвления может пересекаться с кровеносными сосудами либо в трех, либо в четырёх точках. Поэтому точка разветвления может быть не правильно классифицирована. Чтобы избавиться от этой проблемы используется система голосования, изображённая на рис. 8.

Рис. 8. Схема классификации точек бифуркации и пересечения.
В этой системе голосования точка разветвления
 классифицируется для трёх различных радиусов
классифицируется для трёх различных радиусов 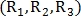 по количеству пересечений окружности с кровеносными сосудами. Радиусы определяются как:
по количеству пересечений окружности с кровеносными сосудами. Радиусы определяются как: 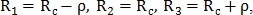 где
где 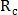 и
и  принимают фиксированные значения. При этом вычисляются два значения
принимают фиксированные значения. При этом вычисляются два значения 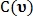 и
и 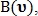 означающие количество голосов за то, чтобы точка
означающие количество голосов за то, чтобы точка  была классифицирована как точка пересечения и как точка бифуркации соответственно:
была классифицирована как точка пересечения и как точка бифуркации соответственно: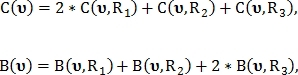
где
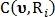 и
и 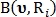 – бинарные значения, указывающие идентифицирована ли точка
– бинарные значения, указывающие идентифицирована ли точка  с использованием радиуса
с использованием радиуса 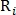 как точка пересечения либо как точка бифуркации соответственно.
как точка пересечения либо как точка бифуркации соответственно.В случае если
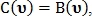 то тип точки
то тип точки  не определён. Если же значение отличаются друг от друга, то при
не определён. Если же значение отличаются друг от друга, то при 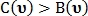 точка
точка  классифицируется как точка пересечения, в противном случае как точка бифуркации.
классифицируется как точка пересечения, в противном случае как точка бифуркации.3.2. Поиск преобразования подобия и определение метрики схожести
После того, как точки найдены, необходимо найти преобразование подобия. Это преобразование описывается 4 параметрами
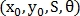 – смещение по оси
– смещение по оси  и
и  , масштаб и вращение соответственно.
, масштаб и вращение соответственно.Само преобразование определяется как:
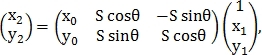
где
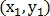 – координаты точки на первом изображении
– координаты точки на первом изображении 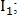
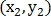 – на втором изображении
– на втором изображении 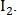
Для нахождения преобразования подобия используются пары контрольных точек. Например, точки
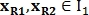 определяют вектор
определяют вектор 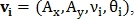 где
где 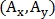 – координаты начала вектора,
– координаты начала вектора, 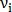 – длина вектора и
– длина вектора и 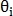 – направление вектора. Таким же образом определяется вектор
– направление вектора. Таким же образом определяется вектор 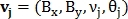 для точек
для точек 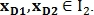 Пример представлен на рис. 9.
Пример представлен на рис. 9.
Рис. 9. Пример двух пар контрольных точек.
Параметры преобразования подобия находятся из следующих равенств:
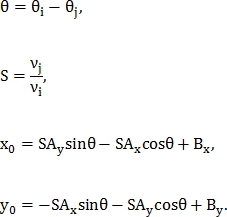
Пусть количество найденных точек на первом изображения равняется M, а на втором N, тогда количество пар контрольных точек на первом изображении равно
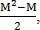 а на втором
а на втором  Таким образом, получаем
Таким образом, получаем 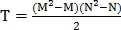 возможных преобразований, среди которых верным выбирается то, при котором количество совпавших точек наибольшее.
возможных преобразований, среди которых верным выбирается то, при котором количество совпавших точек наибольшее.Поскольку значение параметра S близко к единице, то T можно уменьшить, отбрасывая пары точек, неудовлетворяющие следующему неравенству:
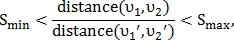
где
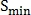 – это минимальный порог для параметра
– это минимальный порог для параметра 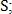
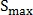 – это максимальный порог для параметра
– это максимальный порог для параметра 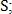
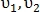 – пара контрольных точек из
– пара контрольных точек из 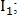
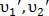 – пара контрольных точек из
– пара контрольных точек из 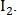
После применения одного из возможных вариантов выравнивания для точек
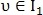 и
и 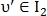 вычисляется показатель схожести:
вычисляется показатель схожести: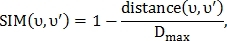
где
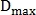 – пороговая максимальная дистанция между точками.
– пороговая максимальная дистанция между точками.В случае если
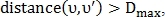 то
то 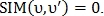
В некоторых случаях обе точки
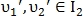 могут иметь хорошее значение похожести с точкой
могут иметь хорошее значение похожести с точкой 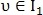 . Это случается, когда
. Это случается, когда 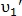 и
и 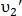 находятся близко друг к другу. Для определения наиболее подходящей пары вычисляется вероятность схожести:
находятся близко друг к другу. Для определения наиболее подходящей пары вычисляется вероятность схожести: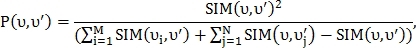
где
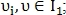
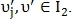
Если
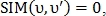 то
то 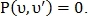
Чтобы найти количество совпавших точек строится матрица Q размера M x N так, что в i-й строке и j-м столбце содержится
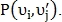
Затем в матрице Q ищется максимальный ненулевой элемент. Пусть этот элемент содержится в
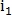 -й строке и
-й строке и 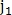 -м столбце, тогда точки
-м столбце, тогда точки 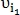 и
и 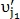 определяются как совпавшие, а
определяются как совпавшие, а 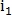 -я строка и
-я строка и 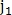 -й столбец обнуляются. После чего опять ищется максимальный элемент. Поиск таких максимумов повторяется до тех пор, пока все элементы матрицы Q не обнулятся. На выходе алгоритма получаем количество совпавших точек C.
-й столбец обнуляются. После чего опять ищется максимальный элемент. Поиск таких максимумов повторяется до тех пор, пока все элементы матрицы Q не обнулятся. На выходе алгоритма получаем количество совпавших точек C.Метрику схожести двух сетчаток можно определить несколькими способами:
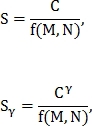
где
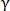 – параметр, который вводится для настройки влияния количества совпавших точек;
– параметр, который вводится для настройки влияния количества совпавших точек;f выбирается одним из следующих вариантов:
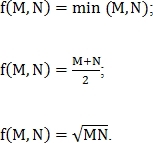
Метрика
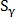 нормализуется одним из двух способов:
нормализуется одним из двух способов: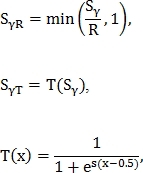
где
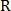 и
и  – некоторые константы.
– некоторые константы.3.3. Дополнительные усложнения алгоритма
Метод, основанный на поиске точек разветвления, можно усложнить, добавляя дополнительные признаки, например углы, как на рис. 10.

Рис. 10. Углы, образованные точками разветвления, в качестве дополнительных признаков.
Также можно применять шифр гаммирования. Как известно, сложение по модулю 2 является абсолютно стойким шифром, когда длина ключа равна длине текста, а поскольку количество точек бифуркации и пересечения не превышает порядка 100, но всё же больше длины обычных паролей, то в качестве ключа можно использовать комбинацию хешей пароля. Это избавляет от необходимости хранить в базе данных сетчатки глаза и хеши паролей. Нужно хранить только координаты, зашифрованные абсолютно стойким шифром.
Заключение
Аутентификация по сетчатке действительно показывает точные результаты. Алгоритм, основанный на методе фазовой корреляции, не допустил ни одной ошибки при тестировании на базе данных VARIA. Также алгоритм был протестирован на неразмеченной базе MESSIDOR с целью проверки алгоритма на ложные срабатывания. Все найденные алгоритмом пары похожих сетчаток были проверены вручную. Они действительно являются одинаковыми. На сравнение кровеносных сосудов двух сетчаток глаз из базы VARIA уходит в среднем 1.2 секунды на двух ядрах процессора Pentium ® Dual-CoreT4500 с частотой 2.30 GHz. Время исполнения алгоритма получилось довольно большое для идентификации, но оно приемлемо для аутентификации.
Также была предпринята попытка реализации алгоритма, использующего углы Харриса, но получить удовлетворительных результатов не удалось. Как и в предыдущем алгоритме, возникла проблема в устранении вращения и смещения при помощи метода фазовой корреляции. Вторая проблема связана с недостатками алгоритма поиска углов Харриса. При одном и том же пороговом значении для отсева точек, количество найденных точек может оказаться либо слишком большим либо слишком малым.
В дальнейших планах стоит разработка алгоритма, основанного на поиске точек разветвления. Он требует гораздо меньше вычислительных ресурсов по сравнению с алгоритмом, основанном на методе фазовой корреляции. Кроме того, существуют возможности для его усложнения в целях сведения к минимуму вероятности взлома системы.
Другим интересным направлением в дальнейших исследованиях является разработка автоматических систем для ранней диагностики заболеваний, таких как глаукома, сахарный диабет, атеросклероз и многие другие.
Список использованных источников и литературы
- Reddy B.S. and Chatterji B.N. An FFT-Based Technique for Translation, Rotation, and Scale-Invariant Image Registration // IEEE Transactions on Image Processing. 1996. Vol. 5. No. 8. pp. 1266-1271.
- Human recognition based on retinal images and using new similarity function / A. Dehghani [et al.] // EURASIP Journal on Image and Video Processing. 2013.
- Hortas M.O. Automatic system for personal authentication using the retinal vessel tree as biometric pattern. PhD Thesis. Universidade da Coruna. La Coruna. 2009.
- VARIA database
- MESSIDOR database
p.s. по немногочисленным просьбам выкладываю ссылку на проект на гитхабе.

