На сайте бесплатных лекций MIT OpenCourseWare выложен курс лекций по космологии Алана Гуса, одного из создателей инфляционной модели вселенной.
Вашему вниманию предлагается перевод третьей лекции: «Инфляционная Космология 3. Эффект Доплера и специальная теория относительности».
Нерелятивистское доплеровское смещение
В конце прошлой лекции мы начали обсуждать доплеровское смещение и ввели обозначения. Речь шла о случае, когда наблюдатель неподвижен, а источник движется со скоростью . Мы рассматривали звуковые волны, которые имели фиксированную скорость относительно некоторой среды.
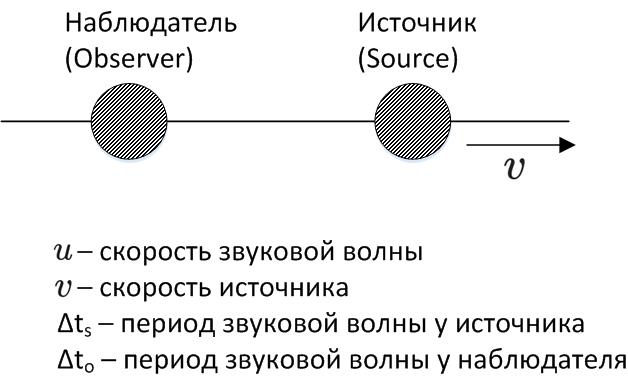
Скорость волны относительно среды обозначим , означает скорость удаления источнка, как показано на рисунке. — интервал времени между гребнями волны, испущенными источником, то есть период волны у источника. обозначает период волны у наблюдателя. Нам нужно вычислить связь между и .
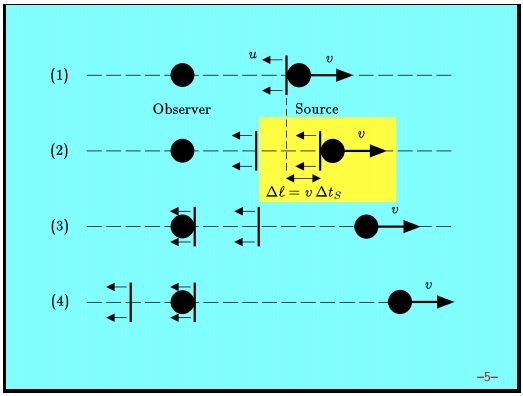
На рисунке показаны различные этапы данного процесса. На первом этапе источник движется вправо и испускает первый гребень волны. Пока ничего особенно интересного.
На втором этапе источник испускает второй гребень волны. Но за это время источник переместился, это перемещение выделено желтым. Время между испусканием гребней волны равно . Поэтому расстояние, которое пройдет источник в течение этого времени, равно . Назовем это расстояние .
Это действительно важный этап, он объясняет доплеровское смещение. Видно, что второй гребень волны должен пройти немного больше чем первый гребень, на величину .
Третий этап — волна прошла расстояние между наблюдателем и источником. На данном этапе первый гребень только что попал к наблюдателю. Четвертый этап — второй гребень попал к наблюдателю.
Чтобы понять, чему равно доплеровское смещение, нужно заметить, что, если бы оба объекта были неподвижны, то не было бы никакой разницы в периоде волны у наблюдателя и источника. Каждый гребень волны попадал бы к наблюдателю с некоторым запозданием, равным времени, за которое звуковая волна проходит расстояние от источника до наблюдателя. Но, в отсутствии движения, это запоздание одинаково для каждого гребня. Таким образом, если источник не движется = .
Но из-за движения источника второму гребню придется пройти расстояние большее на величину . Разница между периодами будет равна времени, которое потребуется волне, чтобы пройти это расстояние.
Мы знаем чему равно . – это просто . Подставляя в наше уравнение получаем:
Это уравнение показывает связь между и . Можно найти отношение и .
Это отношение является также отношением длины волны у наблюдателя и у источника , поскольку длина волны просто равна скорости волны умноженной на ее период .
Для описания доплеровского или красного смещения существует стандартное определение.
называется доплеровским или красным смещением. Астрономы вычитают единицу из отношения длин волн, чтобы в случае, когда оба объекта неподвижны, получилось равным 0. Такой случай соответствует отсутствию красного смещения и означает, что длина волны одна и та же у источника и у наблюдателя.
Таким образом, получаем красное смещение для нерелятивистского движения, или звуковой волны, в случае, когда движется источник:
Теперь перейдем к другому простому случаю, когда движется наблюдатель, а источник неподвижен. Источник у нас по-прежнему справа, а наблюдатель слева. Но на этот раз наблюдатель движется со скоростью . В обоих случаях — это относительная скорость между источником и наблюдателем.
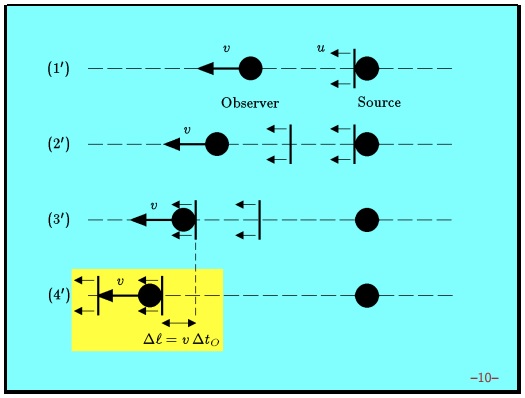
Первый этап снова довольно прост. Источник излучает первый гребень волны. Этап номер два — второй гребень волны испускается источником. Этап номер три — первый гребень волны доходит до наблюдателя. Этап номер четыре — второй гребень волны доходит до наблюдателя.
Между временем, когда первый гребень приходит к наблюдателю, и временем, когда второй гребень приходит к наблюдателю, то есть временем между третьим и четвертым этапами наблюдатель переместился. Он переместился на расстояние равное умноженное на время между этими этапами. Время между этими этапами — это как раз время, которое проходит между получением двух гребней наблюдателем. Это то, что мы обозначили — период волны, измеренный наблюдателем. Пройденное расстояние — это просто . Все нужное для получения ответа происходит внутри желтого прямоугольника на последнем этапе.
Можно выписать уравнения для данного случая. В этот раз все немного сложнее. Начнем с той же идеи. был бы равен , если бы не было движения. Но становится немного больше из-за дополнительного расстояния, которое проходит второй гребень. Это дополнительное расстояние снова назовем . Время задержки снова будет деленное на , скорость волны.
Но на этот раз у нас другая формула для . На этот раз равна , а не , как было в предыдущем случае.
Уравнение становится немного сложнее, потому что появляется с обеих сторон уравнения. Тем не менее, это уравнение с одним неизвестным, из него легко находится . После несложных алгебраических преобразований получаем:
Вычтя единицу получаем окончательное уравнение для , вновь для нерелятивистского случая, когда движется наблюдатель:
Стоит отметить, что, когда скорость мала по сравнению со скоростью волны, что часто бывает если мы рассматриваем световую волну, но также встречается и в случае распространения звука, то обе формулы для почти одинаковы. Они обе пропорциональны , если мало. Единственное различие — это знаменатель.
Во втором случае у нас знаменатель . В первом случае просто равно , и нет никакого знаменателя. Если мало, то знаменатель во втором случае близок к 1. Таким образом, две формулы будут почти одинаковыми. Можно описать это немного более точно, вычислив разницу между z в обоих случаях. Проделав несложные вычисления получаем:
Из формулы явно видно, что разница между пропорциональна , а не просто . Если равна одной тысячной, разница будет одна миллионная. Поэтому для медленных скоростей не имеет значения, движется ли источник или движется наблюдатель. Но ответы, конечно, будут сильно отличаться, если скорость сравнима с .
СТУДЕНТ: Не нарушает ли это принцип относительности Галилея?
ПРЕПОДАВАТЕЛЬ: На самом деле нет. Для наших расчетов критически важным является воздух, в котором движется звуковая волна. В обоих случаях воздух покоится относительно рисунка. Если сделать преобразования Галилея от одной картины к другой, то после преобразования воздух будет двигаться, и получится не совсем та же картина.
Поэтому все согласуется с Галилеевской теорией относительности. Нужно помнить, что воздух здесь играет решающую роль. Когда мы говорим, что наблюдатель или источник находится в покое, в действительности имеется ввиду, что он находится в покое по отношению к среде, в которой движется волна.
СТУДЕНТ: Я заметил, что если больше , то в первом случае ответ всегда положительный, все в порядке. Но если больше во втором случае, то получается отрицательный ответ. Мне кажется это странным.
ПРЕПОДАВАТЕЛЬ: Да, если больше , то в случае движения наблюдателя ответ становится отрицательным. Это означает, что волна никогда не достигнет наблюдателя. Если наблюдатель движется быстрее чем скорость волны, волна никогда не догонит его. Поэтому получается такой необычный ответ. Если источник движется быстрее скорости волны, волна все равно достигает наблюдателя. Поэтому в первом случае мы получаем правильный ответ.
Релятивистское замедление времени
Давайте теперь перейдем к релятивистскому случаю. Нам потребуются некоторые факты из теории относительности. Поскольку существуют специализированные курсы по теории относительности, я не хочу, чтобы наши лекции стали таким курсом. Однако я хочу, чтобы наш курс был полностью понятен людям, не проходившим теорию относительности. Знание специальной теории относительности не является обязательным условием для нашего курса. Поэтому моей целью будет рассказать вам достаточно о специальной теории относительности, чтобы вы могли понимать дальнейшее. Я не буду выводить результаты, их вывод можно найти в других курсах. Если вы не хотите их посещать, то тоже ничего страшного. Но я хочу, чтобы мой курс был логически последовательным.
Итак, мы рассмотрим следствия специальной теории относительности, не пытаясь связать их непосредственно с основополагающими идеями специальной теории относительности. Однако я напомню, откуда взялась специальная теория относительности. Она зародилась в голове у Альберта Эйнштейна, когда он рассматривал Галилеевскую теорию относительности, о которой спрашивали минуту назад. Галилеевская теория относительности гласит, что если вы посмотрите на любой физический процесс в системе отсчета, которая движется с равномерной скоростью относительно другой системы отсчета, то в обоих системах отчета законы физики должны описываться одинаковым образом.
Теория относительности Галилея сыграла очень важную роль в истории физики. Ключевой вопрос во времена Галилея был — двигалась ли Земля вокруг Солнца или Солнце вокруг Земли. Галилей в этом споре принимал активное участие. Один из аргументов, доказывающих, что именно Солнце должно двигаться вокруг Земли, а не наоборот, был такой, что если Земля движется вокруг Солнца, то это означает, что мы движемся вместе с Землей с очень высокой скоростью. Скорость Земли вокруг Солнца высока по обычным меркам. Люди в то время считали, что очевидно, такое движение должно чувствоваться. Это было доказательство того, что Земля неподвижна, а Солнце движется. Потому что, в противном случае, чувствовался бы эффект быстрого движения Земли.
Для точки зрения Галилея, что движется именно Земля, критически важно, что мы такое движение не замечаем. Если мы движемся равномерно, то законы физики остаются точно такими же, какими они были бы, если бы мы оставались в покое. В этом суть теории относительности Галилея. Она была очень четко изложена Галилеем в его трудах.
Все это было справедливо для механических явлений. Однако в 1860-х годах Максвелл вывел свои уравнения. Вернее будет сказать, он завершил их вывод, большинство этих уравнений уже существовало. Из уравнений Максвелла следовало, что свет должен двигаться с фиксированной скоростью, которая может быть выражена через электрическую и магнитную постоянные и . Эту скорость мы обозначаем . Теперь представим, что вы попали на космический корабль, который движется со скоростью равной, скажем, половине , и погнались за лучом света. Согласно физике, которая была известна в то время, получалось, что с точки зрения космического корабля, движущегося со скоростью , световой импульс будет удаляться от него всего со скоростью . Но это означает, что в системе отсчета такого быстро движущегося космического корабля законы физики должны каким-то образом отличаться. Уравнения Максвелла должны отличаться от стандартной формы.
Между физикой Максвелла и физикой Ньютона возникла некоторая напряженность. Напряженность, но не противоречие. Вполне возможно представить, что существует фиксированная система отсчета, в которой уравнения Максвелла имеют простую форму. Но уравнения Ньютона имеют одинаковую форму во всех инерциальных системах отсчета. Чтобы объяснить, почему так происходит, физики изобрели идею эфира, то есть среду, в которой распространяются световые волны, подобно воздуху, в котором распространяются звуковые волны. Система отсчета, в которой уравнения Максвелла имеют простую форму, является системой отсчета, в которой покоится эфир. Если мы движемся относительно эфира, то уравнения становятся другими. Именно так люди думали в 1904 году. Это была последовательная точка зрения, но это означало, что существует двойственность между электромагнетизмом и механикой.
Эйнштейн подумал, что может быть физика не такая нелогичная. Может быть, есть более элегантный способ, который может все объяснить. Он понял, что если модифицировать уравнения, которые используются для преобразования между разными системами отсчета, то можно сделать уравнения Максвелла инвариантными. Можно сделать так, чтобы уравнения Максвелла были действительны во всех системах отсчета. Давайте вернемся к нашему примеру с кораблем, гонящимся за световым лучом. Согласно новым уравнениям преобразования, которые предложил Эйнштейн, получается, хотя это сильно противоречит интуиции, что световой импульс удаляется от корабля со скоростью . Хотя корабль сам движется со скоростью , пытаясь догнать световой импульс.
Не очевидно, как такое может быть. Но, оказывается, именно так все и происходит. В основном это была догадка Эйнштейна. Он предположил, что эфира нет, что законы физики, и электромагнетизма, и механики одинаковы во всех системах отсчета. Для того, чтобы так получалось, уравнения преобразования между различными системами отсчета должны отличаться от тех, которые использовал Галилей.
Эти преобразования называются преобразованиями Лоренца. В этой лекции мы не будем их выписывать. В этой лекции мы поговорим о трех физических эффектах, которые следуют из преобразований Лоренца. Один из таких эффектов – это замедление времени. Немного позже мы обсудим два других основных эффекта, которые необходимы для понимания специальной теории относительности и объяснения, как такое может быть, что скорость света одинакова для всех наблюдателей, даже для тех, которые движутся.

Замедление времени заключается в том, что если наблюдать за движущимися часами, то движущиеся часы «выглядят» идущими медленнее. Замечу, что я поставил слово «выглядят» в кавычки. Мы вернемся к этому и обсудим подробно, что подразумевается под словом «выглядят». Тем не менее, движущиеся часы будут выглядеть в моей системе отсчета идущими всегда медленнее в абсолютно предсказуемое число раз. Это число является известным выражением в специальной теории относительности :
где — это просто обозначение для , скорость движения часов, деленная на скорость света. Если мало, то замедление времени тоже мало, почти равна 1. Замедление времени в 1 раз означает, что время вообще не замедляется. Если близка к 1, то эффект будет незначительным. Но движущиеся часы всегда будут идти медленнее.
Давайте теперь вернемся к слову «выглядят». Тут есть тонкость. В прошлом году на PBS вышел фильм из четырех частей «Ткань космоса» Брайана Грина. Он пытался проиллюстрировать замедление времени. Он показал человека, сидящего в кресле, и человека, идущему к нему и несущего часы над головой. Камера показала, что человек, сидящий в кресле, увидит, как часы при движении начинают идти медленнее. Это не верно. Это не то, что он на самом деле увидит. И это ключевая проблема слова «выглядят».
Когда мы говорим, что движущиеся часы идут медленнее, мы не имеем в виду, что наблюдатель действительно это видит. Сложность ситуации заключается в том, что когда вы смотрите на что-то, вы регистрируете световые импульсы, приходящие к вашим глазам в данный момент времени. Поскольку свет проходит путь за конечное время, это означает, что вы видите разные вещи в разное время. Например, если есть какой-то объект, скажем, лазерная указка, летящая ко мне, я увижу ее заднюю часть там, где она была в более раннее время, чем передняя часть. Потому что свету, который испускается задней частью, требуется большее время, чтобы достичь моего глаза, чем свету, испущенному передней частью указки.
Поэтому, когда объект приближается ко мне, я увижу разные его части в разные моменты времени. Это все усложняет. То, что я увижу, принимая во внимание специальную теорию относительности, довольно сложно. Это можно вычислить, но для этого нет простого выражения. Нужно шаг за шагом вычислять, что я увижу в каждый конкретный момент времени. Это абсолютно не похоже на простую картину.
Таким образом, утверждение, что часы идут медленнее в раз, основано не на том, что на самом деле увидит наблюдатель. Оно основано на том, что увидит система отсчета, а не конкретный человек. Это в конечном итоге приводит к более простой картине. Систему отсчета можно представить как набор линеек, соединенных друг с другом, так, что они образуют координатную сетку, и набор часов, расположенных повсюду внутри этой сетки.
При этом все наблюдения производятся локально. То есть, если мы хотим измерить время в какой-то системе отсчета, мы не используем центральные часы, ожидая, пока световой импульс достигнет этих центральных часов. Вместо этого, система отсчета заполнена часами, которые были синхронизированы друг с другом с самого начала. Если мы хотим знать, в какое время произошло какое-то событие, мы смотрим на часы, расположенные рядом с ним. Эти часы показывают, когда произошло это событие.
Как правило, именно таким образом мы работаем с различными системами координат. Если мы хотим понять, что увидит конкретный наблюдатель, то картина усложняется. Мы должны принять во внимание скорость света. Только исключив время на распространение света и рассчитав, что будут показывать локальные часы, мы увидим замедление времени в простой форме, что движущиеся часы всегда идут медленнее.
В частности, в примере с человеком, сидящим в кресле, и часами, приближающимися к нему. Человек будет испытывать, то, что мы обсуждаем на данной лекции — доплеровское смещение. Поскольку часы приближаются к нему, он будет испытывать синее смещение, а не красное. Он увидит, что часы идут быстрее, а не медленнее, в точности противоположное тому, что было показано в телевизионной программе. Ему будет казаться, что часы идут быстрее из-за того, что каждый последующий световой импульс проходит меньшее расстояние, поскольку часы приближаются к наблюдателю. Этот эффект дает больший вклад, чем эффект замедления движущихся часов, если сравнивать их с неподвижными часами, находящимися непосредственно рядом.
СТУДЕНТ: Если часы очень быстро пролетают мимо нас, могли бы мы увидеть их замедление, когда они находятся строго перпендикулярно к нам?
ПРЕПОДОВАТЕЛЬ: Да, вы совершенно правы. Когда часы пролетают мимо наблюдателя и находятся строго напротив него, скорость часов в его системе отсчета оказывается перпендикулярна скорости фотонов, которые он видит. При этом он увидит чистый эффект замедления времени.
Хочу добавить, что я и еще несколько человек из MIT принимали участие в создании фильма Брайана Грина. Мы долго обсуждали этот вопрос с Брайаном Грином по электронной почте. Мы все говорили, что это неправильно. Однако Брайан Грин занял позицию, что это было сделано намеренно, что он пытался проиллюстрировать эффект замедления времени, без обсуждения доплеровского смещения. Поскольку он не хотел говорить о доплеровском смещении, он просто проигнорировал факт его существования. Мы все считали, что это неправильно с педагогической точки зрения. Но мы не смогли убедить в этом Брайана.
Релятивистское доплеровское смещение
Теперь мы снова вычислим доплеровский сдвиг, на этот раз учитывая, что движущиеся часы идут медленнее в раз. Мы займемся релятивистским случаем, где волна — это световая волна. А скорости могут быть сопоставимы со скоростью света. На этот раз эффект замедления времени достаточно велик, чтобы принимать его во внимание.
На этот раз оба ответа должны получиться одинаковыми. Если ответы получатся разными, то получится, что наша картина мира неверна, противоречива. Не должно иметь значения, движется ли источник или движется наблюдатель. Раньше это имело значение, и мы объясняли это тем, что в процесс был вовлечен воздух. Если сделать преобразование, чтобы перейти от одного случая к другому, от случая, когда движется источник, к случаю, когда движется наблюдатель, воздух в разных случаях будет имеет разную скорость. В одном случае он будет неподвижен, в другом случае он будет двигаться. Поэтому мы не планировали получить один и тот же ответ.
Но теперь, когда мы переходим от случая, где движется источник, к случаю, где движется наблюдатель, то с другой скоростью должен двигаться эфир. Но основная аксиома специальной теории относительности заключается в том, что эфира нет, по крайней мере, нет физических эффектов, возникающих из-за эфира. Так что можно притвориться, что его не существует. Поэтому в специальной теории относительности мы должны получить один и тот же ответ, будь то движущийся источник или движущийся наблюдатель. Это на самом деле одна и та же ситуация, только рассматриваемая из разных систем отсчета. Специальная теория относительности утверждает, что не имеет значения, в какой системе отсчета мы делаем вычисления. Мы воспользуемся теми же рисунками, но на этот раз примем во внимание тот факт, что движущиеся часы идут медленнее в раз.

Для начала давайте подумаем, на каком этапе для нас важно замедление времени движущихся часов? На втором. Именно на этом этапе источник измеряет движущимися часами период между испусканием двух гребней волны. Можно просто представить, что источник испускает серию импульсов, где каждый импульс представляет собой гребень волны. Для меня это выглядит немного проще, потому что не нужно думать о синусоидальной волне, которую на самом деле создает источник.
Время между этими импульсами, измеренное часами источника — это то, что мы обозначили как . Источник движется на нашей картине. Все вычисления мы будем производить в нашей системе отсчета. Это очень важно, так как преобразования между системами отсчета немного сложны в специальной теории относительности. Когда вы решаете какую-нибудь задачу, то очень важно выбрать систему отсчета, которую вы будете использовать для описания задачи, и придерживаться ее. Если что-либо изначально описано в другой системе отсчета, нужно понять, как это выглядит в вашей системе отсчета. Чтобы затем соотнести это с другими событиями, которые описываются в вашей системе отсчета.
Для нашей задачи нашей системой отсчета будет система отсчета картинки, система отсчета, которая находится в покое относительно наблюдателя. Можно также назвать ее системой отсчета наблюдателя. Относительно этой системы отсчета источник движется. Источник испускает последовательность импульсов. Можно представить, что источник — это просто часы. Любое явление, повторяющееся с регулярными интервалами — это часы. Таким образом, источник представляет собой движущиеся часы, которые идут медленнее в раз.
В остальном ничего не меняется. У наблюдателя также имеются часы, которые он использует для измерения времени между гребнями. Но часы наблюдателя покоятся в нашей системе отсчета. Таким образом, нет замедления времени, связанного с часами наблюдателя, есть только замедление времени, связанное с часами источника. И снова, все важное изображено внутри желтого прямоугольника. Теперь нужно взглянуть на уравнения и посмотреть, как они изменятся.
В прошлый раз интервал времени, измеренный наблюдателем, был суммой двух членов. В качестве первого члена был , это был бы единственный член, если бы источник покоился. Это также верно и в нашем случае. Но время у источника идет медленнее в раз. То есть если не учитывать изменений в длине пути — эти изменения мы учтем в следующем члене – то период, измеряемый наблюдателем будет отличаться от периода, измеряемого источника в раз. Но нужно выяснить, будет ли стоять в числителе или знаменателе. Для этого может помочь мысленный пример.
Итак, часы источника идут медленнее. Допустим, мы говорим о временном интервале в одну секунду. Если часы источника идут медленнее, это означает, что у нас должно пройти больше времени, чтобы у источника прошла секунда. Допустим, что часы идут медленнее в два раза. Это означает, что у источника будет проходить только одна секунда каждые наши две секунды. Это означает, что период, который мы увидим, будет длиннее, чем в раз. Таким образом, перед первым членом мы ставим множитель . Второй член по прежнему равен .
Но выражение для также меняется. — это временной интервал, который требуется световому импульсу для перемещения на дополнительное расстояние. Дополнительное расстояние пропорционально времени между импульсами. Это время меняется из-за замедления времени часов источника. Так что второй член также увеличивается в раз.
Таким образом, весь ответ увеличивается в раз. Учитывая, что
и
после алгебраических преобразований получаем
Итак, мы получили ответ, учитывающий специальную теорию относительности, в случае движения источника. При учете теории относительности наш ответ увеличился в раз. Мы ожидаем, что ответ не будет зависеть от того, движется источник или наблюдатель, но, конечно, это нужно проверить при помощи вычислений.
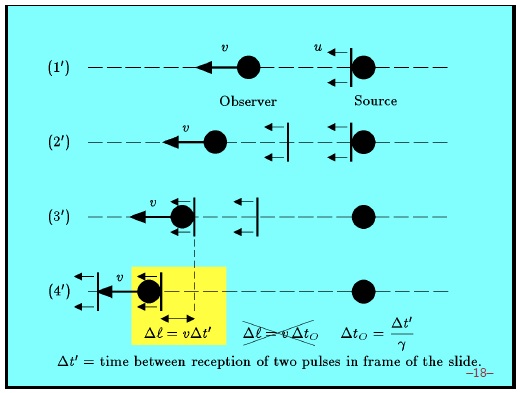
За основу мы возьмем расчет, который мы уже сделали для нерелятивистского случая, с движущимся наблюдателем. Мы попробуем вычислить релятивистский случай. Теперь часы наблюдателя идут медленнее. Они идут медленнее относительно нас, относительно нашей системы отсчета, где наша система отсчета, по определению, система отсчета нашей картинки.
Самое важное опять происходит в желтом прямоугольнике. Источник неподвижен, поэтому — это просто период волны, измеренный нашими часами. Но период, измеренный наблюдателем, , будет другим. Поэтому мы по-другому запишем наше уравнение, заменив выражение для . Для вместо мы запишем .
не равна . — это время, прошедшее между третьим и четвертым этапами, то есть время прошедшее между приходом двух соседних гребней волны к наблюдателю, измеренное в нашей системе отсчета. Мы описываем все с точки зрения нашей системы отсчета. отличается от в раз, потому что по отношению к нам часы наблюдателя работают медленнее в раз.
Опять, нужно немного подумать, где должна находиться , в числителе или знаменателе. Мы знаем, что часы наблюдателя идут медленнее по отношению к нашим. Это означает, что время, которое потребуется для того, чтобы прошла одна секунда у наблюдателя, у нас должно занять больше секунды. Поэтому = . Например, за время, которое часы наблюдателя проходят одну секунду, у нас проходят две секунды.
Мы повторим расчет, который мы делали для нерелятивистского случая, когда наблюдатель двигался. Но в расчет мы добавим замедление времени, которое сделает этот расчет верным. Сначала мы выпишем уравнения, какими они выглядят в нашей системе отсчета, то есть используют интервал :
Теперь мы можем выполнить преобразования, аналогичные тем, которые мы выполняли для нерелятивистского случая и получить выражение для :
Подставляя выражение для получаем:
или:
это выражение верно как в случае движения источника, так и в случае движения наблюдателя.
Красное смещение в релятивистском случае получается:
Итак, мы получили то, что ожидали. Что результат соответствует принципам теории относительности. Наш ответ не зависит от того, движется ли источник или наблюдатель, поскольку не имеет значения, в какой системе отсчета мы выполняем вычисления.
Другие эффекты специальной теории относительности
Теперь я хочу поговорить о двух других кинематических эффектах специальной теории относительности, а именно — Лоренцевом сокращении и изменении понятия одновременности. Но прежде чем заняться этими эффектами, есть еще один вопрос, который мы должны обсудить. Это часы, которые двигаются с ускорением.
Специальная теория относительности описывает инерциальные системы отсчета и то, какие преобразования выполняются при переходе от одной инерциальной системы к другой. Если мы знаем, как идут часы, находящиеся в покое в одной системе отсчета, специальная теория относительности полностью описывает, как будут идти часы в системе отсчета, движущейся с равномерной скоростью по отношению к первоначальной системе отсчета. Или другими словами, она описывает, как будут идти часы, если они двигаются с постоянной скоростью.
Однако в реальном мире, у нас очень мало часов, которые можно считать инерциальными. Любые часы, которые мы видим вокруг себя — часы на стене, которые двигаются вместе с Землей, или мои наручные часы, постоянно подвергаются ускорению. Мы хотим иметь возможность работать с часами, которые ускоряются и двигаются с релятивистской скоростью. Такое, например, происходит в спутниках. Система GPS, как вам, вероятно, известно, не будет работать, если в расчетах не учитывать эффекты специальной теории относительности и даже общей теории относительности. Таким образом, изучение поведения движущихся часов является критически важной технологической задачей.
Что мы можем сказать про ускоряющиеся часы? Существует распространенный миф, что для описания ускорения нужна общая теория относительности. Поэтому мы должны отложить разговор об ускоряющихся часах, пока не пройдем курс общей теории относительности. На самом деле, это не так. Общая теория относительности — это теория гравитации, которая утверждает, что гравитация и ускорение тесно связаны. В этом контексте ускорение появляется в общей теории относительности.
Однако специальной теории относительности достаточно для описания любой системы, которая описывается уравнениями, согласующимися со специальной теорией относительности. Специальная теория относительности не описывает гравитацию. Поэтому в ситуации, когда важна гравитация, специальная теория относительности не в состоянии давать правильные результаты. Но пока гравитация отсутствует, пока мы имеем дело только с электромагнитными силами, никто не мешает нам использовать уравнения специальной теории относительности.
Мы должны использовать уравнения динамики в специальной теории относительности, которые показывают, как тела реагируют на силы. Всякий раз, когда прикладывается сила, появляется ускорение. Такие уравнения существуют. Мы можем объединить, например, электромагнетизм с релятивистской механикой, чтобы описать систему частиц, которые взаимодействуют при помощи электромагнитных сил, в полном соответствии со специальной теорией относительности. И, несмотря на то, что эти частицы ускоряются, мы можем посчитать для них все, что хотим.
В частности, если имеются часы, сделанные из деталей, физику которых мы понимаем, специальная теория относительности может сказать нам, как будут вести себя эти часы, даже когда они ускоряются. Однако этот расчет может быть, очень, очень сложный. Потому что физика любых реальных часов, например, моих наручных часов, очень сложна. Но нам не нужно выписывать уравнения, описывающие мои наручные часы, чтобы понять, как они будут себя вести при ускорении.
Замечу, что у многих из вас уже есть большой опыт работы с ускоряющимися часами, потому что многие из вас носят наручные часы, которые все время ускоряются. И они, как правило, работают. Обычно мы предполагаем, что, хотя часы ускоряются, они сделаны достаточно хорошо, чтобы выдерживать ускорение, которое придает им ваше запястье, и показывать правильное время.
С другой стороны, можно представить себе противоположенную ситуацию. Если взять механические заводные часы, и кинуть их в стену, они разобьются о стену и остановятся. Когда они разбиваются о стену, они испытывают очень большое ускорение. Если ускорение достаточно большое, мы можем предсказать, что случится с часами, даже если это будет сложным взаимодействием. Если ускорение достаточно большое, оно просто сломает часы, и они остановятся. Это один из возможных эффектов, которое ускорение может оказывать на часы.
Другие эффекты похожи на этот. Если движение моей руки оказывает влияние на работу наручных часы, это является механическим эффектом, который можно рассчитать, понимая механику работы часов, а не используя принципы общей теории относительности. Разница со специальной теорией относительности здесь в том, что специальная теория относительности может сделать точный прогноз о том, как будут вести себя часы, если они будут двигаться с постоянной скоростью, даже не зная ничего об устройстве этих часов. Специальная теория относительности может сделать такое предсказание, потому что существует симметрия, симметрия Лоренца, которая связывает движущиеся и покоящиеся часы. Это точная симметрия природы. Независимо от того, из чего сделаны часы, если они движутся с постоянной скоростью, специальная теория относительности утверждает, что они будут идти медленнее в раз.
С другой стороны, ни в специальной теории относительности, ни в общей теории относительности нет подобного принципа, касающегося ускорения. То, как ускорение действует на часы, зависит, конечно, от того, насколько большим является ускорение, как устроены часы, и каким образом ускорение влияет на различные внутренние части часов. Суть в том, что когда мы говорим об ускоряющихся часах, мы всегда предполагаем, что часы сделаны достаточно хорошо, чтобы ускорение не влияло на то, с какой скоростью они идут. Мы предполагаем, что это идеальные часы, что они сделаны идеально хорошо. Когда мы говорим, что ускорение не влияет на скорость работы часов, мы имеем в виду, что в каждый момент времени часы идут с точно такой же скоростью, как и другие часы, которые двигаются одновременно с нашими часами с той же скоростью, но без ускорения.
В любой момент времени мои наручные часы будут иметь определенную скорость. На темп их хода очень незначительно будет влиять , которая в нашем случае будет очень близка к 1. Если мы будем считать мои часы идеальными часами, то мы предполагаем, что в любой момент времени они идут с той же скоростью, что и часы, которые не ускоряются, но которые двигаются с той же скоростью, что и наручные часы. Таким образом, множитель останется, но не будет никакого эффекта ускорения. Скорость работы часов будет определяться только их скоростью относительно нашей системы отсчета.
Теперь я хочу немного поговорить о других следствиях специальной теории относительности. Немного позже мы поговорим о динамических следствиях специальной теории относительности, которые включают в себя хорошо известные уравнения, такие как . Но прежде чем говорить о динамических величинах, таких как энергии и импульсе, мы закончим с рассмотрением кинематических эффектов специальной теории относительности. Под кинематикой я имею в виду следствия специальной теории относительности для измерения времени и расстояния.
Если ограничиться следствиями для измерения времени и расстояний, кинематическими эффектами, то таких следствий специальной теории относительности ровно три. Вся специальная теория относительности, в некотором смысле, воплощена в этих трех эффектах. Замедление времени является одним из таких эффектов.

Второе следствие – это еще один известный эффект специальной теории относительности, сокращение Лоренца, или иногда называемый сокращением Лоренца-Фицджеральда. В его описании снова будет фигурировать слово «выглядит». Я всегда буду писать это слово в кавычках, чтобы напомнить, что это не совсем то, что увидит наблюдатель. Любой стержень, который движется со скоростью вдоль своей длины относительно заданной системы отсчета, будет «выглядеть» для наблюдателя в этой системе отсчета короче своей длины в раз. Длина стержня, который движется перпендикулярно своей длине, не меняется. Это все показано на рисунке.
Это очень известное следствие специальной теории относительности. Оно означает, что ракета становится все короче и короче, по мере того как она движется быстрее и быстрее. Опять же, нужно помнить, что это не то, что вы на самом деле увидите. Это то, что получится, если измерения делаются локальными наблюдателями, и затем длина ракеты вычисляется на основе этих измерений.

Третий и последний эффект немного сложнее описать. Но это очень важный эффект. Первые два эффекта не были бы непротиворечивы, если бы не было третьего эффекта. Третьим эффектом является изменение понятия одновременности, или относительность одновременности.
Допустим у нас есть система, состоящая из двух часов, которые синхронизированы в своей системе отсчета, относительно которой они покоятся. Пусть они также соединены стержнем, который имеет некоторую длину в их системе отсчета, которую мы назовем . Если вся эта система двигается относительно нас со скоростью вдоль стержня, для нас эти часы выглядят не синхронизированными, несмотря на то, что они синхронизированы в своей системе отсчета.
В частности, задние часы будут выглядеть немного забегающими вперед, на время . Напомню, что . — расстояние между часами, измеренное в системе отсчета часов. — это, конечно, скорость света. С другой стороны, если часы двигаются в направлении, перпендикулярном соединяющей их линии, то часы выглядят синхронизованными.
Этот эффект очень важен для целостности всей картины. Мы не будем доказывать, что специальная теория непротиворечива. Мы бы вполне могли это сделать, но не будем этим заниматься, поскольку наш курс не посвящен детальному изучению специальной теории относительности. Однако может показаться, что между следствием специальной теории относительности — что движущиеся часы идут медленнее, и постулатом, что для всех инерциальных наблюдателей верны одни и те же законы физики, существует довольно очевидное несоответствие. Это значит, что если вы двигаетесь относительно меня, то для меня ваши часы идут медленнее. Но в то же время, для вас мои часы идут медленнее. Потому что, с вашей точки зрения, вы находитесь в покое, а я двигаюсь по отношению к вам. С вашей точки зрения двигаются мои часы. И мои часы должны идти медленнее.
Мне кажется, что ваши часы идут медленнее. Вам кажется, что мои часы идут медленнее. Кажется, что это противоречие. Что произойдет, если мы просто поместим часы рядом друг с другом и будем сравнивать, как они идут? Какие из часов будут идти быстрее? Как мы можем договориться друг с другом об этом? Конечно, мы не можем держать часы рядом друг с другом, и в тоже время перемещать их друг относительно друга. Это одна из причин, позволяющих разрешить противоречие. Вспомним, что я на самом деле имею в виду, когда говорю, что ваши часы идут медленнее. Я делаю все свои измерения не наблюдая непосредственно за вашими часами, потому что тогда возникает эффект задержки распространения сигнала, который усложняет картину. Я делаю все свои измерения при помощи множества локальных наблюдателей, окружающих меня и находящихся в покое по отношению ко мне. Они передают мне свои результаты. Только после получения и объединения их результатов я получаю единую картину того, что, где и когда произошло.
Поэтому, когда я говорю, что ваши часы работают медленно, я имею в виду, что у меня есть множество часов, которые находятся в покое по отношению ко мне. Когда ваши часы пролетают мимо меня, локальные наблюдатели сравнивают ваши часы со своими часами. Затем они передают результаты мне. Если ваши часы идут медленнее, скажем, в два раза, это означает, что, когда ваши часы пролетают мимо часов моего наблюдателя и его часы показывают одну секунду, ваши часы будут показывать только полсекунды. Когда они пролетают мимо более отдаленных часов моей системы отсчета, и часы моей системы отсчета показывают две секунды, ваши часы будут показывать одну секунду, и так далее. В этом смысле ваши часы идут медленнее.
Это должно быть совместимо с тем, что согласно вашей точке зрения мои часы также идут медленнее. Если вы предполагаете, что часы в моей системе отсчета синхронизированы, то вы приходите к выводу, что мои часы идут быстрее. Потому что когда ваши часы показывают полсекунды, мои часы показывают одну секунду. Когда ваши часы показывают секунду, мои часы показывают две секунды. Согласно такому прямому сравнению получается, что мои часы идут быстрее.
Но в то же время, мы знаем, что это не верно. Вы должны получить тот же результат, что и я. Если мы движемся по отношению друг к другу, вам должно казаться, что мои часы идут медленнее. Выход из этой затруднительной ситуации заключается в относительности одновременности. С вашей точки зрения последовательность часов из моей системы отсчета, когда они пролетают мимо вас, действительно показывают большее время по сравнению с вашими часами. Однако с вашей точки зрения мои часы не синхронизированы друг с другом. Поэтому вы не можете определить, с какой скоростью идут мои часы, измеряя время на разных часах.
Если вы хотите выяснить, с какой скоростью идут мои часы, вы должны следить за одними из моих часов и смотреть как на них меняются показания с течением времени. Вы не должны сравнивать показания разных часов, потому что мои часы не синхронизированы друг с другом, с вашей точки зрения. Но если вы будете наблюдать за одними из моих часов, используя набор ваших часов, которые неподвижны по отношению к вам, так же, как я использовал набор своих часов, когда измерял скорость работы ваших часов, тогда все встанет на свои места. Вы увидите, что мои часы идут медленнее. Я увижу, что ваши часы идут медленнее. Поскольку мы расходимся во мнении относительно того, какие события происходят одновременно, то противоречия не возникает. Таким образом, относительность одновременности критически важна, иначе мы бы получили вопиющее противоречие во всей картине.
Это все, что я планировал рассказать на сегодняшней лекции. Мы обсудили кинематические следствия специальной теории относительности. Как я сказал, мы не будем пытаться вывести их. Если вам интересно, как они получаются, то вы можете прослушать специализированный курс по специальной теории относительности.
Позже мы обсудим следствия из специальной тории относительности для импульса и энергии, которые будут важны для нас. Энергия и импульс интересны нам только до тех пор, пока они определены таким образом, что они являются сохраняемыми величинами. Именно поэтому энергия и импульс важны в физике. Для замкнутой системы полная энергия и импульс не меняются. Энергия и импульс могут передаваться из одной части системы в другую. Но энергия и импульс не могут быть ни созданы, ни уничтожены.
Если взять определения энергии и импульса из Ньютоновской механики и использовать их в релятивистской кинематике, то окажется, что при, например, столкновении частиц энергия и импульс сохранялись бы в одной системе отсчета и не сохранялись бы в другой системе отсчета. Законы сохранения зависели бы от используемой системы отсчета.
Поэтому Эйнштейн несколько изменил определения энергии и импульса таким образом, что если они сохраняются в одной системе отсчета, то они сохраняются и в любой другой системе отсчета, связанной с первой преобразованиями специальной теории относительности. Как только мы меняем кинематику перехода от одной системы отсчета к другой, нам также нужно изменить определения энергии и импульса, чтобы законы сохранения были справедливы во всех системах отсчета. В дальнейшем мы введем немного модифицированные, немного не Ньютоновские определения энергии и импульса движущихся частиц.
Вашему вниманию предлагается перевод третьей лекции: «Инфляционная Космология 3. Эффект Доплера и специальная теория относительности».
Нерелятивистское доплеровское смещение
В конце прошлой лекции мы начали обсуждать доплеровское смещение и ввели обозначения. Речь шла о случае, когда наблюдатель неподвижен, а источник движется со скоростью . Мы рассматривали звуковые волны, которые имели фиксированную скорость относительно некоторой среды.

Скорость волны относительно среды обозначим , означает скорость удаления источнка, как показано на рисунке. — интервал времени между гребнями волны, испущенными источником, то есть период волны у источника. обозначает период волны у наблюдателя. Нам нужно вычислить связь между и .

На рисунке показаны различные этапы данного процесса. На первом этапе источник движется вправо и испускает первый гребень волны. Пока ничего особенно интересного.
На втором этапе источник испускает второй гребень волны. Но за это время источник переместился, это перемещение выделено желтым. Время между испусканием гребней волны равно . Поэтому расстояние, которое пройдет источник в течение этого времени, равно . Назовем это расстояние .
Это действительно важный этап, он объясняет доплеровское смещение. Видно, что второй гребень волны должен пройти немного больше чем первый гребень, на величину .
Третий этап — волна прошла расстояние между наблюдателем и источником. На данном этапе первый гребень только что попал к наблюдателю. Четвертый этап — второй гребень попал к наблюдателю.
Чтобы понять, чему равно доплеровское смещение, нужно заметить, что, если бы оба объекта были неподвижны, то не было бы никакой разницы в периоде волны у наблюдателя и источника. Каждый гребень волны попадал бы к наблюдателю с некоторым запозданием, равным времени, за которое звуковая волна проходит расстояние от источника до наблюдателя. Но, в отсутствии движения, это запоздание одинаково для каждого гребня. Таким образом, если источник не движется = .
Но из-за движения источника второму гребню придется пройти расстояние большее на величину . Разница между периодами будет равна времени, которое потребуется волне, чтобы пройти это расстояние.
Мы знаем чему равно . – это просто . Подставляя в наше уравнение получаем:
Это уравнение показывает связь между и . Можно найти отношение и .
Это отношение является также отношением длины волны у наблюдателя и у источника , поскольку длина волны просто равна скорости волны умноженной на ее период .
Для описания доплеровского или красного смещения существует стандартное определение.
называется доплеровским или красным смещением. Астрономы вычитают единицу из отношения длин волн, чтобы в случае, когда оба объекта неподвижны, получилось равным 0. Такой случай соответствует отсутствию красного смещения и означает, что длина волны одна и та же у источника и у наблюдателя.
Таким образом, получаем красное смещение для нерелятивистского движения, или звуковой волны, в случае, когда движется источник:
Теперь перейдем к другому простому случаю, когда движется наблюдатель, а источник неподвижен. Источник у нас по-прежнему справа, а наблюдатель слева. Но на этот раз наблюдатель движется со скоростью . В обоих случаях — это относительная скорость между источником и наблюдателем.

Первый этап снова довольно прост. Источник излучает первый гребень волны. Этап номер два — второй гребень волны испускается источником. Этап номер три — первый гребень волны доходит до наблюдателя. Этап номер четыре — второй гребень волны доходит до наблюдателя.
Между временем, когда первый гребень приходит к наблюдателю, и временем, когда второй гребень приходит к наблюдателю, то есть временем между третьим и четвертым этапами наблюдатель переместился. Он переместился на расстояние равное умноженное на время между этими этапами. Время между этими этапами — это как раз время, которое проходит между получением двух гребней наблюдателем. Это то, что мы обозначили — период волны, измеренный наблюдателем. Пройденное расстояние — это просто . Все нужное для получения ответа происходит внутри желтого прямоугольника на последнем этапе.
Можно выписать уравнения для данного случая. В этот раз все немного сложнее. Начнем с той же идеи. был бы равен , если бы не было движения. Но становится немного больше из-за дополнительного расстояния, которое проходит второй гребень. Это дополнительное расстояние снова назовем . Время задержки снова будет деленное на , скорость волны.
Но на этот раз у нас другая формула для . На этот раз равна , а не , как было в предыдущем случае.
Уравнение становится немного сложнее, потому что появляется с обеих сторон уравнения. Тем не менее, это уравнение с одним неизвестным, из него легко находится . После несложных алгебраических преобразований получаем:
Вычтя единицу получаем окончательное уравнение для , вновь для нерелятивистского случая, когда движется наблюдатель:
Стоит отметить, что, когда скорость мала по сравнению со скоростью волны, что часто бывает если мы рассматриваем световую волну, но также встречается и в случае распространения звука, то обе формулы для почти одинаковы. Они обе пропорциональны , если мало. Единственное различие — это знаменатель.
Во втором случае у нас знаменатель . В первом случае просто равно , и нет никакого знаменателя. Если мало, то знаменатель во втором случае близок к 1. Таким образом, две формулы будут почти одинаковыми. Можно описать это немного более точно, вычислив разницу между z в обоих случаях. Проделав несложные вычисления получаем:
Из формулы явно видно, что разница между пропорциональна , а не просто . Если равна одной тысячной, разница будет одна миллионная. Поэтому для медленных скоростей не имеет значения, движется ли источник или движется наблюдатель. Но ответы, конечно, будут сильно отличаться, если скорость сравнима с .
СТУДЕНТ: Не нарушает ли это принцип относительности Галилея?
ПРЕПОДАВАТЕЛЬ: На самом деле нет. Для наших расчетов критически важным является воздух, в котором движется звуковая волна. В обоих случаях воздух покоится относительно рисунка. Если сделать преобразования Галилея от одной картины к другой, то после преобразования воздух будет двигаться, и получится не совсем та же картина.
Поэтому все согласуется с Галилеевской теорией относительности. Нужно помнить, что воздух здесь играет решающую роль. Когда мы говорим, что наблюдатель или источник находится в покое, в действительности имеется ввиду, что он находится в покое по отношению к среде, в которой движется волна.
СТУДЕНТ: Я заметил, что если больше , то в первом случае ответ всегда положительный, все в порядке. Но если больше во втором случае, то получается отрицательный ответ. Мне кажется это странным.
ПРЕПОДАВАТЕЛЬ: Да, если больше , то в случае движения наблюдателя ответ становится отрицательным. Это означает, что волна никогда не достигнет наблюдателя. Если наблюдатель движется быстрее чем скорость волны, волна никогда не догонит его. Поэтому получается такой необычный ответ. Если источник движется быстрее скорости волны, волна все равно достигает наблюдателя. Поэтому в первом случае мы получаем правильный ответ.
Релятивистское замедление времени
Давайте теперь перейдем к релятивистскому случаю. Нам потребуются некоторые факты из теории относительности. Поскольку существуют специализированные курсы по теории относительности, я не хочу, чтобы наши лекции стали таким курсом. Однако я хочу, чтобы наш курс был полностью понятен людям, не проходившим теорию относительности. Знание специальной теории относительности не является обязательным условием для нашего курса. Поэтому моей целью будет рассказать вам достаточно о специальной теории относительности, чтобы вы могли понимать дальнейшее. Я не буду выводить результаты, их вывод можно найти в других курсах. Если вы не хотите их посещать, то тоже ничего страшного. Но я хочу, чтобы мой курс был логически последовательным.
Итак, мы рассмотрим следствия специальной теории относительности, не пытаясь связать их непосредственно с основополагающими идеями специальной теории относительности. Однако я напомню, откуда взялась специальная теория относительности. Она зародилась в голове у Альберта Эйнштейна, когда он рассматривал Галилеевскую теорию относительности, о которой спрашивали минуту назад. Галилеевская теория относительности гласит, что если вы посмотрите на любой физический процесс в системе отсчета, которая движется с равномерной скоростью относительно другой системы отсчета, то в обоих системах отчета законы физики должны описываться одинаковым образом.
Теория относительности Галилея сыграла очень важную роль в истории физики. Ключевой вопрос во времена Галилея был — двигалась ли Земля вокруг Солнца или Солнце вокруг Земли. Галилей в этом споре принимал активное участие. Один из аргументов, доказывающих, что именно Солнце должно двигаться вокруг Земли, а не наоборот, был такой, что если Земля движется вокруг Солнца, то это означает, что мы движемся вместе с Землей с очень высокой скоростью. Скорость Земли вокруг Солнца высока по обычным меркам. Люди в то время считали, что очевидно, такое движение должно чувствоваться. Это было доказательство того, что Земля неподвижна, а Солнце движется. Потому что, в противном случае, чувствовался бы эффект быстрого движения Земли.
Для точки зрения Галилея, что движется именно Земля, критически важно, что мы такое движение не замечаем. Если мы движемся равномерно, то законы физики остаются точно такими же, какими они были бы, если бы мы оставались в покое. В этом суть теории относительности Галилея. Она была очень четко изложена Галилеем в его трудах.
Все это было справедливо для механических явлений. Однако в 1860-х годах Максвелл вывел свои уравнения. Вернее будет сказать, он завершил их вывод, большинство этих уравнений уже существовало. Из уравнений Максвелла следовало, что свет должен двигаться с фиксированной скоростью, которая может быть выражена через электрическую и магнитную постоянные и . Эту скорость мы обозначаем . Теперь представим, что вы попали на космический корабль, который движется со скоростью равной, скажем, половине , и погнались за лучом света. Согласно физике, которая была известна в то время, получалось, что с точки зрения космического корабля, движущегося со скоростью , световой импульс будет удаляться от него всего со скоростью . Но это означает, что в системе отсчета такого быстро движущегося космического корабля законы физики должны каким-то образом отличаться. Уравнения Максвелла должны отличаться от стандартной формы.
Между физикой Максвелла и физикой Ньютона возникла некоторая напряженность. Напряженность, но не противоречие. Вполне возможно представить, что существует фиксированная система отсчета, в которой уравнения Максвелла имеют простую форму. Но уравнения Ньютона имеют одинаковую форму во всех инерциальных системах отсчета. Чтобы объяснить, почему так происходит, физики изобрели идею эфира, то есть среду, в которой распространяются световые волны, подобно воздуху, в котором распространяются звуковые волны. Система отсчета, в которой уравнения Максвелла имеют простую форму, является системой отсчета, в которой покоится эфир. Если мы движемся относительно эфира, то уравнения становятся другими. Именно так люди думали в 1904 году. Это была последовательная точка зрения, но это означало, что существует двойственность между электромагнетизмом и механикой.
Эйнштейн подумал, что может быть физика не такая нелогичная. Может быть, есть более элегантный способ, который может все объяснить. Он понял, что если модифицировать уравнения, которые используются для преобразования между разными системами отсчета, то можно сделать уравнения Максвелла инвариантными. Можно сделать так, чтобы уравнения Максвелла были действительны во всех системах отсчета. Давайте вернемся к нашему примеру с кораблем, гонящимся за световым лучом. Согласно новым уравнениям преобразования, которые предложил Эйнштейн, получается, хотя это сильно противоречит интуиции, что световой импульс удаляется от корабля со скоростью . Хотя корабль сам движется со скоростью , пытаясь догнать световой импульс.
Не очевидно, как такое может быть. Но, оказывается, именно так все и происходит. В основном это была догадка Эйнштейна. Он предположил, что эфира нет, что законы физики, и электромагнетизма, и механики одинаковы во всех системах отсчета. Для того, чтобы так получалось, уравнения преобразования между различными системами отсчета должны отличаться от тех, которые использовал Галилей.
Эти преобразования называются преобразованиями Лоренца. В этой лекции мы не будем их выписывать. В этой лекции мы поговорим о трех физических эффектах, которые следуют из преобразований Лоренца. Один из таких эффектов – это замедление времени. Немного позже мы обсудим два других основных эффекта, которые необходимы для понимания специальной теории относительности и объяснения, как такое может быть, что скорость света одинакова для всех наблюдателей, даже для тех, которые движутся.

Замедление времени заключается в том, что если наблюдать за движущимися часами, то движущиеся часы «выглядят» идущими медленнее. Замечу, что я поставил слово «выглядят» в кавычки. Мы вернемся к этому и обсудим подробно, что подразумевается под словом «выглядят». Тем не менее, движущиеся часы будут выглядеть в моей системе отсчета идущими всегда медленнее в абсолютно предсказуемое число раз. Это число является известным выражением в специальной теории относительности :
где — это просто обозначение для , скорость движения часов, деленная на скорость света. Если мало, то замедление времени тоже мало, почти равна 1. Замедление времени в 1 раз означает, что время вообще не замедляется. Если близка к 1, то эффект будет незначительным. Но движущиеся часы всегда будут идти медленнее.
Давайте теперь вернемся к слову «выглядят». Тут есть тонкость. В прошлом году на PBS вышел фильм из четырех частей «Ткань космоса» Брайана Грина. Он пытался проиллюстрировать замедление времени. Он показал человека, сидящего в кресле, и человека, идущему к нему и несущего часы над головой. Камера показала, что человек, сидящий в кресле, увидит, как часы при движении начинают идти медленнее. Это не верно. Это не то, что он на самом деле увидит. И это ключевая проблема слова «выглядят».
Когда мы говорим, что движущиеся часы идут медленнее, мы не имеем в виду, что наблюдатель действительно это видит. Сложность ситуации заключается в том, что когда вы смотрите на что-то, вы регистрируете световые импульсы, приходящие к вашим глазам в данный момент времени. Поскольку свет проходит путь за конечное время, это означает, что вы видите разные вещи в разное время. Например, если есть какой-то объект, скажем, лазерная указка, летящая ко мне, я увижу ее заднюю часть там, где она была в более раннее время, чем передняя часть. Потому что свету, который испускается задней частью, требуется большее время, чтобы достичь моего глаза, чем свету, испущенному передней частью указки.
Поэтому, когда объект приближается ко мне, я увижу разные его части в разные моменты времени. Это все усложняет. То, что я увижу, принимая во внимание специальную теорию относительности, довольно сложно. Это можно вычислить, но для этого нет простого выражения. Нужно шаг за шагом вычислять, что я увижу в каждый конкретный момент времени. Это абсолютно не похоже на простую картину.
Таким образом, утверждение, что часы идут медленнее в раз, основано не на том, что на самом деле увидит наблюдатель. Оно основано на том, что увидит система отсчета, а не конкретный человек. Это в конечном итоге приводит к более простой картине. Систему отсчета можно представить как набор линеек, соединенных друг с другом, так, что они образуют координатную сетку, и набор часов, расположенных повсюду внутри этой сетки.
При этом все наблюдения производятся локально. То есть, если мы хотим измерить время в какой-то системе отсчета, мы не используем центральные часы, ожидая, пока световой импульс достигнет этих центральных часов. Вместо этого, система отсчета заполнена часами, которые были синхронизированы друг с другом с самого начала. Если мы хотим знать, в какое время произошло какое-то событие, мы смотрим на часы, расположенные рядом с ним. Эти часы показывают, когда произошло это событие.
Как правило, именно таким образом мы работаем с различными системами координат. Если мы хотим понять, что увидит конкретный наблюдатель, то картина усложняется. Мы должны принять во внимание скорость света. Только исключив время на распространение света и рассчитав, что будут показывать локальные часы, мы увидим замедление времени в простой форме, что движущиеся часы всегда идут медленнее.
В частности, в примере с человеком, сидящим в кресле, и часами, приближающимися к нему. Человек будет испытывать, то, что мы обсуждаем на данной лекции — доплеровское смещение. Поскольку часы приближаются к нему, он будет испытывать синее смещение, а не красное. Он увидит, что часы идут быстрее, а не медленнее, в точности противоположное тому, что было показано в телевизионной программе. Ему будет казаться, что часы идут быстрее из-за того, что каждый последующий световой импульс проходит меньшее расстояние, поскольку часы приближаются к наблюдателю. Этот эффект дает больший вклад, чем эффект замедления движущихся часов, если сравнивать их с неподвижными часами, находящимися непосредственно рядом.
СТУДЕНТ: Если часы очень быстро пролетают мимо нас, могли бы мы увидеть их замедление, когда они находятся строго перпендикулярно к нам?
ПРЕПОДОВАТЕЛЬ: Да, вы совершенно правы. Когда часы пролетают мимо наблюдателя и находятся строго напротив него, скорость часов в его системе отсчета оказывается перпендикулярна скорости фотонов, которые он видит. При этом он увидит чистый эффект замедления времени.
Хочу добавить, что я и еще несколько человек из MIT принимали участие в создании фильма Брайана Грина. Мы долго обсуждали этот вопрос с Брайаном Грином по электронной почте. Мы все говорили, что это неправильно. Однако Брайан Грин занял позицию, что это было сделано намеренно, что он пытался проиллюстрировать эффект замедления времени, без обсуждения доплеровского смещения. Поскольку он не хотел говорить о доплеровском смещении, он просто проигнорировал факт его существования. Мы все считали, что это неправильно с педагогической точки зрения. Но мы не смогли убедить в этом Брайана.
Релятивистское доплеровское смещение
Теперь мы снова вычислим доплеровский сдвиг, на этот раз учитывая, что движущиеся часы идут медленнее в раз. Мы займемся релятивистским случаем, где волна — это световая волна. А скорости могут быть сопоставимы со скоростью света. На этот раз эффект замедления времени достаточно велик, чтобы принимать его во внимание.
На этот раз оба ответа должны получиться одинаковыми. Если ответы получатся разными, то получится, что наша картина мира неверна, противоречива. Не должно иметь значения, движется ли источник или движется наблюдатель. Раньше это имело значение, и мы объясняли это тем, что в процесс был вовлечен воздух. Если сделать преобразование, чтобы перейти от одного случая к другому, от случая, когда движется источник, к случаю, когда движется наблюдатель, воздух в разных случаях будет имеет разную скорость. В одном случае он будет неподвижен, в другом случае он будет двигаться. Поэтому мы не планировали получить один и тот же ответ.
Но теперь, когда мы переходим от случая, где движется источник, к случаю, где движется наблюдатель, то с другой скоростью должен двигаться эфир. Но основная аксиома специальной теории относительности заключается в том, что эфира нет, по крайней мере, нет физических эффектов, возникающих из-за эфира. Так что можно притвориться, что его не существует. Поэтому в специальной теории относительности мы должны получить один и тот же ответ, будь то движущийся источник или движущийся наблюдатель. Это на самом деле одна и та же ситуация, только рассматриваемая из разных систем отсчета. Специальная теория относительности утверждает, что не имеет значения, в какой системе отсчета мы делаем вычисления. Мы воспользуемся теми же рисунками, но на этот раз примем во внимание тот факт, что движущиеся часы идут медленнее в раз.

Для начала давайте подумаем, на каком этапе для нас важно замедление времени движущихся часов? На втором. Именно на этом этапе источник измеряет движущимися часами период между испусканием двух гребней волны. Можно просто представить, что источник испускает серию импульсов, где каждый импульс представляет собой гребень волны. Для меня это выглядит немного проще, потому что не нужно думать о синусоидальной волне, которую на самом деле создает источник.
Время между этими импульсами, измеренное часами источника — это то, что мы обозначили как . Источник движется на нашей картине. Все вычисления мы будем производить в нашей системе отсчета. Это очень важно, так как преобразования между системами отсчета немного сложны в специальной теории относительности. Когда вы решаете какую-нибудь задачу, то очень важно выбрать систему отсчета, которую вы будете использовать для описания задачи, и придерживаться ее. Если что-либо изначально описано в другой системе отсчета, нужно понять, как это выглядит в вашей системе отсчета. Чтобы затем соотнести это с другими событиями, которые описываются в вашей системе отсчета.
Для нашей задачи нашей системой отсчета будет система отсчета картинки, система отсчета, которая находится в покое относительно наблюдателя. Можно также назвать ее системой отсчета наблюдателя. Относительно этой системы отсчета источник движется. Источник испускает последовательность импульсов. Можно представить, что источник — это просто часы. Любое явление, повторяющееся с регулярными интервалами — это часы. Таким образом, источник представляет собой движущиеся часы, которые идут медленнее в раз.
В остальном ничего не меняется. У наблюдателя также имеются часы, которые он использует для измерения времени между гребнями. Но часы наблюдателя покоятся в нашей системе отсчета. Таким образом, нет замедления времени, связанного с часами наблюдателя, есть только замедление времени, связанное с часами источника. И снова, все важное изображено внутри желтого прямоугольника. Теперь нужно взглянуть на уравнения и посмотреть, как они изменятся.
В прошлый раз интервал времени, измеренный наблюдателем, был суммой двух членов. В качестве первого члена был , это был бы единственный член, если бы источник покоился. Это также верно и в нашем случае. Но время у источника идет медленнее в раз. То есть если не учитывать изменений в длине пути — эти изменения мы учтем в следующем члене – то период, измеряемый наблюдателем будет отличаться от периода, измеряемого источника в раз. Но нужно выяснить, будет ли стоять в числителе или знаменателе. Для этого может помочь мысленный пример.
Итак, часы источника идут медленнее. Допустим, мы говорим о временном интервале в одну секунду. Если часы источника идут медленнее, это означает, что у нас должно пройти больше времени, чтобы у источника прошла секунда. Допустим, что часы идут медленнее в два раза. Это означает, что у источника будет проходить только одна секунда каждые наши две секунды. Это означает, что период, который мы увидим, будет длиннее, чем в раз. Таким образом, перед первым членом мы ставим множитель . Второй член по прежнему равен .
Но выражение для также меняется. — это временной интервал, который требуется световому импульсу для перемещения на дополнительное расстояние. Дополнительное расстояние пропорционально времени между импульсами. Это время меняется из-за замедления времени часов источника. Так что второй член также увеличивается в раз.
Таким образом, весь ответ увеличивается в раз. Учитывая, что
и
после алгебраических преобразований получаем
Итак, мы получили ответ, учитывающий специальную теорию относительности, в случае движения источника. При учете теории относительности наш ответ увеличился в раз. Мы ожидаем, что ответ не будет зависеть от того, движется источник или наблюдатель, но, конечно, это нужно проверить при помощи вычислений.

За основу мы возьмем расчет, который мы уже сделали для нерелятивистского случая, с движущимся наблюдателем. Мы попробуем вычислить релятивистский случай. Теперь часы наблюдателя идут медленнее. Они идут медленнее относительно нас, относительно нашей системы отсчета, где наша система отсчета, по определению, система отсчета нашей картинки.
Самое важное опять происходит в желтом прямоугольнике. Источник неподвижен, поэтому — это просто период волны, измеренный нашими часами. Но период, измеренный наблюдателем, , будет другим. Поэтому мы по-другому запишем наше уравнение, заменив выражение для . Для вместо мы запишем .
не равна . — это время, прошедшее между третьим и четвертым этапами, то есть время прошедшее между приходом двух соседних гребней волны к наблюдателю, измеренное в нашей системе отсчета. Мы описываем все с точки зрения нашей системы отсчета. отличается от в раз, потому что по отношению к нам часы наблюдателя работают медленнее в раз.
Опять, нужно немного подумать, где должна находиться , в числителе или знаменателе. Мы знаем, что часы наблюдателя идут медленнее по отношению к нашим. Это означает, что время, которое потребуется для того, чтобы прошла одна секунда у наблюдателя, у нас должно занять больше секунды. Поэтому = . Например, за время, которое часы наблюдателя проходят одну секунду, у нас проходят две секунды.
Мы повторим расчет, который мы делали для нерелятивистского случая, когда наблюдатель двигался. Но в расчет мы добавим замедление времени, которое сделает этот расчет верным. Сначала мы выпишем уравнения, какими они выглядят в нашей системе отсчета, то есть используют интервал :
Теперь мы можем выполнить преобразования, аналогичные тем, которые мы выполняли для нерелятивистского случая и получить выражение для :
Подставляя выражение для получаем:
или:
это выражение верно как в случае движения источника, так и в случае движения наблюдателя.
Красное смещение в релятивистском случае получается:
Итак, мы получили то, что ожидали. Что результат соответствует принципам теории относительности. Наш ответ не зависит от того, движется ли источник или наблюдатель, поскольку не имеет значения, в какой системе отсчета мы выполняем вычисления.
Другие эффекты специальной теории относительности
Теперь я хочу поговорить о двух других кинематических эффектах специальной теории относительности, а именно — Лоренцевом сокращении и изменении понятия одновременности. Но прежде чем заняться этими эффектами, есть еще один вопрос, который мы должны обсудить. Это часы, которые двигаются с ускорением.
Специальная теория относительности описывает инерциальные системы отсчета и то, какие преобразования выполняются при переходе от одной инерциальной системы к другой. Если мы знаем, как идут часы, находящиеся в покое в одной системе отсчета, специальная теория относительности полностью описывает, как будут идти часы в системе отсчета, движущейся с равномерной скоростью по отношению к первоначальной системе отсчета. Или другими словами, она описывает, как будут идти часы, если они двигаются с постоянной скоростью.
Однако в реальном мире, у нас очень мало часов, которые можно считать инерциальными. Любые часы, которые мы видим вокруг себя — часы на стене, которые двигаются вместе с Землей, или мои наручные часы, постоянно подвергаются ускорению. Мы хотим иметь возможность работать с часами, которые ускоряются и двигаются с релятивистской скоростью. Такое, например, происходит в спутниках. Система GPS, как вам, вероятно, известно, не будет работать, если в расчетах не учитывать эффекты специальной теории относительности и даже общей теории относительности. Таким образом, изучение поведения движущихся часов является критически важной технологической задачей.
Что мы можем сказать про ускоряющиеся часы? Существует распространенный миф, что для описания ускорения нужна общая теория относительности. Поэтому мы должны отложить разговор об ускоряющихся часах, пока не пройдем курс общей теории относительности. На самом деле, это не так. Общая теория относительности — это теория гравитации, которая утверждает, что гравитация и ускорение тесно связаны. В этом контексте ускорение появляется в общей теории относительности.
Однако специальной теории относительности достаточно для описания любой системы, которая описывается уравнениями, согласующимися со специальной теорией относительности. Специальная теория относительности не описывает гравитацию. Поэтому в ситуации, когда важна гравитация, специальная теория относительности не в состоянии давать правильные результаты. Но пока гравитация отсутствует, пока мы имеем дело только с электромагнитными силами, никто не мешает нам использовать уравнения специальной теории относительности.
Мы должны использовать уравнения динамики в специальной теории относительности, которые показывают, как тела реагируют на силы. Всякий раз, когда прикладывается сила, появляется ускорение. Такие уравнения существуют. Мы можем объединить, например, электромагнетизм с релятивистской механикой, чтобы описать систему частиц, которые взаимодействуют при помощи электромагнитных сил, в полном соответствии со специальной теорией относительности. И, несмотря на то, что эти частицы ускоряются, мы можем посчитать для них все, что хотим.
В частности, если имеются часы, сделанные из деталей, физику которых мы понимаем, специальная теория относительности может сказать нам, как будут вести себя эти часы, даже когда они ускоряются. Однако этот расчет может быть, очень, очень сложный. Потому что физика любых реальных часов, например, моих наручных часов, очень сложна. Но нам не нужно выписывать уравнения, описывающие мои наручные часы, чтобы понять, как они будут себя вести при ускорении.
Замечу, что у многих из вас уже есть большой опыт работы с ускоряющимися часами, потому что многие из вас носят наручные часы, которые все время ускоряются. И они, как правило, работают. Обычно мы предполагаем, что, хотя часы ускоряются, они сделаны достаточно хорошо, чтобы выдерживать ускорение, которое придает им ваше запястье, и показывать правильное время.
С другой стороны, можно представить себе противоположенную ситуацию. Если взять механические заводные часы, и кинуть их в стену, они разобьются о стену и остановятся. Когда они разбиваются о стену, они испытывают очень большое ускорение. Если ускорение достаточно большое, мы можем предсказать, что случится с часами, даже если это будет сложным взаимодействием. Если ускорение достаточно большое, оно просто сломает часы, и они остановятся. Это один из возможных эффектов, которое ускорение может оказывать на часы.
Другие эффекты похожи на этот. Если движение моей руки оказывает влияние на работу наручных часы, это является механическим эффектом, который можно рассчитать, понимая механику работы часов, а не используя принципы общей теории относительности. Разница со специальной теорией относительности здесь в том, что специальная теория относительности может сделать точный прогноз о том, как будут вести себя часы, если они будут двигаться с постоянной скоростью, даже не зная ничего об устройстве этих часов. Специальная теория относительности может сделать такое предсказание, потому что существует симметрия, симметрия Лоренца, которая связывает движущиеся и покоящиеся часы. Это точная симметрия природы. Независимо от того, из чего сделаны часы, если они движутся с постоянной скоростью, специальная теория относительности утверждает, что они будут идти медленнее в раз.
С другой стороны, ни в специальной теории относительности, ни в общей теории относительности нет подобного принципа, касающегося ускорения. То, как ускорение действует на часы, зависит, конечно, от того, насколько большим является ускорение, как устроены часы, и каким образом ускорение влияет на различные внутренние части часов. Суть в том, что когда мы говорим об ускоряющихся часах, мы всегда предполагаем, что часы сделаны достаточно хорошо, чтобы ускорение не влияло на то, с какой скоростью они идут. Мы предполагаем, что это идеальные часы, что они сделаны идеально хорошо. Когда мы говорим, что ускорение не влияет на скорость работы часов, мы имеем в виду, что в каждый момент времени часы идут с точно такой же скоростью, как и другие часы, которые двигаются одновременно с нашими часами с той же скоростью, но без ускорения.
В любой момент времени мои наручные часы будут иметь определенную скорость. На темп их хода очень незначительно будет влиять , которая в нашем случае будет очень близка к 1. Если мы будем считать мои часы идеальными часами, то мы предполагаем, что в любой момент времени они идут с той же скоростью, что и часы, которые не ускоряются, но которые двигаются с той же скоростью, что и наручные часы. Таким образом, множитель останется, но не будет никакого эффекта ускорения. Скорость работы часов будет определяться только их скоростью относительно нашей системы отсчета.
Теперь я хочу немного поговорить о других следствиях специальной теории относительности. Немного позже мы поговорим о динамических следствиях специальной теории относительности, которые включают в себя хорошо известные уравнения, такие как . Но прежде чем говорить о динамических величинах, таких как энергии и импульсе, мы закончим с рассмотрением кинематических эффектов специальной теории относительности. Под кинематикой я имею в виду следствия специальной теории относительности для измерения времени и расстояния.
Если ограничиться следствиями для измерения времени и расстояний, кинематическими эффектами, то таких следствий специальной теории относительности ровно три. Вся специальная теория относительности, в некотором смысле, воплощена в этих трех эффектах. Замедление времени является одним из таких эффектов.

Второе следствие – это еще один известный эффект специальной теории относительности, сокращение Лоренца, или иногда называемый сокращением Лоренца-Фицджеральда. В его описании снова будет фигурировать слово «выглядит». Я всегда буду писать это слово в кавычках, чтобы напомнить, что это не совсем то, что увидит наблюдатель. Любой стержень, который движется со скоростью вдоль своей длины относительно заданной системы отсчета, будет «выглядеть» для наблюдателя в этой системе отсчета короче своей длины в раз. Длина стержня, который движется перпендикулярно своей длине, не меняется. Это все показано на рисунке.
Это очень известное следствие специальной теории относительности. Оно означает, что ракета становится все короче и короче, по мере того как она движется быстрее и быстрее. Опять же, нужно помнить, что это не то, что вы на самом деле увидите. Это то, что получится, если измерения делаются локальными наблюдателями, и затем длина ракеты вычисляется на основе этих измерений.

Третий и последний эффект немного сложнее описать. Но это очень важный эффект. Первые два эффекта не были бы непротиворечивы, если бы не было третьего эффекта. Третьим эффектом является изменение понятия одновременности, или относительность одновременности.
Допустим у нас есть система, состоящая из двух часов, которые синхронизированы в своей системе отсчета, относительно которой они покоятся. Пусть они также соединены стержнем, который имеет некоторую длину в их системе отсчета, которую мы назовем . Если вся эта система двигается относительно нас со скоростью вдоль стержня, для нас эти часы выглядят не синхронизированными, несмотря на то, что они синхронизированы в своей системе отсчета.
В частности, задние часы будут выглядеть немного забегающими вперед, на время . Напомню, что . — расстояние между часами, измеренное в системе отсчета часов. — это, конечно, скорость света. С другой стороны, если часы двигаются в направлении, перпендикулярном соединяющей их линии, то часы выглядят синхронизованными.
Этот эффект очень важен для целостности всей картины. Мы не будем доказывать, что специальная теория непротиворечива. Мы бы вполне могли это сделать, но не будем этим заниматься, поскольку наш курс не посвящен детальному изучению специальной теории относительности. Однако может показаться, что между следствием специальной теории относительности — что движущиеся часы идут медленнее, и постулатом, что для всех инерциальных наблюдателей верны одни и те же законы физики, существует довольно очевидное несоответствие. Это значит, что если вы двигаетесь относительно меня, то для меня ваши часы идут медленнее. Но в то же время, для вас мои часы идут медленнее. Потому что, с вашей точки зрения, вы находитесь в покое, а я двигаюсь по отношению к вам. С вашей точки зрения двигаются мои часы. И мои часы должны идти медленнее.
Мне кажется, что ваши часы идут медленнее. Вам кажется, что мои часы идут медленнее. Кажется, что это противоречие. Что произойдет, если мы просто поместим часы рядом друг с другом и будем сравнивать, как они идут? Какие из часов будут идти быстрее? Как мы можем договориться друг с другом об этом? Конечно, мы не можем держать часы рядом друг с другом, и в тоже время перемещать их друг относительно друга. Это одна из причин, позволяющих разрешить противоречие. Вспомним, что я на самом деле имею в виду, когда говорю, что ваши часы идут медленнее. Я делаю все свои измерения не наблюдая непосредственно за вашими часами, потому что тогда возникает эффект задержки распространения сигнала, который усложняет картину. Я делаю все свои измерения при помощи множества локальных наблюдателей, окружающих меня и находящихся в покое по отношению ко мне. Они передают мне свои результаты. Только после получения и объединения их результатов я получаю единую картину того, что, где и когда произошло.
Поэтому, когда я говорю, что ваши часы работают медленно, я имею в виду, что у меня есть множество часов, которые находятся в покое по отношению ко мне. Когда ваши часы пролетают мимо меня, локальные наблюдатели сравнивают ваши часы со своими часами. Затем они передают результаты мне. Если ваши часы идут медленнее, скажем, в два раза, это означает, что, когда ваши часы пролетают мимо часов моего наблюдателя и его часы показывают одну секунду, ваши часы будут показывать только полсекунды. Когда они пролетают мимо более отдаленных часов моей системы отсчета, и часы моей системы отсчета показывают две секунды, ваши часы будут показывать одну секунду, и так далее. В этом смысле ваши часы идут медленнее.
Это должно быть совместимо с тем, что согласно вашей точке зрения мои часы также идут медленнее. Если вы предполагаете, что часы в моей системе отсчета синхронизированы, то вы приходите к выводу, что мои часы идут быстрее. Потому что когда ваши часы показывают полсекунды, мои часы показывают одну секунду. Когда ваши часы показывают секунду, мои часы показывают две секунды. Согласно такому прямому сравнению получается, что мои часы идут быстрее.
Но в то же время, мы знаем, что это не верно. Вы должны получить тот же результат, что и я. Если мы движемся по отношению друг к другу, вам должно казаться, что мои часы идут медленнее. Выход из этой затруднительной ситуации заключается в относительности одновременности. С вашей точки зрения последовательность часов из моей системы отсчета, когда они пролетают мимо вас, действительно показывают большее время по сравнению с вашими часами. Однако с вашей точки зрения мои часы не синхронизированы друг с другом. Поэтому вы не можете определить, с какой скоростью идут мои часы, измеряя время на разных часах.
Если вы хотите выяснить, с какой скоростью идут мои часы, вы должны следить за одними из моих часов и смотреть как на них меняются показания с течением времени. Вы не должны сравнивать показания разных часов, потому что мои часы не синхронизированы друг с другом, с вашей точки зрения. Но если вы будете наблюдать за одними из моих часов, используя набор ваших часов, которые неподвижны по отношению к вам, так же, как я использовал набор своих часов, когда измерял скорость работы ваших часов, тогда все встанет на свои места. Вы увидите, что мои часы идут медленнее. Я увижу, что ваши часы идут медленнее. Поскольку мы расходимся во мнении относительно того, какие события происходят одновременно, то противоречия не возникает. Таким образом, относительность одновременности критически важна, иначе мы бы получили вопиющее противоречие во всей картине.
Это все, что я планировал рассказать на сегодняшней лекции. Мы обсудили кинематические следствия специальной теории относительности. Как я сказал, мы не будем пытаться вывести их. Если вам интересно, как они получаются, то вы можете прослушать специализированный курс по специальной теории относительности.
Позже мы обсудим следствия из специальной тории относительности для импульса и энергии, которые будут важны для нас. Энергия и импульс интересны нам только до тех пор, пока они определены таким образом, что они являются сохраняемыми величинами. Именно поэтому энергия и импульс важны в физике. Для замкнутой системы полная энергия и импульс не меняются. Энергия и импульс могут передаваться из одной части системы в другую. Но энергия и импульс не могут быть ни созданы, ни уничтожены.
Если взять определения энергии и импульса из Ньютоновской механики и использовать их в релятивистской кинематике, то окажется, что при, например, столкновении частиц энергия и импульс сохранялись бы в одной системе отсчета и не сохранялись бы в другой системе отсчета. Законы сохранения зависели бы от используемой системы отсчета.
Поэтому Эйнштейн несколько изменил определения энергии и импульса таким образом, что если они сохраняются в одной системе отсчета, то они сохраняются и в любой другой системе отсчета, связанной с первой преобразованиями специальной теории относительности. Как только мы меняем кинематику перехода от одной системы отсчета к другой, нам также нужно изменить определения энергии и импульса, чтобы законы сохранения были справедливы во всех системах отсчета. В дальнейшем мы введем немного модифицированные, немного не Ньютоновские определения энергии и импульса движущихся частиц.
Комментарии (4)

4erdak
13.05.2018 16:48Отличное поверхностное ознакомление с СТО, только к чему все это было епт, если уже давным давно всем стало ясно, что космологическое красное смещение это никакой нахрен не эффект Доплера и близко, а это аналогия годится разве, что для домохозяек на канале дискавери, где Алекс Филипенко будет втирать, что это долбаный Эффект Доплера. Короче само пространство расширяется, а вместе с ним и электромагнитные волны, постепенно, и расстояние между отдельными фотонами тоже растягиваются за время полета, в результате чего телескопы засекут вспышку сверновой по длительности в z+1 раз дольше чем оно должно быть. Это так называемое кажущееся замедление времени на удаленных обьектах, но в случае СТО, замедление времни совсем не кажущееся, но то такое,


ExtenZ
Шикарный пост, спасибо.