Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Итак, настал момент применить на практике всё то, о чем мы так долго рассуждали теоретически. Данная заметка будет использовать в основном материал предыдущей статьи, в которой есть ссылки на предыдущие публикации по тензорной тематике.
А заниматься мы будем механикой. Именно решение задач механики и побудило меня разбираться с тензорным исчислением. И поговорим мы об уравнениях Лагранжа 2 рода, которые применяются для анализа движения сложных механических систем. Эти уравнения имеют вид, хорошо известный большинству специалистов в данной области
где s — число степеней свободы механической системы;
Те, кто сталкивался с этими уравнениями наверняка замечали, что после выполнения трехкратного дифференцирования кинетической энергии получаются выражения, представленные линейной комбинацией вторых производных от обобщенных координат и линейной комбинации произведений их первых производных. И это, по крайней мере меня, наводило на мысль о том, что кинетическую энергию можно продифференцировать один раз в общем виде, а потом просто составлять уравнения движения, используя полученные выражения общего вида. Только вот попытки проделать это самостоятельно не приводили меня к успеху.
Тем не менее это можно сделать, если опираться на тензорное исчисление, в общем и не прибегая к дифференцированию кинетической энергии (хотя такой подход тоже возможен). И мы сделаем это в данной статье, правда пока только для точки, и заодно решим какую-нибудь не слишком сложную задачку, иллюстрирующую эффективность рассмотренного подхода.
Что же, начнем!
1. Кинематика материальной точки в произвольных координатах
Традиционным при изложении механики является векторный способ задания движения точки

Рис. 1. Векторный способ задания движения точки
При таком способе задания движения положение точки в пространстве определяется радиус-вектором, выпущенном из некоторой точки O, под которой подразумевают тело отсчета. Этот радиус-вектор есть функция времени
Если функция (1) задана, то говорят, что задан закон движения точки. Зная закон движения точки можно получить её скорость и ускорение
Радиус-вектор, скорость и ускорения — это векторы, а значит будем рассматривать их как тензоры ранга (1,0). Кроме того, мы не будем использовать декартову систему координат. Будем использовать криволинейные координаты
где
Определение числа степеней свободы формулируют двояко
Число степеней свободы тела — разность между число зависимых координат n, однозначно задающих положение тела в пространстве и числом уравнений наложенных на тело связей r
Число координат, которым задается положение точки в пространстве n = 3. Если движение точки не ограничено связями, то число степеней свободы будет так же равно трем.
Если же точка движется по некой поверхности, то её движение ограничено — поверхность и есть связь, налагающая условия на декартовы координаты точки. Это условие — уравнение поверхности по которой движется точки и есть уравнение связи. Число степеней свободы такой точки s = 2. Число обобщенных координат тоже будет равно двум — это будут криволинейные координаты, отсчитываемые вдоль поверхности.
Если точка движется по некоторой кривой, то на неё наложено уже две связи — кривая в пространстве задается как линия пересечения двух поверхностей. Число степеней свободы такой точки s = 1, а обобщенная координата — одна — длина дуги, которую прошла точка по кривой.
Таким образом, координаты (3) автоматически учитывают геометрию наложенных на точку связей, что в аналитической механике позволяет исключить из уравнений движения реакции связей.
Другое определения числа степеней свободы таково
Число степеней свободы тела — число независимых параметров, однозначно определяющих положение тела в пространстве
так же включает в себя представление о связях, но в более завуалированной форме.
Будем называть (3) законом движения точки. Зная закон движения, получим векторы скорости и ускорения точки. Продифференцируем по времени радиус-вектор точки
Напомню, что в (4) работает правило Эйнштейна и в правой части выражения производится суммирование по немым индексам i и j. Очевидно, что частная производная
есть контравариантные компоненты вектора скорости. Теперь, чтобы получить вектор ускорения, продифференцируем по времени (4)
Вспоминаем определение ковариантной производной из предыдущей статьи, запишем производную вектора скорости по обобщенной координате (смотрим формулу (33) из предыдущей публикации
где
Подставляем (6) в (5)
В уравнении (7) первое слагаемое в скобках
- вторая производная от обобщенной координаты по времени. С учетом (8) окончательно записываем выражение для контравариантных компонент вектора ускорения точки
2. Возможное перемещение точки
Начнем с определения
Возможным (или кинематически возможным) называется такое перемещение точки, при котором не нарушаются наложенные на точку связи
Это понятие является базовым в аналитической механике. Рассмотрим движение несвободной точки (рисунок 2). Пусть точка движется по поверхности. Её координаты, могут принимать только такие значения, при которых все точки траектории расположены на данной поверхности. Такие координаты называют кинематически возможными, они связаны между собой уравнением поверхности. В этом случае удобно выбрать криволинейные координаты

Рис. 2. Возможное перемещение несвободной точки.
Проварьируем обобщенные координаты, то есть добавим к закону изменения координат бесконечно малую функцию
и вычислим, какое перемещение совершит при этом точка
Вектор
3. Общее уравнение динамики точки
Снова обратимся к рисунку 2. Пусть несвободная точка движется под действием активных сил, равнодействующая которых равна
Умножим (12) скалярно на возможное перемещение точки (11)
Допустим идеальность наложенных на точку связей, что означает, что их реакции не совершают работы на возможном перемещении точки
Это, в принципе, можно допустить всегда. При наличие неидеальных связей, их реакции при определенных условиях можно перевести в разряд активных сил, что усложняет задачу, но не является принципиальным затруднением. Аналитическая механика оперирует данным допущением, мы пойдем тем же путем, положив справедливость (14) и приходя к уравнению
Теперь, как предлагается в соотношении (11), разложим возможное перемещение через вариации обобщенных координат (подразумевая суммирование по повторяющимся индексам)
В выражении (15) слева стоят ковариантные проекции ускорения точки, а справа — ковариантные проекции равнодействующей активных сил
В аналитической механике
Теперь свернем (9) с метрическим тензором, подставляя результат в (16)
В силу независимости вариаций обобщенных координат, коэффициенты при них можно приравнять, получив s (по числу обобщенных координат) уравнений
Вам ничего не напоминает полученное уравнение (18)? Это очень похоже на уравнения движения, которые получаются после взятия всех производных в уравнениях Лагранжа 2 рода. Более того, это и есть уравнения Лагранжа 2 рода — к уравнениям (18) можно придти дифференцируя кинетическую энергию, выразив её через контравариантные компоненты вектора скорости.
Похожим образом в аналитической механике выводят уравнения Лагранжа 2 рода, опираясь на выражение подобное (15), которое по сути есть общее уравнение динамики, записанное в обобщенных силах. Кроме того, уравнение (15) инвариантно относительно преобразования координат, ибо его левая и правая часть — скалярные произведения векторов. А скалярное произведение, как мы помним, есть инвариант относительно изменения базиса.
Таким образом мы получили дифференциальные уравнения движения материальной точки в обобщенных координатах. Теперь применим их для решения известной задачи.
4. Движение точки под действием центральной силы. Уравнение Бине
Рассмотрим движение тяжелой точки в плоскости, под действием силы, направленной радиально из притягивающего/отталкивающего центра O. Данная задача — типичная задача о движении точки в центральном поле и она имеет простое аналитическое решение. Достаточно простое, чтобы попытаться решить её, применяя уравнения (18) и проверить их
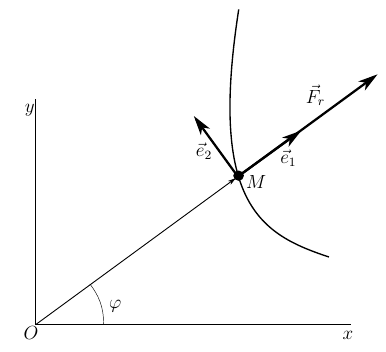
Рис. 3. Движение точки в центральном поле.
Задачу будем решать в полярных координатах
метрика для которых известна (можно посмотреть тут, а можно и получить, но это довольно тривиально)
Для полярных координат нетрудно найти и символы Кристоффеля 2 рода. Пять из них равны нулю, и только три имеют ненулевые значение
Пользуясь этими данными, можно выписать левые части уравнений (18)
Так как сила
То есть получить уравнения движения точки
Уравнение (20) легко интегрируется
причем (21) выражает постоянство секторной скорости, что характерно для движения в центральном поле. Из (21) выразим производную по полярному углу и подставим в (19)
В (22) перейдем от дифференцирования по времени к производной по полярному углу
Подставляем (24) в (22)
И, наконец, умножая обе части (25) на
Данное уравнение известно как дифференциальное уравнение Бине движения точки в центральном поле. Если движение происходит под действием Ньютоновского тяготения, то
И мы получаем общее решение в виде
являющееся уравнение конических сечений (окружностей, эллипсов, парабол и гипербол) в полярных координатах
Заключение
В данной статье показан подход к использованию тензорных соотношений применительно к динамике материальной точки, движение которой может быть описано произвольными обобщенными координатами. Полученные уравнения непосредственно вытекают из общих принципов аналитической механики и равноценны уравнениям Лагранжа 2 рода.
Данный подход может быть применен к описанию движения механической системы. Но об этом я расскажу чуть позже, а пока что спасибо всем кто прочел этот труд за внимание.
Продолжение следует…

