Открывая своё кафе, вы хотели бы узнать ответ на следующий вопрос: «где находится другое, ближайшее к этой точке кафе?» Эта информация помогла бы вам лучше понять ваших конкурентов.

Это пример задачи поиска "ближайшего соседа", которую широко изучают в информатике. Дан набор сведений и новая точка, и требуется найти, к какой точке из уже существующих она окажется ближайшей? Такой вопрос возникает во множестве повседневных ситуаций в таких областях, как исследование генома, поиск картинок и рекомендации на Spotify.

Но, в отличие от примера с кафе, вопросы о ближайшем соседе часто оказываются очень сложными. За последние несколько десятилетий величайшие умы среди специалистов по информатике брались за поиски наилучших способов решения подобной задачи. В частности, они пытались справиться с усложнениями, появляющимися из-за того, что в различных наборах данных могут быть очень разные определения «близости» точек друг к другу.

И вот теперь команда из специалистов по информатике придумала совершенно новый способ решения задачи нахождения ближайшего соседа. В паре работ пять учёных детально описали первый обобщённый метод решения задачи нахождения ближайшего соседа для сложных данных.

«Это первый результат, охватывающий большой набор пространств при помощи единой алгоритмической техники», — сказал Пётр Индик, специалист по информатике из Массачусетского технологического института, влиятельная фигура в области разработок, связанных с этой задачей.

Разница расстояний

Мы так крепко привязаны к единственному способу определения расстояния, что легко упустить из виду возможность существования других способов. Обычно мы измеряем расстояние, как евклидово – как прямую линию между двумя точками. Однако есть ситуации, в которых больше смысла имеют другие определения. К примеру, манхэттенское расстояние заставляет вас делать повороты на 90 градусов, будто перемещаясь по прямоугольной сети дорог. Чтобы измерить такое расстояние, которое по прямой могло бы равняться 5 километрам, вам может потребоваться пересечь город в одном направлении на 3 км, а потом в другом – на 4.

Также возможно рассуждать о расстояниях не в географическом смысле. Каково расстояние между двумя людьми в соцсети, или двумя фильмами, или двумя геномами? В этих примерах расстояние обозначает степень похожести.

Существуют десятки метрик расстояний, каждая из которых подходит к какой-то определенной задаче. Возьмём, к примеру, два генома. Биологи сравнивают их, используя "расстояние Левенштейна", или дистанцию редактирования. Дистанция редактирования между двумя последовательностями генома – это количество добавлений, удалений, вставок и замен, необходимых для превращения одной из них в другую.

Дистанция редактирования и евклидово расстояние – это два различных понятия о расстоянии, и свести одно к другому нельзя. Такая несопоставимость существует для многих пар метрик расстояний, и представляет собой преграду для специалистов по информатике, пытающихся разработать алгоритмы поиска ближайшего соседа. Это означает, что алгоритм, работающий для одного типа расстояний, не будет работать для другого – точнее, так было до сих пор, пока не появился новый вид поиска.


Александр Андони

Квадратура круга

Стандартный подход к поиску ближайшего соседа – разделить существующие данные на подгруппы. Если, допустим, ваши данные описывают расположение коров на пастбище, то вы можете заключить каждую из них в круг. Потом поместим на луг новую корову и зададим вопрос: в какой из кругов она попадает? Практически гарантировано, что ближайший сосед новой коровы окажется в том же самом круге.

Затем повторим процесс. Разделим круги на подкруги, разделим эти ячейки дальше, и так далее. В итоге найдётся ячейка всего с двумя точками: существующей и новой. Эта существующая точка и будет вашим ближайшим соседом.


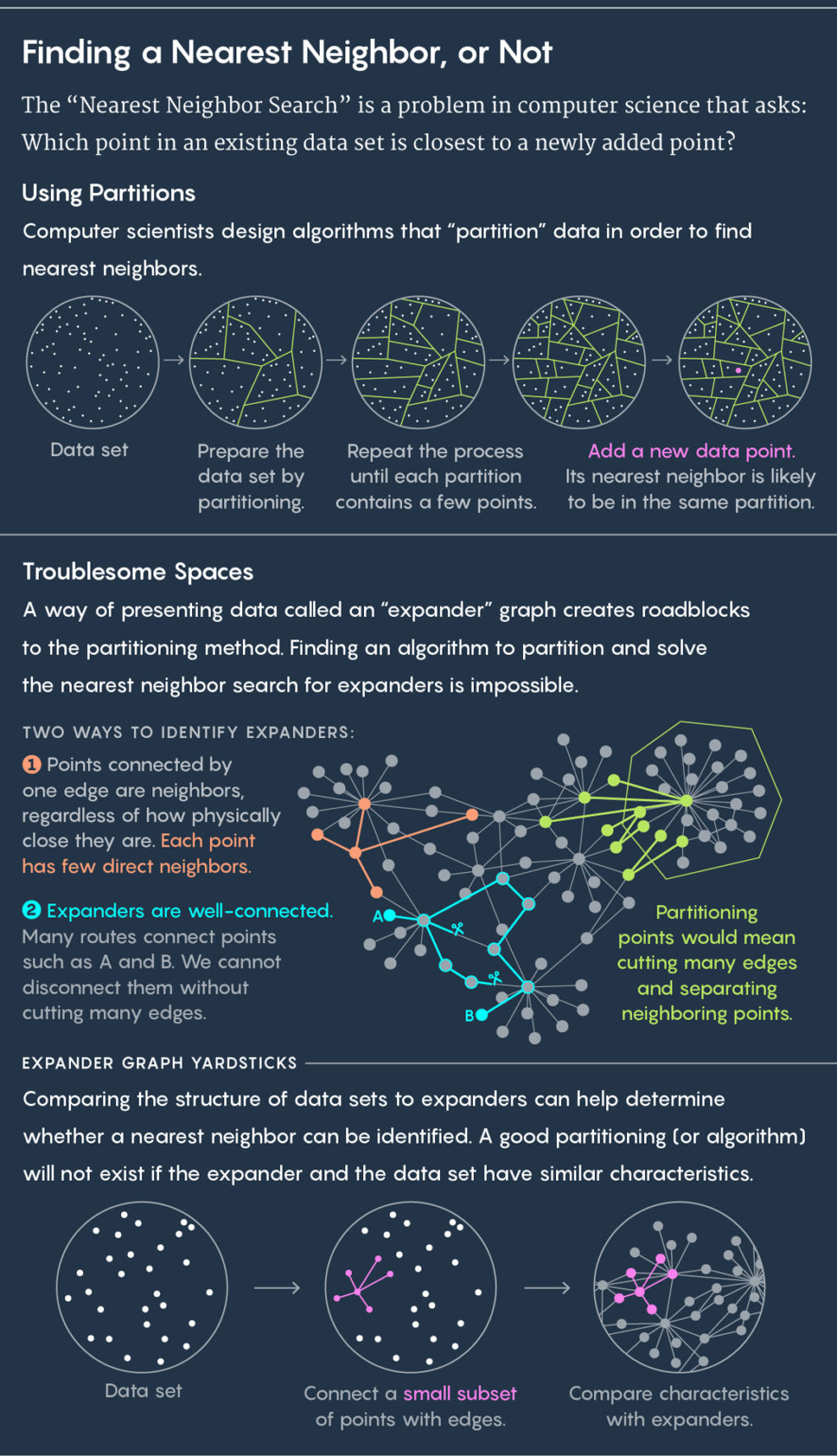
Вверху – разделение данных на ячейки. Внизу – использование расширяющего графа

Алгоритмы рисуют ячейки, хорошие алгоритмы рисуют их быстро и хорошо – то есть так, чтобы не оказалось ситуации, в которой новая корова попадает в круг, а её ближайший сосед оказывается в другом круге. «Мы хотим, чтобы в этих ячейках ближние точки чаще оказывались в одном диске друг с другом, а далёкие – редко», — сказал Илья Разенштейн, специалист по информатике из Microsoft Research, соавтор новой работы, в которой также участвовали Александр Андони из Колумбийского Университета, Ассаф Наор из Принстона, Александр Николов из Университета Торонто и Эрик Вайнгартен из Колумбийского университета.

Многие годы специалисты по информатике придумывали различные алгоритмы по рисованию подобных ячеек. Для маломерных данных – таких, где одна точка определяется небольшим количеством значений, например, расположение коровы на пастбище – алгоритмы создают т.н. "диаграммы Вороного", точно отвечающие на вопрос касательно ближайшего соседа.

Для многомерных данных, у которых одна точка может определяться сотнями или тысячами значений, диаграммы Вороного требуют слишком больших вычислительных мощностей. Вместо этого программисты рисуют ячейки при помощи "локально чувствительного хеширования", впервые описанного Индиком и Радживом Мотвани в 1998. ЛЧХ-алгоритмы рисуют ячейки случайным образом. Поэтому они работают быстрее, но менее точно – вместо того, чтобы находить точного ближайшего соседа, они гарантируют нахождение точки, находящейся не дальше заданного расстояния от реального ближайшего соседа. Это можно представить себе, как рекомендацию фильма от Netflix, которая не идеальна, но достаточно хороша.

С конца 1990-х специалисты по информатике придумали таких ЛЧХ-алгоритмы, которые дают примерные решения для задачи поиска ближайшего соседа для заданных метрик расстояний. Алгоритмы были весьма специализированными, и алгоритм, разработанный для одной метрики расстояний, нельзя было применять для другой.

«Можно придумать очень эффективный алгоритм для евклидового или манхэттенского расстояния, для некоторых специфических случаев. Но у нас не было алгоритма, работавшего бы на большом классе расстояний», — сказал Индик.

Поскольку алгоритмы, работающие с одной метрикой, не получалось использовать для другой, программисты придумали обходную стратегию. Через процесс под названием «встраивание» они накладывали метрику, для которой у них не было хорошего алгоритма, на метрику, для которой он был. Однако соответствие метрик обычно было неточным – что-то типа квадратного колышка в круглом отверстии. В некоторых случаях встраивание вообще не проходило. Было необходимо придумать универсальный способ отвечать на вопрос о ближайшем соседе.


Илья Разенштейн

Неожиданный результат

В новой работе учёные отказались от поиска специальных алгоритмов. Вместо этого они задали более широкий вопрос: что мешает разработать алгоритм на определённой метрике расстояний?

Они решили, что виной тому неприятная ситуация, связанная с расширяющим графом, или экспандером. Экспандер — это особый вид графа, набора точек, соединённых рёбрами. У графов есть своя метрика расстояния. Расстояние между двумя точками графа – это минимальное количество линий, необходимых для того, чтобы пройти из одной точки в другую. Можно представить себе граф, представляющий собой связи между людьми в соцсети, и тогда расстояние между людьми будет равно количеству разделяющих их связей. Если, к примеру, у Джулиан Мур есть френд, у которого есть френд, у которого во френдах состоит Кевин Бэйкон, тогда расстояние от Мур до Бэйкона равняется трём.

Экспандер – особый тип графов, у которого есть два, на первый взгляд, противоречащих друг другу свойства. Он обладает высокой связностью, то есть две точки нельзя разъединить, не разрезав несколько рёбер. В то же время большая часть точек соединена с очень малым количеством других. Из-за этого большая часть точек находится далеко друг от друга.

Уникальная комбинация этих свойств – хорошая связность и малое количество рёбер – приводит к тому, что на экспандерах невозможно провести быстрый поиск ближайшего соседа. Любые попытки разделить его на ячейки будут отделять точки, близко лежащие друг от друга.

«Любой способ разрезания экспандера на две части требует разрезания множества рёбер, что разделяет много близко расположенных вершин», — сказал Вайнгартен, соавтор работы.

К лету 2016 года Андони, Ниоколов, Разенштейн и Ванйгартен знали, что для экспандеров нельзя придумать хорошего алгоритма поиска ближайшего соседа. Но они хотели доказать, что такие алгоритмы невозможно построить для множества других метрик расстояний – метрик, при поиске хороших алгоритмов для которых специалисты по информатике зашли в тупик.

Чтобы найти доказательство невозможности таких алгоритмов, им нужно было найти способ встроить метрику экспандера в другие метрики расстояний. Таким методом они могли определить, что у других метрик имеются свойства, похожие на свойства экспандеров, что и не даёт сделать для них хорошие алгоритмы.


Эрик Вайнгартен

Четыре специалиста по информатике отправились к Ассафу Наору, математику из Принстонского университета, предыдущая работа которого хорошо подходила для темы экспандеров. Они попросили его помочь доказать, что экспандеры можно встроить в различные типы метрик. Наор быстро вернулся с ответом – но не тем, который они от него ждали.

«Мы попросили Ассафа помочь нам с этим утверждением, а он доказал обратное», — сказал Андони.

Наор доказал, что экспандеры не встраиваются в большой класс метрик расстояний, известных, как "нормированные пространства" (куда входят и такие метрики, как евклидово и манхэттенское пространство). Опираясь на доказательства Наора, учёные последовали по следующей логической цепочке: если экспандеры не встраиваются в метрику расстояний, тогда должен быть хороший способ разбивать их на ячейки (поскольку, как они доказали, единственной преградой для этого служат свойства экспандеров). Поэтому должен существовать хороший алгоритм поиска ближайшего соседа – даже если его ещё пока никто не нашёл.

Пять исследователей опубликовали свои результаты в работе, которую они завершили в ноябре и выложили в апреле. За ней последовала вторая работа, которую они закончили в этом году и опубликовали в августе. В ней они использовали информацию, полученную при написании первой работы, чтобы найти быстрый алгоритм поиска ближайшего соседа для нормированных пространств.

«Первая работа продемонстрировала существование способа разбиения метрики на две части, но в ней не было рецепта того, как это сделать быстро, — сказал Вайнгартен. – Во второй работе мы утверждаем, что существует способ разделять точки, и кроме того, что это разделение можно сделать при помощи быстрых алгоритмов».

В итоге новые работы впервые обобщают поиск ближайшего соседа в многомерных данных. Вместо того, чтобы разрабатывать специализированные алгоритмы для определённых метрик, у программистов появился универсальный подход для поиска алгоритмов.

«Это упорядоченный метод разработки алгоритмов поиска ближайшего соседа в любой из нужных вам метрик расстояний», — сказал Вайнгартен.