Крупным математическим достижением стало доказательство гипотезы Циммера, найденное небольшой командой исследователей

У решёток в высших измерениях симметрии не всегда можно перенести в измерения ниже рангом

Успех Роберта Циммера можно определить по-разному. В качестве президента Чикагского университета с 2006 года он попал в заголовки газет, находя девятизначные суммы для финансирования и публикуя статьи в поддержку свободы слова на кампусе. Но до того, как стать президентом университета, он был математиком. И спустя много времени после того, как он оставил серьёзные исследования, запущенный им исследовательский план, наконец, даёт свои результаты.

Год назад три математика доказали гипотезу Циммера, связанную с обстоятельствами, при которых геометрические пространства обладают симметриями определённого типа. Их доказательство стало одним из крупнейших математических достижений в последние годы. Оно ставит точку в вопросе, вставшем перед Циммером в период его интенсивной умственной деятельности в конце 1970-х и начале 1980-х.

«Я бы сказал, что лет пять ложился спать с мыслями об этой задаче, каждую ночь, так что я был ею одержим, и здорово наблюдать, как люди её решили», — сказал Циммер.

Обычно, чем больше у геометрического пространства измерений, тем больше в нём может быть симметрий. Это можно представить, изучая окружность, существующую на двумерной плоскости, и шар, простирающийся в три измерения: способов вращения шара существует больше, чем способов вращения окружности. Дополнительные измерения шара создают дополнительные симметрии.

Гипотеза Циммера относится к симметриям особого вида, известным, как высокоранговые решётки. Она задаёт вопрос, ограничивает ли измерение геометрического пространства применение симметрий этого типа. Авторы новой работы – Аарон Браун и Себастьян Хуртадо-Салазар из Чикагского университета и Дэвид Фишер из Университета Индианы –показали, что при количестве измерений меньше определённого особых симметрий не наблюдается. Таким образом, они доказали правильность гипотезы Циммера.


Роберт Циммер, ныне президент Чикагского университета, разработал гипотезу, названную в его честь, почти 40 лет назад

Их работа отвечает на один важный и давно висевший вопрос, открывая новые способы исследования множества других. Она также открывает внутренние свойства геометрических пространств. Симметрия – одно из наиболее простых свойств подобных пространств. В новой работе говорится, что симметрии могут существовать в пространствах одного типа, и не могут – в других. Это достижение было получено после десятилетий простоя.

«Гипотеза выглядела так, будто способна занять людей на очень долгое время», — сказал Эйми Вилкинсон, математик из Чикагского университета, организовавший в этом году конференцию, посвящённую этому доказательству. «И они относительно просто уничтожили этот вопрос».

Удовлетворяя симметриям

Симметрия – одна из первых геометрических концепций, с которой дети сталкиваются в математике. Собственноручно они узнают, что можно повернуть, перевернуть и сдвигать форму, и в итоге получить ту же самую форму, с которой начали. Сохранение формы объекта в результате изменений отзывается определённым внутренним удовлетворением – это намёк на наличие более глубокого порядка во Вселенной.

У математиков есть свой формальный язык для изучения симметрии. Он даёт им возможность в сжатых терминах рассуждать о различных симметриях, применимых в заданном геометрическом пространстве.

У квадрата, к примеру, есть восемь симметрий – восемь способов перевернуть или повернуть его, снова получив квадрат. Окружность же можно повернуть на любое количество градусов; у неё бесконечное количество симметрий. Математики собирают все симметрии данного геометрического объекта, или пространства, и упаковывают их в «группу».

Группы интересны сами по себе. Они часто появляются в результате изучения определённых геометрических пространств, но иногда появляются и в совершенно не связанном с геометрией контексте. К примеру, группы могут формировать числовые множества (к примеру, есть определённая симметрия в том, чтобы добавить 5 или отнять 5 от числа).

«Группа, в принципе, может появиться как симметрия совершенно разных вещей», — сказал Циммер.

Существуют и более экзотические виды симметрии, чем те, что мы изучаем в школе. Рассмотрим, к примеру, симметрию решёток. Простейшая решётка – это двумерная сетка. На плоскости решётку можно сдвигать вверх, вниз, влево, вправо на любое количество квадратов, и получить решётку, которая выглядит точно так же, как исходная. Также можно отражать решётку через любое количество отдельных клеточек. Пространства с решётками обладают бесконечным количеством различных симметрий решёток.



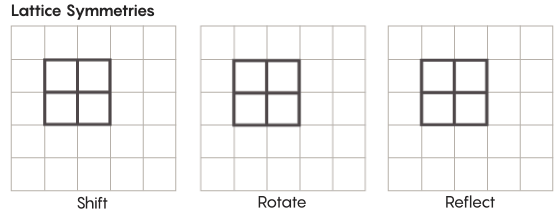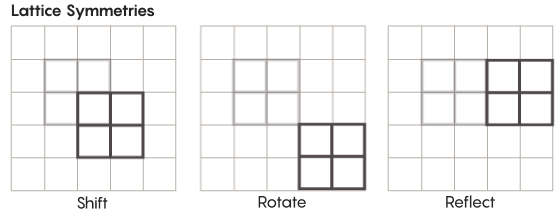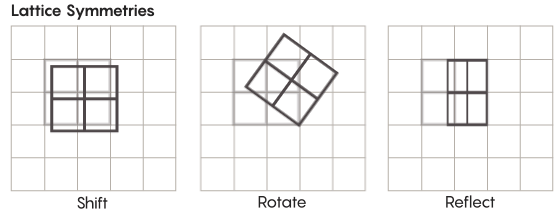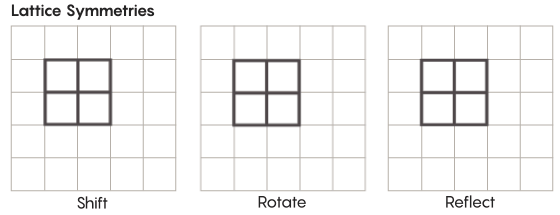
Решётки могут существовать в любом количестве измерений. В трёхмерном пространстве решётка может состоять из кубов, а не из квадратов. В четырёх и более измерениях представить решётку уже не получится, но работает она точно так же; математики могут описать её совершенно точно. Интересующие гипотезу Циммера группы включают в себя решётки «высшего ранга», или решётки в определённых пространствах высших измерений. «Эта странная решётка была бы очень красивой, если бы её можно было увидеть, пусть мне это и не дано, — сказал Хуртадо-Салазар. – Мне кажется, что смотреть на неё было бы очень приятно».

В XX-м веке математики обнаружили эти группы в различных условиях – не только в геометрии, но и в теории чисел, логике и информатике. Открывая новые группы, логично задать вопрос – какого рода пространства обладают такими наборами симметрий?

Иногда группы очевидно невозможно сопоставить пространству. Можно довольно быстро понять, что группу симметрий окружности нельзя применить к квадрату. Поверните квадрат на 10 градусов, и вы не получите исходный квадрат. Но смесь группы с бесконечным количеством симметрий и пространства со многими измерениями затрудняет определение применимости группы.

«При переходе к более сложным группа в большем количестве измерений, — сказал Циммер, — эти вопросы сильно усложняются».

Непрямая связь

Представляя себе симметрию, мы представляем вращение целиком формы – например, квадрат, повёрнутый на 90 градусов. Но на базовом уровне симметрия зависит от движущихся точек. Симметричное преобразование пространства означает, что нужно взять каждую его точку и передвинуть в какую-то другую точку. В этом смысле поворот квадрата на 90 градусов на самом деле означает, что надо взять каждую точку квадрата, и повернуть её на 90 градусов так, чтобы она оказалась не на том ребре, с которого начала.


Дэвид Фишер

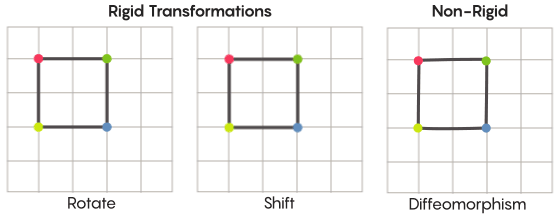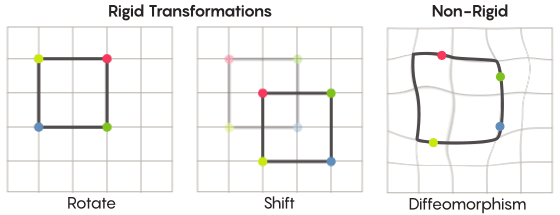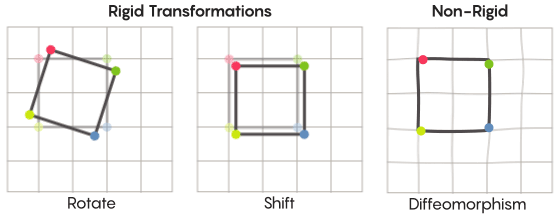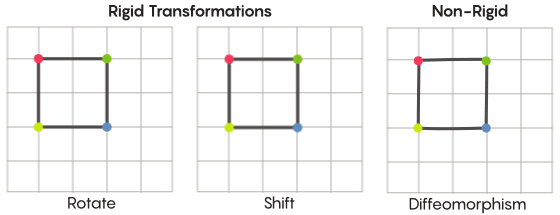
Задачу передвижения точек можно решить более или менее строго. Наиболее знакомые нам симметричные преобразования – отражение квадрата относительно диагонали или поворот его на 90 градусов – весьма строги. Строги в том смысле, что они не перепутывают точки. Точки, бывшие до отражения вершинами, остаются вершинами и после (они просто становятся другими вершинами), а точки, составлявшие прямые рёбра, после отражения всё ещё составляют прямые рёбра (просто другие).

Есть менее строгие, более гибкие виды симметричных преобразований, и именно они интересны в контексте гипотезы Циммера. В таких преобразованиях точки сильнее меняют свою организацию; они не обязательно сохраняют свои прежние связи друг с другом после трансформации. К примеру, можно сдвинуть каждую точку квадрата на три единицы длины по периметру квадрата – это удовлетворяет базовым требованиям симметричного преобразования, то есть, просто сдвига каждой точки в пространстве на другое место. Аарон Браун, соавтор доказательства, описал, как эти, более свободные виды преобразований, могли бы выглядеть в контексте мяча.

«Можно взять северный и южный полюса и перекрутить их в противоположных направлениях. Тогда расстояния между точками увеличатся», — сказал Браун.

В случае сетки, вместо простого сдвига её по плоскости, вы можете искривить её, растянуть в одних местах и сжать в других, так, что преобразованная сетка уже не накладывается на исходную. Такие преобразования менее строги, и называются диффеоморфизмами.



У Циммера были уважительные причины использовать эту, менее строгую версию симметрии в своей гипотезе. Особые решётки высшего ранга, имеющие отношение к этой гипотезе, впервые изучал в 1960-х Григорий Александрович Маргулис, получивший за свою работу Филдсовскую премию. Маргулис составил полное описание того, пространства какого рода можно преобразовывать при помощи этих решёток высшего ранга, если разрешить только строгие преобразования.

Гипотеза Циммера стала естественным продолжением работы Маргулиса. Она начинается со списка пространств, на которых могут работать решётки высшего ранга – этот список обнаружил Маргулис – и спрашивает, расширяется ли этот список, если позволить решёткам менее строгие трансформации.

В новой работе три математика доказали, что ослабление определения симметрии не меняет область применения симметрий решёток высшего ранга. Даже если позволить решёткам весьма нерегулярные преобразования – сдвигаться, изгибаться, растягиваться – решётки всё равно имеют жёсткое ограничение области действия.

«После добавления такой гибкости в условие задачи, интуитивно, конечно, кажется, что решётки смогут действовать шире. Поэтому оказывается удивительным, что на самом деле ответ будет „нет“ – в некоторых случаях не могут», — сказал Фишер.

Математики установили точные соответствия между размерностью пространства и размерностью, или рангом, решёток, для решёток, способных играть роль симметрии в данном пространстве. В целом они показали, что чем выше ранг решётки, тем больше измерений надо пространству, способному её вместить. Даже имея значительную гибкость в деле преобразования пространства, преобразования высокоранговых решёток ограничены высшими измерениями.

«Это говорит о том, что существует нечто весьма фундаментальное в строении пространств, из чего следует их возможность вмещать подобные преобразования», — сказал Уилкинсон.

Гипотеза Циммера – всего лишь первый шаг к более крупной программе. Разобравшись с ней, соавторы работы наложили грубое ограничение на пространства, в которых можно преобразовывать высокоранговые решётки. Следующей, более амбициозной фазой работы будет концентрация на тех пространствах, в которых могут существовать решётки – а потом и классификация всех разных способов преобразования решётками этих пространств.

«В итоге программа должна суметь классифицировать все эти способы. Есть много интересных вопросов за пределами простого установления факта существования определённых мест, в которых решётки не могут действовать», — сказал Циммер.