Уже давно известное быстрое преобразование Фурье используется не только для решения задач цифровой обработки сигналов, распознавания объектов на изображении, но и в компьютерной графике. Джерри Тессендорфом была описана математическая модель, позволяющая синтезировать океанские волны и анимировать их в реальном времени. В основе этой модели лежит двумерное БПФ.
Когда мне была поставлена задача разработать приложение для DSP-процессора, визуализирующее работу БПФ, я понял, что моделирование волн отлично подойдет для этой цели.

Основную идею математической модели волны можно описать таким выражением:
= FFT2D( ), FFT2D обозначим как оператор двумерного БПФ.
— это поле высот водной поверхности (матрица размером , где и могут принимать значения степеней двойки). Элементы этой матрицы являются высотами волн.
– сигнал (матрица размером ), сгенерированный по определенному закону и зависящий от времени.
, где элементы матрицы это , а матрица — комплексно-сопряженная к матрица,
– это элементы матрицы .
— поэлементное умножение матриц.
— поле высот в начальный момент времени t = 0.
— комплексно-сопряженная к матрица (размером ).
Для создания анимации движения волн в реальном времени необходимо пересчитывать матрицы и , меняя t. Матрицы , и вычисляются один раз и переиспользуются.
Теперь перейдем к описанию DSP-процессора, которому, исходя из вышеописанных формул, нужно уметь:
В качестве DSP-процессора использовался 1879ВМ6Я на архитектуре NeuroMatrix, разработанный в компании ЗАО НТЦ «Модуль». Схема на рисунке 1.
Процессор содержит 2 параллельно работающих ядра NMPU0 и NMPU1 (работают на частоте 500 МГц), каждое из которых имеет RISC процессор и векторный сопроцессор (NMCore FPU для плавающей точки и NMCore INT для целочисленной арифметики). Ядро NMPU0 предназначено для обработки данных с плавающей точкой, а NMPU1 – целочисленных данных. NMPU0 имеет 8 банков внутренней памяти SRAM (по 128 кБ каждый), а NMPU1 – 4 банка (по 128 кБ) такой же памяти. На 1879ВМ6Я установлен контроллер DMA и интерфейс DDR2.
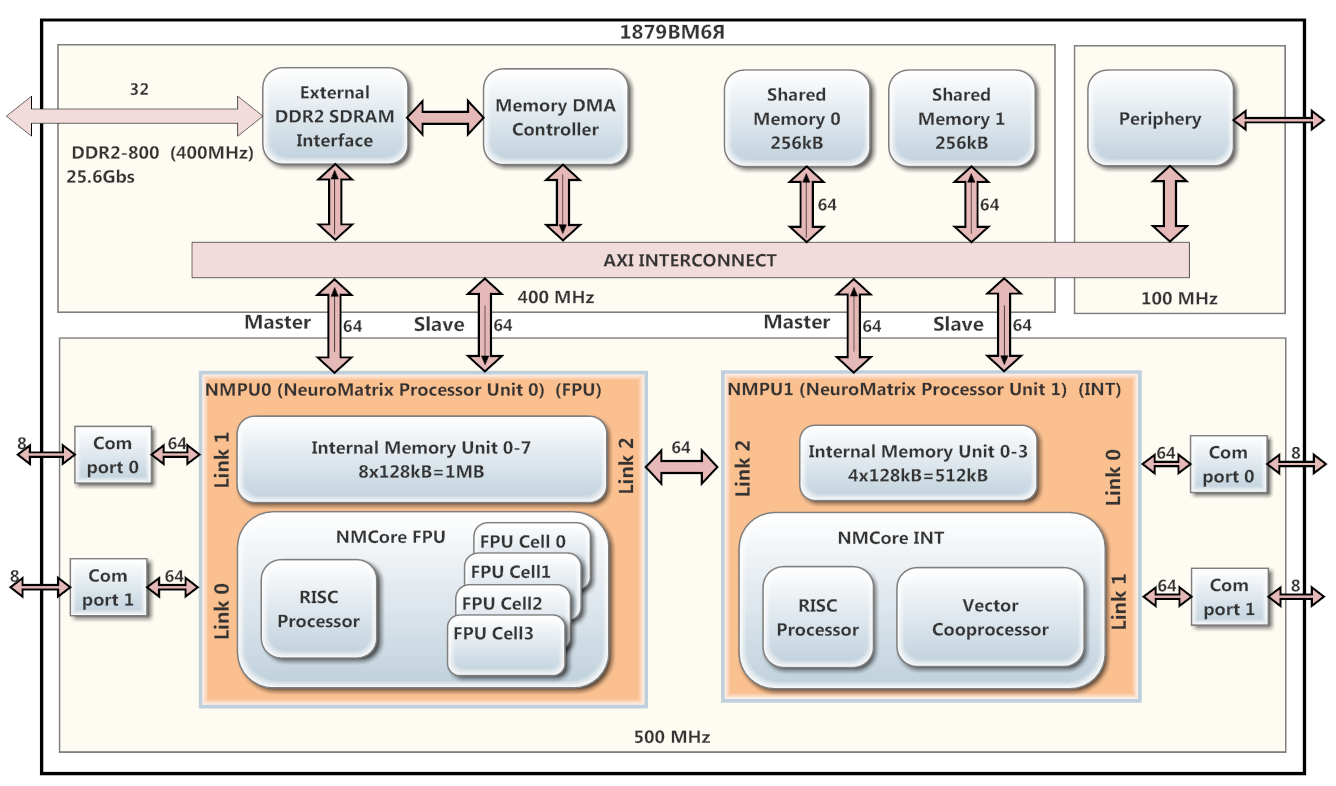
Рис. 1. Схема процессора 1879ВМ6Я
Процессор размещен на инструментальном модуле МС121.01 (см. рис. 2). Также на этом модуле имеется 512 МБ памяти DDR2.

Рис.2. МС121.01
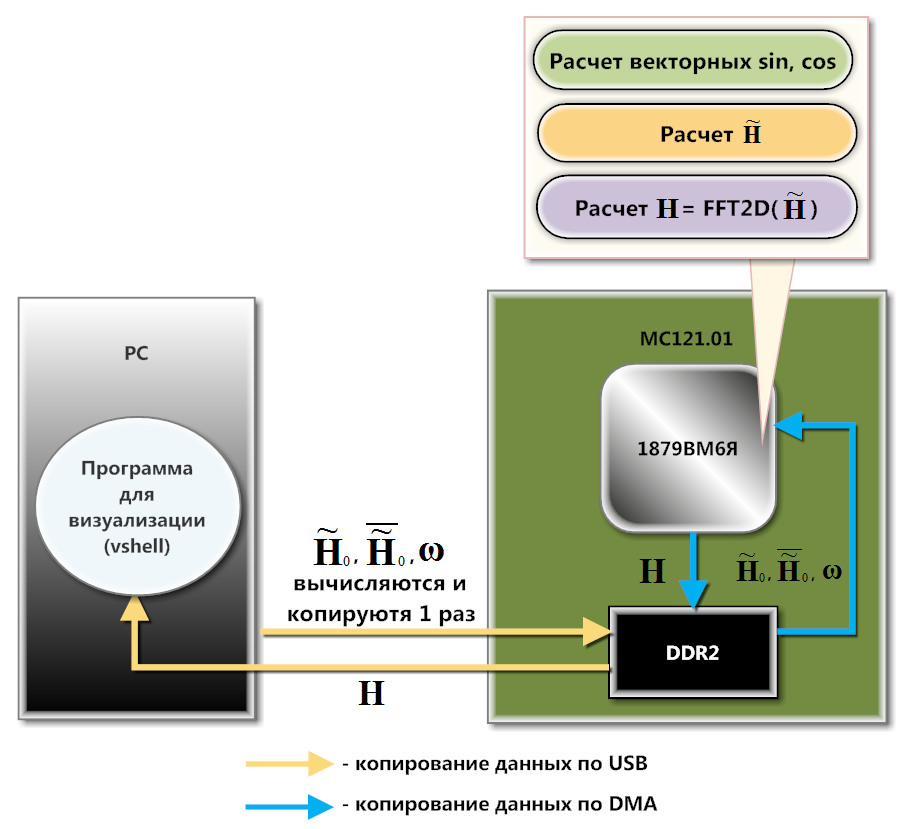
Рис. 3. Схема взаимодействия МС121.01 и PC
МС121.01 взаимодействует с PC по USB (схема на рисунке 3). На программном уровне это взаимодействие организуется с помощью библиотеки загрузки и обмена данными, которая входит в состав SDK этой платы. Заранее вычисленные матрицы , и загружаются в память DDR2 посредством функций библиотеки загрузки и обмена. DMA-контроллер копирует , и построчно во внутреннюю память (SRAM) процессора. Загрузка в DDR2 обусловлена тем, что в SRAM полностью не помещается ни одна из этих матриц. Построчное копирование здесь имеет место, потому что 1879ВМ6Я производит вычисления из SRAM быстрее, чем из DDR2. Причем, существенную часть вычислений можно сделать на фоне работы DMA.
Используя векторные функции библиотеки NMPP для вычисления синусов, косинусов, умножения и сложения векторов, процессор рассчитывает строки матрицы и берет от них одномерное БПФ. Результат отправляется по DMA назад в DDR2. Так в DDR2 формируется промежуточная матрица, от столбцов которой процессор вычисляет одномерное БПФ (предварительно загрузив столбцы промежуточной матрицы по DMA в SRAM). Таким образом в DDR2 формируется матрица . Эта матрица выгружается в PC для отрисовки одного кадра с изображением волновой поверхности. Для анимации картинки в реальном времени нужно по описанному выше алгоритму вычислять матрицу , увеличивая параметр t.
На практике получается, что 1879ВМ6Я вычисляет матрицу быстрее, чем PC ее выкачивает. Из-за этого процессор может простаивать, ожидая, когда PC заберет очередную порцию данных. Решить эту проблему удалось с помощью кольцевого буфера (вмещающего несколько матриц ), организованного в DDR2 памяти платы.
На программном уровне работа с контроллером DMA и кольцевым буфером осуществляется с помощью функций библиотеки HAL (Hardware abstraction Level) для процессоров NeuroMatrix.
Когда матрица поля высот загружена в память PC, можно визуализировать поверхность. Чтобы отобразить ее более понятно, нужно координаты x, y, z, описывающие точки поверхности, умножить на матрицу поворота. Так мы получим новые координаты поверхности x’, y’, z’, повернув ее на определенный угол.
Масштабируя новые координаты и соединяя по ним точки прямыми линиями, можно увидеть анимацию океанских волн (см. на видео ниже). Для визуализации поверхности использовалась библиотека вывода изображения на экран vshell.
В заключение, хочется сказать, что на вычисление и передачу по USB одной матрицы размером 256x256 чисел float тратится ~4.7 млн. тактов (72 такта на float). При этом частота кадров равна ~107. Если не брать в расчет время, затраченное на передачу данных по USB, то вычисления будут стоить ~2.5 млн. тактов (38 тактов на float). Это суммарное время, затраченное процессором 1879ВМ6Я, на поэлементные умножения и сложения матриц, вычисления БПФ, синусов, косинусов и копирования с помощью DMA. Эти вычисления выполняются на фоне передачи данных по USB.
Разница в 2.2 млн. тактов (4.7 млн. — 2.5 млн. = 2.2 млн.) говорит о том, что в системе PC – МС121.01 USB является «бутылочным горлышком», и 1879ВМ6Я можно нагрузить расчетами на 46% больше, не получив просадку FPS.
Также хочется отметить, что на фоне передачи данных по USB и вычислений на сопроцессоре для плавающей точки, может быть задействован сопроцессор для целочисленной арифметики, который в этой задаче не использовался.
В таблице приведена производительность некоторых векторных функций библиотеки nmpp.
NMPP — библиотека примитивов для архитектуры NeuroMatrix
HAL — библиотека абстракции аппаратно-зависимой части NeuroMatrix
VSHELL — библиотека обработки и вывода на экран изображения
Когда мне была поставлена задача разработать приложение для DSP-процессора, визуализирующее работу БПФ, я понял, что моделирование волн отлично подойдет для этой цели.

Математическая модель волны
Основную идею математической модели волны можно описать таким выражением:
= FFT2D( ), FFT2D обозначим как оператор двумерного БПФ.
— это поле высот водной поверхности (матрица размером , где и могут принимать значения степеней двойки). Элементы этой матрицы являются высотами волн.
– сигнал (матрица размером ), сгенерированный по определенному закону и зависящий от времени.
, где элементы матрицы это , а матрица — комплексно-сопряженная к матрица,
– это элементы матрицы .
— поэлементное умножение матриц.
— поле высот в начальный момент времени t = 0.
— комплексно-сопряженная к матрица (размером ).
Для создания анимации движения волн в реальном времени необходимо пересчитывать матрицы и , меняя t. Матрицы , и вычисляются один раз и переиспользуются.
Теперь перейдем к описанию DSP-процессора, которому, исходя из вышеописанных формул, нужно уметь:
- Вычислять БПФ.
- Поэлементно умножать матрицы.
- Складывать матрицы.
- Вычислять вектора синусов и косинусов.
В качестве DSP-процессора использовался 1879ВМ6Я на архитектуре NeuroMatrix, разработанный в компании ЗАО НТЦ «Модуль». Схема на рисунке 1.
Процессор содержит 2 параллельно работающих ядра NMPU0 и NMPU1 (работают на частоте 500 МГц), каждое из которых имеет RISC процессор и векторный сопроцессор (NMCore FPU для плавающей точки и NMCore INT для целочисленной арифметики). Ядро NMPU0 предназначено для обработки данных с плавающей точкой, а NMPU1 – целочисленных данных. NMPU0 имеет 8 банков внутренней памяти SRAM (по 128 кБ каждый), а NMPU1 – 4 банка (по 128 кБ) такой же памяти. На 1879ВМ6Я установлен контроллер DMA и интерфейс DDR2.

Рис. 1. Схема процессора 1879ВМ6Я
Процессор размещен на инструментальном модуле МС121.01 (см. рис. 2). Также на этом модуле имеется 512 МБ памяти DDR2.

Рис.2. МС121.01

Рис. 3. Схема взаимодействия МС121.01 и PC
МС121.01 взаимодействует с PC по USB (схема на рисунке 3). На программном уровне это взаимодействие организуется с помощью библиотеки загрузки и обмена данными, которая входит в состав SDK этой платы. Заранее вычисленные матрицы , и загружаются в память DDR2 посредством функций библиотеки загрузки и обмена. DMA-контроллер копирует , и построчно во внутреннюю память (SRAM) процессора. Загрузка в DDR2 обусловлена тем, что в SRAM полностью не помещается ни одна из этих матриц. Построчное копирование здесь имеет место, потому что 1879ВМ6Я производит вычисления из SRAM быстрее, чем из DDR2. Причем, существенную часть вычислений можно сделать на фоне работы DMA.
Используя векторные функции библиотеки NMPP для вычисления синусов, косинусов, умножения и сложения векторов, процессор рассчитывает строки матрицы и берет от них одномерное БПФ. Результат отправляется по DMA назад в DDR2. Так в DDR2 формируется промежуточная матрица, от столбцов которой процессор вычисляет одномерное БПФ (предварительно загрузив столбцы промежуточной матрицы по DMA в SRAM). Таким образом в DDR2 формируется матрица . Эта матрица выгружается в PC для отрисовки одного кадра с изображением волновой поверхности. Для анимации картинки в реальном времени нужно по описанному выше алгоритму вычислять матрицу , увеличивая параметр t.
На практике получается, что 1879ВМ6Я вычисляет матрицу быстрее, чем PC ее выкачивает. Из-за этого процессор может простаивать, ожидая, когда PC заберет очередную порцию данных. Решить эту проблему удалось с помощью кольцевого буфера (вмещающего несколько матриц ), организованного в DDR2 памяти платы.
На программном уровне работа с контроллером DMA и кольцевым буфером осуществляется с помощью функций библиотеки HAL (Hardware abstraction Level) для процессоров NeuroMatrix.
Визуализация волновой поверхности
Когда матрица поля высот загружена в память PC, можно визуализировать поверхность. Чтобы отобразить ее более понятно, нужно координаты x, y, z, описывающие точки поверхности, умножить на матрицу поворота. Так мы получим новые координаты поверхности x’, y’, z’, повернув ее на определенный угол.
Масштабируя новые координаты и соединяя по ним точки прямыми линиями, можно увидеть анимацию океанских волн (см. на видео ниже). Для визуализации поверхности использовалась библиотека вывода изображения на экран vshell.
Заключение
В заключение, хочется сказать, что на вычисление и передачу по USB одной матрицы размером 256x256 чисел float тратится ~4.7 млн. тактов (72 такта на float). При этом частота кадров равна ~107. Если не брать в расчет время, затраченное на передачу данных по USB, то вычисления будут стоить ~2.5 млн. тактов (38 тактов на float). Это суммарное время, затраченное процессором 1879ВМ6Я, на поэлементные умножения и сложения матриц, вычисления БПФ, синусов, косинусов и копирования с помощью DMA. Эти вычисления выполняются на фоне передачи данных по USB.
Разница в 2.2 млн. тактов (4.7 млн. — 2.5 млн. = 2.2 млн.) говорит о том, что в системе PC – МС121.01 USB является «бутылочным горлышком», и 1879ВМ6Я можно нагрузить расчетами на 46% больше, не получив просадку FPS.
Также хочется отметить, что на фоне передачи данных по USB и вычислений на сопроцессоре для плавающей точки, может быть задействован сопроцессор для целочисленной арифметики, который в этой задаче не использовался.
В таблице приведена производительность некоторых векторных функций библиотеки nmpp.
| Функция | Такты |
|---|---|
| Одномерное БПФ, 256 точек | 1770 |
| Синус, 256 точек | 1400 |
| Косинус, 256 точек | 1400 |
Ссылки:
NMPP — библиотека примитивов для архитектуры NeuroMatrix
HAL — библиотека абстракции аппаратно-зависимой части NeuroMatrix
VSHELL — библиотека обработки и вывода на экран изображения
Комментарии (2)

diktomus Автор
04.12.2018 17:51Это матрица частот. Ее элементы можно найти так: ?_ij = sqrt(g * k_ij), g — это гравитационная постоянная, а k_ij — это длины волновых векторов


Jeka178RUS
А что есть матрица омега?