
17 млрд событий, 60 млн пользовательских сессий и огромное количество виртуальных свиданий происходят в Badoo ежедневно. Каждое событие аккуратно сохраняется в реляционные базы данных для последующего анализа на SQL и не только.
Современные распределённые транзакционные базы данных с десятками терабайт данных — настоящее чудо инженерной мысли. Но SQL как воплощение реляционной алгебры в большинстве стандартных реализаций пока не позволяет формулировать запросы в терминах упорядоченных кортежей.
В последней статье из серии, посвящённой виртуальным машинам, я расскажу про альтернативный подход к поиску интересных сессий — движок регулярных выражений («Поросячий Матчер»), определённых для последовательностей событий.
Виртуальная машина, байт-код и компилятор прилагаются бесплатно!
О событиях и сессиях
Предположим, у нас уже есть хранилище данных, позволяющее быстро и последовательно просматривать события каждой из пользовательских сессий.
Мы хотим находить сессии по запросам вроде «посчитать все сессии, где имеется указанная подпоследовательность событий», «найти части сессии, описанные заданным шаблоном», «вернуть ту часть сессии, которая случилась после заданного шаблона» или «посчитать, сколько сессий достигли определённых частей шаблона». Это может пригодиться для самых разных типов анализа: поиск подозрительных сессий, вороночный анализ и т. д.
Искомые подпоследовательности надо как-то описывать. В самой простой форме эта задача похожа на поиск подстроки в тексте; нам же хочется иметь инструмент помощнее — регулярные выражения. Современные реализации движков регулярных выражений чаще всего используют (вы угадали!) виртуальные машины.
Созданием небольших виртуальных машинок для сопоставления сессий с регулярными выражениями мы и займёмся ниже. Но для начала уточним определения.
Событие состоит из типа события, времени, контекста и набора атрибутов, специфичных для каждого из типов.
Тип и контекст каждого из событий это целые числа из предопределенных списков. Если с типами событий все понятно, то контекст это, например, номер экрана, на котором произошло заданное событие.
Атрибут события это произвольное целое число, смысл которого определяется типом события. Атрибутов у события может не быть, или их может быть несколько..
Сессия — это последовательность событий, отсортированных по времени.
Но давайте, наконец, перейдём к делу. Гул, как говорится, затих, а я вышел на подмостки.
Сравниваем по бумажке
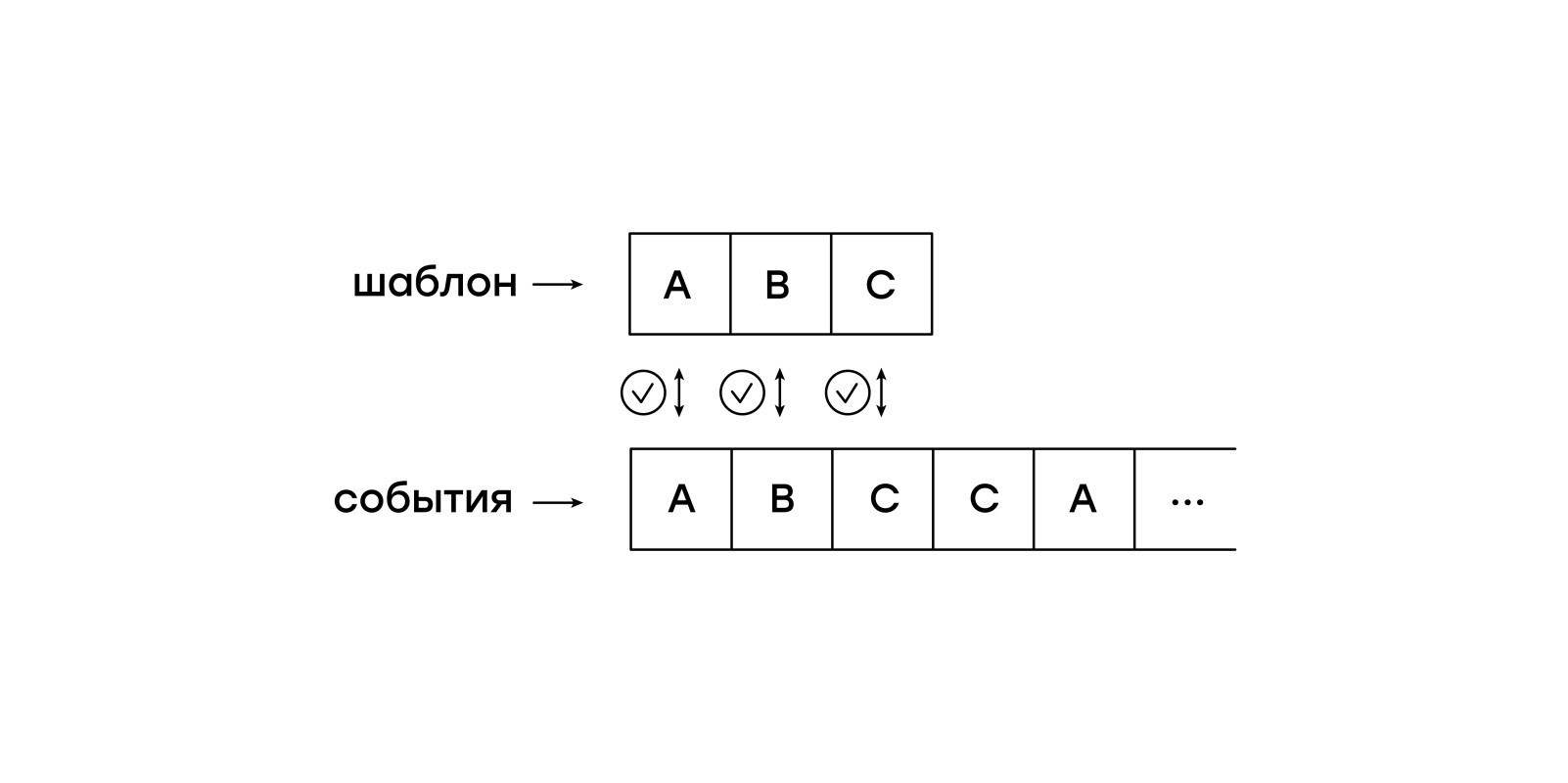
Особенность данной виртуальной машины — пассивность по отношению к входным событиям. Мы не хотим держать всю сессию в памяти и позволять виртуальной машине самостоятельно переходить от события к событию. Вместо этого мы будем одно за другим подавать события из сессии в виртуальную машинку.
Определимся с интерфейсными функциями:
matcher *matcher_create(uint8_t *bytecode);
match_result matcher_accept(matcher *m, uint32_t event);
void matcher_destroy(matcher *matcher);
Если с функциями matcher_create и matcher_destroy всё понятно, то matcher_accept стоит прокомментировать. Функция matcher_accept получает на вход экземпляр виртуальной машины и очередное событие (32 бита, где 16 бит — на тип события и 16 бит — на контекст), а возвращает код, поясняющий, что пользовательскому коду делать дальше:
typedef enum match_result {
// подать на вход еще одно событие
MATCH_NEXT,
// успешно найден искомый шаблон, события больше можно не подавать
MATCH_OK,
// текущая сессия не похожа на искомый шаблон, события можно больше не подавать
MATCH_FAIL,
// внутренняя ошибка в коде
MATCH_ERROR,
} match_result;
Опкоды виртуальной машины:
typedef enum matcher_opcode {
// нулевой опкод, сразу останавливает выполнение с ошибкой
OP_ABORT,
// проверить тип текущего события тип (аргумент - искомый тип)
OP_NAME,
// проверить контекст текущего события (аргумент - искомый контекст)
OP_SCREEN,
// запросить следующее событие
OP_NEXT,
// успешно завершить поиск
OP_MATCH,
} matcher_opcode;
Главный цикл виртуальной машины:
match_result matcher_accept(matcher *m, uint32_t next_event)
{
#define NEXT_OP() (*m->ip++)
#define NEXT_ARG() ((void)(m->ip += 2), (m->ip[-2] << 8) + m->ip[-1])
for (;;) {
uint8_t instruction = NEXT_OP();
switch (instruction) {
case OP_ABORT:{
return MATCH_ERROR;
}
case OP_NAME:{
uint16_t name = NEXT_ARG();
if (event_name(next_event) != name)
return MATCH_FAIL;
break;
}
case OP_SCREEN:{
uint16_t screen = NEXT_ARG();
if (event_screen(next_event) != screen)
return MATCH_FAIL;
break;
}
case OP_NEXT:{
return MATCH_NEXT;
}
case OP_MATCH:{
return MATCH_OK;
}
default:{
return MATCH_ERROR;
}
}
}
#undef NEXT_OP
#undef NEXT_ARG
}В этом простеньком варианте наша виртуальная машина последовательно сопоставляет шаблон, описанный байт-кодом, со входящими событиями. В таком виде это просто не слишком лаконичное сопоставление префиксов двух строк: искомого шаблона и входной строки.
Префиксы префиксами, но мы хотим находить искомые шаблоны не только в начале, но и в произвольном месте сессии. Наивное решение — перезапуск сопоставления с каждого события сессии. Но это подразумевает многократный просмотр каждого из событий и поедание алгоритмических младенцев.
Пример из первой статьи серии, в сущности, имитирует перезапуск сопоставления при помощи отката (англ. backtracking). Код в примере выглядит, конечно, стройней приведённого здесь, но проблема никуда не делась: каждое из событий придётся проверить многократно.
Так жить нельзя.
Я, еще раз я и снова я

Давайте ещё раз обозначим задачу: надо сопоставлять шаблон со входящими событиями, от каждого из событий начиная новое сопоставление. Так почему бы нам именно это и не делать? Пускай виртуальная машина ходит по входящим событиям в несколько потоков!
Для этого нам потребуется завести новую сущность — поток. Каждый поток хранит единственный указатель — на текущую инструкцию:
typedef struct matcher_thread {
uint8_t *ip;
} matcher_thread;
Естественно, и в самой виртуальной машине мы теперь явный указатель хранить не будем. Его заменят два списка потоков (о них чуть ниже):
typedef struct matcher {
uint8_t *bytecode;
/* Threads to be processed using the current event */
matcher_thread current_threads[MAX_THREAD_NUM];
uint8_t current_thread_num;
/* Threads to be processed using the event to follow */
matcher_thread next_threads[MAX_THREAD_NUM];
uint8_t next_thread_num;
} matcher;
А вот и обновлённый главный цикл:
match_result matcher_accept(matcher *m, uint32_t next_event)
{
#define NEXT_OP(thread) (*(thread).ip++)
#define NEXT_ARG(thread) ((void)((thread).ip += 2), ((thread).ip[-2] << 8) + (thread).ip[-1])
/* Каждое полученное событие запускает новый поток с начала байт-кода */
add_current_thread(m, initial_thread(m));
// На полученное событие мы обрабатываем каждый из потоков
for (size_t thread_i = 0; thread_i < m->current_thread_num; thread_i++ ) {
matcher_thread current_thread = m->current_threads[thread_i];
bool thread_done = false;
while (!thread_done) {
uint8_t instruction = NEXT_OP(current_thread);
switch (instruction) {
case OP_ABORT:{
return MATCH_ERROR;
}
case OP_NAME:{
uint16_t name = NEXT_ARG(current_thread);
// если выясняется, что текущее событие не соответствует шаблону, то текущий поток
// не помещается в список next_threads, и завершает выполнение
if (event_name(next_event) != name)
thread_done = true;
break;
}
case OP_SCREEN:{
uint16_t screen = NEXT_ARG(current_thread);
if (event_screen(next_event) != screen)
thread_done = true;
break;
}
case OP_NEXT:{
// поток запросил следующее событие, т.е. должен быть помещен в список
// next_threads
add_next_thread(m, current_thread);
thread_done = true;
break;
}
case OP_MATCH:{
return MATCH_OK;
}
default:{
return MATCH_ERROR;
}
}
}
}
/* Меняем местами текущий и следующий списки, запрашиваем следующее событие */
swap_current_and_next(m);
return MATCH_NEXT;
#undef NEXT_OP
#undef NEXT_ARG
}
На каждом полученном событии мы сначала вносим в список current_threads новый поток, проверяющий шаблон с самого начала, после чего начинаем обход списка current_threads, для каждого из потоков выполняя инструкции по указателю.
Если встречается инструкция NEXT, то поток помещается в список next_threads, то есть ждёт получения следующего события.
Если шаблон потока не совпадает с полученным событием, то такой поток просто не добавляется в список next_threads.
Инструкция MATCH немедленно выходит из функции, сообщая кодом возврата о совпадении шаблона с сессией.
По завершении обхода списка потоков текущий и следующий списки меняются местами.
Собственно, всё. Можно сказать, что мы буквально делаем то, что хотели: одновременно сверяем несколько шаблонов, запуская по одному новому процессу сопоставления на каждое из событий сессии.
Множественные личности и ветвления в шаблонах
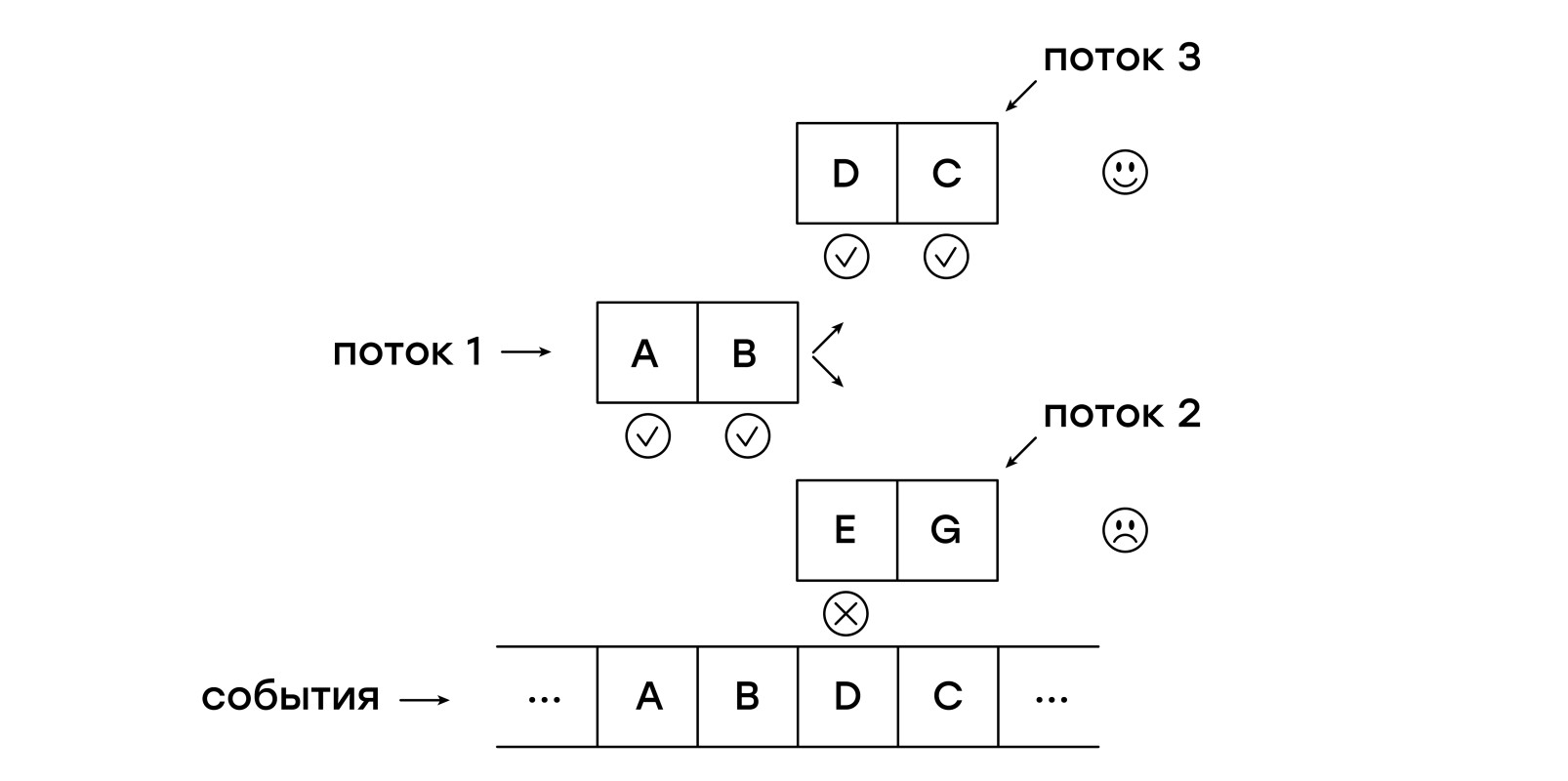
Искать шаблон, описывающий линейную последовательность событий, конечно, полезно, но мы же хотим получить полноценные регулярные выражения. И потоки, которые мы создали на предыдущем этапе, тут тоже пригодятся.
Предположим, мы хотим найти последовательность из двух или трёх интересных нам событий, что-то вроде регулярного выражения на строках: "a?bc". В этой последовательности символ "а" опционален. Как это выразить в байт-коде? Легко!
Мы можем запустить два потока, по одному для каждого случая: с символом "a" и без него. Для этого введём дополнительную инструкцию (вида SPLIT addr1, addr2), которая запускает два потока с указанных адресов. Помимо SPLIT, нам пригодится ещё JUMP, которая просто продолжает исполнение с указанной в непосредственном аргументе инструкции:
typedef enum matcher_opcode {
OP_ABORT,
OP_NAME,
OP_SCREEN,
OP_NEXT,
// перейти к указанной инструкции
OP_JUMP,
// запустить два новых потока с обеих указанных инструкций
OP_SPLIT,
OP_MATCH,
// это просто число инструкций
OP_NUMBER_OF_OPS,
} matcher_opcode;Сам цикл и остальные инструкции не меняются — мы просто внесём два новых обработчика:
// ...
case OP_JUMP:{
/* Добавить новый поток, продолжающий выполнение с нового адреса */
uint16_t offset = NEXT_ARG(current_thread);
add_current_thread(m, create_thread(m, offset));
break;
}
case OP_SPLIT:{
/* внести пару новых потоков в текущий список */
uint16_t left_offset = NEXT_ARG(current_thread);
uint16_t right_offset = NEXT_ARG(current_thread);
add_current_thread(m, create_thread(m, left_offset));
add_current_thread(m, create_thread(m, right_offset));
break;
}
// ...
Обратите внимание на то, что инструкции добавляют потоки в текущий список, то есть они продолжают работу в контексте текущего события. Поток, в рамках которого произошло ветвление, в список следующих потоков уже не попадает.
Самое удивительное в этой виртуальной машине для регулярных выражений то, что наших потоков и этой пары инструкций достаточно для того, чтобы выразить почти все общепринятые при сопоставлении строк конструкции.
Регулярные выражения на событиях
Теперь, когда у нас есть подходящая виртуальная машина и инструменты для неё, можно заняться, собственно, синтаксисом для наших регулярных выражений.
Ручная запись опкодов для более серьёзных программ быстро утомляет. В прошлый раз я не стал делать полноценный парсер, но пользователь true-grue на примере мини-языка PigletC показал возможности своей библиотеки raddsl. Я был так впечатлён лаконичностью кода, что при помощи raddsl написал небольшой компилятор регулярных выражений строк в сто-двести на Python. Компилятор и инструкция по его применению есть на GitHub. Результат работы компилятора на языке ассемблера понимает утилита, читающая два файла (программу для виртуальной машины и список событий сессии для проверки).
Для начала ограничимся типом и контекстом события. Тип события обозначаем единственным числом; если требуется указать контекст, указываем его через двоеточие. Простейший пример:
> python regexp/regexp.py "13" # шаблон, состоящий из типа события 13
NEXT
NAME 13
MATCHТеперь пример с контекстом:
python regexp/regexp.py "13:12" # тип 13, контекст 12
NEXT
NAME 13
SCREEN 12
MATCHПоследовательные события должны быть как-то разделены (например, пробелами):
> python regexp/regexp.py "13 11 10:9" 08:40:52
NEXT
NAME 13
NEXT
NAME 11
NEXT
NAME 10
SCREEN 9
MATCHШаблон поинтереснее:
> python regexp/regexp.py "12|13"
SPLIT L0 L1
L0:
NEXT
NAME 12
JUMP L2
L1:
NEXT
NAME 13
L2:
MATCHОбратите внимание на строки, заканчивающиеся двоеточием. Это метки. Инструкция SPLIT создаёт два потока, продолжающие выполнение с меток L0 и L1, а JUMP в конце первой ветки исполнения просто переходит к концу ветвления.
Можно выбирать между цепочками выражений подлиннее, группируя подпоследовательности скобками:
> python regexp/regexp.py "(1 2 3)|4"
SPLIT L0 L1
L0:
NEXT
NAME 1
NEXT
NAME 2
NEXT
NAME 3
JUMP L2
L1:
NEXT
NAME 4
L2:
MATCHПроизвольное событие обозначается точкой:
> python regexp/regexp.py ". 1"
NEXT
NEXT
NAME 1
MATCHЕсли мы хотим показать, что подпоследовательность опциональна, то ставим после неё знак вопроса:
> python regexp/regexp.py "1 2 3? 4"
NEXT
NAME 1
NEXT
NAME 2
SPLIT L0 L1
L0:
NEXT
NAME 3
L1:
NEXT
NAME 4
MATCHРазумеется, поддерживаются и обычные в регулярных выражениях многократные повторения (плюс или звёздочка):
> python regexp/regexp.py "1+ 2"
L0:
NEXT
NAME 1
SPLIT L0 L1
L1:
NEXT
NAME 2
MATCHЗдесь мы просто многократно выполняем инструкцию SPLIT, запуская на каждом цикле новые потоки.
Аналогично со звёздочкой:
> python regexp/regexp.py "1* 2"
L0:
SPLIT L1 L2
L1:
NEXT
NAME 1
JUMP L0
L2:
NEXT
NAME 2
MATCH
Перспектива
Могут пригодиться и другие расширения описанной виртуальной машины.
Например, её легко можно расширить проверкой атрибутов событий. Для реальной системы я предполагаю использовать синтаксис вроде «1:2{3:4, 5:>3}», что означает: событие 1 в контексте 2 с атрибутом 3, имеющим значение 4, и значением атрибута 5, превышающим 3. Атрибуты здесь можно просто передавать массивом в функцию matcher_accept.
Если передавать в matcher_accept ещё и временной интервал между событиями, то в язык шаблонов можно добавить синтаксис, позволяющий пропускать время между событиями: "1 mindelta(120) 2", что будет означать: событие 1, потом промежуток минимум в 120 секунд, событие 2. В сочетании с сохранением подпоследовательности это позволяет собирать информацию о поведении пользователей между двумя подпоследовательностями событий.
Другие полезные вещи, которые относительно легко добавить: сохранение подпоследовательностей регулярного выражения, разделение «жадных» и обычных операторов звёздочку и плюс и так далее. Наша виртуальная машина в терминах теории автоматов представляет собой недетерминированный конечный автомат, для реализаций которого такие вещи сделать несложно.
Заключение
Наша система разрабатывается под быстрые пользовательские интерфейсы, поэтому и движок хранения сессий самописный и оптимизирован именно под проход по всем сессиям. Все миллиарды событий, разбитые на сессии, проверяются на соответствие шаблонам за секунды на единственном сервере.
Если для вас скорость не столь критична, то похожую систему можно оформить в виде расширения для какой-нибудь более стандартной системы хранения данных вроде традиционной реляционной базы данных или распределённой файловой системы.
К слову, в последних версиях стандарта SQL уже появилась похожая на описанную в статье возможность, и отдельные базы данных (Oracle и Vertica) уже реализовали её. В свою очередь Yandex ClickHouse реализует собственный SQL-подобный язык, но там тоже есть аналогичные функции.
Отвлекаясь от событий и регулярных выражений, хочу повторить, что применимость виртуальных машин гораздо шире, чем может показаться на первый взгляд. Эта техника подходит и широко применяется во всех случаях, когда есть необходимость чётко разделить примитивы, которые понимает движок системы, и «парадную» подсистему, то есть, к примеру, какой-нибудь DSL или язык программирования.
На этом я заканчиваю серию статей, посвящённых различным применениям интерпретаторов байт-кода и виртуальным машинам. Надеюсь, читателям Хабра серия понравилась и, разумеется, буду рад ответить на любые вопросы по теме.
Неформальный список литературы
Интерпретаторы байт-кода для языков программирования тема специфичная, и литературы по ним относительно немного. Лично мне понравилась книга Айана Крейга «Виртуальные машины» ("Virtual Machines"), хотя в ней описываются не столько реализации интерпретаторов, сколько абстрактные машины — математические модели, лежащие в основе различных языков программирования.
В более широком смысле виртуальным машинам посвящена другая книга — «Виртуальные машины: гибкие платформы для систем и процессов» ("Virtual Machines: Versatile Platforms for Systems and Processes"). Это введение в различные сферы применения виртуализации, охватывающее виртуализацию и языков, и процессов, и архитектур компьютеров в целом.
Практические аспекты разработки движков регулярных выражений обсуждаются в популярной литературе по компиляторам редко. «Поросячий Матчер» и пример из первой статьи базируются на идеях из потрясающей серии статей Расса Кокса, одного из разработчиков движка Google RE2.
Теория регулярных выражений излагается во всех академических учебниках, посвящённых компиляторам. Принято ссылаться на знаменитую «Книгу дракона», но я бы рекомендовал начать с приведённой выше ссылки.
Работая над статьёй, я впервые использовал интересную систему для быстрой разработки компиляторов на Python raddsl, принадлежащую перу пользователя true-grue (спасибо, Пётр!). Если перед вами стоит задача прототипирования языка или быстрой разработки какого-то DSL, стоит обратить на неё внимание.
Комментарии (17)

qw1
14.12.2018 20:32+1Чисто теоретически, можно подобрать такое регулярное выражение, и такой вход, что каждый поток будет форкаться на каждом шаге, т.е. кол-во потоков будет удваиваться. Тогда программа либо упадёт из-за исчерпания лимита потоков, либо будет сильно тормозить, если лимит потоков довольно большой, а входная строка специально удерживает кол-во работающих потоков почти на пределе.

VlK Автор
14.12.2018 21:11Вопрос хороший, да. :-)
В практической реализации при добавлении потоков инструкцией SPLIT или любым другим способом мы будем проверять, нет ли уже потока с данной инструкцией. Добавлять новый не имеет смысла — у него то же самое состояние (единственный указатель на текущую инструкцию).
То есть при длине сессии N и длине байт-кода M мы будем иметь максимум M потоков. Для целой сессии мы максимум O(N*M) раз побеспокоим наши потоки.
qw1
14.12.2018 22:18Интересное решение. К сожалению, оно не работает, если в регулярном выражении есть группы и после окончания сопоставления нужно будет также вернуть позицию каждой группы в строке.

VlK Автор
15.12.2018 14:47в моей задаче был нужен сам факт достижения определенной точки регулярного выражения плюс, возможно, счетчик числа достижений, поиск групп там был скорее теоретической возможностью.
Однако, если, допустим, добавить инструкции SAVE, сохраняющие массив, почему вдруг мы не можем извлечь подгруппы..?
qw1
15.12.2018 17:10Потому что сейчас у каждого потока в контексте есть только текущий Instruction Pointer, а если делать с группами, то форк, который делает поток на уже существующий Instruction Pointer, должен иметь свои данные, и сжать два потока в один будет нельзя.

VlK Автор
14.12.2018 21:11Кроме того, мы ж в данном случае контролируем компилятор, то есть генерация адекватного байт-кода — наша ответственность.

qw1
14.12.2018 22:21Тут ничего не сделаешь, это проблема самого принципа.
Например, регулярное выражение (a|a|a)* и входная строка aaaaaaaaaaa… будут утраивать число потоков на каждом шаге.
VlK Автор
15.12.2018 15:16Конкретно в данном случае регулярное выражение можно сжать на этапе преобразования дерева.
Опять же, предложенная оптимизация здесь будет работать, нет?
qw1
15.12.2018 17:11Сжатия — это эвристики, которые всегда можно обмануть. Например, если удаляются одинаковые под-выражения, то
(a|a*)*уже не сожмёшь, потому что формально подвыражения неодинаковые.


ArthurKushman
Если ничего не напутал — вместо
должно быть
для удаления объявленного ранее макроса.
VlK Автор
Точно! Поправил. Спасибо :-)
ksergey01
И лучше макросы заменить на лямбды
VlK Автор
И Си заменить на Си++ :-)
Раз уж на то пошло, тогда уж разумней сделать парочку static inline функций, лямбы тут совершенно ни к чему.
ksergey01
В тегах Си++, по этому предположил что это будет уместно.
VlK Автор
Я подумал, что уместо, т.к. обычно программистам на С++ такие вещи бывают интересны и понятны.
Там зачем там лямбды? :-)