
Но для того, чтобы поступить в ШАД, нужно успешно пройти три этапа — заполнить анкету на сайте, сдать вступительный экзамен и прийти на собеседование. Ежегодно в ШАД поступают старшекурсники, выпускники и аспиранты МГУ, МФТИ, ВШЭ, ИТМО, СПбГУ, УрФУ, НГУ и не все они справляются с нашими испытаниями. В этом году мы получили анкеты от 3500 человек, 1000 из которых была допущена к экзамену, и только 350 сдали его успешно.
Для тех, кто хочет попробовать себя и понять, на что он способен, мы подготовили разбор вступительного экзамена этого года. С вариантом, который мы выбрали для вас, справились 56% решавших его. В этой таблице вы можете увидеть, сколько человек смогли решить каждое из заданий в нём.
| Задание | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Решило | 57% | 68% | 40% | 35% | 29% | 12% | 20% | 6% |
Но для начала хотелось бы объяснить, что мы проверяем экзаменом и как подходим к его составлению. В самые первые годы существования ШАД письменного экзамена не было, так как заявок было ещё немного, и со всеми, кто прошёл онлайн-тестирование, получалось поговорить лично. Но зато и собеседования были дольше; некоторые выпускники вспоминают, как с ними беседовали по шесть часов, предлагая много сложных задач. Потом поступающих стало больше – и в 2012 году появился письменный экзамен.
Созданием варианта занимаются кураторы московской ШАД, одним из которых я являюсь; с подбором заданий им помогают коллеги из филиалов. Число задач в варианте не сильно изменилось за эти четыре года: сначала их было семь, а в прошлом году стало восемь. В каждом варианте есть задачи по математике (от пяти до семи) и задачи на алгоритмы (одна или две).
Что касается математики, мы, конечно же, проверяем, владеют ли поступающие основными разделами программы: алгеброй, математическим анализом, комбинаторикой и теорией вероятностей. Но нам важны не те знания, что достигаются зубрёжкой и забываются через неделю после зачёта или экзамена – вроде ужасных формул из таблицы неопределённых интегралов или функции распределения Стьюдента; именно поэтому мы разрешаем поступающим брать с собой на письменный экзамен любые бумажные источники. Гораздо ценнее понимание сути происходящего, а также умение применять стандартные факты и методы в необычных ситуациях. Вычислительную сложность мы также стараемся свести к минимуму; даже и двузначные числа перемножать приходится нечасто. Так что на экзамене вы не встретите рутинных и утомительных вычислительных упражнений, а многие задания покажутся нестандартными и, может быть, даже олимпиадными.
В части, касающейся алгоритмов, мы избегаем задач, требующих знания специфических структур данных (деревьев поиска, хэш-таблиц и т.д) или алгоритмов (быстрые алгоритмы сортировки, алгоритмы поиска кратчайших путей на графах и т.д.). Кроме того, мы не требуем от поступающих написать реализацию придуманного алгоритма на каком-либо языке программирования; скорее даже наоборот — всячески от этого отговариваем. И действительно, на письменном экзамене нас больше всего интересуют не навыки программирования, а умение внятно описать алгоритм и при необходимости убедить читателя в том, что он удовлетворяет ограничениям на время работы и объём выделяемой памяти. Впрочем, решения, содержащие код на любом языке, который мы в состоянии прочесть, тоже принимаются, но их труднее проверять и, кроме того, они всё равно должны сопровождаться обоснованием корректности.
Задача 1
Найдите предел последовательности (an), для которой
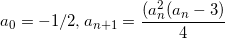
Видим, что при an?(-1;0) имеет место неравенство an < a(n+1), то есть последовательность возрастает. По теореме Вейерштрасса она имеет предел. Чтобы его найти, перейдём к пределу в нашем рекуррентном соотношении:
откуда предел может быть одним из чисел 0, –1 и 4. Нетрудно понять, что это 0.
Задача 2
На плоскости, замощённой одинаковыми прямоугольниками со сторонами 10 и 20 (прямоугольники примыкают сторонами), рисуют случайную окружность радиуса 4. Найдите вероятность того, что окружность имеет общие точки ровно с тремя прямоугольниками.
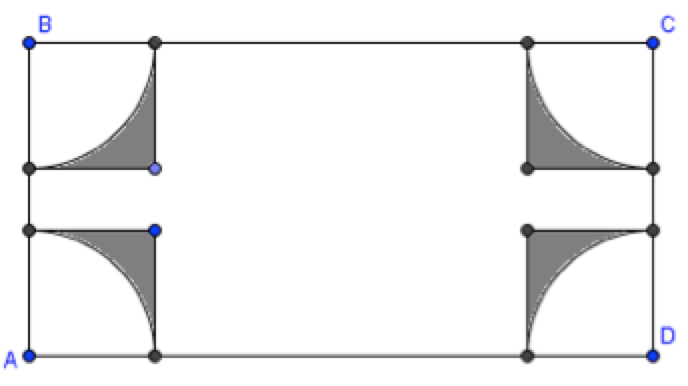
Следовательно, искомая вероятность равна
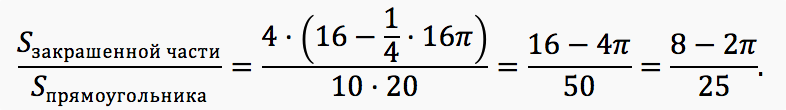
Задача 3
Дима и Ваня по очереди заполняют матрицу размера 2n?2n. Цель Вани – сделать так, чтобы получившаяся в итоге матрица имела собственное значение 1, а цель Димы – помешать ему. Дима ходит первым. Есть ли у кого-нибудь из них выигрышная стратегия?
Задача 4
Найдите определитель матрицы A=(aij), где
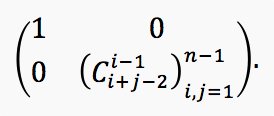
Продолжая рассуждение по индукции, убеждаемся, что определитель исходной матрицы равен определителю единичной, т.е. 1.
Задача 5
Даны два массива целых чисел a[1..n] и b[1..k], причём все элементы b различны. Требуется найти набор индексов i_1 < i_2 <… < i_k, для которого набор a[i_1],...,a[i_k] является перестановкой элементов массива b, причём разность i_k — i_1 минимально возможная. Ограничение по времени — O(nk) (но, может быть, вы сможете быстрее), по памяти — O(n).
Оценка O(n) по памяти очевидна. Оценка O(nk) по сложности может быть обоснована следующим образом: мы всё делаем в один проход (отсюда n) и на каждом шаге должны искать элемент в массиве b (отсюда k). Ясно, что алгоритм можно улучшить: если вначале отсортировать b и использовать двоичный поиск, получим O(n log k). Если же использовать совершенное хеширование, то можно добиться сложности O(n+k).
Задача 6
В 2222 году волейбольные турниры проводят по новой системе. Говорят, что команда А превосходит команду В, если А выиграла у В или у какой-либо команды, выигравшей у В. Каждая пара команд играет по 1 разу. Ничья исключается волейбольными правилами. Чемпионом объявляют команду, превзошедшую все другие команды. (а) Докажите, что чемпион обязательно найдётся (б) Докажите, что не может быть ровно двух чемпионов.
Лемма.Пусть команда Е не превосходит команду К. Тогда К набрала больше очков, чем Е.
Доказательство. Если Е не превосходит К, то К победила команду Е, а также все команды, которые победила команда Е.
Теперь пусть Х – команда, которую превзошла команда Е. Если Е выиграла у Х, то К также выиграла у Х. Значит, К превосходит Х. Если же Е выиграла у команды F, которая выиграла у Х, то заметим, что К тоже выиграла у F. Значит, К выиграла у F, которая выиграла у Х, то есть К превосходит Х. Итого, К превосходит все команды, которые превзошла Е, да ещё и Е в придачу, то есть как минимум на одну команду больше, чем Е. Лемма доказана.
(а) Пусть А – команда, заработавшая максимальное число очков. Докажем, что А – чемпион. Допустим, это не так, тогда есть команда В, которую А не превзошла. По лемме получаем, что В заработала больше очков, чем А. Противоречие.
(б) Пусть у нас есть два чемпиона: А и В. Друг с другом они играли; пусть, к примеру, победила А. Так как В превосходит все другие команды (и А в частности), то В победила некоторую команду, которая выиграла у А.
Допустим для начала, что есть команды, которые победили и А, и В. Тогда можно показать, что та из них (назовём её С), которая набрала больше всего очков, и будет третьим чемпионом. В самом деле, пусть Е – команда, которую не превзошла С. Тогда, во-первых Е победила и А, и В, а во-вторых, Е заработала больше очков, чем С. Противоречие.
Пусть теперь нет команд, которые победили и А, и В. Рассмотрим множество всех таких команд, которые победили А, но проиграли В. Отметим, что оно непусто (см. выше). Среди них возьмём команду с наибольшим числом очков. Тогда пользуясь леммой мы можем установить, что эта команда является третьим чемпионом.
Задача 7
Вычислите интеграл

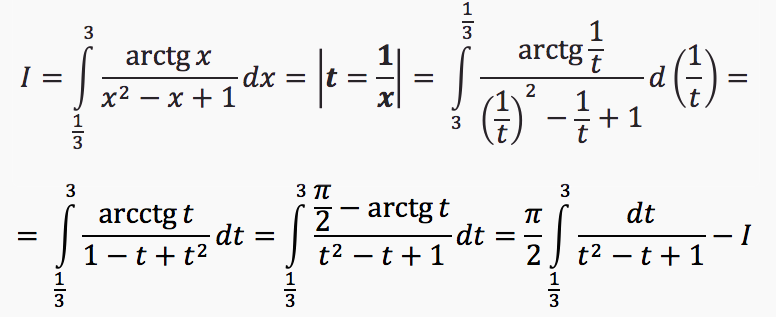
Отсюда
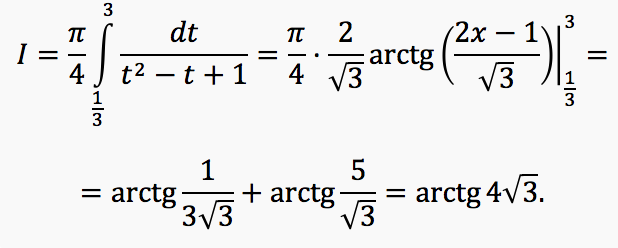
Этот интеграл уже берётся непосредственно.
Задача 8
На плоскости нарисована ломаная с n звеньями. Длина каждого звена равна 1, ориентированный угол между соседними звеньями с равной вероятностью равен ? или –?. Найдите математическое ожидание квадрата расстояния от её начальной точки до конечной.
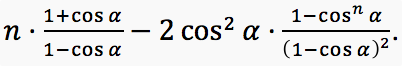
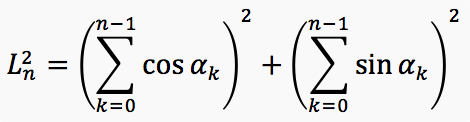
Наша задача – найти математическое ожидание этой случайной величины. Имеем:
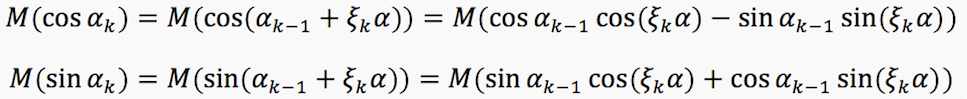
Пользуясь тем, что
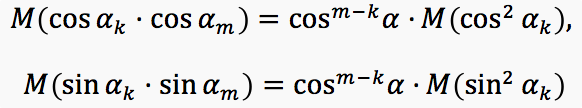
Следовательно,
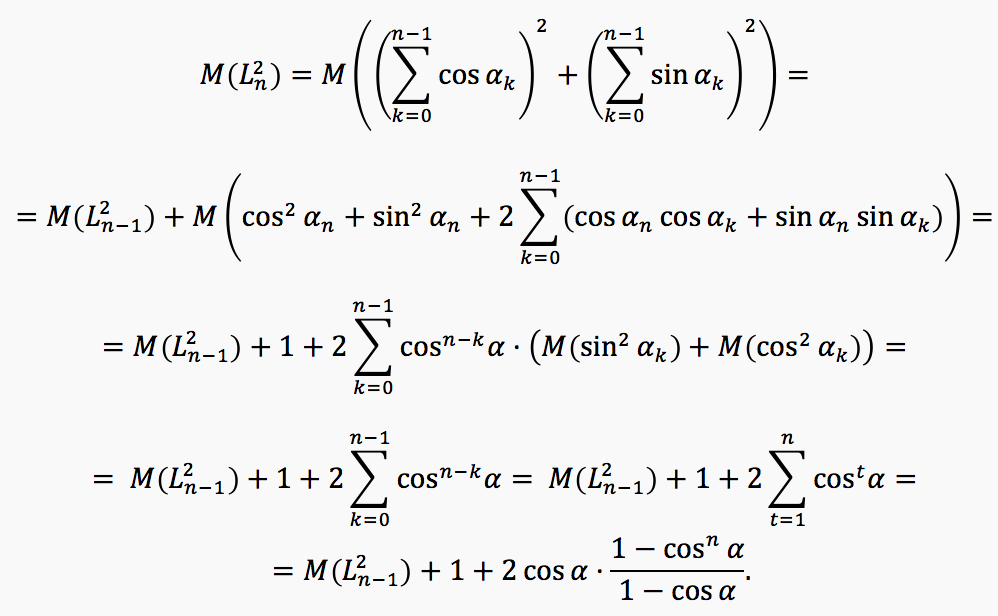
Отсюда уже нетрудно вывести ответ.
Комментарии (41)

AndrewNikolaevich
14.07.2015 19:18+16Я чего-то не понимаю, скорее всего не понимаю всего. ©

Z80A
15.07.2015 00:28+21Пост чувства собственного ничтожества.

SerafimArts
15.07.2015 06:19-2Да не, если задуматься, что-то решить можно, но задумываться и вспоминать университетский курс матана и ангема ой как не хочется, тем более он забыт, намертво и сверху заколочен досками, с удовольствием, превиликим.

kenoma
14.07.2015 20:04+5В Задаче 2 вы пишете что плоскость замощена прямоугольниками 10 на 20, но при этом не пишете, каким образом эти прямоугольники размещены относительно друг друга. А ведь если к длинной стороне прямоугольника могут примыкать короткие стороны двух других прямоугольников то решение должно быть другим.

Mrrl
14.07.2015 20:10«прямоугольники примыкают сторонами» — обычно означает «сторона к стороне». А не «сторона к двум сторонам». И если есть разумная интерпретация, в которой ответ один и не зависит от дополнительных параметров — лучше считать, что она правильная.

kenoma
14.07.2015 20:13+2Рад, что вы увидели здесь однозначность.

Mrrl
14.07.2015 20:24+3Вот здесь про это хорошо написано.

zagayevskiy
15.07.2015 07:30+3В той статье все доведено до абсурда, а тут
прямоугольники примыкают сторонами
стороны — во множественном числе, значит и «сторона к двум сторонам» — тоже возможно.

mik
15.07.2015 10:18Кроме того, если углы прямоугольников совпадают, то окружность всегда будет иметь общие точки с четным количеством прямоугольников, поскольку любая точка из сторон любого прямоугольника будет принадлежать либо двум, либо четырем (угол) прямоугольникам. Без пояснения, как именно размещены прямоугольники, задача некорректна.

Direvius
15.07.2015 11:24+2Один прямоугольник может быть пересечен дважды. Но я тоже подумал про неоднозначность размещения.

imwode
14.07.2015 23:19Задача 6:
Чемпионом объявляют команду, превзошедшую все другие команды
В доказательстве многократно используется «набрала больше очков». На самом деле победитель (по условиям) найдется тогда и только тогда, когда одна команда проиграет всем остальным, вторая выиграет только у первой, третья только у второй и первой и т.д. Можно найти вероятность этого события. Она будет отлична от 1, соответственно доказать, что победитель найдется всегда — невозможно.
imwode
14.07.2015 23:24Там засада, на самом деле в этом «или»:
если А выиграла у В или у какой-либо команды, выигравшей у В
То есть отношение команд не ограничивается «превосходством», а возможны три отношения:
A>B
A<B
A~B
Ramires
15.07.2015 11:25Не до конца понял систему правил для определения победителя в задаче 6.
Каждая пара команд играет по 1 разу.
Берем 3 команды: A, B, C.
A выигрывает у B, B выигрывает у C, C выигрывает у A.
Кто победитель?
maximw
15.07.2015 11:33+2Между C и A матч вообще не состоится, т.к. по правилам A уже превосходит C по результатам двух предыдущих игр.

Ramires
15.07.2015 11:48Тогда фраза «Каждая пара команд играет по 1 разу.» должна звучать «Каждая пара не превосходящих друг друга команд играет по 1 разу.»
Спасибо за уточнение.

Rasifiel
15.07.2015 11:56+1Мне кажется, что вы неправы. В тексте явно написано, что играет каждый с каждым. Отношение превосходства не обязательно односторонее. Если А превосходит В, то это не значит, что В не превосходит А.

ToPP
15.07.2015 16:10Тогда скажите пожалуйста, я правильно понял по условию, что все играю со всеми вне зависимости от результатов матчей?

Mrrl
15.07.2015 16:12Правильно. Получается полный граф, у каждого ребра — какое-то направление. Чемпион — та вершина, из которой до любой другой можно добраться за один или два шага.

st-fedotov Автор
15.07.2015 15:09Победителей может быть много. Так, если играют три команды А, В и С, причём А выиграла у В, В выиграла у С, а С выиграла у А, то все три команды являются победителями.

Error_403_Forbidden
14.07.2015 23:26+4а 30-40-50-летние могут проходить экзамены? Есть какие-то возрастные ограничения?

monah_tuk
15.07.2015 03:58+3Посмотрел на задачи, понял, что не все могут… Всё такое знакомое, но отсутствие необходимости в реальной жизни пользоваться чем-то сложнее: отнять, сложить и поделить, накладывает отпечаток. Т.е. ограничение может больше накладывает не возраст как таковой, а дальность отстояния от окончания ВУЗа и отсутствие повседневной необходимости использовать «вышку».

Mrrl
15.07.2015 04:06+1Да, там уже идёт расслоение — либо ты про это уже забыл, и тогда задачи просто не решатся, либо всё это умеешь — и тогда, скорее всего, тебе будет просто скучно.

Sayonji
15.07.2015 03:34Мне кажется, что даже если тест и для школьников, все равно нельзя давать формулировки в роде вероятности того, что что-то, без указания распределения. Математика — точная наука.

Mrrl
15.07.2015 04:11С распределениями здесь тоже всё хорошо. Случайная окружность на плоскости с периодическим рисунком — понятно, что координаты центра распределены равномерно по фундаментальной области. А про ломаную явно сказано «с равной вероятностью».

Sayonji
15.07.2015 04:34Я не знаю, что такое фундаментальная область, но в задаче говорится про плоскость, по которой равномерно ничего распределить не получится.

Mrrl
15.07.2015 04:58Ну как же — вот она. Для паркета из прямоугольников — будет самим прямоугольником (если брать группу параллельных переносов). А на нём распределить точки равномерно — не проблема.

Sayonji
15.07.2015 06:52+2Да, хороший термин. Однако я же не говорю, что есть проблема с пониманием того, что имелось в виду в задаче. Я только считаю, что формулировки такие нельзя давать.


Mrrl
В последней задаче что-то не то. В конце (после последней формулы) у нас получается
n*(1+2*cos(a)/(1-cos(a))-2*cos(a)/(1-cos(a))*sum(cos(a)^(n-1)). Но сумма степеней косинусов равна (1-cos(a)^n)/(1-cos(a)), так что в знаменателе в ответе должно получиться (1-cos(a))^2, a не (1+cos(a)^n)…
st-fedotov Автор
Спасибо, что обратили внимание. К сожалению, правильные формулы потерялись в процессе оформления. Жаль, конечно, что Хабр не поддерживает TEX. Я всё поправил.