
Недавно в журнале Quanta вышел материал, в котором автор рассказывал про удивительный с точки зрения неискушенных читателей феномен, доказанный математиками. Его суть в том, что почти все многочлены определенного типа — неприводимые, то есть не поддаются разложению. Это доказательство применяется во многих областях чистой математики. Но также это хорошая новость для одного из столпов современной жизни — цифрового шифрования.
Для надежного хранения цифровой информации широко используется шифрование с помощью алгоритма RSA. Это прокачанная версия схемы, которую может придумать даже семиклассник, чтобы обмениваться сообщениями с друзьями: каждой букве присваивается свой номер, который умножается на некий секретный, заранее оговоренный ключ. Чтобы расшифровать сообщение, достаточно просто поделить его на секретный ключ.
RSA-шифрование работает схожим образом. Приведем сильно упрощенное объяснение. Пользователь придумывает сообщение и выполняет над ним определенные математические операции, включающие в себя умножение на очень большое число (длиной в несколько сотен цифр). Единственный способ расшифровать сообщение — найти простые множители полученного результата*.
Безопасность RSA-шифрования базируется на том факте, что математике неизвестны быстрые способы найти простые множители очень больших чисел. И если зашифрованное сообщение предназначалось не вам, и у вас нет ключа для его расшифровки, то попытки найти этот ключ могут занять добрую тысячу лет. Причем это справедливо и для самых современных компьютеров, с помощью которых все равно не удастся подобрать правильные простые множители.
Но есть и обходной путь. Каждое число может быть представлено в виде уникального алгебраического уравнения. И, в отличие от поиска простых множителей числа, поиск простых множителей многочлена выполнить гораздо легче. И как только многочлен будет разложен на такие простые множители, эту информацию можно использовать для поиска простых множителей первоначального числа.
Вот как это работает.
Шаг первый: Выбирается любое число, простые множители которого нужно узнать. Для простоты возьмем число 15.
Шаг второй: 15 переводится в двоичную систему:
1111.
Шаг третий: Это двоичное выражение превращается в многочлен путем перевода всех двоичных чисел в коэффициенты многочлена:
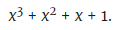
(Обратите внимание: этот многочлен равен 15, если x=2. Число 2 — основание двоичной системы.)
Шаг четвертый: Многочлен раскладывается на множители:
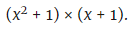
Шаг пятый: x=2 подставляется в каждый из этих множителей:
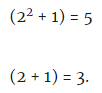
Заключение: 5 и 3 — простые множители числа 15.
Да, это излишне сложный способ поиска простых множителей небольшого числа вроде 15, которые легко вычислить в уме. Однако когда дело доходит до крупных чисел, состоящих из сотен цифр, этот многочленный метод дает удивительное преимущество. Для разложения простых чисел быстрых алгоритмов не существует. Но для разложения крупных многочленов такие алгоритмы есть. Поэтому как только удастся превратить большое число в большой многочлен, можно очень близко подобраться к поиску простых множителей числа.
Означает ли это, что RSA-шифрование находится под угрозой? На самом деле нет. И новая, недавно доказанная закономерность по поводу многочленов как раз связана с этим.
Математики Эммануэль Брулья и Петер Варью из Кембриджского университета доказали, что по мере удлинения многочленов с коэффициентами 0 и 1 вероятность того, что их вообще можно будет разложить, становится все ниже. А если многочлен не удастся разложить, значит, его нельзя будет использовать для поиска простых множителей числа, которое требуется вычислить.
Доказательство Брулья и Варью фактически говорит о том, что обходной путь для взлома RSA-шифрования ведет в никуда. Используемые в RSA очень большие числа соответствуют очень длинным многочленам. Кембриджские ученые утверждают, что практически невозможно найти многочлены такой длины, поддающиеся при этом разложению. Как криптографы, так и математики давно подозревали, что это так. Однако когда мировая кибербезопасность зависит от невозможности использования некоторого математического приема, всегда хорошо иметь доказательство, что этот прием действительно не работает.

Комментарии (35)

SUA
16.01.2019 17:54+1>>что по мере удлинения многочленов с коэффициентами 0 и 1 вероятность того, что их вообще можно будет разложить, становится все ниже
Странно…
— Как минимум половина таких многочленов (любой длины) оканчивается на 0 и поэтому раскладывается (с ожидаемым корнем x=2)
— И, с другой стороны, многочлен полученный из ключа RSA гарантированно раскладывается на ровно 2 множителя т.к. рассуждение описанное в (шаг четвертый) работает в обе стороны
К сожалению, препринта нет…
Mad__Max
17.01.2019 06:43Есть, просто далековато лежит, т.к. это перевод простой поясняющей журалисткой статьи к журналисткой статьи более сложного уровня, написанной по мотивам исходной научной статьи математиков.
Первоисточник всей этой цепочки тут: Irreducibility of random polynomials of large degree
SUA
17.01.2019 14:45+1Спасибо!
В очередной раз журналисты такие журналисты…
" Suppose that the Riemann hypothesis holds… "
т.е. вероятно (но исходное предположение не доказано), что многочлен с коэффициентами 0 и 1, полученный из открытого ключа RSA, статистически неразложим если рассматривать его как случайный многочлен (допустимость чего не доказывалось — или я этого не вижу в статье).

qwez
17.01.2019 11:30Как минимум половина таких многочленов (любой длины) оканчивается на 0 и поэтому раскладывается (с ожидаемым корнем x=2)
У всех чисел, полученных перемножением двух больших простых чисел, не будет множителя 2. Значит все многочлены, полученные из ключей RSA будут оканчиваться на 1.

mtivkov
17.01.2019 13:34Между такими многочленами и числами взаимно-однозначное соответствие, т.е. в статье якобы есть утверждение, что доля простых чисел возрастает при повышении разрядности чисел.
Но она убывает.
Sirion
17.01.2019 13:39Между многочленами и числами — взаимно-однозначное соответствие. А вот между неприводимыми многочленами и простыми числами — нет. Неприводимый многочлен может соответствовать составному числу.

soomrack
17.01.2019 14:54> Неприводимый многочлен может соответствовать составному числу.
Очевидно, что нет.
Sirion
17.01.2019 15:1115

saluev
17.01.2019 15:24Многочлен для 15 приводим, это даже в статье показано.

Sirion
17.01.2019 15:29+1Прошу пардона, я допустил опечатку в 50% символов своего сообщения.
25.
soomrack
17.01.2019 15:44(x^2+1)(x^2+1)

Sirion
17.01.2019 15:4625 — это x^4 + x^3 + 1. А не то, что написали вы.

soomrack
17.01.2019 15:56Я почти правильно написал:
25 = 5 * 5 = (x^2+1)(x^2+1) [при x = 2] = x^4 + 2 x^2 + 1
но поскольку коэффициент 2 недопустим, то его надо заменить на x, и получаем
x^4 + x^3 + 1
этот многочлен, действительно неприводим над Z.
Sorry, затупил, забыл, что от коэффициентов неравных 0 и 1 надо будет избавляться.

Cerberuser
17.01.2019 15:00Чему будет соответствовать произведение многочленов, соответствующих простым множителям данного составного числа?

alex005
16.01.2019 18:24-1тут вопрос в какой проекции смотреть на числа, если в лоб, то сложно, а если с другой стороны — то все видно. осталось только нужную проекцию найти. может есть возможность представлять числа не многочленами, а какими-то другими математическими объектами…

staticlab
16.01.2019 20:34А если взять не двоичную систему, а, например, троичную или другую, то полученный многочлен можно будет быстро разложить?

tbl
17.01.2019 07:57Так как раз и ищут многочлен с коэффициентами 1 и 0, т.е. задача сводится к поиску системы счисления в котором число будет состоять только из 1 и 0. Вырожденный и очевидный вариант 2 не подходит из-за слишком большой длины многочлена.

vlanko
17.01.2019 15:12Наверное предполагалось, что многочлен с единичными коефициентами разложить проще. 1 на 1 всегда поделится.

worldmind
17.01.2019 09:54Если я правильно понимаю, то стоит оговариваться, что это не означает что решения нет, просто именно таким способом решить не получится.
Чтобы никто не подумал, что это окончательное доказательство надёжности алгоритма.
mk2
17.01.2019 12:33Это точно. Для постквантовой криптографии RSA всё равно не годится, потому что существует алгоритм Шора.

DoNotPanic
17.01.2019 13:01На самом деле полином любой степени можно разложить на одночлены с в общем случае комплексными коэффициентами. То есть и разложение любого числа возможно — на комплексные множители. И вопрос в том, можно ли затем эти комплексные множители так свернуть перемножением части из них, чтобы получить целые множители…

soomrack
17.01.2019 15:01+1> На самом деле полином любой степени можно разложить на одночлены с в общем случае комплексными коэффициентами. То есть и разложение любого числа возможно — на комплексные множители. И вопрос в том, можно ли затем эти комплексные множители так свернуть перемножением части из них, чтобы получить целые множители…
Конечно, можно. Если коэффициенты вещественны, то все комплексные корни будут попарно сопряжены. Проблема в том, что быстрых алгоритмов нахождения комплексных корней тоже мало. Когда вы говорите о нахождении комплексных корней многочлена с целыми коэффициентами, причем (очевидно из условий задачи) корни многочлена должны быть целые (и мнимая, и вещественная часть), то фактически вы пытаетесь решить диофантово уравнение с двумя переменными. А для них расстояние от корня до нуля может иметь экспоненциальную зависимость относительно степени многочлена.

vlanko
17.01.2019 15:18кстати да. стандартные алгоритмы проверки делимости многочленов (подбором) — как раз деление на число.

Apache02
17.01.2019 13:57И если зашифрованное сообщение предназначалось не вам, и у вас нет ключа для его расшифровки, то попытки найти этот ключ могут занять добрую тысячу лет.
Условия вводят в заблуждение — будто для расшифровывания достаточно выполнения одного из двух условий: либо быть получателем либо иметь ключ.

unC0Rr
17.01.2019 15:25придумывает сообщение и выполняет над ним определенные математические операции, включающие в себя умножение на очень большое число
Не умножение, а возведение в степень по модулю очень большого числа.
Единственный способ расшифровать сообщение — найти простые множители полученного результата
Не результата, а модуля, который известен из открытого ключа.


usdglander
Наверное потому что простое число и нельзя разложить на сомножители за исключением 1 и самого числа?
khim
И именно потому, что простые числа так устроены для них как раз подобный алгоритм существует.
Это кто-то пытался сказать «попроще», а получилось… как получилось.
Разлагать на множители нужно всё-таки составное число, являющееся произведением двух простых… и вот это уже быстро сделать не получается.
P.S. И как раз если бы быстро искать простые было бы нельзя RSA и не работал бы. Так что в результате упрощения фраза изменила свой смысл на, фактически, противоположную…
staticlab
Да это просто переводчик как всегда ошибся:
9660
Почему двух? Или вы частный случай берете?
Sirion
Потому что на этом случае основан шифр RSA.