Нет, ну я, конечно, не всерьез. Должен же быть предел, до какой степени возможно упрощать предмет. Но для первых этапов, понимания базовых концепций и быстрого «въезжания» в тему, может быть, и допустимо. А как правильно поименовать данный материал (варианты: «Машинное обучение для чайников», «Анализ данных с пеленок», «Алгоритмы для самых маленьких»), обсудим в конце.

К делу. Написал несколько прикладных программ на MS Excel для визуализации и наглядного представления процессов, которые происходят в разных методах машинного обучения при анализе данных. Seeing is believing, в конце концов, как говорят носители культуры, которая и разработала большинство этих методов (кстати, далеко не все. Мощнейший «метод опорных векторов», или SVM, support vector machine – изобретение нашего соотечественника Владимира Вапника, Московский Институт управления. 1963 год, между прочим! Сейчас он, правда, преподает и работает в США).

Три файла на обозрение

1. Кластеризация методом k-средних

Задачи этого вида относятся к «обучению без учителя», когда нам нужно разбить исходные данные на некоторое заранее известное число категорий, но при этом у нас нет никакого количества «правильных ответов», их мы должны извлечь из самих данных. Фундаментальная классическая задача нахождения подвидов цветков ириса (Рональд Фишер, 1936 год!), которая считается первой ласточкой этой области знания – как раз такой природы.

Метод достаточно прост. У нас есть набор объектов, представленных в виде векторов (наборов N чисел). У ирисов это – наборы 4 чисел, характеризующие цветок: длина и ширина наружной и внутренней доли околоцветника, соответственно (Ирисы Фишера — Википедия). В качестве расстояния, или меры близости между объектами, выбирается обычная декартова метрика.

Далее, произвольным образом (или не произвольным, смотрите дальше) выбираются центры кластеров, и подсчитываются расстояния от каждого объекта до центров кластеров. Каждый объект на данном шаге итерации помечается как принадлежащий к самому близкому центру. Затем центр каждого кластера переносится в среднее арифметическое координат своих членов (по аналогии с физикой его называют еще «центром масс»), и процедура повторяется.

Процесс достаточно быстро сходится. На картинках в двумерии это выглядит так:

1. Первоначальное случайное распределение точек на плоскости и число кластеров



2. Задание центров кластеров и отнесение точек к своим кластерам



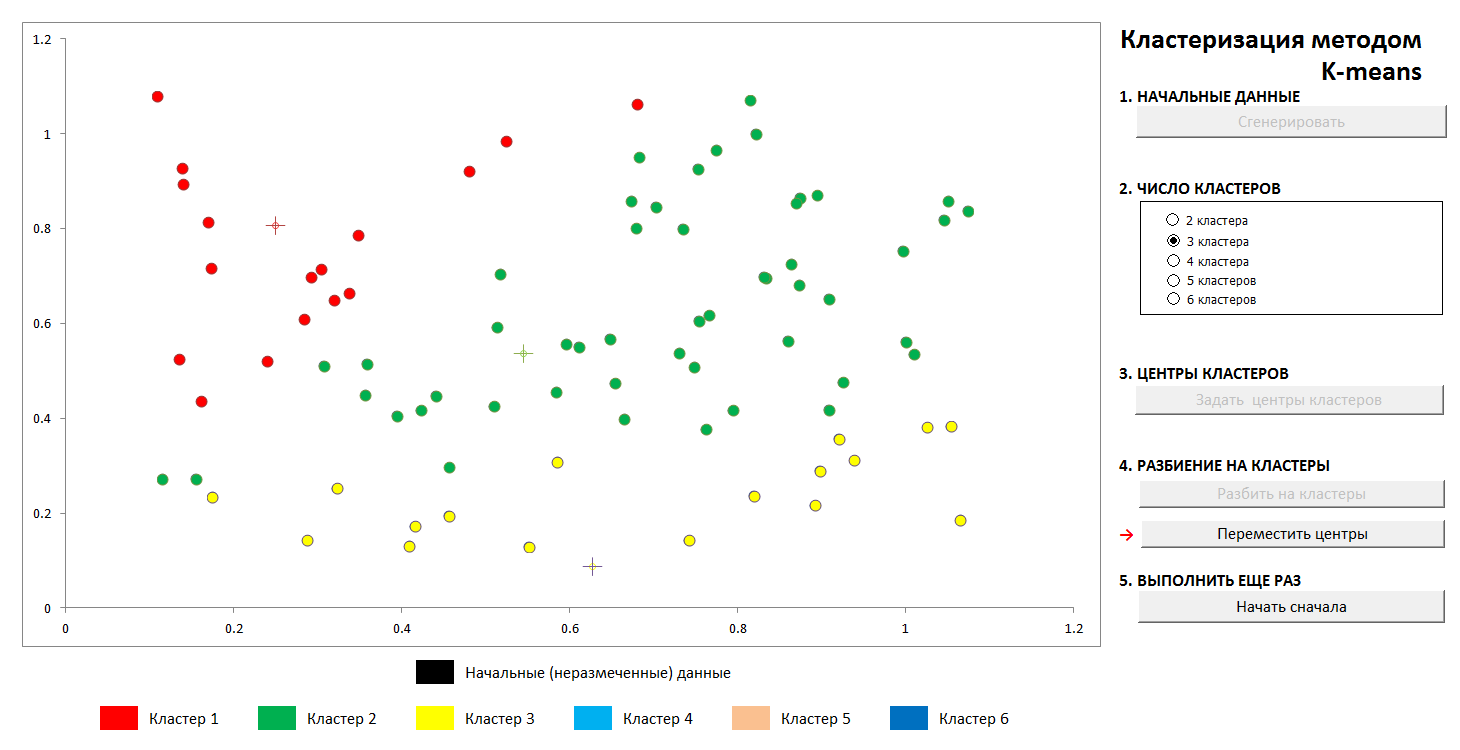
3. Перенесение координат центров кластеров, перерасчет принадлежности точек, пока центры не стабилизируются. Видна траектория движения центра кластера в оконечное положение.



В любой момент можно задать новые центры кластеров (не генерируя новое распределение точек!) и увидеть, что процесс разбиения не всегда является однозначным. Математически это означает, что у оптимизируемой функции (сумме квадратов расстояний от точек до центров своих кластеров) мы находим не глобальный, а локальный минимум. Победить эту проблему можно либо неслучайным выбором начальных центров кластеров, либо перебором возможных центров (иногда их выгодно поместить точно в какую-нибудь из точек, тогда хотя бы есть гарантия, что мы не получим пустых кластеров). В любом случае, у конечного множества всегда есть точная нижняя грань.

Поиграться с этим файлом можно по этой ссылке (не забудьте включить поддержку макросов. На вирусы файлы проверены)

Описание метода в Википедии — Метод k-средних

2. Аппроксимация многочленами и разбивка данных. Переобучение

Замечательный ученый и популяризатор науки о данных К.В. Воронцов коротко говорит о методах машинного обучения как о «науке о проведении кривых через точки». В этом примере будем находить закономерность в данных методом наименьших квадратов.

Показана техника разбиения исходных данных на «обучающие» и «контрольные», а также такой феномен, как переобучение, или «переподстройка» под данные. При правильной аппроксимации мы будем иметь некую ошибку на обучающих данных и несколько бoльшую – на контрольных. При неправильной – точную подстройку под обучающие данные и огромную ошибку на контрольных.

(Известный факт, что через N точек можно провести единственную кривую N-1 й степени, и этот способ в общем случае не дает нужного результата. Интерполяционный многочлен Лагранжа в Википедии)

1. Задаем изначальное распределение



2. Делим точки на «обучающие» и «контрольные» в соотношении 70 на 30.



3. Проводим аппроксимирующую кривую по обучающим точкам, видим ошибку, которую она дает на контрольных данных



4. Проводим точную кривую через обучающие точки, и видим чудовищную ошибку на контрольных данных (и нулевую на обучающих, но что толку?).



Показан, конечно, простейший вариант с единственным разбиением на «обучающие» и «контрольные» подмножества, в общем случае это делается многократно для наилучшей подстройки коэффициентов.

Файл доступен тут, антивирусом проверен. Включите макросы для корректной работы

3. Градиентный спуск и динамика изменения ошибки

Здесь будет 4-мерный случай и линейная регрессия. Коэффициенты линейной регрессии будут определяться по шагам методом градиентного спуска, изначально все коэффициенты – нули. На отдельном графике видна динамика уменьшения ошибки по мере все более точной подстройки коэффициентов. Есть возможность посмотреть все четыре 2-мерные проекции.

Если задать слишком большой шаг градиентного спуска, то видно, что всякий раз мы будем проскакивать минимум и к результату придем за большее число шагов, хотя, в конце концов, все равно придем (если только не слишком сильно задерем шаг спуска — тогда алгоритм пойдет «в разнос»). И график зависимости ошибки от шага итерации будет не плавным, а «дерганным».

1. Генерируем данные, задаем шаг градиентного спуска



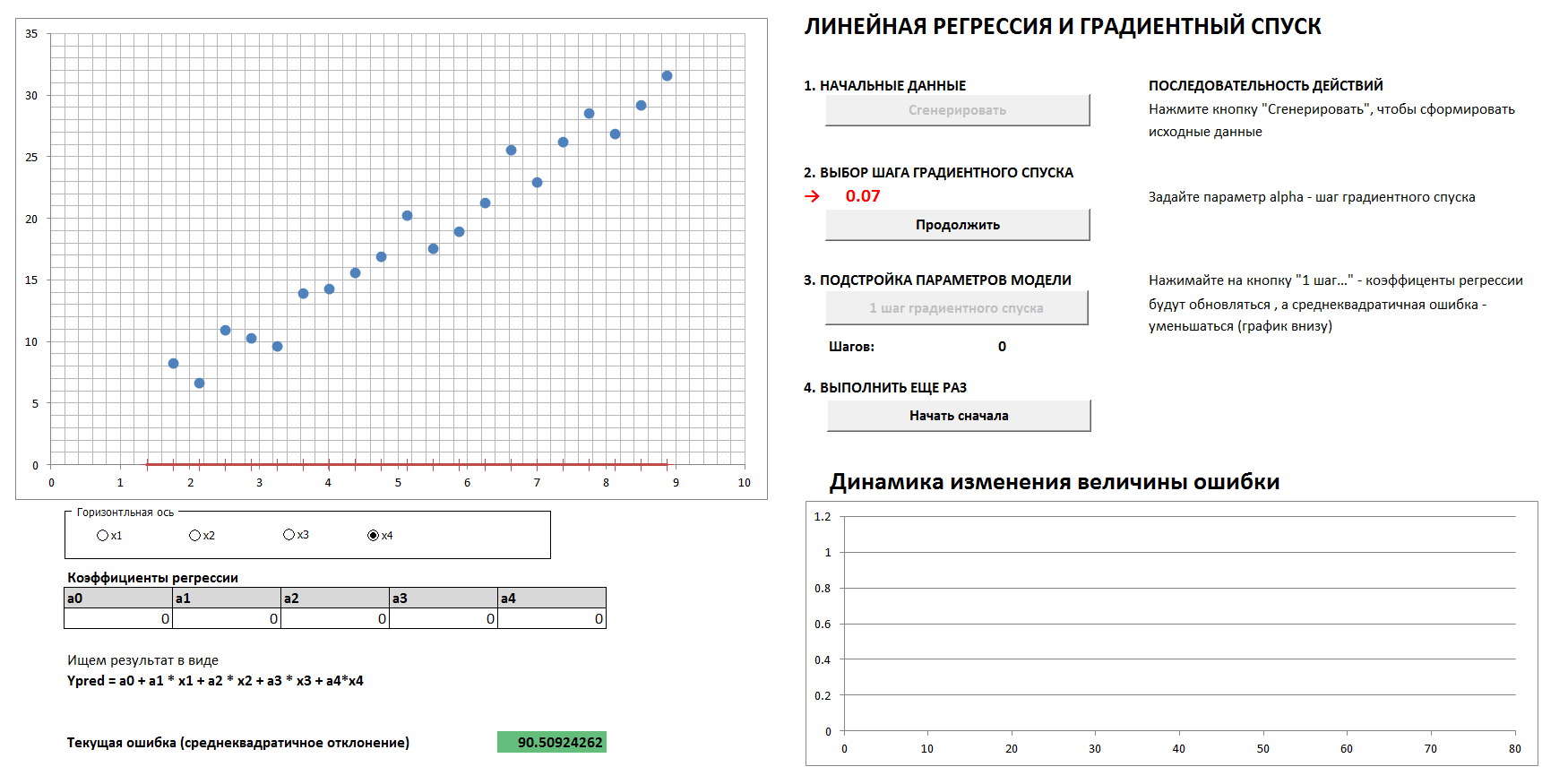
2. При правильном подборе шага градиентного спуска плавно и достаточно быстро приходим к минимуму



3. При неправильном подборе шага градиентного спуска проскакиваем максимум, график ошибки – «дерганный», сходимость занимает большее число шагов


и



4. При совсем неправильном подборе шага градиентного спуска удаляемся от минимума



(Чтобы воспроизвести процесс при показанных на картинках значениях шага градиентного спуска, поставьте галочку «эталонные данные»).

Файл – по этой ссылке, нужно включить макросы, вирусов нет.

Как считает уважаемое сообщество, допустимо ли такое упрощение и метод подачи материала? Стоит ли перевести статью на английский?