
Введение
Настоящая статья описывает результаты эксперимента проведенного в рамках проекта “Абсолютный курс валют”. Протокол эксперимента можно увидеть перейдя по ссылке.
Проект “Абсолютный курс валют” занимается анализом парных валютных курсов, выделением из них абсолютных валютных курсов и их анализом. В рамках проекта получена методика преобразования от парных курсов к абсолютным валютным курсам. Для этого определена абсолютная валюта ABS. Курсы всех имеющихся валют выражаются в отношении к ABS.
Детальное описание технологии приводится в статье “От валютных пар к абсолютным курсам валют”.
На сегодняшний день уже вышли несколько статей по применению метода абсолютных валютных курсов. Привожу две последние.
В статье “Исследование связанности мировых валют через корреляцию абсолютных курсов” описывается одно из применений технологии абсолютных валютных курсов. Дается формальный метод вычисления связи между различными валютами.
В статье “Портфельный метод Марковица применительно к валютному рынку” дается описывается недоступная ранее технология оптимизации валютного портфеля.
В далее описывается методика преобразования от парных (относительных) валютных курсов к абсолютным. Приводятся числовые параметры преобразования и методика их вычисления.
В файле-источнике ежедневно в автоматическом режиме подгружаются парные валютные курсы и из них вычисляются абсолютные.
Матрица преобразования была получена в 2017 году. Вычислялась она на реальных парных валютных курсах путем минимизации ошибки отклонения восстановленных парных курсов из абсолютных. С тех пор не проводился анализ ошибки на современных данных.
Описанные ниже неожиданные результаты проверки заставили разработать новую методику получения матрицы преобразования. Кроме того была обнаружена ошибка обработки импортируемых котировок.
Теоретические основания
Для получения абсолютных валютных курсов необходимо проделать следующее преобразование. Для начала парные курсы логарифмируем. Далее умножаем их на матрицу обратного преобразования. В конце обратно возвращаем из логарифмической шкалы применением экспоненты.
Для дальнейшего перехода к парным курсам необходимо абсолютные курсы прологарифмировать. Затем умножить на матрицу прямого преобразования. Завершаем как и ранее применением экспоненты.
Более детально технология описана в статье “От валютных пар к абсолютным курсам отдельных валют” (только в этой статье 2018 года дается транспонированное представление матриц преобразования в отличии от представления настоящей статьи).
Прямая матрица легко определяется. Строки в ней соответствуют валютам, а столбцы валютным парам. Матрица сильно разрежена и состоит из нулей, единиц и минус единиц.
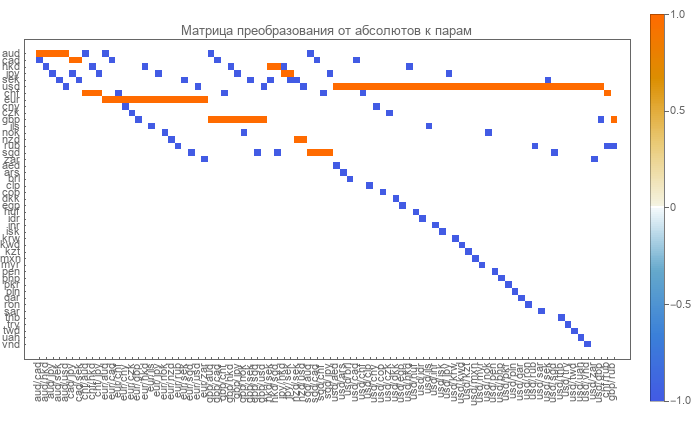
Нули говорят об отсутствии такой пары и валюты. Единица соответствует валюте в числителе пары. Минус единица обозначает валюту в знаменателе пары.
Обратная матрица преобразования от пар к абсолютным курсам не определена. Ее необходимо вычислять. Наиболее очевидный метод — это минимизировать ошибку восстановления парных курсов. Что и было сделано для вычисления этой матрицы в 2017 году. Приводим графическое представление этой матрицы.
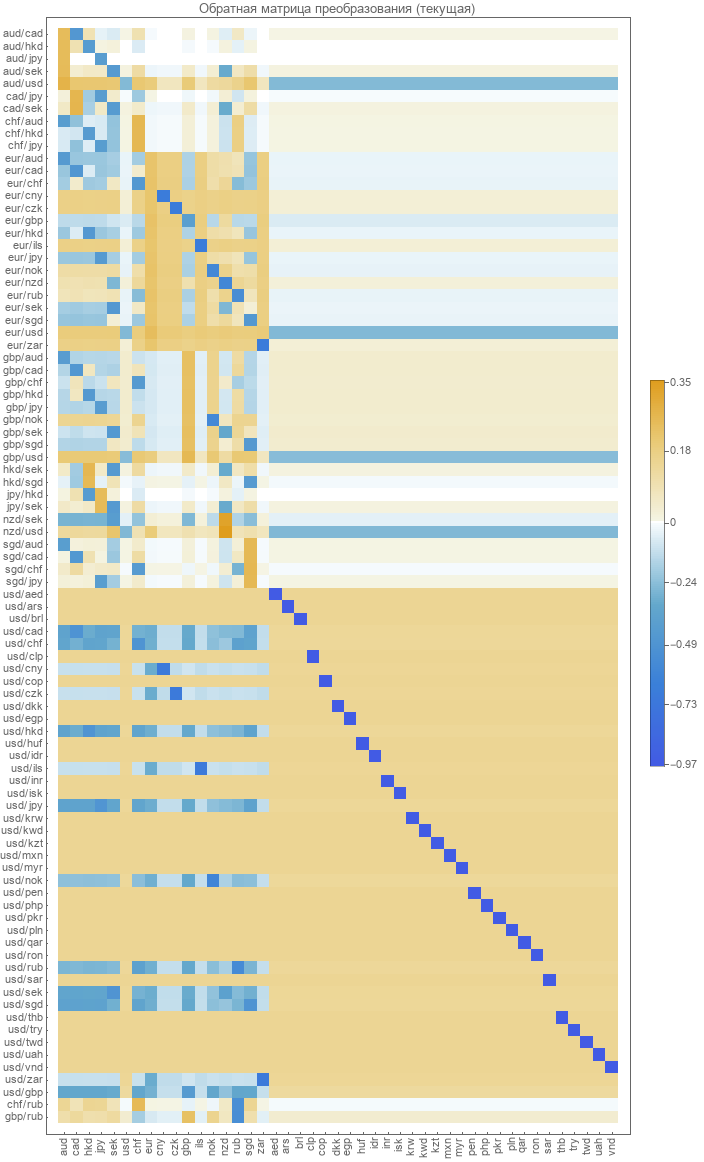
Проверка точности существующей модели
Для действующей матрицы были получены абсолютные и восстановленные парные валютные курсы. Были обнаружены резкие отличия между исходными и восстановленными парными курсами.

Далее был произведен расчет ошибок восстановления для всех пар.
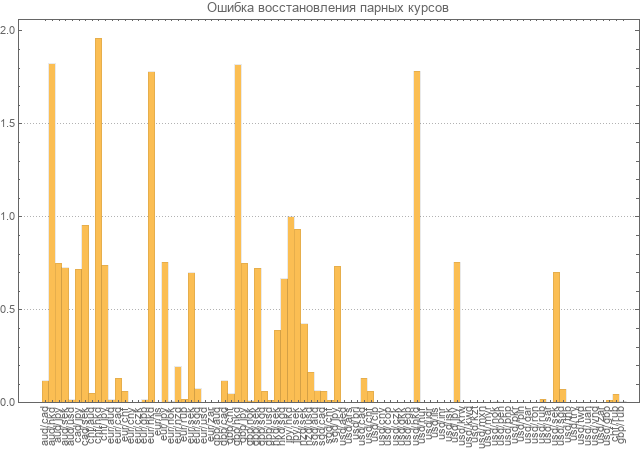
Ошибка считалась как среднее относительных отклонений взятых по модулю. Как можно видеть на диаграмме ошибки по многим парам почти в два раза больше самих значений.
Конечно такой уровень ошибки не позволяет считать модель состоятельной и требует пересчета.
Псевдообратная матрица от прямой
Первое что мы попробуем — это посчитаем просто обратную матрицу для матрицы прямого преобразования. Ввиду того что матрица у нас неквадратная придется использовать псевдообратное преобразование. Результат имеет следующий.
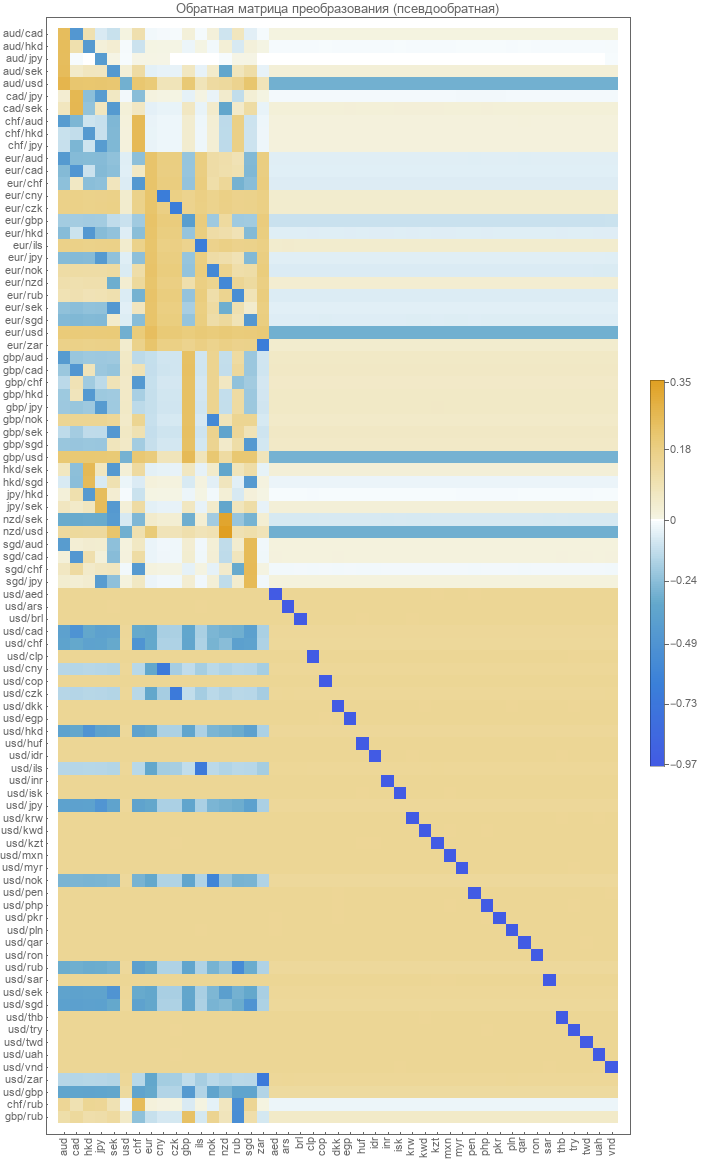
Очень похоже на то что мы получили ранее используя для оптимизации реальные парные курсы валют.
Рассчитаем абсолютные курсы. Затем восстановим из абсолютных парные курсы. Диаграмма ошибок получилась следующая.

Ошибки тоже получились большие как и в оценке выше. Эта модель тоже не может нас устроить.
Расчет обратной матрицы через линейно независимые компоненты
Если детально проанализировать матрицу прямого преобразования, то можно обнаружить, что она имеет вырожденный вид (ранг матрицы меньше чем число строк-валют). Другими словами в прямой матрице есть линейно зависимые строки. И потому получить приемлемую обратную матрицу нам не получится.
Для выхода из сложившейся ситуации было предложено следующее решение. При переходе от абсолютных курсов к парным необходимо сначала переходить к линейно-независимым компонентам. И уже потом переходить к парам. Матрицы перехода от абсолютных курсов к компонентам и от компонент к парным курсам будут невырожденными и можно будет получить обратные матрицы.
Для поиска линейно-независимых компонент необходимо к матрице прямого преобразования присоединить единичную матрицу парных курсов. Таким образом мы получим две матрицы перехода от абсолютных курсов к парным и присоединенную матрицу перехода от парных к парным.

Теперь будем производить стандартные преобразования к ступенчатому виду верхней части этой совмещенной матрицы (на самом деле стандартные средства математического пакета Wolfram Mathematica приводят дальше к диагональному виду). В результате удалось получить следующую преобразованную матрицу.

Теперь в столбцах этой матрицы имеем линейно-независимые компоненты. Причем мы можем к ним перейти как от абсолютных курсов (верхняя часть матрицы) так и от парных курсов (нижняя часть совмещенной преобразованной матрицы).
Выделим эти матрицы перехода к линейно-независимым компонентам. Вот матрица перехода к компонентам от абсолютных курсов.
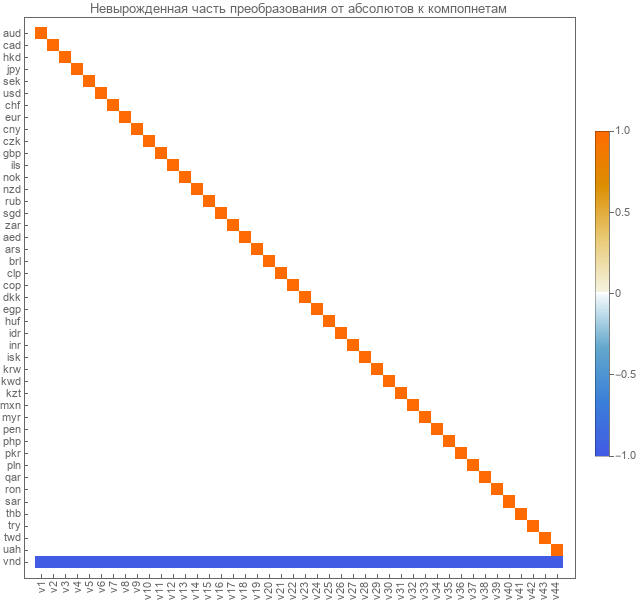
Вот матрица перехода от парных курсов к линейно-независимым компонентам.

Переход от абсолютов к компонентам происходит через рассчитанную выше матрицу. Обратное преобразование от компонент к абсолютам делаем через обратную матрицу. Ввиду того что она будет невырожденной можно получить хорошую обратную матрицу. Будем получать как псевдообратную. Вот ее вид.

Теперь можно получить полную матрицу обратного преобразования от пар к абсолютам. Для этого умножим матрицу преобразования от пар к компонентам на обратную матрицу преобразования от компонент к абсолютам. Вид она имеет такой.

Хотя подобное мы уже видели выше, но все же матрица другая. Исследуем результаты которые она дает. Рассчитаем абсолютные курсы, а из них уже восстановим парные. Ошибка восстановления получилась следующая.

На всех парах кроме двух практически нулевые ошибки. Выясняем что с этими парами.
Оказывается в двух валютных парах неверные данные принимаются. Для jpy/hkd и jpy/sek данные идут лотами по 10000 и 100 шт. Необходимо исправить и заново проверить.
После исправлений входных парных курсов (избавления от лотов) и повторных вычислений абсолютных и восстановленных парных курсов смотрим ошибку восстановления.

Получили ошибку в пределах 0.3%. Вполне приемлемый уровень ошибки.
Вот пример графика абсолютного курса.
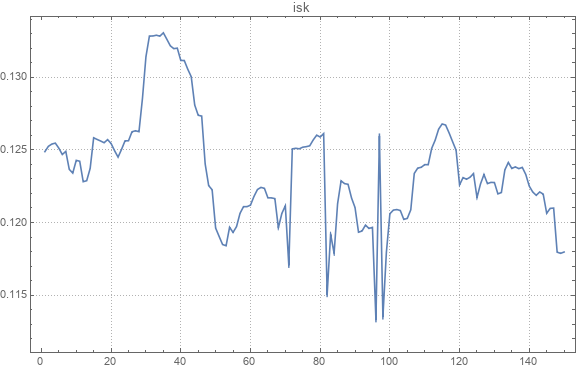
Вот пример исходного и восстановленного парных валютных курсов.

Раз уж пересчитали новую матрицу обратного преобразования снова приводим данные по последним абсолютным курсам всех участвующих валют.
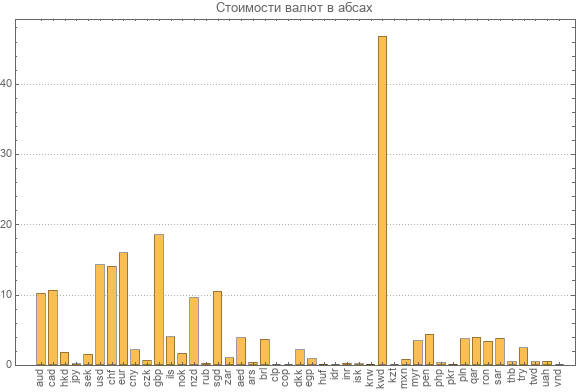
Можно увидеть самую дорогую валюту. Это кувейтский динар стоимостью почти 47 абсов. Самая маленькая абсолютная стоимость у вьетнамского донга — 0.003 абса.
Выводы
В результате проведенных исследований выяснили, что существующий метод расчета абсолютных курсов дает существенную погрешность. Кроме того обнаружена ошибка в исходных данных.
Обратную матрицу преобразования от пар к абсолютам удалось получить лишь используя метод преобразования к меньшему количеству линейно-независимых компонент с невырожденной матрицей преобразования.
Метод получения обратной матрицы преобразования не использовал данные парных курсов. И потому от них независим.
Проверка преобразования на реальных курсах показала низкий уровень ошибки. Из чего был сделан вывод о применимости найденной матрицы обратного преобразования от парных валютных курсов к абсолютным.
Метод не претендует на статус законченного и математически выверенного, но как приемлемое решение будет применяется для дальнейших исследований свой абсолютных валютных курсов.
Комментарии (38)

ANIDEANI
21.04.2019 21:06+2Всех волнует не текущий точный курс — а точный будущий КУРС.
Предикшен лёрнинг, те предсказание будущих данных — сложная тема.
Но раскрою немного инсайда.
И да, PI = 1
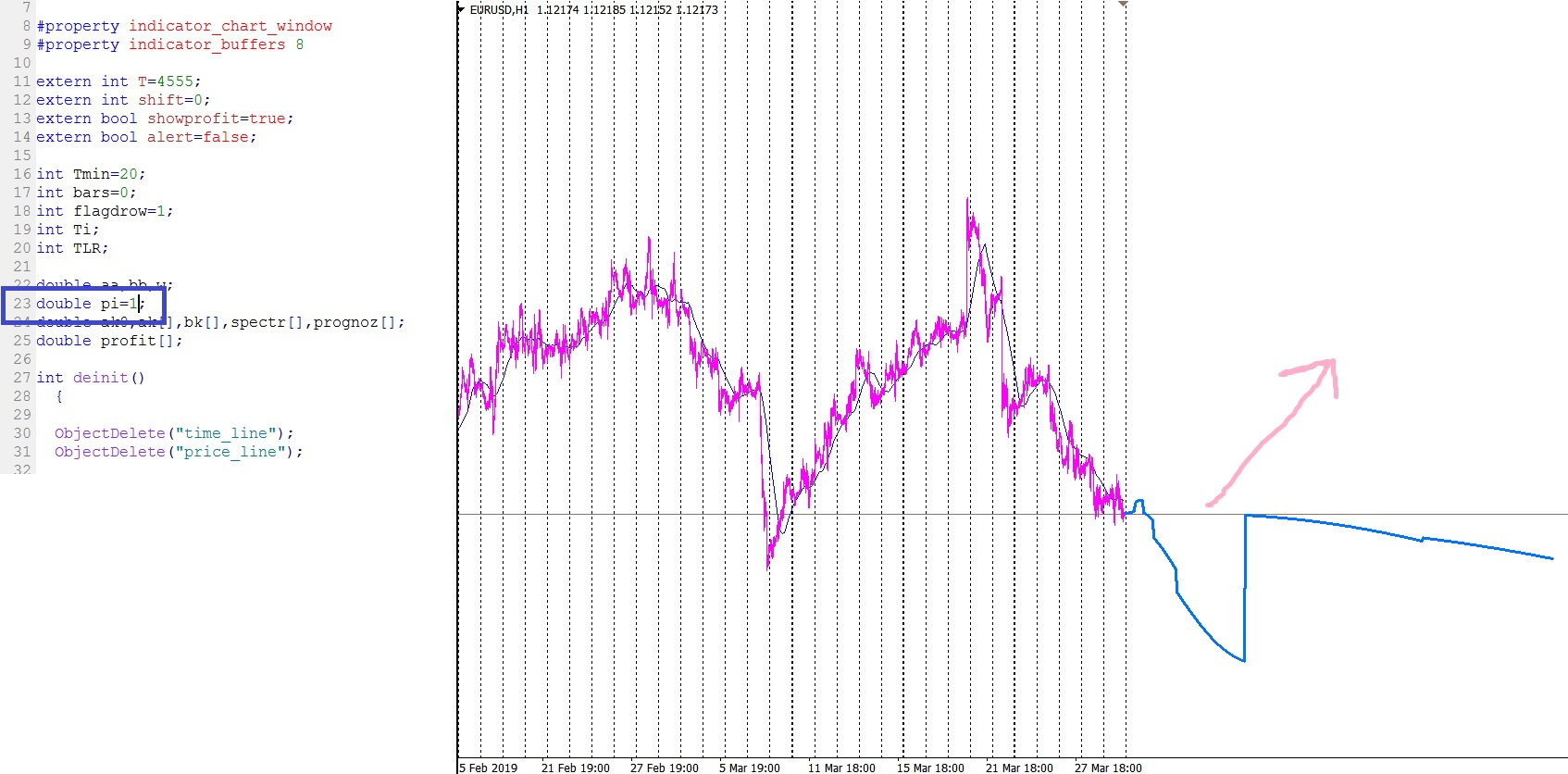

RusakovMxL
21.04.2019 21:53Смысл тут может быть: сильное отклонение от абса какой-нибудь валюты говорит о том, что ее стоит покупать или продавать. А изменения произошли в силу какого-то политического события (или иного события), которое рано или поздно устаканится, а валюта откатится к абсу. Но на этом можно сыграть. Мне так видится.

Stas911
22.04.2019 02:53Речь про арбитраж или что-то другое?

RusakovMxL
22.04.2019 07:58Косвенно, да. Извлечение прибыли из разницы в ценах. А Abs — как индикатор (вроде перекупленности или перепроданности).

eavprog Автор
22.04.2019 14:54Именно это хотел месяц назад проверять. Даже название придумал «Использование дисбаланса абсолютных курсов для принятия решения...». Только столкнулся с проблемой резких отличий между исходными парными курсами и восстановленными. Пришлось заново пересмотреть технологию получения матрицы преобразования от парных курсов к абсолютным.
Теперь можно задуматься о проверке дисбаланса в абсолютных курсах. Возможно это даст сигналы.
Только меня смущает получившаяся ошибка. Она малая на последних парах и больше в начале ряда пар. Это следствие перехода к линейно-независимым компонентам. Наверное придется делать что-то на подобие разворота главных компонент. Тогда есть шанс что ошибка распределится по всем парам и модель абсолютных курсов действительно примет центральное место.
RusakovMxL
22.04.2019 16:02Удачи Вам в поиске священного грааля! Единственное, события (как в нашей стране — политического характера) могут затянуться на длительный срок под давлением других политических сил. Можно не дождаться отмены действия сигнала. Эти сигналы будут носить характер лонгов. Есть смысл скрещивать с другими сигналами всяких там скользящих средних, пересечений и т.п.

eavprog Автор
22.04.2019 16:10Спасибо. Только я не делал эту теорию исключительно для российского рынка. Детального анализа абсолютных курсов тоже пока не делал. Все впереди.

Druu
22.04.2019 03:50Для этого определена абсолютная валюта ABS. Курсы всех имеющихся валют выражаются в отношении к ABS.
Так это не абсолютный курс, а относительный относительно случайного тугрика (ABS).
В статье “Портфельный метод Марковица применительно к валютному рынку” дается описывается недоступная ранее технология оптимизации валютного портфеля.
Это чем она недоступная, если портфельная теория Марковица к валютным портфелям напрямую применяется без каких-либо проблем?

eavprog Автор
22.04.2019 15:15Попробуйте применить теорию Марковица к парным валютным курсам. Допустим у вас есть история парных валютных курсов usd_jpy, jpy_chf, eur_usd, usd_rub. Соответственно имеем ряд валют в нашем портфеле: usd, jpy, chf, eur, rub.
Внимание вопрос!!! Сколько единиц каждой валюты нужно приобрести чтобы через месяц быть в плюсе (разрешается применить теорию портфельного инвестирования Марковица)?
================================
В сети можно найти пример применения теории Марковица к валютному портфелю. Но есть одно «НО». Все парные валютные курсы в знаменателе имели одну валюту — доллар. Т.е. курсы всех валют были выражены через доллар. Но кто вам сказал о стабильности самого доллара? Если посмотреть на абсолютный курс доллара, то можно видеть как он пляшет.
Кстати, именно невозможность применения теории Марковица несколько лет назад заставила меня придумывать этот метод перехода к абсолютным курсам.
Druu
22.04.2019 15:30Допустим у вас есть история парных валютных курсов usd_jpy, jpy_chf, eur_usd, usd_rub
Можно все пересчитать по кросскурсам и привести к виду x\usd.
Но кто вам сказал о стабильности самого доллара?
А зачем ему быть стабильным? Это для портфельной теории не требуется. Кроме того — вы, например, стоимость акций в портфеле в долларах меряете и никаких проблем не возникает.
И, к слову, чем ABS более стабилен чем USD?

eavprog Автор
22.04.2019 15:56Пока у меня нет доказательства этого утверждения. Формальное доказательство в планах. Но изначально искалось общее стабильное основание. Предполагалось что это основание будет значительно стабильнее чем любая из имеющихся валют.

eavprog Автор
22.04.2019 16:03Кстати, есть еще одно применение этой теории. Пока еще описывал, обязательно сделаю.
Теория Марковица позволит вам распределить средства в различных неденежных финансовых инструментах (акции, облигации, товары и т.д.), но она не подскажет когда вывести средства в деньги.
А теперь представьте что портфель — это ряд указанных выше неденежных финансовых инструментов и присоединенных к ним валют. В этом случае выразив все через абсолютные курсы есть возможность получать и такую рекомендацию (когда выводить средства в валюту).

tretyakovpe
22.04.2019 08:53а теперь преобразуем эту матрицу с помощью другой матрицы чтобы можно было преобразовать полученную матрицу с помощью вот этой матрицы.
простите, не удержался.

sergeyns
22.04.2019 10:49Тема всемирного заговора и Ящеров не раскрыта.
ЗЫ — это из той же серии что и мысли о существовании некой «единой валюты»…

mayorovp
22.04.2019 11:49+1Настораживает вид матрицы перехода от курсов к компонентам. Выглядит так, как будто вы просто приравняли ABS=VND, и теперь оцениваете мировую экономику во вьетнамских донгах. Тоже интересное исследование, но пафосного названия "абсолютный курс" такой подход не заслуживает.

eavprog Автор
22.04.2019 15:32Согласен, что момент перехода к компонентам описал недостаточно четко.
После избавления от линейных зависимостей столбцах совмещенной матрицы в первых 44 столбцах остаются линейно-независимые компоненты.
В первых 45 строках содержится матрица перехода к компонентам от абсолютных курсов.
В оставшихся 88 строках находится матрица перехода перехода от парных курсов к этим же линейно-независимым компонентам.
Таким образом можно получить матричное уравнение:
X_abs * M_abs2comp = X_par * M_par2comp
Из него можно получить следующее решение:
X_abs = X_par * M_par2comp * (M_abs2comp^-1)
Именно это и позволяет нам получить матрицу преобразования от валютных пар к абсолютным курсам валют (конечно есть небольшая поправка — X_abs и X_par — это прологарифмированные исходные курсы).
Про «пафосность» согласен, но выбор такого наименования был не первым. Просто биржевого тикера «ABS» не обнаружил и решил быстрее застолбить его за этой синтетической валютой. Надеюсь приживется.
mayorovp
22.04.2019 16:22После избавления от линейных зависимостей столбцах совмещенной матрицы в первых 44 столбцах остаются линейно-независимые компоненты...
… которыми у вас стали все валюты кроме VND, каждой валюте — своя компонента, а VND влияет на все курсы сразу. Причём "особой" валютой VND стала не из-за благодаря какому-то особо умному алгоритму, а просто потому что шла последней в списке. Ну нельзя же так делать!
По-хорошему, именно тут вы должны что-нибудь придумать, чтобы получить именно абсолютный курс, а не просто курс относительно вьетнамского донга. Например, потребовав минимальной средней корреляции между абсолютными курсами. Но тут МНК вас уже не спасёт...
По-простому, вы можете выбрать в качестве базовой валюты любую из мировых резервных (по возможности, SDR), и повторить расчёты исходя из этого.

eavprog Автор
22.04.2019 18:39Да. Я вижу эту особенность преобразования. Если посмотреть на ошибку восстановления, то можно видеть, что вначале ряда она значительно больше чем в конце. Это связано с особенностью устранения линейных зависимостей в столбцах совместной матрицы. Решение тоже есть. Нужно сделать что-то подобное развороту собственных векторов главных компонент.

MaximRV
22.04.2019 15:33Такое впечатление, что статьи стали появляться, которые обычно были в журналах ВАК. Интересно, научно, но для чего непонятно.

eavprog Автор
22.04.2019 15:35Боюсь на ВАК пока не потяну. Решил пока откатать на родном Хабре. Но если подскажете еще место для публикации такого материала буду благодарен.
Кстати еще публикую эти материалы на vc.ru. Только там аудитория менее подкованная чем здесь.

lorc
22.04.2019 23:34Я полистал ваши статьи. Идея конечно интересная, но вы как-то слишком уж переусложнили расчеты. Вам не нужны логарифмы. Да и без матриц на самом деле можно обойтись.
Давайте обозначим V{x} ваш "абсолютный" курс валюты x. Тогда очевидно что V{ABS} = 1. А обычный курс любой пары валют можно записать как V{x}/V{y} = a{x}{y}. Например V{RUB}/V{USD} = 70.
Теперь для каждой валютной пары x-y можно записать уравнение V{x}/V{y} = a{x}{y}. Перепишем его по другому: V{x} — a{x}{y}V{y} = 0.
Если выписать эти уравнения для всех известных курсов, вы получите систему линейных уравнений относительно неизвестных V{}. Но решить вы ее не сможете потому что валютных пар сильно больше чем валют — уравнений больше чем неизвестных. Зато можно найти приближенное решение, например методом наименьших квадратов, достаточно сложить квадраты всех уравнений и минимизировать полученную функцию.
Таким образом вы получите нечто вроде абсолютного курса для каждой валюты. Но что потом делать с этими цифрами? Ведь нет никакой гарантии что на следующий день абсолютный курс не поменяется. Вы получите какие-то новые решения, но где гарантия что V{ABS1} = V{ABS2}?
Впрочем, получившиеся данные все равно можно попробовать использовать для арбитража. Наверное можно посмотреть какая из компонент целевой функции (той что вам надо минимизировать) вносит наибольший вклад в ошибку.

mayorovp
23.04.2019 10:48В лоб тут МНК не поможет, ибо матрица-то если и не вырожденная, то точно очень нехорошая. Все равно одну из валют нужно принять за ABS, то есть постулировать единичный абсолютный курс. Но получается всё равно проще чем у автора.

lorc
23.04.2019 14:22Ну о вырожденности тут говорить не приходится, потому что количество уравнений сильно больше количества неизвестных, т.е. матрица будет прямоугольной, а СЛАУ — переопределенной.

mayorovp
23.04.2019 14:33Посмотрите на систему, она однородна, т.е. умножение всех абсолютных курсов на одну и ту же величину не меняет решения. В частности, все нули — всегда решение системы. Боюсь, именно нулевое решение системы МНК и найдет.

lorc
23.04.2019 23:33Да, вы абсолютно правы. Об очевидном решении я и не подумал. Вся эта затея с абсолютными курсом получается ещё более глупой, чем мне казалось вначале.


amarao
Тысяча объяснений «как», но ни одного слова про то, «что» и «зачем».
eavprog Автор
Боюсь вам придется потерпеть мой низкий уровень квалификации в оформлении результатов научных изысканий. Но надеюсь с вашей помощью я быстро поднаторею.
В начале статьи есть ссылки на две предыдущие работы. В них дается описание двух применений технологии абсолютных курсов «исследование связанности мировых рынков...» и «формирование валютного портфеля».
Дальнейшие применения этой технологии ищу и пробую. Думаю вы мне еще подскажете.
amarao
У вас ссылка на googledrive, а не на работу. Просто опубликуйте краткое описание. Желательно ещё, с объяснением, почему именно ваше определение наиболее подходящее.
eavprog Автор
Спасибо за подсказку. Ссылки действительно были битые. Поправил. Теперь должно работать.
eavprog Автор
Касательно краткого описания согласен. Но это уже в следующих работах.
По поводу наиболее подходящего пока ответа нет. Предполагаю, что найденное решение должно давать наиболее стабильное основание. Предполагаю что значительно стабильнее чем любой финансовый инструмент. Но с доказательством такового пока еще далеко.
Возможно подсказки направления куда копать подскажут здесь. На это я тоже надеюсь.