
Проект: “Абсолютный курс валют”
Введение
О проекте
Проект “Абсолютный курс валют” занимается анализом парных валютных курсов, выделением из них абсолютных валютных курсов и их анализом.
В рамках проекта получена методика преобразования от парных курсов к абсолютным валютным курсам. Для этого определена абсолютная валюта ABS. Курсы всех имеющихся валют выражаются в отношении к ABS.
В проекте исследуются свойства абсолютных курсов. Исследуются различные применения абсолютных курсов валют.
Зачем это...?
На сегодняшний день уже вышли несколько статей по применению метода абсолютных валютных курсов. Привожу две последние.
В статье “Исследование связанности мировых валют через корреляцию абсолютных курсов” описывается одно из применений технологии абсолютных валютных курсов. Дается формальный метод вычисления связи между различными валютами.
В статье “Портфельный метод Марковица применительно к валютному рынку” дается описывается недоступная ранее технология оптимизации валютного портфеля.
На этих двух применениях исследования не останавливаются. Проверяются другие применения технологии. Если у читателей есть свои видения о прочих возможных применениях их можно писать в обсуждениях к статье. Ссылки на места обсуждений приводятся.
Методика получения абсолютных курсов
Детальное описание технологии приводится в статье “От валютных пар к абсолютным курсам валют”.
В основе метода лежит разбор представления парных курсов. Парный валютный курс — это отношение ценности одной валюты к ценности другой. А если ввести некоторую универсальную абсолютную валюту ABS, то имеет место быть следующее преобразование.
Парный валютный курс есть отношение двух абсолютных курсов.
Для того чтобы получить абсолютные курсы нужно сначала прологарифмировать это уравнение.
Соответственно можно видеть, что логарифмы парных курсов линейно связаны с логарифмами абсолютных курсов валют. И значит можно поискать между ними простое линейное преобразование. Логарифмы абсолютных курсов можно умножать на матрицу прямого преобразования и получать логарифмы парных курсов.
И стоит ожидать что существует обратное линейное преобразование для перехода от парных курсов к абсолютным.
Соответственно вся методика получения абсолютных курсов записывается следующим образом.
Нужно просто логарифмировать парные курсы, умножать их на обратную матрицу и применять экспоненту.
О проблеме
Выше было описано как получать абсолютные курсы из парных. Это делается при помощи линейного преобразования логарифмированных парных курсов и возврата через экспоненту.
Прямое линейное преобразование от абсолютных курсов к парным производится при помощи прямой матрицы. Получить ее весьма просто. Она состоит из нулей, единиц и минус единиц (“0” — нет связи пары и валюты, “+1” — валюта в числителе пары, “-1” — валюта в знаменателе пары). Ниже можно будет ее увидеть.
Наибольшую проблему представляет получение обратной матрицы (точнее необходимо использовать псевдообратное преобразование). С ее помощью можно перейти от парных курсов к абсолютным. Но получение этой матрицы нетривиально вследствии вырожденности матрицы прямого преобразования.
В предыдущей статье дается описание одного метода получения такой матрицы. В статье “Детали перехода от парных (относительных) валютных курсов к абсолютным. Работа над ошибками” раскрывается метод получения абсолютных курсов. В эксперименте мы воспользовались приемом перехода к линейно-независимым компонентам. Таким образом удалось избавится от вырожденности в псевдообратном преобразовании.
Метод настоящего эксперимента
В этой работе предлагается другой метод ухода от вырожденности в матрице прямого преобразования. В настоящее время используются парные курсы которые предоставляет РБЦ. Там 88 пар валют для экспорта. Для них существует следующая матрица прямого преобразования.
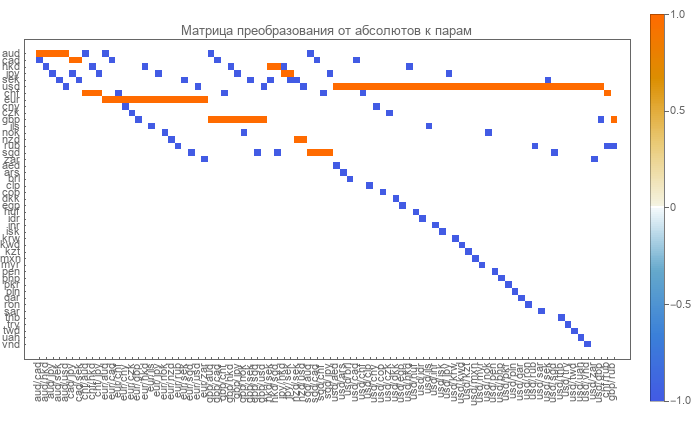
Белое в ней нули, синее -1 и красное это единицы. Но она вырожденная. Т.е. от нее не получится обратная матрица.
При проведении предыдущего эксперимента удалось заметить что диагонально подобная матрица имеет обратное преобразование. Соответственно было сделано предложение перейти к кросс-курсам и невырожденной матрице преобразования.
Весь расчет проводился в системе Wolfram Mathematica. Система позволяет получать кросс-курсы прямо внутри системы.
Детали эксперимента (малый пример)
Всего имеются 45 валют. Для наглядности сначала рассмотрим случай с малым количеством валют и валютных пар. Расчет доступен по ссылке в облаке Wolfram Cloud.
Список валют и валютных пар
Были отобраны следующие 10 валют: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK. Из них определили 9 валютных пар: AUD/CAD, CAD/HKD, HKD/JPY, JPY/SEK, SEK/USD, USD/CHF, CHF/EUR, EUR/CNY, CNY/CZK.
Матрица прямого преобразования
Матрица прямого преобразования имеет следующий вид.

Расцвеченный вариант выглядит так.

Размер матрицы — 10х9. Ранг матрицы — 9. Матрица невырожденная. Можно свободно искать обратную к ней.
Матрица обратного преобразования от парных курсов к абсолютным
В результате применения метода псевдообратного преобразования получаем обратную матрицу.

В расцвеченном виде так.

Размер обратной матрицы — 9х10.
Проверка обратной матрицы
Прежде чем двигаться дальше проверяем полученную матрицу. Для этого обратную матрицу умножим на прямую. Результат видим следующий.

И в расцвеченном виде.
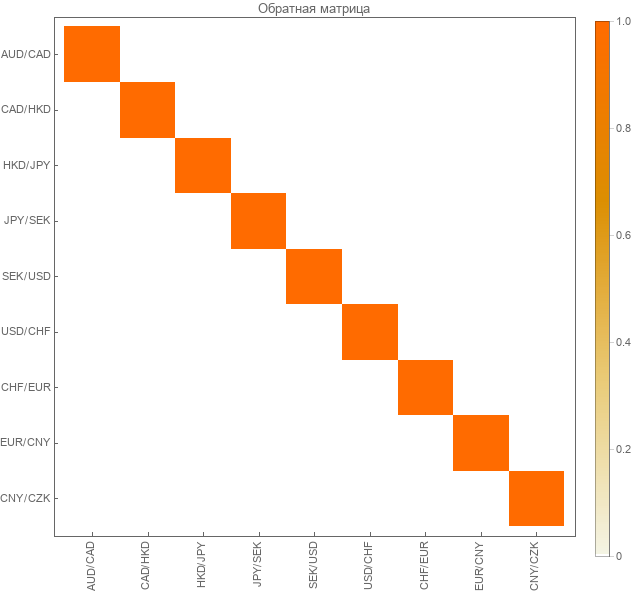
Действительно получили единичную диагональную матрицу. Значит обратная верна.
В предыдущем эксперименте проводили проверку метода получения абсолютных курсов. Для этого из полученных абсолютных курсов восстанавливали парные курсы через матрицу прямого преобразования. Дальше сравнивали восстановленные парные курсы с исходными и смотрели ошибку. В нашем случае ошибка при такой проверке будет в пределах машинной точности.
Проверка на реальных курсах
Теперь посмотрим результаты на реальных данных. Возьмем реальные котировки парных валютных кросс-курсов и рассчитаем для них абсолютные курсы.
Были взяты ежедневные кросс-курсы за 30 дней с 28.03.2019 по 27.04.2019.
Курсы валютных пар
Вот матрица парных валютных курсов. Это столбцы парных валютных курсов для следующих пар AUD/CAD, CAD/HKD, HKD/JPY, JPY/SEK, SEK/USD, USD/CHF, CHF/EUR, EUR/CNY, CNY/CZK.

Вот график курса для одной из валютных пар.

Средние значения для парных курсов получились следующими.
Теперь попробуем оценить вариативность данных. Для этого используем стандартное отклонение. Но для стандартизации разделим его на среднее значение. Результаты отобразим на диаграмме.
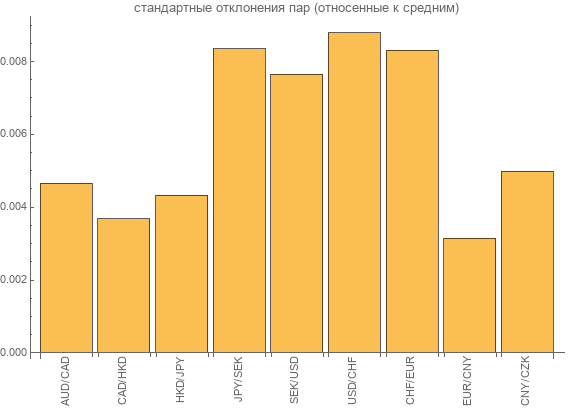
Как можно видеть стандартные отклонения для каждой валютной пары находятся в пределах 0, 2% — 0, 9% от средних значений парных курсов.
Абсолютные курсы
Теперь вычисляем для парных абсолютные курсы (методика описана в разделе Методика получения абсолютных курсов). После вычислений получаем следующие ряды данных.
Это столбцы абсолютных курсов для следующих валют AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK.

Приведем график абсолютного курса одной из валют.
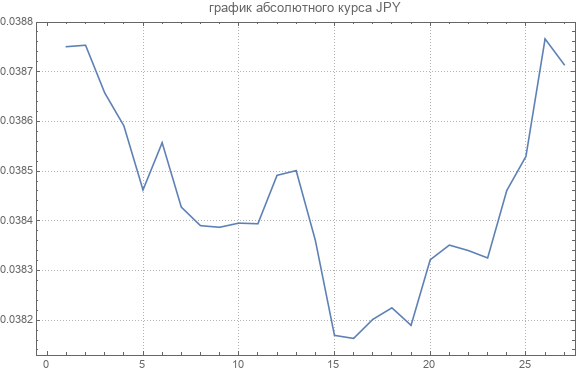
Средние значения для абсолютных курсов следующие.

Оценим вариативность абсолютных валютных курсов.

Стандартные отклонения для абсолютных курсов каждой валюты находятся в пределах 0, 2% — 0, 7% от средних значений абсолютных курсов. И это согласуется с данными для валютных пар.
Результаты на всех валютах
Теперь рассмотрим результаты на всех имеющихся валютах. Исходник расчета доступен по ссылке.
Список валют и валютных пар
Полный перечень содержит следующие 45 валют: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK, GBP, ILS, NOK, NZD, RUB, SGD, ZAR, AED, ARS, BRL, CLP, COP, DKK, EGP, HUF, IDR, INR, ISK, KRW, KWD, KZT, MXN, MYR, PEN, PHP, PKR, PLN, QAR, RON, SAR, THB, TRY, TWD, UAH, VND. Для них выбраны следующие 44 валютные пары: AUD/CAD, CAD/HKD, HKD/JPY, JPY/SEK, SEK/USD, USD/CHF, CHF/EUR, EUR/CNY, CNY/CZK, CZK/GBP, GBP/ILS, ILS/NOK, NOK/NZD, NZD/RUB, RUB/SGD, SGD/ZAR, ZAR/AED, AED/ARS, ARS/BRL, BRL/CLP, CLP/COP, COP/DKK, DKK/EGP, EGP/HUF, HUF/IDR, IDR/INR, INR/ISK, ISK/KRW, KRW/KWD, KWD/KZT, KZT/MXN, MXN/MYR, MYR/PEN, PEN/PHP, PHP/PKR, PKR/PLN, PLN/QAR, QAR/RON, RON/SAR, SAR/THB, THB/TRY, TRY/TWD, TWD/UAH, UAH/VND.
Матрица прямого преобразования
Получили матрицу прямого преобразования размером 45 на 44. Ранг у нее равен 44.
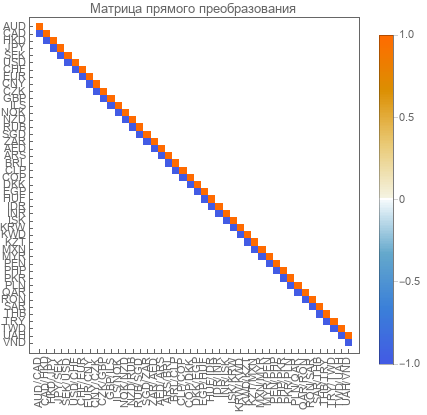
Матрица обратного преобразования
Обратная матрица получилась в результате применения обратно псевдопреобразования. Размер матрицы 44 на 45.
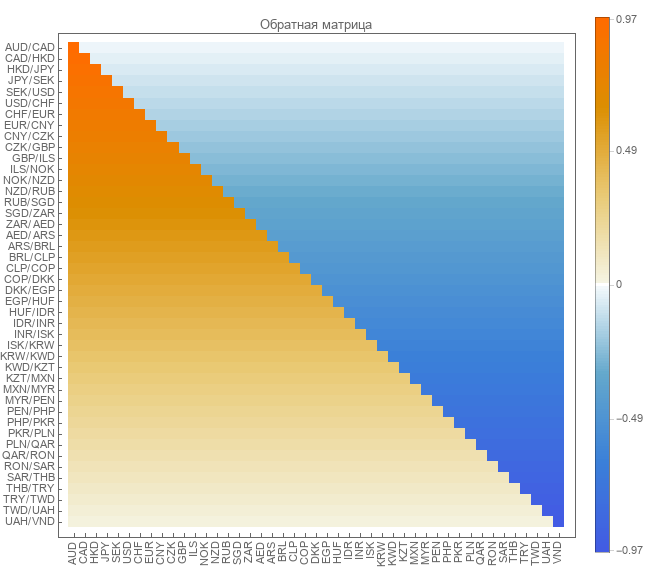
Проверка обратной матрицы
После умножения обратной матрицы на прямую получили единичную матрицу.
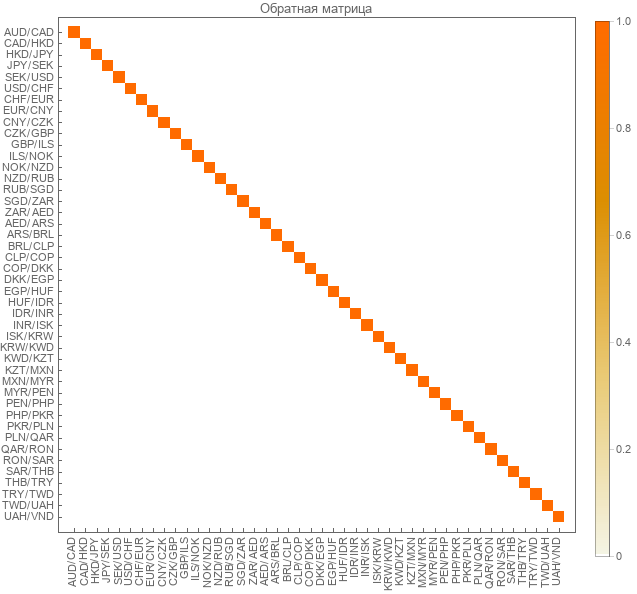
Проверка на реальных курсах
Подгрузили 44 парных валютных кросс-курса. Пример одного приводим на следующем графике.
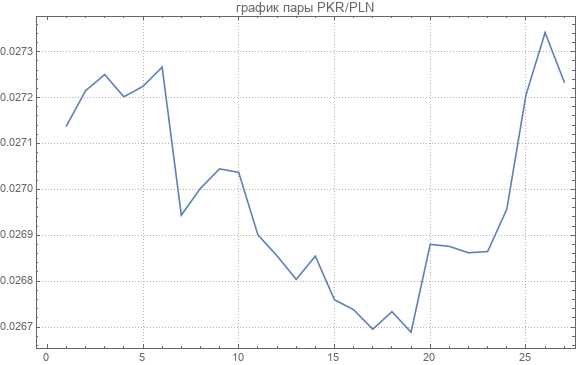
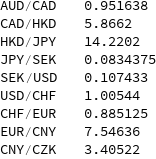
Вот данные о средних значениях курсов для каждой валютной пары.
AUD/CAD 0.951638
CAD/HKD 5.8662
HKD/JPY 14.2202
JPY/SEK 0.0834375
SEK/USD 0.107433
USD/CHF 1.00544
CHF/EUR 0.885125
EUR/CNY 7.54636
CNY/CZK 3.40522
CZK/GBP 0.0335481
GBP/ILS 4.69022
ILS/NOK 2.38106
NOK/NZD 0.173451
NZD/RUB 43.5338
RUB/SGD 0.0209621
SGD/ZAR 10.4641
ZAR/AED 0.259015
AED/ARS 11.7136
ARS/BRL 0.0907021
BRL/CLP 171.256
CLP/COP 4.72058
COP/DKK 0.00210715
DKK/EGP 2.60095
EGP/HUF 16.5291
HUF/IDR 49.5307
IDR/INR 0.00490364
INR/ISK 1.73912
ISK/KRW 9.44975
KRW/KWD 0.000266945
KWD/KZT 1248.05
KZT/MXN 0.050062
MXN/MYR 0.216251
MYR/PEN 0.803967
PEN/PHP 15.7631
PHP/PKR 2.71475
PKR/PLN 0.0269842
PLN/QAR 0.954411
QAR/RON 1.16298
RON/SAR 0.885697
SAR/THB 8.48908
THB/TRY 0.179564
TRY/TWD 5.39876
TWD/UAH 0.871089
UAH/VND 863.675
Для каждой валютной пары смотрим вариативность как и в эксперименте выше.

Стандартное отклонение для всех валютных пар находится в пределах от 0,2% до 2,5% от среднего значения.
После пересчета получаем абсолютные курсы. Вот график абсолютного курса одной из валют.
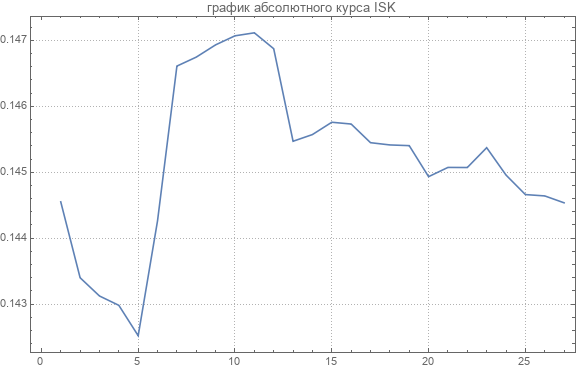
Средние значения абсолютных курсов получилось следующими.
AUD 12.4626
CAD 13.096
HKD 2.23247
JPY 0.156996
SEK 1.88165
USD 17.5149
CHF 17.4213
EUR 19.6824
CNY 2.60821
CZK 0.765955
GBP 22.832
ILS 4.86814
NOK 2.04455
NZD 11.7884
RUB 0.270822
SGD 12.9197
ZAR 1.23485
AED 4.76765
ARS 0.407218
BRL 4.49018
CLP 0.0262207
COP 0.0055548
DKK 2.63619
EGP 1.01359
HUF 0.0613224
IDR 0.00123809
INR 0.25249
ISK 0.145194
KRW 0.0153652
KWD 57.5605
KZT 0.0461203
MXN 0.921362
MYR 4.26106
PEN 5.30007
PHP 0.336241
PKR 0.123862
PLN 4.59025
QAR 4.8096
RON 4.1356
SAR 4.66938
THB 0.550046
TRY 3.06473
TWD 0.567676
UAH 0.651731
VND 0.000754602
Вариативность абсолютных курсов можно оценить по диаграмме.

Стандартное отклонение всех абсолютных курсов находится в пределах от 0,2% до 2,5% от среднего значения. Что согласуется с данными валютных пар.
Выводы
Эксперимент с получением абсолютных курсов из парных кросс-курсов удался. Получен новый метод расчета абсолютных курсов. Метод работает и легко применим. Для дальнейших исследований достаточно легко получать абсолютные курсы.
Точность метода ограничена лишь точностью выдаваемых кросс-курсов.
К сожалению открытых источников кросс-курсов обнаружить в сети не получается. И соответственно не получится этот метод применить на сайте. Но при первичном сравнении абсолютных курсов с сайта и полученных в настоящем эксперименте различия были выявлены лишь в четвертом знаке после запятой. Детальное сравнение проведем в следующих работах.
Последнюю версию настоящей статьи в PDF формате можно скачать по ссылке.
Енин А.В.
Оренбург.
02.05.2019
Комментарии (26)

gurovofficial
03.05.2019 21:57Есть такое понятие как ценообразование, оно выглядит как: фундаментальные факторы + спекулятивные факторы. На современных рынках эти факторы отражаются не просто в будущем, а заранее(т.е. новость планируется, а рынке уже её учитывают). А что такое абсолютный курс валюты лично мне не совсем ясно. И как он может помочь в трейдинге тоже.

EndUser
04.05.2019 00:19Универсальный курс валюты — это гипотеза о том, что все N? валютных пар реальных курсов можно заменить на N пар абсолютных курсов без потери информации.
Это статическая модель для каждого выбранного дня, динамика в ней не подразумевается. Хотя даёт надежду наблюдать обобщённую тенденцию единичной валюты и, как следствие, перспективы арбитража с ней. Например, внезапно вычленить устойчивый тренд какого нть реала к какому нть донгу.
Лично мне бы для подтверждения хотелось бы проверить гипотезу просто: показать, что произвольная цепочка ощутимой длины конверсий (без учёта маржи обменника) в меру длинная, что-то вроде AUD->USD->GPB->AED->RUB->INR->TRY->JPY-> равна AUD->ABS->JPY. При этом независимо от выбранной длинной цепочки.
Arqwer
04.05.2019 09:19На сколько мне известно, это почти так. Есть небольшая погрешность, и это позволяет зарабатывать high frequency trading.

Arqwer
04.05.2019 09:33Без дополнительных условий никаких надежд на анализ тренда здесь быть не должно. Можно же просто любую валюту (или комбинацию валют) объявить абсолютной, и все курсы выражать через неё.
Вот если добавить какую-нибудь регуляризацию, например, что абсолютная валюта не только корректна с точки зрения курсов, но и минимизирует какую-то меру колебания валют относительно "абсолютной", тогда да, надежду можно будет поискать.

konst90
04.05.2019 18:47А почему гипотеза?
Ма же можем принять любую валюту за 1 и от нее через кросс-курсы посчитать все остальные.
Или проблема в том, что по разным цепям получится разное значение?
EndUser
05.05.2019 12:17Неплохо. Но суть в том, что одна валюта собственно колеблется.
Плюс — да, я чувствую, что по разным цепочкам результат будет разным.
А коллеги выискивают некий средневзвешенный курс ABS, который наиболее консервативен, имеет минимальную динамику (в идеале const, но это не получится) так, чтобы колебания единичных курсов иных валют ярко вылазили.

kinall
05.05.2019 13:02по разным цепям получится разное значение
Если это так, то получается отличная задача на комбинаторику – найти такую закольцованную цепочку, которая с учётом комиссии биржи даёт профит. Идея для стартапа!=)

eavprog Автор
06.05.2019 13:18Если принять одну из валют за 1, то заранее обречь весь метод на неудачу. Значит это сразу предположение, что эта валюта имеет максимальную стабильность и весь мир крутится вокруг нее. В применяемом методе ни одна из валют таким статусом не обладает. Абсолютный курс каждой валюты получается из имеющихся парных курсов прямым нелинейным преобразованием.

eavprog Автор
06.05.2019 13:37Думаю — это вопрос расчета кросс-курса. К сожалению мне не видно как он выдается из математического пакета Wolfram Mathematica. Но полагаю алгоритм следующий.
Если необходимо вычислить кросс-курс для двух валют система ищет минимальную цепочку имеющихся парных курсов и производит преобразование.

Accounter
04.05.2019 22:47Абсолютная валюта существует. Называется — «золото».

kinall
04.05.2019 23:05Увы, нет — золотой стандарт отменён.

Accounter
04.05.2019 23:23Золото не отменено. Поэтому золотой стандарт, на самом деле существует. Только он выражен неявно, через другие валюты.

kinall
05.05.2019 00:17Если курс золота по отношению к некой валюте постоянен, то да, у этой валюты есть золотой стандарт. Если же нет (а сейчас таких валют, насколько я понимаю, не осталось), то говорить о «золотом» стандарте для неё столь же правомерно, как о «долларовом», «фунтовом» или «рублёвом».

eavprog Автор
06.05.2019 13:24Не силен в экономике. Но следующая работа будет как раз касательно абсолютной стоимости золота. Буду накапливать информацию касательно доказательства стабильности абсолютной валюты ABS. Полагаю что в абсолютном исчислении колебания золота, электроэнергии и т.п. будут меньше чем колебания абсолютных стоимостей других финансовых инструментов.

pashkov
05.05.2019 10:21Интересно, ваш метод применим для криптовалют?
Сейчас на coinmarketcap.com зарегистрировано более 2000 криптовалют.
Но не все они одинаково значимы. Какие-то курсы, наверняка, задаются искусственно.
eavprog Автор
06.05.2019 13:10он применим к любым инструментам. Криптовалюты имеют отношение к другим валютам. Значит можно вычислить криптовалюты в абсолютном исчислении.

vladb00mer
06.05.2019 13:29я всегда считал курс доллара абсолютным, но может я неправильно понял мировую экономику)

eavprog Автор
06.05.2019 13:33))) в этой теории я как раз и ищу максимально стабильное основание — валюту ABS. И все валюты выражаю через нее. А как пляшут абсолютные курсы валю можно глянуть на сайте проекта. И доллар там не самая стабильная валюта. Кстати, сейчас готовлю статью с анализом абсолютных курсов. Думаю в течение недели выпущу.

vladb00mer
06.05.2019 13:50надеюсь доллар не вечен, поэтому удачи! не забывайте про индекс бигмака, вдруг поможет)

Alexey_mosc
06.05.2019 17:27Маленький пример операций с матрицами на R:
library(MASS) A <- matrix( c(5, 1, 3,1, 3,-1, 0,-1, 4, 0,-2,2), nrow=3, byrow=TRUE) solve(A) Error in solve.default(A) : 'a' (3 x 4) must be square #expected ## #Moore-Penrose Generalized Inverse of A. #ginv(A) requires loading the MASS package. ## B2=MASS::ginv(A) round(A%*%B2, 4) [,1] [,2] [,3] [1,] 1 0 0 [2,] 0 1 0 [3,] 0 0 1 # as expected
А можно уточнить,
… матрице прямого преобразования
Как у вас из валютных пар получается исходная матрица?
UPD: кажется, понял, 1 если валюта в числителе пары, -1 в знаменателе. Верно?

Alexey_mosc
06.05.2019 17:32И еще замечание строго статистического толка.
Вот здесь по вашей ссылке корреляции несмотря на то, что я не копался в скрипте, я вижу по матрице корреляций, исходя из их значений, — что вы брали интегрированные абсолютные курсы, применяя к ним Пирсона, что является ошибочной методологией, так как они не стационарны. Полученные коэффициенты не показывают ожидаемой связи, а только ложные корреляции. Надо мерять корреляцию в данном случае между временными рядами первых разниц (returns). (Но если вы делали не так, сорри за коммент, было бы интересно знать — как.)


mwambanatanga
Заново изобрели Frankel-Wei regression?
eavprog Автор
Не могу найти приличного описания. Подскажите где почитать или здесь небольшое объяснение киньте. Спасибо.