
Если прошлая статья была скорее для затравки, то теперь пришло время проверить способности Джулии в распараллеливании на своей машине.
Многоядерная или распределенная обработка
Реализация параллельных вычислений с распределенной памятью обеспечивается модулем Distributed как часть стандартной библиотеки, поставляемой с Julia. Большинство современных компьютеров имеют более одного процессора, и несколько компьютеров могут быть объединены в кластер. Использование мощностей этих нескольких процессоров позволяет быстрее выполнять многие вычисления. На производительность влияют два основных фактора: скорость самих процессоров и скорость их доступа к памяти. В кластере совершенно очевидно, что данный ЦП будет иметь самый быстрый доступ к ОЗУ на том же компьютере (узле). Возможно еще более удивительно, что подобные проблемы актуальны на типичном многоядерном ноутбуке из-за различий в скорости основной памяти и кеша. Следовательно, хорошая многопроцессорная среда должна позволять контролировать «владение» частью памяти конкретным процессором. Julia предоставляет многопроцессорную среду, основанную на передаче сообщений, позволяющую программам запускаться одновременно на нескольких процессах в разных доменах памяти.
Реализация передачи сообщений в Julia отличается от других сред, таких как MPI [1]. Общение в Julia обычно "одностороннее", что означает, что программисту необходимо явно управлять только одним процессом в двухпроцессной операции. Кроме того, эти операции обычно не выглядят как «отправка сообщения» и «получение сообщения», а скорее напоминают операции более высокого уровня, такие как вызовы пользовательских функций.
Распределенное программирование в Julia построено на двух примитивах: удаленных ссылках и удаленных вызовах. Удаленная ссылка — это объект, который можно использовать из любого процесса для ссылки на объект, сохраненный в конкретном процессе. Удаленный вызов — это запрос одного процесса на вызов определенной функции по определенным аргументам другого (возможно, того же) процесса.
Удаленные ссылки бывают двух видов: Future и RemoteChannel.
Удаленный вызов возвращает Future и делает это немедленно; процесс, который сделал вызов, переходит к своей следующей операции, в то время как удаленный вызов происходит где-то еще. Вы можете дождаться завершения удаленного вызова командой wait для возвращенного Future, а также можете получить полное значение результата, используя fetch.
С другой стороны, у нас есть RemoteChannel'ы, которые перезаписываются. Например, несколько процессов могут координировать свою обработку, ссылаясь на один и тот же удаленный канал. У каждого процесса есть связанный идентификатор. Процесс, обеспечивающий интерактивное приглашение Julia, всегда имеет идентификатор, равный 1. Процессы, используемые по умолчанию для параллельных операций, называются «работниками». Когда существует только один процесс, процесс 1 считается рабочим. В противном случае рабочими считаются все процессы, отличные от процесса 1.

Приступим же. Запуск с припиской julia -p n предоставляет n рабочих процессов на локальном компьютере. Обычно имеет смысл, чтобы n равнялось количеству потоков ЦП (логических ядер) на машине. Обратите внимание, что аргумент -p неявно загружает модуль Distributed.
Для пользователей Linux действия с консолью не должны вызывать затруднений, т.ч. этот ликбез предназначен для малоопытных пользователей Windows.
Терминал Julia (REPL) предоставляет возможность использования системных команд:
julia> pwd() # узнать текущую рабочую директорию
"C:\\Users\\User\\AppData\\Local\\Julia-1.1.0"
julia> cd("C:/Users/User/Desktop") # изменить ее
julia> run(`calc`) # запуск программы или файла
# в данном случае калькулятора Windows.
# Кавычки которые на клавише Ё
Process(`calc`, ProcessExited(0))используя эти команды, можно запустить Julia из Julia, но лучше не увлекаться
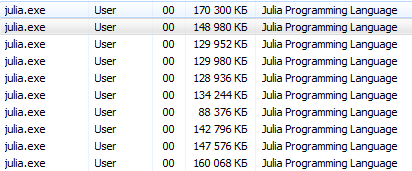
Более правильно будет запустить cmd из julia/bin/ и выполнить там команду julia -p 2 или вариант для любителей запуска с ярлыка: на рабочем столе создать блокнотовский документ с таким содержимым C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 (адрес и количество процессов указываете своё) и сохранить его как текстовый документ с именем run.bat. Вот, теперь у Вас на рабочем столе есть системный файл запуска Julia на 4 ядра.
$ ./julia -p 2
julia> r = remotecall(rand, 2, 2, 2)
Future(2, 1, 4, nothing)
julia> s = @spawnat 2 1 .+ fetch(r)
Future(2, 1, 5, nothing)
julia> fetch(s)
2?2 Array{Float64,2}:
1.18526 1.50912
1.16296 1.60607
Первый аргумент для remotecall — это вызываемая функция.
Большинство параллельных программ в Julia не ссылаются на конкретные процессы или количество доступных процессов, но удаленный вызов считается низкоуровневым интерфейсом, обеспечивающим более точное управление.
Второй аргумент для remotecall — это идентификатор процесса, который будет выполнять работу, а остальные аргументы будут переданы вызываемой функции. Как видите, в первой строке мы попросили процесс 2 построить случайную матрицу 2 на 2, а во второй строке мы попросили добавить 1 к ней. Результат обоих вычислений доступен в двух фьючерсах, r и s. Макрос spawnat оценивает выражение во втором аргументе процесса, указанного в первом аргументе. Иногда вам может понадобиться удаленно вычисленное значение. Обычно это происходит, когда вы читаете из удаленного объекта, чтобы получить данные, необходимые для следующей локальной операции. Для этого существует функция remotecall_fetch. Это эквивалентно fetch (remotecall (...)), но более эффективно.
Помните, что getindex(r, 1,1) эквивалентен r[1,1], поэтому этот вызов извлекает первый элемент будущего r.
Синтаксис удаленного вызова remotecall не особенно удобен. Макрос @spawn упрощает работу. Он работает с выражением, а не с функцией, и выбирает, где выполнить операцию за вас:
julia> r = @spawn rand(2,2)
Future(2, 1, 4, nothing)
julia> s = @spawn 1 .+ fetch(r)
Future(3, 1, 5, nothing)
julia> fetch(s)
2?2 Array{Float64,2}:
1.38854 1.9098
1.20939 1.57158Обратите внимание, что мы использовали 1 .+ Fetch(r) вместо 1 .+ r. Это потому, что мы не знаем, где будет выполняться код, поэтому в общем случае может потребоваться выборка для перемещения r в процесс, выполняющий сложение. В этом случае @spawn достаточно умен, чтобы выполнять вычисления для процесса, которому принадлежит r, поэтому fetch будет неоперативной (никакая работа не выполняется). (Стоит отметить, что spawn не встроен, но определен в Джулии как макрос. Можно определить свои собственные такие конструкции.)
Важно помнить, что после извлечения Future будет кэшировать свое значение локально. Дальнейшие вызовы fetch не влекут за собой сетевой скачок. После того, как все ссылающиеся фьючерсы выбраны, удаленное сохраненное значение удаляется.
@async похож на @spawn, но запускает задачи только в локальном процессе. Мы используем его для создания задачи «подачи» для каждого процесса. Каждая задача выбирает следующий индекс, который должен быть рассчитан, затем ожидает завершения процесса и повторяется до тех пор, пока у нас не закончатся индексы.
Обратите внимание, что задачи фидера не начинают выполняться до тех пор, пока основная задача не достигнет конца блока @sync, после чего она сдает управление и ожидает завершения всех локальных задач, прежде чем вернуться из функции.
Что касается v0.7 и выше, задачи фидера могут совместно использовать состояние через nextidx, потому что все они выполняются в одном и том же процессе. Даже если задачи планируются совместно, в некоторых контекстах может потребоваться блокировка, например, при асинхронном вводе / выводе. Это означает, что переключение контекста происходит только в четко определенных точках: в этом случае, когда вызывается remotecall_fetch. Это текущее состояние реализации, и оно может измениться в будущих версиях Julia, так как оно предназначено для того, чтобы можно было выполнить до N задач в M процессах, или M:N Threading. Тогда потребуется модель получения / освобождения блокировки для nextidx, поскольку небезопасно разрешать нескольким процессам читать и записывать ресурсы одновременно.
Ваш код должен быть доступен для любого процесса, который его запускает. Например, введите в командной строке Julia следующее:
julia> function rand2(dims...)
return 2*rand(dims...)
end
julia> rand2(2,2)
2?2 Array{Float64,2}:
0.153756 0.368514
1.15119 0.918912
julia> fetch(@spawn rand2(2,2))
ERROR: RemoteException(2, CapturedException(UndefVarError(Symbol("#rand2"))
Stacktrace:
[...]Процесс 1 знал о функции rand2, а процесс 2 — нет. Чаще всего вы будете загружать код из файлов или пакетов, и у вас будет значительная гибкость в управлении тем, какие процессы загружают код. Рассмотрим файл DummyModule.jl, содержащий следующий код:
module DummyModule
export MyType, f
mutable struct MyType
a::Int
end
f(x) = x^2+1
println("loaded")
endЧтобы ссылаться на MyType во всех процессах, DummyModule.jl должен быть загружен в каждом процессе. Вызов include ('DummyModule.jl') загружает его только для одного процесса. Чтобы загрузить его в каждый процесс, используйте макрос @everywhere (запустите Julia командой julia -p 2):
julia> @everywhere include("DummyModule.jl")
loaded
From worker 3: loaded
From worker 2: loadedКак обычно, это не делает DummyModule доступным для любого процесса, который требует использования или импорта. Более того, когда DummyModule включается в область действия одного процесса, он не включается ни в один другой:
julia> using .DummyModule
julia> MyType(7)
MyType(7)
julia> fetch(@spawnat 2 MyType(7))
ERROR: On worker 2:
UndefVarError: MyType not defined
?
julia> fetch(@spawnat 2 DummyModule.MyType(7))
MyType(7)Тем не менее, все еще возможно, например, отправить MyType процессу, который загрузил DummyModule, даже если он не находится в области видимости:
julia> put!(RemoteChannel(2), MyType(7))
RemoteChannel{Channel{Any}}(2, 1, 13)Файл также может быть предварительно загружен в несколько процессов при запуске с флагом -L, а сценарий драйвера может использоваться для управления вычислениями:
julia -p <n> -L file1.jl -L file2.jl driver.jlПроцесс Julia, выполняющий скрипт драйвера в приведенном выше примере, имеет идентификатор, равный 1, точно так же, как процесс, обеспечивающий интерактивное приглашение. Наконец, если DummyModule.jl является не отдельным файлом, а пакетом, то использование DummyModule загрузит DummyModule.jl во всех процессах, но только перенесет его в область действия процесса, для которого было вызвано использование.
Запуск и управление рабочими процессами
Базовая установка Julia имеет встроенную поддержку двух типов кластеров:
- Локальный кластер, указанный с параметром -p, как показано выше.
- Кластерные машины, использующие опцию --machine-file. При этом используется логин ssh без пароля для запуска рабочих процессов Julia (по тому же пути, что и текущий хост) на указанных машинах.

Функции addprocs, rmprocs, worker и другие доступны в качестве программного средства добавления, удаления и запроса процессов в кластере.
julia> using Distributed
julia> addprocs(2)
2-element Array{Int64,1}:
2
3Модуль Distributed должен быть явно загружен в главный процесс перед вызовом addprocs. Он автоматически становится доступным для рабочих процессов. Обратите внимание, что рабочие не запускают сценарий запуска ~/.julia/config/startup.jl и при этом они не синхронизируют свое глобальное состояние (такое как глобальные переменные, определения новых методов и загруженные модули) с любым из других запущенных процессов. Другие типы кластеров можно поддержать, написав свой собственный ClusterManager, как описано ниже в разделе ClusterManager.
Действия с данными
Отправка сообщений и перемещение данных составляют большую часть накладных расходов в распределенной программе. Сокращение количества сообщений и объема отправляемых данных имеет решающее значение для достижения производительности и масштабируемости. Для этого важно понимать движение данных, выполняемое различными конструкциями распределенного программирования Джулии.
fetch можно рассматривать как явную операцию перемещения данных, поскольку она напрямую запрашивает перемещение объекта на локальную машину. @spawn (и несколько связанных конструкций) также перемещает данные, но это не так очевидно, поэтому это можно назвать неявной операцией перемещения данных. Рассмотрим эти два подхода к построению и возведению в квадрат случайной матрицы:
Способ раз:
julia> A = rand(1000,1000);
julia> Bref = @spawn A^2;
[...]
julia> fetch(Bref);способ два:
julia> Bref = @spawn rand(1000,1000)^2;
[...]
julia> fetch(Bref);Разница кажется тривиальной, но на самом деле она довольно значительна из-за поведения @spawn. В первом методе случайная матрица строится локально, а затем отправляется в другой процесс, где она возводится в квадрат. Во втором методе случайная матрица строится и возводится в квадрат на другом процессе. Поэтому второй метод отправляет намного меньше данных, чем первый. В этом игрушечном примере два метода легко отличить и выбрать из них. Тем не менее, в реальной программе проектирование перемещения данных может потребовать больших умственных затрат и, вероятно, некоторых измерений.
Например, если первый процесс нуждается в матрице А, тогда первый метод может быть лучше. Или, если вычисление A является дорогостоящим и его пользует только текущий процесс, то его перемещение в другой процесс может быть неизбежным. Или, если текущий процесс имеет очень мало общего между spawn и fetch(Bref), может быть лучше полностью исключить параллелизм. Или представьте, что rand(1000, 1000) заменен более дорогой операцией. Тогда может иметь смысл добавить еще один оператор spawn только для этого шага.
Глобальные переменные
Выражения, выполняемые удаленно через spawn, или замыкания, указанные для удаленного выполнения с использованием remotecall, могут ссылаться на глобальные переменные. Глобальные привязки в модуле Main обрабатываются немного иначе, чем глобальные привязки в других модулях. Рассмотрим следующий фрагмент кода:
A = rand(10,10)
remotecall_fetch(()->sum(A), 2)В этом случае sum ДОЛЖНА быть определена в удаленном процессе. Обратите внимание, что A является глобальной переменной, определенной в локальной рабочей области. У работника 2 нет переменной с именем A в разделе Main. Отправка функции замыкания () -> sum(A) для работника 2 приводит к тому, что Main.A определяется на 2. Main.A продолжает существовать на работнике 2 даже после возврата вызова remotecall_fetch.

Удаленные вызовы со встроенными глобальными ссылками (только в главном модуле) управляют глобальными переменными следующим образом:
- Новые глобальные привязки создаются на рабочих местах назначения, если на них ссылаются как на часть удаленного вызова.
- Глобальные константы объявляются как константы и на удаленных узлах.
- Globals повторно отправляются целевому работнику только в контексте удаленного вызова и только в том случае, если его значение изменилось. Кроме того, кластер не синхронизирует глобальные привязки между узлами. Например:
A = rand(10,10)
remotecall_fetch(()->sum(A), 2) # worker 2
A = rand(10,10)
remotecall_fetch(()->sum(A), 3) # worker 3
A = nothingВыполнение приведенного выше фрагмента приводит к тому, что Main.A на работнике 2 имеет значение, отличное от Main.A на работнике 3, тогда как значение Main.A на узле 1 равно нулю.
Как вы, наверное, поняли, хотя память, связанная с глобальными переменными, может быть собрана, когда они переназначаются на ведущем устройстве, такие действия не предпринимаются для рабочих, поскольку привязки продолжают действовать. clear! может использоваться для ручного переназначения определенных глобальных переменных на nothing, если они больше не требуются. Это освободит любую память, связанную с ними, как часть обычного цикла сборки мусора. Таким образом, программы должны быть осторожны при обращении к глобальным переменным в удаленных вызовах. На самом деле, по возможности, лучше избегать их вообще. Если вы должны ссылаться на глобальные переменные, рассмотрите возможность использования блоков let для локализации глобальных переменных. Например:
julia> A = rand(10,10);
julia> remotecall_fetch(()->A, 2);
julia> B = rand(10,10);
julia> let B = B
remotecall_fetch(()->B, 2)
end;
julia> @fetchfrom 2 InteractiveUtils.varinfo()
name size summary
––––––––– ––––––––– ––––––––––––––––––––––
A 800 bytes 10?10 Array{Float64,2}
Base Module
Core Module
Main ModuleНетрудно заметить, что глобальная переменная A определена на работнике 2, но B записывается как локальная переменная, и, следовательно, привязка для B не существует на работнике 2.
Параллельные циклы

К счастью, многие полезные параллельные вычисления не требуют перемещения данных. Типичным примером является симуляция Монте-Карло, где несколько процессов могут одновременно обрабатывать независимые симуляционные испытания. Мы можем использовать @spawn, чтобы подбрасывать монеты на два процесса. Сначала напишите следующую функцию в count_heads.jl:
function count_heads(n)
c::Int = 0
for i = 1:n
c += rand(Bool)
end
c
endФункция count_heads просто складывает n случайных битов. Вот как мы можем провести несколько испытаний на двух машинах и сложить результаты:
julia> @everywhere include_string(Main, $(read("count_heads.jl", String)), "count_heads.jl")
julia> a = @spawn count_heads(100000000)
Future(2, 1, 6, nothing)
julia> b = @spawn count_heads(100000000)
Future(3, 1, 7, nothing)
julia> fetch(a)+fetch(b)
100001564Этот пример демонстрирует мощный и часто используемый шаблон параллельного программирования. Многие итерации выполняются независимо в нескольких процессах, а затем их результаты объединяются с использованием некоторой функции. Процесс объединения называется редукцией, поскольку он обычно уменьшает тензорный ранг: вектор чисел сокращается до одного числа, или матрица сводится к одной строке или столбцу и т.д. В коде это обычно выглядит следующим образом: шаблон x = f(x, v [i]), где x — аккумулятор, f — функция сокращения, а v[i] — сокращаемые элементы.
Желательно, чтобы f был ассоциативным, чтобы не имело значения, в каком порядке выполняются операции. Обратите внимание, что наше использование этого шаблона с count_heads может быть обобщено. Мы использовали два явных оператора spawn, что ограничивает параллелизм двумя процессами. Для запуска на любом количестве процессов мы можем использовать параллельный цикл for, работающий в распределенной памяти, который можно записать в Julia с помощью distributed, например:
nheads = @distributed (+) for i = 1:200000000
Int(rand(Bool))
endЭта конструкция реализует шаблон раскидывания итераций по нескольким процессам и объединения их с указанным сокращением (в данном случае (+)). Результат каждой итерации принимается как значение последнего выражения внутри цикла. Само выражение в параллельном цикле вычисляется до окончательного ответа.
Обратите внимание, что хотя параллельные циклы for выглядят как последовательные циклы, их поведение существенно отличается. В частности, итерации не происходят в указанном порядке, и записи в переменные или массивы не будут видны глобально, поскольку итерации выполняются в разных процессах. Любые переменные, используемые внутри параллельного цикла, будут скопированы и переданы каждому процессу. Например, следующий код не будет работать должным образом:
a = zeros(100000)
@distributed for i = 1:100000
a[i] = i
endЭтот код не будет инициализировать все, поскольку каждый процесс будет иметь только отдельную копию. Следует избегать параллельных циклов, подобных этим. К счастью, Shared Arrays могут быть использованы, чтобы обойти это ограничение:
using SharedArrays
a = SharedArray{Float64}(10)
@distributed for i = 1:10
a[i] = i
endИспользование «внешних» переменных в параллельных циклах вполне разумно, если переменные доступны только для чтения:
a = randn(1000)
@distributed (+) for i = 1:100000
f(a[rand(1:end)])
endЗдесь каждая итерация применяет f к случайно выбранному образцу из вектора, общего для всех процессов. Как вы могли заметить, оператор сокращения можно опустить, если он не нужен. В этом случае цикл выполняется асинхронно, то есть он порождает независимые задачи на всех доступных рабочих потоках и возвращает массив Future немедленно, не ожидая завершения. Вызывающий может дождаться завершения Future на более позднем этапе, вызвав для них fetch, или дождаться завершения в конце цикла, добавив префикс @sync, например @sync distributed for.
В некоторых случаях оператор сокращения не требуется, и мы просто хотим применить функцию ко всем целым числам в некотором диапазоне (или, в более общем случае, ко всем элементам в некоторой коллекции). Это еще одна полезная операция, называемая параллельной картой, реализованная в Julia как функция pmap. Например, мы можем вычислить сингулярные значения нескольких больших случайных матриц параллельно следующим образом:
julia> M = Matrix{Float64}[rand(1000,1000) for i = 1:10];
julia> pmap(svdvals, M);pmap Джулии разработан для случая, когда каждый вызов функции выполняет большой объем работы. Напротив, distributed for может обрабатывать ситуации, когда каждая итерация крошечная, возможно, просто суммируя два числа. Только рабочие процессы используются как pmap, так и distributed для параллельного вычисления. В случае distributed for окончательное сокращение выполняется во время вызова.
Общие массивы (Shared Arrays)

Shared Arrays используют системную разделяемую память для отображения одного и того же массива во многих процессах. Хоть он и имеет некоторое сходство с DArray, поведение у SharedArray совершенно иное. В DArray каждый процесс имеет локальный доступ только к фрагменту данных, и никакие два процесса не используют один и тот же блок памяти; напротив, в SharedArray каждый участвующий процесс имеет доступ ко всему массиву.
SharedArray — хороший выбор, если вы хотите, чтобы большой объем данных был доступен для двух или более процессов на одном компьютере. Поддержка Shared Array доступна через модуль SharedArrays, который должен быть явно загружен на всех участвующих работников. У SharedArray индексирование (присваивание и доступ к значениям) работает так же, как и с обычными массивами не теряя эффективности, потому что основная память доступна локальному процессу. Поэтому большинство алгоритмов работают естественным образом на SharedArray, хоть и в однопроцессном режиме. В случаях, когда алгоритм настаивает на вводе Array, базовый массив можно получить из SharedArray, вызвав sdata. Для других типов AbstractArray sdata просто возвращает сам объект, поэтому безопасно использовать sdata для любого объекта типа Array. Конструктор для разделяемого массива имеет вид:
SharedArray{T,N}(dims::NTuple; init=false, pids=Int[])который создает N-размерный общий массив битов типа T и размера dims для процессов, указанных в pids. В отличие от распределенных массивов, общий массив доступен только для тех участвующих рабочих, которые определены аргументом с именем pids (и процессом создания, если он находится на том же хосте).
Если указана функция init с подписью initfn(S :: SharedArray), она вызывается для всех участвующих работников. Вы можете указать, что каждый работник запускает функцию init в отдельной части массива, распараллеливая инициализацию.
Вот краткий пример:
julia> using Distributed
julia> addprocs(3)
3-element Array{Int64,1}:
2
3
4
julia> @everywhere using SharedArrays
julia> S = SharedArray{Int,2}((3,4), init = S -> S[localindices(S)] = myid())
3?4 SharedArray{Int64,2}:
2 2 3 4
2 3 3 4
2 3 4 4
julia> S[3,2] = 7
7
julia> S
3?4 SharedArray{Int64,2}:
2 2 3 4
2 3 3 4
2 7 4 4SharedArrays.localindices обеспечивает непересекающиеся одномерные диапазоны индексов и иногда удобен для разделения задач между процессами. Конечно, вы можете разделить работу любым способом, каким пожелаете:
julia> S = SharedArray{Int,2}((3,4), init = S -> S[indexpids(S):length(procs(S)):length(S)] = myid())
3?4 SharedArray{Int64,2}:
2 2 2 2
3 3 3 3
4 4 4 4Поскольку все процессы имеют доступ к базовым данным, вы должны быть осторожны, чтобы не создавать конфликты. Например:
@sync begin
for p in procs(S)
@async begin
remotecall_wait(fill!, p, S, p)
end
end
endприведет к неопределенному поведению. Поскольку каждый процесс заполняет весь массив своим собственным pid, любой процесс, который будет выполнен последним (для любого конкретного элементаS), сохранит свой pid.
В качестве более расширенного и сложного примера рассмотрим параллельное выполнение следующего «ядра»:
q[i,j,t+1] = q[i,j,t] + u[i,j,t]В этом случае, если мы попытаемся разделить работу, используя одномерный индекс, мы, скорее всего, столкнемся с проблемой: если q [i,j,t] ближе к концу блока, назначенного одному работнику и q[i,j,t+1] находится рядом с началом блока, назначенного другому, очень вероятно, что q[i,j,t] будет не готова в тот момент, когда это необходимо для вычисления q[i,j,t+1]. В таких случаях лучше разбить массив на части вручную. Давайте разделимся по второму измерению. Определите функцию, которая возвращает индексы (irange, jrange), присвоенные этому работнику:
julia> @everywhere function myrange(q::SharedArray)
idx = indexpids(q)
if idx == 0 # This worker is not assigned a piece
return 1:0, 1:0
end
nchunks = length(procs(q))
splits = [round(Int, s) for s in range(0, stop=size(q,2), length=nchunks+1)]
1:size(q,1), splits[idx]+1:splits[idx+1]
endДалее определим ядро:
julia> @everywhere function advection_chunk!(q, u, irange, jrange, trange)
@show (irange, jrange, trange) # display so we can see what's happening
for t in trange, j in jrange, i in irange
q[i,j,t+1] = q[i,j,t] + u[i,j,t]
end
q
endМы также определяем вспомогательную оболочку для реализации SharedArray
julia> @everywhere advection_shared_chunk!(q, u) =
advection_chunk!(q, u, myrange(q)..., 1:size(q,3)-1)Теперь давайте сравним три разные версии, одна из которых работает в одном процессе:
julia> advection_serial!(q, u) = advection_chunk!(q, u, 1:size(q,1), 1:size(q,2), 1:size(q,3)-1);который использует @distributed:
julia> function advection_parallel!(q, u)
for t = 1:size(q,3)-1
@sync @distributed for j = 1:size(q,2)
for i = 1:size(q,1)
q[i,j,t+1]= q[i,j,t] + u[i,j,t]
end
end
end
q
end;и тот, который делегирует кусками:
julia> function advection_shared!(q, u)
@sync begin
for p in procs(q)
@async remotecall_wait(advection_shared_chunk!, p, q, u)
end
end
q
end;Если мы создадим SharedArray и синхронизируем эти функции, мы получим следующие результаты (с помощью julia -p 4):
julia> q = SharedArray{Float64,3}((500,500,500));
julia> u = SharedArray{Float64,3}((500,500,500));Запустите функции один раз для JIT-компиляции и замерьте время выполнения @time при втором запуске:
julia> @time advection_serial!(q, u);
(irange,jrange,trange) = (1:500,1:500,1:499)
830.220 milliseconds (216 allocations: 13820 bytes)
julia> @time advection_parallel!(q, u);
2.495 seconds (3999 k allocations: 289 MB, 2.09% gc time)
julia> @time advection_shared!(q,u);
From worker 2: (irange,jrange,trange) = (1:500,1:125,1:499)
From worker 4: (irange,jrange,trange) = (1:500,251:375,1:499)
From worker 3: (irange,jrange,trange) = (1:500,126:250,1:499)
From worker 5: (irange,jrange,trange) = (1:500,376:500,1:499)
238.119 milliseconds (2264 allocations: 169 KB)Самым большим преимуществом advection_shared! Является то, что он минимизирует трафик среди рабочих, позволяя каждому вычислять в течение продолжительного времени назначенный фрагмент.
Общие массивы и распределенная сборка мусора
Как и удаленные ссылки, общие массивы также зависят от сборки мусора на узле создания. Код, который создает много недолговечных объектов совместно используемых массивов, выигрывает от явного завершения этих объектов как можно скорее.
Это приводит к тому, что дескрипторы памяти и файлов, отображающие общий сегмент, освобождаются быстрее.
Параллельный Монте-Карло в Julia
И вот, когда Вы пролистали всю эту скучную теорию остановившись лишь на гифке с куркой, можно приступить к примеру, с которым будет интересно поиграться на своей машине.
В качестве довольно параллельного алгоритма для примера вычислим , отношение длины окружности к ее диаметру, используя симуляцию Монте-Карло. Из определения следует, что площадь круга равна , где — радиус круга. Мы можем разработать алгоритм Монте-Карло для вычисления путем случайных бросков дротиков, т.е. генерирования равномерно распределенных случайных чисел в поле в плоскости и подсчета доли точек, которые приземляются внутри круга.
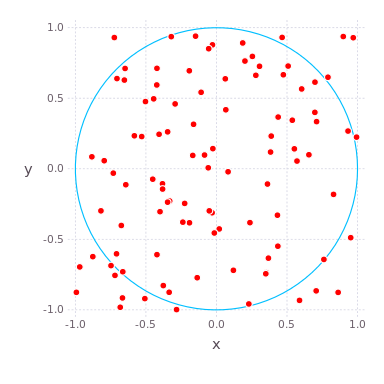
Поскольку отношение площади круга (, поскольку здесь ) к площади квадрата () равно , оно должно быть равно доле точек, которые приземляются в круге, если мы бросим бесконечное количество случайных дротиков в этом поле. Таким образом, наша оценка в четыре раза превышает долю точек, которые попадают в круг. Ниже приведена функция compute_pi (N), которая вычисляет оценку , используя дротиков.
function compute_pi(N::Int)
# counts number of points that have radial coordinate < 1, i.e. in circle
n_landed_in_circle = 0
for i = 1:N
x = rand() * 2 - 1 # uniformly distributed number on x-axis
y = rand() * 2 - 1 # uniformly distributed number on y-axis
r2 = x*x + y*y # radius squared, in radial coordinates
if r2 < 1.0
n_landed_in_circle += 1
end
end
return n_landed_in_circle / N * 4.0
endПонятное дело, чем больше точек в симуляции, тем точнее посчитается . Этот процесс просто напрашивается на распараллеливание: точки генерируются независимо, и вместо того чтобы считать сто точек на одном ядре, мы можем посчитать по 25 на четырех.
Запустим Julia на четырех ядрах и подключим к сеансу файл Pi.jl (его можно создать в Sublime Text, либо просто скопируйте содержимое и правым щелчком вставьте в терминал):
C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4
julia> include("C:/Users/User/Desktop/Pi.jl")@everywhere function compute_pi(N::Int)
n_landed_in_circle = 0
# counts number of points that have radial coordinate < 1, i.e. in circle
for i = 1:N
x = rand() * 2 - 1 # uniformly distributed number on x-axis
y = rand() * 2 - 1 # uniformly distributed number on y-axis
r2 = x*x + y*y # radius squared, in radial coordinates
if r2 < 1.0
n_landed_in_circle += 1
end
end
return n_landed_in_circle / N * 4.0
end
function parallel_pi_computation(N::Int; ncores::Int=4)
# раздаем каждому ядру равную порцию вычислений
sum_of_pis = @distributed (+) for i=1:ncores
compute_pi(ceil(Int, N / ncores))
end
return sum_of_pis / ncores # average value
end
# ceil (T, x) возвращает ближайшее целое значение
# типа T, которое больше или равно x.И можно пускать с разным количеством ядер, при этом замеряя время:
julia> @time parallel_pi_computation(1000000000, ncores = 1)
6.818123 seconds (1.96 M allocations: 99.838 MiB, 0.42% gc time)
3.141562892
julia> @time parallel_pi_computation(1000000000, ncores = 1)
5.081638 seconds (1.12 k allocations: 62.953 KiB)
3.141657252
julia> @time parallel_pi_computation(1000000000, ncores = 2)
3.504871 seconds (1.84 k allocations: 109.382 KiB)
3.1415942599999997
julia> @time parallel_pi_computation(1000000000, ncores = 4)
3.093918 seconds (1.12 k allocations: 71.938 KiB)
3.1416889400000003
julia> pi
? = 3.1415926535897...Особенность JIT-компиляции — первый пуск будет отрабатывать дольше. Как видите, параллельные вычисления в Julia это просто. Конечно, чтоб достигнуть более существенного прироста в производительности следует глубже разобраться в теме (Здесь не рассматривались еще такие возможности как Multi-Threading, Atomic Operations, Channels и Coroutines).
Полезные ссылки
Помимо встроенных средств, существует множество внешних пакетов, которые следует упомянуть. Например MPI.jl это обертка Джулии для протокола MPI, или
DistributedArrays.jl для работы с распределенными массивами.
Необходимо упомянуть экосистему Джулии программирования на GPU, которая включает в себя:
- Низкоуровневая (на ядре C) OpenCL.jl и CUDAdrv.jl которые являются соответственно интерфейсом OpenCL и оболочкой CUDA.
- Низкоуровневые (на чистой Julia) интерфэйсы CUDAnative.jl которая является родной реализацией CUDA Джулии.
- Высокоуровневые абстракции, характерные для конкретных задач, такие как CuArrays.jl и CLArrays.jl
- Библиотеки высокого уровня, такие как ArrayFire.jl и GPUArrays.jl
- Параллельный Монте-Карло
- Более детально читаем в руководстве
- Курка и скришнот из игры Kynseed
- Источник арта
На этом, пожалуй, закончим. Всем умеренного процессорного тепла!


d5v
Ну что ж, буду первым подопытным:
julia> @time parallel_pi_computation(1000000000, ncores = 60)
0.094249 seconds (5.60 k allocations: 260.203 KiB)
3.1416588651668227
Спасибо за интересный материал и готовый пример.
Yermack Автор
60 ядер?! Круууть!
d5v
Кстати, зависимость времени от кол-ва точек практически идеально линейная (вплоть до 1e12 точек).
julia> @time parallel_pi_computation(1000000000, ncores = 60)
0.094249 seconds (5.60 k allocations: 260.203 KiB)
3.1416588651668227
julia> @time parallel_pi_computation(10000000000, ncores = 60)
0.923575 seconds (5.63 k allocations: 277.953 KiB)
3.141592570116815
julia> @time parallel_pi_computation(100000000000, ncores = 60)
9.466933 seconds (5.61 k allocations: 261.125 KiB)
3.14159586009168
julia> @time parallel_pi_computation(1000000000000, ncores = 60)
90.969203 seconds (5.72 k allocations: 270.672 KiB)
3.141590758957169
Yermack Автор
Триллион точек, чтоб получить точность до пятого знака — этот алгоритм мой самый любимый из самых непрактичных
P.S. Тут кстати большие числа можно так
1_000_000_000_000задавать, такой вот синтаксический сахарPand5461
А с чего ей-то быть нелинейной?
Вот насколько будет близко к обратной пропорциональности при изменении числа ядер и фиксированном количестве точек — это более важный для практики вопрос.
d5v
Pand5461
А что быстрее выходит — нативный
Distributed.jlилиMPI.jlс OpenMPI / MVAPICH?homocomputeris
Плохо, что нет CLArrays и CLBLAS для Julia 1.0, и без Nvidia делать нечего.
antonbatenev
И вот ощущение, что они сначала создают себе проблемы, а потом героически их преодолевают не покидает и во время чтения документации.
UA3MQJ
Если б не арты, я бы и не зашел )))