Что представляет собой цикл вычислений на квантовом компьютере?
1. Приготовили кубиты в нужном количестве и нужном нам начальном состоянии.
2. Собрали кубиты в квантовый регистр.
3. Применили к квантовому регистру последовательность операций.
4. Произвели измерение кубитов, составляющих квантовый регистр. Получили в итоге двоичное число, размерность которого совпадает с размерностью квантового регистра.
5. Поразмыслили над полученным результатом.
6. Повторили цикл вычислений (пункты с 1. по 5.), возможно, много раз.
7. Поразмыслили над результатом.
За каждым из пунктов стоят тома непрошибаемой теории. Но мы же программисты. Многие ли из нас знают так уж хорошо, что там и как крутится-вертится в классических процессорах. Да, практически, никто. Да оно, вроде бы, не очень и надо. Может и здесь как-нибудь так. Нам бы среду (IDE-шку какую-никакую, или чего там есть?), пару тезисов… мы чего-нибудь накалякаем, ткнём кнопочку “run”, квантовый компилятор (или чего там у них) выдаст нам синтаксис, мы его подправим. Глядишь, потихонечку пойдёт-поедет!
Отчего же не попробовать? Кто нам, в конце концов, запретит? Google нам в руки. Осмотримся! Во-первых, что там с ассортиментом квантовых компьютеров на рынке? Так. Понятно. Глухо! Поработать с живой железкой ещё не скоро доведётся. Люди даже выражают сомнения, доведётся ли вообще когда-нибудь. Ну, я имею в виду, с такой нормальной железкой, с несколькими сотнями кубитов, размером с ноутбук, и чтобы купить можно было недорого в любом ближайшем хозяйственном магазине. Да. Нескоро.
Ну и ладно. Но руки-то чешутся! А интуиция и образование подсказывают, что всё это квантовое вычислительное хозяйство вполне должно поддаваться (с какими-то ограничениями) моделированию на классических компьютерах. Поищем в этом направлении. Здесь уже получше ситуация. Но, всё-таки, на удивление мало живых/активных проектов. Совсем молодая область! Но кое-что есть. Особенно долго копаться, и привередничать не будем, возьмём первое, более-менее понятное и более-менее работающее. И, желательно, попроще. Например, QCad
Ну вот! Среда есть, кнопки есть. Нифига непонятно пока, по ходу разберёмся. Бегло пробежали глазами мануальчик и в бой!
Значит так: слева в главном окне – кубиты.
Есть панель-toolbox с иконками элементарных преобразований (гейтов), которые мы будем нанизывать на горизонтальные линейки с рисками.
По нажатию кнопки “run”, эти наши кубиты, как бы, побегут слева направо и будут последовательно пробегать сквозь гейты (т.е. претерпевать соответствующие преобразования) и, в конце концов, прибегут к правому краю окошка, полностью преобразованные в соответствии с нашей «программой» (последовательностью гейтов). А на правый конец линеек (всех или не всех, это уж как мы пожелаем), мы повесим иконки, символизирующие процесс измерения, которым заканчивается всякий цикл вычислений на квантовом компьютере. Сам же результат измерений в разных видах мы можем просмотреть в отдельном окошке.
Результат измерения квантового регистра – одно двоичное число. И процесс измерения – это вероятностный процесс. Т.е. мы на выходе получаем одно из возможных (вероятных) значений результата вычислений. А нам практически всегда требуется оценить распределение вероятностей. Чтобы оценить это искомое распределение, процесс вычисления надо бы повторить много раз. В окошке результата измерений (на вкладке «Measured», т.е. «Измеренное») разработчик QCAD выдаёт нам результат сразу в виде искомого распределения вероятностей каждого из возможных состояний регистра. Так разработчику намного проще моделировать, а пользователю намного проще анализировать результат.
Сходу может быть неочевидно, что кубит № 1 – это самый младший кубит регистра и в окошке результата в состоянии регистра он находится в позиции младшего бита, т.е – крайний справа.
Очень, конечно, интересно, как это реализовано (или, вернее будет сказать, может быть реализовано, потенциально) в железе, но первые же несколько робких и безуспешных попыток продраться сквозь зубодробительную теорию, основательно охлаждают этот интерес. Ну и ладно.
Кубит – это квантовомеханическая система. Кубит потому так и называется (ку — БИТ), что для нас, программистов, он выглядит имеющим всего два базисных состояния. А, стало быть, как учат нас первые строчки учебников квантовой механики, мы вправе ожидать, что, в общем случае, кубит будет скорее находиться в суперпозиции базисных состояний, чем в одном из «чистых» базисных. А в симуляторе мы видим слева (на входе) кубиты в состояниях |0> и |1>. Как так? Метнёмся в Google, осмотримся. Да, действительно. Квантовые инженеры-железячники уже научились «приготавливать» кубиты в «чистых» базисных состояниях. Ну и славно.
А чем замечательно базисное состояние (|0> или |1>)? Замечательно оно тем, что сколько бы раз мы ни применяли процедуру измерения к кубиту в одном из этих состояний, мы всегда будем получать определённый результат (0 или 1). Измерение в квантовой механике, как мы знаем, процесс вероятностный, а тут у нас результат будет определённый, т.е. вероятность будет равна 1.
Итак, приступаем к экспериментам с нашим симулятором! С чего начнём? Ну, вот все говорят: «Квантовые вычисления …, квантовые вычисления …»! Хочется уже понять, что это за квантовые вычисления такие? Идёшь, естественно, в Google, набираешь: «квантовые вычисления», и вываливается тебе много всего, но среди всего того, что вываливается, ты находишь либо какие-то общие слова, либо убойную математику, либо убойную физику. И хочется спросить: а где же собственно сами вычисления?! Но спросить особенно некого. Ну, вот давайте, пожалуй, с этого и начнём, попробуем смоделировать на нашей модели квантового компьютера самые обычные арифметические операции с двоичными числами.
Реализуем операцию сложения двух двухразрядных чисел. Три кубита используем для хранения результата (Q1, Q2, Q3), два кубита под первое слагаемое (Q4, Q5), два кубита под второе слагаемое (Q6, Q7) и ещё понадобится какое-то количество вспомогательных кубитов (для хранения бита переноса, например, и т.п.).
Первое, что мы делаем – создаём шаблон модели:
File -> new ->…
В появившемся диалоге
выбираем требуемое количество строк (т.е. кубитов) и столбцов (тактов вычислений) и жмём ОК.
В открывшемся пустом окне справа вешаем в нужных позициях иконки измерения,
и получаем готовый шаблон приложения.
Теперь, используя доступные нам гейты (элементарные преобразования), мы должны «собрать» искомую программу (сложение двух двухразрядных двоичных чисел). Я использовал для этого гейты «controlled not» и «controlled controlled not». Что они собой представляют и как работают, всякий может подсмотреть в своём «Карманном справочнике для квантового программиста».
Ниже на картинке приведена моя реализация решения задачи:
Очень возможно, что это решение покажется кому-то чудовищным, но, несомненно, — оно является решением! А как это проверить?
Если дважды кликнуть на квадратике с символом состояния кубита.
Откроется диалог:
c помощью которого можно выбрать начальное состояние каждого конкретного кубита.
Таким образом, задавая различные начальные состояния кубитам операндов, мы будем получать разные значения результата после нажатия кнопки “RUN”. А что у нас здесь будет результатом и как его посмотреть? Идём в окошке Qubits status на вкладку Measured и находим там состояние регистра, напротив которого стоит число (суть вероятность) 1.0.
Это и будет результат наших вычислений!
Ну что же, для самого первого знакомства с темой, пожалуй, хватит. Засим, позвольте откланяться.
Искренне ваш!
1. Приготовили кубиты в нужном количестве и нужном нам начальном состоянии.
2. Собрали кубиты в квантовый регистр.
3. Применили к квантовому регистру последовательность операций.
4. Произвели измерение кубитов, составляющих квантовый регистр. Получили в итоге двоичное число, размерность которого совпадает с размерностью квантового регистра.
5. Поразмыслили над полученным результатом.
6. Повторили цикл вычислений (пункты с 1. по 5.), возможно, много раз.
7. Поразмыслили над результатом.
За каждым из пунктов стоят тома непрошибаемой теории. Но мы же программисты. Многие ли из нас знают так уж хорошо, что там и как крутится-вертится в классических процессорах. Да, практически, никто. Да оно, вроде бы, не очень и надо. Может и здесь как-нибудь так. Нам бы среду (IDE-шку какую-никакую, или чего там есть?), пару тезисов… мы чего-нибудь накалякаем, ткнём кнопочку “run”, квантовый компилятор (или чего там у них) выдаст нам синтаксис, мы его подправим. Глядишь, потихонечку пойдёт-поедет!
Отчего же не попробовать? Кто нам, в конце концов, запретит? Google нам в руки. Осмотримся! Во-первых, что там с ассортиментом квантовых компьютеров на рынке? Так. Понятно. Глухо! Поработать с живой железкой ещё не скоро доведётся. Люди даже выражают сомнения, доведётся ли вообще когда-нибудь. Ну, я имею в виду, с такой нормальной железкой, с несколькими сотнями кубитов, размером с ноутбук, и чтобы купить можно было недорого в любом ближайшем хозяйственном магазине. Да. Нескоро.
Ну и ладно. Но руки-то чешутся! А интуиция и образование подсказывают, что всё это квантовое вычислительное хозяйство вполне должно поддаваться (с какими-то ограничениями) моделированию на классических компьютерах. Поищем в этом направлении. Здесь уже получше ситуация. Но, всё-таки, на удивление мало живых/активных проектов. Совсем молодая область! Но кое-что есть. Особенно долго копаться, и привередничать не будем, возьмём первое, более-менее понятное и более-менее работающее. И, желательно, попроще. Например, QCad
Ну вот! Среда есть, кнопки есть. Нифига непонятно пока, по ходу разберёмся. Бегло пробежали глазами мануальчик и в бой!
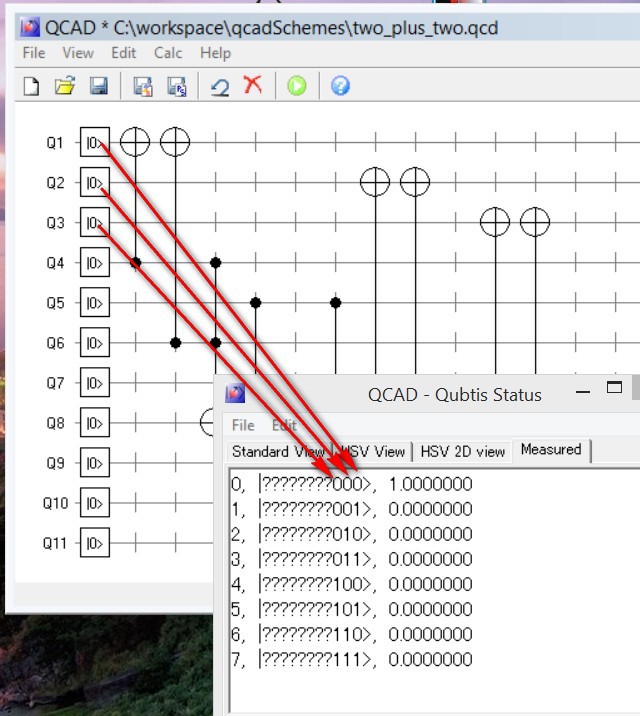
Значит так: слева в главном окне – кубиты.
Есть панель-toolbox с иконками элементарных преобразований (гейтов), которые мы будем нанизывать на горизонтальные линейки с рисками.
По нажатию кнопки “run”, эти наши кубиты, как бы, побегут слева направо и будут последовательно пробегать сквозь гейты (т.е. претерпевать соответствующие преобразования) и, в конце концов, прибегут к правому краю окошка, полностью преобразованные в соответствии с нашей «программой» (последовательностью гейтов). А на правый конец линеек (всех или не всех, это уж как мы пожелаем), мы повесим иконки, символизирующие процесс измерения, которым заканчивается всякий цикл вычислений на квантовом компьютере. Сам же результат измерений в разных видах мы можем просмотреть в отдельном окошке.
Хозяйке на заметку № 1
Результат измерения квантового регистра – одно двоичное число. И процесс измерения – это вероятностный процесс. Т.е. мы на выходе получаем одно из возможных (вероятных) значений результата вычислений. А нам практически всегда требуется оценить распределение вероятностей. Чтобы оценить это искомое распределение, процесс вычисления надо бы повторить много раз. В окошке результата измерений (на вкладке «Measured», т.е. «Измеренное») разработчик QCAD выдаёт нам результат сразу в виде искомого распределения вероятностей каждого из возможных состояний регистра. Так разработчику намного проще моделировать, а пользователю намного проще анализировать результат.
Хозяйке на заметку № 2
Сходу может быть неочевидно, что кубит № 1 – это самый младший кубит регистра и в окошке результата в состоянии регистра он находится в позиции младшего бита, т.е – крайний справа.
Очень, конечно, интересно, как это реализовано (или, вернее будет сказать, может быть реализовано, потенциально) в железе, но первые же несколько робких и безуспешных попыток продраться сквозь зубодробительную теорию, основательно охлаждают этот интерес. Ну и ладно.
Непонятка № 1
Кубит – это квантовомеханическая система. Кубит потому так и называется (ку — БИТ), что для нас, программистов, он выглядит имеющим всего два базисных состояния. А, стало быть, как учат нас первые строчки учебников квантовой механики, мы вправе ожидать, что, в общем случае, кубит будет скорее находиться в суперпозиции базисных состояний, чем в одном из «чистых» базисных. А в симуляторе мы видим слева (на входе) кубиты в состояниях |0> и |1>. Как так? Метнёмся в Google, осмотримся. Да, действительно. Квантовые инженеры-железячники уже научились «приготавливать» кубиты в «чистых» базисных состояниях. Ну и славно.
А чем замечательно базисное состояние (|0> или |1>)? Замечательно оно тем, что сколько бы раз мы ни применяли процедуру измерения к кубиту в одном из этих состояний, мы всегда будем получать определённый результат (0 или 1). Измерение в квантовой механике, как мы знаем, процесс вероятностный, а тут у нас результат будет определённый, т.е. вероятность будет равна 1.
Итак, приступаем к экспериментам с нашим симулятором! С чего начнём? Ну, вот все говорят: «Квантовые вычисления …, квантовые вычисления …»! Хочется уже понять, что это за квантовые вычисления такие? Идёшь, естественно, в Google, набираешь: «квантовые вычисления», и вываливается тебе много всего, но среди всего того, что вываливается, ты находишь либо какие-то общие слова, либо убойную математику, либо убойную физику. И хочется спросить: а где же собственно сами вычисления?! Но спросить особенно некого. Ну, вот давайте, пожалуй, с этого и начнём, попробуем смоделировать на нашей модели квантового компьютера самые обычные арифметические операции с двоичными числами.
Эксперимент № 1
Реализуем операцию сложения двух двухразрядных чисел. Три кубита используем для хранения результата (Q1, Q2, Q3), два кубита под первое слагаемое (Q4, Q5), два кубита под второе слагаемое (Q6, Q7) и ещё понадобится какое-то количество вспомогательных кубитов (для хранения бита переноса, например, и т.п.).
Первое, что мы делаем – создаём шаблон модели:
File -> new ->…
В появившемся диалоге
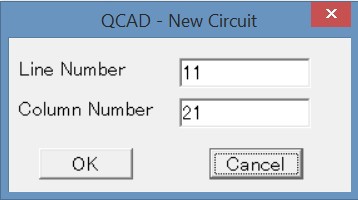
выбираем требуемое количество строк (т.е. кубитов) и столбцов (тактов вычислений) и жмём ОК.
В открывшемся пустом окне справа вешаем в нужных позициях иконки измерения,
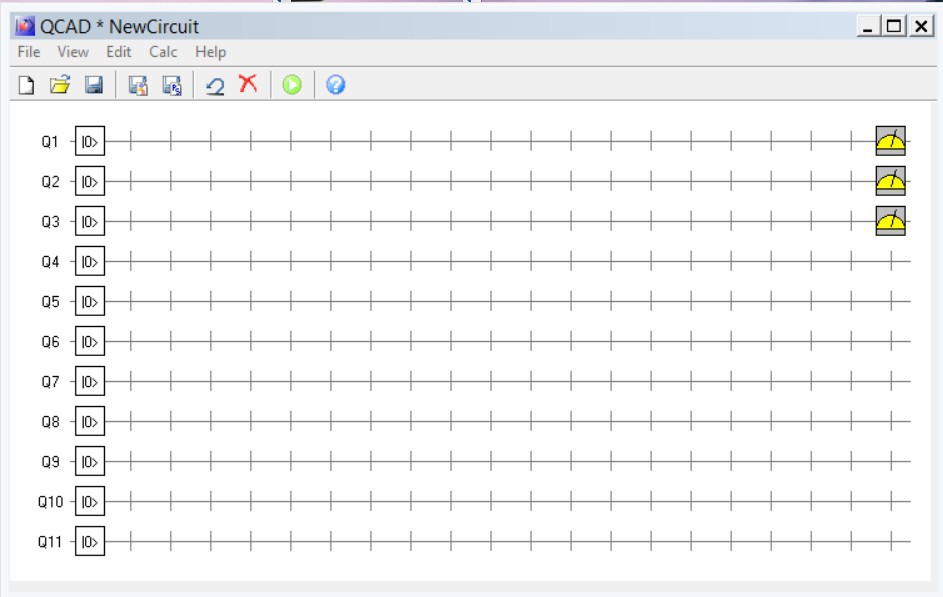
и получаем готовый шаблон приложения.
Теперь, используя доступные нам гейты (элементарные преобразования), мы должны «собрать» искомую программу (сложение двух двухразрядных двоичных чисел). Я использовал для этого гейты «controlled not» и «controlled controlled not». Что они собой представляют и как работают, всякий может подсмотреть в своём «Карманном справочнике для квантового программиста».
Ниже на картинке приведена моя реализация решения задачи:
Очень возможно, что это решение покажется кому-то чудовищным, но, несомненно, — оно является решением! А как это проверить?
Хозяйке на заметку № 3
Если дважды кликнуть на квадратике с символом состояния кубита.
Откроется диалог:
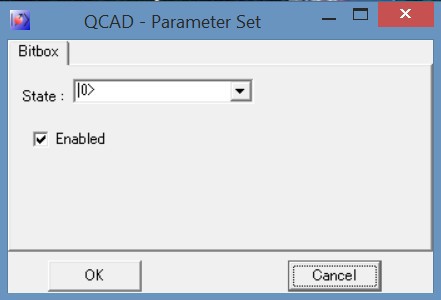
c помощью которого можно выбрать начальное состояние каждого конкретного кубита.
Таким образом, задавая различные начальные состояния кубитам операндов, мы будем получать разные значения результата после нажатия кнопки “RUN”. А что у нас здесь будет результатом и как его посмотреть? Идём в окошке Qubits status на вкладку Measured и находим там состояние регистра, напротив которого стоит число (суть вероятность) 1.0.
Это и будет результат наших вычислений!
Ну что же, для самого первого знакомства с темой, пожалуй, хватит. Засим, позвольте откланяться.
Искренне ваш!
Комментарии (27)
TheDeadOne
08.04.2015 14:55+9Многие ли из нас знают так уж хорошо, что там и как крутится-вертится в классических процессорах. Да, практически, никто.
В этом месте грустно вздохнул и укоризненно покачал головой.
dtestyk
08.04.2015 20:08мне кажется, и классический компьютер выдавал бы вероятности, если бы в схемах верхний порог напряжения низкого логического уровня совпадал с нижним высокого
zuborg
08.04.2015 21:24Было бы интересно увидеть игру на эту тему, что-то типа SpaceChem — составлять такие вот конвейеры из квантовых гейтов…
nckma
08.04.2015 23:26Я не знаю прав ли я или нет… Иногда думаю про квантовые компьютеры…
Представляю себе его так:
1) исходные биты — это несколько точечных синхронных источников света.
2) операция NAND (И-НЕ) — это точка в пространстве, где волны складываясь в противофазе подавляют друг друга. То есть, если недалеко от 2х источников света поставить черный экран с проколотой точкой, то она будет светиться только когда горит только один из двух входных сигналов — источников света. Если есть и первый и второй сигналы — на выходе ноль — сложение волн в противофазе.
3) теоретически из элементов NAND можно собрать любую логику
Проблема такого компьютера — сигнал после такого гейта сильно ослаблен.
dtestyk
09.04.2015 04:50сигнал после такого гейта сильно ослаблен
должен помочь аналог линзы Френеля, кроме того можно брать сразу много точек
а как вам такая модель: несколько слоев полупрозрачных зеркал. на границах слоев фотон может или пройти, или отразиться и находится в суперпозиции, пока его не задетектируют
можно варьировать толщину(фазовый сдвиг), коэффициент отражения, угол входа, потенциально можно добавить голографические и активные(допускающие накачку как в лазере) слои
назвал это активная ассоциативная рефлективная среда
p.s. идею подсказала архитектура иерархической темпоральной памяти
mwizard
09.04.2015 09:17К сожалению, вы придумали элемент XOR, а не NAND. Когда оба аргумента ложны, в вашем случае на выходе тоже будет ложь, тогда как в NAND для двух ложных аргументов на выходе должна быть истина.
Можно подумать о схеме с тремя лучами — двумя аргументами и одним опорным, который всегда включен. Т.е. с таблицей истинности типа такой:
x • y • P 0 • 0 • 0 ›› ? 0 • 1 • 0 ›› ? 1 • 0 • 0 ›› ? 1 • 1 • 0 ›› ? 0 • 0 • 1 ›› 1 0 • 1 • 1 ›› 1 1 • 0 • 1 ›› 1 1 • 1 • 1 ›› 0mwizard
09.04.2015 10:12ну или NOR, как вариант:
x • y • P 0 • 0 • 0 ›› ? 0 • 1 • 0 ›› ? 1 • 0 • 0 ›› ? 1 • 1 • 0 ›› ? 0 • 0 • 1 ›› 1 0 • 1 • 1 ›› 0 1 • 0 • 1 ›› 0 1 • 1 • 1 ›› 0
Если бы получилось сделать так, чтобы интерференция любого количества лучей больше одного приводила бы к «тишине», то получилось бы то, что нужно.dtestyk
09.04.2015 14:36тут написано:
Если фотоны посылать на границу раздела фаз строго в одной фазе движения, то… мы будем наблюдать только отраженный или только преломленный луч
Значит, можно настроить источник на пропускание. Пусть эта фаза будет +, противоположная ей: –.
+ • +| • – ›› + + • –| • – ›› – – • +| • – ›› – – • –| • – ›› –mwizard
09.04.2015 14:39Вы что, серьезно ссылаетесь на этот сайт? Или я не оценил шутку?
Блин, это просто восхитительно, одни только «вопросы-ответы» чего стоят! Весь этот сборник ахинеи можно разобрать на цитаты.dtestyk
09.04.2015 15:12Ссылаюсь только на экспериментальные данные(и то не как на факт, а скорее как на возможность), а не рассуждения автора.
Утверждение про фотон на границе можно проверить(людям, работающим в соответствующей области), но не так то просто найти достоверный источник.
Monnoroch
Вот это глупость. Вероятность 1 не гарантирует определенности эксперимента.
Например, вероятность того, что две прямые на плоскости непараллельны равна именно 1, но это же не исключает наличия параллельных прямых.
mark_ablov
ээ, а откуда у вас такая вероятность? стремится к 1, но не равно же.
niosus
Да нет, Monnoroch совершенно прав (с некоторыми необходимыми, как мне кажется, уточнениями).
Пусть нам дана прямая на плоскости и точка не на данной прямой. Вероятность провести прямую через эту точку, которая не будет параллельна данной будет как раз равна 1, ведь этих непараллельных прямых «ровно» бесконечность, а параллельная — всего одна: 1/INF == 0
mark_ablov
Насколько я знаю, обычно оперируют пределами, типа lim (1/x) = 0, при x -> inf, а записей 1/inf стараются избегать.
niosus
Конечно, но вы не можете избежать бесконечности, если она есть :)
alexzzam
Предел бывает у последовательности или у функции.
где n — количество случайных экспериментов, a — количество непараллельных прямых среди них. Предел в точности равен 1.
А вероятность это конкретное число, которое не может куда-то стремиться.
Если хотите, вероятность непараллельности прямых это значение предела
mikhanoid
Неа. Вероятность — это не такой предел в данном случае. Этот предел может быть равен вероятности, а может и не быть равен. Обычно в таких случаях вообще исследуют и определяют сходимость по вероятности, а не обычный предел из математического анализа. Ну, и неверно утверждать, что вероятность — это число. Вероятность — это мера множества, со всеми вытекающими свойствами, в том числе и с возможностью вычислять пределы.
alexzzam
Ну, вот есть у нас заданная прямая. Мы выбираем случайную точку на плоскости и проводим через неё случайную прямую. Вероятность того, что эта прямая окажется непараллельна заданной это же именно число, разве нет? Учитывая, что для любых заранее выбранных прямой и точки не на ней оно будет одинаковое. (Потому что аффинные преобразования не меняют параллельность) И тогда это число будет значением того предела, кажется.
Я не спорю, я правда плохо помню, объясните, пожалуйста.
mikhanoid
Направления, в которых будут проводится прямые образуют несчётное множество. В этом случае вероятность надо задавать функцией плотности вероятности, ну, а потом считать пределы и интегралы. Потому что вероятность — это всё же мера, а не число.
Тонкость вот в чём. Если бы вероятность была просто числом и нулевым в данном случае, то параллельной прямой просто не существовало бы.
А так можно задаваться таким вопросом: какова вероятность того, что в случайно выбранном конусе будет параллельная заданной прямая? И тому подобными.
blueboar2
У меня была такая задача — мы берем три точки на окружности, соединяем их линиями, и нужно найти вероятность получения равностороннего треугольника.
PsyHaSTe
Можно сказать более научным языком. Пусть мы случайном образом проводим прямую. Прямая задается уравнением y = ax с точностью до константы. Случайно выбирая a получаем всевозможные прямые. Нам требуется c равное нашей исходной прямой (иначе они будут не параллельны). Таким образом нам нужно найти вероятность того, что действительное число a будет равно с. Эта вероятность в точности равна нулю, т.к. это вероятность того, что непрерывная величина примет конкретное значение.
ChessShire
Отнюдь не единица, пока вы не определите механизм выбора прямой. Я, к примеру, собираюсь выбирать в 50% случаев параллельную прямую и в 50% случаев фиксированную непараллельную. У меня вероятность 0,5.
Подробнее — читайте про парадокс Бертрана.
Monnoroch
Я имел ввиду равномерный выбор среди всех пар прямых. Вы, разумеется, это поняли, но так же классно попридираться, да?
ChessShire
Разумеется, особенно когда в результате придирок кто-то может узнать что-то новое.
Monnoroch
Только вот оригинальный комментарий был совсем не про прямые, они вообще просто наглядной иллюстрацией служили, а ваши придирки получились совсем не в тему ни статьи ни моего комментария.
mikhanoid
Чтобы рассуждать о вероятности провести параллельную прямую, нужно сначала построить систему элементарных событий. Если Мы строим систему событий так: выбираем случайное направление, и в этом направлении строим прямую, то распределение вероятностей здесь будет совсем не таким, как распределение вероятностей при целенаправленном построении параллельной прямой.
Но даже если строить случайное равномерное распределение, то не всё так просто. Потому что вероятность провести параллельную прямую будет вычисляться как предел интеграла от дельта-функции по равномерной плотности. А это и будет сходимость с вероятностью, а не абсолютная сходимость.
В квантовой же механике, если вероятность равна 1, то именно этот результат измерения и получим. Ну. По крайней мере в случае с кубитами. Есть и другие, конечно, распределения. Например, вероятность поймать частицу в точке X ведёт себя точно так же, как вероятность провести параллельную прямую к заданной.
tendzin1966 Автор
Мне кажется, следует всё-таки проводить границу между теоретическими построениями (математикой) и результатами лабораторных опытов.
Допустим, у себя на кухне из чугунного котелка, газовой горелки, трёх клистирных трубок и магнита от сабвуфера я собрал установку, моделирующую один кубит. Я с ней долго экспериментирую, что-то вычисляю, а потом, укоризненно качая головой, сажусь за стол и пишу письмо.
«Гильберту (копия фон Нейману).
Уважаемые господа, из того, что я прочитал в ваших знаменитых работах, я понял, что вы искренне считаете, будто бы если, скажем, H – сепарабельное гильбертово пространство, A – ограниченный самосопряжённый оператор на этом пространстве, x0 –собственный вектор этого оператора, а0 – соответствующее собственное число, то всегда будет выполняться равенство
Ax0 = a*x0, где а = а0
Я провёл тщательнейшую проверку этого утверждения [приводится чертёж установки] и вынужден сообщить вам, что оно не верно. На самом деле, равенство выполняется примерно в 999999 случаях из миллиона. В остальных случаях мы имеем
Ax0 = a*x0, где a = 0.715
Надеюсь на ваше мужество и научную честность и ожидаю, что в ближайшем будущем вы сами опубликуете опровержение ваших работ в «Nature», «Physical Review» и «Успехах физических наук».
Искренне ваш!»
Понятно, что я на этом не успокаиваюсь. Я беру большую линейку, угольник, калькулятор и пневматический пистолет, строю какие-то линии и точки на стене своей комнаты, а потом начинаю в эту стену стрелять. После каждого выстрела что-то измеряю и вычисляю. Потом снова, укоризненно качая головой, сажусь за стол и пишу новое письмо.
«Лебегу (копия Борелю и Колмогорову)
Уважаемый господин Лебег. Я подверг тщательнейшей проверке ваше утверждение о том, что мера Лебега одиночной точки равна нулю [приводится фотография метровой деревянной линейки, угольника и пневматического пистолета] и вынужден вам сообщить, что оно не верно.
На самом деле, мера (Лебега) одиночной точки равна (примерно) 0.00267, поскольку примерно на 375-м выстреле (я там немножко сбился со счёта в конце, но это не так важно) я попал ровно в точку, через которую сумел провести прямую параллельную заданной.
Надеюсь в скором времени увидеть на полках магазинов новые, исправленные редакции учебников по матанализу (а заодно и по теории вероятностей).
Искренне ваш!»
Безусловно, я как и вы (Monnoroch) считаю, что в реальных экспериментах с физическими («железными») реализациями кубитов мы будем получать всё что угодно, независимо от того, кто там и как определял пространства, операторы и вероятности (ведь именно в этом и был главный посыл вашего комментария, я прав?). Но это только с одной стороны. С другой стороны, результат применения оператора к собственному вектору останется определённым независимо от того, что мы там намеряем со своими клистирными трубками.
А экспериментатору, который измеряя свои кубиты вдруг обнаруживает что-то, чего совсем не ожидал, остаётся только считать, что либо состояние, которое он «приготовил» было не совсем «чистым», либо при измерении что-то не заладилось, ну или писать такие вот письма Гильберту и Колмогорову.
Последнее я лично ему делать не советовал бы, ибо, как говорил Воланд: «…Над вами потешаться будут...»