Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.
Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.

Список лекций
Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.
Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.
Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:
- Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
- Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
- Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка
- Случайные процессы. Белый шум. Функция плотности вероятностей
- Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция
- Фильтрация сигналов: БИХ, КИХ фильтры
- Оконные функции в задачах фильтрации. Детектирование слабых сигналов.
- Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего
Список лекций — достаточный
Где найти?
Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).
Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!
Сигналы. Z-преобразование
Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).
Все сигналы по способу представления на множестве можно разделить на четыре группы:
- аналоговые — описываются непрерывными во времени функциями,
- дискретные — прерываются во времени с шагом заданным дискретизации,
- квантованные — имеют набор конечных уровней (как правило, по амплитуде),
- цифровые — комбинация свойств дискретных и квантованных сигналов.
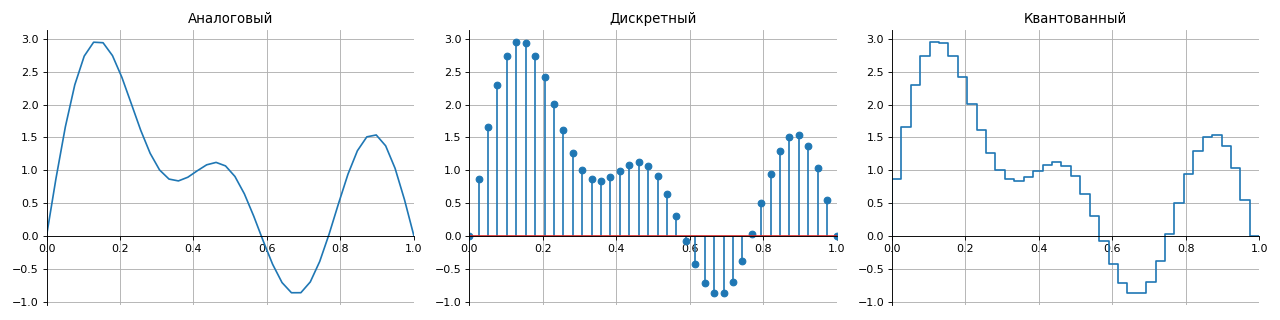
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.
Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.
Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.
Пример конечной дискретной последовательности:
x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}Пример этой же последовательности в Z-форме:
X(z) = 2 + z-1 — 2z-2 + 2z-4 + 3z-5 + 1z-6
Преобразование Фурье. Свойства. ДПФ и БПФ
В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.
В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).
Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.
Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.
Спектр гармонического сигнала:
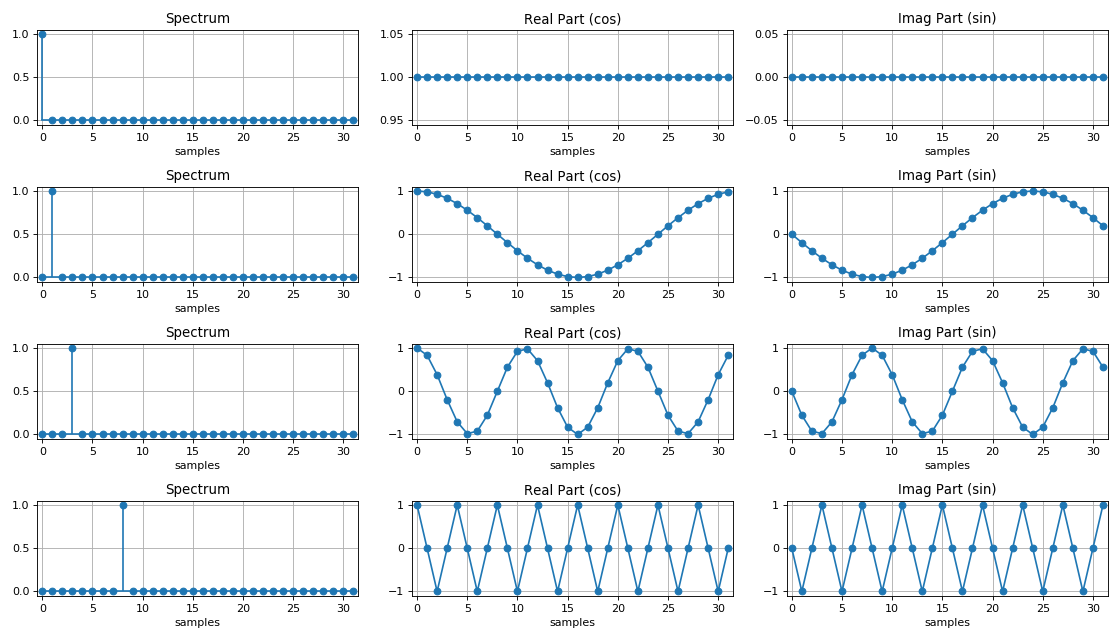
Сравнение эффективности ДПФ и БПФ
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:
| N | ДПФ | БПФ | Отношение числа комплексных сложений | Отношение числа комплексных умножений | ||
|---|---|---|---|---|---|---|
| Число операций умножения | Число операций сложения | Число операций умножения | Число операций сложения | |||
| 2 | 4 | 2 | 1 | 2 | 4 | 1 |
| 4 | 16 | 12 | 4 | 8 | 4 | 1.5 |
| 8 | 64 | 56 | 12 | 24 | 5.3 | 2.3 |
| 16 | 256 | 240 | 32 | 64 | 8 | 3.75 |
| 32 | 1024 | 992 | 80 | 160 | 12.8 | 6.2 |
| 64 | 4096 | 4032 | 192 | 384 | 21.3 | 10.5 |
| 128 | 16384 | 16256 | 448 | 896 | 36.6 | 18.1 |
| ... | ... | ... | ... | ... | ... | ... |
| 4096 | 16777216 | 16773120 | 24576 | 49152 | 683 | 341 |
| 8192 | 67108864 | 67100672 | 53248 | 106496 | 1260 | 630 |
Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!
Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.

Свертка и корреляция
В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.
В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.
Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).
В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).
Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.
| N | Свертка | Быстрая свертка | Отношение |
|---|---|---|---|
| 8 | 64 | 448 | 0.14 |
| 16 | 256 | 1088 | 0.24 |
| 32 | 1024 | 2560 | 0.4 |
| 64 | 4096 | 5888 | 0.7 |
| 128 | 16K | 13312 | 1.23 |
| ... | ... | .. | ... |
| 2048 | 4M | 311296 | 13.5 |
Случайные сигналы и шум
В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
- закон распределения (относительное время пребывания значения сигнала в определенном интервале),
- спектральное распределение мощности сигнала.
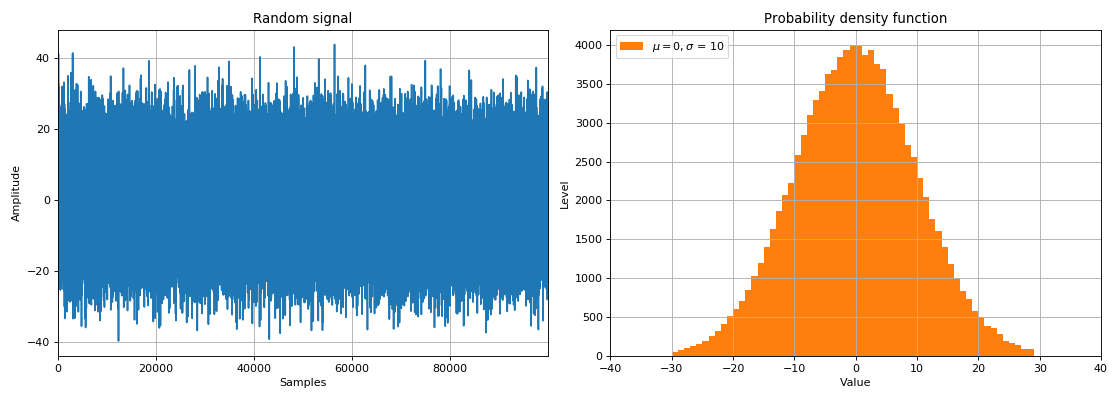
В задачах ЦОС случайные сигналы делятся на два класса:
- шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
- сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.
С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).
Сигналы, модуляция и манипуляция
В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.

Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
"""
Create Chirp signal
Parameters
----------
amp : float
Signal magnitude
beta : float
Modulation bandwidth: beta < N for complex, beta < 0.5N for real
freq : float or int
Linear frequency of signal
period : integer
Number of points for signal (same as period)
kwargs : bool
Complex signal if is_complex = True
Modulated by half-sine wave if is_modsine = True
"""
is_complex = kwargs.get('is_complex', False)
is_modsine = kwargs.get('is_modsine', False)
t = np.linspace(0, 1, period)
tt = np.pi * (freq * t + beta * t ** 2)
if is_complex is True:
res = amp * (np.cos(tt) + 1j * np.sin(tt))
else:
res = amp * np.cos(tt)
if is_modsine is True:
return res * np.sin(np.pi * t)
return res
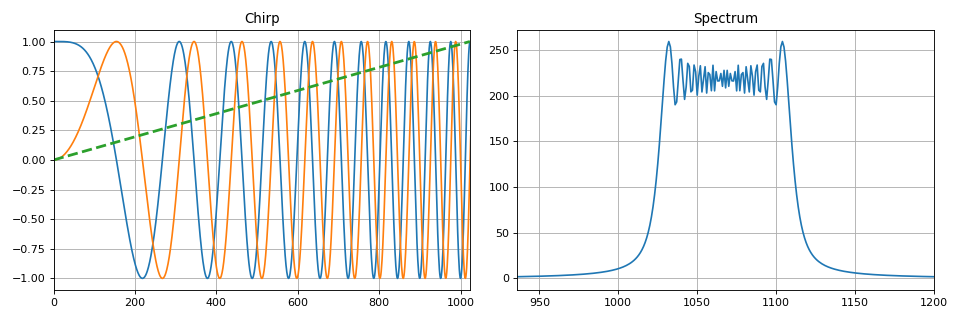
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).

Цифровые фильтры — БИХ и КИХ
Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.

В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.
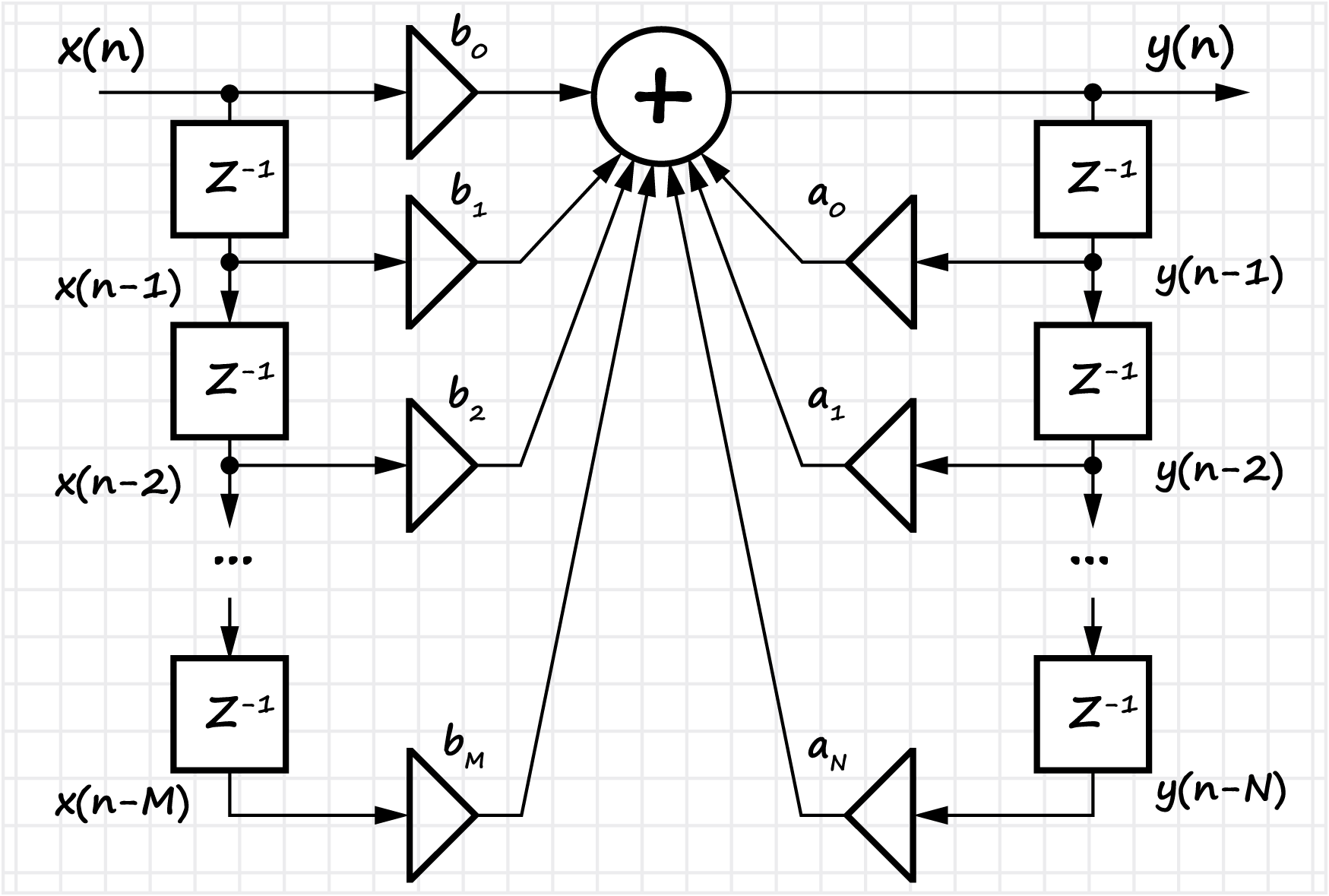
Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.

Оконные функции в задачах фильтрации
В задачах цифровой обработки сигналов используются оконные функции различной формы, которые при наложении на сигнал во временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Правило:
Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).
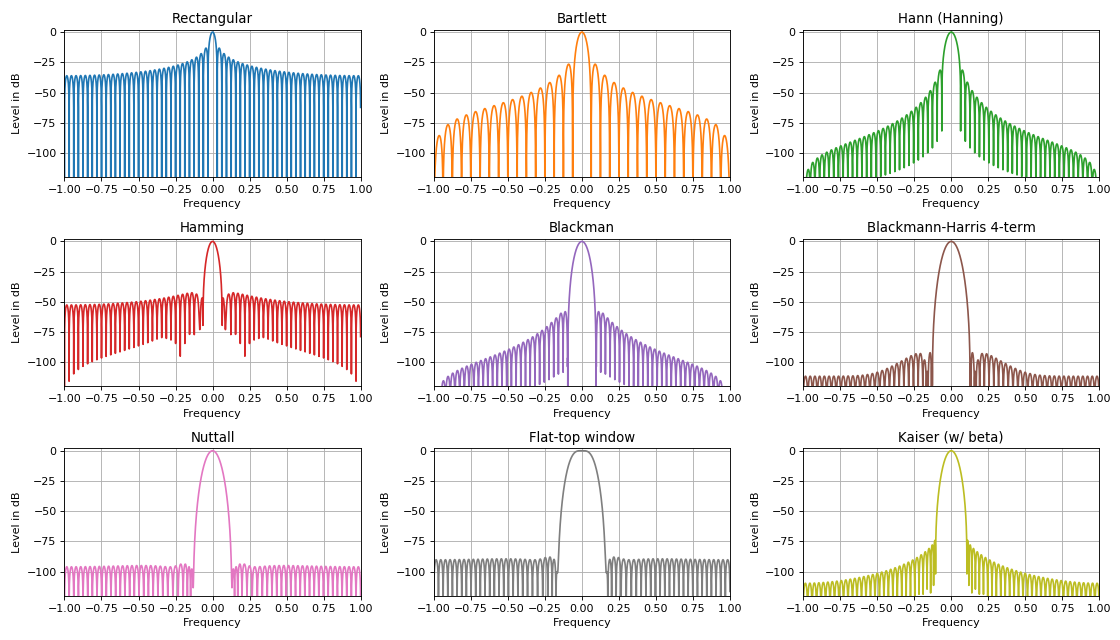
Ресемплинг. Децимация и интерполяция
В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.
Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.
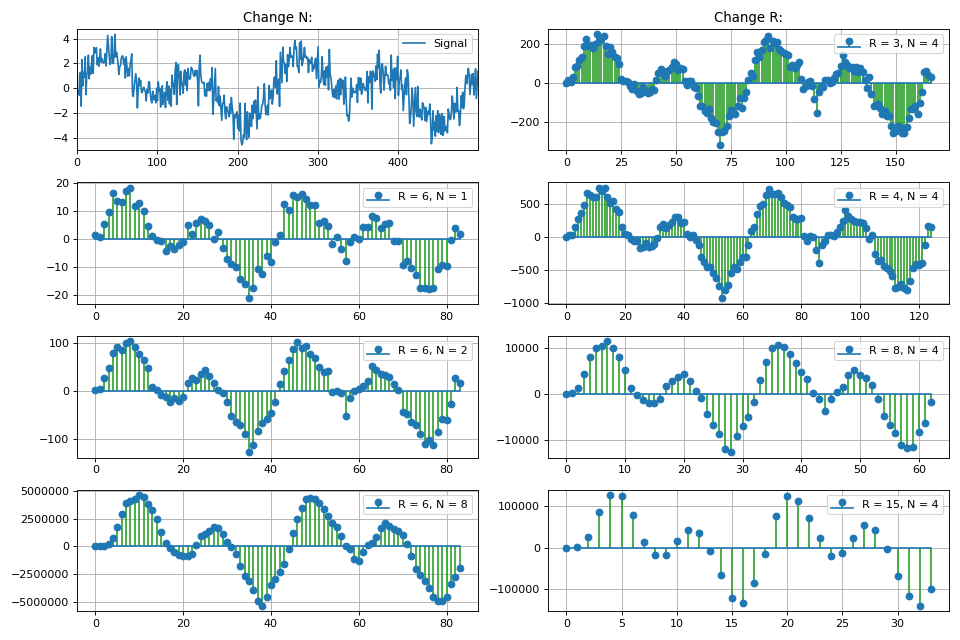
Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.
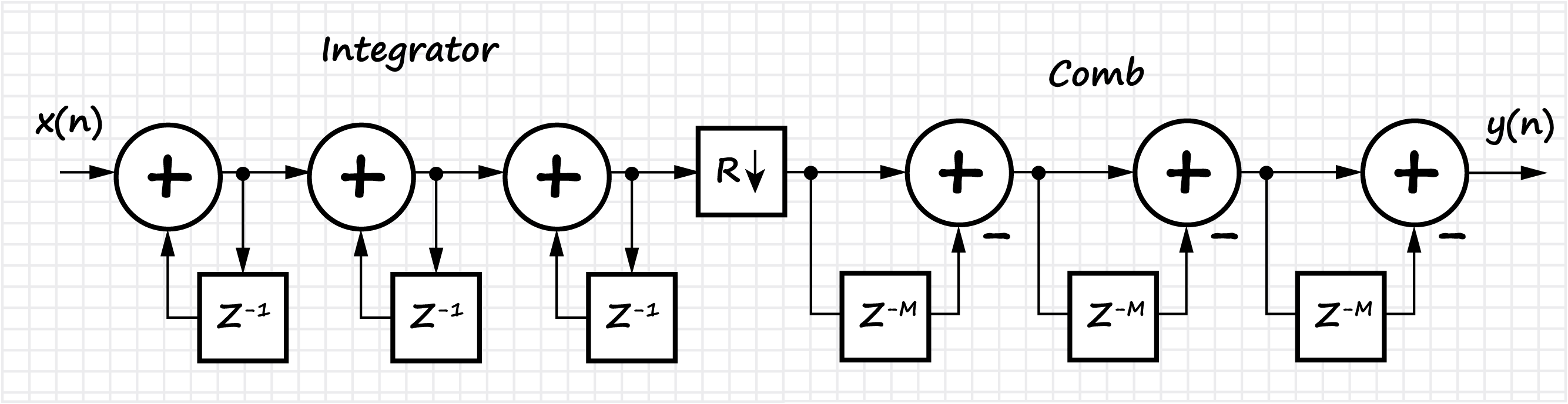
График АЧХ фильтра в зависимости от коэффициента децимации:
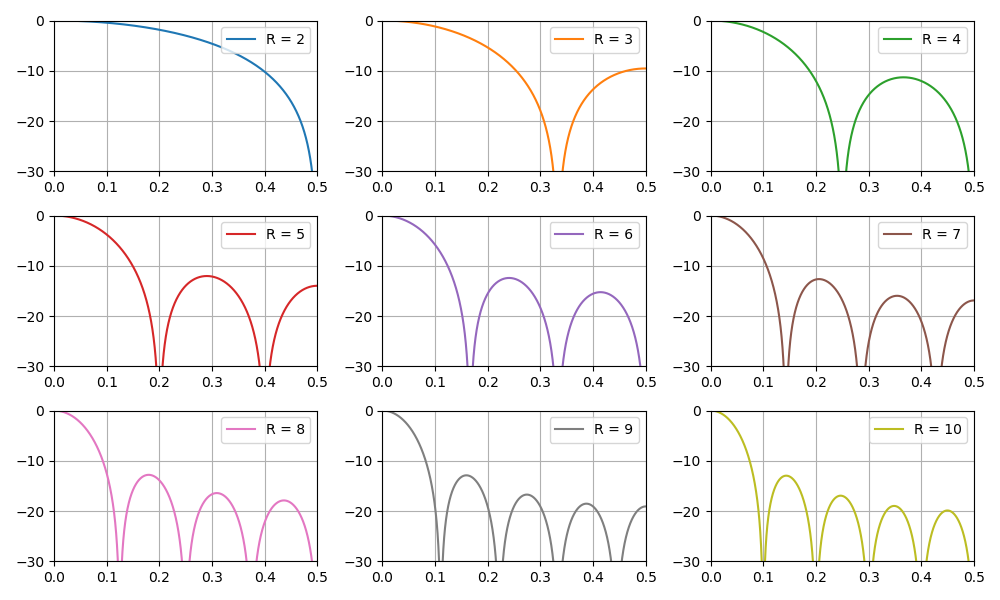
Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.
Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.
class CicFilter:
"""
Cascaded Integrator-Comb (CIC) filter is an optimized class of
finite impulse response (FIR) filter.
CIC filter combines an interpolator or decimator, so it has some
parameters:
R - decimation or interpolation ratio,
N - number of stages in filter (or filter order)
M - number of samples per stage (1 or 2)*
* for this realisation of CIC filter just leave M = 1.
CIC filter is used in multi-rate processing. In hardware
applications CIC filter doesn't need multipliers, just only
adders / subtractors and delay lines.
Equation for 1st order CIC filter:
y[n] = x[n] - x[n-RM] + y[n-1].
Parameters
----------
x : np.array
input signal
"""
def __init__(self, x):
self.x = x
def decimator(self, r, n):
"""
CIC decimator: Integrator + Decimator + Comb
Parameters
----------
r : int
decimation rate
n : int
filter order
"""
# integrator
y = self.x[:]
for i in range(n):
y = np.cumsum(y)
# decimator
y = y[::r]
# comb stage
return np.diff(y, n=n, prepend=np.zeros(n))
def interpolator(self, r, n, mode=False):
"""
CIC inteprolator: Comb + Decimator + Integrator
Parameters
----------
r : int
interpolation rate
n : int
filter order
mode : bool
False - zero padding, True - value padding.
"""
# comb stage
y = np.diff(self.x, n=n,
prepend=np.zeros(n), append=np.zeros(n))
# interpolation
if mode:
y = np.repeat(y, r)
else:
y = np.array([i if j == 0 else 0 for i in y for j in range(r)])
# integrator
for i in range(n):
y = np.cumsum(y)
if mode:
return y[1:1 - n * r]
else:
return y[r - 1:-n * r + r - 1]
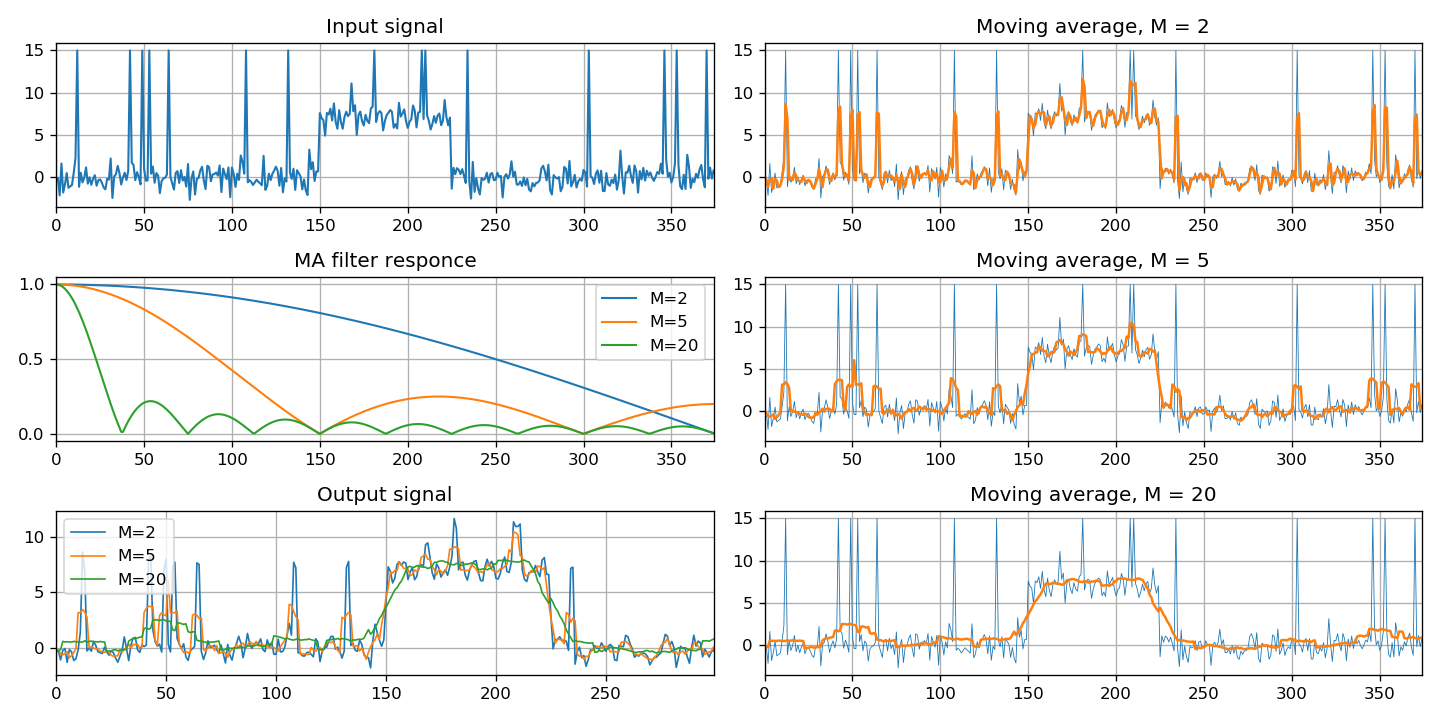
Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.
Заключение
Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!
Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).
Спасибо за внимание!
Комментарии (57)

chaffinch
18.07.2019 14:31+1ИМХО — все подобные курсы позиционируют себя для изучения обработки сигналов, в реальности же они хороши только для освежения забытых знаний. Если базовых знаний нет — надо курить опенгеймера…

Gryphon88
18.07.2019 15:56Можете посоветовать разбор теоремы Найквиста с последовательным усложнением? Типа вначале вводится бесшумный бесконечный по времени сигнал и дискретизация с дельта-функцией, потом сигнал становится конечным, появляется шум, АЦП тоже становится неидеальным (интегрирование по времени вместо точечного «выкалывания»)…

Egrace
18.07.2019 19:07+1Я считаю, что более правильно эту теорему называть теоремой Котельникова. А вот частоту, равную половине частоты дискретизации (о которой идет речь в теореме) — частотой Найквиста.

red-cat-fat
18.07.2019 19:07Огромное спасибо! Мне, как студенту эти материалы очень пригодятся для ознакомления!

Occamlab
18.07.2019 23:48Очень круто, главное не забросить…
Очень нехватает вейвлетов.
тут цифровая обработка сигналов, глазами химика, постоянно обновляется:
terpconnect.umd.edu/~toh/spectrum/IntroToSignalProcessing.pdf
capitanov Автор
19.07.2019 03:30Вейвлеты есть в планах. В принципе набор тем, которые я планирую добавить тянет на полноценный курс, не меньший этого. Спасибо :)

ZEvS_Poisk
19.07.2019 00:53Отличная статья!
Однако хотел-бы поправить:
Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (среднеквадратическое отклонение).
Дисперсия и среднеквадратичное отклонение это не одно и то-же. СКО это корень из дисперсии.
capitanov Автор
19.07.2019 03:31Про дисперсию и ско сделаю уточнение, дабы не вводить в заблуждение, спасибо!

Navigator_Pirks
19.07.2019 03:27+1Цитата: «Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.»
На самом деле:
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной ширины полосы частот, занимаемой спектром непрерывного сигнала.
capitanov Автор
19.07.2019 03:39Либо добавить уточнение, что спектр сигнала лежит в диапазоне от 0 до fв. Спасибо за замечание!

Refridgerator
19.07.2019 05:44Да — часто забывают, что теорема Котельникова в оригинале рассматривает полосы частот в радиоэфире. Соответственно и для дискретизации узкополосных гигагерцовых сигналов вовсе не нужен гигагерцовый АЦП.

AAE
19.07.2019 12:24Позвольте вопрос, чтобы понять Вашу терминологию. Прямой спектр действительного сигнала отличен от нуля в полосе частот от 1 до 3 кГц. Какая ширина (в кГц) полосы этого сигнала?

Navigator_Pirks
19.07.2019 14:26Без сомнения, ширина полосы частот, занимаемой указанным сигналом — 2 кГц. И для обеспечения возможности его дальнейшего восстановления достаточно частоты сэмплирования > 4 кГц.

AAE
19.07.2019 14:35А по какой формуле Вы сможете восстановить сигнал без потерь с такой частотой дискретизации?
Я к тому спрашиваю, что Ваше утверждение «Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной ширины полосы частот, занимаемой спектром непрерывного сигнала» не верно, место я указал курсивом.
Refridgerator
19.07.2019 20:15Да вроде всё правильно — теоремы Котельникова IV и V говорят же об этом прямым текстом. Математически это выглядит как-то так: непрерывный сигнал восстанавливается свёрткой дискретного с функцией sinc, затем приводится к аналитическому виду, затем линейно сдвигается вверх по частоте умножением на комплексную синусоиду. Если сдвиг по частоте выше частотной полосы, можно просто умножить на синусоиду и отфильтровать отрицательную часть частот.

AAE
19.07.2019 21:03Не совсем так. Посмотрите, что у Котельникова в теореме V:
1. Дискретизация с частотой f1+f2 (в действительности с частотой 2(f2+f1), если без временного сдвига делать) — получение отсчетов F1 и F2, то есть, отсчетов квадратур.
2. Восстановление квадратур F1 и F2 рядами Котельникова по синкам — получение непрерывных F1(t) и F2(t).
3. И только теперь их дискретизация с частотой 2(f2-f1).
4. Передача отсчетов квадратур по каналу связи (это те самые «числа», которые фигурируют в формулировке теоремы V).
5. Восстановление квадратур F1 и F2 рядами Котельникова по синкам получение непрерывных F1(t) и F2(t).
6. Восстановление F(t) по формуле (13) из теоремы IV.
То есть, Вы сформулировали всё правильно, за исключением того, что исходный сигнал F(t) восстанавливается не по своим отсчетам, а по отсчетам F1(t) и F2(t).
Но автор в формулировке теоремы Котельникова написал про восстановление именно по своим дискретным отсчетам, как у Котельникова и Шеннона и звучит. Вот поэтому, по-моему, Вы не корректно поправили автора.
Refridgerator
19.07.2019 21:14что исходный сигнал F(t) восстанавливается не по своим отсчетам, а по отсчетам F1(t) и F2(t)
Дискретизируется-то по своим же. Вот так это происходит:

При идеальном восстановлении отсчёты будут совпадать.
AAE
19.07.2019 21:22Нет, не по своим.
Пусть f1=1, f2=4. По теореме V у Котельникова частота дискретизации равна f1+f2=5 (или 10 без временного сдвига). Передаваемые по каналу отсчеты квадратур получаются с частотой 2(f2-f1)=6. При частоте 2(f2-f1)=6 отсчеты квадратур не равны отсчетам исходного сигнала.
Refridgerator
19.07.2019 21:35частота дискретизации равна f1+f2=5
Разве? А не 2*(f2-f1)=6? Откуда сложение-то взялось?
AAE
19.07.2019 22:00В теореме V у Котельникова. Я же выше написал, как там (в этой теореме) доказательство делается.
Давайте по другому. В самом начале я привел пример действительного сигнала, у которого спектр отличен от нуля в полосе частот от 1 до 3 кГц. Дискретизируем его с частотой 2*(f2-f1)=4 кГц. Теперь напишите формулу (формулы), по которой можно восстановить сигнал без потерь по полученным так отсчетам.
Refridgerator
20.07.2019 09:34Хорошо, давайте по-другому.
При дискретизации непрерывный сигнал умножается на гребёнку Дирака. Его отсчёты, совпадающие с отсчётами гребёнки Дирака, никуда не деваются.
При этом их спектры сворачиваются. И если период решётки меньше длины спектра — произойдёт их наложение и восстановление будет невозможно.
Ну а поскольку вследствие свёртки спектр «размножился», то восстановление происходит простой фильтрацией в частотном домене в исходной полосе частот. Исходные отсчёты исходного сигнала продолжают оставаться на своих местах.

AAE
20.07.2019 10:20У Вас при дискретизации с частотой 2(f2-f1) и будут наложения, вплоть до полного обнуления. И вот пример.
Возьмем функцию S(t)=sin(2pif1t)/(2pif1t), f1=1 кГц. Функция четная, её спектр действителен и имеет форму прямоугольника на интервале частот от минус f1 до f1, высота прямоугольника равна 1/(2f1). Центральная частота прямоугольника = 0. Нули функции расположены в моменты времени kdt1=k/(2f1), k целое, не равное 0.
Теперь пусть функция F(t)=S(t)*sin(2pi(f2-f1)t)=sin(2pif1t)/(2pif1t)*sin(2pi(f2-f1)t), f2=3 кГц. F(t) — нечетная, её спектр чисто мнимый и состоит из двух прямоугольников (по форме как у функции S(t)) — один прямоугольник (прямой спектр)
c центральной частотой (f2-f1), второй прямоугольник (инверсный спектр) с центральной частотой минус (f2-f1) и с противоположным знаком по отношению к первому. Нули F(t) расположены в моменты времени kdt1=k/(2f1) и ndt2=n/(2(f2-f1)), k,n — целые. Заметим, что моменты времени kdt1=k/(2f1) вложены в моменты ndt2=n/(2(f2-f1)), то есть (совсем не важно для примера, но для порядку) нули функции F(t)=sin(2pif1t)/(2pif1t)*sin(2pi(f2-f1)t) для наших значений f1 и f2 расположены в моменты времени ndt2=n/(2(f2-f1)), n — целое.
Что имеем при дискретизации F(t) с частотой Fs=2(f2-f1) в моменты времени ndt2=n/(2(f2-f1)):
— в частотной области — полное наложение прямого и инверсного спектров на интервале частот от f1 до f2 (а прямой и инверсный спектры одинаковы по форме — прямоугольники — и с противоположными знаками) с результатом наложения в виде тождественного нуля на всем диапазоне частот от 0 до Fs;
— во временной области — те же самые нули (в нули функции F(t) мы попали).
Весьма предсказуемый результат в данном примере от дискретизации с частотой 2(f2-f1).
Посмотрим внимательно на F(t)=sin(2pif1t)/(2pif1t)*sin(2pi(f2-f1)t). Разложение на квадратуры очевидно: F1(t)=0, F2(t)=sin(2pif1t)/(2pif1t). Функцию F2(t) без потерь можно дискретизировать с частотой Fs=2(f2-f1) в моменты времени
ndt2=n/(2(f2-f1), результатом будут все нули, кроме одной единицы при t=0. Можно ли восстановить после такой дискретизации F2(t) без потерь? Можно.
Можно ли восстановить после такой дискретизации F(t) без потерь? Тоже можно.
Об этом и говорит Котоельников в теореме V. Для доказательства он четыре (!) раза производит дискретизацию:
— первый раз исходную F(t) с частотой f1+f2 в моменты времени k/(f1+f2) для получения отсчетов F1(t);
— второй раз исходную F(t) с частотой f1+f2, но в моменты времени (k+0.5)/(f1+f2) для получения отсчетов F2(t);
— третий раз функцию F1(t) с частотой f2-f1 в моменты времени k/(f2-f1) для получения отсчетов F1(t), эта дискретизация отличается по частоте от первой (!);
— четвертый раз функцию F2(t) с частотой f2-f1 в моменты времени k/(f2-f1) для получения отсчетов F2(t), эта дискретизация отличается по частоте от второй (!).
Полученные в третьей и четвертой дискретизациях отсчеты он передает как «числа» (термин из теоремы V), но поскольку одному моменту дискретизации соответствуют два «числа» (от третьей и четвертой дискретизаций), то частоту следования этих
чисел он определяет как 2(f2-f1), то есть в 2 раза больше, чем при третьей и четвертой дискретизациях.
Восстановление по этим «числам» очевидно — сначала через ряд (1) восстанавливаются F1(t) и F2(t), затем вычисляется F(t) по формуле (13).
Убедил?:)
По поводу умножения на гребёнку Дирака — это отдельная и на мой взгляд весьма любопытная тема. Если хотите, можно её обсудить, но не в рамках этой ветки. Можно и по электронной почте. Для затравки — спектры при дискретизации не «размножаются» и периодически не повторяются.
Прошу прощения за «много букв».

Refridgerator
20.07.2019 10:41Нет, не убедили. Но и продолжать спорить мне жалко времени. Кроме того, в ваших выкладках я не обнаружил сумму дельта-функций Дирака, описывающих дискретный сигнал.
Для затравки — спектры при дискретизации не «размножаются» и периодически не повторяются.
Вроде бы как спектр от гребёнки Дирака — это тоже гребёнка Дирака, и теорему о свёртке вроде бы тоже никто не отменял.
AAE
20.07.2019 10:54А без «гребёнки Дирака» у Вас не получается? А ведь «гребёнки Дирака» только один из методов (способов) упрощения жизни, и не более того.
Давайте с ней. Сверните F(t) из моего примера с гребёнкой Дирака, и получите те же самые наложения прямого и инверсного спектров. В примере прямой спектр весь лежит между двумя дельта-функциями (первая пара), а инверсный тоже лежит между двумя дельта-функциями (вторая пара), но только не между первыми двумя, а между соседней парой (а не между первыми двумя, как надо бы, чтобы потерь не было). При свёртке спектры между соседними парами тупо складываются, в моем примере полностью перекрываются — возникают наложения и потери.
Refridgerator
20.07.2019 11:47А без «гребёнки Дирака» у Вас не получается? А ведь «гребёнки Дирака» только один из методов (способов) упрощения жизни, и не более того.
Гребёнка Дирака — это функция, хорошо подходящая для строго математического описания процедуры дискретизации. Когда Котельников сформулировал свою теорему — законченной теории ЦОС ещё попросту не было, поэтому он оперировал теми понятиями, которые были ему доступны на тот момент.
В примере прямой спектр весь лежит между двумя дельта-функциями (первая пара), а инверсный тоже лежит между двумя дельта-функциями (вторая пара), но только не между первыми двумя
Инверсный спектр мы (я) обнулили приведением сигнала к аналитическому виду, поэтому он ни на что не наложится.
AAE
20.07.2019 12:51Про гребёнку Дирака и строгую математику Вы несколько неправы. Строгая математика тут — функциональный анализ и изоморфизм L2 и l2(эль малое), а не предложенное (кем и когда, подсказать?) и притянутое за уши (чтобы воткнуть между L2 и l2 что-то такое, что аппаратом обобщенных функций не переваривается ни под каким соусом) нечто, да еще с паровозом в виде периодизации спектра и бесконечных энергий.
И очень интересно, где это Вы при дискретизации инверсный спектр обнулили? А если перед дискретизацией Вы привели сигнал к аналитическому виду, то откуда в процессе дискретизации аналитического (или его же в ноль смещенного) отсчеты исходной функции взяли?
Еще раз — с частотой дискретизации Fs=2(f2-f1) можно без потерь дискретизировать квадратуры (функции F1(t) и минус F2(t)), мгновенные значения которых (отсчеты) в моменты времени k/Fs не равны исходной функции в те же моменты времени, о которых написал Navigator_Pirks в своём замечании.

AAE
20.07.2019 13:01У меня есть к Вам просьба — подскажите, пожалуйста, литературу, в которой определена операция умножения дельта-функции Дирака с произвольной функцией.

Refridgerator
20.07.2019 16:21«On the Duality of Discrete and Periodic Functions», например. Ну и Wolfram с этим тоже прекрасно справляется.

AAE
20.07.2019 17:18Конечно, хотелось бы что-то из Владимирова. Но это не важно.
И у Владимирова и в указанных Вами материалах я не встретил определения операции умножения дельта-функции на другую функцию. Скалярное произведение есть. Но определения простого умножения, которое встречается у Вас в тексте («При дискретизации непрерывный сигнал умножается на гребёнку Дирака»), там нет. И не ищите. Эта операция не определена. Это к вопросу о математической строгости. В литературе встречается результат свертки гребёнки дирака с взвешенной дискретизируемой функцией — взвешенная (пропорционально отсчетам) сумма дельта-функций. Но никак не результат «умножения».
И, простите, пожалуйста, но «Гребёнка Дирака — это функция» (Ваши слова) — это совсем неправда.
Но у нас речь о дискретизации с частотой 2(f2-f1). Вы принимаете мои слова «с частотой дискретизации Fs=2(f2-f1) можно без потерь дискретизировать квадратуры» (и только квадратуры, если f1 > 0), но никак не исходный сигнал? Или настаиваете на версии Navigator_Pirks?
И если Вам интересно, подскажу кто и когда (и литературу Вам в электронном виде смогу переслать) ввел в дискретизацию гребёнку Дирака и зачем.

Gryphon88
20.07.2019 18:24И если Вам интересно, подскажу кто и когда (и литературу Вам в электронном виде смогу переслать) ввел в дискретизацию гребёнку Дирака и зачем.
Мне интересно, так что прошу. В книгах, которые мне попадались, comb function появляется как-то вдруг.
AAE
20.07.2019 18:27Я тут совсем недавно, поэтому прицепить сюда пока не знаю как. Можно по электронной почте, напишите мне на 729@inbox.ru, в ответе перешлю книгу в djvu. Или подскажите, пожалуйста, как тут файл прицепить.

AAE
20.07.2019 20:04Ссылка на книгу, о которой писал — yadi.sk/i/rEAbcdNoH8OnIw. Там достаточно первые 12 страниц прочитать, особенно 10-ю.
В двух словах: использование дельта-функций — только метод (способ) представления сигнала, к которому может быть применён матаппарат классического анализа (литература [10] 1959 год). Там же и то, что вместо дельта-функции можно применять и просто sinc, но возни с интегралами будет больше.
Метод так прижился, что теперь без него дискретизацию и не мыслят вовсе. Но это всё же только метод, и не единственный.

Refridgerator
20.07.2019 19:07Но определения простого умножения, которое встречается у Вас в тексте («При дискретизации непрерывный сигнал умножается на гребёнку Дирака»), там нет. И не ищите. Эта операция не определена.
Если эта операция не определена, то как же Wolfram Alpha/Mathematica смогла выполнить над ней преобразование Фурье?
AAE
20.07.2019 19:10Всё правильно — преобразование Фурье от произведения, как скалярное произведение дельта-функции с чем-то, определено в обобщенном смысле. Тут нет противоречия со строгой математикой.

Refridgerator
20.07.2019 19:13«Гребёнка Дирака — это функция» (Ваши слова) — это совсем неправда.
Dirac comb also known as sampling function, constructed from Dirac delta functions
AAE
20.07.2019 19:19Дельта-функция Дирака не является функцией. Её значения в точках не определены. На википедию лучше не ссылаться. Я там для пробы писал всякую откровенную фигню — висело всё это месяцами, пока сам не исправил.

Refridgerator
20.07.2019 19:29На хабре тоже, бывает, фигню пишут. И что характерно — исправлению не подлежащую в принципе.

AAE
20.07.2019 19:44Про дельта-функцию Дирака и её значения в точках можно спросить любого математика — даже студент МехМата МГУ Вам повторит то, что я написал. Сам символ дельта-функции — ?(x) — только символ, обозначающий линейный непрерывный (уже не обязательно) функционал (Владимиров, «Обобщенные функции в математической физике»). То есть, вне интеграла не живет.

Refridgerator
20.07.2019 20:05Что значит «вне интеграла не живёт»? Если я её продифференцирую, она что, умрёт?

AAE
20.07.2019 20:27Продифференцировать её Вы можете только двумя способами (получите два совершенно разных результата) — в обобщенном смысле (опять интеграл, но зато математики примут), либо сконструировать дельта-образующую последовательность (предел которой Вы назовёте дельта-функцией), продифференцировать каждый член её, найти предел последовательности уже производных (опять же, если он есть) и назвать этот предел производной Вами определённой дельта-функции (математики Вас за этот финт высекут, но физики так делают без всякого сумления). Второй вариант не является математически строгим, но работает. И в нематематической литературе встречается довольно часто. В теории сигналов используется только он.

AAE
20.07.2019 10:33Немного добавлю, для нашего примера (f1=1 кГц, f2=3 кГц) величины f2-f1 и (f1+f2)/2 равны. Так, по-моему, будет понятней.

ViacheslavMezentsev
19.07.2019 06:31Может быть интересным разложение в ряд Фурье при помощи метода БПФ. В качестве домашнего задания можно вывести соответствие между спектральными компонентами и коэффициентами ряда.


Oscillator
19.07.2019 08:36+1Раз сюда зайдут люди, интересующиеся ЦОС, то не могу не оставить здесь рекомендацию книги (да простит меня автор), которая на мой взгляд наиболее проста в понимании и чтении именно новичками, при этом не теряя в полноте изложения: Стивен Смит: Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников
Цена правда как у Айчифера почти, но она стоит своих денег абсолютно.

Hedgehogues
19.07.2019 11:11Начал смотреть ваши ноутбуки. Да, все, замечательно, много примеров, с графтками, с примерами кода, по-феншую.
Но… Честно… Расстроен. Вы не приводите решение не одной задачи. Как мне, человеку, который с дпф занимался примерно нисколько, начать все это добро юзать? Вот, например, есть задача про эпилептиков. Нужно дать предикт заблаговременно: будет припадок или нет. Как это добро мне поможет решить ее? Для меня оказывается куда проще нагенерить фичей и пихнуть это в бустинг, чем городить огород из преобразований, хаотично из применяя

dsmv2014
19.07.2019 12:48Надо изучать матчасть. Ваша задача из совершенно другой области и конечно её надо решать по другому.

ViacheslavMezentsev
20.07.2019 06:19Дополнительные материалы для начинающих.
Курс видеоуроков на youtube: Основы ЦОС в Matlab (2018).
Можно скачать целиком (update.lst для возможной докачки):
youtube-dl.exe --download-archive update.lst --ignore-errors -f best -o "%%(title)s.%%(ext)s" https://www.youtube.com/playlist?list=PLmu_y3-DV2_kpP8oX_Uug0IbgH2T4hRPL

Sanja_K
22.07.2019 10:50Огромное спасибо за то, что Вы делаете такие статьи и вкладываете в это свой труд!


Refridgerator
Поглядел ваш курс и он мне показался слишком, слишком поверхностным. Помимо этого, он так же страдает теми же недостатками, что и прочие курсы того же типа — вводятся понятия и функции без объяснения, откуда они взялись, зачем и почему (та же функция Хевисайда).
Ну вот например.
Вы рисуете прямоугольную функцию, я рядом его спектр — но уже в абсолютном значении, причём в линейном масштабе. Ну а как новичок должен догадаться, что там изображена «выпрямленная» функция sinc? Как он должен догадаться, что и наоборот, спектр от sinc — прямоугольный?
Или вы рассматриваете оконные функции. Ну а как из них выбирать подходящую? А где описания отличий — например, что окно Нуттала гладкое (с нулевой первой производной) на краях? А где окно Дольфа-Чебышева, которая позволяет явно задавать величину боковых лепестков непосредственно в децибелах?
А почему ресемленг вы сводите исключительно к CIC, в то время как CIC — это лишь один из вариантов реализации, причём не идеальной?
capitanov Автор
В процессе подготовки этого материала у меня постоянно возникало желание выкинуть из курса лишнего, дабы не получилось много теории в ущерб практическим примерам. Плюс, какие-то слишком очевидные (для меня) вещи я мог удалить за ненужностью. С другой стороны — я не позиционирую курс как подробное издание или полноценную законченную книгу (на этот счёт есть библия в виде книги Айфичера).
Ресемлинг планировался в нескольких частях. Дабы не раздувать тетрадку примерами, я решил обойтись CIC в первой части. Фильтры Фарроу обязательно добавлю. С остальными замечаниями согласен и по возможности доработаю эти моменты.
Спасибо за фидбек!
mphys
А можно сделать два издания, стартовое и подробное?
:)
chnav
Не люблю читать с экрана )) Спасибо.
capitanov Автор
К сожалению, я не смог нагуглить первое издание вообще, поэтому не могу сравнить их, но если вы говорите, что разница только в интерактивной поддержке, то по критерию цены выбор за первым изданием. Примеры MATLAB всегда можно будет скачать и посмотреть в электронной версии второго издания.
Кстати, свою книгу я покупал ~10 лет назад за 600 рублей и это было второе издание. Можете скинуть ссылку в ЛС на первое издание для сравнения?
chnav
Про первое издание я прочитал в предисловии ко второму, там сказано про MatLab.
Спасибо за вашу работу.
imwode
Я бы больше сказал — теорему Котельникова надо по словам разбирать, предварительно разжевав, что такое спектр. Я слушал этот курс в универе, и сейчас со стыдом понял, что я теорему Котельникова не понимаю, и статья не помогла разобраться.
capitanov Автор
Рекомендую к прочтению адаптированную статью, УФН от 2006 года "О пропускной способности эфира и проволоки в электросвязи", в которой содержатся все семь теорем Котельникова. Это адаптированный вариант оригинальных трудов Котельникова. Добавил её в репозиторий.